Data Pruning of Tomographic Data for the Calibration of Strain Localization Models
Abstract
:1. Introduction
2. Notations
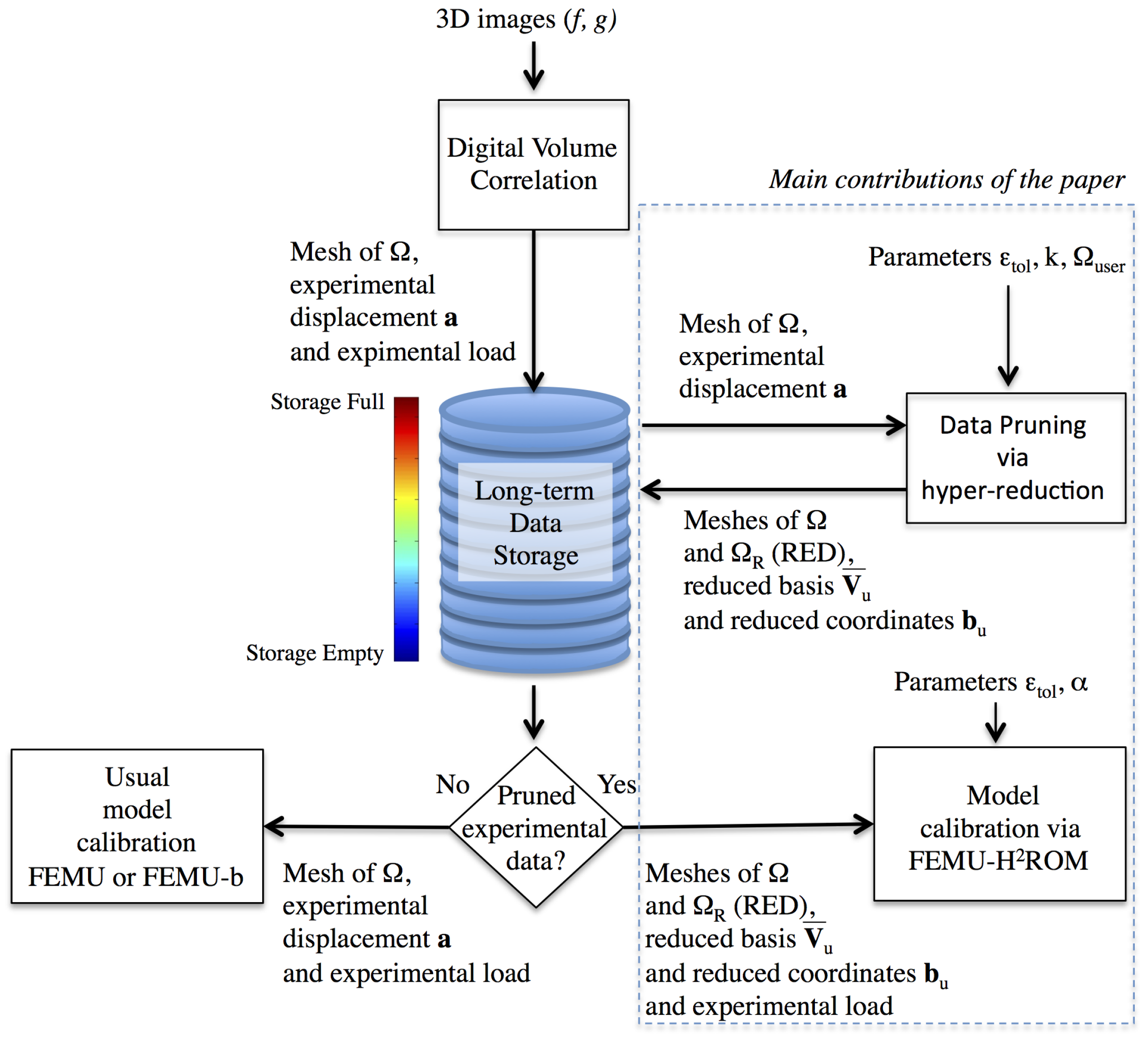
3. Data Pruning by Following an Hyper-Reduction Scheme
3.1. Digital Volume Correlation
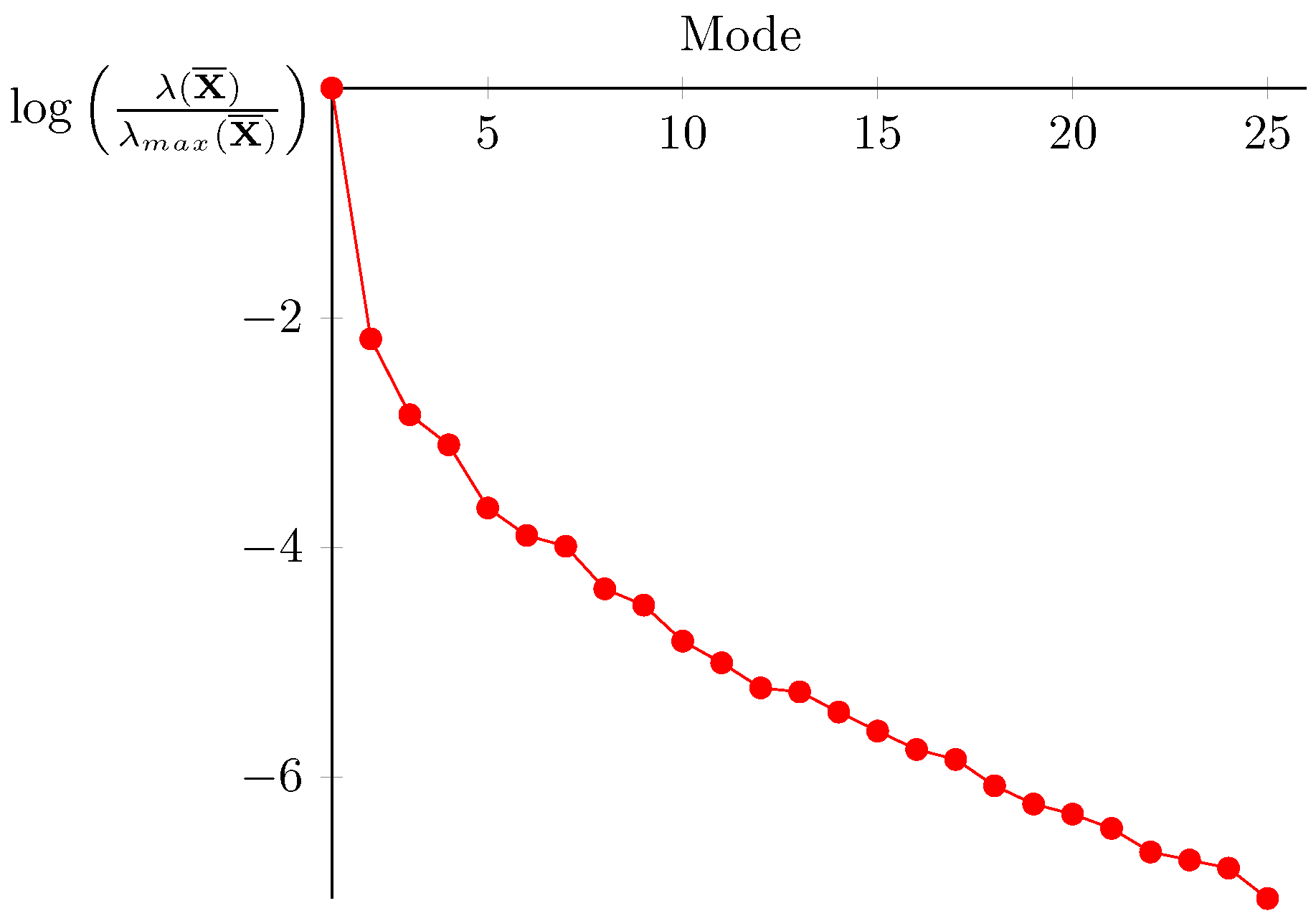
3.2. Dimensionality Reduction
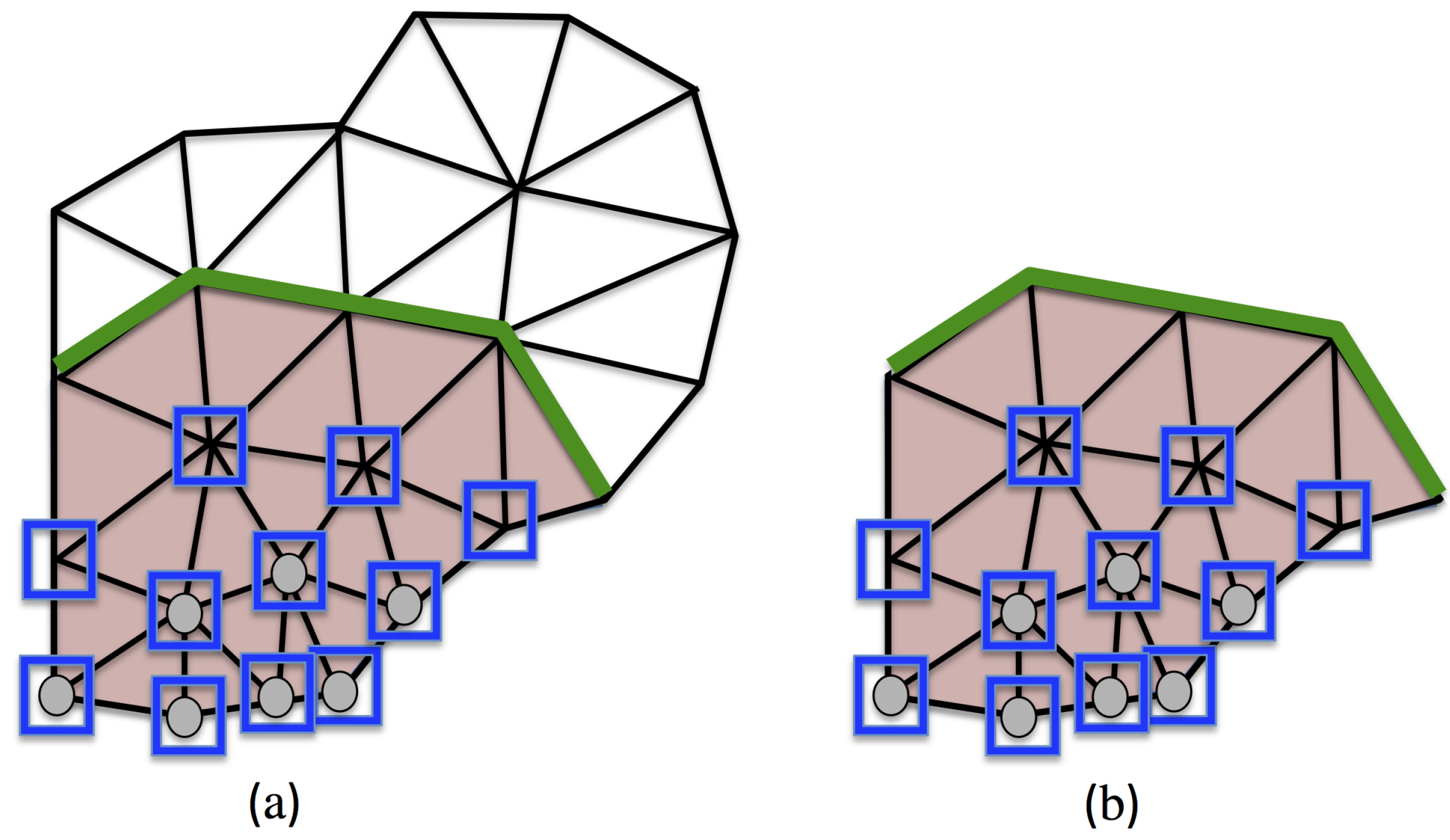
3.3. Reduced Experimental Domain
| Algorithm 1:k-SWIM Selection of Variables with EmpIrical Modes |
 |
3.4. Experimental Data Restricted to the RED
- The pruned reduced basis , and the consecutive reduced coordinates .
- The full mesh of and the mesh of ( and ).
- The load history applied to the specimen on the subdomain .
- Usual metadata related to the experiment (temperature, material parameters, etc.).
3.5. Reduced Mechanical Equations Set Up on the Reduced Experimental Domain
4. Illustrating Example: Polyurethane Bonded Sand Studied with X-ray CT
4.1. Material and Test Description
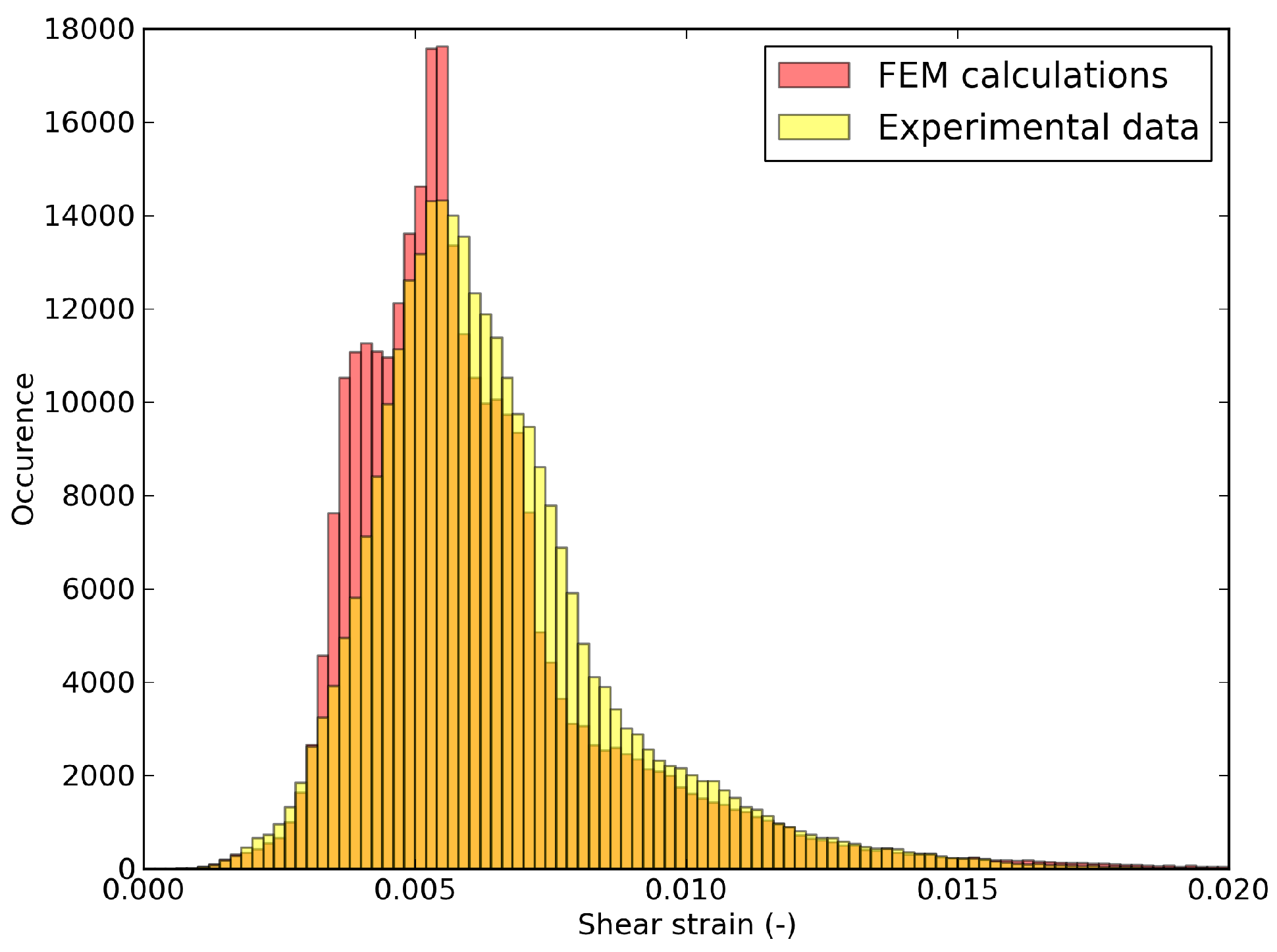
4.2. DVC and Error Estimation
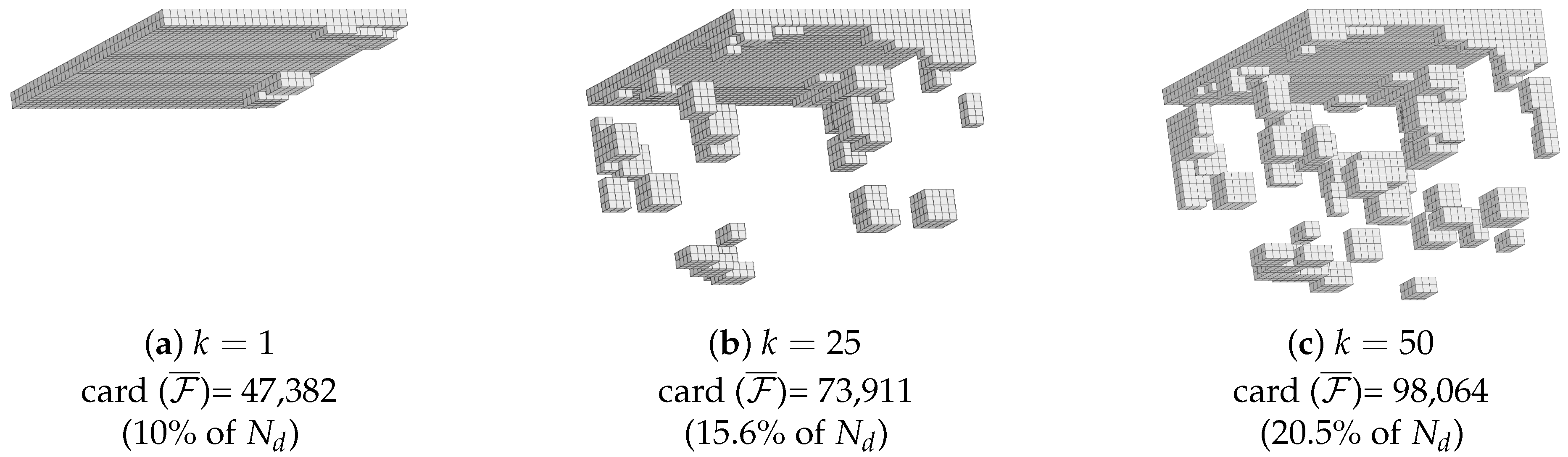
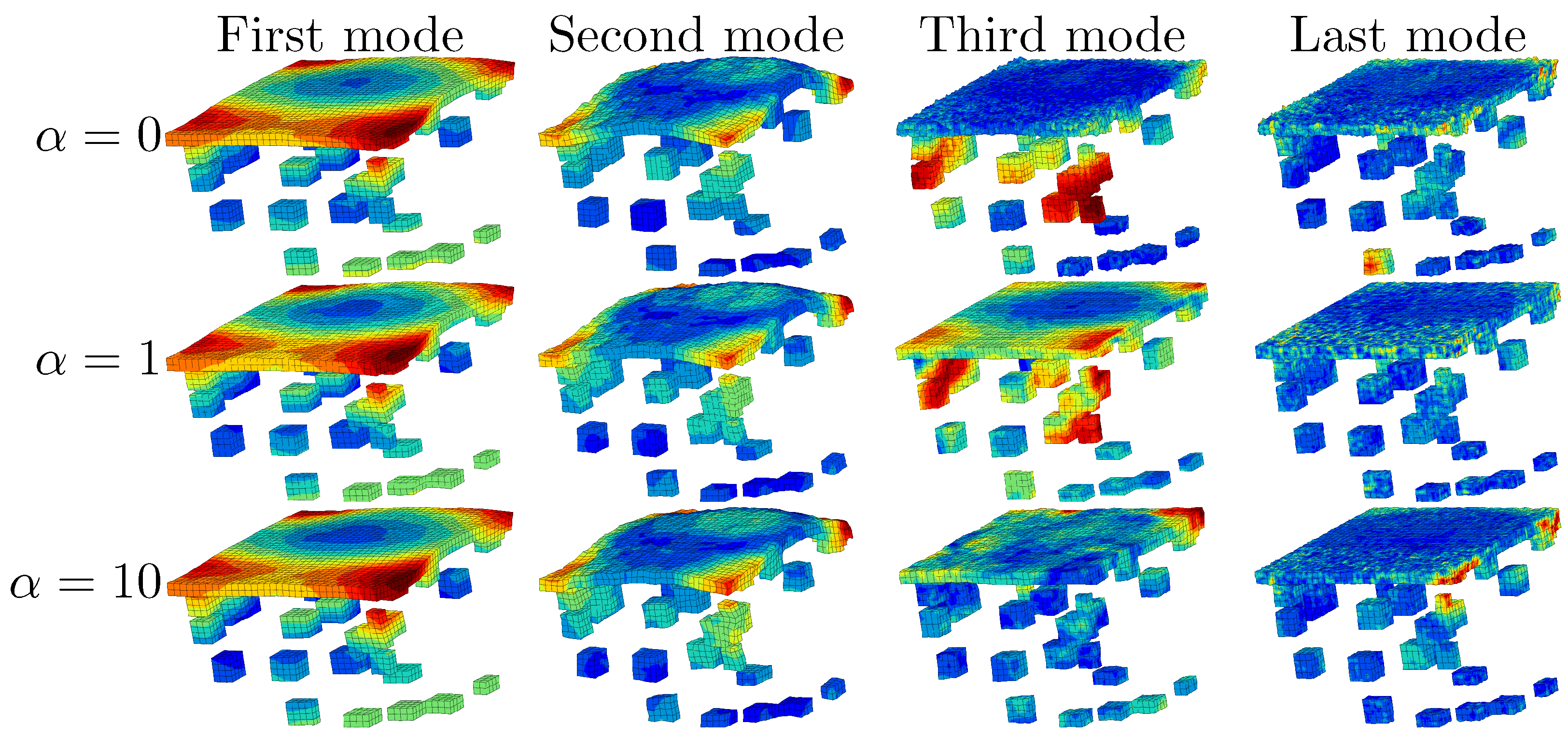
4.3. Building the Reduced Experimental Basis
4.4. RED after DVC on the Specimen
5. Assessing the Relevance of the Pruned Data via Finite Element Model Updating-HROM
5.1. Constitutive Model MC-CASM
5.1.1. Presentation
- Addition of a damage law whose equation is phenomenological (based on cycled compressive tests).
- The hardening law of the bonding parameter b is different: A first hardening precedes the softening. It is supposed here that the polyurethane resin goes through a first hardening before breaking.
5.1.2. Yield Function and Plastic Flow
5.1.3. Hardening and Damage Laws
5.2. Calibration Protocol by Using the Hybrid Hyper-Reduction Method
- One initial calculation where , which gives ;
- m parameters sensibility calculations where , which give for
5.3. Discussion on Dirichlet Boundary Conditions
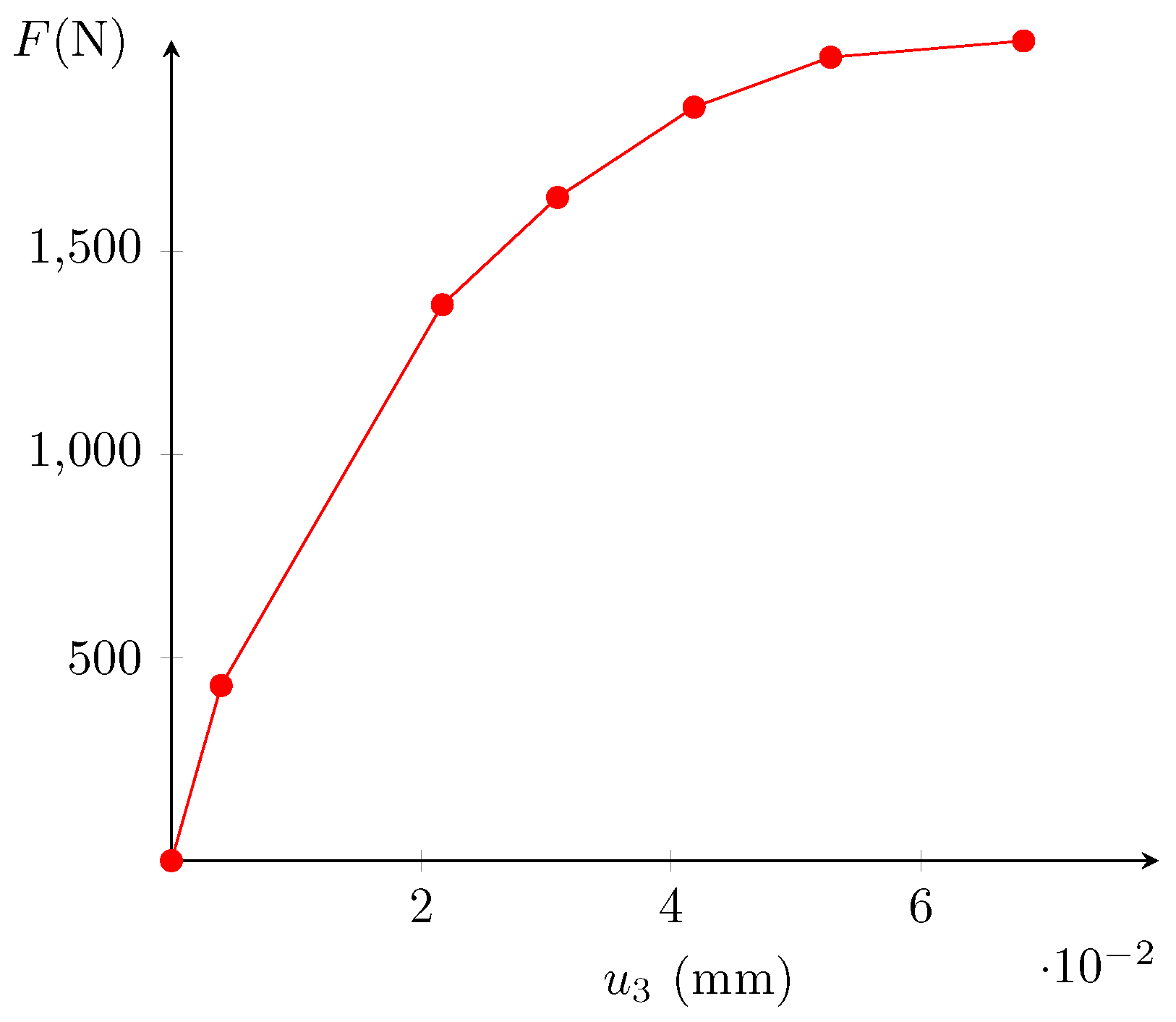
5.4. Parameters Updating
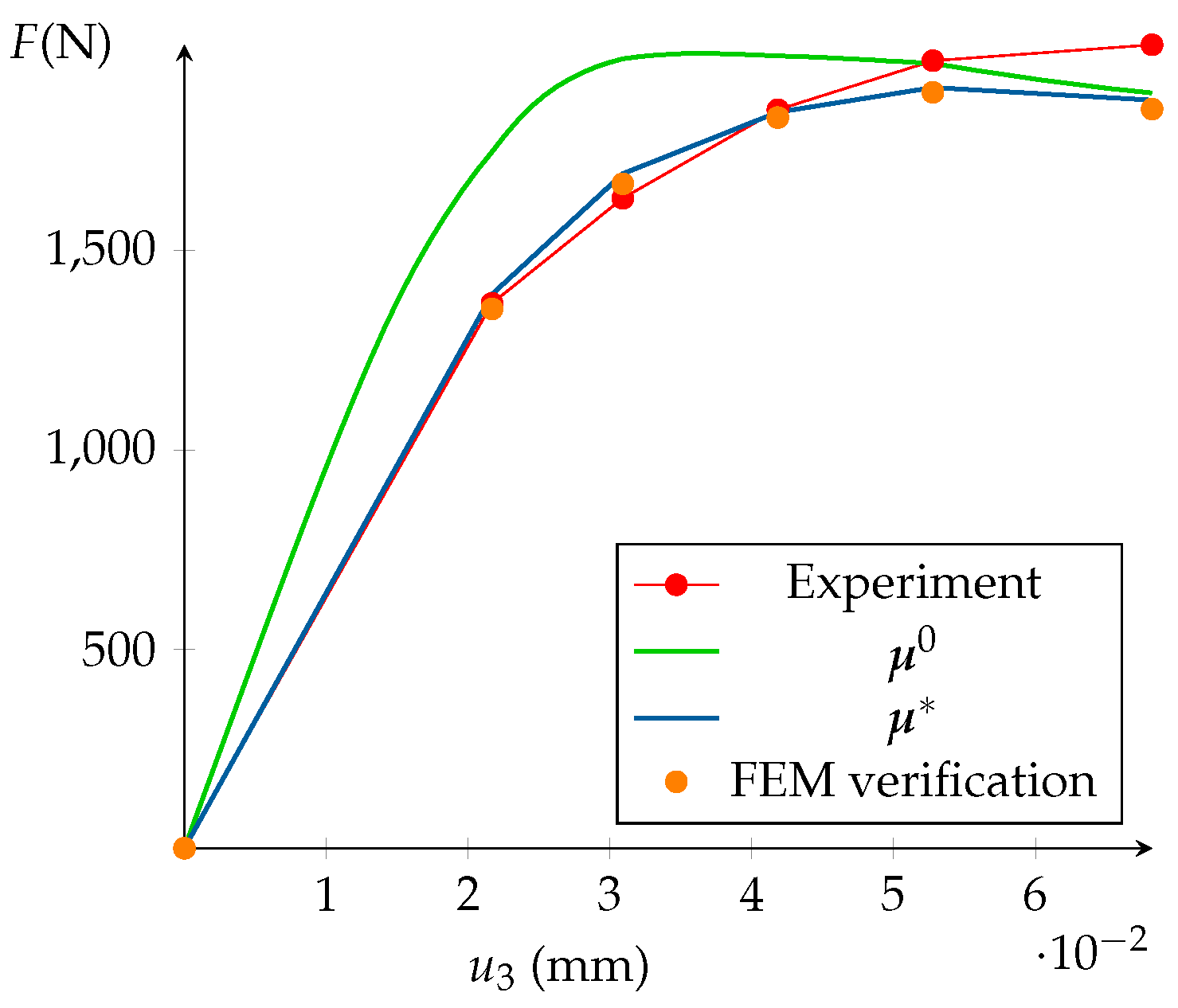
5.5. Model Calibration and FEM Validation
- Perform again the whole parameters sensibility study with .
- Concatenate the previously determined matrix from Equation (42) with and perform a new truncated SVD to determine ultimately an enriched reduced basis . No new FEM calculations are needed.
6. Discussion
6.1. Limitations of the Pruning Procedure
6.2. About the Reconstruction of Data outside the RED
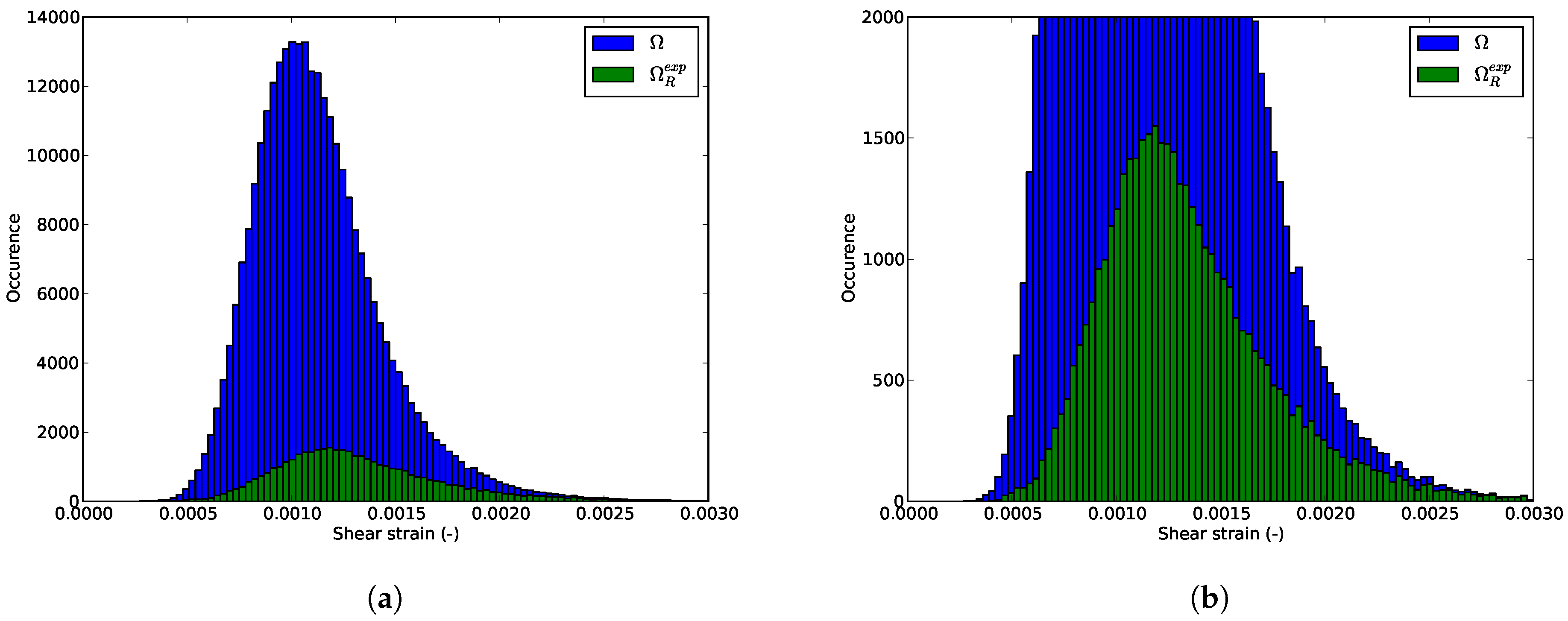
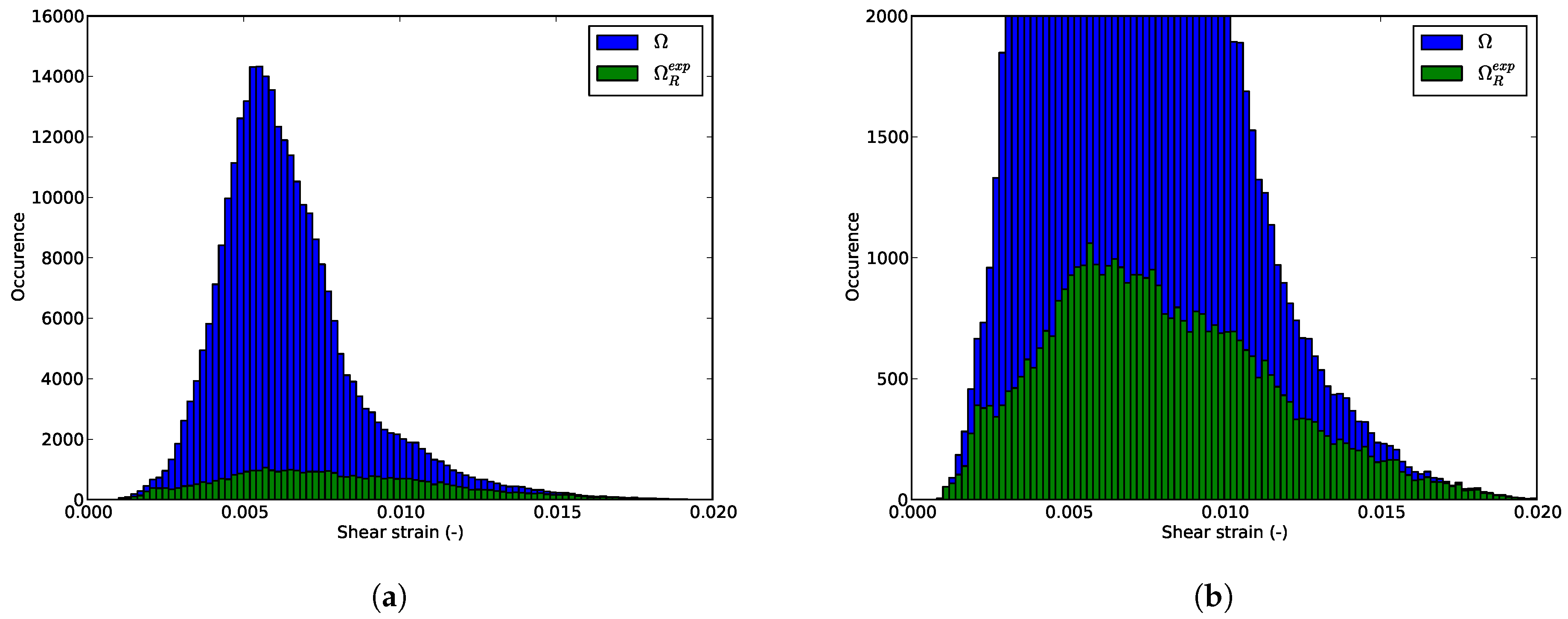
6.3. Shear Strain Distributions in the RED
7. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Chu, T.; Ranson, W.; Sutton, M.; Peters, W. Application of digital-image-dorrelation techniques to experimental mechanics. Exp. Mech. 1985, 25, 232–244. [Google Scholar] [CrossRef]
- Bay, B.; Smith, T.; Fyhrie, D.; Saad, M. Digital volume correlation: Three-dimensional strain mapping using X-ray tomography. Exp. Mech. 1999, 39, 217–226. [Google Scholar] [CrossRef]
- Van Ooijen, P.M.A.; Broekema, A.; Oudkerk, M. Use of a Thin-Section Archive and Enterprise 3-Dimensional Software for Long-Term Storage of Thin-Slice CT Datasets—A Reviewers’ Response. J. Digit. Imag. 2008, 21, 188–192. [Google Scholar] [CrossRef] [PubMed]
- Pan, D. A tutorial on MPEG/audio compression. IEEE MultiMed. 1995, 2, 60–74. [Google Scholar] [CrossRef]
- Cioaca, A.; Sandu, A. Low-rank approximations for computing observation impact in 4D-Var data assimilation. Comput. Math. Appl. 2014, 67, 2112–2126. [Google Scholar] [CrossRef]
- Réthoré, J.; Roux, S.; Hild, F. From pictures to extended finite elements: Extended digital image correlation (X-DIC). C. R. Méc. 2007, 335, 131–137. [Google Scholar] [CrossRef]
- Rojanaarpa, T.; Kataeva, I. Density-Based Data Pruning Method for Deep Reinforcement Learning. In Proceedings of the 2016 15th IEEE International Conference on Machine Learning and Applications (ICMLA), Anaheim, CA, USA, 18–20 December 2016; pp. 266–271. [Google Scholar]
- Hu, Y.; Chen, H.; Li, G.; Li, H.; Xu, R.; Li, J. A statistical training data cleaning strategy for the PCA-based chiller sensor fault detection, diagnosis and data reconstruction method. Energy Build. 2016, 112, 270–278. [Google Scholar] [CrossRef]
- Hong, Y.; Kwong, S.; Chang, Y.; Ren, Q. Unsupervised data pruning for clustering of noisy data. Knowl. Based Syst. 2008, 21, 612–616. [Google Scholar] [CrossRef]
- Kavanagh, K.T.; Clough, R.W. Finite element applications in the characterization of elastic solids. Int. J. Solids Struct. 1971, 7, 11–23. [Google Scholar] [CrossRef]
- Kavanagh, K.T. Extension of classical experimental techniques for characterizing composite-material behavior. Exp. Mech. 1972, 12, 50–56. [Google Scholar] [CrossRef]
- Ienny, P.; Caro-Bretelle, A.S.; Pagnacco, E. Identification from measurements of mechanical fields by finite element model updating strategies. Eur. J. Comput. Mech. 2009, 18, 353–376. [Google Scholar] [CrossRef]
- Lecompte, D.; Smits, A.; Sol, H.; Vantomme, J.; Hemelrijck, D.V. Mixed numerical–experimental technique for orthotropic parameter identification using biaxial tensile tests on cruciform specimens. Int. J. Solids Struct. 2007, 44, 1643–1656. [Google Scholar] [CrossRef]
- Molimard, J.; Le Riche, R.; Vautrin, A.; Lee, J.R. Identification of the four orthotropic plate stiffnesses using a single open-hole tensile test. Exp. Mech. 2005, 45, 404–411. [Google Scholar] [CrossRef]
- Meijer, R.; Douven, L.F.A.; Oomens, C.W.J. Characterisation of Anisotropic and Non-linear Behaviour of Human Skin In Vivo. Comput. Methods Biomech. Biomed. Eng. 1999, 2, 13–27. [Google Scholar] [CrossRef] [PubMed]
- Bruno, L. Mechanical characterization of composite materials by optical techniques: A review. Opt. Lasers Eng. 2018, 104, 192–203. [Google Scholar] [CrossRef]
- Mahnken, R.; Stein, E. A unified approach for parameter identification of inelastic material models in the frame of the finite element method. Comput. Methods Appl. Mech. Eng. 1996, 136, 225–258. [Google Scholar] [CrossRef]
- Forestier, R.; Massoni, E.; Chastel, Y. Estimation of constitutive parameters using an inverse method coupled to a 3D finite element software. J. Mater. Process. Technol. 2002, 125–126, 594–601. [Google Scholar] [CrossRef]
- Giton, M.; Caro-Bretelle, A.S.; Ienny, P. Hyperelastic Behaviour Identification by a Forward Problem Resolution: Application to a Tear Test of a Silicone-Rubber. Strain 2006, 42, 291–297. [Google Scholar] [CrossRef]
- Cugnoni, J.; Botsis, J.; Janczak-Rusch, J. Size and Constraining Effects in Lead-Free Solder Joints. Adv. Eng. Mater. 2006, 8, 184–191. [Google Scholar] [CrossRef]
- Latourte, F.; Chrysochoos, A.; Pagano, S.; Wattrisse, B. Elastoplastic behavior identification for heterogeneous loadings and materials. Exp. Mech. 2008, 48, 435–449. [Google Scholar] [CrossRef]
- Padmanabhan, S.; Hubner, J.P.; Kumar, A.V.; Ifju, P.G. Load and Boundary Condition Calibration Using Full-field Strain Measurement. Exp. Mech. 2006, 46, 569–578. [Google Scholar] [CrossRef]
- Neggers, J.; Allix, O.; Hild, F.; Roux, S. Big Data in Experimental Mechanics and Model Order Reduction: Today’s Challenges and Tomorrow’s Opportunities. Arch. Comput. Methods Eng. 2017. [Google Scholar] [CrossRef]
- Cugnoni, J.; Gmür, T.; Schorderet, A. Inverse method based on modal analysis for characterizing the constitutive properties of thick composite plates. Comput. Struct. 2007, 85, 1310–1320. [Google Scholar] [CrossRef]
- Aubry, N.; Holmes, P.; Lumley, J.L.; Stone, E. The dynamics of coherent structures in the wall region of a turbulent boundary layer. J. Fluid Mech. 1988, 192, 115–173. [Google Scholar] [CrossRef]
- Passieux, J.C.; Perie, J.N. High resolution digital image correlation using proper generalized decomposition: PGD-DIC. Int. J. Numer. Methods Eng. 2012, 92, 531–550. [Google Scholar] [CrossRef]
- Ryckelynck, D. A priori hyperreduction method: An adaptive approach. J. Comput. Phys. 2005, 202, 346–366. [Google Scholar] [CrossRef]
- Hernandez, J.A.; Caicedo, M.A.; Ferrer, A. Dimensional hyper-reduction of nonlinear finite element models via empirical cubature. Comput. Methods Appl. Mech. Eng. 2017, 313, 687–722. [Google Scholar] [CrossRef]
- Baiges, J.; Codina, R.; Idelson, S. A domain decomposition strategy for reduced order models. Application to the incompressible Navier-Stokes equations. Comput. Methods Appl. Mech. Eng. 2013, 267, 23–42. [Google Scholar] [CrossRef]
- Ryckelynck, D.; Lampoh, K.; Quilici, S. Hyper-reduced predictions for lifetime assessment of elasto-plastic structures. Meccanica 2015. [Google Scholar] [CrossRef]
- Liu, J.; Musialski, P.; Wonka, P.; Ye, J. Tensor Completion for Estimating Missing Values in Visual Data. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 208–220. [Google Scholar] [CrossRef] [PubMed]
- Shang, Q.; Yang, Z.; Gao, S.; Tan, D. An Imputation Method for Missing Traffic Data Based on FCM Optimized by PSO-SVR. J. Adv. Transp. 2018. [Google Scholar] [CrossRef]
- Chaturantabut, S.; Sorensen, D.C. Nonlinear Model Reduction via Discrete Empirical Interpolation. J. Sci. Comput. 2010, 32, 2737–2764. [Google Scholar] [CrossRef]
- Chaturantabut, S.; Sorensen, D.C. A state space error estimate for POD-DEIM nonlinear model reduction. J. Numer. Anal. 2012, 50, 46–63. [Google Scholar] [CrossRef]
- Fauque, J.; Ramière, I.; Ryckelynck, D. Hybrid hyper-reduced modeling for contact mechanics problems. Int. J. Numer. Methods Eng. 2018, 115, 117–139. [Google Scholar] [CrossRef]
- Schmidt, A.; Potschka, A.; Koerkel, S.; Bock, H.G. Derivative-Extended POD Reduced-Order Modeling for Parameter Estimation. J. Sci. Comput. 2013, 35, A2696–A2717. [Google Scholar] [CrossRef]
- Jomaa, G.; Goblet, P.; Coquelet, C.; Morlot, V. Kinetic modeling of polyurethane pyrolysis using non-isothermal thermogravimetric analysis. Thermochim. Acta 2015, 612, 10–18. [Google Scholar] [CrossRef]
- Bargaoui, H.; Azzouz, F.; Thibault, D.; Cailletaud, G. Thermomechanical behavior of resin bonded foundry sand cores during casting. J. Mater. Process. Technol. 2017, 246, 30–41. [Google Scholar] [CrossRef]
- Yu, H.S. CASM: A unified state parameter model for clay and sand. Int. J. Numer. Anal. Methods Geomechan. 1998, 22, 621–653. [Google Scholar] [CrossRef]
- Gens, A.; Nova, R. Conceptual bases for a constitutive model for bonded soils and weak rocks. Geotech. Eng. Hard Soils Soft Rocks 1993, 1, 485–494. [Google Scholar]
- Rios, S.; Ciantia, M.; Gonzalez, N.; Arroyo, M.; Viana da Fonseca, A. Simplifying calibration of bonded elasto-plastic models. Comput. Geotech. 2016, 73, 100–108. [Google Scholar] [CrossRef]
- Roscoe, K.; Schofield, A.; Wroth, C. On the yielding of soils. Geotechnique 1958, 8, 22–52. [Google Scholar] [CrossRef]
- Ryckelynck, D.; Missoum Benziane, D. Hyper-reduction framework for model calibration in plasticity-induced fatigue. Adv. Model. Simul. Eng. Sci. 2016, 3, 15. [Google Scholar] [CrossRef]
- Ghavamian, F.; Tiso, P.; Simone, A. POD-DEIM model order reduction for strain-softening viscoplasticity. Comput. Methods Appl. Mech. Eng. 2017, 317, 458–479. [Google Scholar] [CrossRef]
- Peherstorfer, B.; Butnaru, D.; Willcox, K.; Bungartz, H.J. Localized Discrete Empirical Interpolation Method. J. Sci. Comput. 2014, 36, 168–192. [Google Scholar] [CrossRef]
- Haasdonk, B.; Dihlmann, M.; Ohlberger, M. A training set and multiple bases generation approach for parameterized model reduction based on adaptive grids in parameter space. Math. Comput. Model. Dyn. Syst. 2011, 17, 423–442. [Google Scholar] [CrossRef]
- Tarantola, A. Inverse Problem Theory: Methods For Data Fitting and Model Parameter Estimation; Elsevier: Amsterdam, The Netherlands, 1987. [Google Scholar]
- Kaipio, J.; Somersalo, E. Statistical Inverse Problems: Discretization, Model Reduction and Inverse Crimes. J. Comput. Appl. Math. 2007, 198, 493–504. [Google Scholar] [CrossRef]


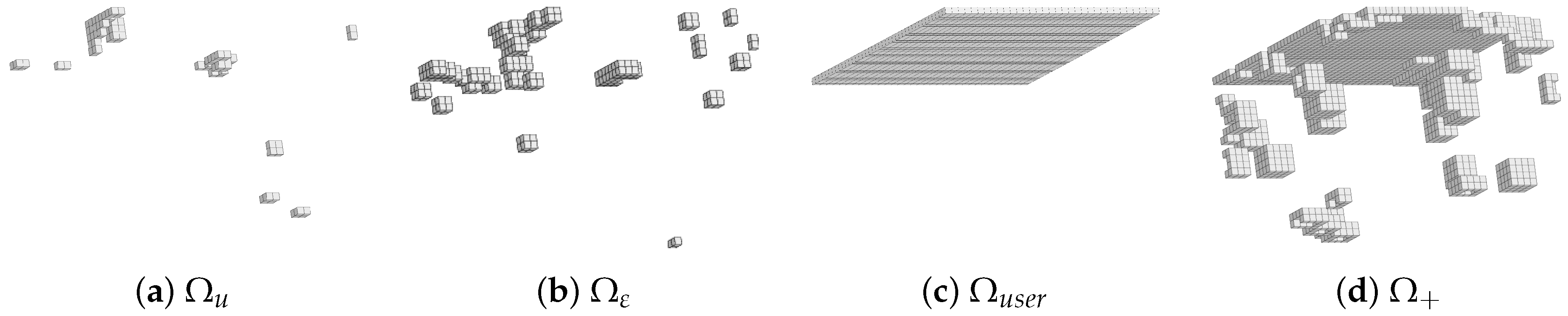

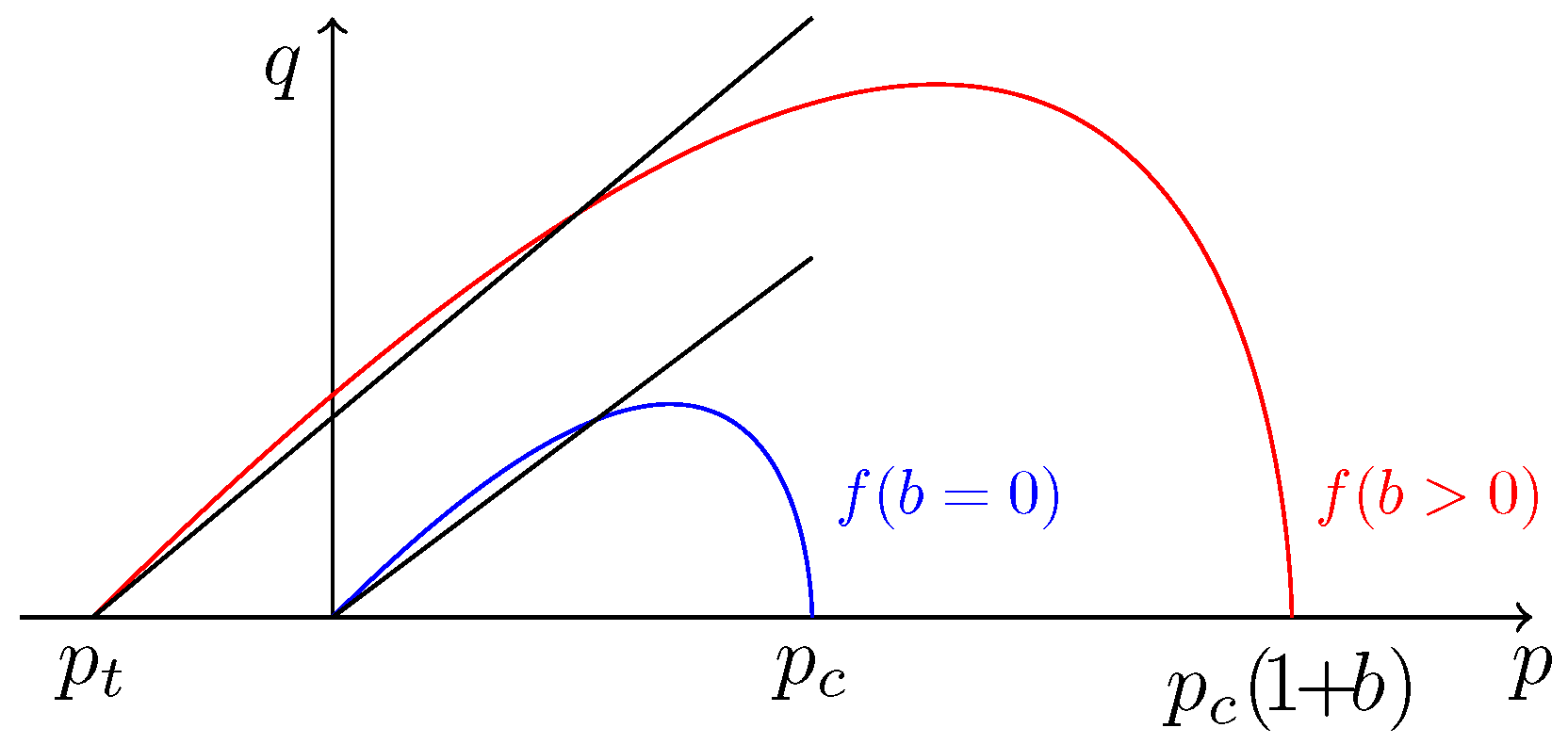
| Experimental Data | Empirical Modes | Pruned Data | |||
|---|---|---|---|---|---|
| 474,405 × 7 | 474,405 × 6 | 73,911 × 6 | |||
| 6 × 7 | 6 × 7 | ||||
| Memory Saved | 15% | 85% | |||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hilth, W.; Ryckelynck, D.; Menet, C. Data Pruning of Tomographic Data for the Calibration of Strain Localization Models. Math. Comput. Appl. 2019, 24, 18. https://doi.org/10.3390/mca24010018
Hilth W, Ryckelynck D, Menet C. Data Pruning of Tomographic Data for the Calibration of Strain Localization Models. Mathematical and Computational Applications. 2019; 24(1):18. https://doi.org/10.3390/mca24010018
Chicago/Turabian StyleHilth, William, David Ryckelynck, and Claire Menet. 2019. "Data Pruning of Tomographic Data for the Calibration of Strain Localization Models" Mathematical and Computational Applications 24, no. 1: 18. https://doi.org/10.3390/mca24010018
APA StyleHilth, W., Ryckelynck, D., & Menet, C. (2019). Data Pruning of Tomographic Data for the Calibration of Strain Localization Models. Mathematical and Computational Applications, 24(1), 18. https://doi.org/10.3390/mca24010018






