A (p,q)-Averaged Hausdorff Distance for Arbitrary Measurable Sets
Abstract
1. Introduction
2. Preliminaries
2.1. Integral Power Means
2.2. Multi-objective Optimization
- (i)
- Let and . Then the vector v is less than w (denoted ), if for all . The relation is defined analogously.
- (ii)
- A vector is dominated by a vector (in short: ) with respect to (2) if and , i.e., there exists a such that .
- (iii)
- A point is called Pareto optimal or a Pareto point if there is no which dominates x.
- (iv)
- The set of all Pareto optimal solutions is called the Pareto set, denoted by .
- (v)
- The image of the Pareto set, , is called the Pareto front.
- (i)
- ,
- (ii)
- ,
- (iii)
- .
3. The -Averaged Hausdorff Distance for Measurable Sets
3.1. Properties of Integral Power Means
- (i)
- If and , then and .
- (ii)
- For any , we have .
- (iii)
- If , then .
- (iv)
- If and for all , then .
- (v)
- For with , we have that .
3.2. Definition of for Measurable Sets
3.3. Metric Properties
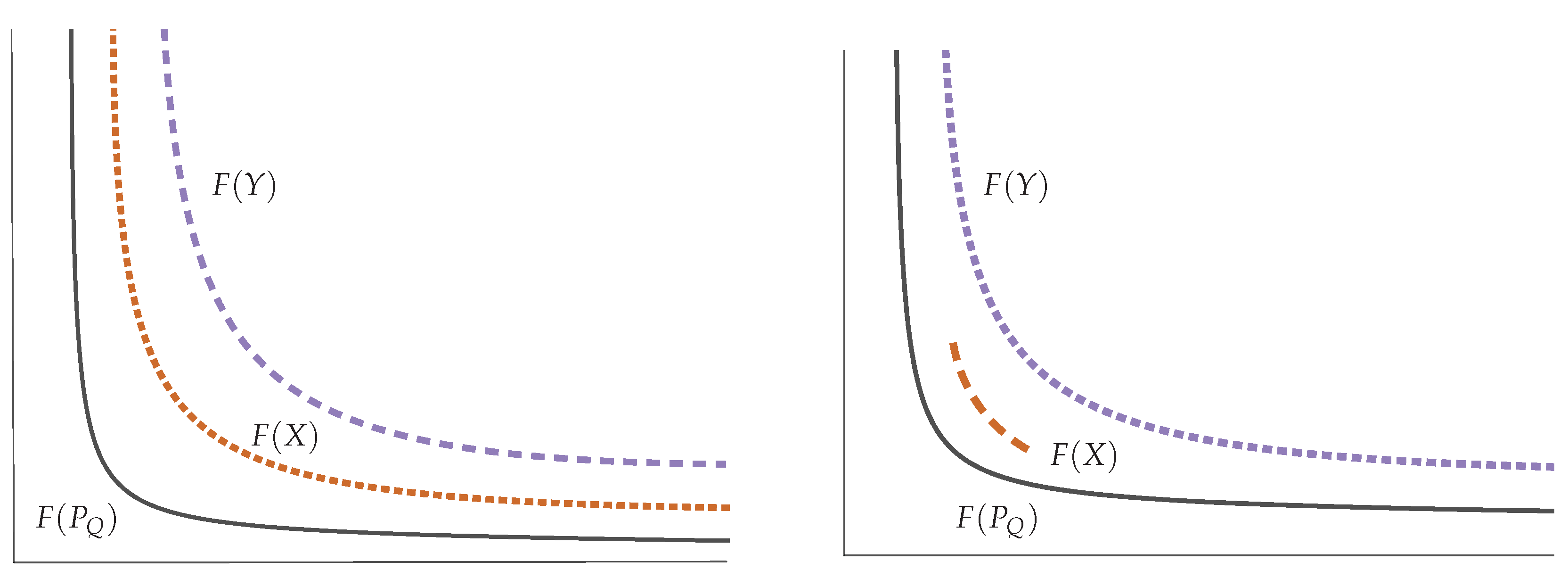
3.4. Pareto-Compliance
- (i)
- X and Y admit finite partitions and such that for each :
- (a)
- and are subsets of non-null finite measure.
- (b)
- , : ,
- (ii)
- , : if .
- (a’)
- (i.e., , such that ), and
- (b’)
- , such that .
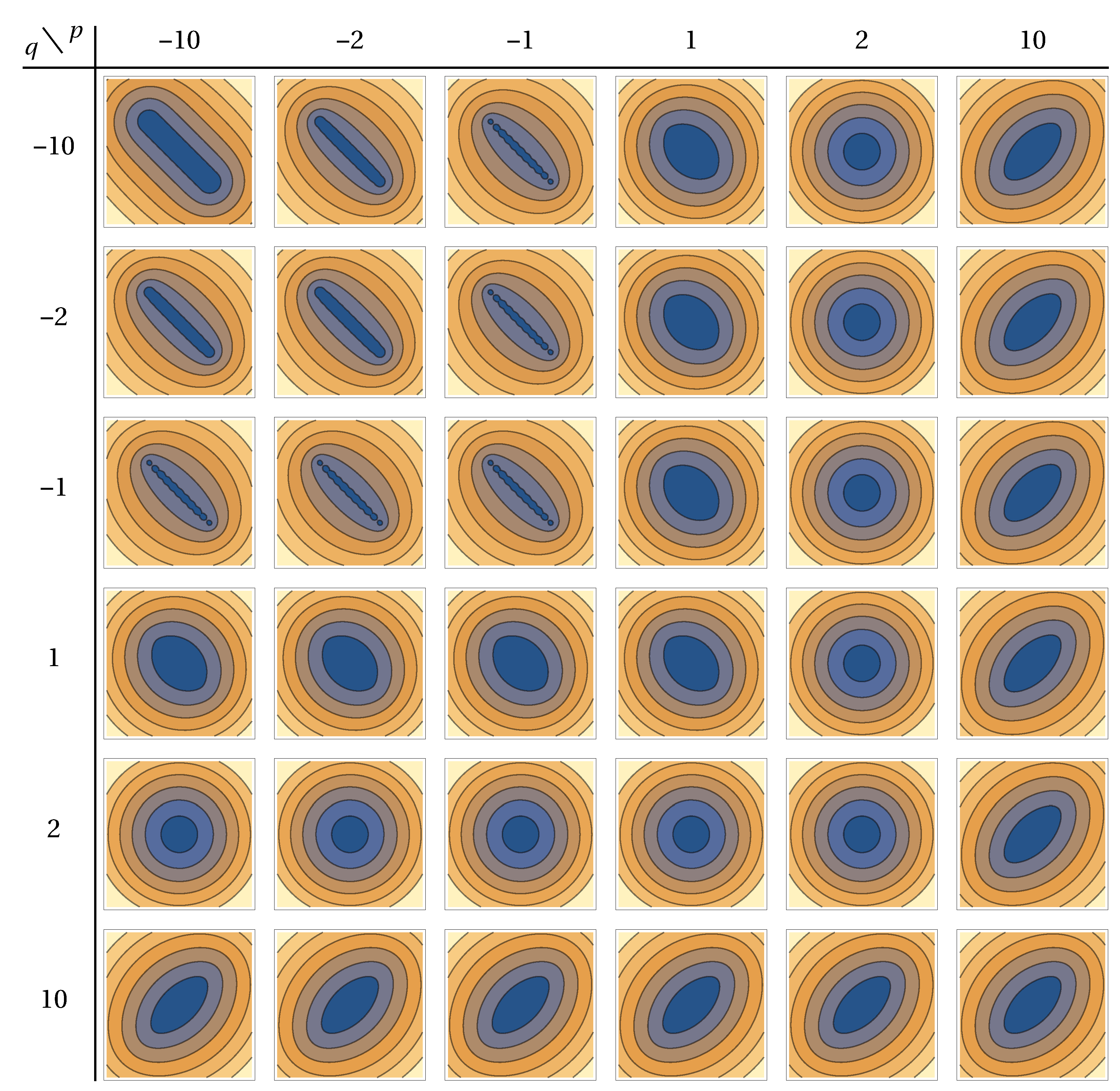
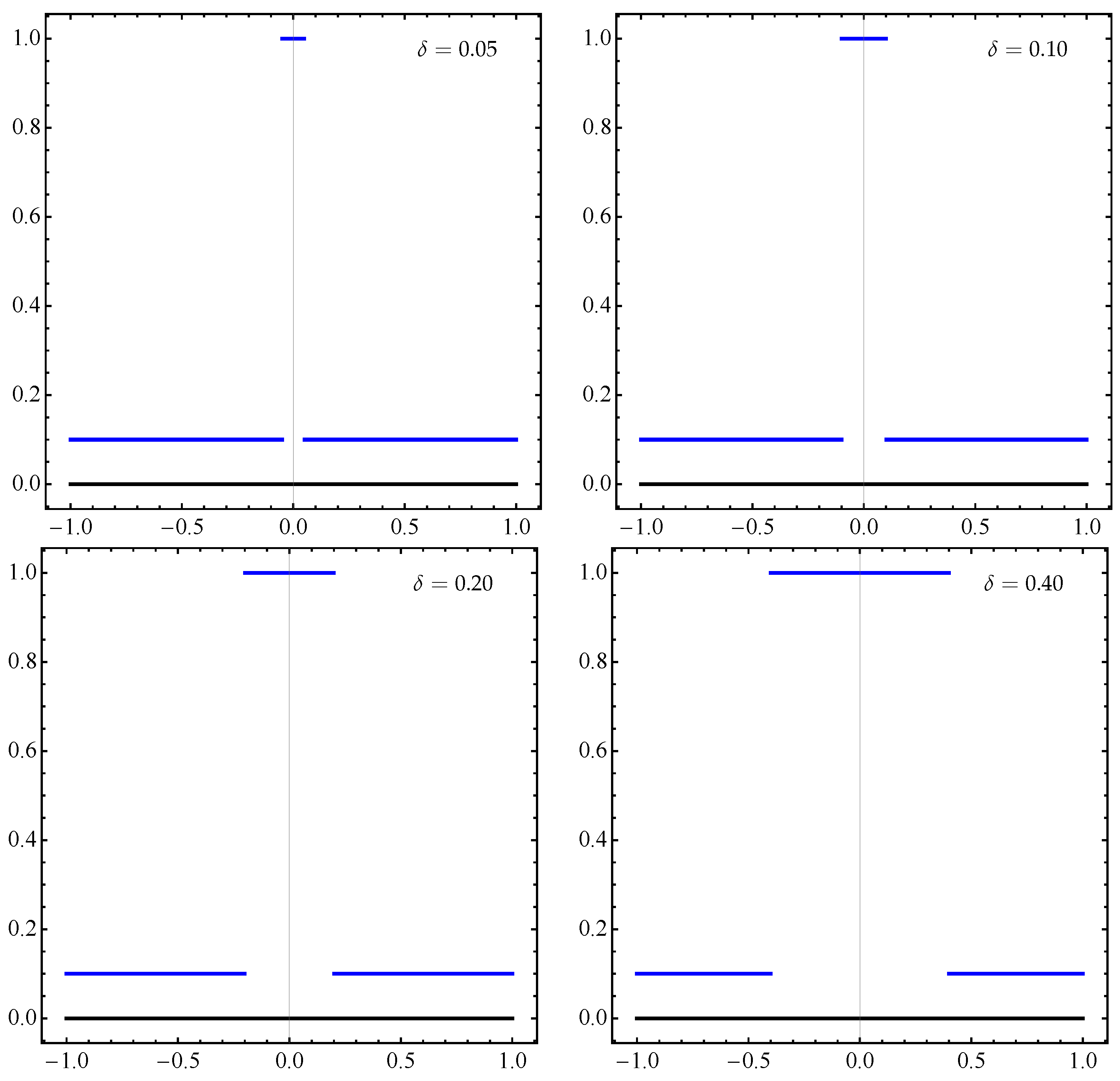
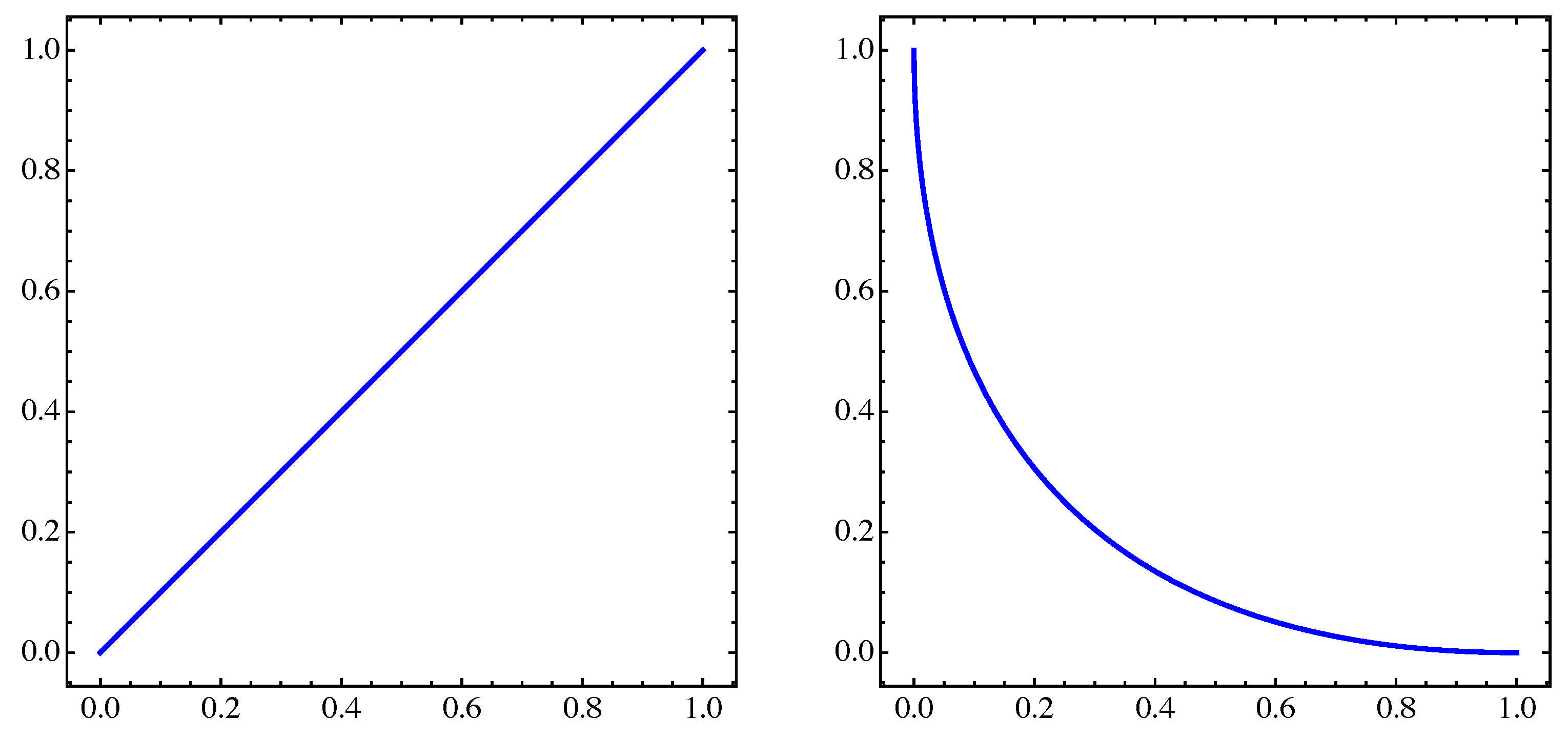
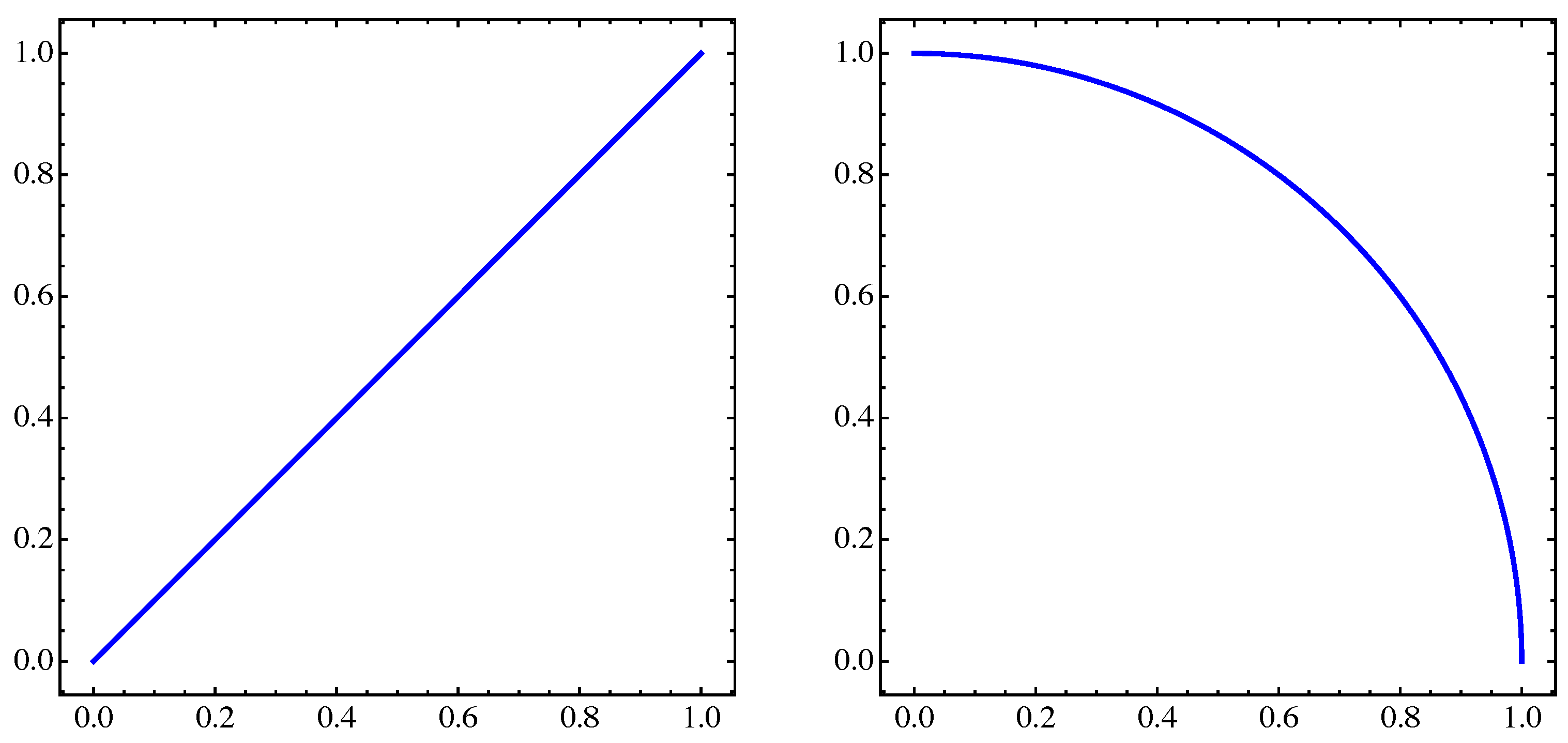
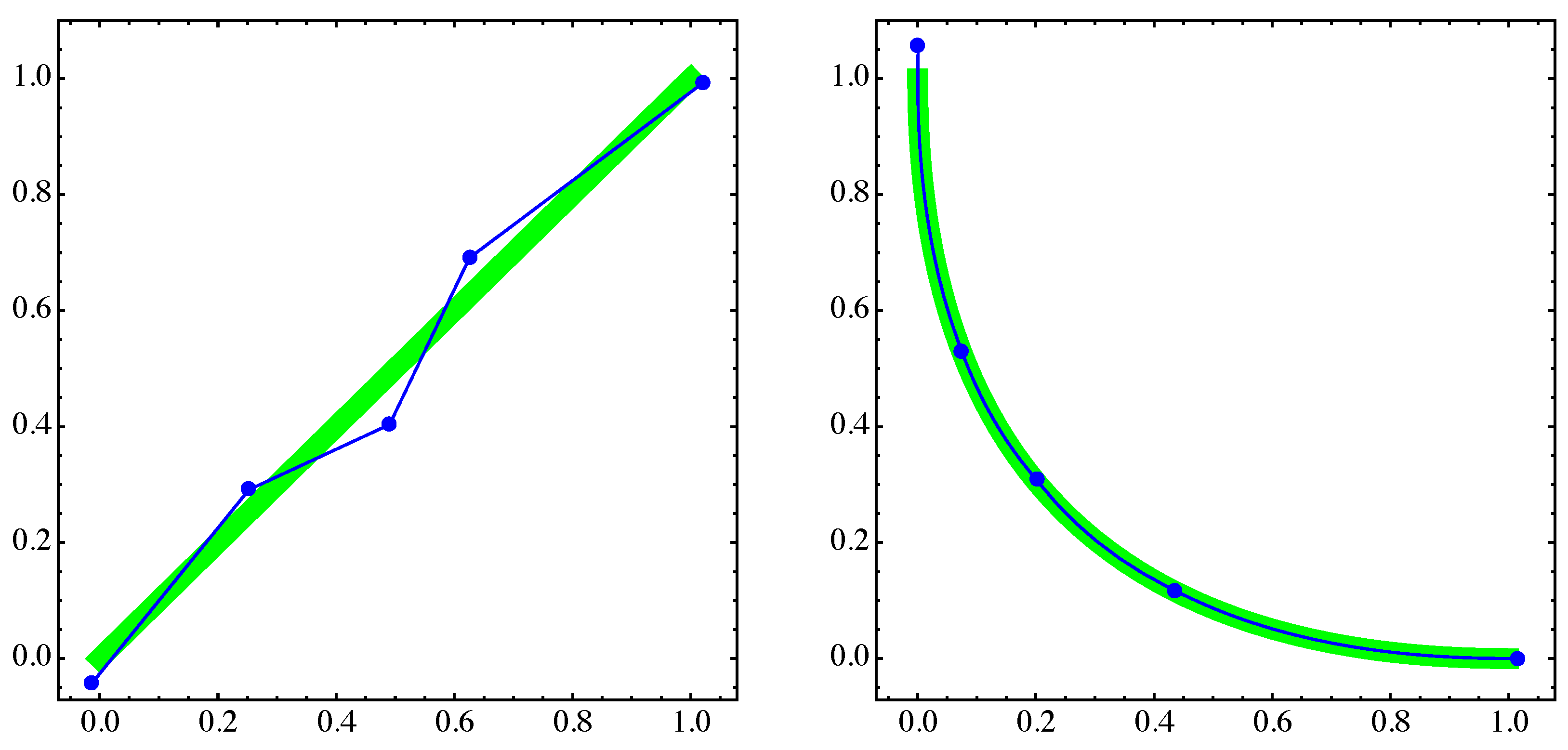
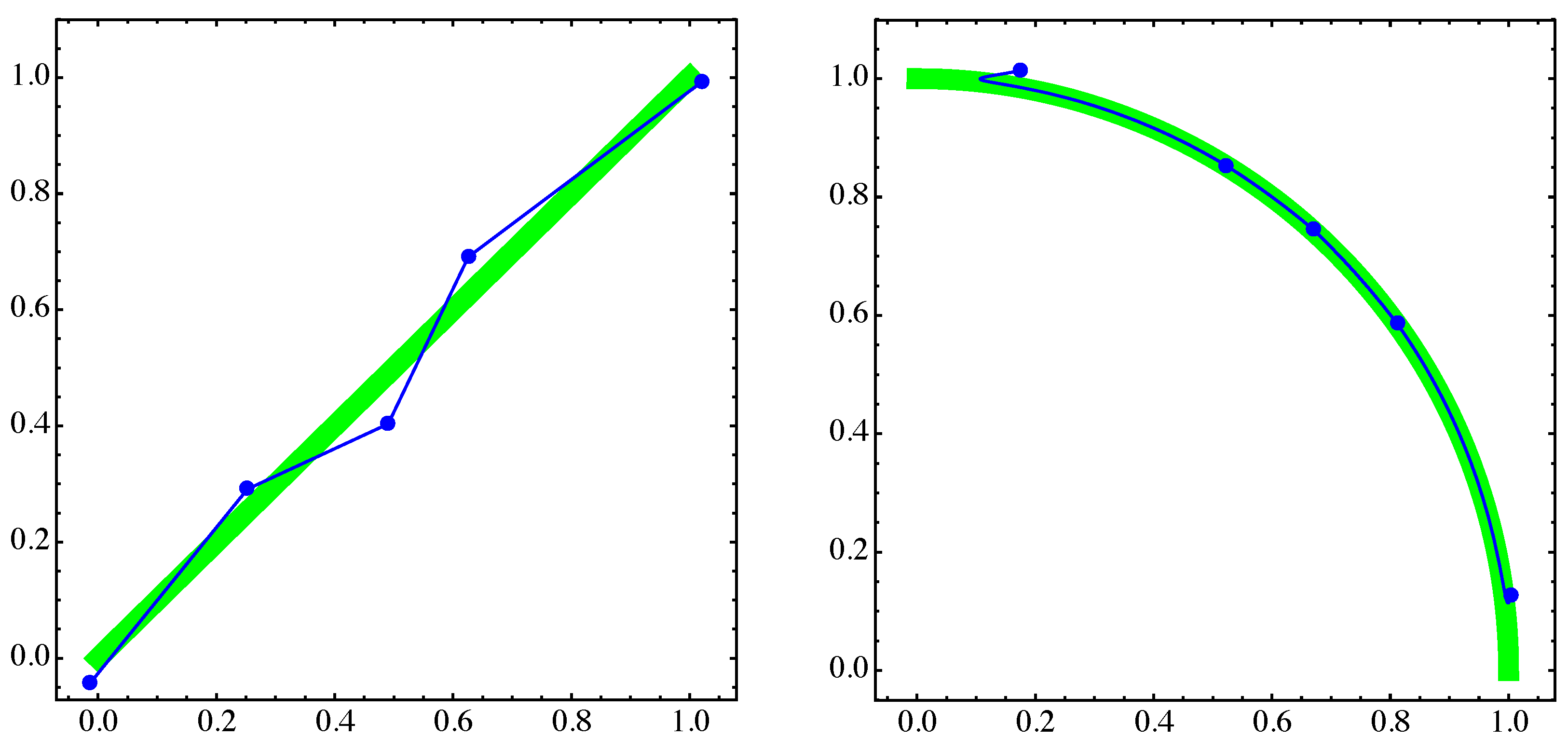
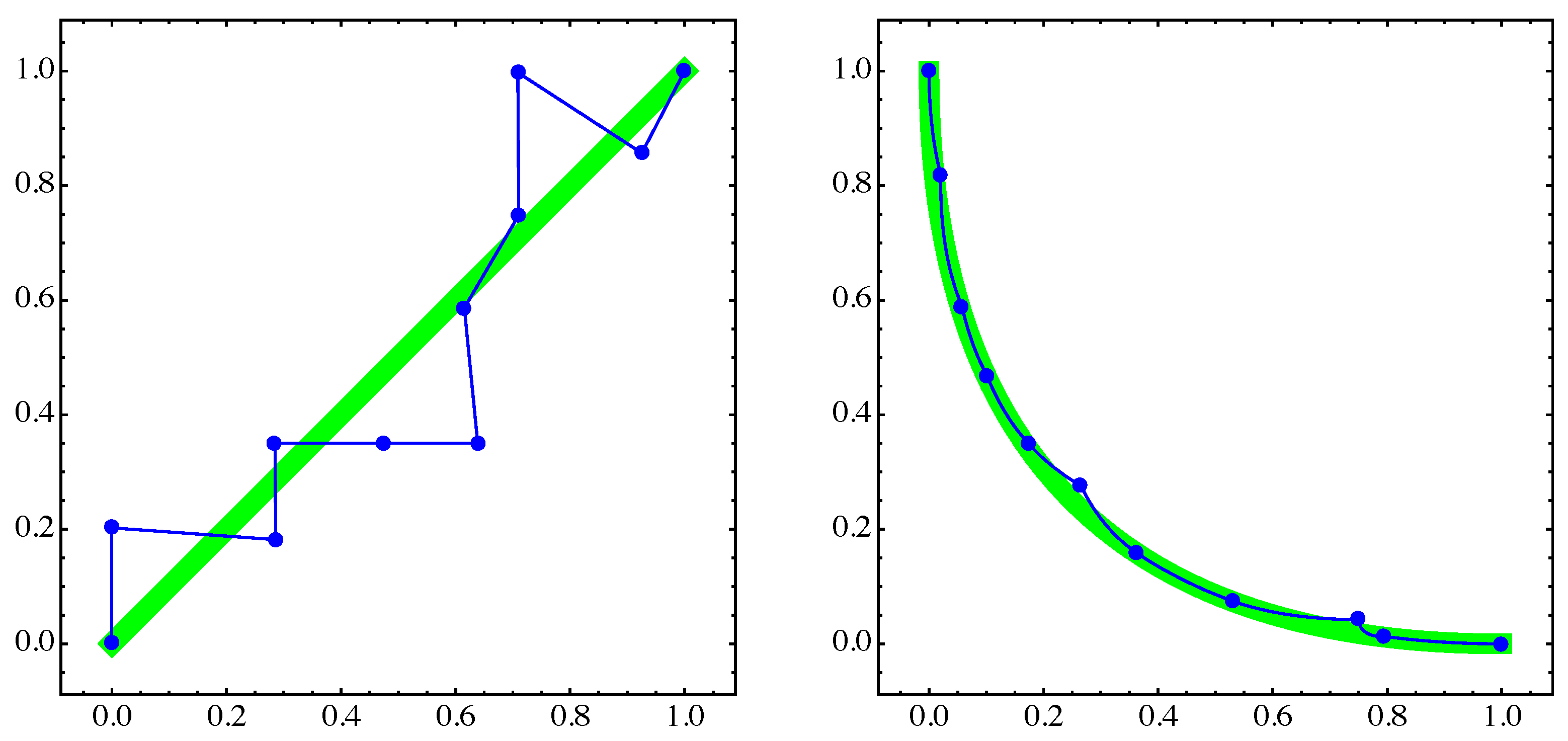
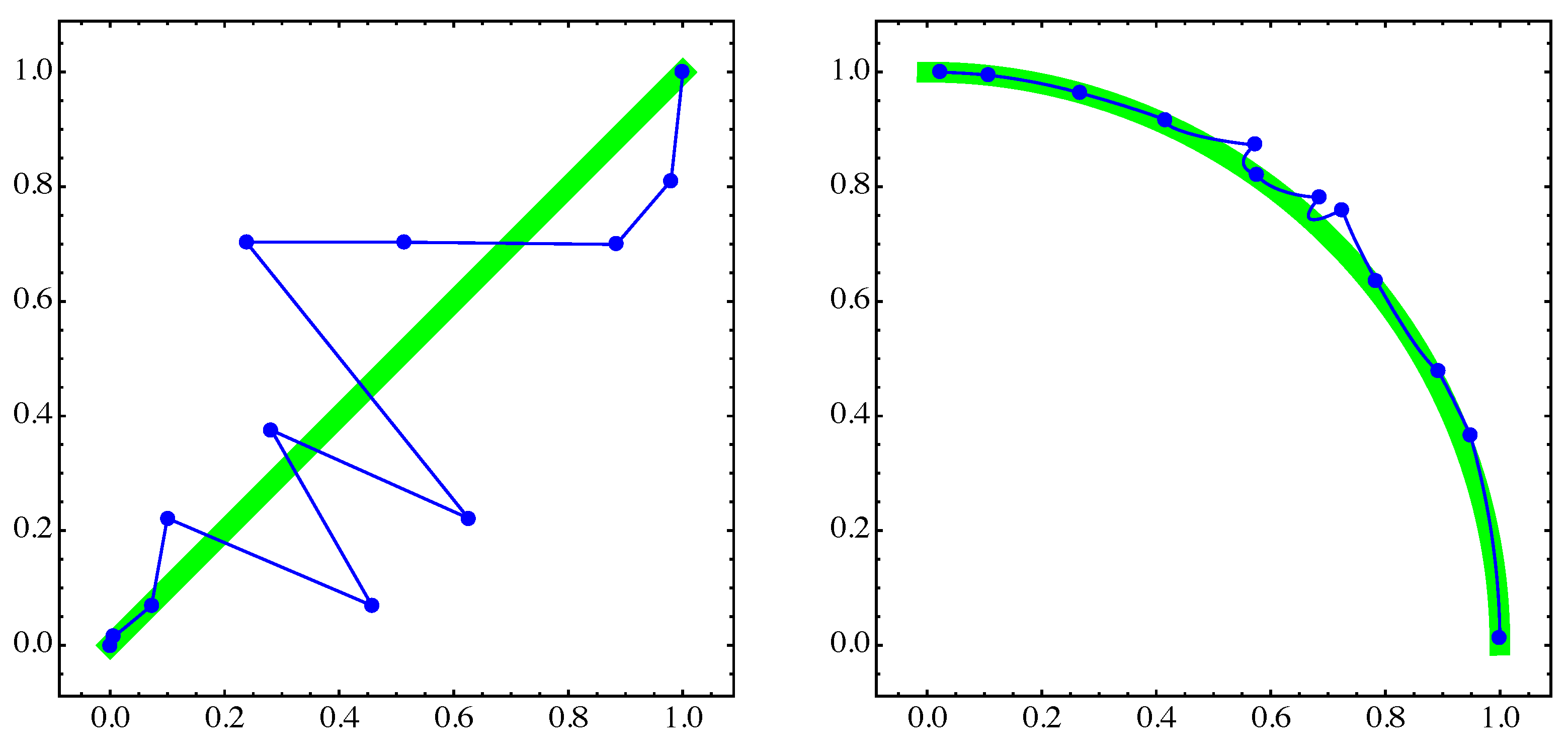
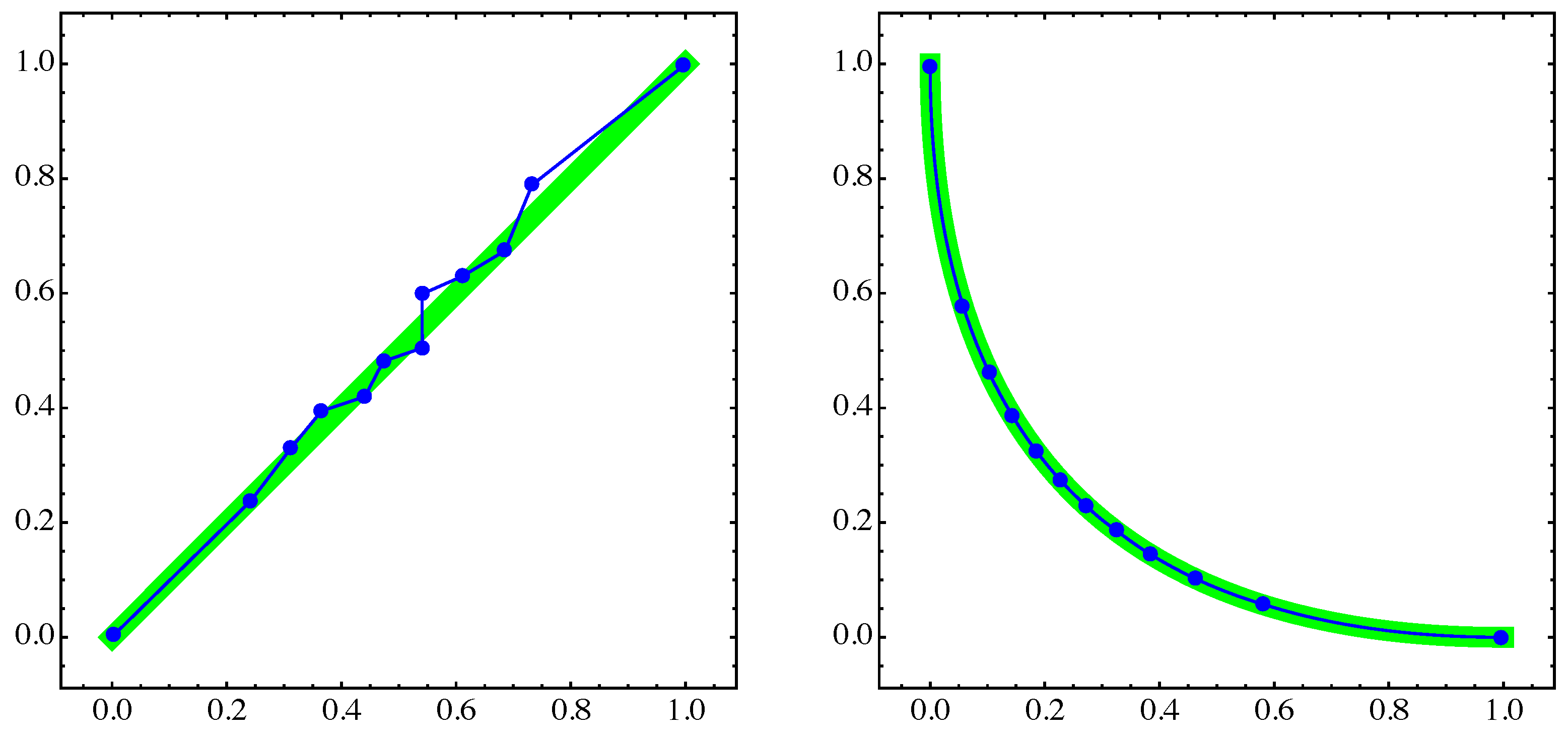
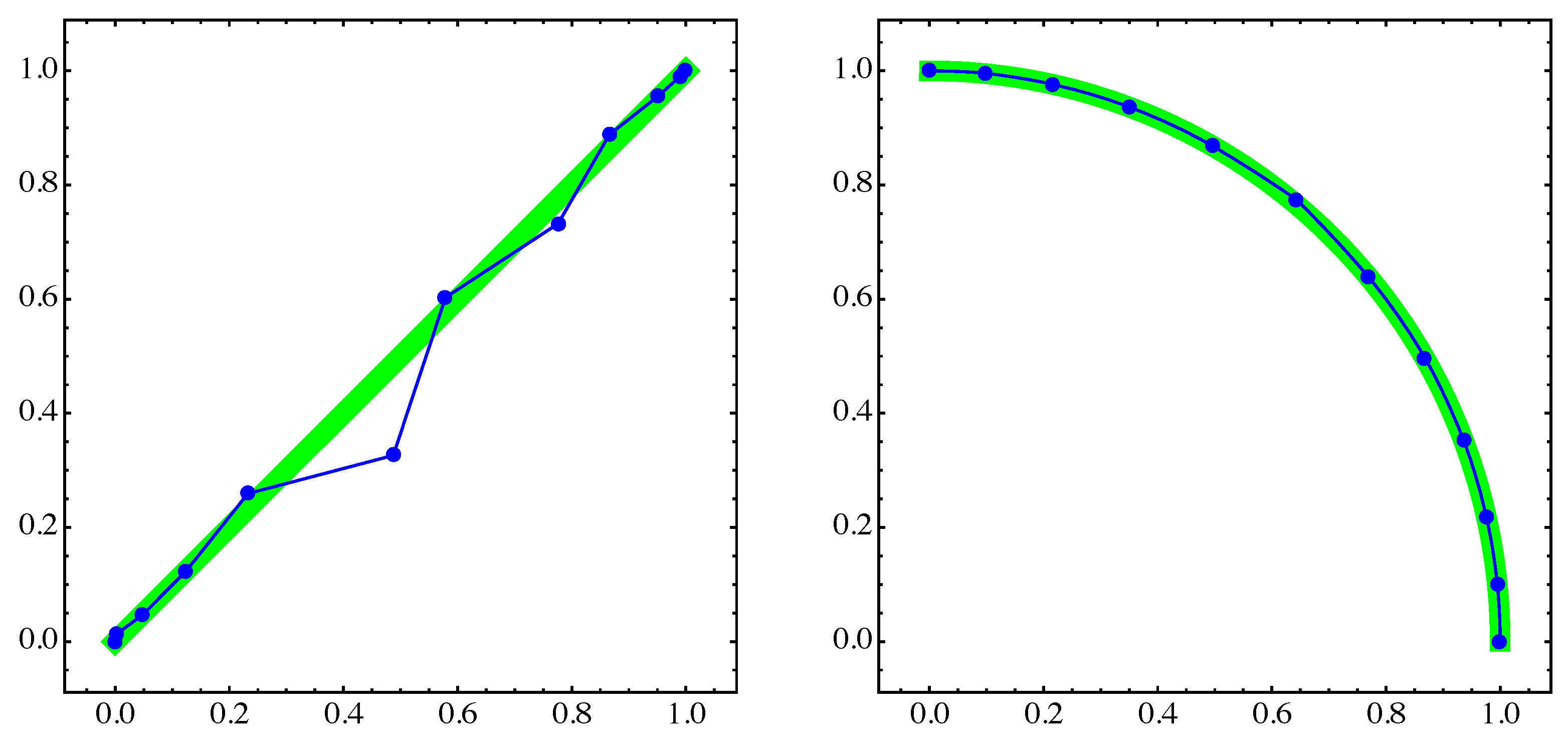
4. Numerical Examples
4.1. General Example
4.2. Approximation of Pareto Sets/Fronts
5. Conclusions and Future Work
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Heinonen, J. Lectures on Analysis on Metric Spaces; Springer: New York, NY, USA, 2001. [Google Scholar]
- Huttenlocher, D.P.; Klanderman, G.A.; Rucklidge, W.A. Comparing Images Using the Hausdorff Distance. IEEE Trans. Pattern Anal. Mach. Intell. 1993, 15, 850–863. [Google Scholar] [CrossRef]
- Yi, X.; Camps, O.I. Line-Based Recognition Using A Multidimensional Hausdorff Distance. IEEE Trans. Pattern Anal. Mach. Intell. 1999, 21, 901–916. [Google Scholar]
- De Carvalho, F.; de Souza, R.; Chavent, M.; Lechevallier, Y. Adaptive Hausdorff distances and dynamic clustering of symbolic interval data. Pattern Recognit. Lett. 2006, 27, 167–179. [Google Scholar] [CrossRef]
- Dellnitz, M.; Hohmann, A. A subdivision algorithm for the computation of unstable manifolds and global attractors. Numerische Mathematik 1997, 75, 293–317. [Google Scholar] [CrossRef]
- Aulbach, B.; Rasmussen, M.; Siegmund, S. Approximation of attractors of nonautonomous dynamical systems. Discret. Contin. Dyn. Syst. Ser. B 2005, 5, 215–238. [Google Scholar]
- Emmerich, M.; Deutz, A.H. Test Problems Based on Lamé Superspheres. In Proceedings of the 4th International Conference on Evolutionary Multi-criterion Optimization, Matsushima, Japan, 5–8 March 2007; Springer: Berlin/Heidelberg, Germany, 2007; pp. 922–936. [Google Scholar]
- Falconer, K. Fractal Geometry: Mathematical Foundations and Applications, 2nd ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2003. [Google Scholar]
- Schütze, O. Set Oriented Methods for Global Optimization. Ph.D. Thesis, University of Paderborn, Paderborn, Germany, 2004. [Google Scholar]
- Dellnitz, M.; Schütze, O.; Hestermeyer, T. Covering Pareto Sets by Multilevel Subdivision Techniques. J. Optim. Theory Appl. 2005, 124, 113–155. [Google Scholar] [CrossRef]
- Padberg, K. Numerical Analysis of Transport in Dynamical Systems. Ph.D. Thesis, University of Paderborn, Paderborn, Germany, 2005. [Google Scholar]
- Schütze, O.; Coello Coello, C.A.; Mostaghim, S.; Talbi, E.G.; Dellnitz, M. Hybridizing Evolutionary Strategies with Continuation Methods for Solving Multi-Objective Problems. Eng. Optim. 2008, 40, 383–402. [Google Scholar] [CrossRef]
- Schütze, O.; Laumanns, M.; Coello Coello, C.A.; Dellnitz, M.; Talbi, E.G. Convergence of Stochastic Search Algorithms to Finite Size Pareto Set Approximations. J. Glob. Optim. 2008, 41, 559–577. [Google Scholar] [CrossRef]
- Schütze, O.; Esquivel, X.; Lara, A.; Coello Coello, C.A. Using the averaged Hausdorff distance as a performance measure in evolutionary multiobjective optimization. IEEE Trans. Evol. Comput. 2012, 16, 504–522. [Google Scholar] [CrossRef]
- Hernández, C.; Naranjani, Y.; Sardahi, Y.; Liang, W.; Schütze, O.; Sun, J.Q. Simple Cell Mapping Method for Multi-objective Optimal Feedback Control Design. Int. J. Dyn. Control 2013, 1, 231–238. [Google Scholar] [CrossRef]
- Siwel, J.; Yew-Soon, O.; Jie, Z.; Liang, F. Consistencies and contradictions of performance metrics in multiobjective optimization. IEEE Trans. Evol. Comput. 2014, 44, 2329–2404. [Google Scholar]
- Sun, J.Q.; Xiong, F.R.; Schütze, O.; Hernández, C. Cell Mapping Methods—Algorithmic Approaches and Applications; Springer: Singapore, 2019. [Google Scholar]
- Jahn, J. Multiobjective search algorithm with subdivision technique. Comput. Optim. Appl. 2006, 35, 161–175. [Google Scholar] [CrossRef]
- Schütze, O.; Vasile, M.; Junge, O.; Dellnitz, M.; Izzo, D. Designing optimal low thrust gravity assist trajectories using space pruning and a multi-objective approach. Eng. Optim. 2009, 41, 155–181. [Google Scholar] [CrossRef]
- Deb, K. Multi-Objective Optimization Using Evolutionary Algorithms; John Wiley & Sons: Chichester, UK, 2001. [Google Scholar]
- Beume, N.; Naujoks, B.; Emmerich, M. SMS-EMOA: Multiobjective selection based on dominated hypervolume. Eur. J. Oper. Res. 2007, 181, 1653–1669. [Google Scholar] [CrossRef]
- Garg, H. Solving structural engineering design optimization problems using an artificial bee colony algorithm. J. Ind. Manag. Optim. 2014, 10, 777–794. [Google Scholar] [CrossRef]
- Garg, H. A hybrid PSO-GA algorithm for constrained optimization problems. Appl. Math. Comput. 2016, 274, 292–305. [Google Scholar] [CrossRef]
- Zapotecas-Martínez, S.; López-Jaimes, A.; García-Nájera, A. LIBEA: A Lebesgue Indicator-Based Evolutionary Algorithm for Multi-objective Optimization. Swarm Evolut. Comput. 2018. [Google Scholar] [CrossRef]
- Hartikainen, M.; Miettinen, K.; Wiecek, M. PAINT: Pareto front interpolation for nonlinear multiobjective optimization. Comput. Optim. Appl. 2012, 52, 845–867. [Google Scholar] [CrossRef]
- Vargas, A.; Bogoya, J.M. A generalization of the averaged Hausdorff distance. Computación y Sistemas 2018, 22, 331–345. [Google Scholar] [CrossRef]
- Tao, T. An Introduction to Measure Theory (Graduate Studies in Mathematics); American Mathematical Society: Providence, RI, USA, 2011. [Google Scholar]
- Jones, F. Lebesgue Integration on Euclidean Space; Jones and Bartlett Publishers: Boston, MA, USA, 2001. [Google Scholar]
- Hardy, G.H.; Littlewood, J.E.; Pólya, G. Inequalities, 2nd ed.; Cambridge University Press: Cambridge, UK, 1952. [Google Scholar]
- Bullen, P.S. Handbook of Means and Their Inequalities; Kluwer Academic Publishers Group: Dordrecht, The Netherlands, 2003. [Google Scholar]
- Pareto, V. Manual of Political Economy; The Macmillan Press: London, UK, 1971. [Google Scholar]
- Hillermeier, C. Nonlinear Multiobjective Optimization: A Generalized Homotopy Approach; Springer Science & Business Media: Berlin, Germany, 2001. [Google Scholar]
- Zitzler, E.; Thiele, L. Multiobjective evolutionary algorithms: A comparative case study and the strength Pareto approach. IEEE Trans. Evol. Comput. 1999, 3, 257–271. [Google Scholar] [CrossRef]
- Brockhoff, D.; Wagner, T.; Trautmann, H. On the Properties of the R2 Indicator. In Proceedings of the 14th Annual Conference on Genetic and Evolutionary Computation, Philadelphia, PA, USA, 7–11 July 2012; ACM: New York, NY, USA, 2012; pp. 465–472. [Google Scholar]
- Ishibuchi, H.; Masuda, H.; Nojima, Y. A Study on Performance Evaluation Ability of a Modified Inverted Generational Distance Indicator. In Proceedings of the 2015 Annual Conference on Genetic and Evolutionary Computation, Madrid, Spain, 11–15 July 2015; ACM: New York, NY, USA, 2015; pp. 695–702. [Google Scholar]
- Dilettoso, E.; Rizzo, S.A.; Salerno, N. A Weakly Pareto Compliant Quality Indicator. Math. Comput. Appl. 2017, 22, 25. [Google Scholar]
- Garg, H.; Kumar, K. Distance measures for connection number sets based on set pair analysis and its applications to decision-making process. Appl. Intell. 2018, 48, 1–14. [Google Scholar] [CrossRef]
- Singh, S.; Garg, H. Distance measures between type-2 intuitionistic fuzzy sets and their application to multicriteria decision-making process. Appl. Intell. 2017, 46, 788–799. [Google Scholar] [CrossRef]
- Van Veldhuizen, D.A.; Lamont, G.B. Multiobjective evolutionary algorithm test suites. In Proceedings of the 1999 ACM Symposium on Applied Computing, San Antonio, TX, USA, 28 February–2 March 1999; ACM: New York, NY, USA, 1999; pp. 351–357. [Google Scholar]
- Coello Coello, C.A.; Cruz Cortés, N. Solving Multiobjective Optimization Problems using an Artificial Immune System. Genet. Program. Evolvable Mach. 2005, 6, 163–190. [Google Scholar] [CrossRef]
- Rudolph, G.; Schütze, O.; Grimme, C.; Domínguez-Medina, C.; Trautmann, H. Optimal averaged Hausdorff archives for bi-objective problems: Theoretical and numerical results. Comput. Optim. Appl. 2016, 64, 589–618. [Google Scholar] [CrossRef]
- Zitzler, E.; Thiele, L.; Laumanns, M.; Fonseca, C.M.; da Fonseca, V.G. Performance assessment of multiobjective optimizers: An analysis and review. IEEE Trans. Evol. Comput. 2003, 7, 117–132. [Google Scholar] [CrossRef]
- Witkowski, A. A new proof of the monotonicity property of power means. JIPAM. J. Inequal. Pure Appl. Math. 2004, 5, 73. [Google Scholar]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, H. MOEA/D: A Multiobjective Evolutionary Algorithm Based on Decomposition. IEEE Trans. Evol. Comput. 2007, 11, 712–731. [Google Scholar] [CrossRef]
- Schütze, O.; Domínguez-Medina, C.; Cruz-Cortés, N.; de la Fraga, L.G.; Sun, J.Q.; Toscano, G.; Landa, R. A scalar optimization approach for averaged Hausdorff approximations of the Pareto front. Eng. Optim. 2016, 48, 1593–1617. [Google Scholar] [CrossRef]
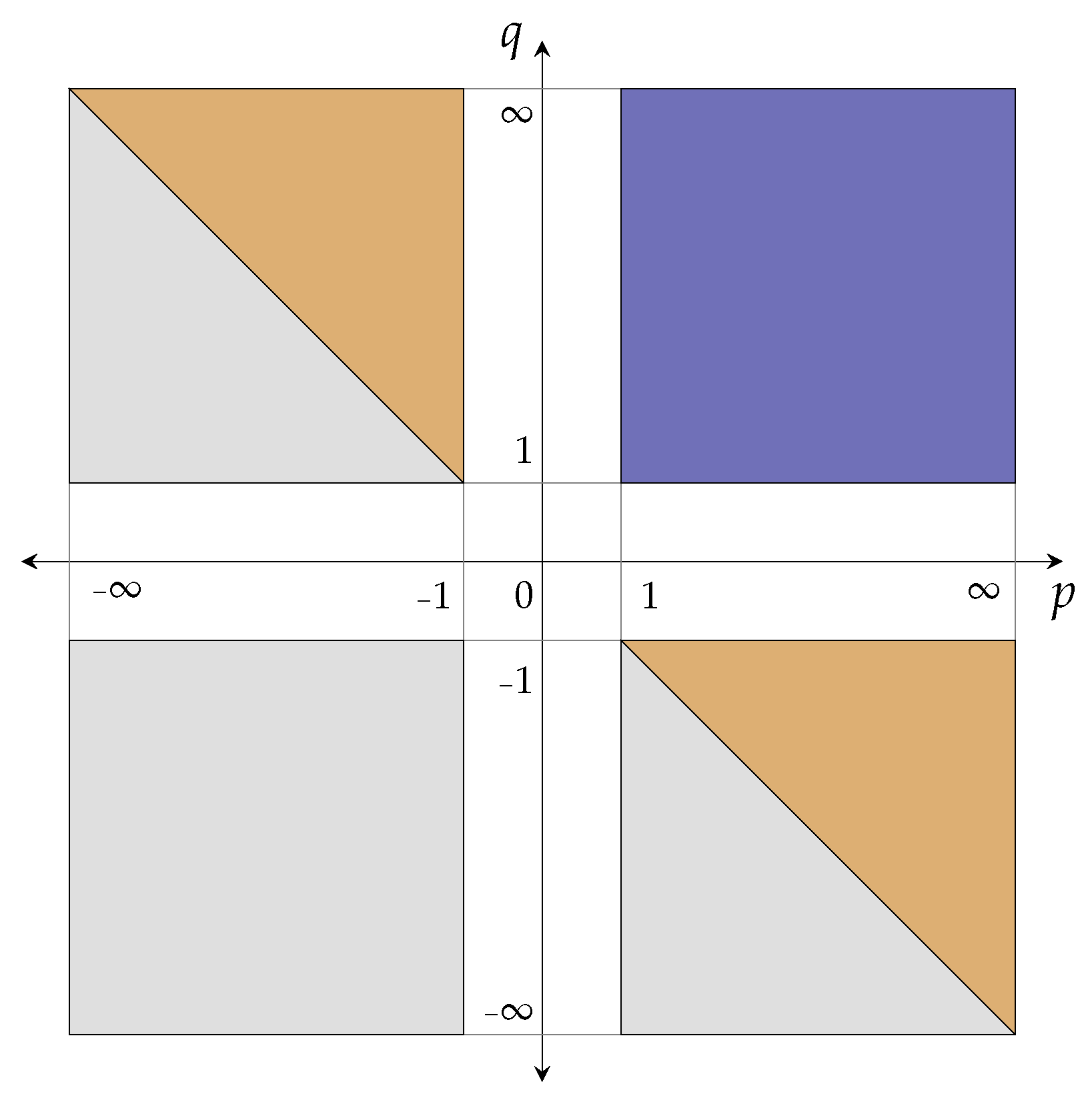
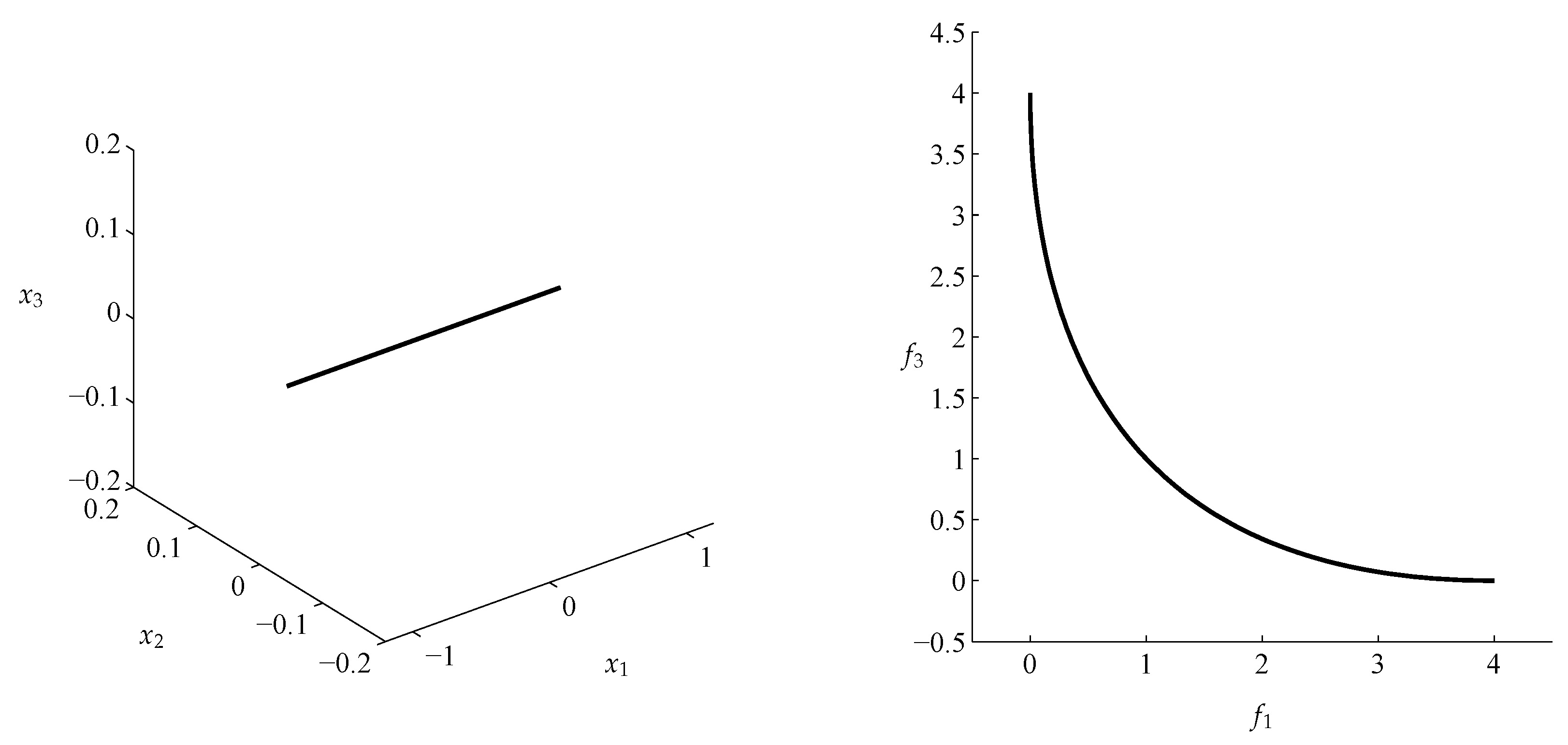
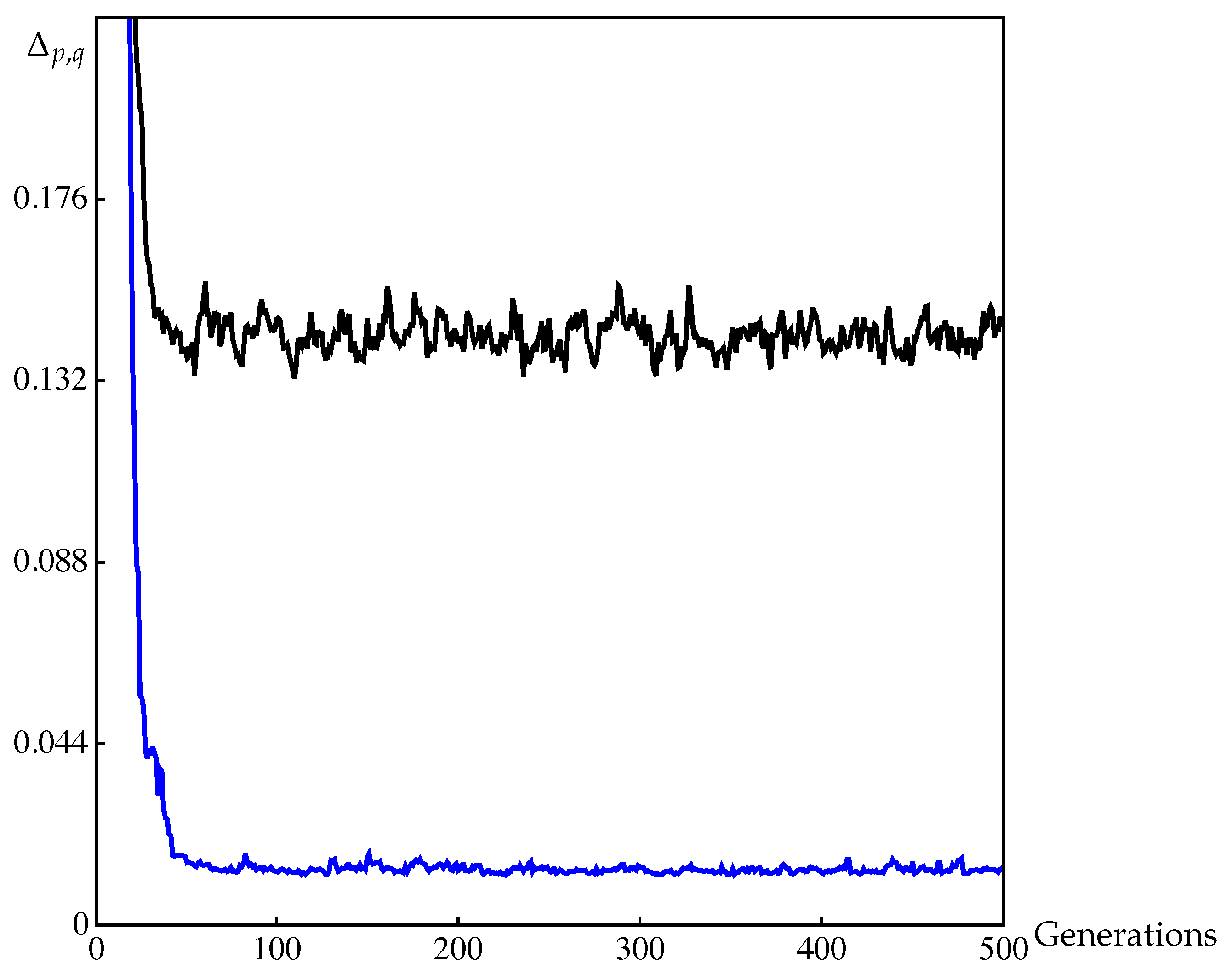
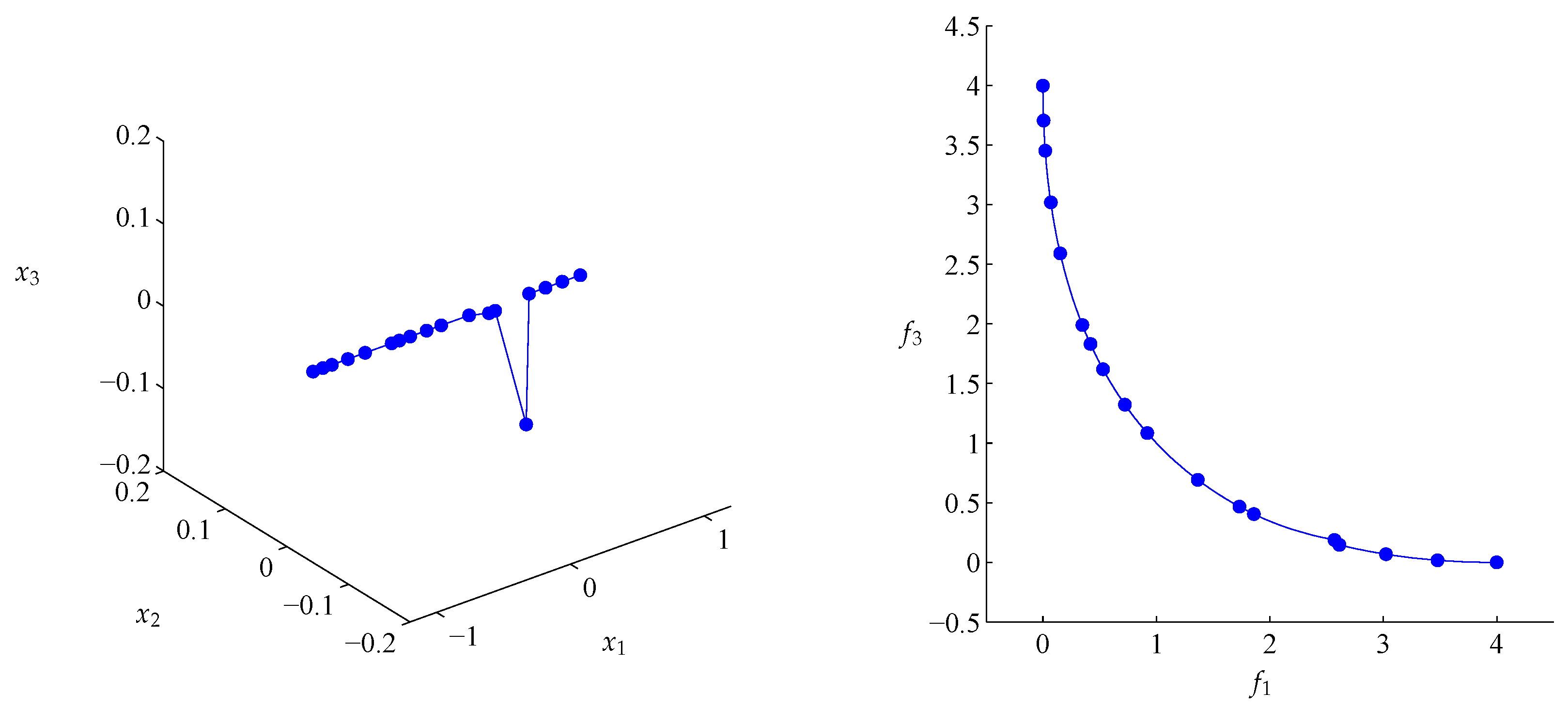
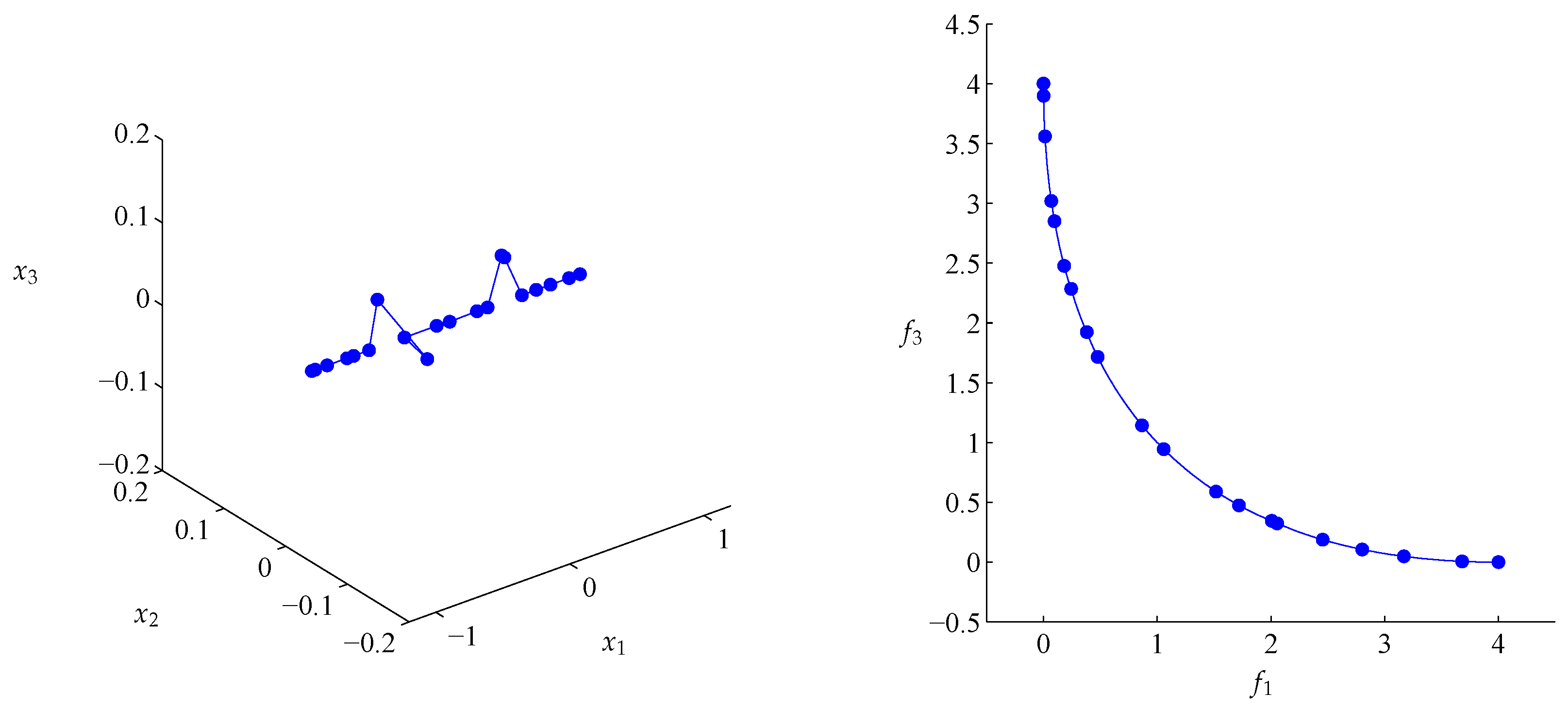
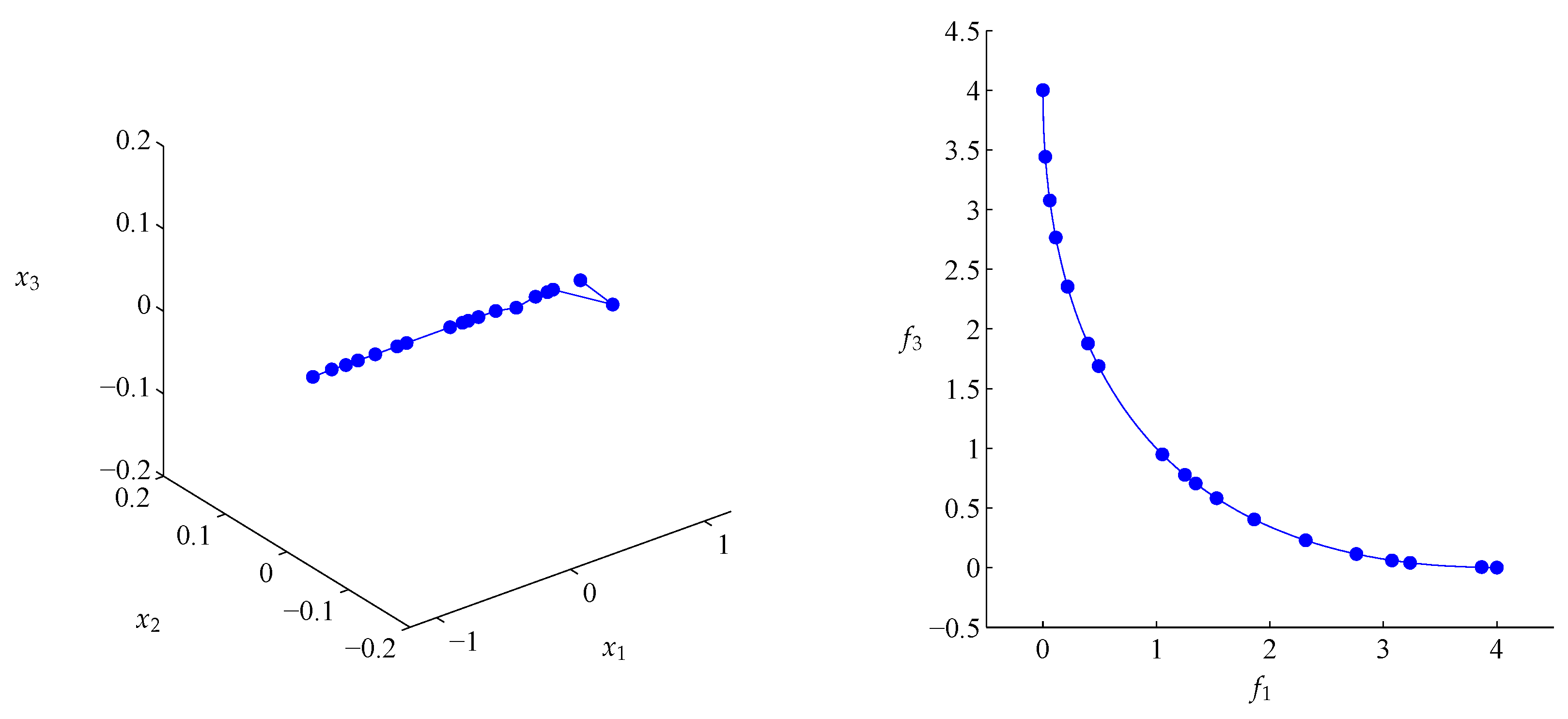
| p | q | ||||
|---|---|---|---|---|---|
| 1 | 1 | ||||
| 1 | |||||
| 1 | |||||
| 1 | |||||
| 1 |
| p | q | Decision Space | Objective Space | |||
|---|---|---|---|---|---|---|
| Finite Archive | Continuous Archive | Finite Archive | Continuous Archive | |||
| 1 | 1 | |||||
| 1 | ||||||
| 1 | ||||||
| 1 | ||||||
| 1 | ||||||
| 1 | 1 | |||||
| 1 | ||||||
| 1 | ||||||
| 1 | ||||||
| 1 | ||||||
| Algorithm | Parameter | Value |
|---|---|---|
| NSGA-II | Population size | 12 |
| Number of generations | 500 | |
| Crossover probability | 0.8 | |
| Mutation probability | ||
| Distribution index for crossover | 20 | |
| Distribution index for mutation | 20 | |
| MOEA/D | Population size | 12 |
| # weight vectors | 12 | |
| Number of generations | 500 | |
| Crossover probability | 1 | |
| Mutation probability | ||
| Distribution index for crossover | 30 | |
| Distribution index for mutation | 20 | |
| Aggregation function | Tchebycheff | |
| Neighborhood size | 3 |
| Generation | ||||
|---|---|---|---|---|
| Finite Archive | Continuous Archive | Finite Archive | Continuous Archive | |
| 50 | ||||
| 100 | ||||
| 200 | ||||
| 250 | ||||
| 400 | ||||
| 450 | ||||
| 460 | ||||
| 470 | ||||
| 480 | ||||
| 490 | ||||
| 500 | ||||
| Generation | ||||
|---|---|---|---|---|
| Finite Archive | Continuous Archive | Finite Archive | Continuous Archive | |
| 50 | ||||
| 100 | ||||
| 200 | ||||
| 250 | ||||
| 400 | ||||
| 450 | ||||
| 460 | ||||
| 470 | ||||
| 480 | ||||
| 490 | ||||
| 500 | ||||
| Generation | Continuous Archive | Finite Archive |
|---|---|---|
| 20 | ||
| 40 | ||
| 60 | ||
| 80 | ||
| 100 | ||
| 120 | ||
| 140 | ||
| 160 | ||
| 180 | ||
| 200 | ||
| 220 | ||
| 240 | ||
| 260 | ||
| 280 | ||
| 300 | ||
| 320 | ||
| 340 | ||
| 360 | ||
| 380 | ||
| 400 | ||
| 420 | ||
| 440 | ||
| 460 | ||
| 480 | ||
| 500 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bogoya, J.M.; Vargas, A.; Cuate, O.; Schütze, O. A (p,q)-Averaged Hausdorff Distance for Arbitrary Measurable Sets. Math. Comput. Appl. 2018, 23, 51. https://doi.org/10.3390/mca23030051
Bogoya JM, Vargas A, Cuate O, Schütze O. A (p,q)-Averaged Hausdorff Distance for Arbitrary Measurable Sets. Mathematical and Computational Applications. 2018; 23(3):51. https://doi.org/10.3390/mca23030051
Chicago/Turabian StyleBogoya, Johan M., Andrés Vargas, Oliver Cuate, and Oliver Schütze. 2018. "A (p,q)-Averaged Hausdorff Distance for Arbitrary Measurable Sets" Mathematical and Computational Applications 23, no. 3: 51. https://doi.org/10.3390/mca23030051
APA StyleBogoya, J. M., Vargas, A., Cuate, O., & Schütze, O. (2018). A (p,q)-Averaged Hausdorff Distance for Arbitrary Measurable Sets. Mathematical and Computational Applications, 23(3), 51. https://doi.org/10.3390/mca23030051






