Abstract
Planning conflict-free trajectories is a long-standing problem in Air Traffic Management. Navigation functions designed specifically to produce flyable trajectories have been previously considered, but lack the robustness to uncertain weather conditions needed for use in an operational context. These uncertainties can be taken into account be modifying the boundary of the domain on which the navigation function is computed. In the following work, we present a method for efficiently taking into account boundary variations, using the Hadamard variation.
1. Introduction
The aviation industry currently faces meaningful challenges to overcome the increasing traffic across the world. Safety solutions are a demand in all flight phases in order to cope with traffic capacity, all-weather conditions and efficiency. In order to address the 5% per year increase in air traffic, the Single European Sky ATM Research (SESAR) program in Europe and the NextGen program in the USA have been initiated to design new rules and tools for future air traffic management (ATM).
Each flight phase has specific operational constraints. Of interest here is the en-route flight phase. This phase is comprised from completion of initial climb through cruise altitude and completion of controlled descent to the initial approach fix. En-route air traffic is currently managed by subdividing airspace into sectors and air routes. In each sector, a team of air traffic controllers supervises the transiting aircraft and prevents conflicts by deviating some aircraft from their planned route. Each team communicates with the teams responsible for neighbouring sectors to transfer aircraft flying through several sectors.
As traffic grows, the workload in a sector may exceed air traffic controller capabilities. In this case, the sector is subdivided into smaller sectors, thus lowering the number of aircraft under the responsibility of an air traffic controller at any given time. However, this increases the time spent transferring aircraft between sectors up to the point where coordinating between sectors takes precedence over separating aircraft and solving conflicts. The SESAR program overcomes this pitfall by delegating most of the separation task to the aircraft themselves, thus inducing a higher level of automation. In this context, fixed air routes will no longer be necessary and trajectories will be planned in 4D in such a way that conflicts are avoided by design.
A major challenge associated with aircraft trajectory planning, in addition to operational constraints and flight dynamics, is the influence of wind. Much research has been conducted to plan such routes several days in advance. However, no algorithm is known to produce planning such that the resulting aircraft trajectories be robust to uncertain head- or tailwind. Artificial potential fields, as first used by [1], enable a mobile to reach a destination while avoiding obstacles in a complex environment. This method has been extended to dynamic environments, with multiple mobile trajectory planning as in [2], coordinating between mobiles in [3] and moving obstacles in [4]. Navigation functions, a specific case of artificial potential fields, introduced originally for robots trajectory planning by [5,6], were extended to generate aircraft trajectories under speed constraints in [7]. Such trajectories also exhibit low curvature on simulated situations, although a theoretical bound is yet to be obtained. Furthermore, conflict avoidance is guaranteed.
Navigation functions have also been used to plan trajectories under a wind constraint in [8] for sailboat navigation. Recent developments in navigation functions also include their application to the case of real-time spacecraft guidance [9], or in uncertain environments [10].
However, the navigation function works under the assumption that aircraft or other mobiles move in a deterministic way. We present in this paper a method to account for time uncertainty in aircraft trajectory planning. To account for this uncertainty, we consider the variation of the navigation function with respect to variations of the boundary of the configuration space. Of interest in this paper is the practical construction of Hadamard’s variational formula, as presented in [11], for the Green’s function of the Laplace equation on a two-dimensional sphere world.
The purpose of this paper is to present a method for computing the Hadamard variational formula given a specific domain perturbation. This variational formula requires knowledge of the Green’s function on the initial domain. Numerical evaluations of the Green’s function for certain problems, such as the Helmholtz operator on periodic structures [12], heat diffusion in 1D [13], the elliptic problem [14], or the exterior Neumann problem [15].
An analytical expression of the Green’s function for Laplace’s equation has also been obtained in multiply connected domaines [16]. However, this formulation is difficult to implement in practice, as it relies on the Schottky–Klein prime function [17].
The motivation for this paper is from designing schemes to plan trajectories for multiple mobiles under uncertainty using harmonic navigation functions.
After a state of the art on navigation functions in Section 2.1, Section 2.2 presents a method for numerically computing the Green’s function of the Laplacian operator, and Section 2.3 applies this method to the computation of the variation of the navigation function with respect to the domain boundary variation. The methods are illustrated and the results for this method are exhibited in Section 3. Finally, future work is outlined in Section 4.
2. Materials and Methods
2.1. Navigation Functions
Navigation functions on an arbitrary sphere world were introduced by Rimon and Koditschek [18] in the context of robot navigation for generating trajectories that present a guarantee of obstacle avoidance. Navigation functions are a family of potential functions, with their maximum on the boundary of the obstacles, their minimum at the destination and no interior local minimum or maximum. Formally, navigation functions are defined as follows:
Definition 1.
A map is a navigation function on a compact connected smooth manifold if it is:
- 1.
- Analytic on the interior of ,
- 2.
- Polar on with a minimum at an interior point ,
- 3.
- Admissible on ,
- 4.
- Morse on Ω.
Once the navigation function is computed, robot trajectories are determined by following at non critical points or the steepest descent given by the Hessian at critical points. The trajectories hereby obtained reach the destination while avoiding obstacles.
Navigation functions have been extended to aircraft trajectory planning [19], taking into account ATM considerations such as limits on speed and curvature, as aircraft can only fly at [%, %] of their nominal speed [20].
Of present interest are harmonic navigation functions on a manifold of with non-overlapping spherical boundaries. Such a domain is referred to as a sphere world. Let be a sphere world as described and the destination point in the interior of .
Consider the Dirichlet problem
where
is the Laplacian operator in two dimensions. As stated in [21], the function on defined by this problem is a navigation function. Indeed, no interior point can be a local extrema so that is polar. is admissible by construction and is Morse on .
However, navigation functions work under the assumption that trajectories are deterministic. The kind of trajectory obtained by this method is not robust against uncertainties, and thus phenomenon such as wind may cause the separation norms to be violated. This prevents navigation functions from being deployed in an operational context. The purpose of this work is to provide tools for extending navigation functions to the case of aircraft trajectories under a wind uncertainty.
In the following sections, we will introduce the Green’s function and a numerical method to obtain it on sphere worlds, and its application to navigation function under a domain boundary uncertainty.
2.2. Semi-Analytical Approximation of the Green’s Function for the Laplacian Operator
2.2.1. Green’s Function
Let be a planar bounded domain with the boundary such that be non intersecting circles and be exterior to all other circles, as illustrated in Figure 1. The centers of circles are noted and the radii . In this configuration, is Lipschitz-continuous and is a Lipschitz domain.
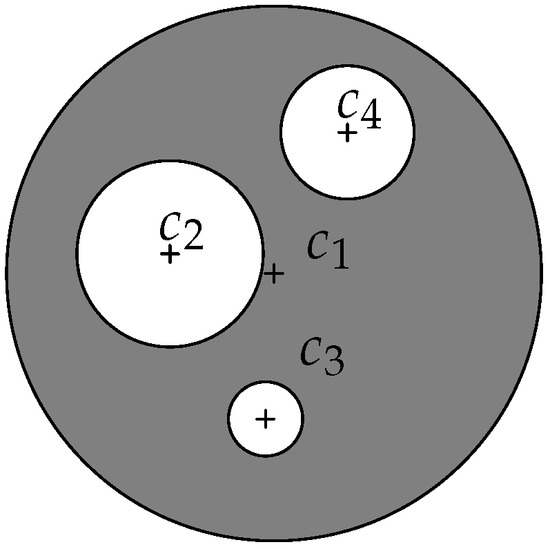
Figure 1.
A sphere world bounded by an outer circle of center and three non overlapping inner circles of centers , and , respectively.
Let us consider the equation
where is a given function. If the domain boundary is sufficiently smooth, then Equation (3) admits a unique solution .
The Green’s function, noted is the solution of
where is the Dirac distribution centered in . Contrary to Equation (3), the right-hand term in Equation (4) is not . However, the -integrability of the Green’s function for elliptical equations on Lipschitz domains is given by [22]. Furthermore, as presented in [23], it follows from Equation (4) that the solution u to Equation (3) has the form
2.2.2. Green’s Function from Conformal Mappings
Definition 2.
Let be a domain. A fundamental solution of the Laplace equation is a mapping such that is harmonic in for any and:
A representation theorem for such a G is given in [24]:
Theorem 1.
Let G be a fundamental solution of Laplace equation in a domain Ω. Then, there exists a function , harmonic in its first argument, and a real constant such that for any :
For a given , h, hence G, is uniquely defined by its values at the boundary . The special choice and vanishing boundary conditions yields the so-called Green’s function of the Laplace equation. It can be obtained by solving for h the system:
Theorem 2.
Let G be Green’s function for the Laplace equation in the domain Ω. The following relation holds in the distributional sense for any :
Proof.
Using the standard operators , it comes: . For an arbitrary function holomorphic in , continuous on :
By Stokes theorem:
Since , Equation (10) yields:
and finally, using the relation:
the right-hand side term equals:
☐
Using the system defining h to obtain an approximate solution is not an easy task from a numerical point of view as it requires solving a Laplace equation that becomes increasingly ill-conditioned as approaches the boundary of the domain. This is mainly due to the fact that the singularity lies within the domain of interest.
In order to transform this inconvenient geometry into a more convenient one, we choose a conformal mapping that eliminates the singularity at .
Consider the following conformal mapping
Provided that is interior to , the map of by noted , as illustrated in Figure 2, is the unbounded region exterior to a set of non-overlapping circles of center and of radii defined by
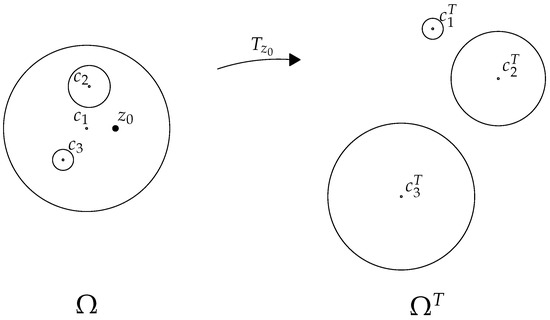
Figure 2.
Mapping of the sphere world by . is the space exterior to three circles.
Let . Given that is a conformal mapping, H is the harmonic solution exterior to non-overlapping disks that vanishes on the disk boundaries and such that as . Furthermore, contrary to , function H has no singularity on its domain. Function can then be determined given the knowledge of function H
In the following subsection, we present a method for approximating H.
2.2.3. Harmonic Function Exterior to Non-Overlapping Disks
We seek a function H on domain as defined previously. We use the following Laurent expansion [25] for H
with
and where , , and are scalars to be determined. This function is harmonic with as and vanishing values on the boundary of .
This series can be approximated by its N first terms. Thus, we consider the approximation h of function H
The Green’s function can then be approximated by the function . This function g has the additional benefit of being easily derived to any order as it is the composition of standard functions. Given Equation (18), the derivatives of h are
The derivatives of g are thus obtained by combining Equations (12), (15) and (19). Once the coefficients for h are determined, these derivatives come for free, as no additional coefficients need to be computed. This property is of interest to us for the purpose of the Hadamard variation covered in Section 2.3 as the normal derivatives on the domain boundary are required.
The values of coefficients of the expansion of h are obtained by a numerical method derived from that of [26], using collocation points equally spaced on the set of boundary circles, to approach the coefficients of (18) given a domain . A least squares method can be used to set the boundary conditions. To ensure that the vanishing condition on the boundary is satisfied, a number n of collocation points denoted by are set on each circle. Values for the coefficients are chosen by minimizing the sum of squares of . Finding the coefficients of h is then equivalent to solving the optimization problem:
where X and v are two vectors of length
and A is an n by matrix.
The problem set in Equation (20) can be turned into a set of linear equations by using Lagrange multipliers [27]. Given enough collocation points, this problem has a unique solution X as defined in Equation (21), from which we obtain the approximation h from Equation (18) of the harmonic function on and the approximation g of the Green’s function, with function g defined for a fixed point as
2.3. First Order Variation of the Harmonic Solution
The purpose of this section is to present the main results relating the behavior of the solution of an elliptic problem with Dirichlet boundary conditions to the variation of its border. Let be a connected orientable smooth Riemannian manifold of dimension d and let be a finite set of disjoint embedded smooth submanifolds of dimension that partition into two disjoint components that are manifolds of dimension d with common boundary . is assumed to be relatively compact. Finally, let X be a smooth vector field on with flow that is transversal to (except perhaps at a finite number of points). The flow of X will be denoted by , with as usual . For a fixed t, will denote the function . The flow will model an admissible deformation of the manifold with boundary . Following [28], the deformed boundary at will be defined as and the perturbed problem as:
Since the primary goal is to obtain a formula for the Green’s function variation, the problem stated in Equation (24) will be reformulated to accommodate a distribution in the right-hand term of Equation (24). Likewise, boundary condition (25) will be simplified later to . The final problem in distributional form is then:
where is the Riemannian volume form and T is the right-hand term distribution. Recalling that , it comes:
where the subscript N denotes the component of the vector normal to and , with N the normal vector to . Any test function v is the image by of a test function . The perturbed problem (27) can thus be rewritten so as to involve only integrals on :
Taking the derivative of the first integral on the left-hand side of (28) with respect to t at yields:
By Cartan’s formula, = , thus:
Putting it in (29), the derivative becomes:
The derivative with respect to t at of the boundary term:
can be expressed as:
with the boundary condition , the first term vanishes. However, it will be kept in the sequel to obtain a more general variation formula. Gathering things together yields:
Considering the problem:
and putting back its solution as v in (33) and using:
gives for the derivative of the solution:
Finally, if u is taken to be the green function of the original problem, the well known Hadamard formula is obtained [29]:
3. Results and Discussion
3.1. Numerical Validation of the Green’s Function Approximation
In this section, we discuss the results obtained by implementing the above method and verify that the resulting functions present certain expected properties. We also justify the decisions regarding the choice of parameters for Equation (18) in light of the relative error and the computation time. We finally discuss the relevance of this method for the application at hand, namely computing navigation functions.
Python 2.7 was used to implement the method described in Section 2.2 on an office computer with an Intel Core i7-4710MQ CPU, 2.50 GHz, eight cores.
The code is freely available on the HAL repository [30].
3.1.1. Convergence of the Method
3.1.1.1. Reconstruction of the Harmonic Solution for Constant Boundary Conditions
Given the Green’s function G on a domain , the harmonic solution can be found for any Dirichlet boundary conditions from Equation (5). In particular, one important property of the Green function is that if the function u in Equation (5) is constant and equal to 1, then we find that for any
We build function g to estimate the Green’s function as defined in Equation (23) on a domain featuring two inner circle boundaries of centers and and of radii and , respectively, and bounded by an outer circle of radius centered at the origin. We then evaluate the quality of the estimation by comparing the integral of its normal derivative to 1:
The integral is computed using the quad function from the scipy Python library [31], and based on a technique from the Fortran library QUADPACK.
Figure 3 is a measure of the quality of the estimation from Equation (37), given by the logarithm of , relative to the number of collocation points at a given point interior to the domain and for a given number of terms in the Laurent expansion , or . Overall, this value follows a decreasing curve, thus the distance decreases as the number of collocation points increases. There is a steep increase of the curve for values of around .
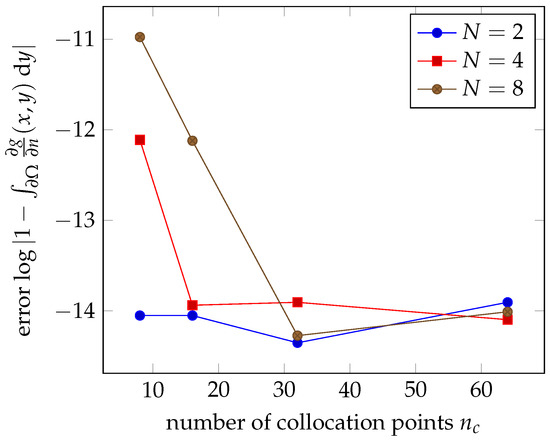
Figure 3.
with and a fixed N for values of ranging from 2 to 64 in the configuration described in Section 3.1.1.1. The x-axis is the number of collocation points .
For higher fixed values of N, the curve starts at a higher point, and converges for higher values of , but, in either case, the distance from to 1 plateau around for . This indicates that the obtained values are constrained by round-off errors.
There is no improvement for , since the problem is over-constrained, as can be seen in the linear problem stated in Equation (20), where coefficients are to be determined from equations.
In the following section, we will further evaluate the quality of the approximation of the Green’s function derived from our method by integrating over the domain boundary to find the harmonic solution for non-constant boundary conditions, similar to those of the foreseen application of our method.
3.1.1.2. Reconstruction for Non-Constant Boundary Conditions
On certain sphere worlds, an analytical solution can be found to Equation (3). Here, we consider the crown defined by the unit circle as an outer boundary, and the circle of center and of radius as an inner boundary as pictured in Figure 4.
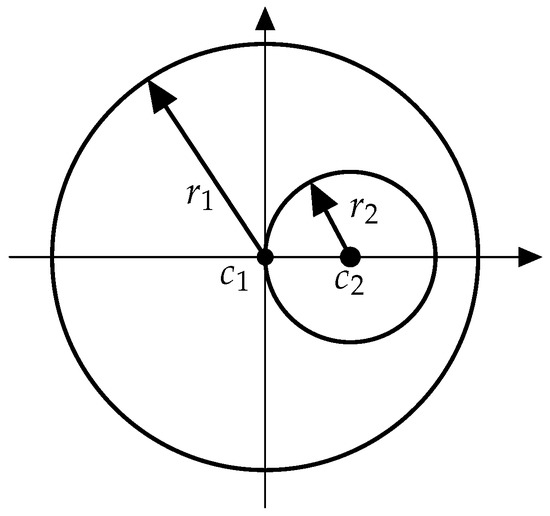
Figure 4.
Domain on which an exact solution is computed. The outer boundary is the unit circle. The inner boundary is the circle of center and of radius . The Dirichlet boundary conditions used are such that the value is on the inner boundary and on the outer boundary.
For a domain bounded by two concentric circles, with constant Dirichlet conditions on each circle, the harmonic solution to this problem is a function of the form with constants A and B chosen to fit the boundary condition. A Möbius mapping [32] can be found that transforms this symmetrical problem into that described in Figure 4. From here, and given Dirichlet boundary conditions such that the value on the inner boundary be constant equal to scalar and the value on the outer boundary be constant equal to , then the harmonic potential on this domain is function
We can thus compare the solution reconstructed with the Green’s function as described in Equation (5), noted
The in this equation are placed on a fine enough Cartesian grid, such that the result has converged.
In Figure 5a, the logarithm of the distance between both solutions is presented. As the number of terms used in the Laurent series increases, the difference decreases for high numbers of collocation points. As discussed previously, the error converges for values of greater than . As such, as the number of terms N in the Laurent expansion increases, the error converges for larger numbers of collocation points, but converges towards a lower value.
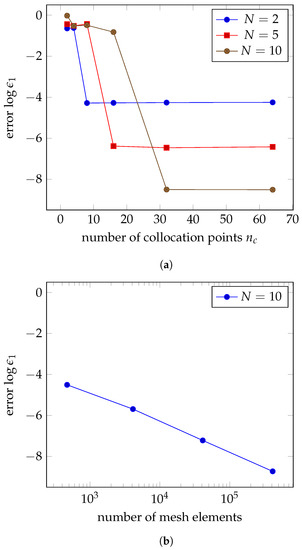
Figure 5.
with our method based on the Green’s function compared to that obtained with the finite elements method. (a) as a function of for a fixed number of terms in the Laurent expansion , or ; (b) as a function of the number of mesh vertices for the finite element method with Lagrangian elements of order 2.
In Figure 5b, is represented for the comparison between the analytical solution and that obtained with the finite elements method using Lagrange elements of order 2. Here, we observe that the error for the solution computed with the Green’s function is comparable to that for the finite elements method.
Although we compare the results obtained using the reconstruction from the Green’s function to those of the finite element method, it is to be noted that reconstructing the harmonic solution from the Green’s function is more time-consuming than solving the finite elements problem, as the Green’s function simultaneously gives the harmonic solution for all boundary conditions. As such, our method is not appropriate for solving single navigation functions. However, in the context of solving boundary variation problems, the hereby presented method computing the Green’s function is superior. We further illustrate this in the following paragraphs by exhibiting the time complexity.
3.1.2. Time Complexity
In this section, we consider the execution time to compute the approximation of the Green’s function at one point, noted as g in Section 2.2. We normalize the resulting times relative to the execution time in the test case where and . The results are presented in Figure 6 for different values of N and of .
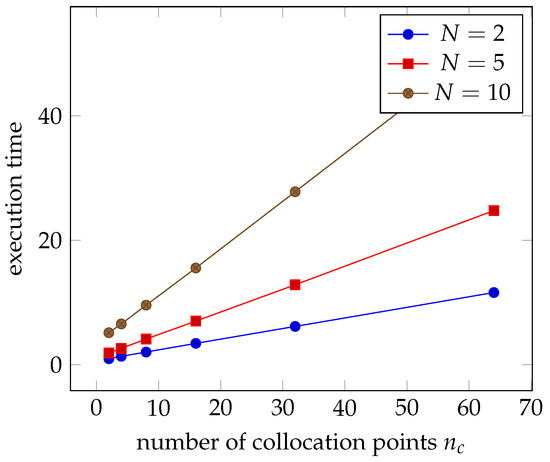
Figure 6.
Normalized execution as a function of for a fixed number of terms in the Laurent expansion , , or .
As can be seen in Figure 6, the time required to compute the Green’s function rapidly increases as the number of terms in the Laurent expansion increases. However, as seen in Section 3.1.1.1 and Section 3.1.1.2, the solution rapidly converges and good results can be obtained with small values of N.
The order of magnitude for the base case in our configuration, with and , is a millisecond. This relatively small amount of time must be put in perspective with the fact that the approximation g of the Green’s function may be computed hundreds of times for different points of the domain in order to estimate the value of the harmonic solution in one point.
In the following section, we will present a practical example of our method, relevant to the application at hand.
3.1.3. Possible Applications of the Solution
3.1.3.1. Green’s Function of Sphere Worlds
Having constructed a semi-analytical method for carrying out the computations of the Green’s function, we now include representative examples illustrating our construction on sphere worlds.
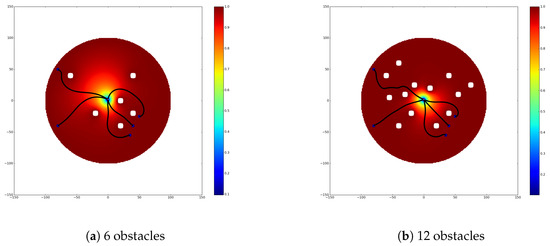
Figure 7 depicts examples of sphere worlds with one obstacle and the singularity placed at different points in the domain. The resulting function vanishes except in the vicinity of the singularity. In each of the Laurent expansion, ten terms are used. Thirty collocation points are set on the domain boundaries at regular intervals.
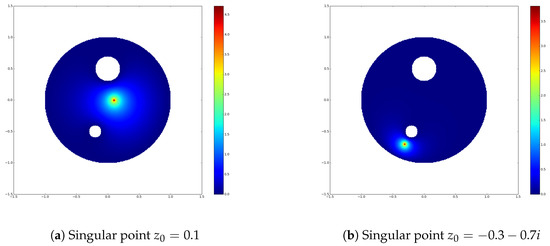
Figure 7.
Approximation g of the Green’s function on unit disc with obstacle of radius centered at and destination disc of radius centered at .
Sphere worlds with more obstacles can be tackled with no additional difficulty.
3.2. Numerical Validation of the Hadamard Variation of the Green’s Function
In the present section, we will exhibit the results obtained with the aforementioned method for variations of the domain boundary. We consider here a sphere world bounded by one destination disc , one obstacle disc and an outer boundary disc , such as the one presented in Figure 7. We hereby study two manners of disturbing the domain boundary
- by varying the center of the obstacle disc, which is representative of the effect of a locally constant wind on an aircraft.
- and by varying the radius of the obstacle disc.
The domain resulting from disturbing the domain boundary is denoted by . In any case, the form of as introduced in Equation (36) can be explicitly expressed for the entire domain border. Let and be respectively the variation of the obstacle disc center and radius. Then, the domain variation is
where is the normal vector to the domain boundary at point . For a pure translation of the disc, the term is null. For a pure variation of the obstacle disc radius, the term is null.
In practice, for determining aircraft trajectories, only the center of the obstacle disc is submitted to uncertainty, since the radius obstacle disc is defined by the aircraft separation norms. However, when the wind field cannot be considered to be locally constant, it makes sense to allow the disc to deform to an ellipse to account for the anisotropic nature of the perturbation. Extensive simulations with various wind fields is an ongoing work within the frame of the STARGATE project.
In the following paragraphs, we will consider the variation of the Green’s function for small variations of the obstacle radius.
We first introduce notations. Let be the Green’s function computed at each from Equation (23). Given the study of parameters in Section 3.1, the values of N and in computing the Green’s function are set respectively to 10 and 30. denotes the variation of the Green’s function as defined in Equation (36) and the Green’s function estimated using the Hadamard variation is noted . The Green’s function on the perturbed domain is noted and is similarly computed at each from Equation (23). Finally, , the Hadamard variation of the Green’s function is compared to , the actual variation of the Green’s function on the entire domain using the relative error for the variation as a metric
where the norm is computed on by discretizing the domain along a Cartesian grid as was done for Equation (40). This error, which is expected to approach 0 for small values of , is given in Figure 9 for perturbations of decreasing amplitudes, for a dilation of the radius of the inner disc.
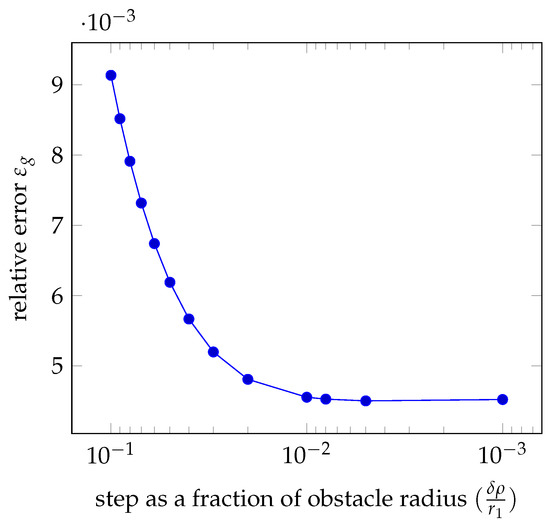
Figure 9.
Relative error of the variation of the Green’s function deduced from the Hadamard variation for a perturbation of the radius of the inner disc (displacement component is null). The x-axis is the logarithm of the inverse of the step by which the inner disc is modified.
4. Conclusions
In this article, a method for effectively computing the navigation function when the domain boundary is uncertain was presented. It is a two-fold method, where Section 2.2 aims at determining the Green’s function for the Laplacian operator and Section 2.3 uses the resulting Green’s function for determining the Hadamard variation. This promising method can be extended to the case of stochastic partial differential equations used within the frame of aircraft trajectory planning by harmonic navigation functions. Future work includes an extensive performance assessment for tactical conflict solving in air traffic management applications. This study will be conducted in the final validation part of the STARGATE project and will be made available on the project Website [34]. Key performance indicators addressed will include at least: fuel consumption increase, average/worst case deviation from the initial flight plan, and average/worst case delay.
Finally, based on the work presented in [35], the stochastic extension to biharmonic navigation functions will be investigated. It is already known that a Hadamard variation formula exists for such problems, but it remains to find an adequate semi-analytical formulation for the Green’s function.
Author Contributions
I.S. contributed for the numerical implementation of the algorithm and for designing the semi-analytical approach. S.P. worked on the Hadamard formula and G.D. was in charge of finite elements algorithms. All authors contributed to testing.
Acknowledgments
This work was funded by the grant ANR-14-CE27-0006 from the French National Research Agency (ANR).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Khatib, O. Real-time obstacle avoidance for manipulators and mobile robots. Int. J. Robot. Res. 1986, 5, 90–98. [Google Scholar] [CrossRef]
- Kim, D.H.; Wang, H.; Shin, S. Decentralized control of autonomous swarm systems using artificial potential functions: Analytical design guidelines. J. Intell. Robot. Syst. 2006, 45, 369–394. [Google Scholar] [CrossRef]
- Zeghal, K. Vers une Théorie de la Coordination D’actions. Application à la Navigation Aérienne. Ph.D. Thesis, Université Pierre et Marie Curie, Paris, France, 1994. [Google Scholar]
- Ge, S.S.; Cui, Y.J. Dynamic motion planning for mobile robots using potential field method. Auton. Robots 2002, 13, 207–222. [Google Scholar] [CrossRef]
- Dimarogonas, D.V.; Kyriakopoulos, K.J.; Theodorakatos, D. Totally distributed motion control of sphere world multi-agent systems using decentralized navigation functions. In Proceedings of the 2006 IEEE International Conference on Robotics and Automation, Orlando, FL, USA, 15–19 May 2006; pp. 2430–2435. [Google Scholar]
- Rimon, E.; Koditschek, D.E. Exact robot navigation using artificial potential functions. IEEE Trans. Robot. Autom. 1992, 8, 501–518. [Google Scholar] [CrossRef]
- Guys, L. Planification de Trajectoires d’Avions sans Conflit: Fonctions Biharmoniques et Fonction de Navigation Harmonique. Ph.D. Thesis, Université Toulouse 3 Paul Sabatier, Toulouse, France, 2014. [Google Scholar]
- Pêtrès, C.; Romero-Ramirez, M.-A.; Plumet, F. Reactive path planning for autonomous sailboat. In Proceedings of the 2011 15th International Conference on Advanced Robotics (ICAR), Tallinn, Estonia, 20–23 June 2011; pp. 112–117. [Google Scholar]
- Romano, M.; Virgili-Llop, J.; Zappulla, R., II. Near-optimal real-time spacecraft guidance and control using harmonic potential functions and a modified rrt. In Proceedings of the 27th AAS/AIAA Spaceflight Mechanics Meeting, San Antonio, TX, USA, 6–9 February 2017. [Google Scholar]
- Hacohen, S.; Shoval, S.; Shvalb, N. Applying probability navigation function in dynamic uncertain environments. Robot. Auton. Syst. 2017, 87, 237–246. [Google Scholar] [CrossRef]
- Hadamard, J.; Fréchet, M. Leçons Sur le Calcul des Variations; A. Hermann et fils: Paris, France, 1910; Volume 1. [Google Scholar]
- Jordan, K.E.; Richter, G.R.; Sheng, P. An efficient numerical evaluation of the green’s function for the helmholtz operator on periodic structures. J. Comput. Phys. 1986, 63, 222–235. [Google Scholar] [CrossRef]
- Beck, J.V.; Cole, K.D.; Haji-Sheikh, A.; Litkouhi, B. Heat Conduction Using Green’s Functions; Hemisphere Publishing Corporation: London, UK, 1992. [Google Scholar]
- Bertoluzza, S.; Decoene, A.; Lacouture, L.; Martin, S. Local error estimates of the finite element method for an elliptic problem with a dirac source term. arXiv, 2015; arXiv:1505.03032. [Google Scholar] [CrossRef]
- Sadybekov, M.A.; Torebek, B.T.; Turmetov, B.K. Representation of the green’s function of the exterior neumann problem for the laplace operator. Sib. Math. J. 2017, 58, 153–158. [Google Scholar] [CrossRef]
- Crowdy, D.; Marshall, J. Green’s functions for laplace’s equation in multiply connected domains. IMA J. Appl. Math. 2007, 72, 78–301. [Google Scholar] [CrossRef]
- Crowdy, D.G.; Kropf, E.H.; Green, C.C.; Nasser, M.M.S. The schottky–klein prime function: A theoretical and computational tool for applications. IMA J. Appl. Math. 2016, 81, 589–628. [Google Scholar] [CrossRef]
- Koditschek, D.E.; Rimon, E. Robot navigation functions on manifolds with boundary. Adv. Appl. Math. 1990, 11, 412–442. [Google Scholar] [CrossRef]
- Roussos, G.P.; Dimarogonas, D.V.; Kyriakopoulos, K.J. 3d navigation and collision avoidance for a non-holonomic vehicle. In Proceedings of the 2008 American Control Conference, Seattle, WA, USA, 11–13 June 2008; pp. 3512–3517. [Google Scholar]
- Delgado, L.; Prats, X. Fuel consumption assessment for speed variation concepts during the cruise phase. In Proceedings of the Conference on Air Traffic Management (ATM) Economics, Belgrade, Serbia, 10 September 2009. [Google Scholar]
- Rimon, E.; Koditschek, D.E. Exact robot navigation using cost functions: The case of distinct spherical boundaries in e/sup n. In Proceedings of the 1988 IEEE International Conference on Robotics and Automation, Philadelphia, PA, USA, 24–29 April 1988; pp. 1791–1796. [Google Scholar]
- Maeda, F.-Y.; Suzuki, N. The integrability of superharmonic functions on lipschitz domains. Bull. Lond. Math. Soc. 1989, 21, 270–278. [Google Scholar] [CrossRef]
- Nevanlinna, R.; Behnke, H.; Grauert, H. Analytic Functions; Springer: Berlin/Heidelberg, Germany, 1970; Volume 3. [Google Scholar]
- Henrici, P. Applied and Computational Complex Analysis; John Wiley & Sons: Hoboken, NJ, USA, 1993; Volume 3. [Google Scholar]
- Krantz, S.G. Handbook of Complex Variables; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Trefethen, L.N. Ten digit algorithms. Presented at the A. R. Mitchell Lecture at the 2005 Dundee Biennial Conference on Numerical Analysis, Dundee, UK, 28 June–1 July 2005. [Google Scholar]
- Lagrange, J.L. Mécanique Analytique; Mallet-Bachelier: Paris, France, 1853; Volume 1. [Google Scholar]
- Peetre, J. On Hadamard’s variational formula. J. Differ. Equ. 1980, 36, 335–346. [Google Scholar] [CrossRef]
- Suzuki, T.; Tsuchiya, T. First and second hadamard variational formulae of the green function for general domain perturbations. J. Math. Soc. Japan 2016, 68, 1389–1419. [Google Scholar] [CrossRef]
- Santos, I.; Puechmorel, S. Stochastic Navigation Function Implementation by a Semi-Analytical Algorithm. Available online: https://hal.inria.fr/hal-01869860 (accessed on 9 September 2018).
- Jones, E.; Oliphant, T.; Peterson, P. SciPy: Open Source Scientific Tools for Python. 2001. Available online: https://www.scipy.org/ (accessed on 9 September 2018).
- Needham, T. Visual Complex Analysis; Oxford University Press: Oxford, UK, 1998. [Google Scholar]
- Fletcher, R. Practical Methods of Optimization; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Stargate Consortium. The Stargate Project. Available online: https://stargate.recherche.enac.fr/ (accessed on 9 September 2018).
- Guys, L.; Puechmorel, S.; Lapasset, L.; Amodei, L.; Maréchal, P. Génération automatique de trajectoires aériennes sans conflit à l’aide de fonctions biharmoniques. In Proceedings of the ROADEF 2012, 13ème Congrès Annuel de la Société Française de Recherche Opérationnelle et d’Aide à la Décision, Angers, France, 11–13 April 2012. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).