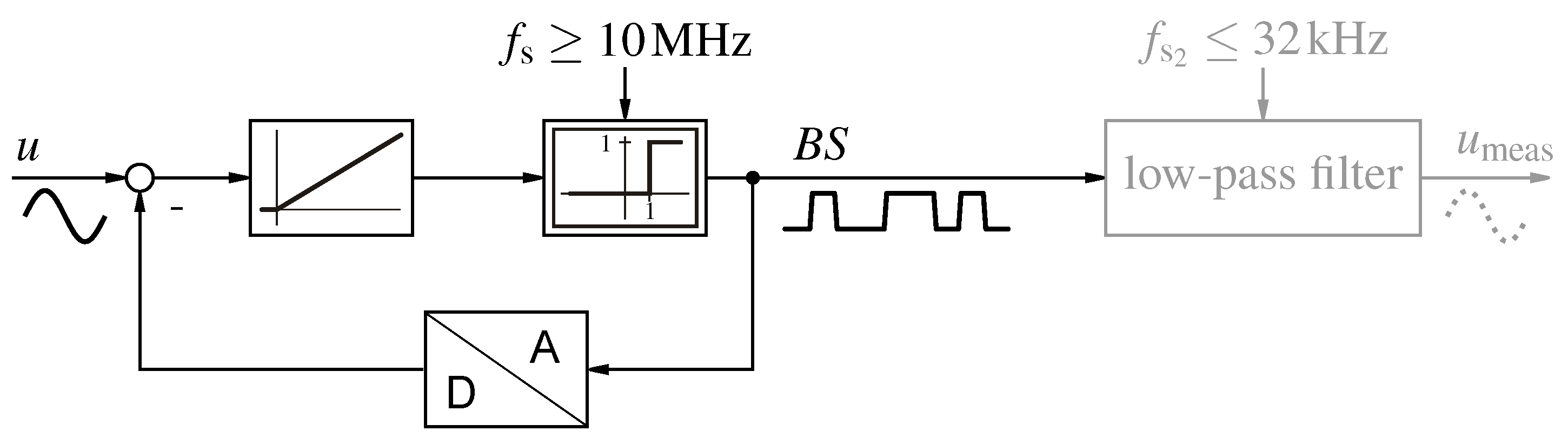
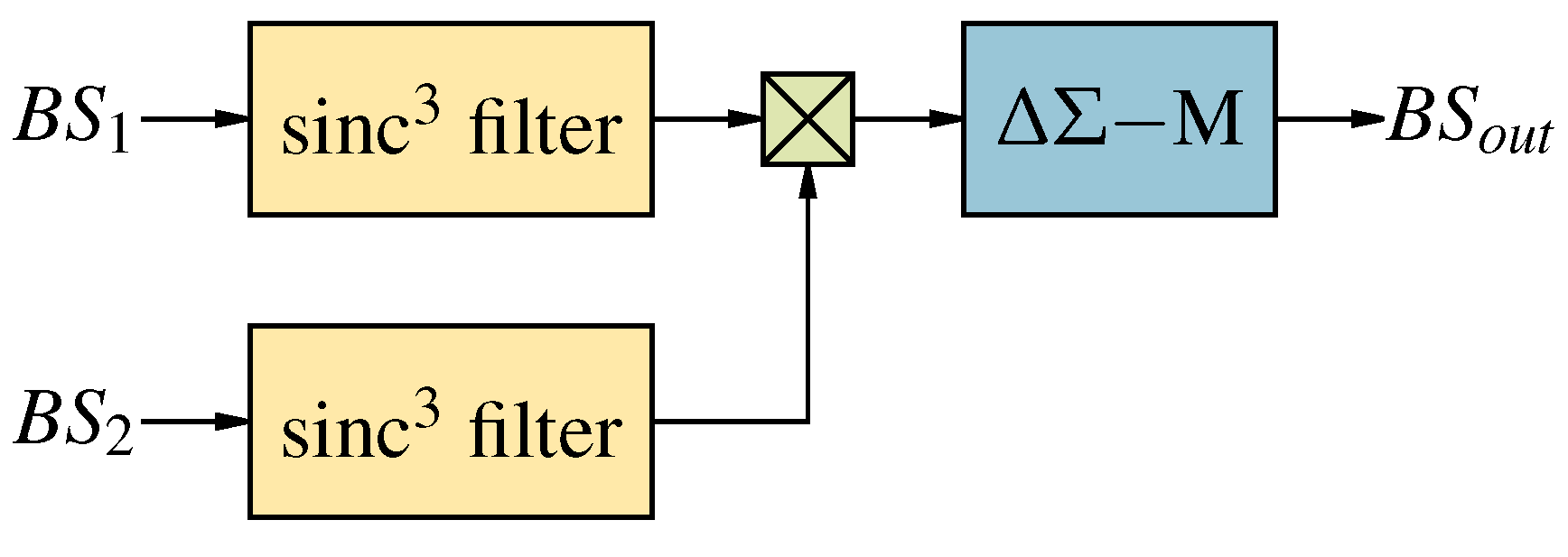
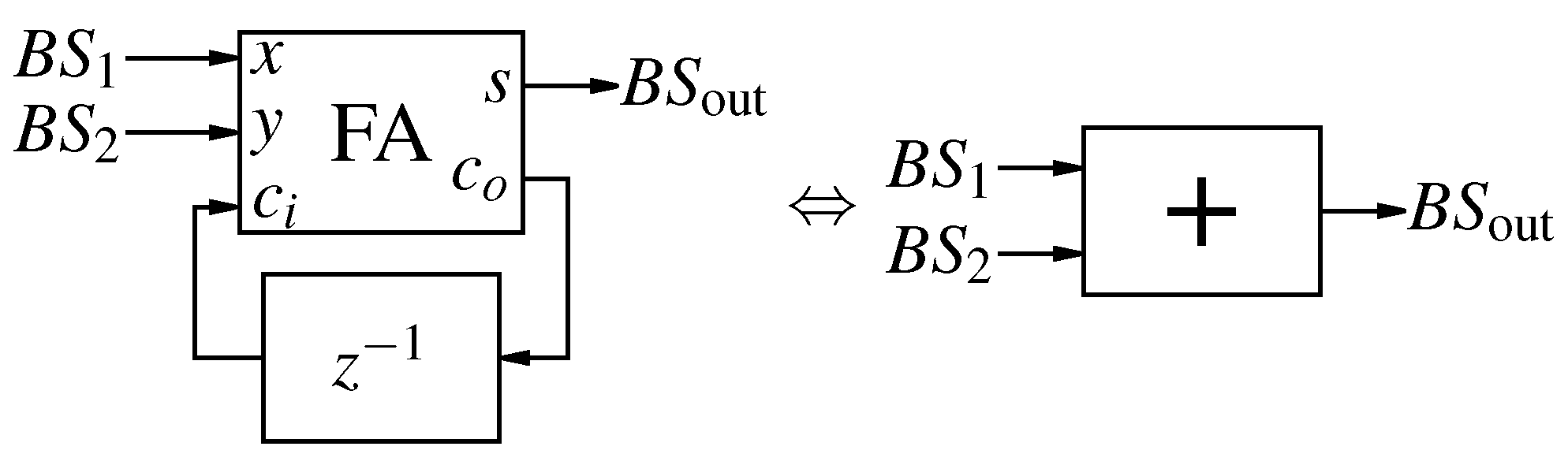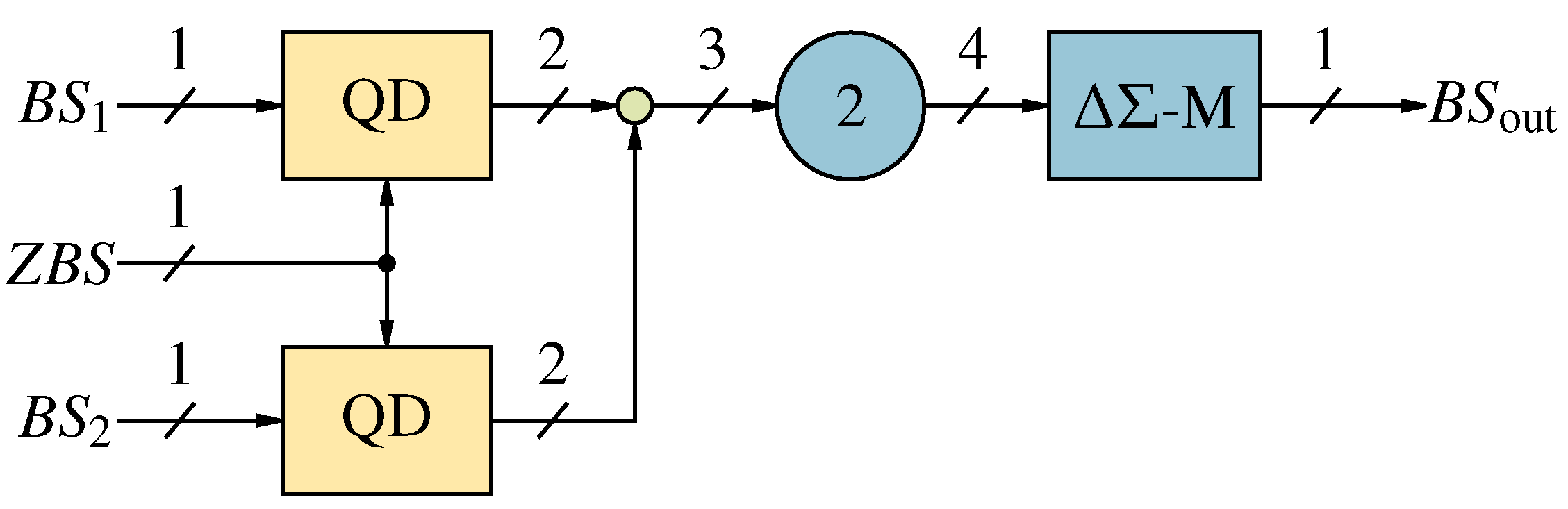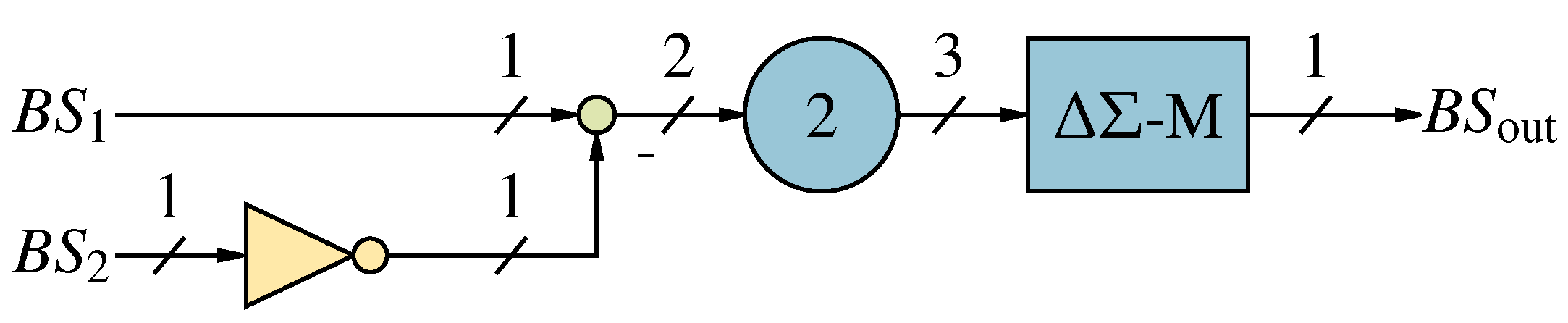Figure 1.
-M with lowpass filter in gray.
Figure 1.
-M with lowpass filter in gray.
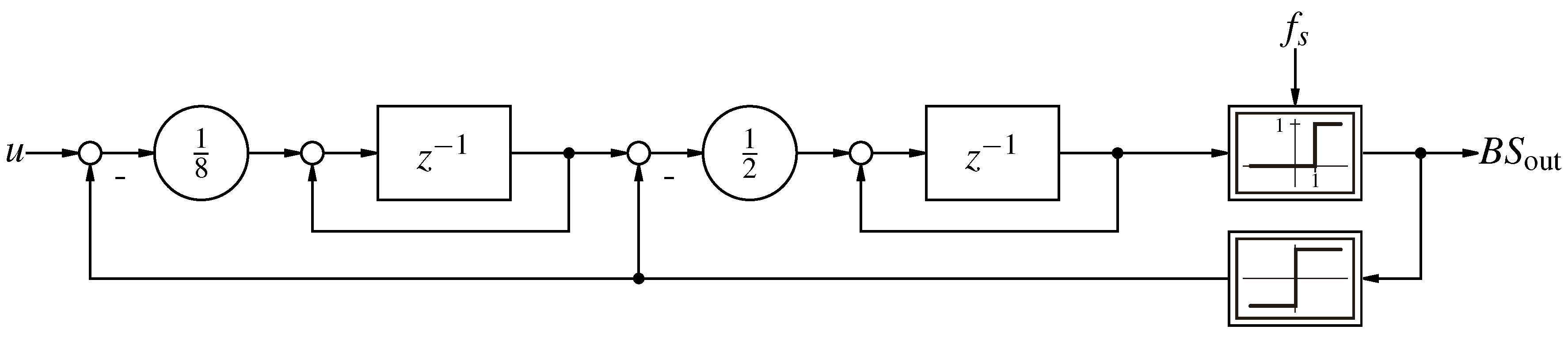
Figure 2.
Utilized second order
-M as proposed in [
16].
Figure 2.
Utilized second order
-M as proposed in [
16].
Figure 3.
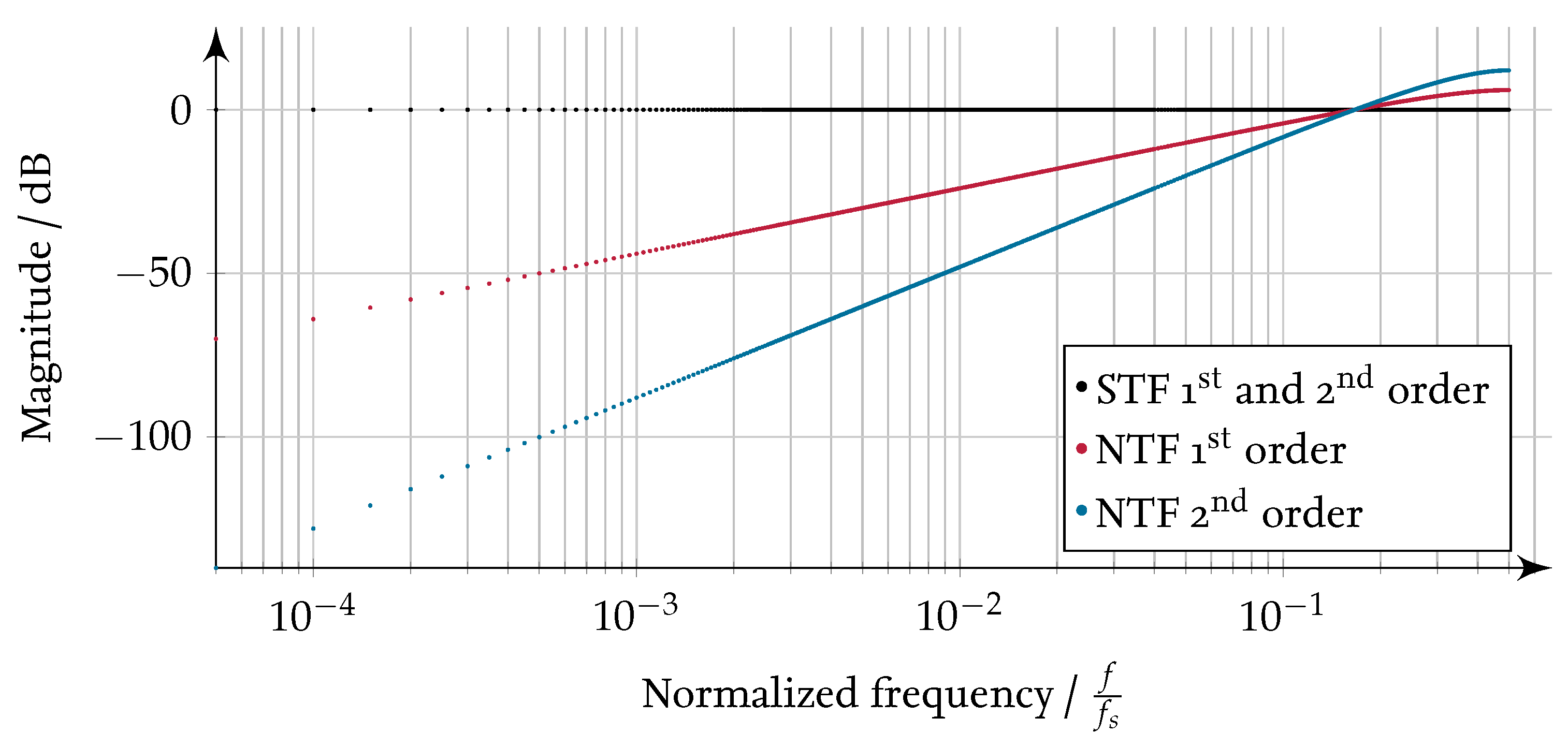
Magnitude of the signal transfer function (STF) and noise transfer function (NTF) of a first order and a second order
-M [
11] over the frequency related to the sampling frequency (
).
Figure 3.
Magnitude of the signal transfer function (STF) and noise transfer function (NTF) of a first order and a second order
-M [
11] over the frequency related to the sampling frequency (
).
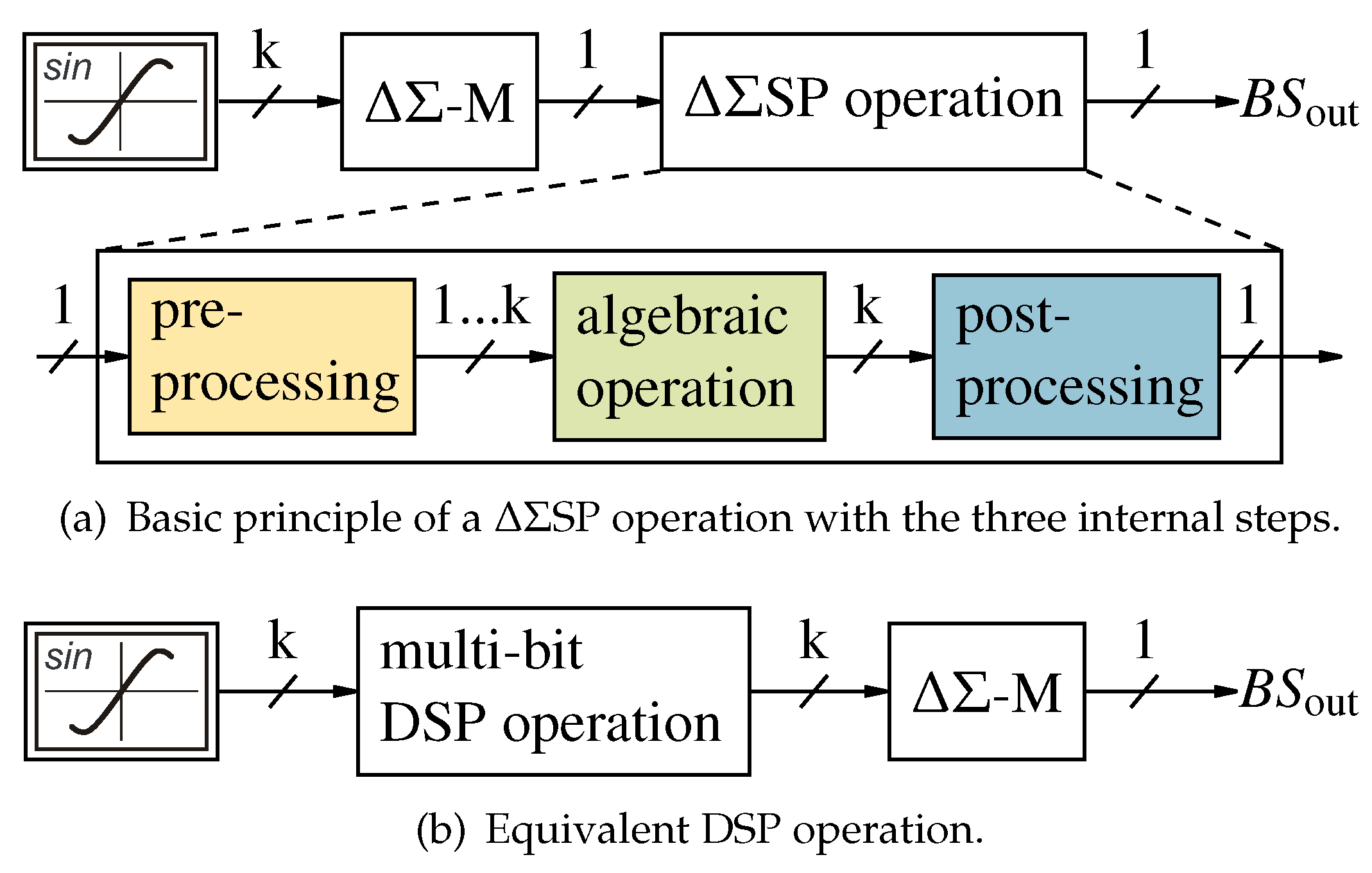
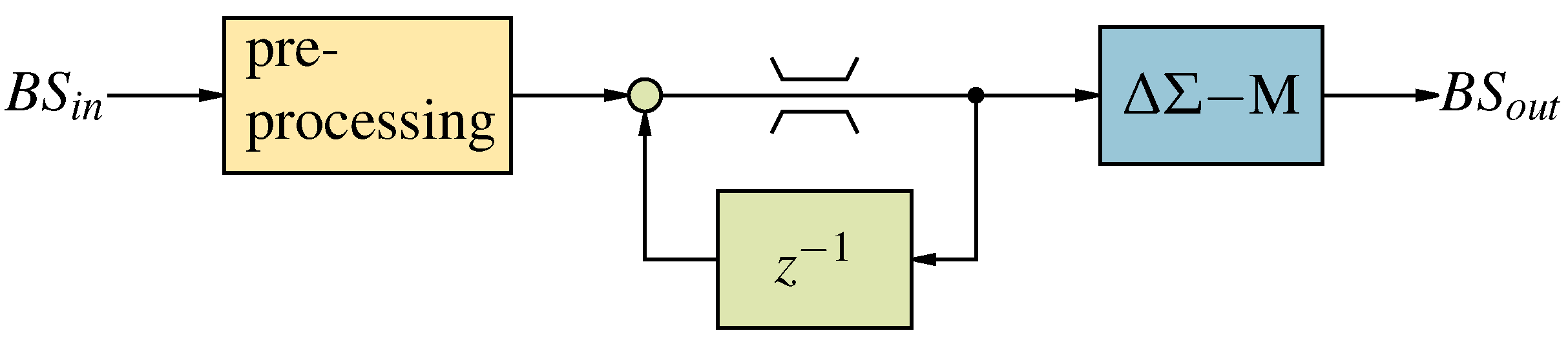
Figure 4.
Basic principle of a ΔΣSP operation with three internal steps and the equivalent DSP operation.
Figure 4.
Basic principle of a ΔΣSP operation with three internal steps and the equivalent DSP operation.
Figure 5.
Delta Adder in classical implementation [
18] and its corresponding symbol.
Figure 5.
Delta Adder in classical implementation [
18] and its corresponding symbol.
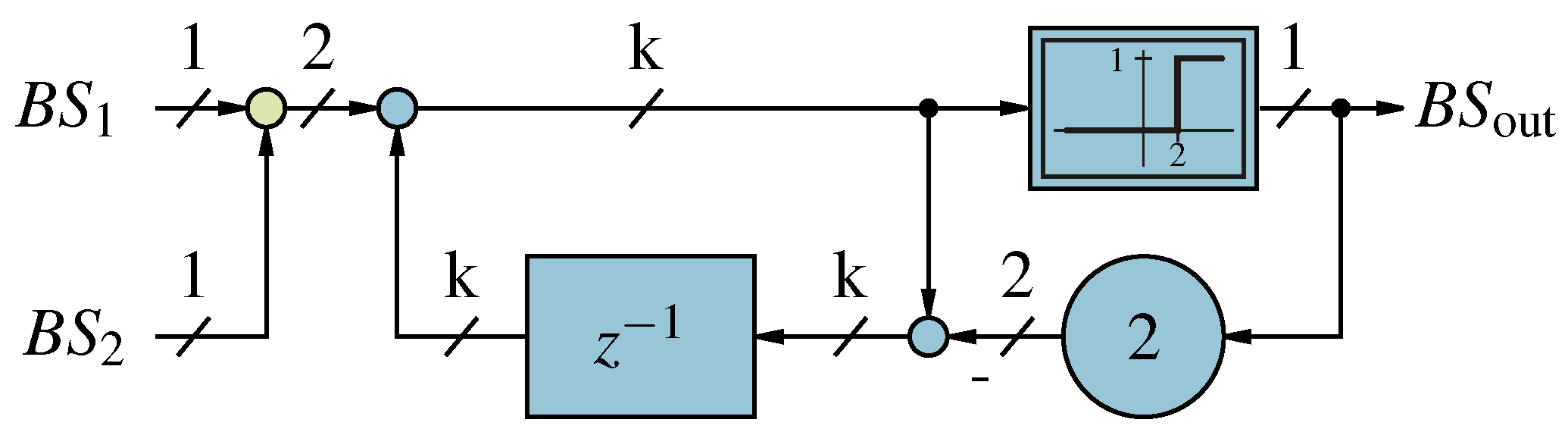
Figure 6.
Equivalent control scheme for Delta Adder [
11].
Figure 6.
Equivalent control scheme for Delta Adder [
11].
Figure 7.
Scaling based on Delta Adder, where
is the i
th bit from the MSB [
18].
Figure 7.
Scaling based on Delta Adder, where
is the i
th bit from the MSB [
18].
Figure 8.
Addition of two bit-streams using bit-stream modification with detailed description of the block .
Figure 8.
Addition of two bit-streams using bit-stream modification with detailed description of the block .
Figure 9.
Control system for adding a fixed value to a bit-stream.
Figure 9.
Control system for adding a fixed value to a bit-stream.
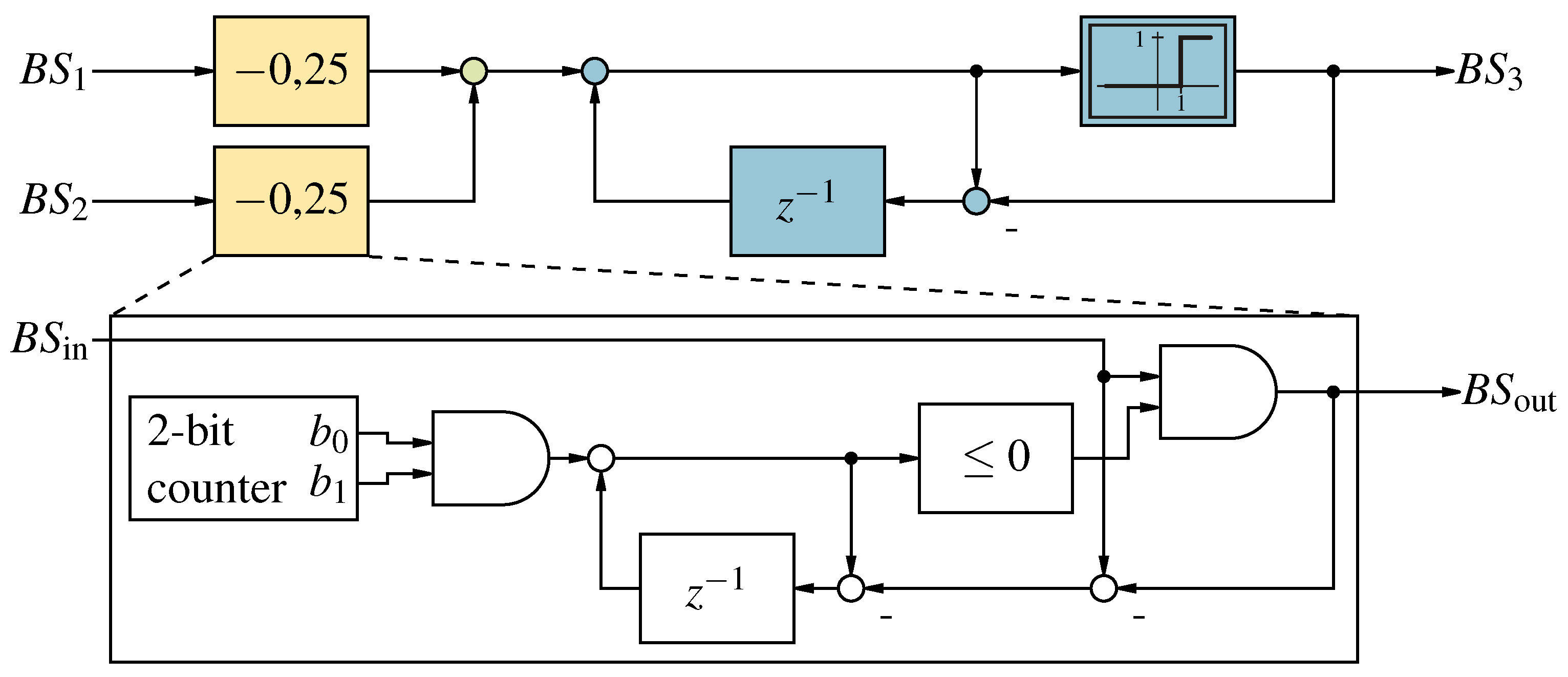
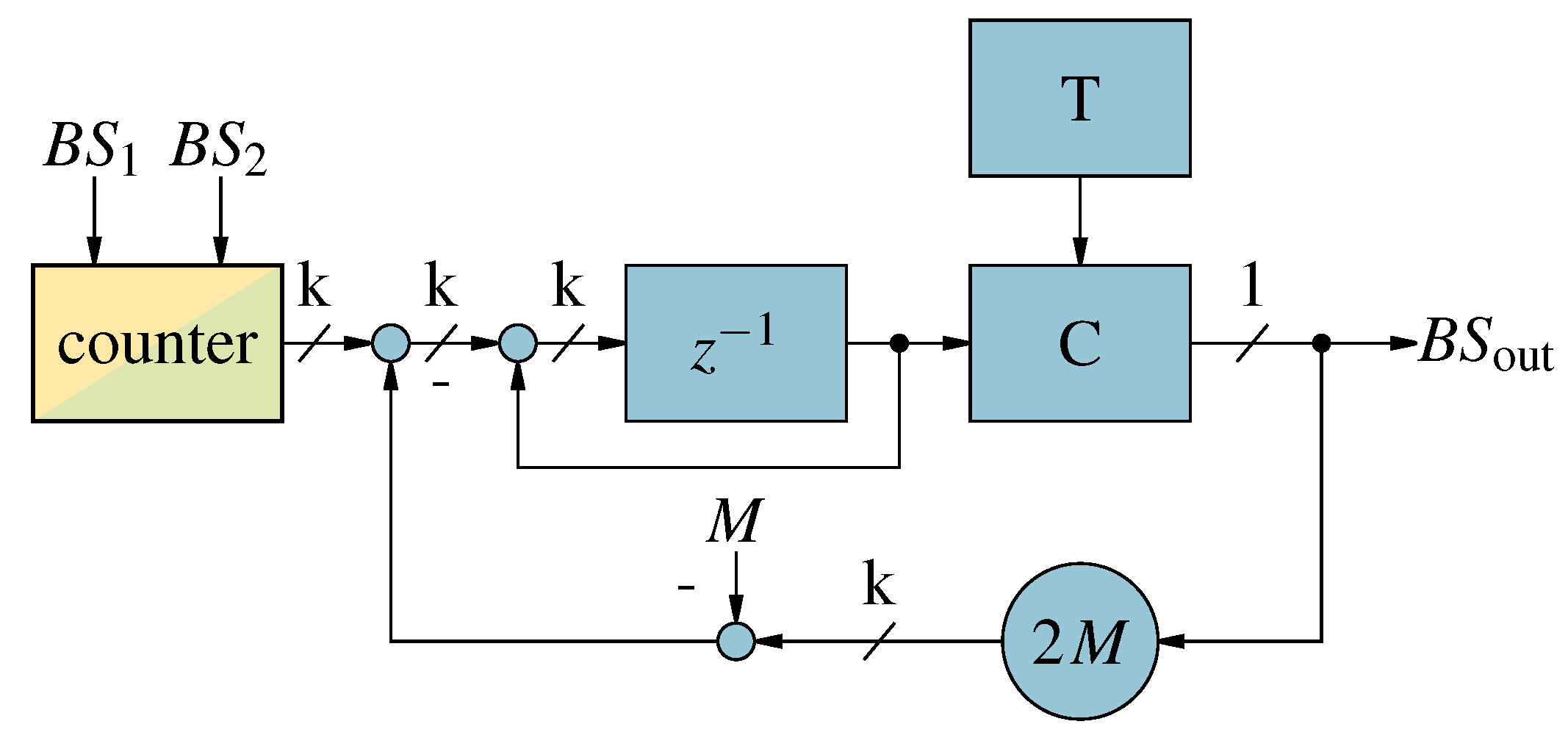
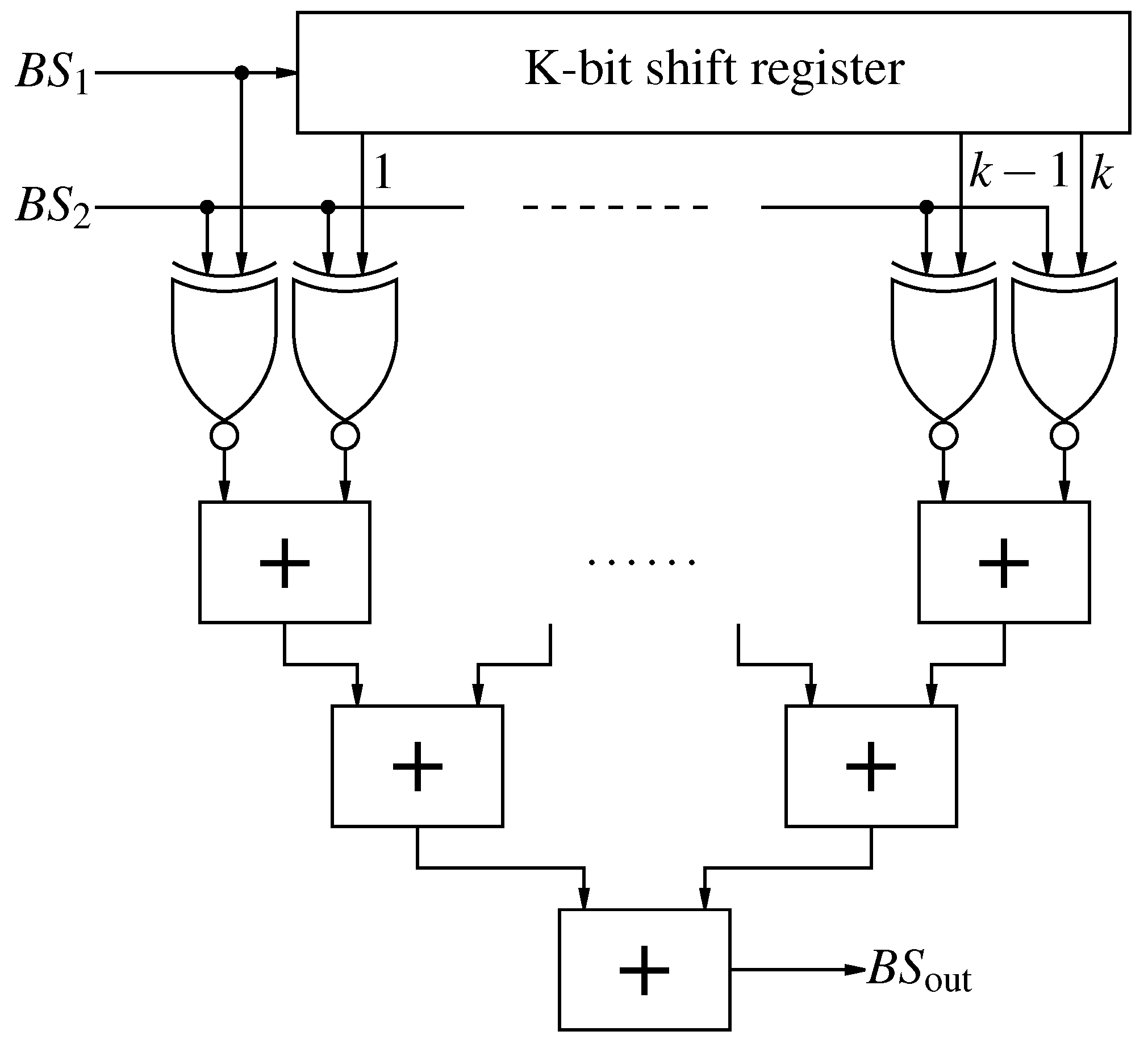
Figure 10.
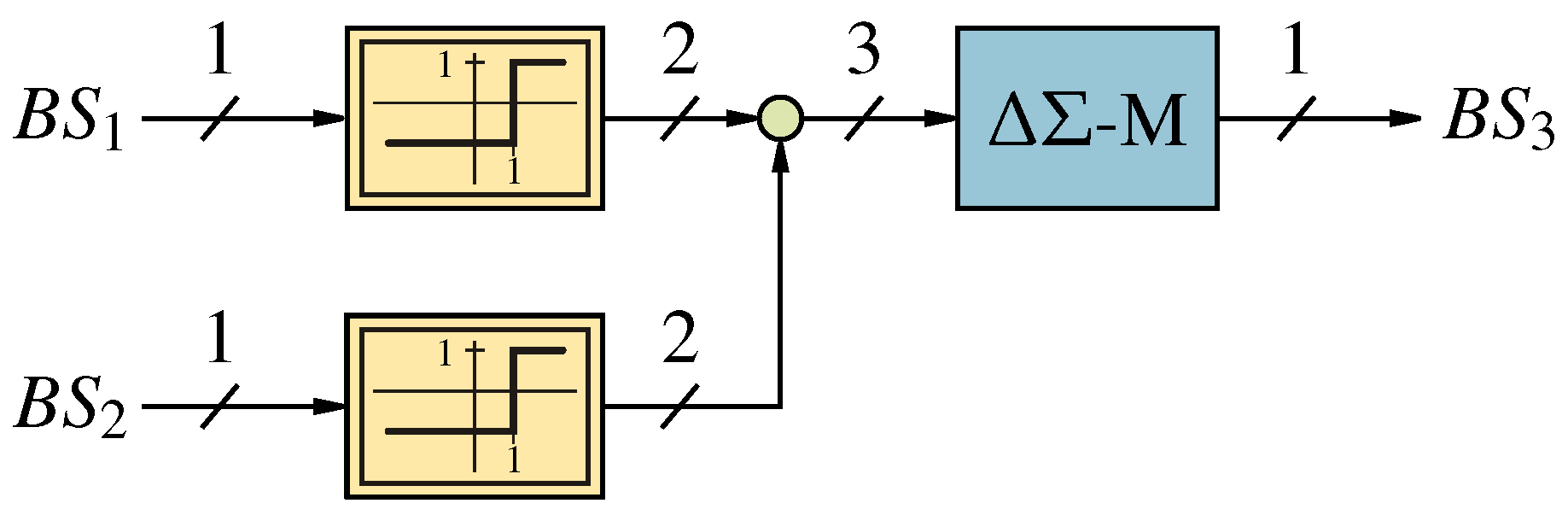
First order Counter Based addition of two bit-streams.
Figure 10.
First order Counter Based addition of two bit-streams.
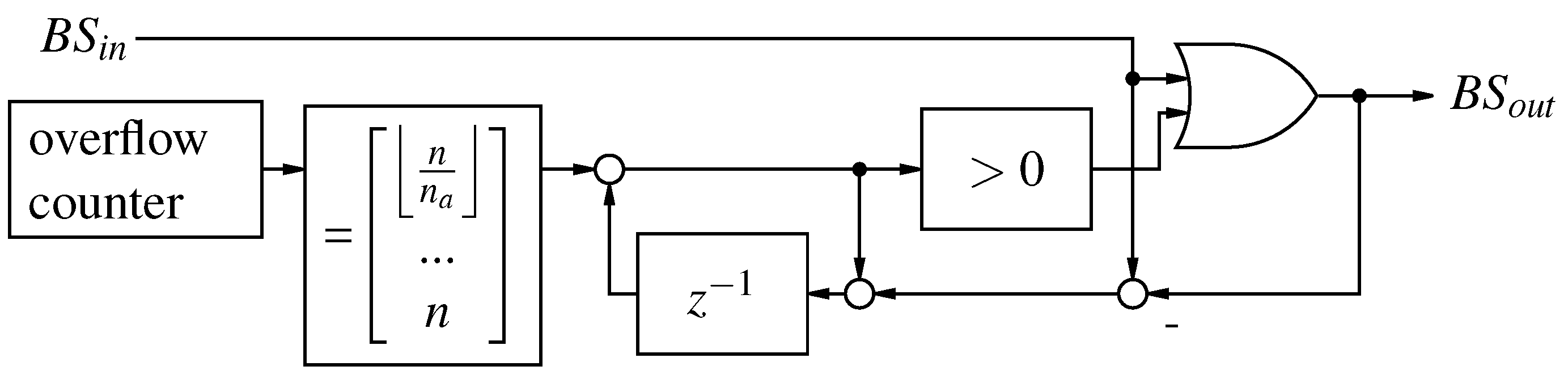
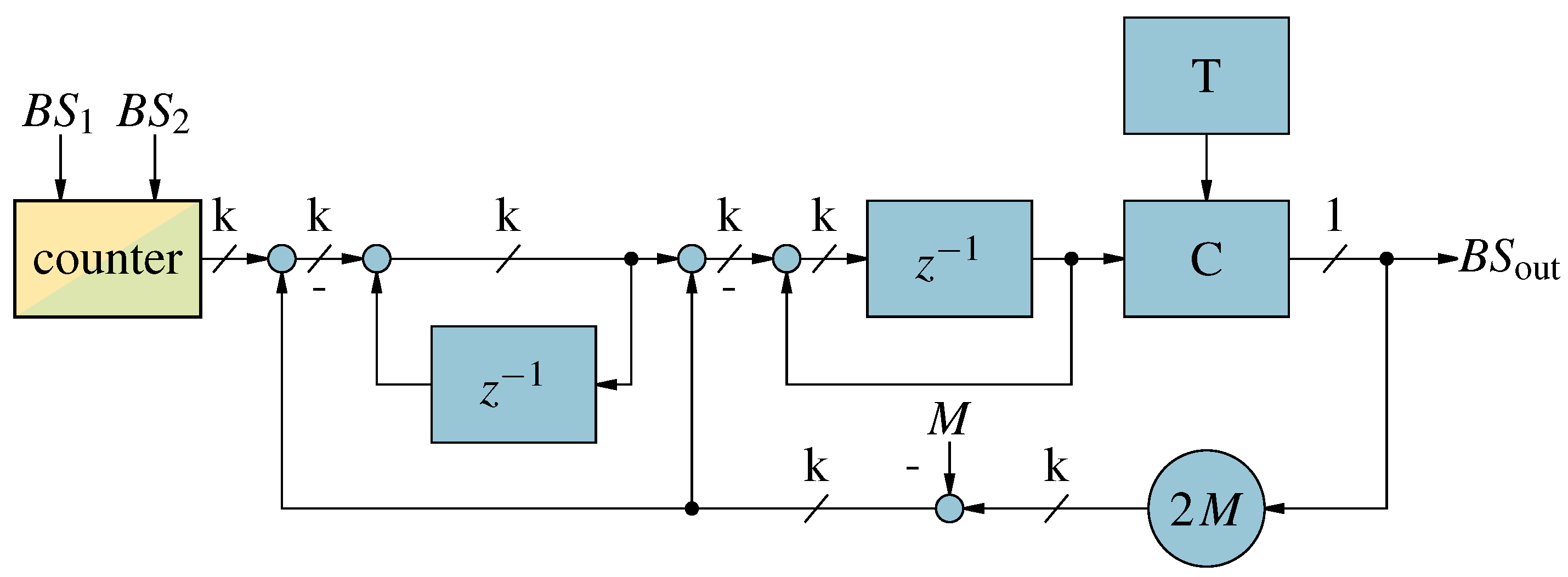
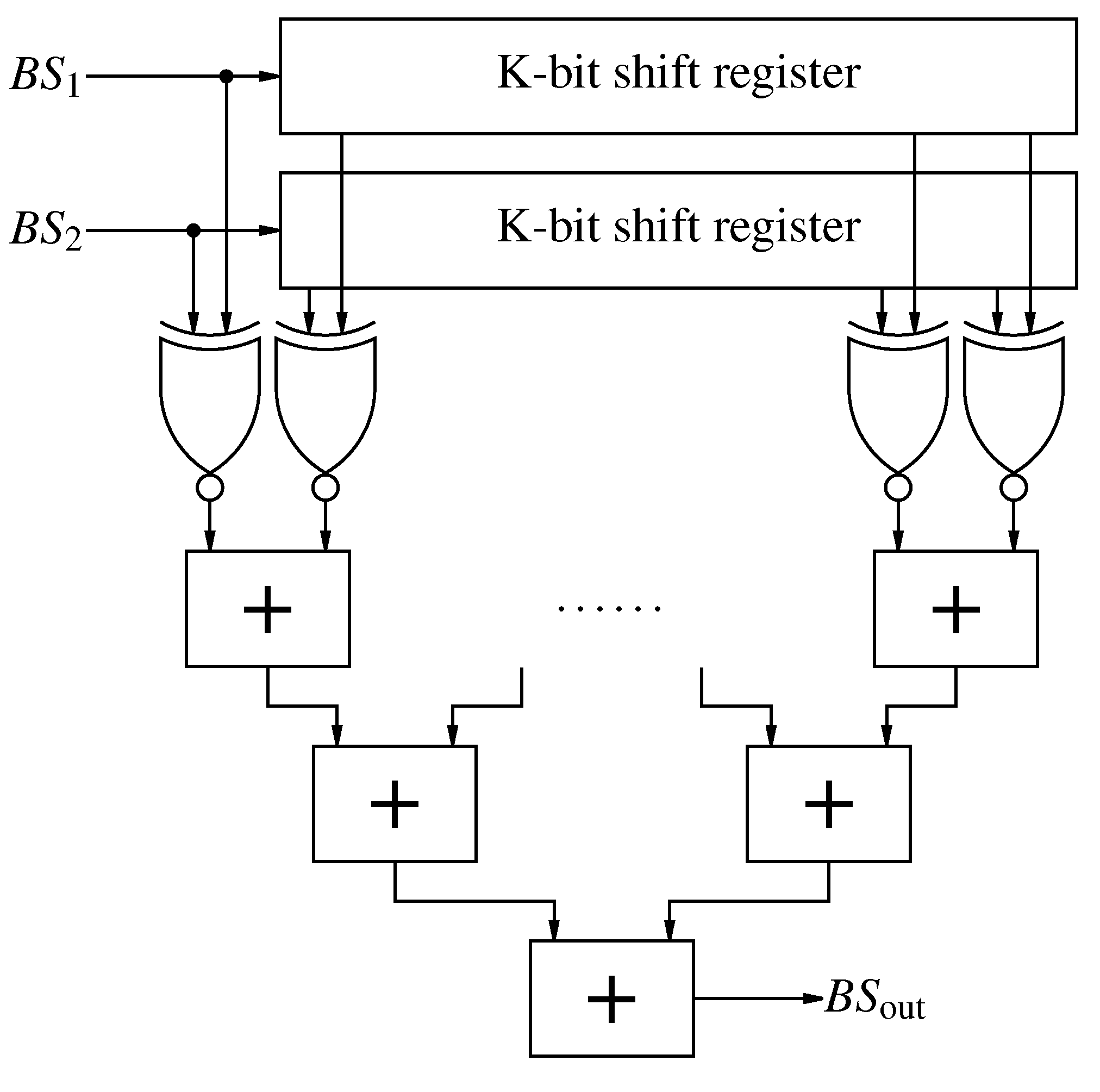
Figure 11.
Second order Counter Based addition of two bit-streams.
Figure 11.
Second order Counter Based addition of two bit-streams.
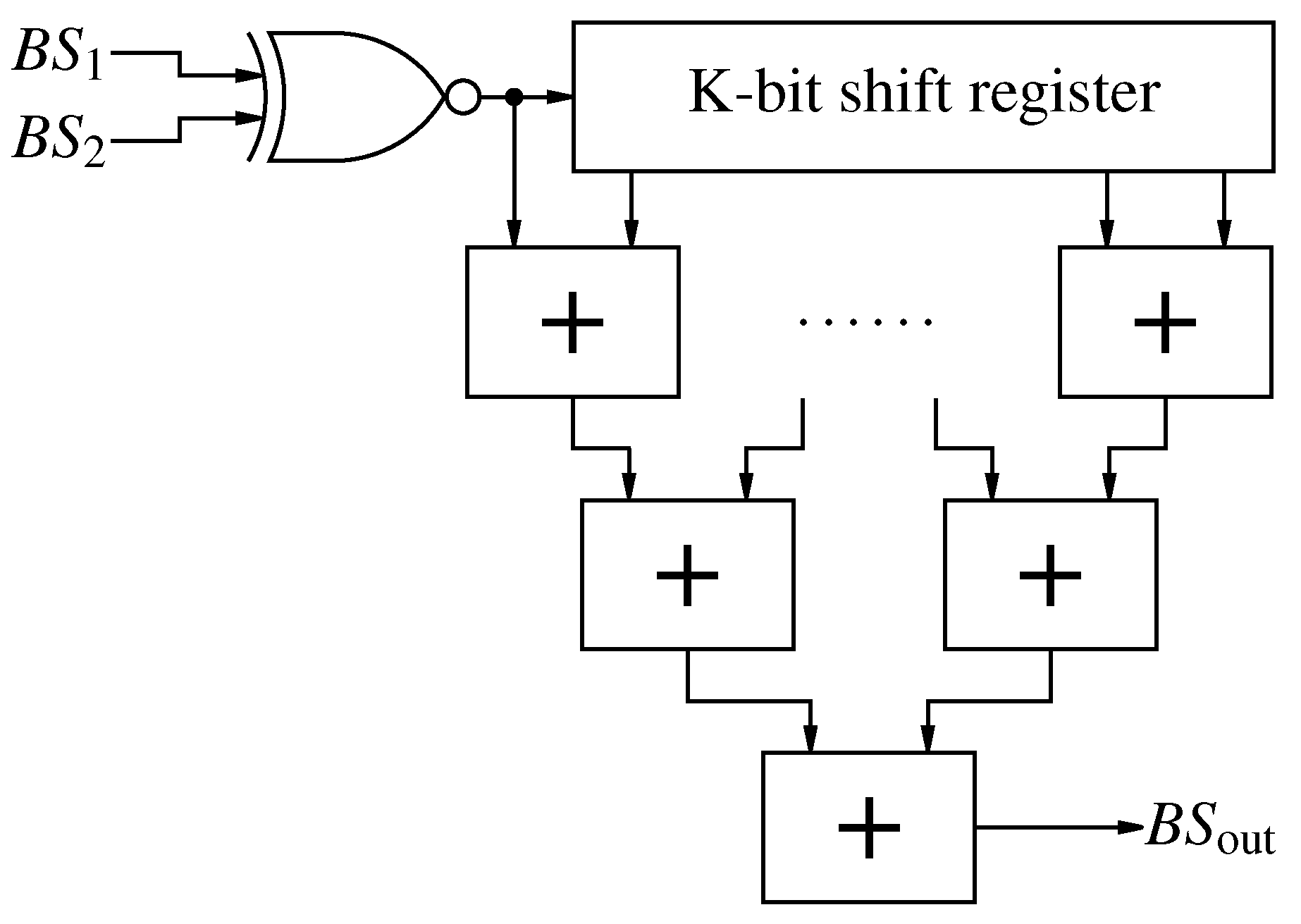
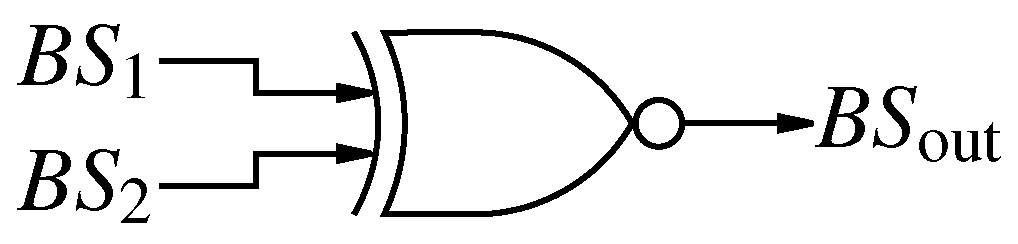
Figure 12.
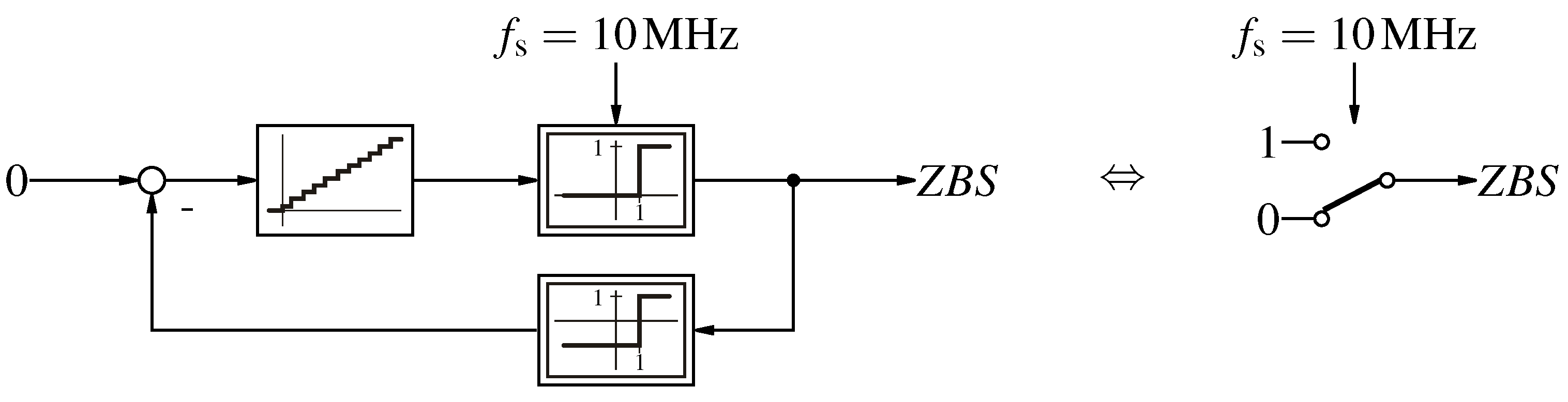
Zero bit-stream generator based on a first order -M and a simplified implementation.
Figure 12.
Zero bit-stream generator based on a first order -M and a simplified implementation.
Figure 13.
The SP operation addition performed with Quanta Decoding.
Figure 13.
The SP operation addition performed with Quanta Decoding.
Figure 14.
The SP operation addition performed with Advanced Quanta Decoding.
Figure 14.
The SP operation addition performed with Advanced Quanta Decoding.
Figure 15.
Fundamental algebraic operation Bipolar Interpretation.
Figure 15.
Fundamental algebraic operation Bipolar Interpretation.
Figure 16.
The SP operation addition operated with Bipolar Interpretation.
Figure 16.
The SP operation addition operated with Bipolar Interpretation.
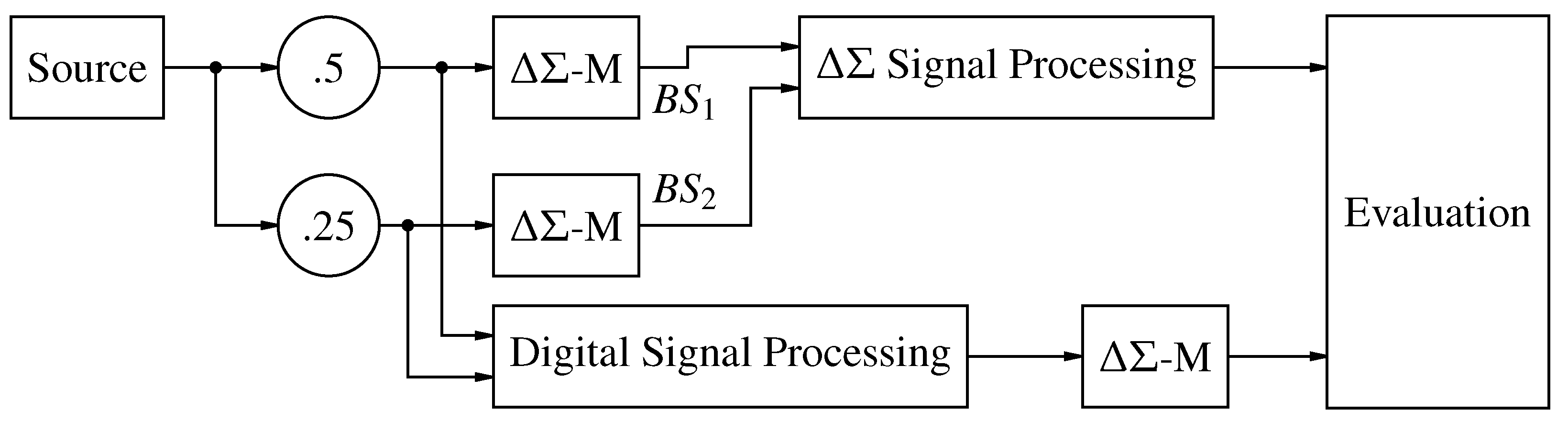
Figure 17.
Test bench for evaluating linear SP.
Figure 17.
Test bench for evaluating linear SP.
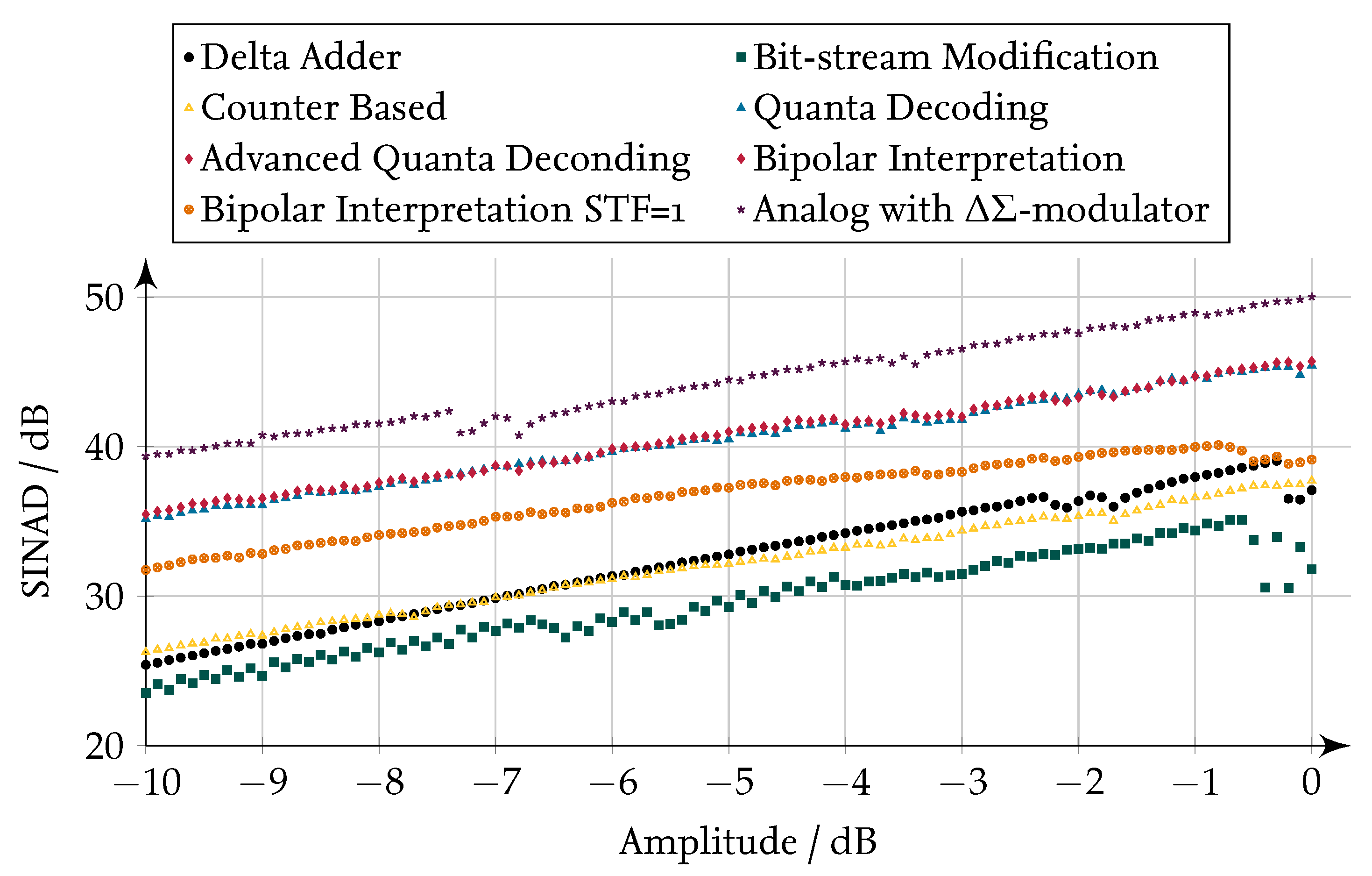
Figure 18.
Resulting SINAD after the linear operation add with different SP implementations for a sine wave excitation with different magnitudes.
Figure 18.
Resulting SINAD after the linear operation add with different SP implementations for a sine wave excitation with different magnitudes.
Figure 19.
Generalized linear operation integration in SP.
Figure 19.
Generalized linear operation integration in SP.
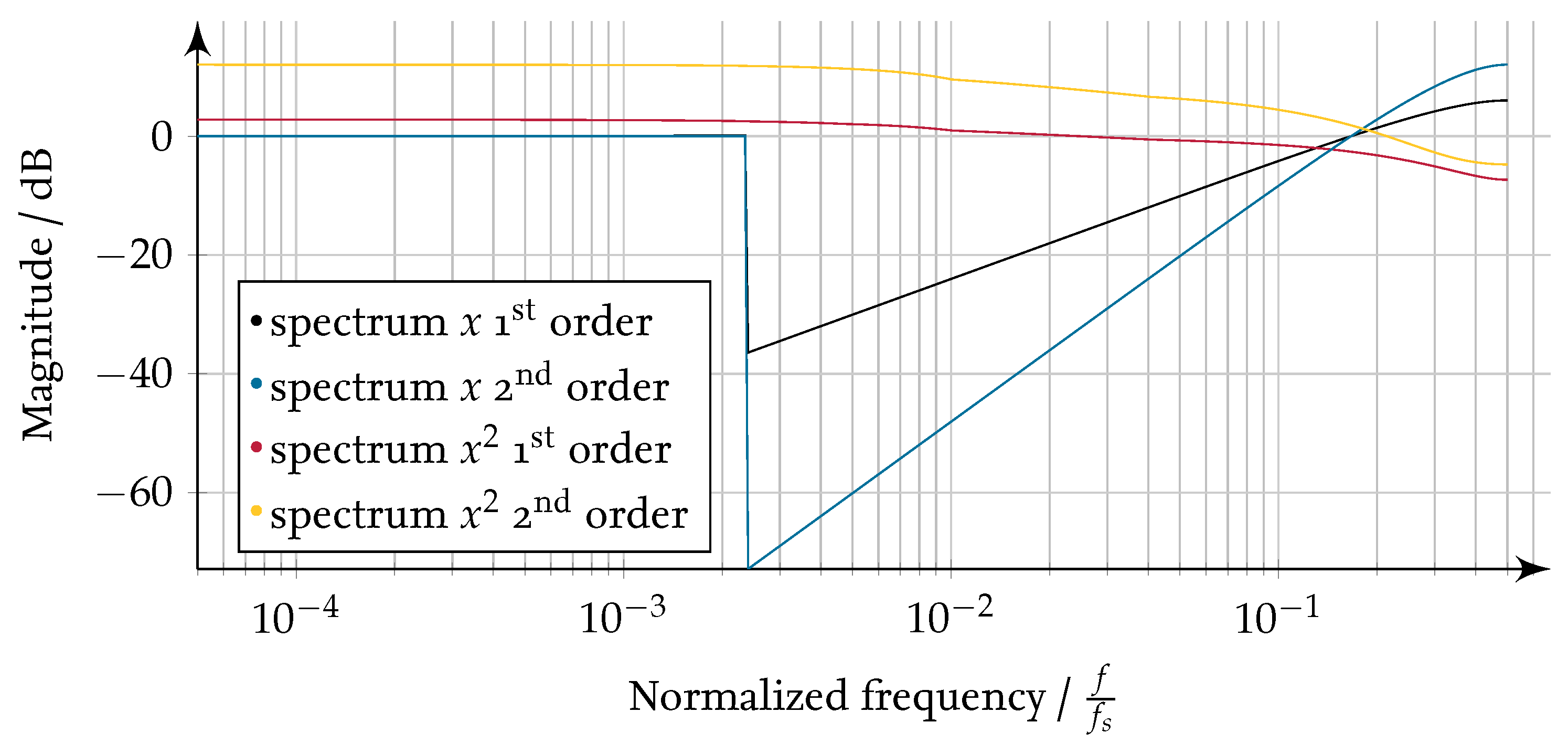
Figure 20.
Output spectra of a first and a second order -Ms and of the signals squared in time domain.
Figure 20.
Output spectra of a first and a second order -Ms and of the signals squared in time domain.
Figure 21.
Multiplication of two bit-streams based on Delta Adder [
29].
Figure 21.
Multiplication of two bit-streams based on Delta Adder [
29].
Figure 22.
Modified multiplication of two bit-streams based on Delta Adder.
Figure 22.
Modified multiplication of two bit-streams based on Delta Adder.
Figure 23.
Modified multiplication of two bit-streams based on Delta Adder with simpler implementation.
Figure 23.
Modified multiplication of two bit-streams based on Delta Adder with simpler implementation.
Figure 24.
Multiplication of two bit-streams using logic operations.
Figure 24.
Multiplication of two bit-streams using logic operations.
Figure 25.
Generalized nonlinear SP operation based an short sinc filters and DSP.
Figure 25.
Generalized nonlinear SP operation based an short sinc filters and DSP.
Figure 26.
Multiplication of two bit-streams using sinc filters and DSP operations.
Figure 26.
Multiplication of two bit-streams using sinc filters and DSP operations.
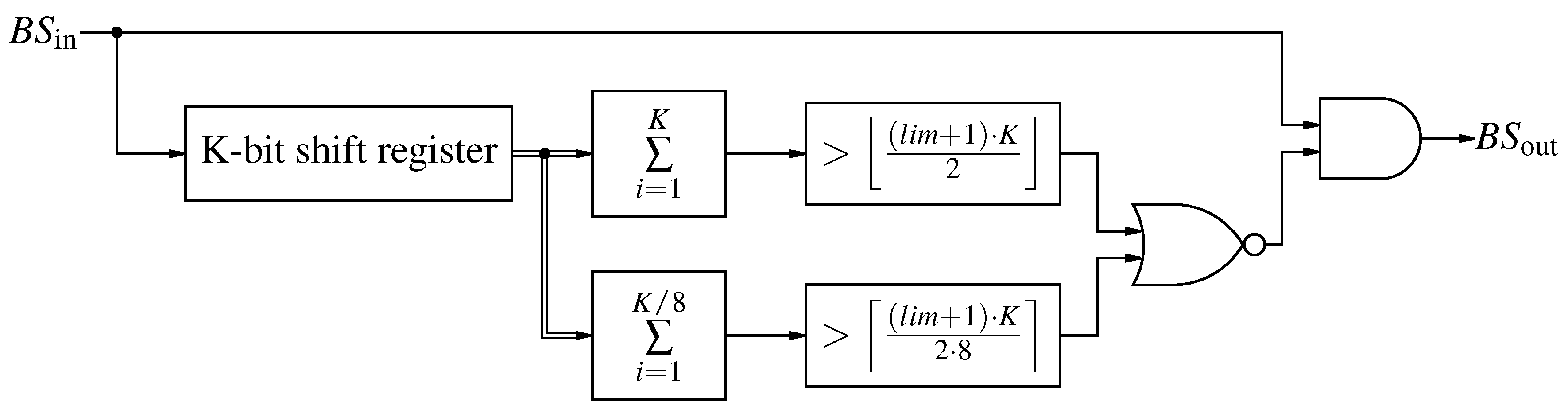
Figure 27.
Limiting the upper value of a bit-stream using delay taps for averaging.
Figure 27.
Limiting the upper value of a bit-stream using delay taps for averaging.
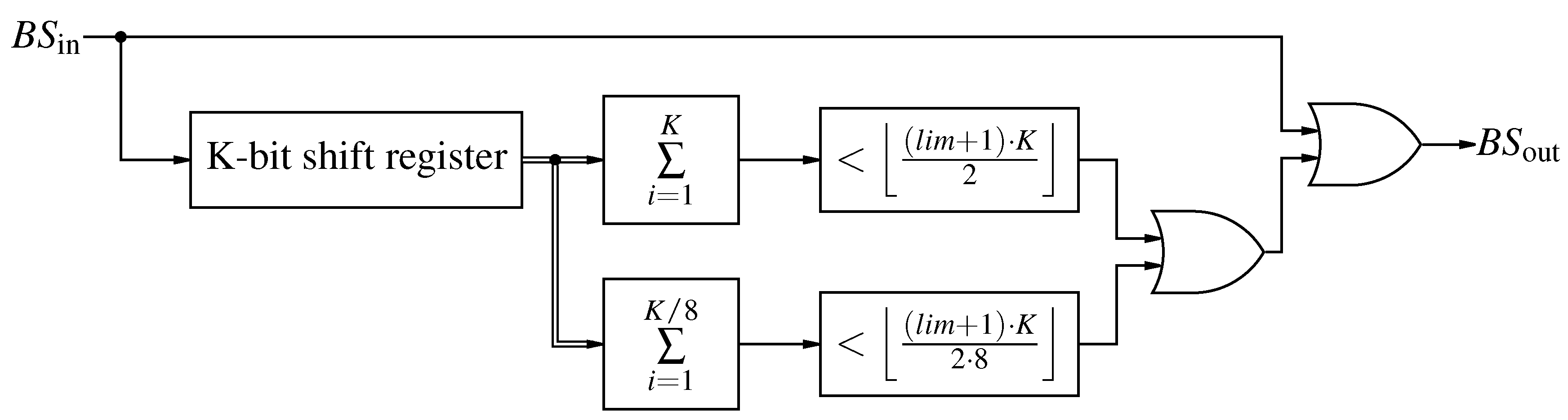
Figure 28.
Limiting the lower value of a bit-stream using delay taps for averaging.
Figure 28.
Limiting the lower value of a bit-stream using delay taps for averaging.
Figure 29.
Limiting the the value of a bit-stream utilizing DSP.
Figure 29.
Limiting the the value of a bit-stream utilizing DSP.
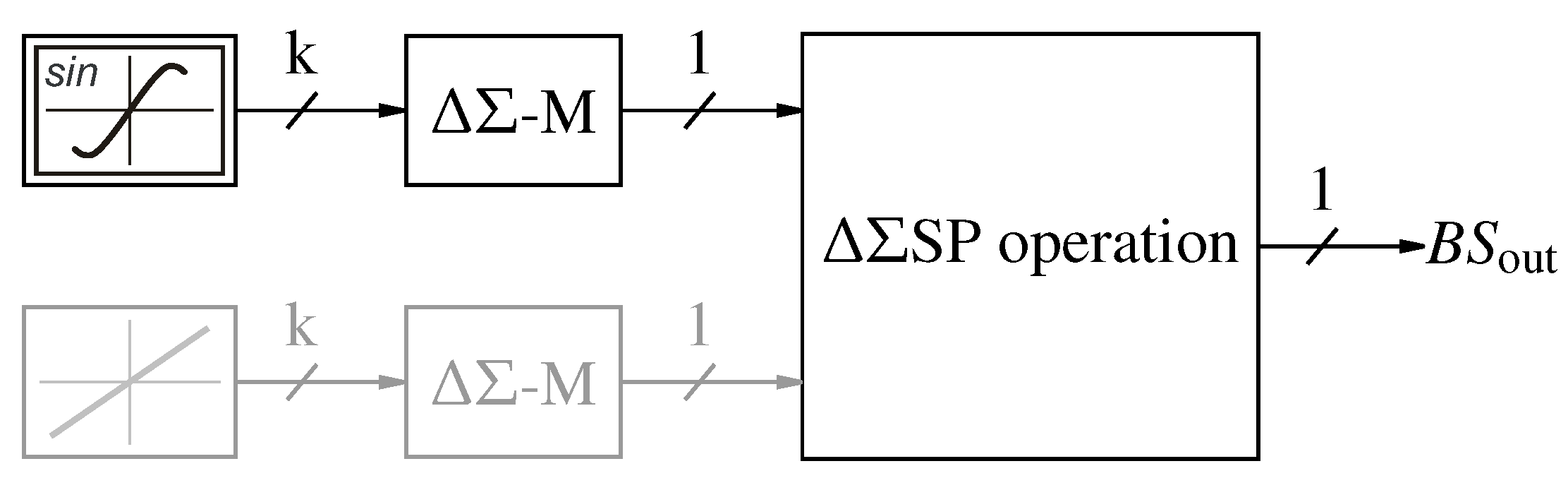
Figure 30.
Test bench for non linear functions with optional second input in gray.
Figure 30.
Test bench for non linear functions with optional second input in gray.
Figure 31.
Sinc filtered results for the multiplication with a decimation rate of 200.
Figure 31.
Sinc filtered results for the multiplication with a decimation rate of 200.
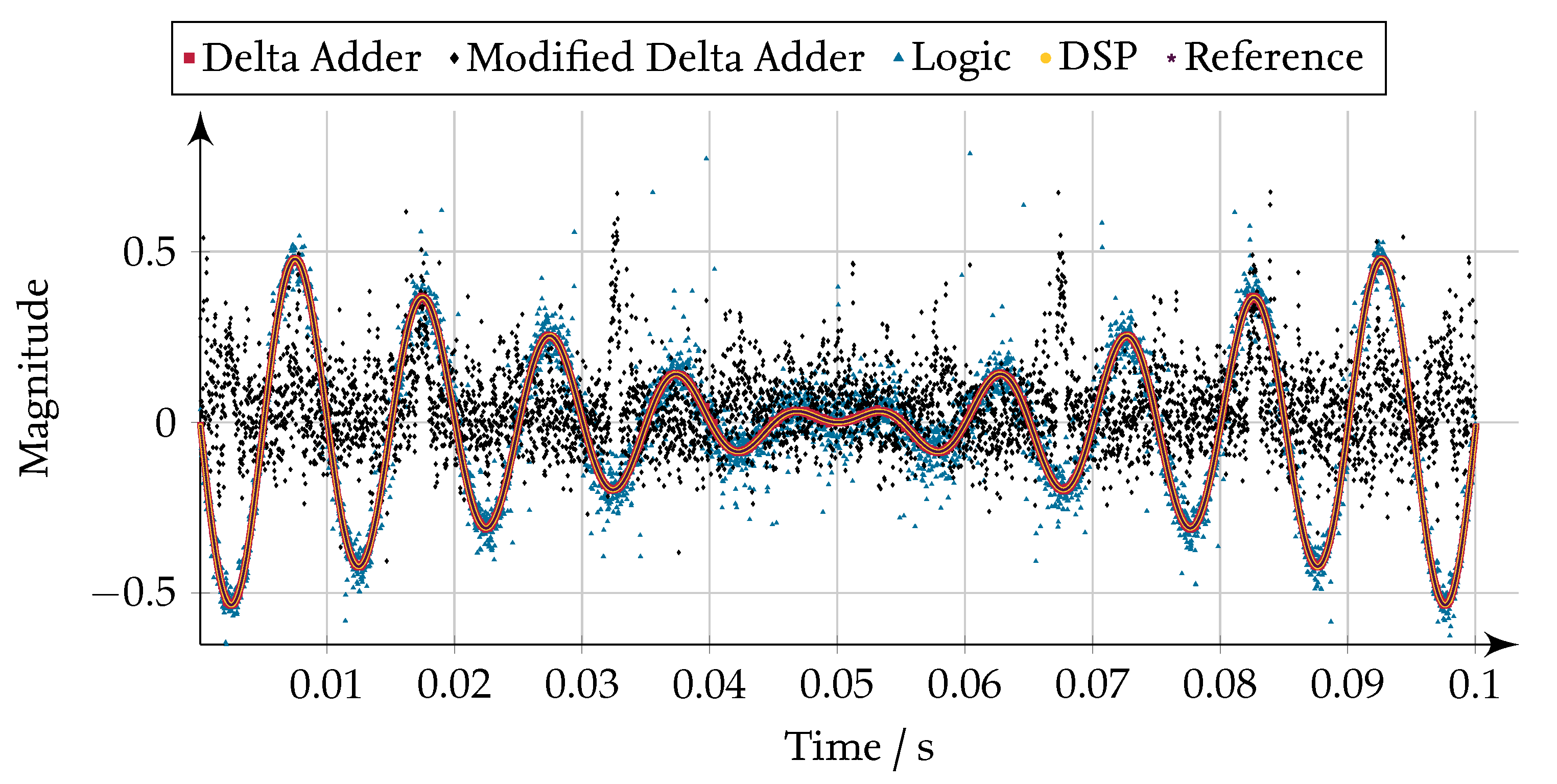
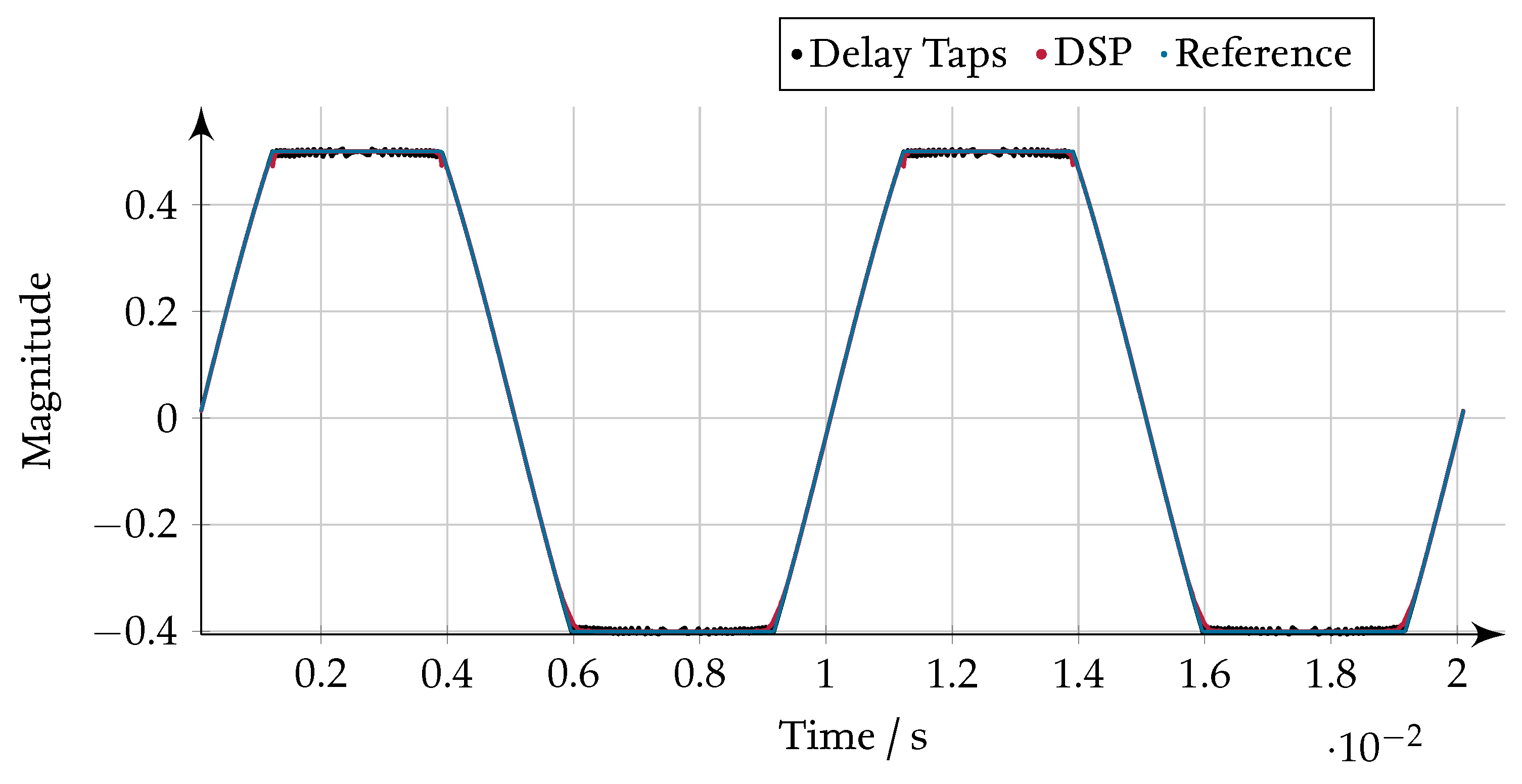
Figure 32.
Sinc filtered results for the limitation with a decimation rate of 20.
Figure 32.
Sinc filtered results for the limitation with a decimation rate of 20.
Table 1.
Truth table of quantizer utilized by counter based operations.
Table 1.
Truth table of quantizer utilized by counter based operations.
| C | C | T |
|---|
| <0 | 0 | T |
| >0 | 1 | T |
| 0 | T | NOT(T) |
Table 2.
Truth table of a bit-stream (BS) minus the ZBS resulting in the quanta decoded value (QD).
Table 2.
Truth table of a bit-stream (BS) minus the ZBS resulting in the quanta decoded value (QD).
Table 3.
Logic table of two bit-streams (BS) and their “zero bit-streams” (ZBS), the quanta decoded value (QD) and the subtraction and addition of the quanta decoded values and direct operated bit-streams. In the highlighted rows, the “zero bit-streams” are equal.
Table 3.
Logic table of two bit-streams (BS) and their “zero bit-streams” (ZBS), the quanta decoded value (QD) and the subtraction and addition of the quanta decoded values and direct operated bit-streams. In the highlighted rows, the “zero bit-streams” are equal.
| ZBS | BS | ZBS | BS | QD | QD | − | + |
|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1 | 0 | 1 | −1 | −1 | 1 | 1 |
| 0 | 0 | 1 | 0 | 0 | −1 | 1 | 0 | −1 | 0 |
| 0 | 0 | 1 | 1 | 0 | 0 | 0 | −1 | 0 | 1 |
| 0 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 1 |
| 0 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 2 | 2 |
| 0 | 1 | 1 | 0 | 1 | −1 | 2 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 2 |
| 1 | 0 | 0 | 0 | −1 | 0 | −1 | 0 | −1 | 0 |
| 1 | 0 | 0 | 1 | −1 | 1 | −2 | −1 | 0 | 1 |
| 1 | 0 | 1 | 0 | −1 | −1 | 0 | 0 | −2 | 0 |
| 1 | 0 | 1 | 1 | −1 | 0 | −1 | −1 | −1 | 1 |
| 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 1 | 0 | 1 | −1 | 0 | 1 | 2 |
| 1 | 1 | 1 | 0 | 0 | −1 | 1 | 1 | −1 | 1 |
| 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 2 |
Table 4.
Phase delay in clock cycles of linear operation classes.
Table 4.
Phase delay in clock cycles of linear operation classes.
| Operation Class | Delay |
|---|
| Delta Adder | 0 |
| Bit-stream Modification | 1 |
| Quanta Decoding | 9 |
| Advanced Quanta Decoding | 9 |
| Bipolar Interpretation | 9 |
| Bipolar Interpretation | 0 |
| Counter Based | 2 |
Table 5.
Resource consumption of the implementations for addition on a FPGA.
Table 5.
Resource consumption of the implementations for addition on a FPGA.
| Implementation | Logic Cells |
|---|
| Delta Adder | 6 |
| Bit-stream Modification | 29 |
| Quanta Decoding | 31 |
| Advanced Quanta Decoding | 28 |
| Bipolar Interpretation | 28 |
| Bipolar Interpretation | 31 |
| Counter Based | 17 |
Table 6.
Simulation parameters.
Table 6.
Simulation parameters.
| Parameter | Value |
|---|
| Sampling frequency | 10 |
| Simulation time | 0.10 s |
| Setup time | 50 |
| Sinusoidal amplitude | 0.75 |
| Sinusoidal frequency | 100 |
| Ramp start value | −0.75 |
| Ramp slope | 15 s−1 |
| DSP sinc filter length | 4 |
| Evaluation sinc filter length | 128 |
Table 7.
Variance and delay of the arithmetic operation multiplication (second input, if different).
Table 7.
Variance and delay of the arithmetic operation multiplication (second input, if different).
| Implementation | Variance | Delay |
|---|
| Delta Adder | 5.2934 × 10−6 | 17 (0) |
| Logic Operations | 3.4792 × 10−3 | 6 |
| DSP | 1.8948 × 10−7 | 12 |
Table 8.
Resource consumption of the implementations for multiplying on a FPGA.
Table 8.
Resource consumption of the implementations for multiplying on a FPGA.
| Implementation | Logic Cells | Multiplier (9 × 9) |
|---|
| Delta Adder | 318 | 0 |
| Logic Operations | 2 | 0 |
| DSP | 243 | 1 |
Table 9.
Variance and delay of the arithmetic operation limiting.
Table 9.
Variance and delay of the arithmetic operation limiting.
| Implementation | Variance | Delay |
|---|
| Delay Taps | 8.7516 × 10−6 | 1 |
| DSP | 1.3405 × 10−5 | 15 |
Table 10.
Resource consumption of the implementations for limiting on a FPGA.
Table 10.
Resource consumption of the implementations for limiting on a FPGA.
| Implementation | Logic cells |
|---|
| Delay Taps | 303 |
| DSP | 181 |