An Improved Differential Evolution Algorithm for Crop Planning in the Northeastern Region of Thailand
Abstract
1. Introduction
2. Literature Review
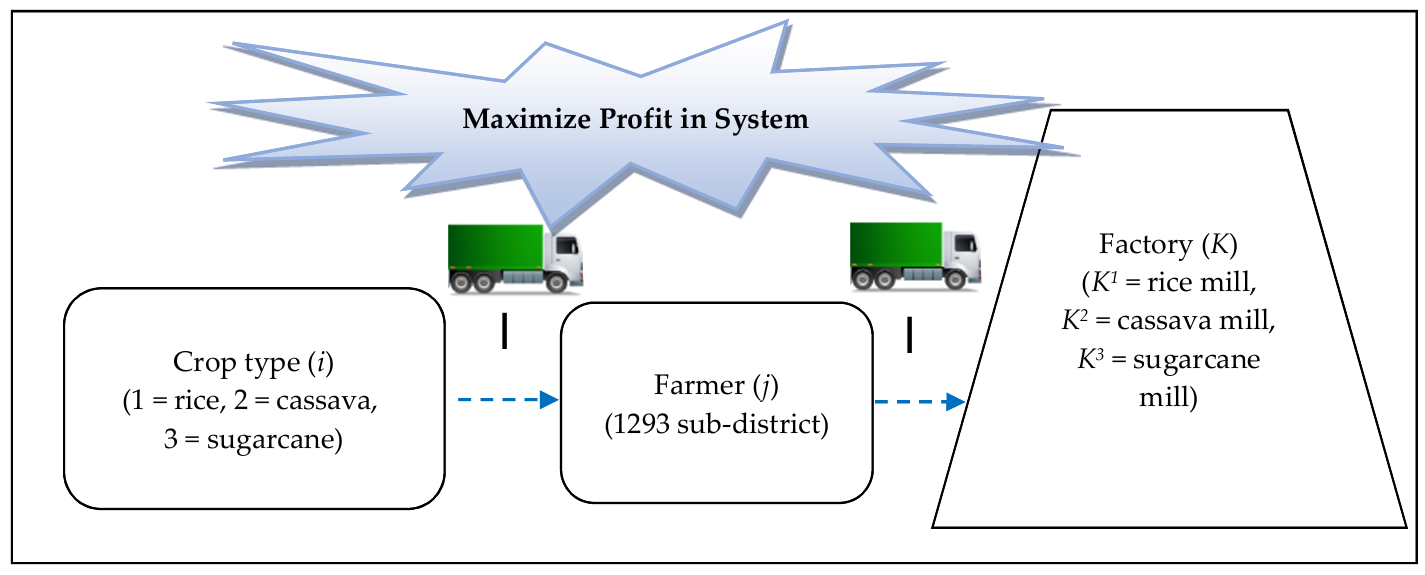
3. Mathematical Model for Crop Planning
3.1. Indices
| i | stands for crop type (1 = rice, 2 = cassava, 3 = sugarcane) |
| j | stands for planning area/famer (j = 1, 2, …, J) |
| K | stands for factory (K = K1, …, Ki, when K1 = rice mill, K2 = cassava mill, K3 = sugarcane mill) |
3.2. Parameters
| Pij | stands for crop price i planted by farmer j (Baht/Kilogram) |
| C1ij | stands for cost of planning i planted by farmer j (Baht/Rai) |
| Bij | stands for rate of crop yield i planted by farmer j (Ton/Rai) |
| Aj | stands for planning area in each district (Rai) |
| Djk | stands for distance from planning area j to factory k (kilometer) |
| C2i | stands for transportation costs of each crop i (Baht/Kilometer) |
| CK | stands for factory purchase capacity (Ton) |
| C3ij | stands for cost of crop cultivation i planted by farmer j (Baht/Rai) |
| Vj | stands for transportation capacity (Ton) |
| M | stands for maximum production capacity |
3.3. Decision Variables
3.4. Objective Function
3.5. Constraints
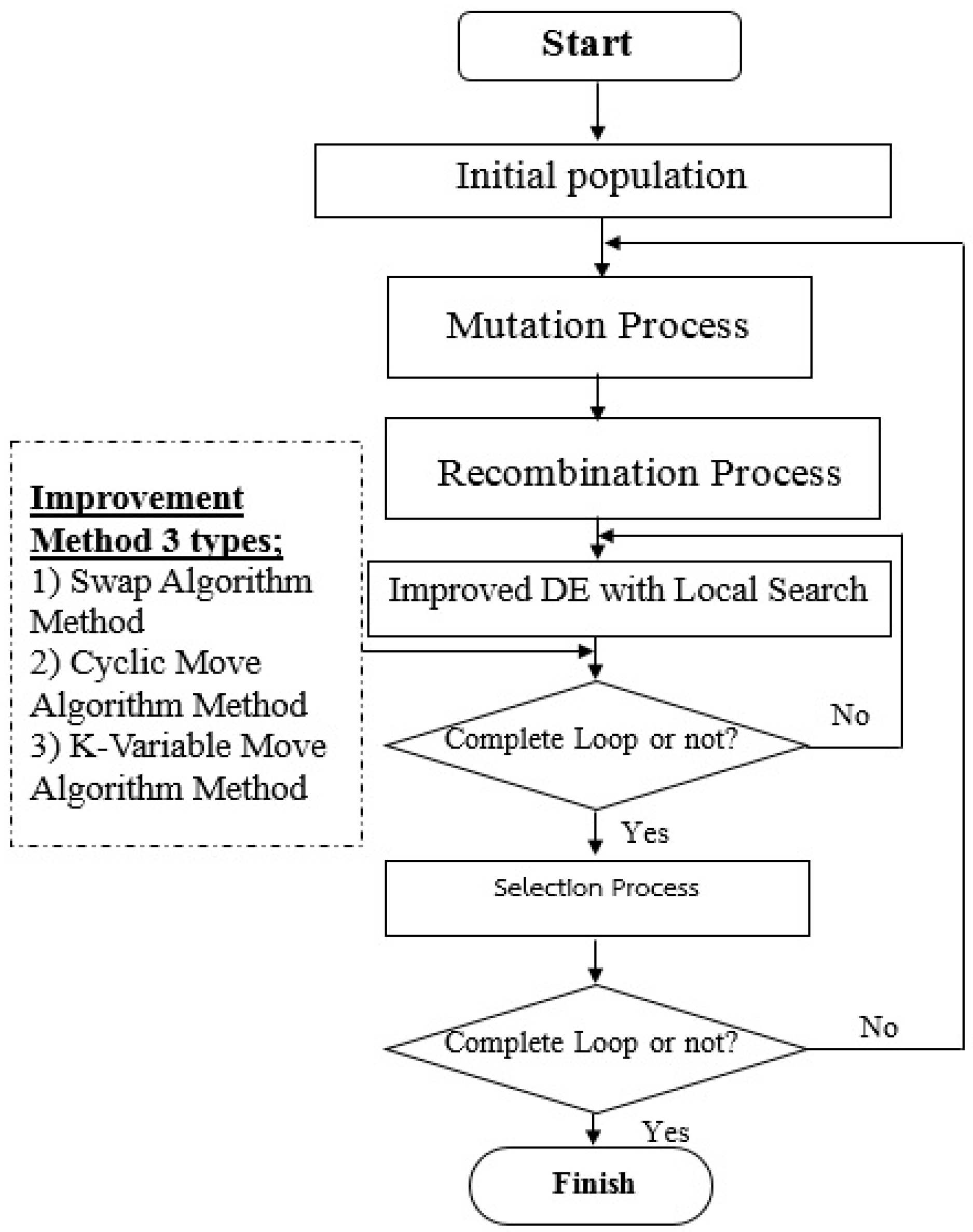
4. Original Differential Evolution Algorithm
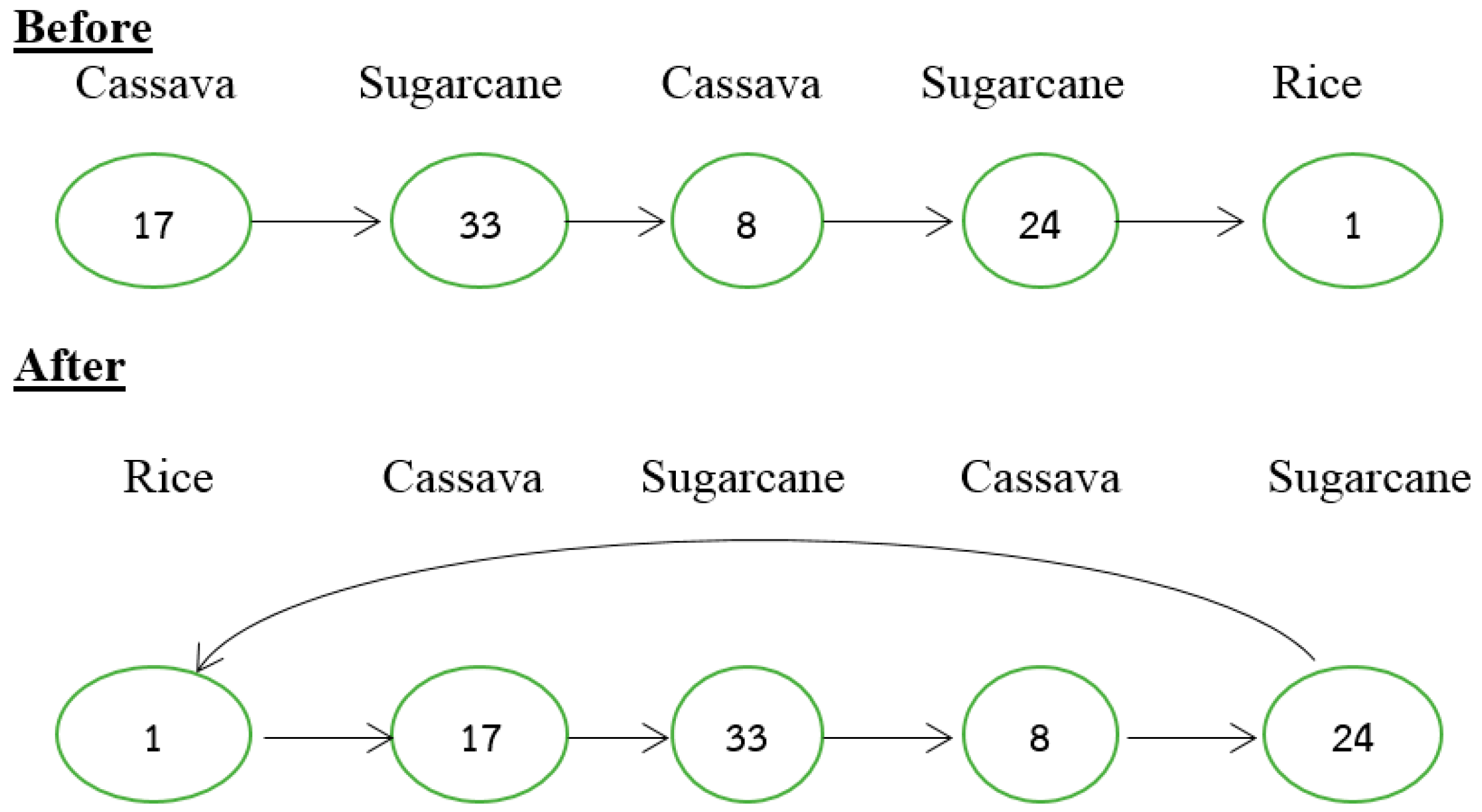
4.1. Initial Population
4.2. Decoding Method
- (1)
- Arrange the numbers in the vectors (value in position of each vector) in increasing order. For example, for Vector 1, the result of sorting is shown in Table 4.
- (2)
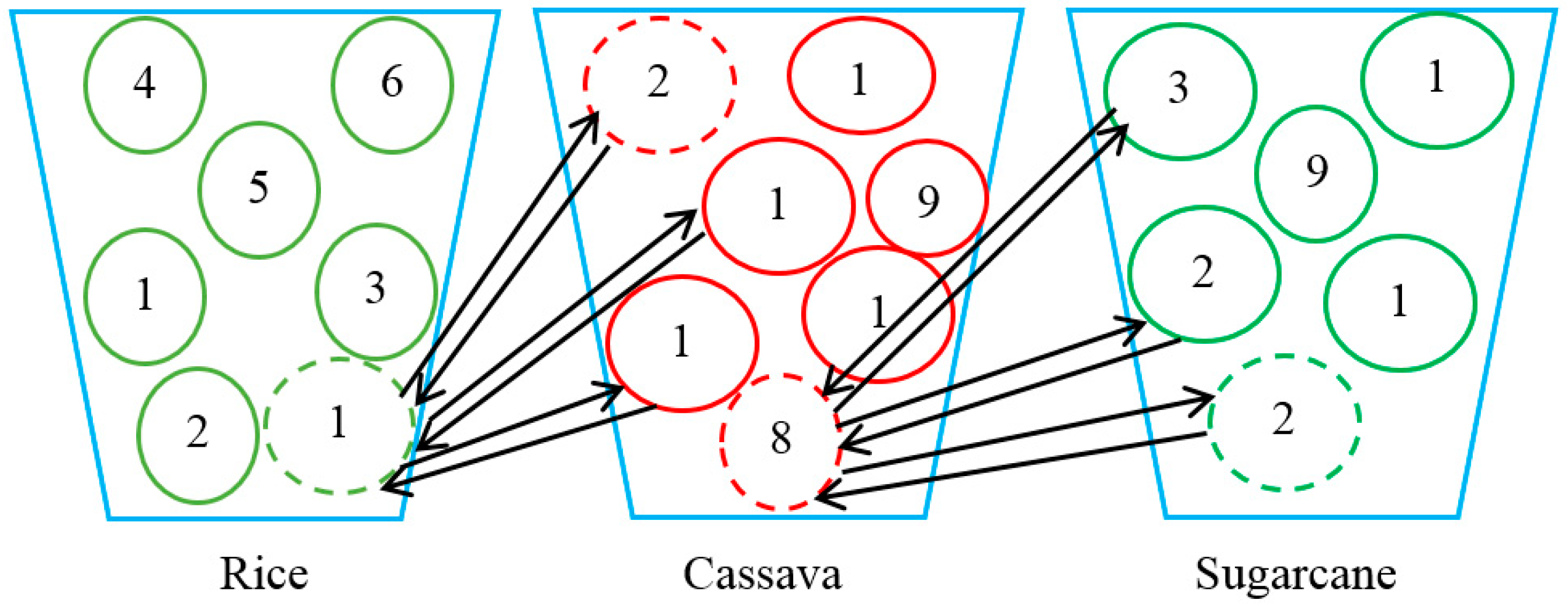
- Assign the type of plant to a field and assign the field to the factory. The roulette wheel idea was used to assign the plants to the field. The probability of each plant to be selected can be determined by any idea, such as: (1) equal probability (0.333 each); (2) average productivity rate, such as rice, sugarcane, and cassava having average productivity rates of 19, 17, and 23 tons/km2, with probabilities of 0.32, 0.29, and 0.39, respectively; (3) price per kilogram of the plants, for example, if the prices of rice, sugarcane, and cassava are 1000, 1200, and 900 baht per ton, the probability of each plant is 0.32, 0.39, and 0.29, respectively; (4) the ratio of factories that will take all the products. There is one rice mill, which has a capacity of 120 tons. There are two sugar mills, each of which has a capacity of 80 tons and, thus, a combined total capacity of 160 tons. There is one tapioca starch mill, which has a capacity of 90 tons. Therefore, each type of plant has a probability of 0.32, 0.43, and 0.25, respectively. During this research, we used the price per kilogram of the plants as the probability to select the plants to maximize the profits generated from the algorithm. Taken from the probability above (using price as the probability), a plant will be assigned to a field according to the value in the position of vector and that field will be assigned to the closest factory, as long as it has enough capacity. The assignment process is shown in Steps (a)–(d).
- (a)
- Calculate the probability of assigning the plants to the fields. Using the proposed algorithm, we applied the price of the plants to calculate this. The probabilities of assigning rice, sugarcane, and cassava were 0.32, 0.39, and 0.29, respectively, for the current example.
- (b)
- Calculate the cumulative probability of each type of plant. Taken from Step (2), the cumulative probabilities of rice, sugarcane, and cassava were 0.32, 0.71, and 1.0, respectively. Use the value in the vector position to decide which plants to grow. The Vector 1 position, which is Field 5, had value of 0.06. This value (0.06) falls in the rice area of the roulette wheel; therefore, Field 5 is assigned to grow rice. Then, Field 5 is assigned to the rice factory (using the information shown in Table 3). This rice factory has a 120-ton capacity and Field 5 can produce 15 tons. Thus, the rice mill has 105 tons remaining to receive rice from other fields.
- (c)
- Redo Step (b) until all fields are assigned to grow exactly one type of plant. This step is needed to evaluate whether a factory has enough capacity to receive the product from all fields that fall into the area of that type of plant. When the factory does not have enough capacity, the field that has a higher value in that position needs to be changed to grow other types of plants. Fields 6, 1, 7, and 3 grow cassava because the values in the Vector 1 positions for these fields were 0.72, 0.84, 0.85, and 0.92, which fall in the area of cassava, for example. However, if all addressed fields grow cassava, this will generate 104 tons of cassava. The tapioca starch mill has only a 90-ton capacity, thus the last field needs to be changed to produce other types of plants. Field 3 needs to change to produce rice in this case. The total cassava that will be produced will decrease from 104 to 75 tons and the amount of rice that will be produced in the plan will increase from 60 to 78 tons (using the information given in Table 2). The assignment of the field to the factory, in case there is more than one factory to select, can be executed by selecting to deliver the product to the factory from that field. Field 4, which grows sugarcane, needs to deliver the sugarcane to the sugar mill and there are two sugar mills, for example. Field 4 has a distance to SM1 and SM2 of 323 and 202 km, respectively (using the information given in Table 3). Therefore, Field 4 will deliver sugarcane to SM2 at a distance of 202 km.
- (d)
- Calculate all profit and cost terms according to the assignment obtained from Step (b).
4.3. Mutation Process
4.4. Crossover or Recombination Process
4.5. Selection Process
5. Improved Differential Evolution Algorithm
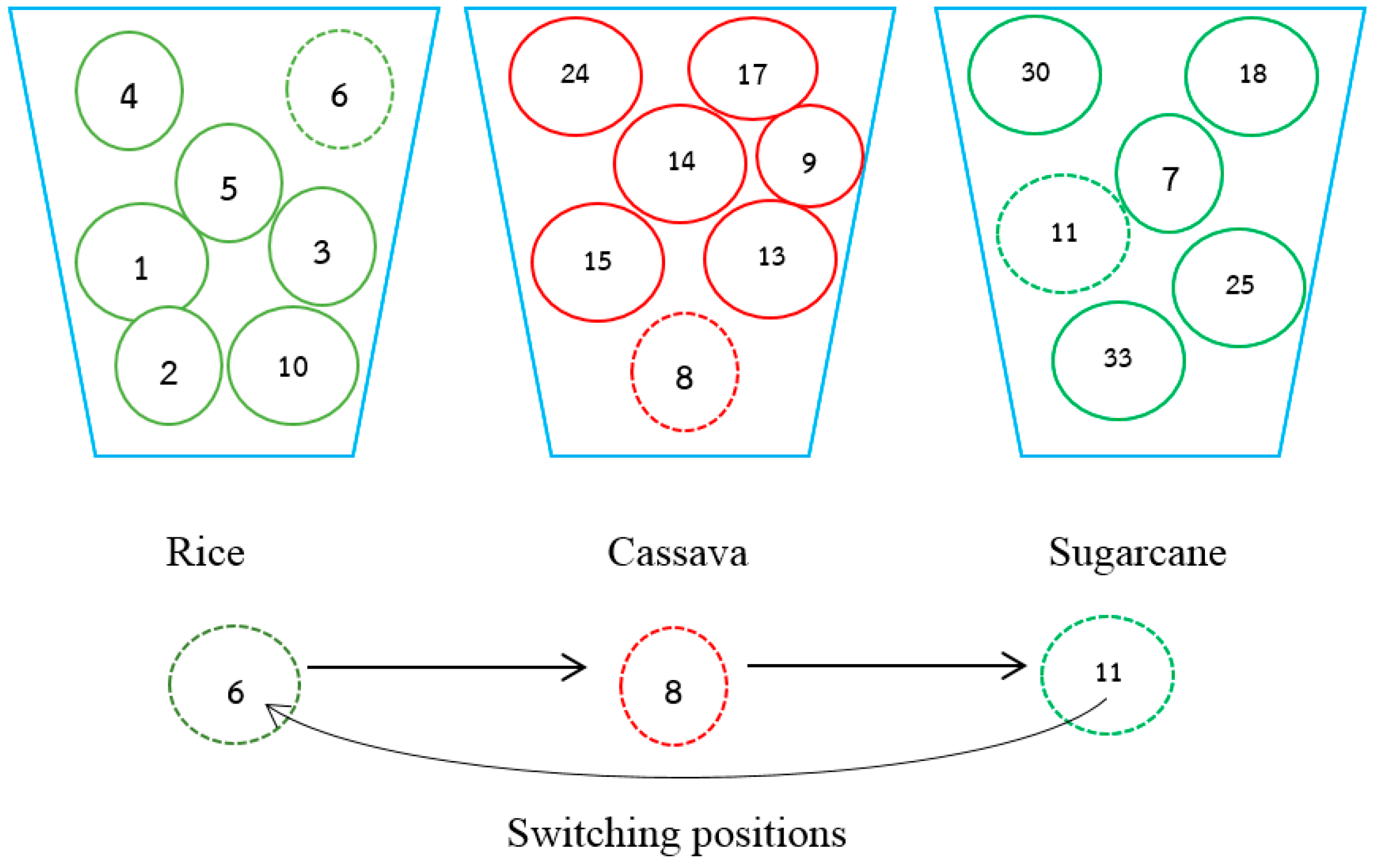
5.1. Swap Algorithm
5.2. Cyclic Move Algorithm
5.3. K-Variable Move Algorithm
6. Computational Experiment and Results
6.1. Experimental Results of Differential Evolution Algorithm (DE) Compared with Lingo V.11
6.2. Experimental Results of DE Compared with Modified DE
7. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Agricultural Information Office. Agricultural Information; Agricultural Economics, Ministry of Agriculture and Cooperatives: Bangkok, Thailand, 2016. [Google Scholar]
- Thongdee, T.; Pitakaso, R. Differential Evolution Algorithms Solving a Multi-Objective, Source and Stage Location-Allocation Problem. Ind. Eng. Manag. Syst. 2015, 14, 11–21. [Google Scholar] [CrossRef]
- Sethanan, K.; Pitakaso, R. Improved differential evolution algorithms for solving generalized assignment problem. Expert Syst. Appl. 2016, 45, 450–459. [Google Scholar] [CrossRef]
- Wang, G.; Tan, Y. Improving Metaheuristic Algorithms with Information Feedback Models. IEEE Trans. Cybern. 2017, 99, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Wang, G.; Guo, L.; Gandomi, A.H.; Hao, G.; Wang, H. Chaotic Krill Herd algorithm. Inf. Sci. 2014, 274, 17–34. [Google Scholar] [CrossRef]
- Wang, G.; Gandomi, A.H.; Alavi, A.H. An effective krill herd algorithm with migration operator in biogeography-based optimization. Appl. Math. Model. 2014, 38, 2454–2462. [Google Scholar] [CrossRef]
- Cui, Z.; Sun, B.; Wang, G.; Xue, Y.; Chen, J. A novel oriented cuckoo search algorithm to improve DV-Hop performance for cyber-physical systems. J. Parallel Distrib. Comput. 2016, 103. [Google Scholar] [CrossRef]
- Wang, G.; Alavi, A.H.; Zhao, X.J.; Hai, C.C. Hybridizing harmony search algorithm with cuckoo search for global numerical optimization. Soft Comput. 2016, 20, 273–285. [Google Scholar] [CrossRef]
- Feng, Y.; Wang, G. Binary Moth Search Algorithm for Discounted {0–1} Knapsack Problem. IEEE Access 2018. [Google Scholar] [CrossRef]
- Wang, G.; Deb, S.; Cui, Z. Monarch Butterfly Optimization. Neural Comput. Appl. 2015. [Google Scholar] [CrossRef]
- Wang, G.; Guo, L.; Gandomi, A.H.; Cao, L.; Alavi, A.H.; Duan, H.; Li, J. Lévy-Flight Krill Herd Algorithm. Math. Probl. Eng. 2013. [Google Scholar] [CrossRef]
- Wang, G.; Guo, L.; Duan, H.; Wang, H.; Liu, L.; Shao, M. Hybridizing Harmony Search with Biogeography Based Optimization for Global Numerical Optimization. J. Comput. Theor. Nanosci. 2013, 10, 2312–2322. [Google Scholar] [CrossRef]
- Wei, Z.J.; Wang, G. Image Matching Using a Bat Algorithm with Mutation. Appl. Mech. Mater. 2012, 203, 88–93. [Google Scholar] [CrossRef]
- Wang, G.; Coelho, L.; Gao, X.Z.; Deb, S. A new metaheuristic optimisation algorithm motivated by elephant herding behavior. Int. J. Bio-Inspired Comput. 2016, 8. [Google Scholar] [CrossRef]
- Wang, G.; Deb, S.; Coelho, L.D.S. Earthworm optimization algorithm: A bio-inspired metaheuristic algorithm for global optimization problems. Int. J. Bio-Inspired Comput. 2018, 12, 1–12. [Google Scholar] [CrossRef]
- Wang, G.; Guo, L.; Wang, H.; Duan, H.; Liu, L.; Li, J. Incorporating mutation scheme into krill herd algorithm for global numerical optimization. Neural Comput. Appl. 2014, 24, 853–871. [Google Scholar] [CrossRef]
- Wang, G.; Gandomi, A.H.; Alavi, A.H. Stud krill herd algorithm. Neurocomputing 2014, 128, 363–370. [Google Scholar] [CrossRef]
- Wang, G.; Gandomi, A.H.; Yang, X.; Alavi, A.H. A new hybrid method based on krill herd and cuckoo search for global optimisation tasks. Int. J. Bio-Inspired Comput. 2016, 8, 286–299. [Google Scholar] [CrossRef]
- Wang, H.; Yi, J.H. An improved optimization method based on krill herd and artificial bee colony with information exchange. Memet. Comput. 2017, 10, 177–198. [Google Scholar] [CrossRef]
- Wang, G.; Gandomi, A.H.; Alavi, A.H.; Deb, S. A hybrid method based on krill herd and quantum-behaved particle swarm optimization. Neural Comput. Appl. 2016, 27, 989–1006. [Google Scholar] [CrossRef]
- Wang, G.; Guo, L.; Gandomi, A.H.; Alavi, A.H.; Duan, H. Simulated Annealing-Based Krill Herd Algorithm for Global Optimization. Abstr. Appl. Anal. 2013. [Google Scholar] [CrossRef]
- Guo, L.; Wang, G.; Gandomi, A.H.; Alavi, A.H.; Duan, H. A new improved krill herd algorithm for global numerical optimization. Neurocomputing 2014, 138, 392–402. [Google Scholar] [CrossRef]
- Wang, G.; Gandomi, A.H.; Alavi, A.H. Study of Lagrangian and Evolutionary Parameters in Krill Herd Algorithm. In Adaptation and Hybridization in Computational Intelligence. Adaptation, Learning, and Optimization; Fister, I., Fister, I., Jr., Eds.; Springer: Cham, Switzerland, 2015. [Google Scholar]
- Wang, G.; Gandomi, A.H.; Alavi, A.H.; Deb, S. A Multi-Stage Krill Herd Algorithm for Global Numerical Optimization. Int. J. Artif. Intell. Tools 2016, 25. [Google Scholar] [CrossRef]
- Wang, G.; Deb, S.; Gandomi, A.H.; Alavi, A.H.A. Opposition-based krill herd algorithm with Cauchy mutation and position clamping. Neurocomputing 2016, 177, 147–157. [Google Scholar] [CrossRef]
- Wang, G.; Gandomi, A.H.; Alavi, A.H.; Gong, D. A comprehensive review of krill herd algorithm: Variants, hybrids and applications. Artif. Intell. Rev. 2017. [Google Scholar] [CrossRef]
- Rizk, M.; Rizk, A.; Ragab, A.; El-Sehiemy, R.A.; Wang, G. A novel parallel hurricane optimization algorithm for secure emission/economic load dispatch solution. Appl. Soft Comput. 2018, 63, 206–222. [Google Scholar] [CrossRef]
- Wang, G.; Gandomi, A.H.; Alavi, A.H.; Dong, Y. A Hybrid Meta-Heuristic Method Based on Firefly Algorithm and Krill Herd. In Handbook of Research on Advanced Computational Techniques for Simulation-Based Engineering; IGI: Hershey, PA, USA, 2016; pp. 521–540. [Google Scholar]
- Wang, G. Moth search algorithm: A bio-inspired metaheuristic algorithm for global optimization problems. Memet. Comput. 2018, 10, 151–164. [Google Scholar] [CrossRef]
- Feng, Y.; Wang, G.; Deb, S.; Lu, M.; Zhao, X. Solving 0–1 knapsack problem by a novel binary monarch butterfly optimization. Neural Comput. Appl. 2017, 28, 1619–1634. [Google Scholar] [CrossRef]
- Feng, Y. Solving 0–1 knapsack problems by chaotic monarch butterfly optimization algorithm with Gaussian mutation. Memet. Comput. 2016. [Google Scholar] [CrossRef]
- Wang, G.; Deb, S.; Zhao, X.; Cui, Z. A new monarch butterfly optimization with an improved crossover operator. Oper. Res. 2016. [Google Scholar] [CrossRef]
- Wu, G. Across neighborhood search for numerical optimization. Inf. Sci. 2016, 329, 597–618. [Google Scholar] [CrossRef]
- Wang, G.; Gandomi, A.H.; Alavi, A.H. A chaotic particle-swarm krill herd algorithm for global numerical optimization. Kybernetes 2013, 42, 962–978. [Google Scholar] [CrossRef]
- Wang, G.; Deb, S.; Gandomi, A.H.; Zhang, Z.; Alavi, A.H. Haotic cuckoo search. Soft Comput. Fusion Found. Methodol. Appl. 2016, 20, 3349–3362. [Google Scholar]
- Yi, J.; Wang, J.; Wang, G. Improved probabilistic neural networks with self-adaptive strategies for transformer fault diagnosis problem. Adv. Mech. Eng. 2016, 8. [Google Scholar] [CrossRef]
- Storn, R.; Price, K.V. Differential evolution: A simple and efficient adaptive scheme for global optimization over continuous spaces. J. Glob. Optim. 1995, 11, 341–359. [Google Scholar] [CrossRef]
- Erbao, C.; Lai, M. A Hybrid differential evolution algorithm to vehicle routing problem with fuzzy demands. J. Comput. Appl. Math. 2009, 231, 302–310. [Google Scholar] [CrossRef]
- Dechampai, D.; Tanwannichkul, L.; Sethanan, K.; Pitakaso, R. A differential evolution algorithm for the capacitated VRP with Flexibility for mixing pickup and delivery services and the maximum duration route in poultry industry. J. Intell. Manuf. 2017, 28, 1357–1376. [Google Scholar] [CrossRef]
- Sethanan, K.; Pitakaso, R. Differential evolution algorithms for scheduling raw milk transportation. Comput. Electron. Agric. 2016, 121, 245–259. [Google Scholar] [CrossRef]
- Das, S.; Suganthan, P.N. Differential Evolution: A Survey of the State-of-the-Art. IEEE Trans. Evol. Comput. 2011, 15, 4–31. [Google Scholar] [CrossRef]
- Glen, J.J. Mathematical models in farm planning: A survey. Oper. Res. 1987, 35, 641–666. [Google Scholar] [CrossRef]
- Itoh, T.; Ishii, H.; Nanseki, T. A model of crop planning under uncertainty in agricultural management. Int. J. Prod. Econ. 2003, 81, 555–558. [Google Scholar] [CrossRef]
- Sarker, R.A.; Talukdar, S.; Haque, A. Determination of optimum crop mix for crop cultivation in Bangladesh. Appl. Math. Model. 1997, 21, 621–632. [Google Scholar] [CrossRef]
- Santosa, B.; Sunarto, A.; Rahman, A. Using Differential Evolution Method to Solve Crew Rostering Problem. Appl. Math. 2010, 1, 316–325. [Google Scholar] [CrossRef]
- Adeyemo, J.; Otieno, F. Differential evolution algorithm for solving multi-objective crop planning model. Agric. Water Manag. 2010, 97, 848–856. [Google Scholar] [CrossRef]
- Mallipeddi, R.; Suganthan, P.N.; Pan, Q.K.; Tasgetiren, M.F. Differential evolution algorithm with ensemble of parameters and mutation strategies. Appl. Soft Comput. 2010, 11, 1679–1696. [Google Scholar] [CrossRef]
- Adekanmbi, O.A.; Olugbara, O.O.; Adeyemo, J. A Comparative Study of State-of-the-Art Evolutionary Multi-objective Algorithms for Optimal Crop-mix planning. Int. J. Agric. Sci. Technol. 2014, 2, 8–16. [Google Scholar] [CrossRef]
- Adeyemo, J.; Bux, F.; Otieno, F. Differential evolution algorithm for crop planning: Single and multi-objective optimization model. Int. J. Phys. Sci. 2010, 5, 1592–1599. [Google Scholar]
- Pant, M.; Radha, T.; Rani, D.; Abraham, A.; Srivastava, D.K. Estimation Using Differential Evolution for Optimal Crop Plan. In Proceedings of the HAIS 2008 International Conference on Hybrid Artificial Intelligence Systems, Oviedo, Spain, 20–22 June 2008; pp. 289–297. [Google Scholar]
- Yi, H.; Duan, Q.; Liao, T.W. Three improved hybrid metaheuristic algorithms for engineering design optimization. Appl. Soft Comput. 2013, 13, 2433–2444. [Google Scholar] [CrossRef]
- Wang, G.; Cheng, H.; Chu, E.; Mirjalili, S. Three-dimensional path planning for UCAV using an improved bat algorithm. Aerosp. Sci. Technol. 2016, 49, 231–238. [Google Scholar] [CrossRef]
- Wang, G.; Gandomi, A.H.; Alavi, A.H.; Hao, G. Hybrid krill herd algorithm with differential evolution for global numerical optimization. Neural Comput. Appl. 2014, 25, 297–308. [Google Scholar] [CrossRef]
- Wang, G.; Gandomi, A.H.; Yang, Z.; Alavi, A.H. A novel improved accelerated particle swarm optimization algorithm for global numerical optimization. Eng. Comput. 2014, 31, 1198–1220. [Google Scholar] [CrossRef]
- Wu, G.; Shen, X.; Li, H.; Chen, H.; Lin, A.; Suganthan, P.N. Ensemble of differential evolution variants. Inf. Sci. 2018, 423, 172–186. [Google Scholar] [CrossRef]
- Wu, G.; Pedrycz, W.; Suganthan, P.N.; Lie, H. Using variable reduction strategy to accelerate evolutionary optimization. Appl. Soft Comput. 2017, 61, 283–293. [Google Scholar] [CrossRef]
- Wang, R.; Purshouse, R.C.; Fleming, P.J. Preference-Inspired Coevolutionary Algorithms for Many-Objective Optimization. IEEE Trans. Evol. Comput. 2013, 17, 474–494. [Google Scholar] [CrossRef]
- Wang, R.; Zhang, O.; Zhang, T. Decomposition-Based Algorithms Using Pareto Adaptive Scalarizing Methods. IEEE Trans. Evol. Comput. 2016, 20, 821–837. [Google Scholar] [CrossRef]
- Wu, G.; Pedrycz, W.; Li, H.; Ma, M.; Liu, J. Coordinated Planning of Heterogeneous Earth Observation Resources. IEEE Trans. Syst. Man Cybern. Syst. 2016, 46, 109–125. [Google Scholar] [CrossRef]
- Wang, G.; Guo, L.; Duan, H.; Wang, H. A New Improved Firefly Algorithm for Global Numerical Optimization. J. Comput. Theor. Nanosci. 2014, 11, 477–485. [Google Scholar] [CrossRef]
- Wang, G.; Cai, X.; Cui, Z.; Min, G.; Chen, J. High Performance Computing for Cyber Physical Social Systems by Using Evolutionary Multi-Objective Optimization Algorithm. IEEE Trans. Emerg. Top. Comput. 2017. [Google Scholar] [CrossRef]
- Ke, L.; Gong, D.W.; Meng, F.L.; Chen, H.H.; Wang, G. Gesture segmentation based on a two-phase estimation of distribution algorithm. Inf. Sci. 2017. [Google Scholar] [CrossRef]
- Rizk, R.M.; El-Sehiemy, R.A.; Deb, S.; Wang, G. A novel fruit fly framework for multi-objective shape design of tubular linear synchronous motor. J. Supercomput. 2017, 73, 1235–1256. [Google Scholar] [CrossRef]
- Wang, R.; Zhou, Z.; Ishibuchi, H.; Liao, T.; Zhang, T. Localized Weighted Sum Method for Many-Objective Optimization. IEEE Trans. Evol. Comput. 2018, 22, 3–18. [Google Scholar] [CrossRef]
- Qin, A.K.; Huang, V.L.; Suganthan, P.N. Differential evolution algorithm with strategy adaptation for global numerical optimization. IEEE Trans. Evolut. Comput. 2009, 13, 398–417. [Google Scholar] [CrossRef]
- Diaz, J.A.; Fernandez, E. A Tabu search heuristic for the generalized assignment problem. Eur. J. Oper. Res. 2001, 132, 22–38. [Google Scholar] [CrossRef]
| Farmer Vector | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.84 | 0.39 | 0.92 | 0.56 | 0.06 | 0.72 | 0.85 | 0.19 | 0.27 | 0.09 |
| 2 | 0.71 | 0.45 | 0.40 | 0.63 | 0.78 | 0.07 | 0.49 | 0.81 | 0.71 | 0.30 |
| 3 | 0.55 | 0.20 | 0.63 | 0.34 | 0.39 | 0.14 | 0.50 | 0.43 | 0.69 | 0.17 |
| 4 | 0.80 | 0.75 | 0.49 | 0.76 | 0.74 | 0.55 | 0.11 | 0.34 | 0.65 | 0.51 |
| 5 | 0.22 | 0.20 | 0.12 | 0.42 | 0.74 | 0.90 | 0.49 | 0.44 | 0.73 | 0.40 |
| - | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| Rice | 15 | 20 | 18 | 8 | 15 | 13 | 19 | 21 | 19 | 15 |
| Sugarcane | 18 | 18 | 20 | 10 | 12 | 16 | 23 | 21 | 23 | 15 |
| Cassava | 25 | 16 | 29 | 9 | 14 | 20 | 30 | 19 | 23 | 16 |
| Factory Field | RM | SM1 | SM2 | TS |
|---|---|---|---|---|
| 1 | 279 | 210 | 148 | 141 |
| 2 | 319 | 186 | 252 | 332 |
| 3 | 107 | 316 | 199 | 234 |
| 4 | 305 | 323 | 202 | 272 |
| 5 | 285 | 150 | 158 | 308 |
| 6 | 200 | 245 | 203 | 179 |
| 7 | 189 | 283 | 173 | 301 |
| 8 | 185 | 122 | 102 | 326 |
| 9 | 291 | 130 | 141 | 229 |
| 10 | 320 | 125 | 111 | 141 |
| Farmer Vector | 5 | 10 | 8 | 9 | 2 | 4 | 6 | 1 | 7 | 3 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.06 | 0.09 | 0.19 | 0.27 | 0.39 | 0.56 | 0.72 | 0.84 | 0.85 | 0.92 |
| Factory | Field | Plant |
|---|---|---|
| RM | 5, 10, 8, 9, 3 | Rice |
| SM1 | 2 | Sugarcane |
| SM2 | 4 | Sugarcane |
| TS | 6, 1, 7 | Cassava |
| Problem Group | Farmer or Subdistrict | Rice | Cassava | Sugarcane | Methods | |||
|---|---|---|---|---|---|---|---|---|
| Number of Factories | Number of Factories | Number of Factories | Lingo | Differential Evolution Algorithm (DE) | ||||
| - | - | - | - | - | Solution (Baht) | Time (s) | Solution | Time (s) |
| 1 (Small Size) | 5 | 3 | 3 | 4 | 153,040 | 00:00:02 | 153,040 | 00:00:01 |
| 10 | 3 | 3 | 4 | 538,909 | 00:00:05 | 538,909 | 00:00:03 | |
| 15 | 3 | 3 | 4 | 704,463 | 00:00:27 | 704,463 | 00:00:05 | |
| 20 | 7 | 7 | 5 | 1.1175 × 106 | 00:00:46 | 1.1175 × 106 | 00:00:14 | |
| 2 (Medium size) | 40 | 16 | 30 | 5 | 2.4585 × 106 | 00:03:39 | 2.4585 × 106 | 00:00:23 |
| 60 | 30 | 50 | 5 | 3.73617 × 106 | 00:06:50 | 3.73617 × 106 | 00:01:38 | |
| 70 | 35 | 55 | 3 | 4.31865 × 106 | 00:10:25 | 4.31865 × 106 | 00:03:37 | |
| 3 (Large Size) | 80 | 45 | 60 | 5 | 4.3341 × 106 | 250 h * | 4.45924 × 106 | 00:02:13 |
| 80 | 50 | 70 | 7 | 4.3378 × 106 | 250 h * | 4.75384 × 106 | 00:03:26 | |
| 80 | 55 | 70 | 10 | 4.3467 × 106 | 250 h * | 4.68498 × 106 | 00:03:69 | |
| 100 | 60 | 70 | 10 | 4.3593 × 106 | 250 h * | 4.54516 × 106 | 00:10:16 | |
| 100 | 60 | 80 | 10 | 4.4355 × 106 | 250 h * | 4.61473 × 106 | 00:13:10 | |
| 100 | 60 | 80 | 10 | 4.4355 × 106 | 250 h * | 4.51473 × 106 | 00:13:10 | |
| 500 | 70 | 85 | 13 | 5.13148 × 106 | 250 h | 5.18148 × 106 | 00:16:34 | |
| Case study | 1293 | 95 | 98 | 19 | 1.39234 × 107 | 250 h * | 1.41761 × 107 | 00:21:82 |
| Problem Size | N | Solution (Profit: Baht) | |||
|---|---|---|---|---|---|
| (A-B-C) | DE | I-DE-SW | I-DE-CY | I-DE-KV | |
| Small size | 5 (3-3-4) | 153,040 | 208,933 | 153,040 | 208,933 |
| 10 (3-3-4) | 538,909 | 565,109 | 554,117 | 565,109 | |
| 15 (3-3-4) | 704,463 | 704,463 | 704,219 | 704,219 | |
| 20 (7-7-5) | 1.1175 × 106 | 1.10857 × 106 | 1.11875 × 106 | 1.11877 × 106 | |
| Medium size | 40 (16-30-5) | 2.4585 × 106 | 2.4585 × 106 | 2.4585 × 106 | 2.4585 × 106 |
| 60 (30-50-5) | 3.73617 × 106 | 3.73617 × 106 | 3.73617 × 106 | 3.73711 × 106 | |
| 70 (35-55-3) | 4.31865 × 106 | 4.31865 × 106 | 4.31865 × 106 | 4.31865 × 106 | |
| Large size | 80 (45-60-5) | 4.55924 × 106 | 4.55924 × 106 | 4.55924 × 106 | 4.56032 × 106 |
| 80 (50-70-7) | 4.47249 × 106 | 4.65214 × 106 | 4.69214 × 106 | 4.71241 ×106 | |
| 80 (55-70-10) | 4.78129 × 106 | 4.79241 × 106 | 4.79201 × 106 | 4.84542 × 106 | |
| 100 (60-70-10) | 4.55681 × 106 | 4.60241 × 106 | 4.61042 × 106 | 4.72124 × 106 | |
| 100 (60-80-10) | 4.64981 × 106 | 4.76292 × 106 | 4.75124 × 106 | 4.78419 × 106 | |
| 100 (60-80-10) | 4.65924 × 106 | 4.71105 × 106 | 4.70924 × 106 | 4.72149 × 106 | |
| 500 (70-85-13) | 5.23148 × 106 | 5.36866 × 106 | 5.3548 × 106 | 5.37866 × 106 | |
| Case study | 1293 (95-98-19) | 1.427614 × 107 | 1.457129 × 107 | 14.32278 × 106 | 14.59643 × 106 |
| Method | I-DE-SW | I-DE-CY | I-DE-KV |
|---|---|---|---|
| DE | ≤(0.02 *) | ≤(0.012 *) | ≤(0.009 *) |
| I-DE-SW | - | =(0.403) | ≤(0.038 *) |
| I-DE-CY | - | - | ≤(0.036 *) |
| Time | Method | 200 h | 250 h | 300 h | 350 h | 400 h |
|---|---|---|---|---|---|---|
| Instance | ||||||
| 80 (45-60-5) | Upper Bound | 4.58894 × 106 | 4.58894 × 106 | 4.58894 × 106 | 4.57591 × 106 | 4.57591 × 106 |
| Best Objective | 4.55145 × 106 | 4.55145 × 106 | 4.55981 × 106 | 4.55981 × 106 | 4.55981 × 106 | |
| I-DE-KV | 4.56032 × 106 | |||||
| 80 (50-70-7) | Upper Bound | 4.80512 × 106 | 4.80512 × 106 | 4.78214 × 106 | 4.78214 × 106 | 4.76542 × 106 |
| Best Objective | 4.56821 × 106 | 4.56995 × 106 | 4.58912 × 106 | 4.60156 × 106 | 4.60156 × 106 | |
| I-DE-KV | 4.71241 × 106 | |||||
| 80 (55-70-10) | Upper Bound | 4.90124 × 106 | 4.90259 × 106 | 4.899128 × 106 | 4.899128 × 106 | 4.899128 × 106 |
| Best Objective | 4.71249 × 106 | 4.71249 × 106 | 4.71249 × 106 | 4.71249 × 106 | 4.71249 × 106 | |
| I-DE-KV | 4.84542 × 106 | |||||
| 100 (60-70-10) | Upper Bound | 4.98241 × 106 | 4.85215 × 106 | 4.79242 × 106 | 4.79242 × 106 | 4.79242 × 106 |
| Best Objective | 4.61983 × 106 | 4.62488 × 106 | 4.62488 × 106 | 4.62488 × 106 | 4.63245 × 106 | |
| I-DE-KV | 4.72124 × 106 | |||||
| 100 (60-80-10) | Upper Bound | 4.88812 × 106 | 4.88812 × 106 | 4.85289 × 106 | 4.85289 × 106 | 4.81457 × 106 |
| Best Objective | 4.62388 × 106 | 4.62388 × 106 | 4.62388 × 106 | 4.64514 × 106 | 4.64514× 106 | |
| I-DE-KV | 4.73419 × 106 | |||||
| 100 (60-80-10) | Upper Bound | 4.8190 × 106 | 4.8190 × 106 | 4.8024 × 106 | 4.8024 × 106 | 4.79842 × 106 |
| Best Objective | 4.6786 × 106 | 4.69782 × 106 | 4.70113 × 106 | 4.70113 × 106 | 4.70113 × 106 | |
| I-DE-KV | 4.71105 × 106 | |||||
| 500 (70-85-13) | Upper Bound | 5.46991 × 106 | 5.46991 × 106 | 5.46892 × 106 | 5.46892 × 106 | 5.44412 × 106 |
| Best Objective | 5.34917 × 106 | 5.35178 × 106 | 5.35178 × 106 | 5.35980 × 106 | 5.35991 × 106 | |
| I-DE-KV | 5.37866 × 106 | |||||
| 1293 (95-98-19) | Upper Bound | 14.7919 × 106 | 14.7919 × 106 | 14.7919 × 106 | 14.7814 × 106 | 14.7814 × 106 |
| Best Objective | 14.56891 × 106 | 14.56891 × 106 | 14.57129 × 106 | 14.57643 × 106 | 14.57610 × 106 | |
| I-DE-KV | 14.59643 × 106 | |||||
| Time | Method | 200 h | 250 h | 300 h | 350 h | 400 h |
|---|---|---|---|---|---|---|
| Instance | ||||||
| 80 (45-60-5) | Upper Bound | 0.628 | 0.628 | 0.628 | 0.342 | 0.342 |
| Best Objective | –0.195 | −0.195 | −0.011 | −0.011 | −0.011 | |
| 80 (50-70-7) | Upper Bound | 1.967 | 1.967 | 1.480 | 1.480 | 1.125 |
| Best Objective | −3.060 | −3.023 | −2.616 | −2.352 | −2.352 | |
| 80 (55-70-10) | Upper Bound | 1.152 | 1.180 | 1.108 | 1.108 | 1.108 |
| Best Objective | −2.743 | −2.743 | −2.743 | −2.743 | −2.743 | |
| 100 (60-70-10) | Upper Bound | 5.532 | 2.773 | 1.508 | 1.508 | 1.508 |
| Best Objective | −2.148 | −2.041 | −2.041 | −2.041 | −1.881 | |
| 100 (60-80-10) | Upper Bound | 3.251 | 3.251 | 2.507 | 2.507 | 1.698 |
| Best Objective | −2.330 | −2.330 | −2.330 | −1.881 | −1.881 | |
| 100 (60-80-10) | Upper Bound | 2.291 | 2.291 | 1.939 | 1.939 | 1.855 |
| Best Objective | −0.689 | −0.281 | −0.211 | −0.211 | −0.211 | |
| 500 (70-85-13) | Upper Bound | 1.697 | 1.697 | 1.678 | 1.678 | 1.217 |
| Best Objective | −0.548 | −0.500 | −0.500 | −0.351 | −0.349 | |
| 1293 (95-98-19) | Upper Bound | 1.339 | 1.339 | 1.339 | 1.267 | 1.267 |
| Best Objective | −0.189 | −0.189 | −0.172 | −0.137 | −0.139 | |
| Average | Upper Bound | 2.232 | 1.891 | 1.523 | 1.479 | 1.265 |
| Best Objective | −1.488 | −1.413 | −1.328 | −1.216 | −1.196 |
| Method | Best Objective | I-DE-KV | |
|---|---|---|---|
| Lingo | Upper Bound | ≥(0.001 *) | ≥(0.003 *) |
| Best Objective | - | ≤(0.003 *) | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ketsripongsa, U.; Pitakaso, R.; Sethanan, K.; Srivarapongse, T. An Improved Differential Evolution Algorithm for Crop Planning in the Northeastern Region of Thailand. Math. Comput. Appl. 2018, 23, 40. https://doi.org/10.3390/mca23030040
Ketsripongsa U, Pitakaso R, Sethanan K, Srivarapongse T. An Improved Differential Evolution Algorithm for Crop Planning in the Northeastern Region of Thailand. Mathematical and Computational Applications. 2018; 23(3):40. https://doi.org/10.3390/mca23030040
Chicago/Turabian StyleKetsripongsa, Udompong, Rapeepan Pitakaso, Kanchana Sethanan, and Tassin Srivarapongse. 2018. "An Improved Differential Evolution Algorithm for Crop Planning in the Northeastern Region of Thailand" Mathematical and Computational Applications 23, no. 3: 40. https://doi.org/10.3390/mca23030040
APA StyleKetsripongsa, U., Pitakaso, R., Sethanan, K., & Srivarapongse, T. (2018). An Improved Differential Evolution Algorithm for Crop Planning in the Northeastern Region of Thailand. Mathematical and Computational Applications, 23(3), 40. https://doi.org/10.3390/mca23030040





