Rapid Modeling and Parameter Estimation of Partial Differential Algebraic Equations by a Functional Spreadsheet Paradigm
Abstract
1. Introduction
2. Description of PDAE System and Solution Method
2.1. Boundary Conditions
- Dirichlet: a constant or time-dependent boundary condition, , specified for an individual state variable .
- Neumann: a constant or time-dependent boundary condition, , specified for an individual state variable derivative .
- Robin: a general boundary condition involving an algebraic expression of state variables and possibly their first derivatives.
- Continuity: a special condition that enforces continuity of a flux across an interface separating two regions with discontinuous material properties. A flux is defined as the product of a property , and the first derivative of a differential variable.
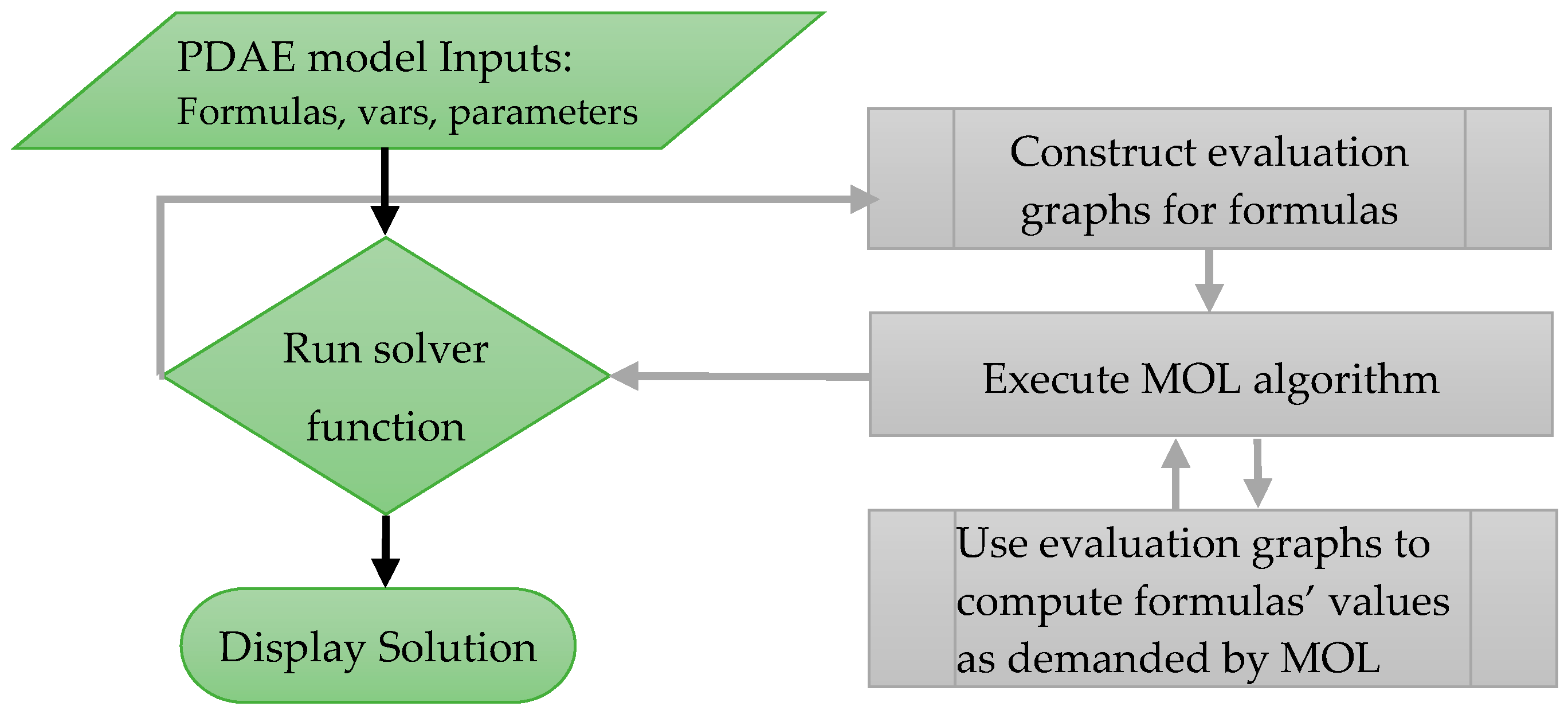
2.2. Solution Strategy
- An initial spatial grid consisting of fixed geometrical points for the problem is constructed. The geometrical points include system equation subregions’ end points, , and boundary condition points. The grid is then refined to satisfy that a minimum number of nodes is generated between any two consecutive geometrical points, as well as the distance between any two nodes is within a specified limit.
- Mapping data structures are constructed to record topological relationships between grid nodes, differential equations, regions and boundary conditions. The data structures support efficient retrieval of information pertaining to a grid node, including whether it is boundary condition node, an interior node, or a region end point, as well as its immediate neighbors and associated differential equations.
- A higher order finite difference scheme is used to approximate the first and second derivatives in terms of the state variables on the spatial grid. Since grid spacing across geometrical points may vary, a variable-step difference scheme is used when neighboring nodes have nonuniform spacing. Dirichlet and Neumann boundary conditions are incorporated at this step by substituting their direct values into the difference scheme.
- The spatial discretization in the previous step eliminates one degree of freedom, which transforms the PDAE into a banded initial value DAE system that can be integrated on an independent time grid using an appropriate DAE algorithm. In particular, we employ the RADAU5 algorithm, which is based on an adaptive implicit Runge–Kutta scheme of order five and supports implicit time-coupled DAE equations [20].
- Robin and Continuity-type boundary conditions are discretized in similar way but imposed as additional algebraic equations on the DAE system. In particular, for flux continuity conditions, each side of Equation (7) is computed using a one-sided difference scheme, and the residual is imposed as an algebraic constraint of zero value at the respective nodes.
3. Description of PDASOLVE Function Interface
3.1. Input Parameters
- Reference to formulas corresponding to the system right-hand-side functions including algabraic constraint equations if present.
- Reference to the system variables in the following order .
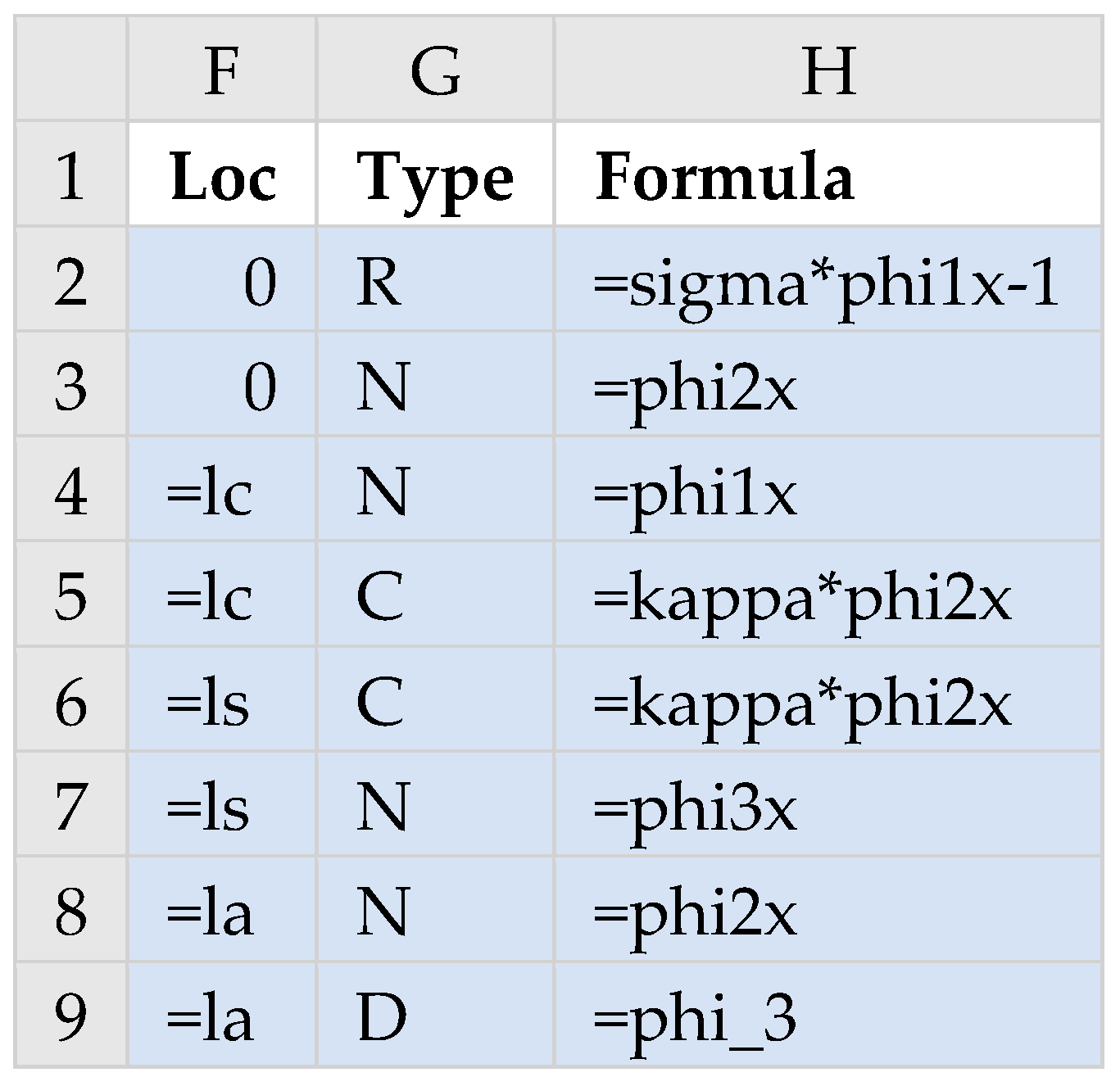
- Reference to a three-column array containing definitions for the system’s boundary conditions. The first column specifies the positions of the boundary conditions; the second column specifies the types that are identified by any of the letters ‘D’, ‘N’, ‘R’ or ‘C’, corresponding respectively to Dirichlet, Neumann, Robin, or Continuity; and the third column specifies the boundary condition formulas defined with respect to zero on one side.
- Spatial domain limits and output control.
- Time interval limit and output control.Optional parameters which may be omitted if not applicable.
- Mass matrix or number of algebraic equations in PDAE with identity mass matrix.
- Reference to a two-column array containing end points for each equation’s subregion.
- Tolerances for the time integration scheme.
- Reference to a two-column array containing key/value pairs for algorithm settings, grid control, and output solution format.
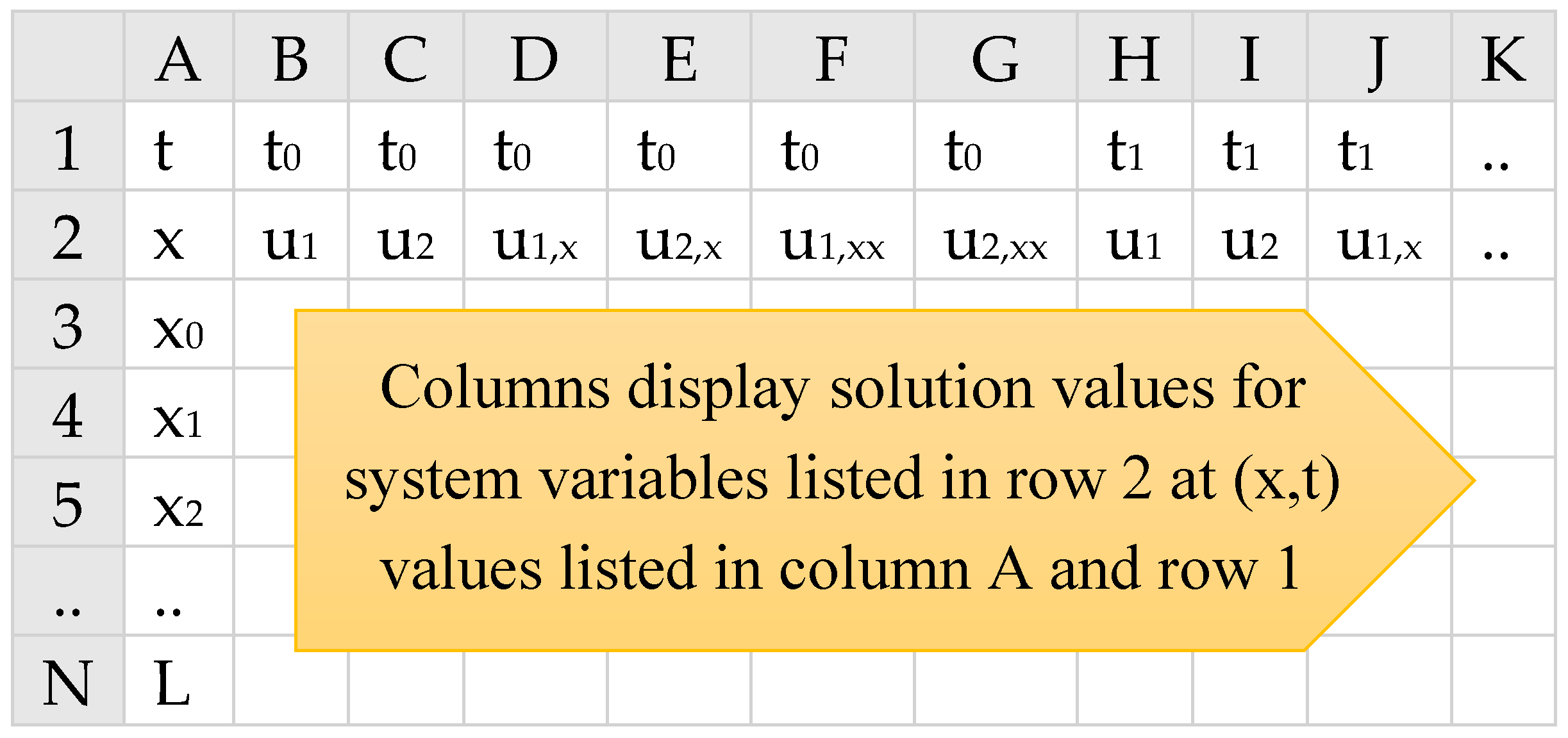
3.2. Output
4. Numerical Examples
4.1. A Continuous PDE System
4.1.1. Spreadsheet Model
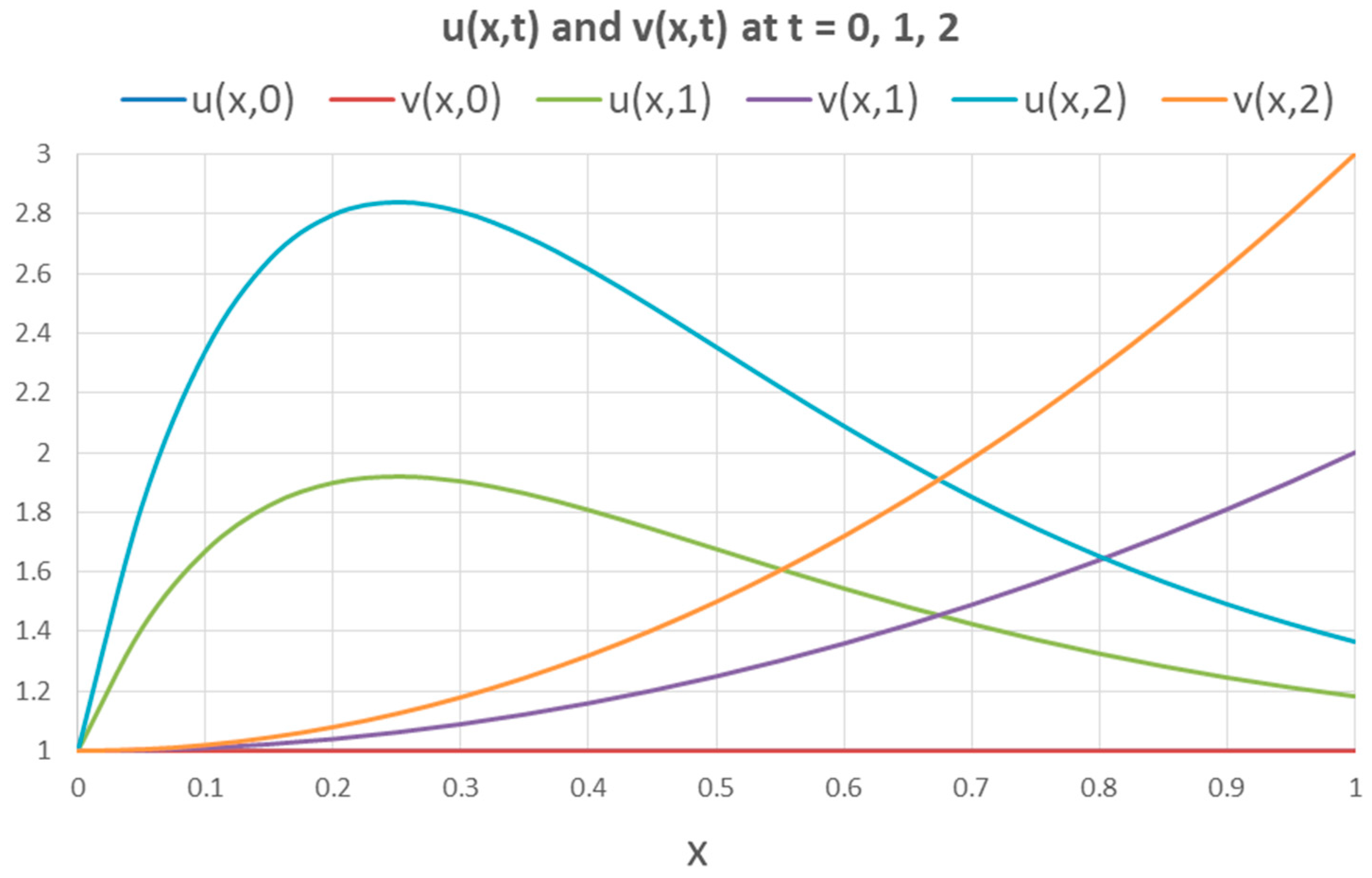
4.1.2. Solution by PDASOLVE Function
4.2. A Discontinuous PDAE System
4.2.1. Mathematical Model
4.2.2. Boundary Conditions
4.2.3. Problem Objective
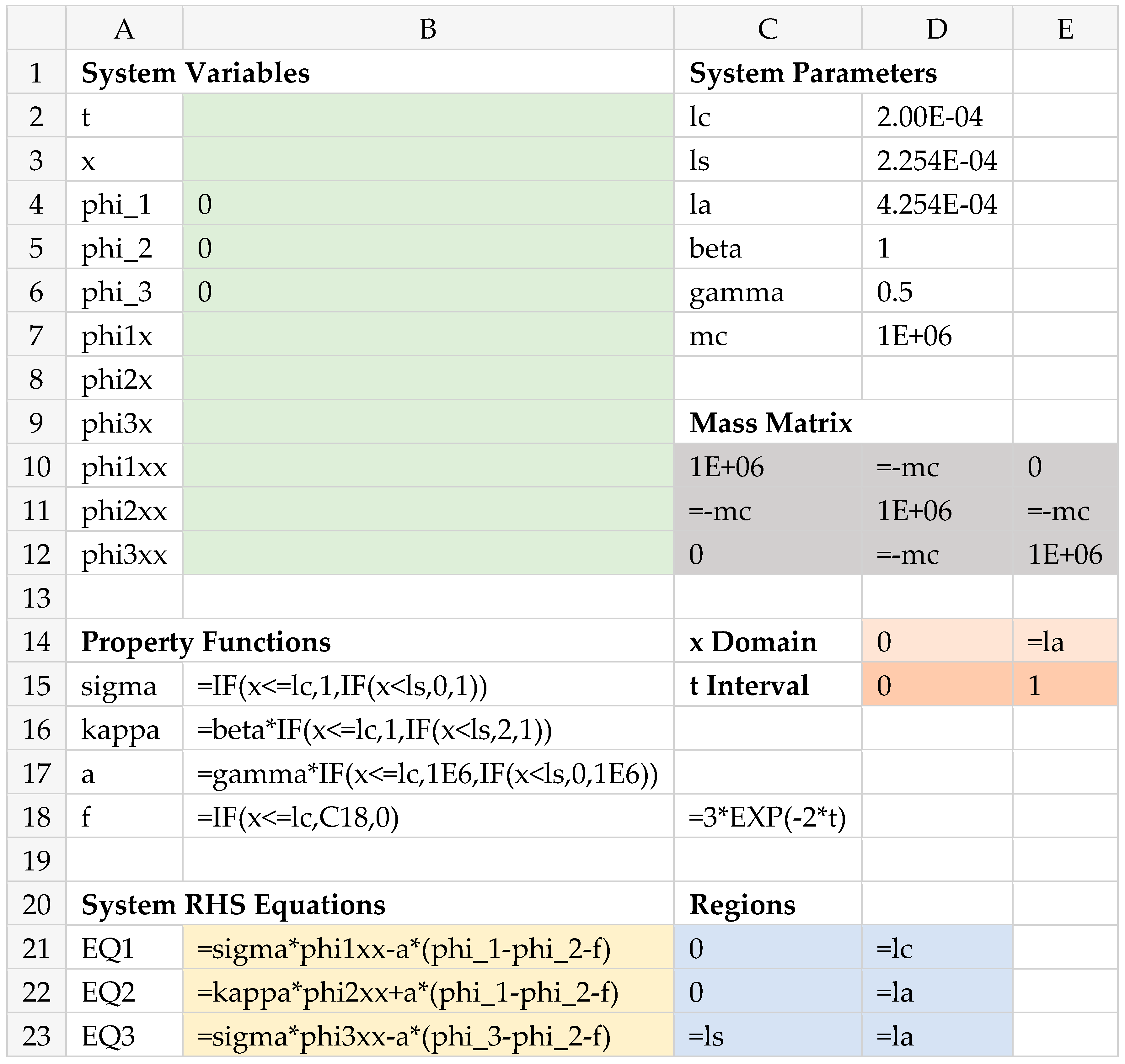
4.2.4. Spreadsheet Model
4.2.5. Computing the Solution by PDASOLVE Function
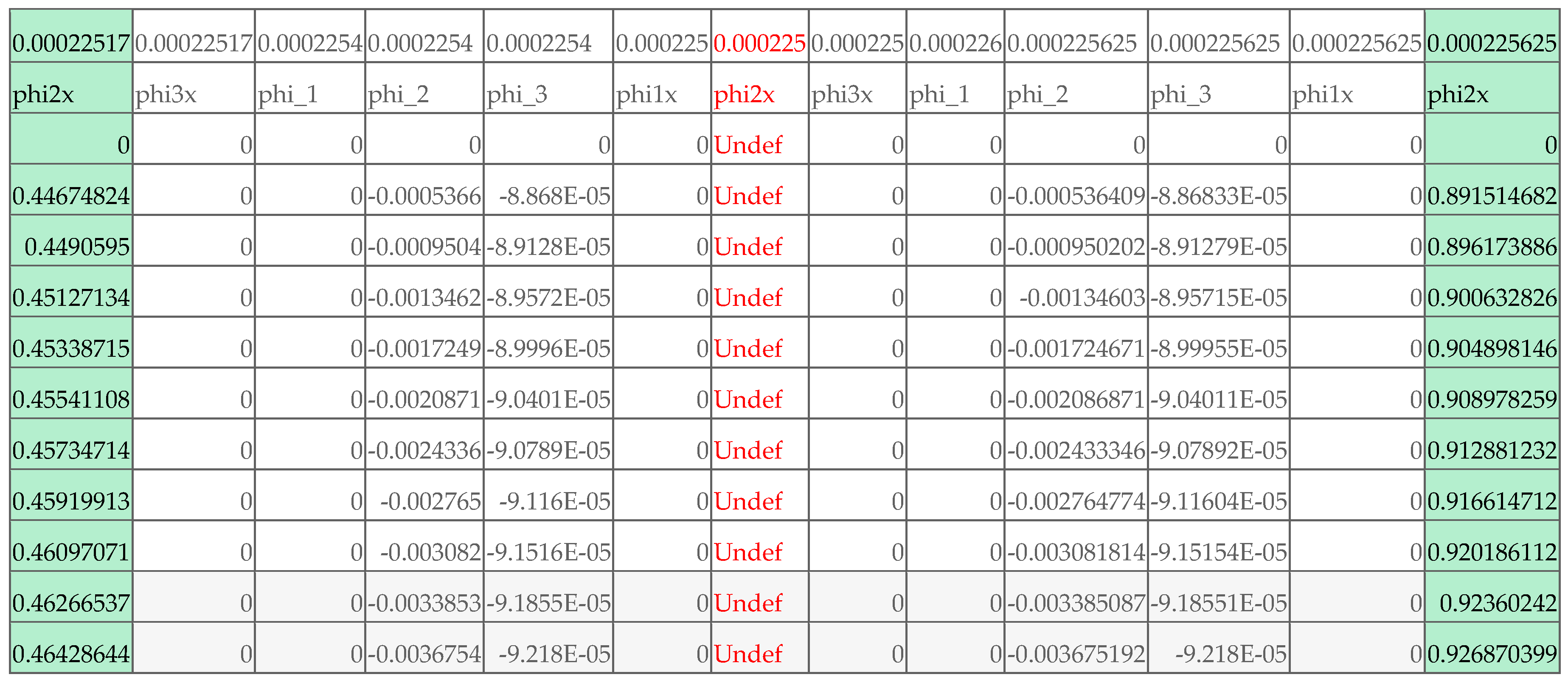
4.2.6. Verification of Continuity Boundary Conditions
5. Parameter Estimation via Dynamical Minimization
- Task 1:
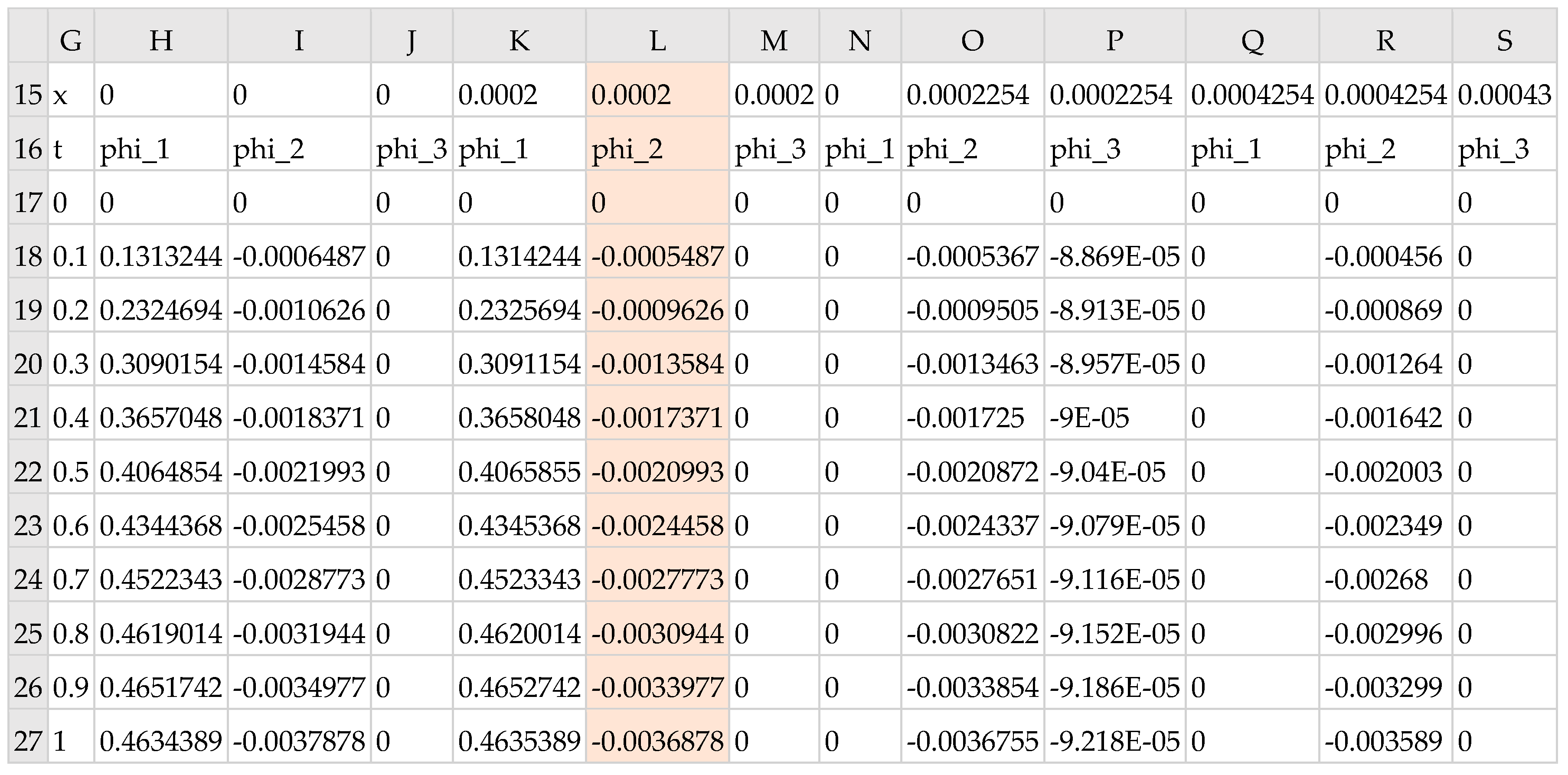
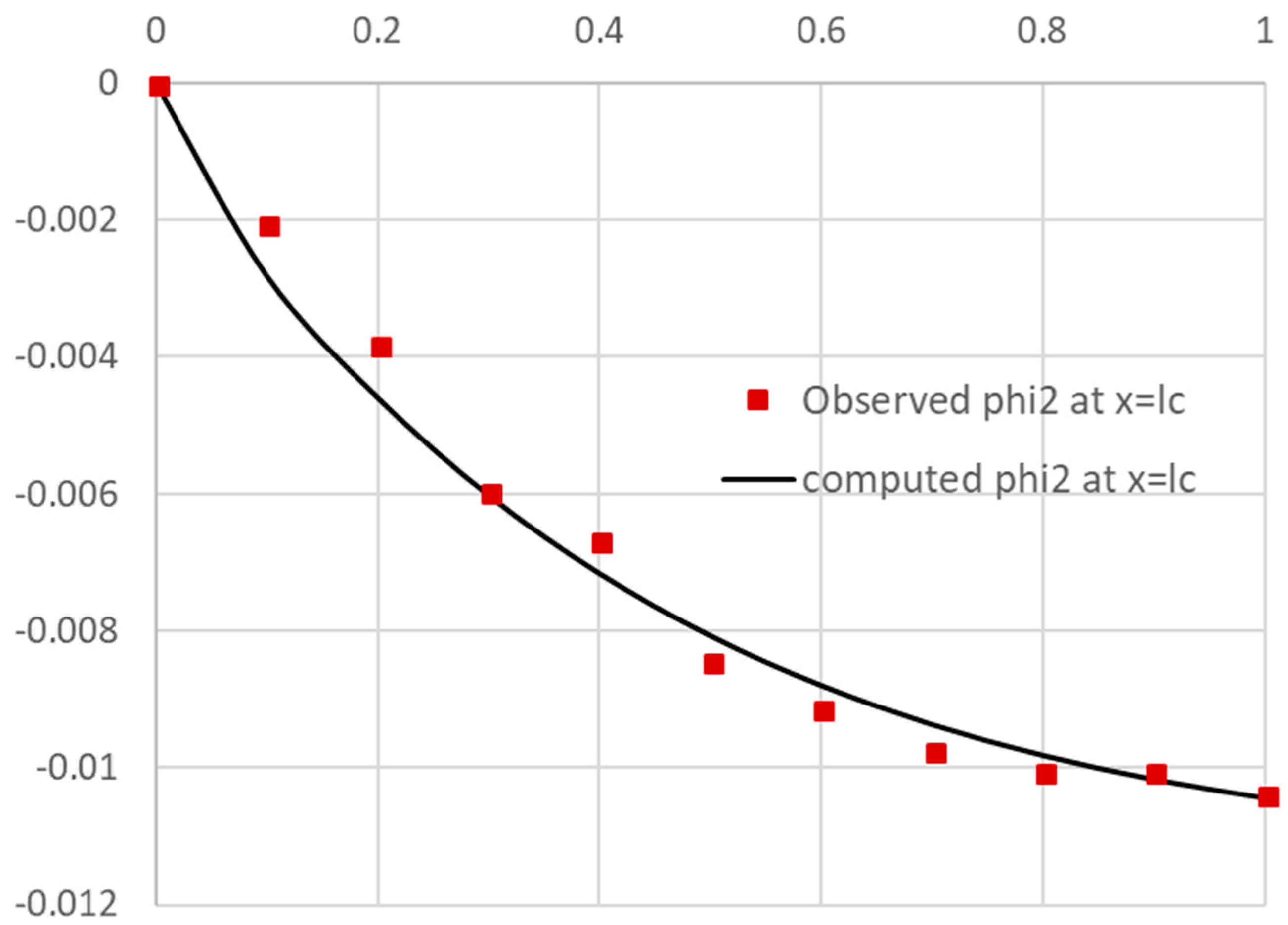
- We obtain an initial solution of the parameterized PDAE model in an allocated array of the spreadsheet as shown in Figure 10. Depending on the problem requirements, it may be advantageous to switch between a transient or snapshot format for the output layout, as well as customize the output to display values of interest.
- Task 2:
- Based on the output result obtained in Task 1 and given observed values, we define an objective formula to be minimized. The objective formula calculates the summation of the square residuals between the observed values and their corresponding computed values from the output result. The spreadsheet is perfectly suited for performing this task given its AutoFill feature and built in math function SUM. Definition of the objective formula for our example is shown in cell S2 of Figure 14. The definition is based on the computed values shown in Figure 10 and observed values stored in range V18:V27.
- Task 3:
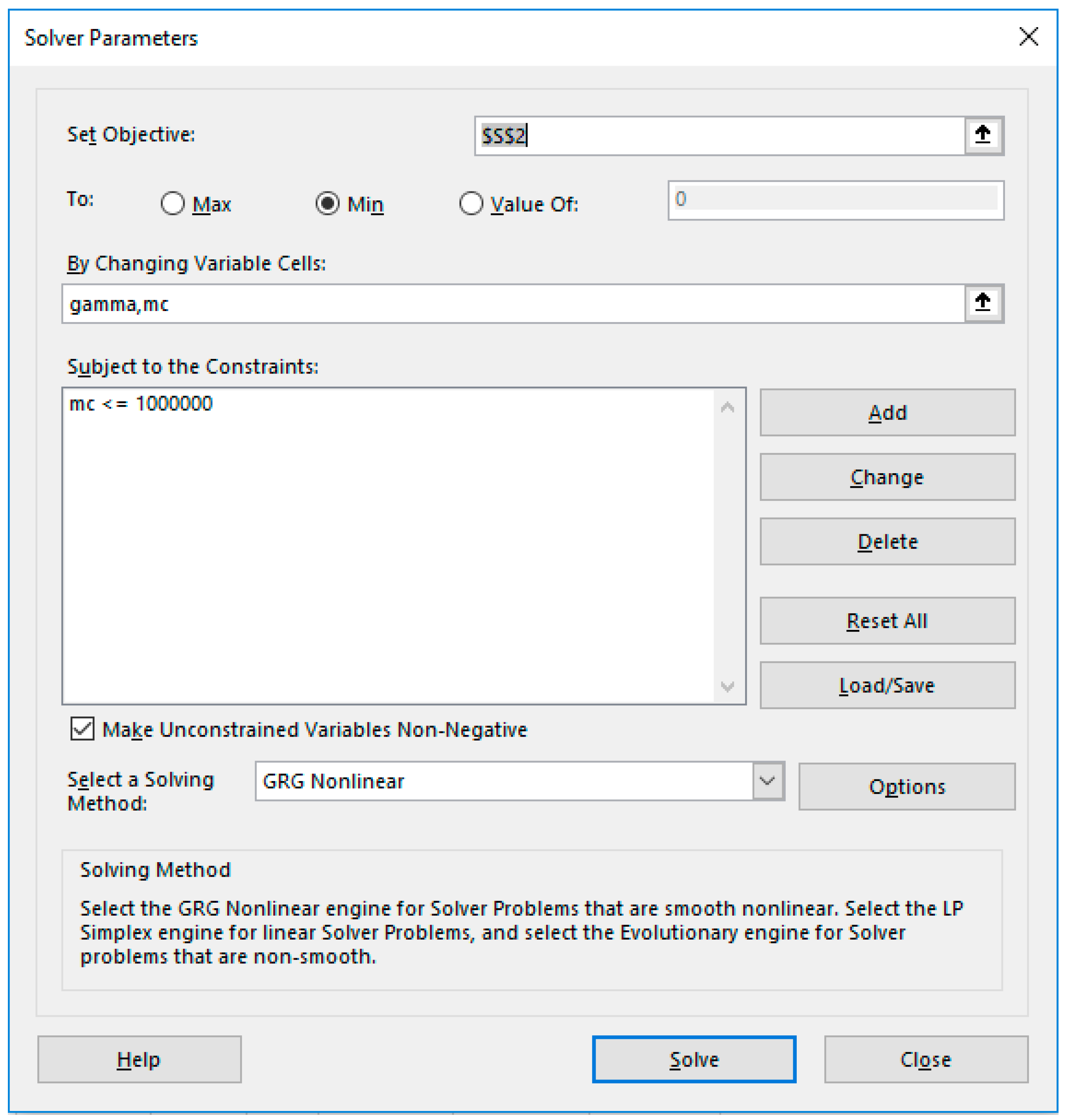
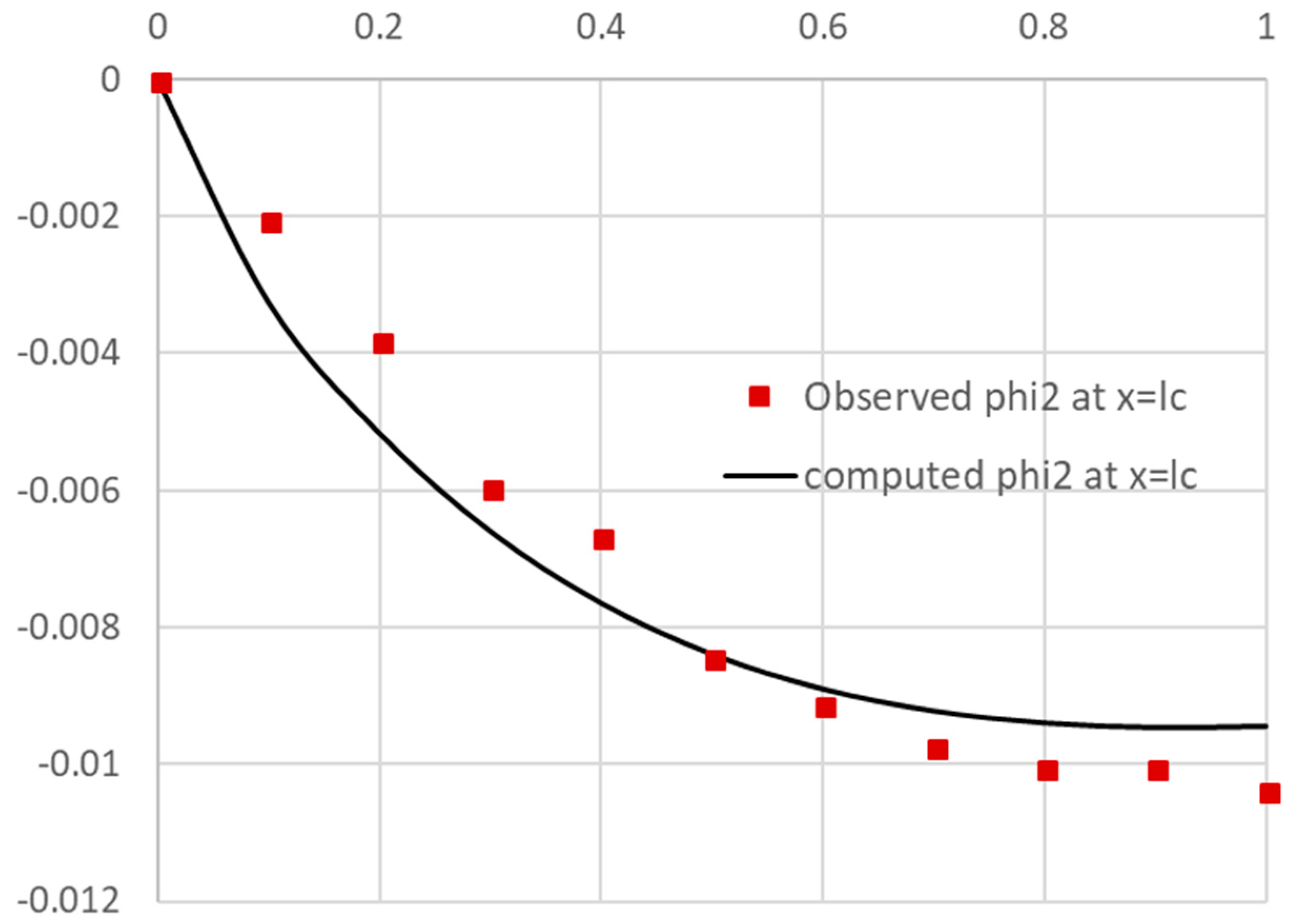
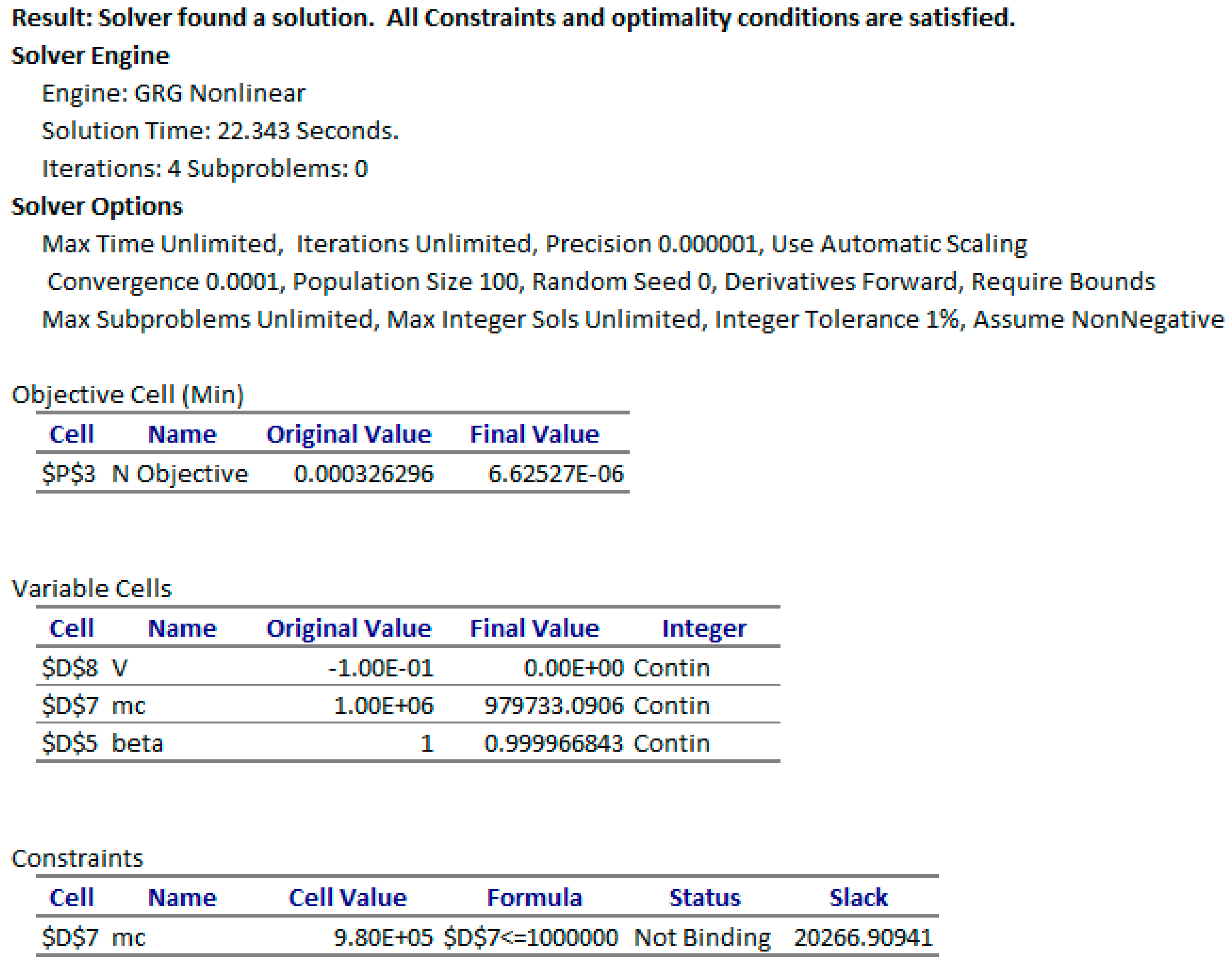
- The remaining task is to configure and run the Excel NLP solver command. Excel solver is invoked from the Data Tab in the Ribbon and displays a simple dialog, which can be configured to minimize or maximize an objective formula by changing variables cells, subject to added constraint formulas. Figure 15 shows the configuration for our example, where we select to minimize the objective Formula S2, by varying gamma and mc variable cells, subject to the upper bound constraint mc ≤ 10 × 106. The bound constraint was added for numerical stability since larger values for the off-diagonal mass matrix element leads to a divergent system. We have also imposed the condition that gamma and mc are nonnegative as shown in Figure 15. We ran the solver that reported a feasible solution in about 48 s of computing time as shown in the Answer Report generated by the solver in Figure 16. The Answer Report shows the original objective value of 3.26 × 10−4 has been reduced to 1.89 × 10−6 in 11 iterations. Upon accepting the solution, Excel automatically updates the spreadsheet to reflect the optimal computed values. The optimized PDAE solution for phi2 is shown in Figure 17, exhibiting excellent agreement with observed values.
5.1. Relative Influence of Design Parameters
5.2. Investigating Effect of Initial Condition and Additional Parameters
6. Alternative Spreadsheet Dynamical Minimization Strategy
7. Conclusions
Supplementary Materials
Conflicts of Interest
Appendix A. Spreadsheet Tips
- Naming spreadsheet variables (e.g., B1 as t) makes it easier to read the formulas and to spot errors. However, it is also recommended to restrict the scope of a named variable to the specific sheet it will be used on, and not the whole workbook. This prevents accidental interdependence between multiple problems on different sheets sharing same named variables. Defining and restricting the scope of named variables is done using the Name Manager in Excel.
- Excel gives precedence to the unary negation operator over the power operator ‘^’. For example, Excel evaluates the formula ‘=−X1^2′ as ‘=(−X1)^2′ when the intention may have been to do ‘-(X1^2)’ instead. A simple fix is to use parentheses or to use the POWER function instead of the operator ‘^’. When using the IF statement in a formula, it is also important to verify the formula always evaluates to a numeric value for all possible conditions. Otherwise, the formula may evaluate to a nonnumeric Boolean condition leading to solver error.
- PDASOLVE function is designed to operate in two modes: a silent mode where only standard spreadsheet errors are returned like #VALUE! and a verbose mode where the function may display informative error or warning message alert in a popup window. It is recommended to work in the verbose mode when modeling and solving a PDAE problem, but switch to the silent mode before running the NLP Solver. Switching between the two modes is triggered by evaluating the formula ‘=VERBOSE(TRUE)’ or ‘=VERBOSE(FALSE)’ in any cell in the workbook. This was not needed in the example of this paper but for other problems, it is possible the NLP Solver may wander into illegal input space before it recovers and adjusts its search. The silent mode blocks any occasional error alerts from the calculus functions. Switching to the silent mode is not required with the alternative NLSOLVE method.
References
- Ghaddar, C.K. Unconventional Calculus Spreadsheet Functions. World Academy of Science, Engineering and Technology, International Science Index 112. Int. J. Math. Comput. Phys. Electr. Comput. Eng. 2016, 10, 160–166. Available online: http://waset.org/publications/10004374 (accessed on 1 August 2018).
- Schittkowski, K. Numerical Data Fitting in Dynamical Systems: A Practical Introduction with Applications and Software; Springer: New York, NY, USA, 2002. [Google Scholar]
- Gieschke, R.; Serafin, D. Development of Innovative Drugs via Modeling with MATLAB: A Practical Guide; Springer: New York, NY, USA, 2014. [Google Scholar]
- Lasdon, L.S.; Waren, A.D.; Jain, A.; Ratner, M. Design and Testing of a Generalized Reduced Gradient Code for Nonlinear Programming. ACM Trans. Math. Softw. 1978, 4, 34–50. [Google Scholar] [CrossRef]
- Schiesser, W.E. The Numerical Method of Lines; Academic Press: San Diego, CA, USA, 1991. [Google Scholar]
- Lam, C.-Y.; Alan Koh, F.H. A Partial Differential Equation Solver for the Classroom. Int. J. Eng. Ed. 2006, 22, 868–875. [Google Scholar]
- Hagler, M. Spreadsheet Solution of Partial Differential Equations. IEEE Trans. Educ. 1987, 3, 130–134. [Google Scholar] [CrossRef]
- Fae’q, A.A. Solutions of Partial Differential Equations Using Excel. Pak. J. Appl. Sci. 2001, 1, 458–465. [Google Scholar]
- Olsthoorn, T.N. Groundwater Modelling: Calibration and the Use of Spreadsheets; Delft University Press: Delft, The Netherlands, 1998. [Google Scholar]
- Karahan, H. Unconditional stable explicit finite difference technique for the advection-diffusion equation using spreadsheets. Adv. Eng. Softw. 2007, 38, 80–86. [Google Scholar] [CrossRef]
- Karahan, H.; Ayvaz, M.T. Time-Dependent Groundwater Modelling Using Spreadsheets. Comput. Appl. Eng. Educ. 2005, 13, 192–199. [Google Scholar] [CrossRef]
- Karahan, H. Implicit finite difference techniques for the advection-diffusion equation using spreadsheets. Adv. Eng. Softw. 2006, 37, 601–608. [Google Scholar] [CrossRef]
- Bhattacharjya, R.K. Solving groundwater flow inverse problem using spreadsheet solver. J. Hydrol. Eng. 2011, 16, 472–477. [Google Scholar] [CrossRef]
- Karahan, H. Predicting Muskingum flood routing parameters using spreadsheets. Comput. Appl. Eng. Educ. 2012, 20, 280–286. [Google Scholar] [CrossRef]
- Ghaddar, C.K. Method, Apparatus, and Computer Program Product for Optimizing Parameterized Models Using Functional Paradigm of Spreadsheet Software. U.S. Patent 9,286,286, 15 March 2016. [Google Scholar]
- Ghaddar, C.K. Method, Apparatus, and Computer Program Product for Solving Equation System Models Using Spreadsheet Software. U.S. Patent 9,892,108, 13 February 2018. [Google Scholar]
- Ghaddar, C.K. Method, Apparatus, and Computer Program Product for Solving an Equation System Using Pure Spreadsheet Functions. USA Patent. to be Issued 2018, in press.
- Levenberg, K. A Method for the Solution of Certain Non-Linear Problems in Least Squares. Q. Appl. Math. 1944, 2, 164–168. [Google Scholar] [CrossRef]
- Marquardt, D. An Algorithm for Least-Squares Estimation of Nonlinear Parameters. SIAM J. Appl. Math. 1963, 11, 431–441. [Google Scholar] [CrossRef]
- Hairer, E.; Wanner, G. Solving Ordinary Differential Equations II: Stiff and Differential-Algebraic Problems; Springer: Berlin/Heidelberg, Germany, 1996. [Google Scholar]
- Ghaddar, C.K. Unlocking the Spreadsheet Utility for Calculus: A Pure Worksheet Solver for Differential Equations. Spreadsheets Educ. 2016, 9, 5. [Google Scholar]
- ExceLab Calculus Add-in for Excel and Reference Manual. Available online: https://excel-works.com (accessed on 1 August 2018).
- Madsen, N.K.; Sincovec, R.F. Software for Partial Differential Equations. In Numerical Methods for Differential Systems; Lapidus, L., Schiesser, W.E., Eds.; Academic Press: New York, NY, USA, 1976. [Google Scholar]
- Ghaddar, C.K. Novel Spreadsheet Direct Method for Optimal Control Problems. Math. Comput. Appl. 2018, 23, 6. [Google Scholar] [CrossRef]











| Time Interval | |
| Spatial Domain | |
| Initial Values | |
| Left Boundary Conditions | |
| Right Boundary Conditions |
| x | ∆u(x, 1) | ∆u(x, 1) | ∆u(x, 2) | ∆v(x, 2) |
|---|---|---|---|---|
| 0.05 | −0.00161 | 0.001883 | −0.01313 | 0.016772 |
| 0.1 | −0.00768 | 0.003858 | −0.06329 | 0.034044 |
| 0.15 | −0.00233 | 0.005022 | −0.01932 | 0.044291 |
| 0.2 | 0.000774 | 0.005024 | 0.006273 | 0.044588 |
| 0.25 | 0.001279 | 0.004289 | 0.010422 | 0.038574 |
| 0.3 | 0.001003 | 0.003155 | 0.008158 | 0.028998 |
| 0.35 | 0.000714 | 0.001945 | 0.005796 | 0.018687 |
| 0.4 | 0.000539 | 0.000855 | 0.00435 | 0.00929 |
| 0.45 | 0.000441 | −1.1 × 10−6 | 0.003543 | 0.001819 |
| 0.5 | 0.000381 | −0.0006 | 0.003056 | −0.0035 |
| 0.55 | 0.000338 | −0.00095 | 0.002701 | −0.00678 |
| 0.6 | 0.000299 | −0.00111 | 0.002391 | −0.00832 |
| 0.65 | 0.000261 | −0.0011 | 0.002086 | −0.00848 |
| 0.7 | 0.000222 | −0.00095 | 0.001773 | −0.00741 |
| 0.75 | 0.000181 | −0.00066 | 0.001446 | −0.0052 |
| 0.8 | 0.00014 | −0.00019 | 0.001118 | −0.00138 |
| 0.85 | 0.000106 | 0.000522 | 0.000849 | 0.004463 |
| 0.9 | 9.24 × 10−5 | 0.001689 | 0.000741 | 0.014098 |
| 0.95 | −6.1 × 10−5 | 0.003434 | −0.00051 | 0.028505 |
| 1.0 | 0.005702 | 0.006291 | 0.047117 | 0.052134 |
| Fixed Parameters | Design Parameters | Initial Conditions |
|---|---|---|
| 254 | ||
| Excel Range | Assigned Name |
|---|---|
| B21:B23 | Eqns |
| B2:B12 | Vars |
| F:2:H9 | BCs |
| D14:E14 | xDom |
| D15:E15 | tDom |
| C10:E12 | M |
| C21:D23 | Rgns |
| t | Ratio at lc | Ratio at ls |
|---|---|---|
| 0.1 | 2.000009 | 0.501111 |
| 0.2 | 1.9999213 | 0.501085 |
| 0.3 | 1.9998514 | 0.50106 |
| 0.4 | 1.9997839 | 0.501037 |
| 0.5 | 1.9997196 | 0.501014 |
| 0.6 | 1.999658 | 0.500993 |
| 0.7 | 1.9995992 | 0.500973 |
| 0.8 | 1.9995428 | 0.500954 |
| 0.9 | 1.999489 | 0.500936 |
| 1 | 1.9994374 | 0.500918 |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ghaddar, C.K. Rapid Modeling and Parameter Estimation of Partial Differential Algebraic Equations by a Functional Spreadsheet Paradigm. Math. Comput. Appl. 2018, 23, 39. https://doi.org/10.3390/mca23030039
Ghaddar CK. Rapid Modeling and Parameter Estimation of Partial Differential Algebraic Equations by a Functional Spreadsheet Paradigm. Mathematical and Computational Applications. 2018; 23(3):39. https://doi.org/10.3390/mca23030039
Chicago/Turabian StyleGhaddar, Chahid Kamel. 2018. "Rapid Modeling and Parameter Estimation of Partial Differential Algebraic Equations by a Functional Spreadsheet Paradigm" Mathematical and Computational Applications 23, no. 3: 39. https://doi.org/10.3390/mca23030039
APA StyleGhaddar, C. K. (2018). Rapid Modeling and Parameter Estimation of Partial Differential Algebraic Equations by a Functional Spreadsheet Paradigm. Mathematical and Computational Applications, 23(3), 39. https://doi.org/10.3390/mca23030039





