Nonlinear Elimination of Drugs in One-Compartment Pharmacokinetic Models: Nonstandard Finite Difference Approach for Various Routes of Administration
Abstract
:1. Introduction
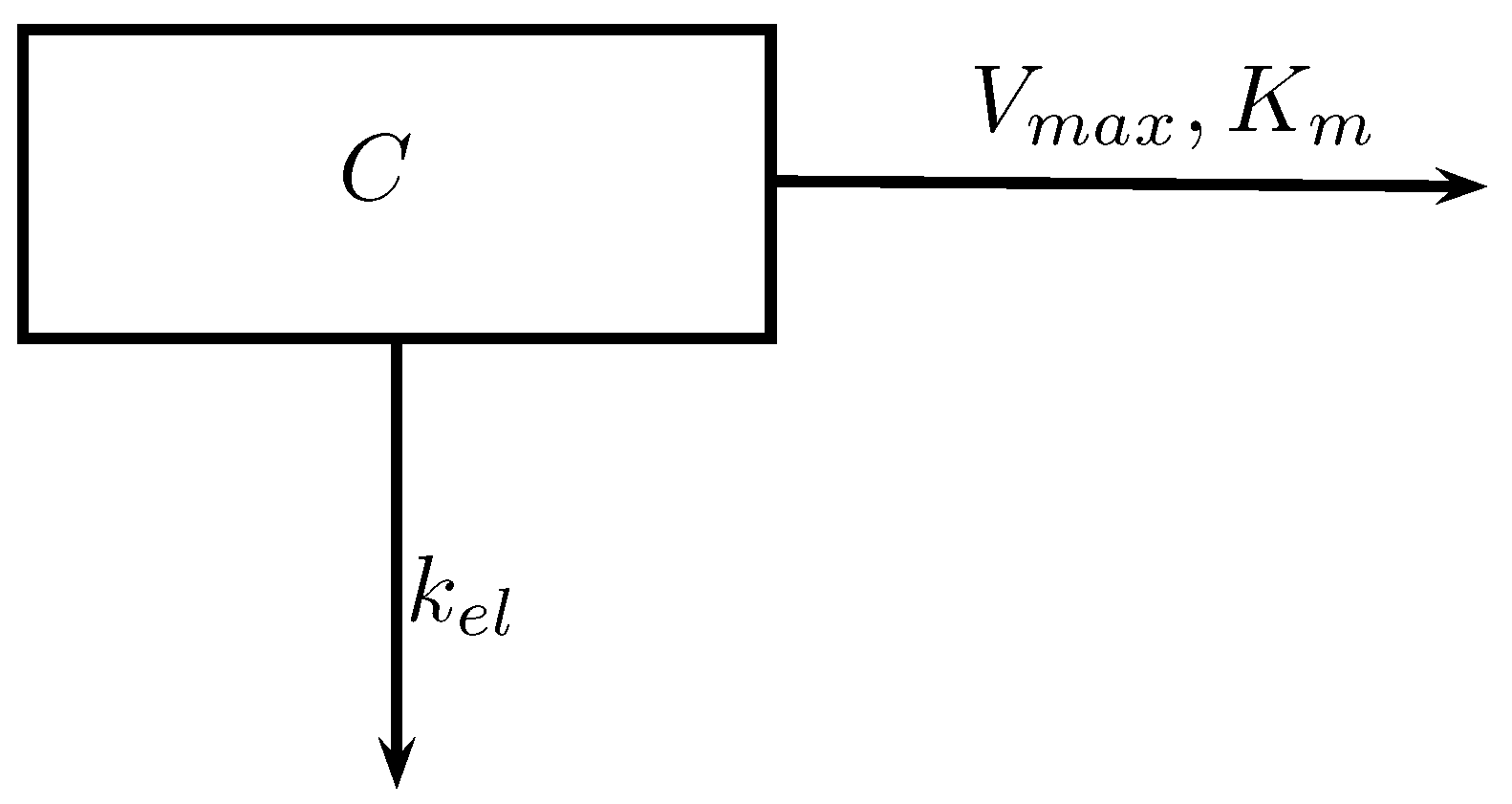
- One-compartment model—I.V. bolus injection,
- One-compartment model—I.V. bolus infusion,
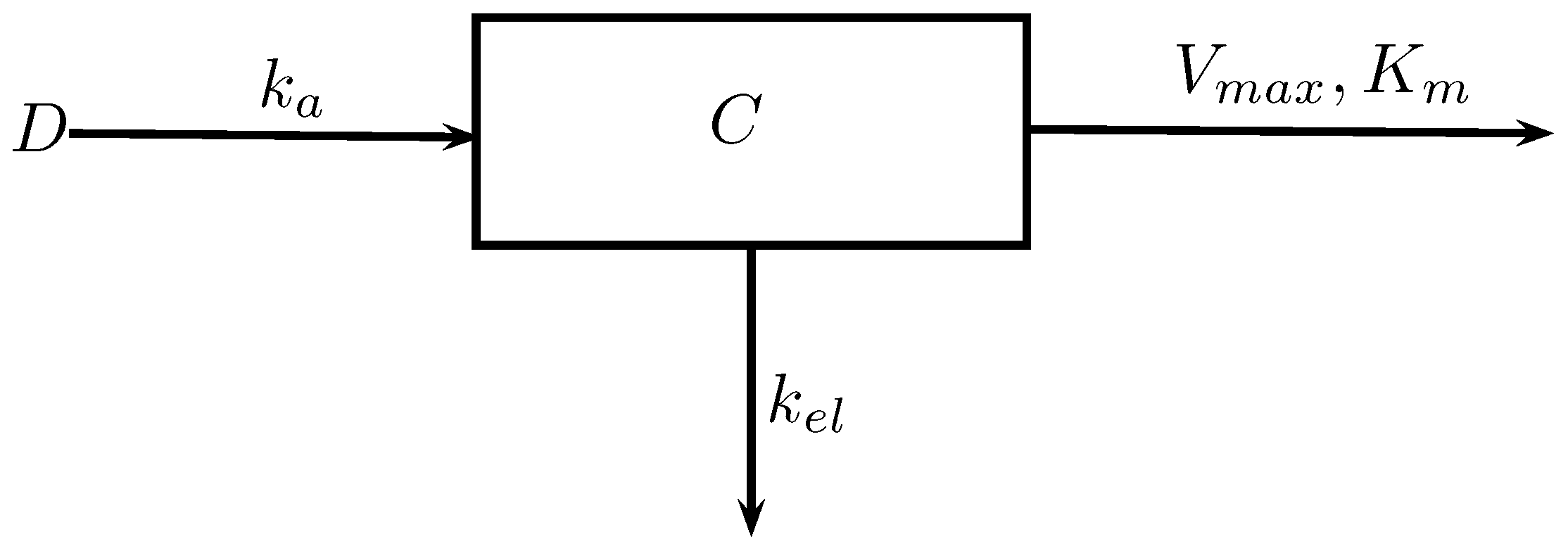
- One-compartment model—Extravascular administration.
- C: Drug concentration in the central compartment.
- : The maximum rate of change of concentration.
- : The Michaelis-Menten constant.
- : The absorption rate constant for oral administration.
- : Elimination rate of the drug leaving the central compartment.
- : The apparent volume of distribution.
2. Methods
2.1. NSFD Modeling Fundamental Principles
- Rule 1
- The orders of the discrete representation of the derivative must be equal to the orders of the corresponding derivatives appearing in the differential equations.
- Rule 2
- Denominator functions for the discrete representations for derivatives must, in general, be expressed in terms of more complicated functions of the step-sizes than those conventionally used.
- Rule 3
- Nonlinear terms must, in general, be modeled by nonlocal discrete representations.
- Rule 4
- All the special conditions that correspond to either the differential equation and/or its solutions should also correspond to the difference equation and/or its solutions.
- Rule 5
- The discrete scheme should not introduce extraneous or spurious solutions.
2.2. Runge-Kutta Method
3. Results
3.1. I.V. Bolus Injection
- (i)
- if , monotonically tends to 0,
- (ii)
- if , for ,
- (iii)
- if , tends to 0 with an oscillating amplitude via an alternating sign at each step,
- (iv)
- if , oscillates with a constant amplitude , and
- (v)
- if , oscillates with an increasing amplitude,
3.1.1. I.V. Bolus Injection: Nonlinear Pharmacokinetic Elimination
Case 1: Semi-Implicit Forward-Euler
Case 2: Implicit Forward-Euler
Case 3: Explicit Forward-Euler
3.1.2. I.V. Bolus Injection: Mixed Drug Elimination
3.2. I.V. Bolus Infusion
- (i)
- if , monotonically tends to ,
- (ii)
- if , for ,
- (iii)
- if , tends to with an oscillating amplitude via an alternating sign at each step,
- (iv)
- if , oscillates with a constant amplitude , and
- (v)
- if , oscillates with an increasing amplitude.
3.2.1. I.V. Bolus Infusion: Nonlinear Pharmacokinetic Elimination
3.2.2. I.V. Bolus Infusion: Mixed Drug Elimination
3.3. Extravasular Administration
3.3.1. Extravasular Administration: Linear Pharmacokinetic Elimination
3.3.2. Extravascular Administration: Mixed Drug Elimination
4. Numerical Simulations and Discussion
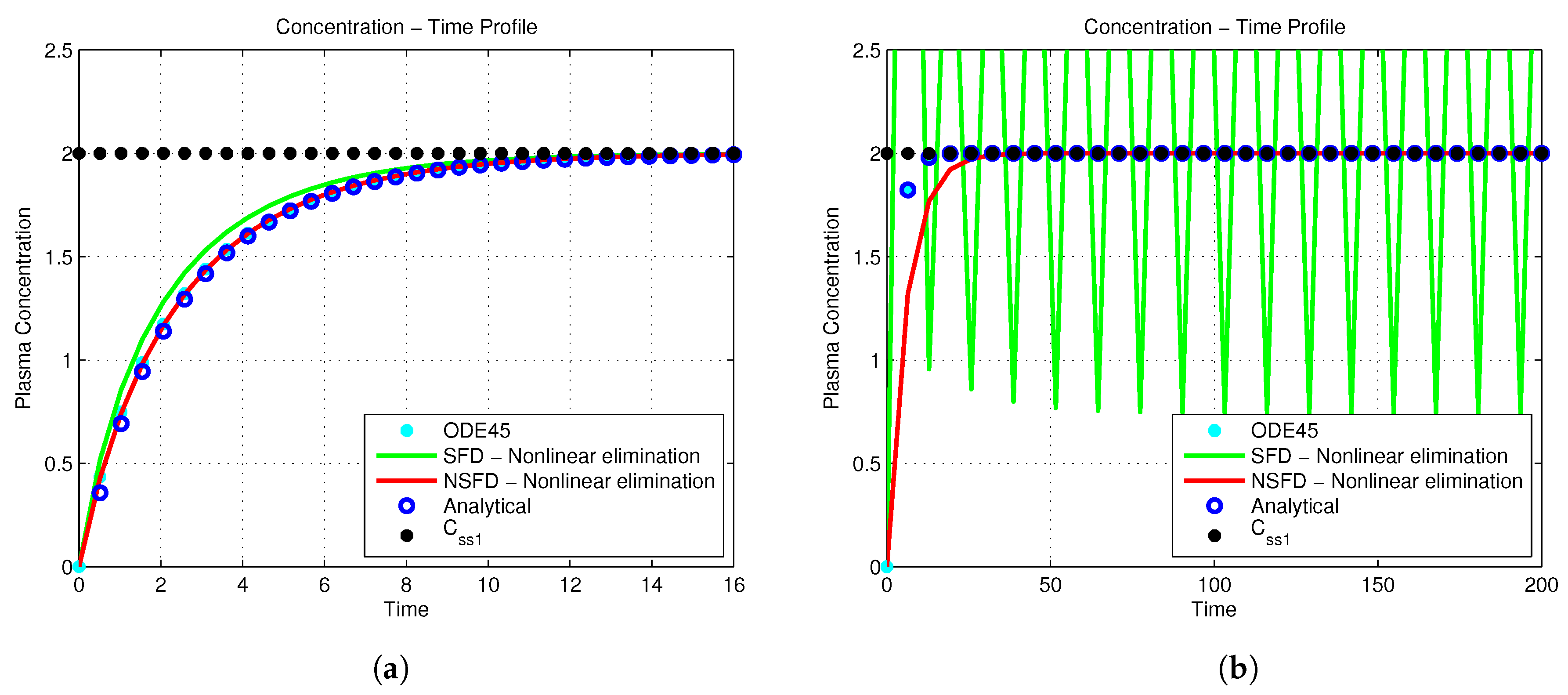
4.1. I.V. Bolus Injection: Simulations
4.1.1. Results Describing Nonlinear Pharmacokinetic Elimination
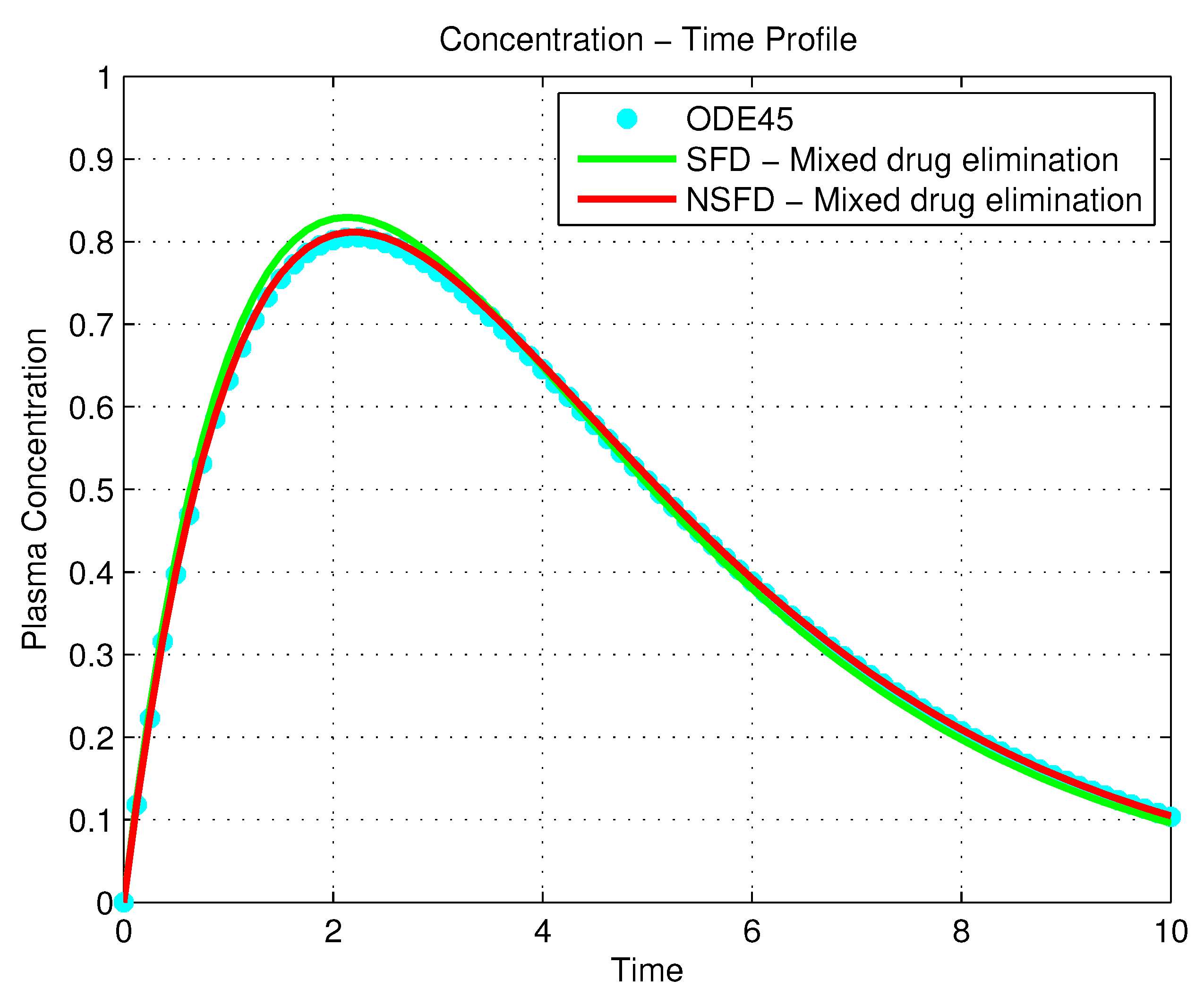
4.1.2. Results Describing Mixed Drug Elimination
4.2. I.V. Bolus Infusion: Simulations
4.2.1. Results Describing Nonlinear Pharmacokinetic Elimination
4.2.2. Results Describing Mixed Drug Elimination
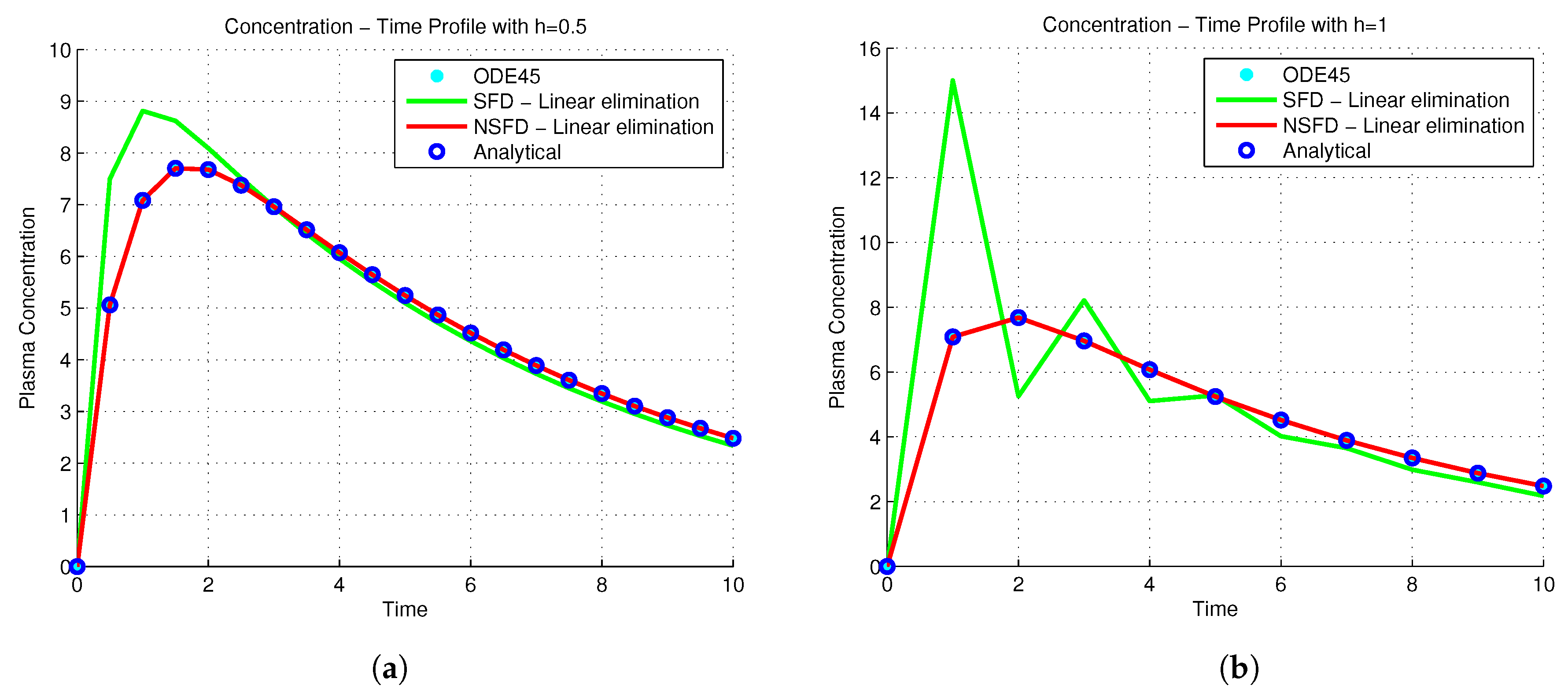
4.3. Extravasular Administration: Simulations
4.3.1. Results Describing Linear Pharmacokinetic Elimination
4.3.2. Results Describing Mixed Drug Elimination
5. Conclusions
Acknowledgments
Conflicts of Interest
Abbreviations
| PK | pharmacokinetic |
| I.V. | intravenous |
| NSFD | nonstandard finite difference |
| SFD | standard finite difference |
| Exact FD | exact finite difference |
| GIT | gastrointestinal tract |
References
- Widmark, E.M.P. Die Theoretischen Grundlagen und die Praktische Verwendbzrkeit der Gerichtlichmedizinischen Alkoholbestimmung; Urban & Schwarzenberg: Berlin, Germany, 1932. [Google Scholar]
- Shargel, L.; Yu, A.; Wu-Pong, S. Introduction to Biopharmaceutics and Pharmacokinetics. In Applied Biopharmaceutics & Pharmacokinetics, 6th ed.; McGraw-Hill: New York, NY, USA, 2012; Chapter 1; pp. 1–17. [Google Scholar]
- Shargel, L.; Yu, A.; Wu-Pong, S. Multicompartment Models: Intravenous Bolus Administration. In Applied Biopharmaceutics & Pharmacokinetics, 6th ed.; McGraw-Hill: New York, NY, USA, 2012; Chapter 4; pp. 58–79. [Google Scholar]
- Beňová, M.; Gombárska, D.; Dobrcký, B. Using Euler’s and Taylor’s expansion method for solution of non-linear differential equation system in pharmacokinetics. Electr. Rev. 2013, 89, 259–261. [Google Scholar]
- Sharma, K.R. On single compartment pharmacokinetics model systems that obey Michaelis-Menten kinetics and systems that obey Krebs Cycle kinetics. JEAS 2011, 1, 43–50. [Google Scholar] [CrossRef]
- Mickens, R.E. Lie methods in mathematical modelling: Difference equation models of differential equation. Math. Comput. Model. 1988, 11, 528–530. [Google Scholar] [CrossRef]
- Villatoro, F.R. Exact finite-difference methods based on nonlinear means. J. Differ. Equ. Appl. 2008, 14, 681–691. [Google Scholar] [CrossRef]
- Roeger, L.W. Exact finite-difference schemes for two-dimensional linear systems with constant coefficients. J. Comput. Appl. Math. 2008, 219, 102–109. [Google Scholar] [CrossRef]
- Ibijola, E.A.; Obayomi, A.A. Derivation of new non-standard finite difference schemes for non-autonomous ordinary differential equation. AJSIR 2012. [Google Scholar] [CrossRef]
- Manning, P.M.; Margrave, G.F. Introduction to Non-Standard Finite-Difference Modelling; CREWES Research Report 18; CREWES: Calgary, AL, Canada, 2006. [Google Scholar]
- Mickens, R.E. Exact solutions to a finite-difference model of a nonlinear reaction-advection equation: Implications for numerical analysis. J. Differ. Equ. Appl. 1989, 9, 995–1006. [Google Scholar] [CrossRef]
- Mickens, R.E. Application of Nonstandard Finite Difference Schemes, 1st ed.; World Scientific: Singapore, 2000. [Google Scholar]
- Mickens, R.E. Nonstandard finite difference schemes for differential equations. J. Differ. Equ. Appl. 2002, 8, 823–847. [Google Scholar] [CrossRef]
- Mickens, R.E. A nonstandard finite difference scheme for the diffusionless Burgers equation with logistic reaction. Math. Comput. Simul. 2003, 62, 117–124. [Google Scholar] [CrossRef]
- Mickens, R.E. Dynamic consistency: A fundamental principle for constructing nonstandard finite difference schemes for differential equations. J. Differ. Equ. Appl. 2005, 11, 645–653. [Google Scholar] [CrossRef]
- Mickens, R.E. A numerical integration technique for conservative oscillators combining nonstandard finite-difference methods with a Hamilton’s principle. J. Sound Vib. 2005, 285, 477–482. [Google Scholar] [CrossRef]
- Sunday, J. On exact finite-difference scheme for numerical solution of initial value problems in ordinary differential equations. PJST 2010, 11, 260–267. [Google Scholar]
- Gander, J.J.; Meyer-Spasche, R. An introduction to numerical integrators preserving physical properties. In Applications of Nonstandard Finite Difference Schemes; Mickens, R.E., Ed.; World Scientific: Singapore, 2000; Volume 1, pp. 181–246. [Google Scholar]
- Mickens, R.E. Nonstandard Finite Difference Models of Differential Equations; World Scientific: Singapore, 1994. [Google Scholar]
- Mickens, R.E. Difference equation models of differential equations. Math. Comput. Model. 1988, 11, 528–530. [Google Scholar] [CrossRef]
- Anguelov, R.; Lubuma, J.M.-S. Nonstandard finite difference method by nonlocal approximation. Math. Comput. Simul. 2003, 61, 465–475. [Google Scholar] [CrossRef]
- Egbelowo, O.; Harley, C.; Jacobs, B. Nonstandard finite difference method applied to a linear pharmacokinetics model. Bioengineering 2017, 4, 40. [Google Scholar] [CrossRef] [PubMed]
- Shargel, L.; Wu-Pong, S.; Yu, A. Introduction to Biopharmaceutics and Pharmacokinetics. In Applied Biopharmaceutics & Pharmacokinetics, 5th ed.; McGraw-Hill: New York, NY, USA, 2007; Chapter 9; pp. 159–180. [Google Scholar]
- Sanyi, T.; Yanni, X. One-compartment model with Michaelis-Menten elimination kinetics and therapeutic window: An analytical approach. J. Pharmacokinet. Pharmacodyn. 2007, 34, 807–827. [Google Scholar]
- Mickens, R.E. An exact discretization of Michaelis-Menten type population equations. J. Biol. Dyn. 2011, 5, 391–397. [Google Scholar] [CrossRef]
- Chapwanya, M.; Lubuma, J.M.-S.; Mickens, R.E. From enzyme kinetics to epidemiological models with Michaelis–Menten contact rate: Design of nonstandard finite difference schemes. Comput. Math. Appl. 2012, 64, 201–213. [Google Scholar] [CrossRef]
- Chapwanya, M.; Lubuma, J.M.-S.; Mickens, R.E. Nonstandard Finite Difference Schemes for Michaelis-Menten Type Reaction-Diffusion Equations. Available online: http://onlinelibrary.wiley.com/doi/10.1002/num.21733/epdf (accessed on 6 September 2017).
- Shargel, L.; Wu-Pong, S.; Yu, A. Introduction to Biopharmaceutics and Pharmacokinetics. In Applied Biopharmaceutics & Pharmacokinetics, 5th ed.; McGraw-Hill: New York, NY, USA, 2007; Chapter 7; pp. 116–136. [Google Scholar]







| Absolute Error for C | |||
|---|---|---|---|
| N | h | Error in Scheme 50 (SFD) | Error in Scheme 49 (NSFD) |
| 2 | 4.000 | 1.027 | 0.108 |
| 4 | 2.000 | 0.338 | 0.030 |
| 8 | 1.000 | 0.115 | 0.007 |
| 16 | 0.500 | 0.051 | 0.002 |
| 32 | 0.250 | 0.024 | 0.000 |
| 64 | 0.125 | 0.012 | 0.000 |
| 128 | 0.062 | 0.006 | 0.000 |
| 256 | 0.031 | 0.003 | 0.000 |
| 512 | 0.016 | 0.001 | 0.000 |
| 1024 | 0.008 | 0.001 | 0.000 |
| Numerical Results | |||||
|---|---|---|---|---|---|
| h | Euler | Heun | Runge-Kutta | Exact FD | Exact |
| 0.0 | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.00000 |
| 0.1 | 0.15000 | 0.13763 | 0.13823 | 0.13823 | 0.13823 |
| 0.2 | 0.27525 | 0.25411 | 0.25514 | 0.25514 | 0.25514 |
| 0.3 | 0.37950 | 0.35241 | 0.35374 | 0.35374 | 0.35374 |
| 0.4 | 0.46592 | 0.43508 | 0.43661 | 0.43661 | 0.43661 |
| 0.5 | 0.53723 | 0.50432 | 0.50597 | 0.50597 | 0.50597 |
| 0.6 | 0.59573 | 0.56203 | 0.56373 | 0.56374 | 0.56374 |
| 0.7 | 0.64337 | 0.60983 | 0.61154 | 0.61154 | 0.61154 |
| 0.8 | 0.68180 | 0.64912 | 0.65080 | 0.65081 | 0.65081 |
| 0.9 | 0.71245 | 0.68112 | 0.68275 | 0.68275 | 0.68275 |
| 1.0 | 0.73651 | 0.70686 | 0.70842 | 0.70842 | 0.70842 |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Egbelowo, O. Nonlinear Elimination of Drugs in One-Compartment Pharmacokinetic Models: Nonstandard Finite Difference Approach for Various Routes of Administration. Math. Comput. Appl. 2018, 23, 27. https://doi.org/10.3390/mca23020027
Egbelowo O. Nonlinear Elimination of Drugs in One-Compartment Pharmacokinetic Models: Nonstandard Finite Difference Approach for Various Routes of Administration. Mathematical and Computational Applications. 2018; 23(2):27. https://doi.org/10.3390/mca23020027
Chicago/Turabian StyleEgbelowo, Oluwaseun. 2018. "Nonlinear Elimination of Drugs in One-Compartment Pharmacokinetic Models: Nonstandard Finite Difference Approach for Various Routes of Administration" Mathematical and Computational Applications 23, no. 2: 27. https://doi.org/10.3390/mca23020027
APA StyleEgbelowo, O. (2018). Nonlinear Elimination of Drugs in One-Compartment Pharmacokinetic Models: Nonstandard Finite Difference Approach for Various Routes of Administration. Mathematical and Computational Applications, 23(2), 27. https://doi.org/10.3390/mca23020027





