1. Introduction
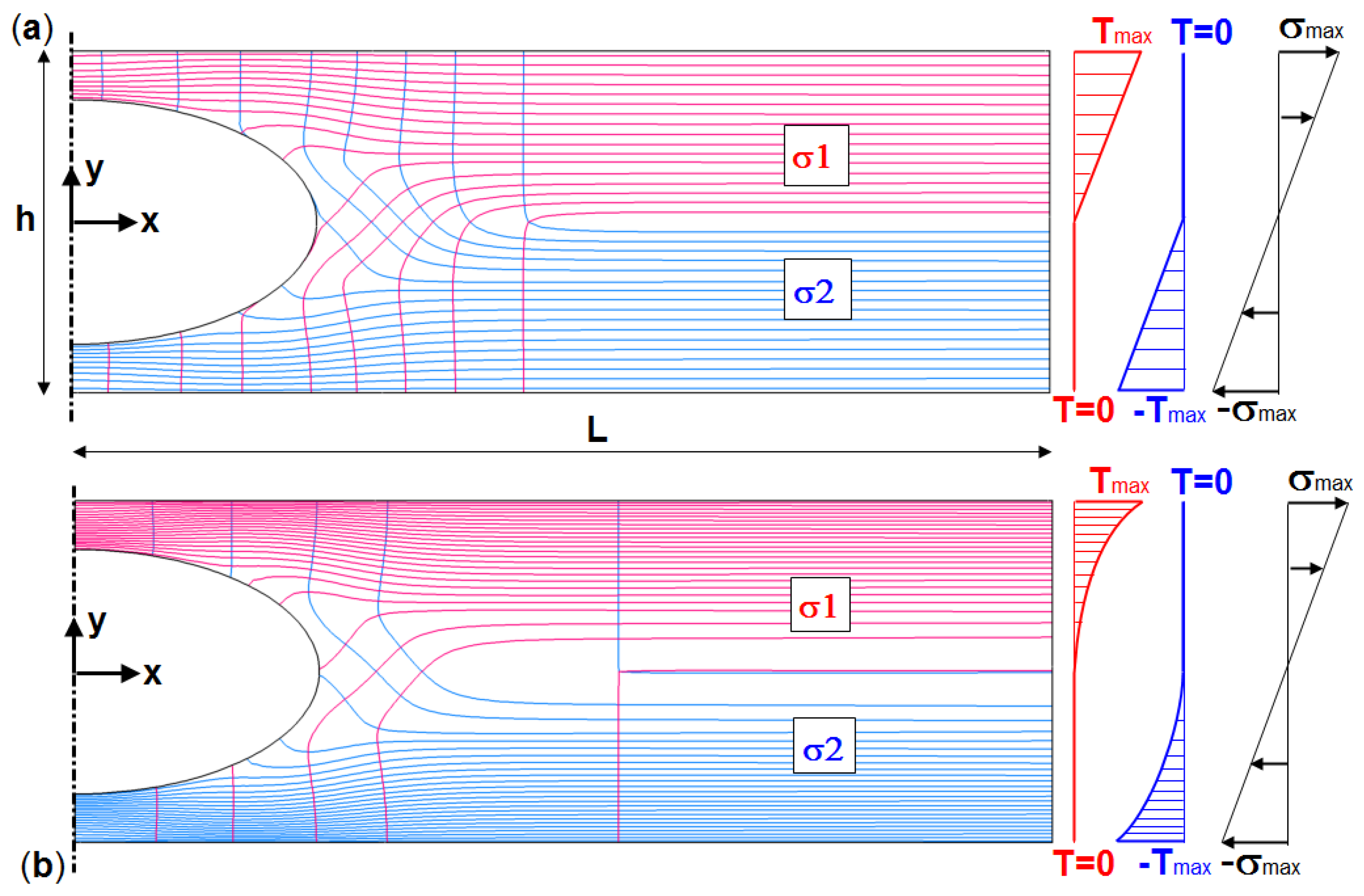
Orthotropic materials can have extremely different thermal conductivities, for example, in printed circuit boards. The tracks conducting current are made of copper (Cu) and are electrically insulated against the plastic plate. Due to its low thermal conductivity (k
2), the Cu conducting track (k
1) is heated to a constant, relatively high temperature. It can be considered as an isothermal line. The thermal heat flow in the plastic due to conduction is very low. For example, if there are two Cu conducting tracks with constant but different temperatures, then a steady temperature gradient independent of k
2 prevails in the plastic between them, even if k
2→0. The Cu-tracks can be described by their position y = y(x), and they control the temperature distribution in the insulator. Alternatively, the position can be described by y’(x) together with their starting positions. If these tracks are infinitely densely distributed, the direction field of the Cu-conductance k
1 is described by y´ = f(x,y). Insulation works perpendicular to the Cu-tracks when k
2 << k
1. Should the (infinitely densely) guided conduction paths be directed parallel to an arbitrary direction field y’ = f(x,y), then the following hypothesis shall be mathematically verified:
Hypothesis: The isotherms of an orthotropic steady-state 2D thermal conduction problem with the thermal conductivities k1 and k2 are tangential to an arbitrarily prescribed direction field y´ = f(x,y) provided that the local orientation of k1 follows the direction field y´, and perfect insulation exists perpendicular to this (k2 = 0).
The integration method, which can be derived from the hypothesis, is the topic of the dissertation by the author [
1]; however, this was published without mathematical verification. Two-dimensional direction fields of the type y´ = f(x,y) can describe physically different processes. In fluid mechanics, the vectorial direction field y´ = v(x,y)/u(x,y) of the velocity components u and v are tangential to the streamlines. The general solution of the direction field to be integrated provides the flow field in the form of streamlines. This task is solved by default in Computational Fluid Dynamics (CFD) codes and is therefore not pursued further here. In stress analysis, the visualization of principal stress (PS) lines is not present in commercial FE programs. The visualization of stream and tensor lines is the subject of numerous investigations. A representative selection is given by [
2,
3,
4,
5,
6].
Beyer [
2] investigated in his dissertation principal stress trajectories arising in civil engineering and in constructions of fiber-reinforced plastics. He established an algorithm for their visualization in two and three dimensions. The procedure is similar to the method shown in
Figure 1; however, improved accuracy is gained with his variable and iterative step control.
Delmarcelle [
3,
4] investigated symmetric tensor fields by studying their topological structure. The basic constituents of tensor topology are the degenerate points where eigenvalues (or principal stress values) are equal to each other. Separatrices and degenerate points are the basic constituents of tensor field topology. A separatice is the tensor line (PS line) between two degenerate points. Knowledge of the topological structure of tensor fields is important, as standard integration methods need this information.
With standard integration methods the uniform distribution of tensor lines depends critically on the placement of starting points (elements), see
Figure 1. Jobard’s algorithm [
5] for the placement of evenly-spaced PS lines (in his paper: streamlines) is based on a separating distance between adjacent PS lines to control their density. If a PS line is too close to another one, it is abruptly cut. With respect to fiber placement in FRP construction this may have adverse consequences. Trichoche [
6] extends the work of Delmarcelle [
3,
4] to broaden the scope of topology-based vector and tensor field visualization. One focus in his work is on turbulent flows. The streamline distribution is extremely complex for turbulent flows with its local, small-scale details. Another focus is instabilities in structural problems. Visualization of stress trajectories should permit detection and identification of bifurcation to provide insight into the time-dependent structural evolution. These issues are beyond the scope of this paper.
All these papers lead to specialized algorithms, which are not public. Therefore, it is desirable to investigate the possibilities of integrating vectorial and tensorial direction fields within FE programs without programming efforts or additional software. PS lines in FRP constructions are of particular interest since fiber courses, which follow the local PS directions, make use of the superior stiffness and strength properties of the fibers [
1,
7,
8,
9,
10].
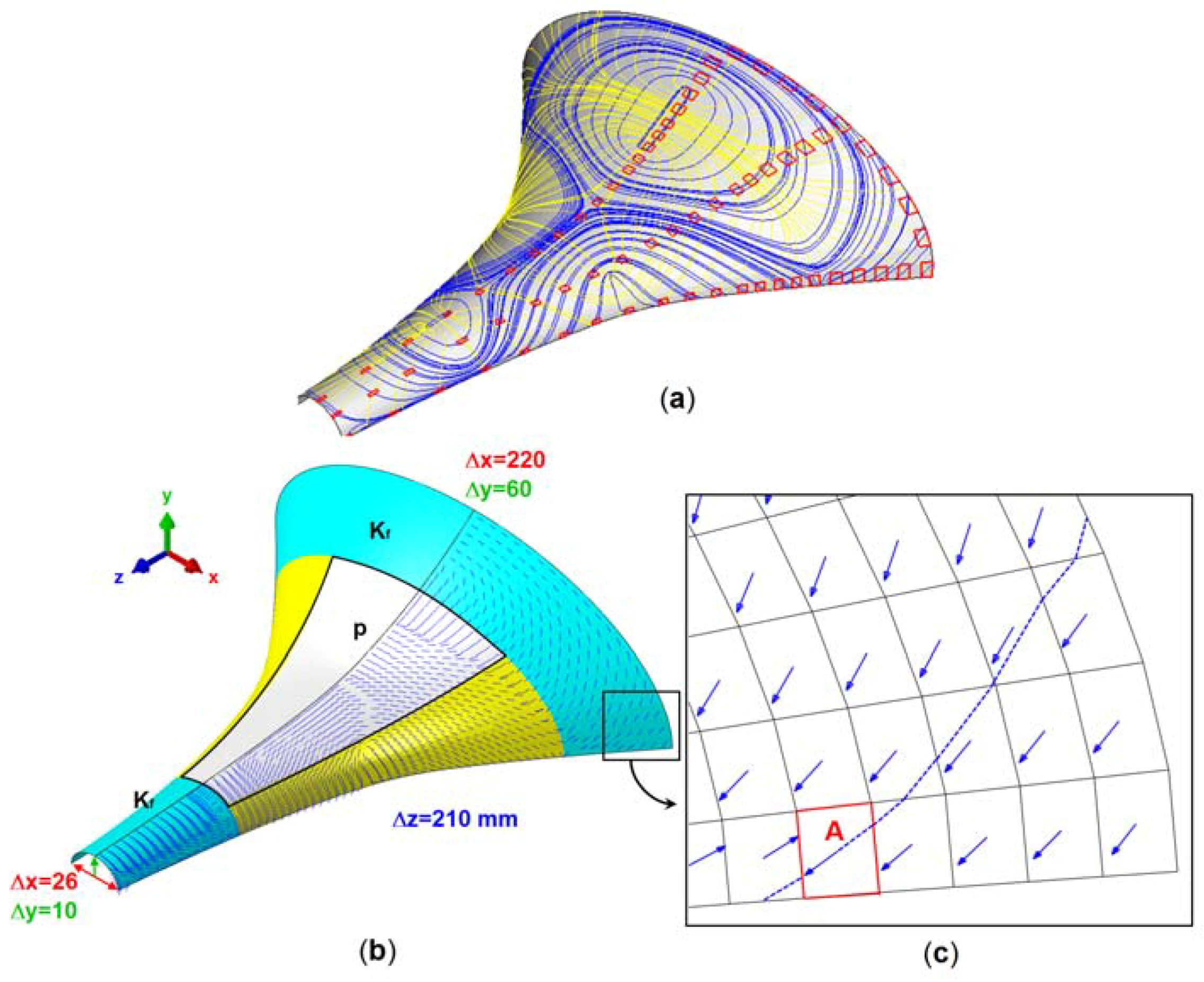
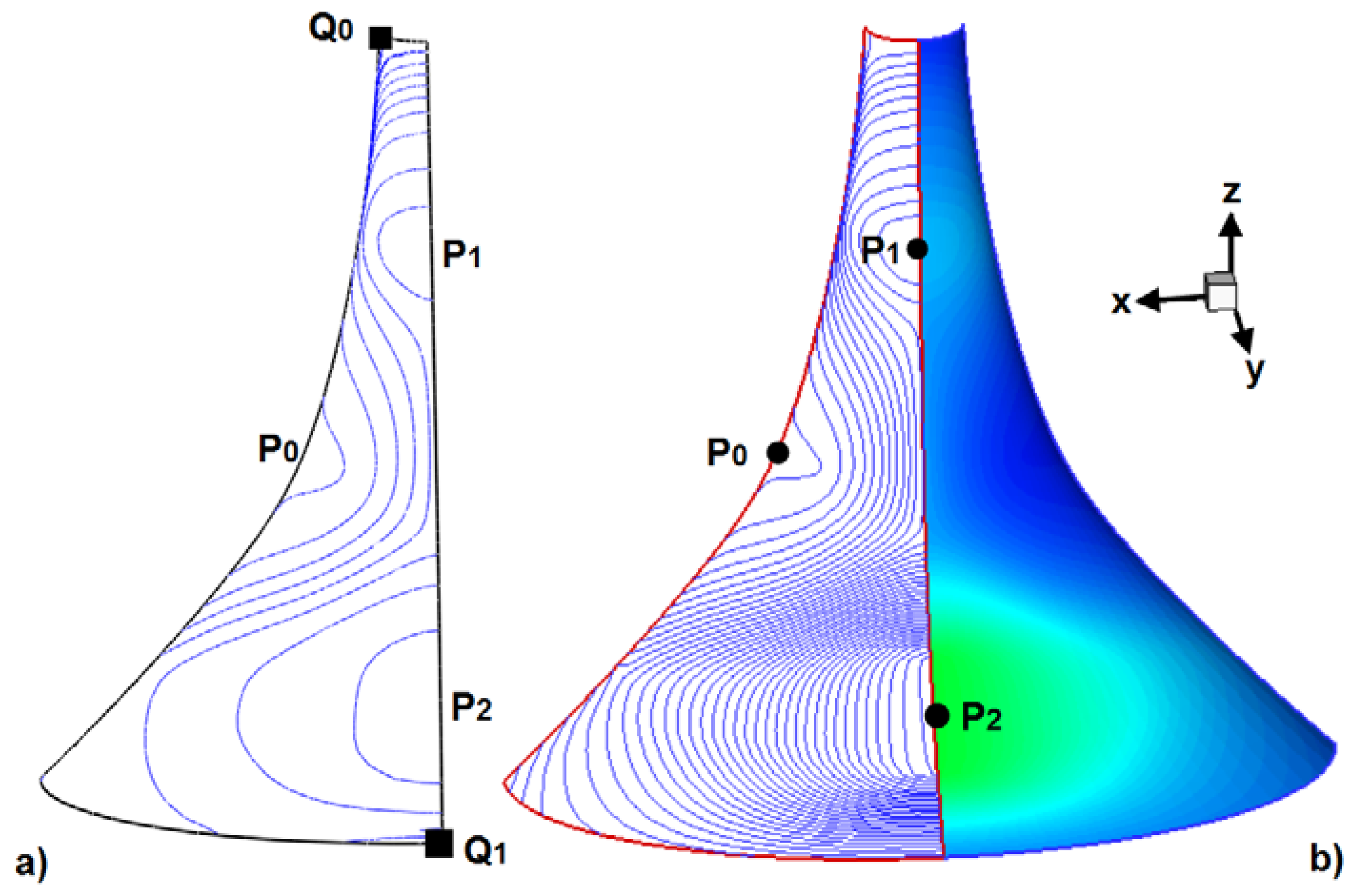
To demonstrate some disadvantages with conventional standard integration methods,
Figure 1 shows an integration procedure developed by the author [
1] (p. 16) applied to the bottom of a shell structure.
Figure 1b shows the PS directions of the blue principal stress trajectories on the bottom of the shell. In the middle plane and on the top of the shell there are other PS directions since membrane and bending stresses occur simultaneously. These directions stem from an eigenvalue problem of the stress tensor, whose eigenvectors (principal stress directions) remain indefinite in the sign. The PS directions can therefore switch the sign from one element to its neighboring element. The integration pattern in
Figure 1c takes this problematic situation into account by replacing the direction vector with a bidirectional element. The bidirectional element intersects two opposing element sides and thereby allows the integration to be continued in the two neighboring elements with their directional elements. Each start element (marked in red) in
Figure 1a provides two individual fiber courses with the procedure just described, corresponding to the two PS directions. A regular placement of the start elements in no way guarantees a uniform distribution of the PS lines. A homogenization of the fiber courses is achieved only with considerable effort. A further disadvantage of this procedure is immediately apparent; each individual trajectory (fiber) must be calculated separately. Should the designer change the fiber volume ratio for reasons of strength, then the procedure must be repeated from the beginning.
This problem is substantially simplified through the hypothesis set out above, which can be modeled by means of the orthotropic heat conduction in FE programs. Since the two-dimensional direction field of the principal stresses describes a planar stress condition, shells with an arbitrary boundary can also be processed. An additional advantage is that all of the PS trajectories (fiber courses) can be calculated by means of a single thermal analysis. If the fiber volume ratio is subsequently increased, correspondingly more isotherms (fiber courses) are extracted from the existing continuous temperature field.
The recommended calculation alternative for the integration of
y´ = f(x,y) is based on the drastically changing properties of Fourier’s law for k
1/k
2→∞. The following section provides a mathematical verification of the hypothesis set out above. The practicability of the integration method is based on independence from thermal boundary conditions; the isotherms always follow the direction field in nonsingular areas. However, the (weighted) distance of the isotherms from each other is influenced by the boundary conditions and can be controlled by them. In
Section 3, the procedure is based on some rules and these are demonstrated practically through examples. The influence of the orthotropy ratio k
1/k
2, as well as the influence of singularities on the course of the isotherms, is investigated.
3. Procedure and Application Examples
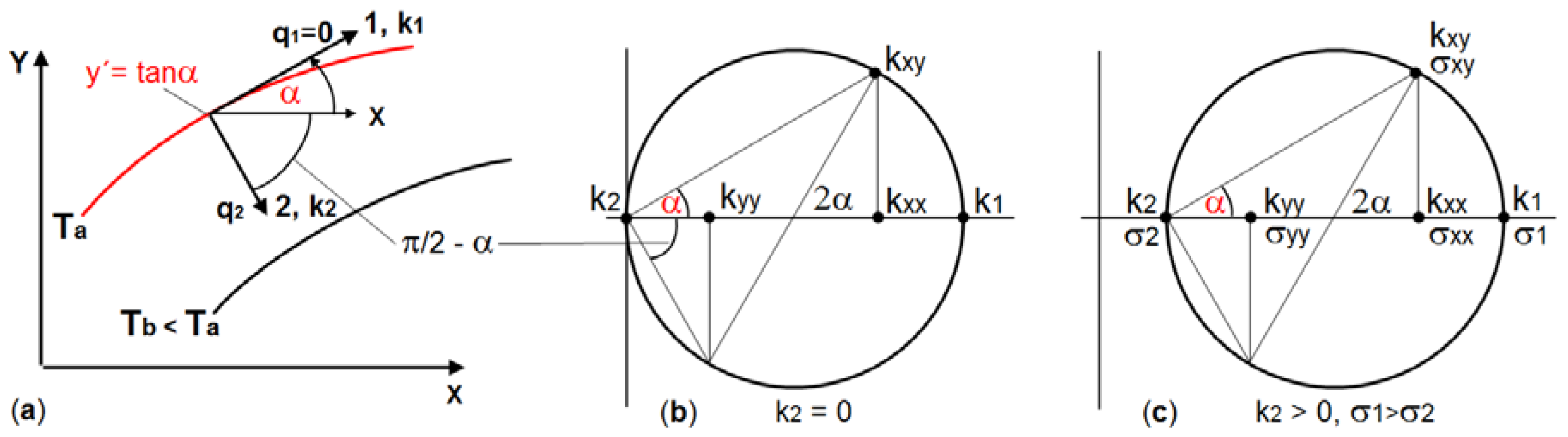
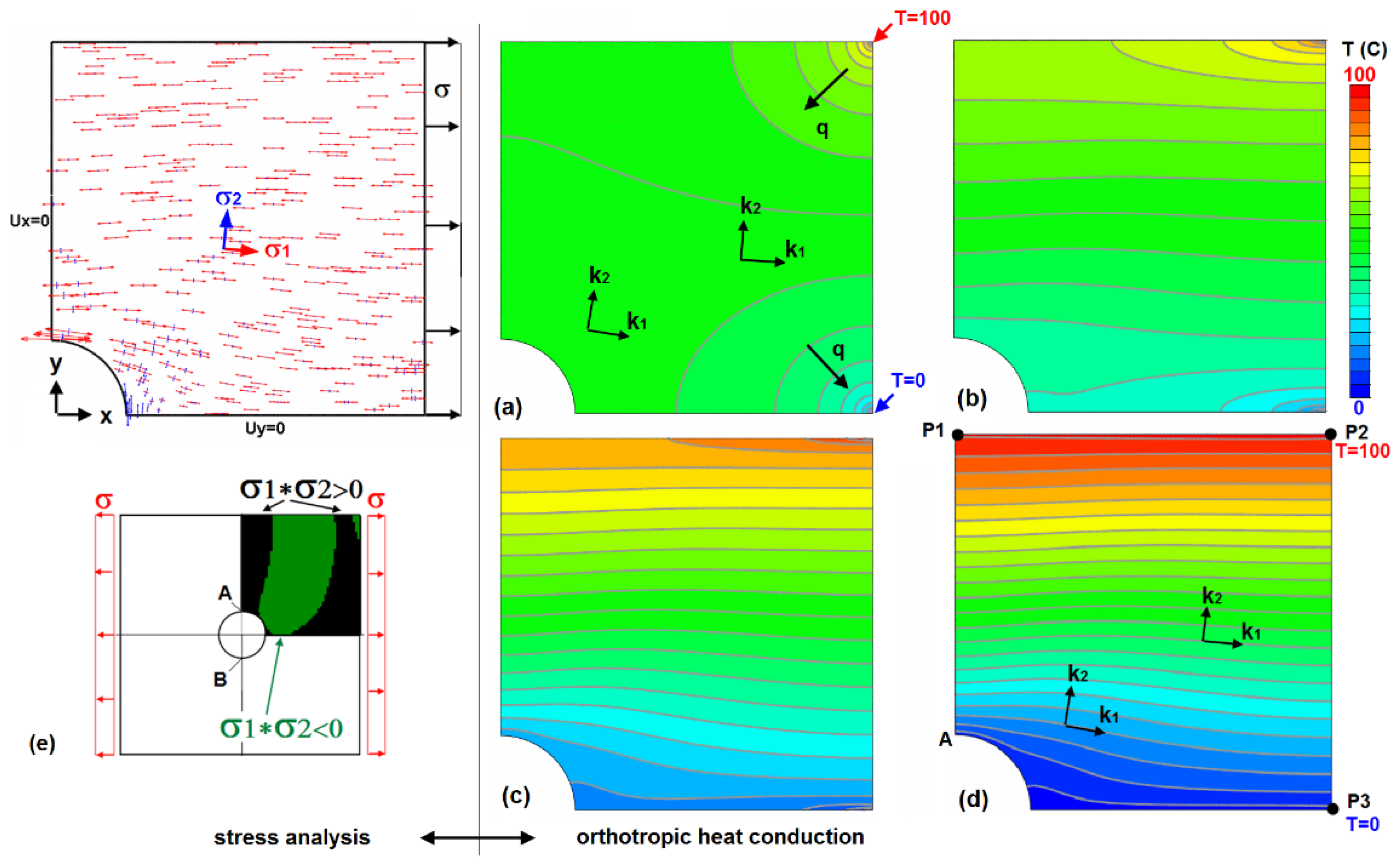
The direction field y´ = f(x,y) to be integrated very often originates from FE analysis in the form of PS directions. The procedure for their integration shall be determined with the help of some rules:
Calculation of the PS directions in all elements (disc, plate, or shell). If this is not provided by the respective FE program used, they can be calculated via the stress components [
σxx σyy σxy]. For example,
y´ = dy/dx = tan
α =
σxy/(σxx − σ2); see also
Figure 2c. Plates and shells have variable stresses across the thicknesses. The direction field therefore must be evaluated for every “thickness integration point”.
Replacement of the structural elements with thermal elements.
Transmission of the PS directions (Step 1) to local systems, depending on the FE program used, (ABAQUS: *Orientation).
Assignment of orthotropic thermal conductivities k1 and k2 in these local systems with extreme ratios, e.g., k1/k2 > 104. (k2 = 0 is permitted in ABAQUS.)
Definition of thermal boundary conditions according to
Section 2.3.
The ratios k1/k2 > 104 and k2/k1 > 104 provide the PS trajectories for the first and for the second principal stress, respectively.
It should be emphasized that the integration of the PS directions for the calculation of the real fiber course is a separate task, independent of the structural analysis. The PS direction field of the structural calculation is adopted as material orientation for the thermal conductivities in the thermal analysis. The boundary conditions are independent in both analyses and have nothing in common with each other.
3.1. Influence of the Orthotropy Ratio k1/k2 on the Integration Accuracy
The influence of the orthotropy ratio
k1/k2 on the integration accuracy is demonstrated by the following example.
Figure 7 shows a perforated disc under axial tension. Due to symmetry, a quarter model is sufficient (
Ux = 0,
Uy = 0). The
supplementary material accompanying this paper includes the ABAQUS input for this example.
The task is to place the fibers in the direction of the largest principal stress for an FRP construction. The PS directions portray the direction field
y´ = f(x,y), which shall be integrated. The elements of the mechanical model are replaced with heat conduction elements whose heat conduction
k1 is oriented parallel to the previously calculated PS directions of σ
1. The
k2 direction is orthogonal to
k1. Now the ratio
k1/k2 is successively increased, thus the isotherms get more and more tangential to the PS direction of σ
1. The influence of the two-node temperature boundary condition at points P2 and P3 (
Figure 7d) on the course of isotherms is no longer perceptible for
k1/k2 > 10
4. Under such simple boundary conditions, it must be ensured that their positions are meaningful. If both temperatures are determined at points P1 and P2, then, practically, two different temperatures are defined on one isotherm.
The relatively uniform distribution of the PS trajectories is remarkable, although only a very simple temperature boundary condition was selected. Should the desired outcome be a distribution of isotherms exactly equidistant between P2 and P3, the temperature along this line must be specified as linearly increasing. Since the isotherms represent the fiber course, the constant line load along P3P2 is uniformly carried by the fibers. The maximum load in the perforated disc at points A and B in
Figure 7e is approximately three times the applied tension, which is well reflected by the fiber course.
At this point, the transport character of the Fourier heat conduction equation in
Figure 7d and Equations (14) and (15) shall be emphasized again. The specification of a linear temperature distribution on the boundary P3P2 is transported along its characteristics without diffusion effects, and these characteristics follow the user defined direction field
y´ = f(x,y).
3.2. The Influence of Singularities on the Course of the Isotherms
In cases of stress singularities, the following distinctions are made: An isotropic (or neutral) point with an undefined PS direction occurs if the two principal stresses σ
1 and σ
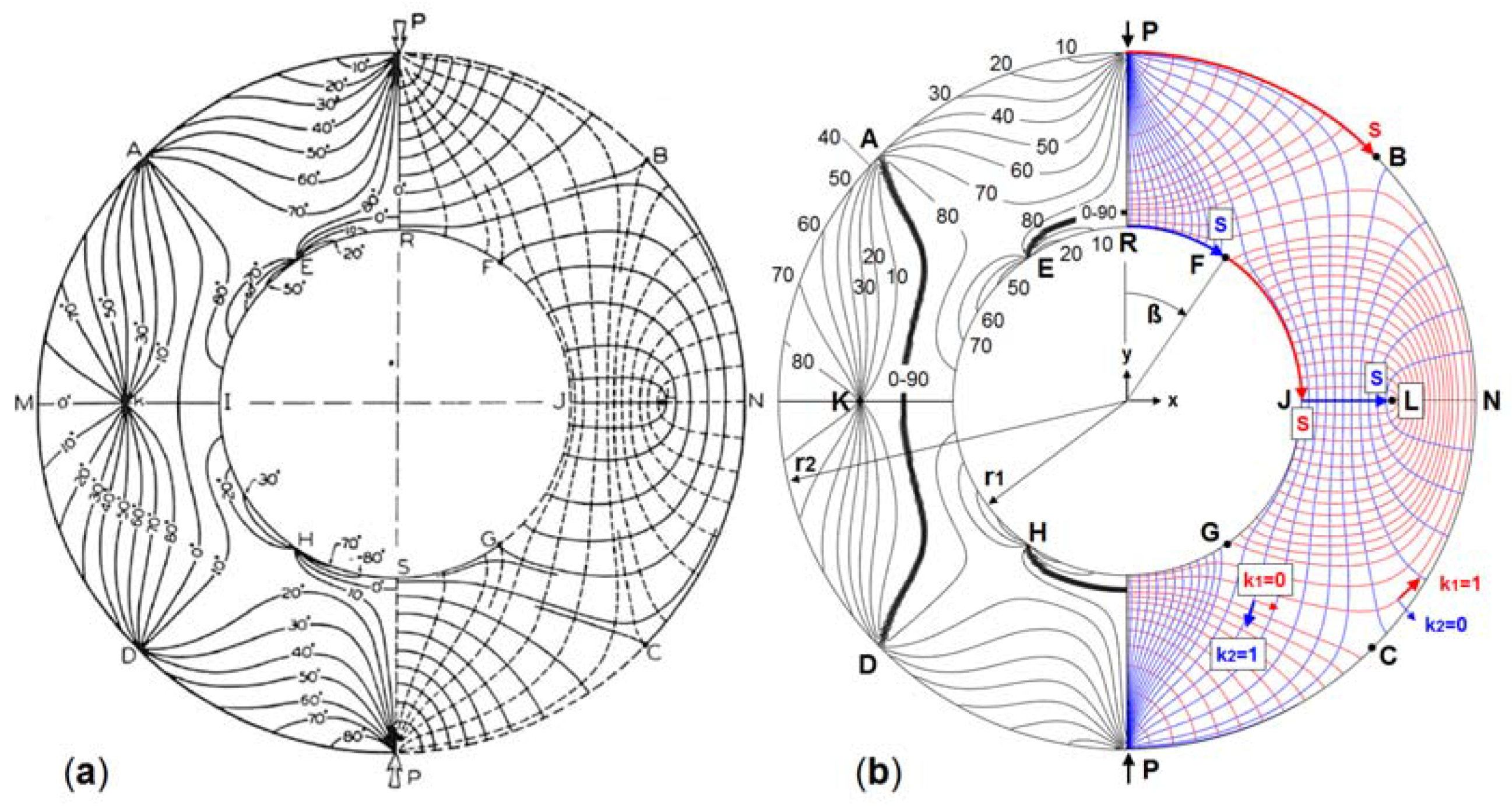
2 are identical. If both principal stresses are zero, then a classic singularity is present. Points with concentrated loads are neither one nor the other. Their isoclines are particularly concentrated at the point of force transmission. What does the course of stress trajectories (represented by isotherms) look like in the vicinity of these points? This can be studied using an example of a circular ring under diametrically opposed single forces.
Figure 8a shows the course of the isoclines and stress trajectories that were determined photoelastically by Frocht [
15].
The experimental results were verified through an FE stress analysis (ABAQUS) followed by an orthotropic heat conduction analysis in order to determine the trajectories, as shown in
Figure 8b. Modeling a quarter of the disc is sufficient due to the symmetry. The stress calculation provides the PS directions. In the subsequent heat conduction calculation, these PS directions serve as local systems for the thermal conductivities k
1 and
k2. Two of these systems are illustratively plotted in the fourth quadrant of
Figure 8b. The system
k1 = 1,
k2 = 0 provides the isotherms as σ
1 trajectories. With
k1 = 0,
k2 = 1, the σ
2 trajectories are determined. The calculation of the isoclines is helpful in order to localize the singular points A, D, E, H, and K (
Figure 8b, left). The isoclines result from Equation (16), i.e., the contour lines of the stress expression on the right side must be visualized; see also
Figure 2c.
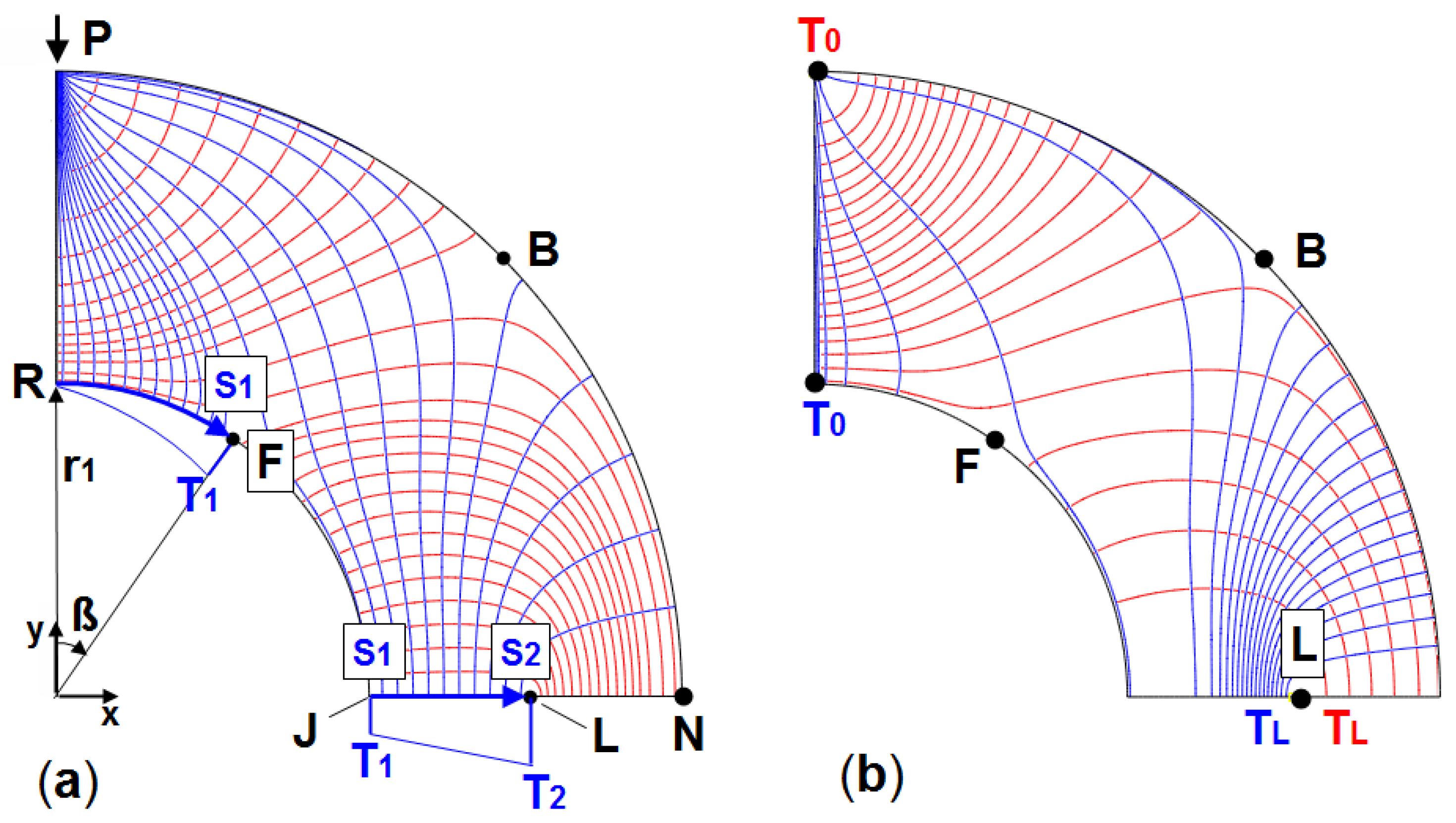
In the trajectories image (right), the singular points appear with the designations B, C, F, G, and L, and are either of the “non-interlocking” type (B, C, F, G) or “interlocking” type (L). This evaluation is useful since a uniform distribution of the isotherms (fibers) is desirable, which is only achievable with knowledge of the singularities. This is shown in
Figure 9a for the σ
2 trajectories (with
σ2 <
σ1). A uniform distribution is achieved through a linearly increasing temperature along RF, with continuation along JL.
Specifying a linear increase in temperature from R to J is incorrect since the σ2 trajectory along RF turns into the σ1 trajectory at point F along FJ. The FJ boundary segment itself is an isotherm and no variable temperature specification is allowed there.
The existence of a singular point on a load-free boundary of a 2D structure always results in this change of trajectories. This property is responsible for the fact that efforts need to be made regarding the specification of suitable temperature boundary conditions in order to obtain uniformly distributed isotherms. Should the temperature be defined only along RF, then only a part of the structure will show isotherms. A further boundary segment with temperature boundary conditions must then be applied in order to capture the rest of the structure. In
Figure 9a, this is segment JL. The procedure is the same when looking for σ
1 trajectories. The temperature is defined as linearly increasing along PB with continuation along LN.
The aim of calculating strictly uniformly distributed isotherms (trajectories) can only be achieved locally.
Figure 9a shows uniformly distributed σ
1 trajectories along PB; however, these end up unevenly distributed on the PR boundary.
On the perforated disc (
Figure 7), the trajectory change mentioned above does not occur along the right boundary of P2P3. This boundary is free from singularities. The specification of two temperatures at points P2 and P3 is sufficient. We can generally use this simple two-node boundary condition (
Section 2.3) for all 2D discs and 3D shells and get—depending on the number of singularities—correspondingly weighted isotherm distributions.
Figure 9b shows this simple procedure for the circular ring with its singularities. The isotherms shown there are less uniformly distributed than in
Figure 9a, but this is adequate for a first overview.
The circular ring problem (
Figure 8) contains the most important forms of singularities: Isotropic points of the “interlocking” and “non-interlocking” type, as well as concentrated point loads. Errors in representation of isotherms are inevitable since they do not fulfil
y´ = f(x,y) in the near vicinity of the singularity. In fact, the isotherms in close proximity there evade in a sideways direction depending on the model mesh size. The model in
Figure 8b, in comparison to
Figure 8a, is clearly fine enough to minimize this error. The element size is virtually the same all over; 60 elements were used (with four nodes respectively) along JN. Through further mesh refinement in the area of singularities, the error can be kept arbitrary small.
3.3. The Principal Stress Trajectories in Shell Structures
A conventional method for the calculation of principal stress trajectories in a shell was shown in
Figure 1. Disadvantages resulted from the uneven fiber placement, which originates from the separate calculation of each individual fiber. In integrating the direction field, it is not practically possible to select optimal start positions (start elements) beforehand.
In contrast to this is the method of integration by means of an orthotropic heat conduction calculation. Even with a two-node temperature boundary condition with Q
0: T = 0 °C, Q
1: T = 1 °C in
Figure 10a, a better fiber distribution can be attained than is depicted in
Figure 1a. This temperature distribution, shown in
Figure 10a, provides the approximate position of three local temperature extremes at the positions P
0, P
1 and P
2.
By repeating the heat conduction analysis with a three-node temperature boundary condition (P
0:
T = 0 °C, P
1:
T = 1 °C, P
2:
T = 2 °C,
Figure 10b), the uniformity of the isotherms is improved. A specification of the linear varying temperatures along boundary segments analogous to the previous section would yield further improvement. However, in light of the result in
Figure 10b, it does not appear to be crucial.
The right half of
Figure 8b highlights another aspect: The continuous temperature field is infinitely dense with respect to the isotherms, so an arbitrary number of contours can be visualized, avoiding calculation of trajectories one after another (
Figure 1).
3.4. Optimization of Fiber Placement in FRP Constructions
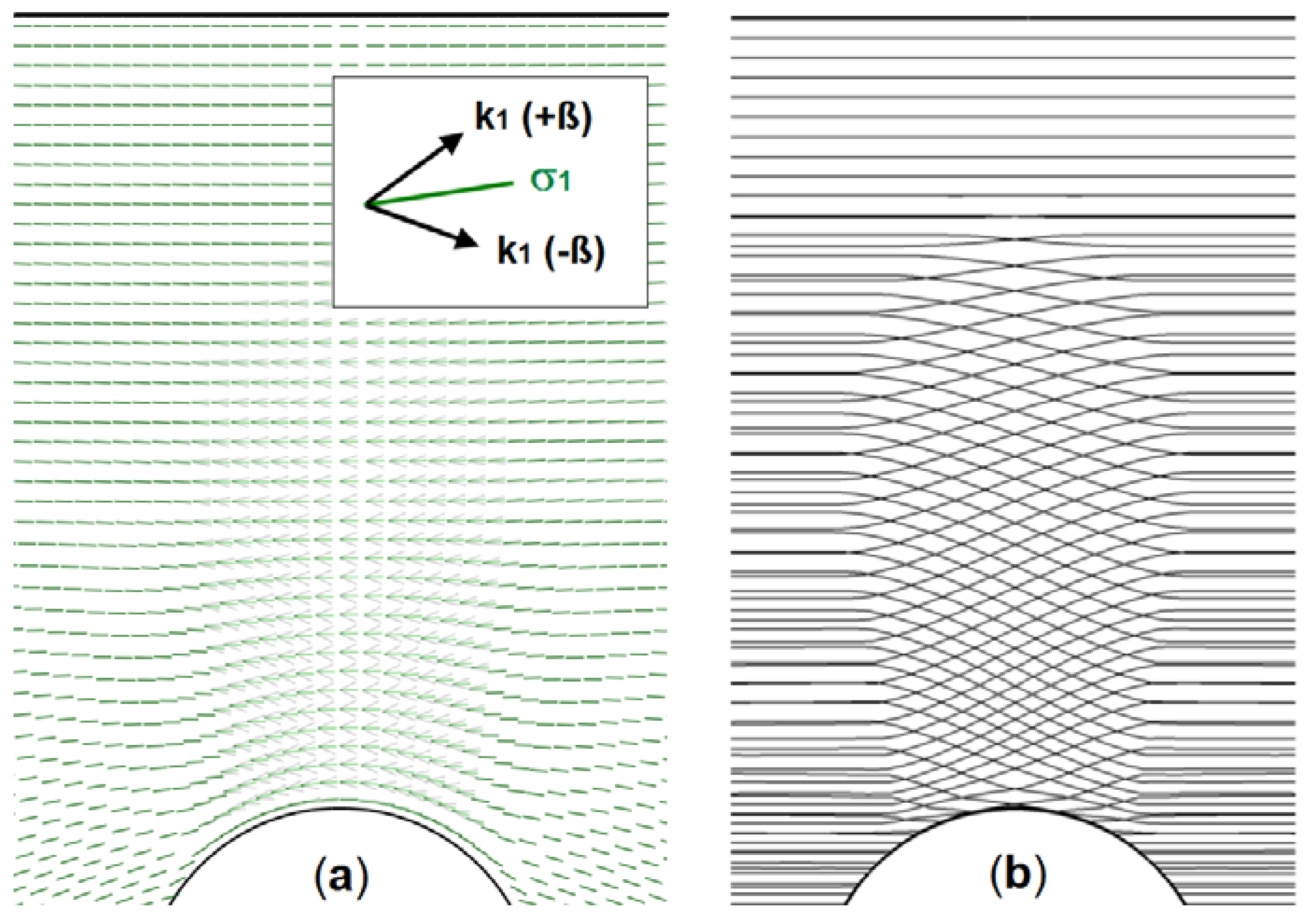
In order to demonstrate a useful application beyond the visualization of tensor lines, the fiber placement in FRP constructions is highlighted. Fiber courses, which follow local PS directions, use the superior stiffness and strength properties of the fibers. In plane stress structures the fiber courses due to σ1 and σ2 are perpendicular to each other, forming a curvilinear cross-ply (CCP) laminate. With regard to optimality, attention must be paid to the algebraic signs of principal stresses.
Fiber placement in the direction of principal stresses is optimal according to net theory [
16], and this is also valid for CCP-laminates if ignoring the support of the matrix. To be on the safe side, the carrying capacity of the construction can be calculated by using a fiber failure criterion. A design based on an inter-fiber failure must additionally take into account the contribution of the matrix. In this case CCP-laminates are optimal only in areas with principal stresses showing different algebraic signs. However, if the algebraic signs are the same, then the curvilinear balanced angle-ply (CBAP) laminate is the better choice according to classical lamination theory [
17]. This design differs from the (right-angled) CCP-laminate through a correction angle ±β regarding the σ
1 direction. The direction field y´ for the largest principal stress σ
1 is then represented by two direction fields: y´ + β and y´ − β, as shown in
Figure 11.
For example, the perforated disc (
Figure 7e) contains the areas
σ1·σ2 < 0 (CCP-laminate is optimal) and
σ1·σ2 > 0 (CBAP-laminate is optimal). In the latter case the modified direction fields can also be integrated without restriction by means of the orthotropic heat conduction analysis. The correction angle β is dependent on the material and the principal stress ratio
σ1/σ2 [
17]. It should be noted that the orthotropic heat conduction is suitable for the integration of arbitrary direction fields even if they are modified for reasons determined by the engineer. Reference is made to Moldenhauer [
1] (pp. 54–60] and [
18] for further details and consideration of particular aspects of load-related optimization (layer thickness distribution, loading condition range, and nonlinearity of stress distribution over the shell thickness).
4. Discussion and Conclusions
The method presented in this paper is suitable for integrating arbitrary vectorial and tensorial 2D direction fields by means of commercial FE programs, provided that the FE programs have options for the analysis of orthotropic heat conduction. The calculated isotherms represent the integral curves of these direction fields inside and on the edge of the 2D structure (disc or shell). The procedure is based on some rules (
Section 3), which concern only the standard input of the FE program. Additional programming is not required. Two temperatures at two different positions shall be specified as a minimum for thermal boundary conditions. The isotherms arising from this can still run in a non-uniform way. Uniformity is achieved while linearly varying temperatures along a boundary segment are specified (
Figure 5a). Should the direction field or the differential equation
y´ = f(x,y) exhibit singularities on the boundary, then the definition of the boundary conditions must be carefully adjusted (
Figure 9). In this case, a preliminary visualization of the isoclines, Equation (16), and/or an analysis with the two-node temperature boundary condition is helpful. The precision of the integration depends on the element size of the FE model.
In comparison with the traditional integration methods, significant improvements arise with the new procedure:
The integration of the direction fields can take place with standard FE programs with options for an orthotropic heat conduction analysis. No additional programming is necessary.
Any number of isotherms can be extracted from the integrated continuous temperature field.
Quick and accurate results are obtained with a simple two-node temperature boundary condition; however, the distribution of isotherms may be non-uniform if singular points are present in the direction field.
As the computed temperature field is continuous, valuable additional information can be extracted from this field. For example, the density of the isotherms (tensor lines) can be computed by displaying the temperature gradients, see [
1] (p. 96).
Applying the proposed integration method to stress tensors it should be noted that principal stress direction fields can originate from linear or nonlinear analyses, see [
1] (p. 74). If principal shear stress (or strain) directions are evaluated in the plastic range then the trajectories can be regarded as slip-lines, see [
1] (pp. 41–44).
Civil engineering: Aligning reinforcement in concrete structures parallel to PS directions is a meaningful tool to effectively increase the low tension strength of concrete, see also [
1] (p. 78).
Mathematical aspects were the focus of this paper. An important application seems to be on FRP constructions. Aligning fiber courses along PS lines make the most of the superior stiffness and strength properties of fibers. Calculation of these fiber courses by integrating the PS directions followed by the evaluation of this optimized FRP design can be done with one and the same FE program. To evaluate and optimize an FRP construction based on PS lines, some practical aspects should be highlighted.
As with all FRP problems, the optimization success is greatest when a special load case is investigated. In reality, loads and boundary conditions change frequently, and the principal stress directions change accordingly. However, the associated degradation of the optimization method affects alternative optimization strategies as well. If one load case dominates other load cases, the optimization effort can be worthwhile nevertheless. A CCP- or CBAP-laminate can be combined with textile preforms and can be stitched onto standard laminates. This technique is known as tailored fiber placement (TFP). The layer with the fiber course aligned to the trajectories covers the critical load case, and the standard laminate the other load cases. In 2D, the TFP stitching technique has been used for a long time [
10]. In 3D, textile preforming or tape laying are possible options.
The effort for the proposed method appears to be very high in the case of plates and shells, since the PS directions for superimposed membrane and bending stress vary across the thickness. The integration of the stress components [
σxx σyy σxy] over the thickness produces normal forces
N = [
Nxx Nyy Nxy] and bending moments
M = [
Mxx Myy Mxy]. FE programs generally provide these section forces and moments
N and
M, which are both constant across the thickness. Their principal directions (1,2) can be computed in analogy to Equation (16), i.e., y
1´ =
Nxy/(
Nxx −
N2), y
2´ = −1/y
1´. It makes sense to arrange the M-layers on the inside and outside and the N-layers in the middle of the shell. Symmetric layers are then obtained with [
M1/M2/N1/N2]
S, see also [
1] (pp. 64–73).
When evaluating a TFP laminate, one is faced with the variable fiber volume fraction due to the diverging and converging streamline nature of the fiber course. The fiber volume fraction is an important input quantity to define laminate stiffness with dependence on local fiber volume and local fiber orientation. The gradient of the temperature field is a measure for the local fiber volume. Displaying the gradient of the temperature field is identical to displaying the isotropic heat flux,
q =
k∙grad(T) with
k =
k1 =
k2. For extreme orthotropy (
k1/k2→∞) we have an orthotropic heat flux, which is zero everywhere, see Equation (11). If the temperature field is based on isotropic conduction with constant k, then the isotropic heat flux is the correct gradient. For this reason, the nodal temperatures from the orthotropic analysis must be used as prescribed nodal temperatures in an additional thermal run. More details can be found in [
1] (p. 96).
Provided that the course of the isotherms (trajectories) shall be used for fiber placement in FRP constructions, the visualized isotherms must be converted into polylines with x-, y-, and z-coordinates. TECPLOT (Bellevue, WA, USA) is suitable as a commercial solution for this. Alternatively, a Fortran program can be used, for which the source code is contained in DeVries [
19].