A Five-Point Subdivision Scheme with Two Parameters and a Four-Point Shape-Preserving Scheme
Abstract
:1. Introduction
2. Preliminaries
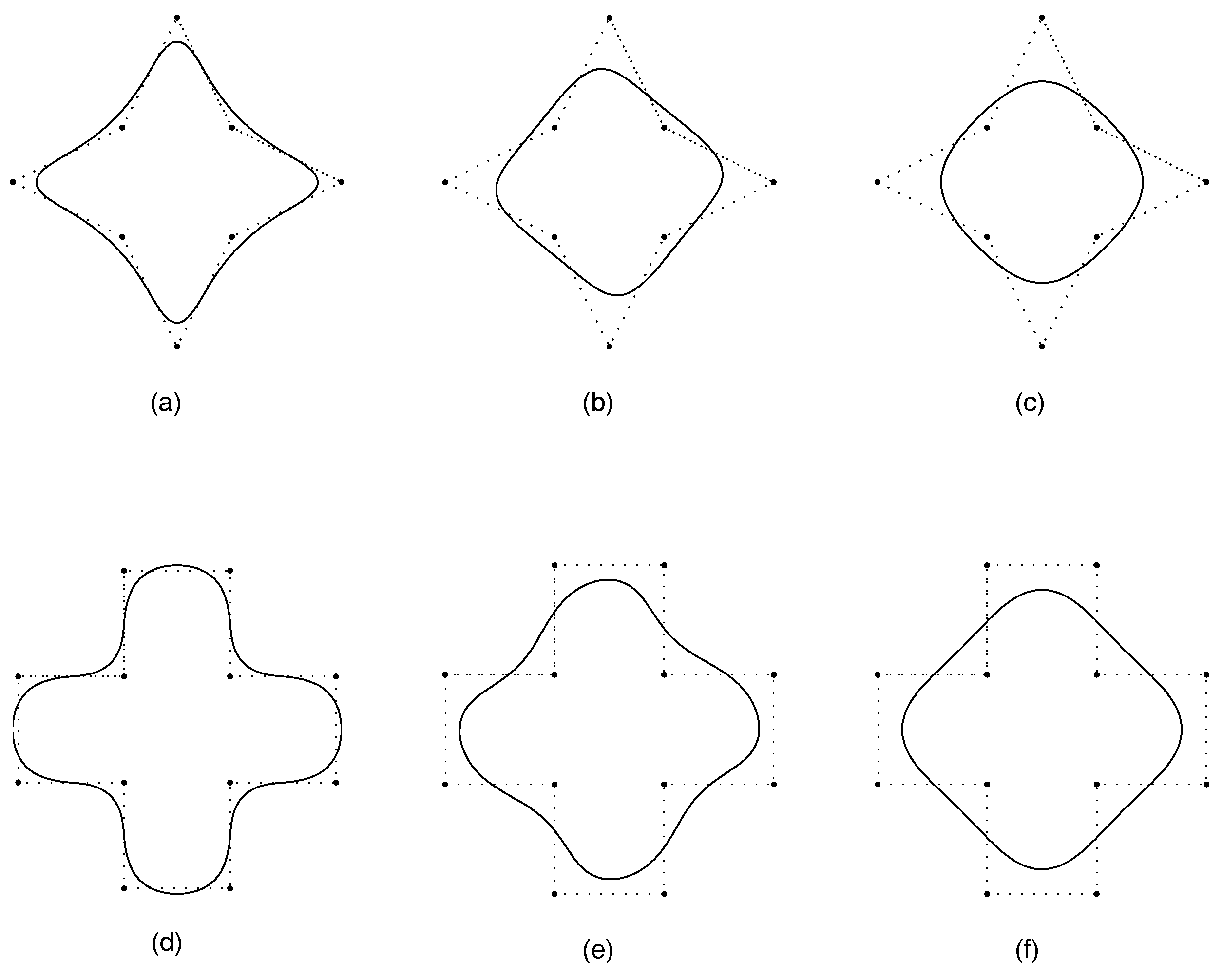
3. A Five-Point Binary Subdivision Scheme with Two Parameters
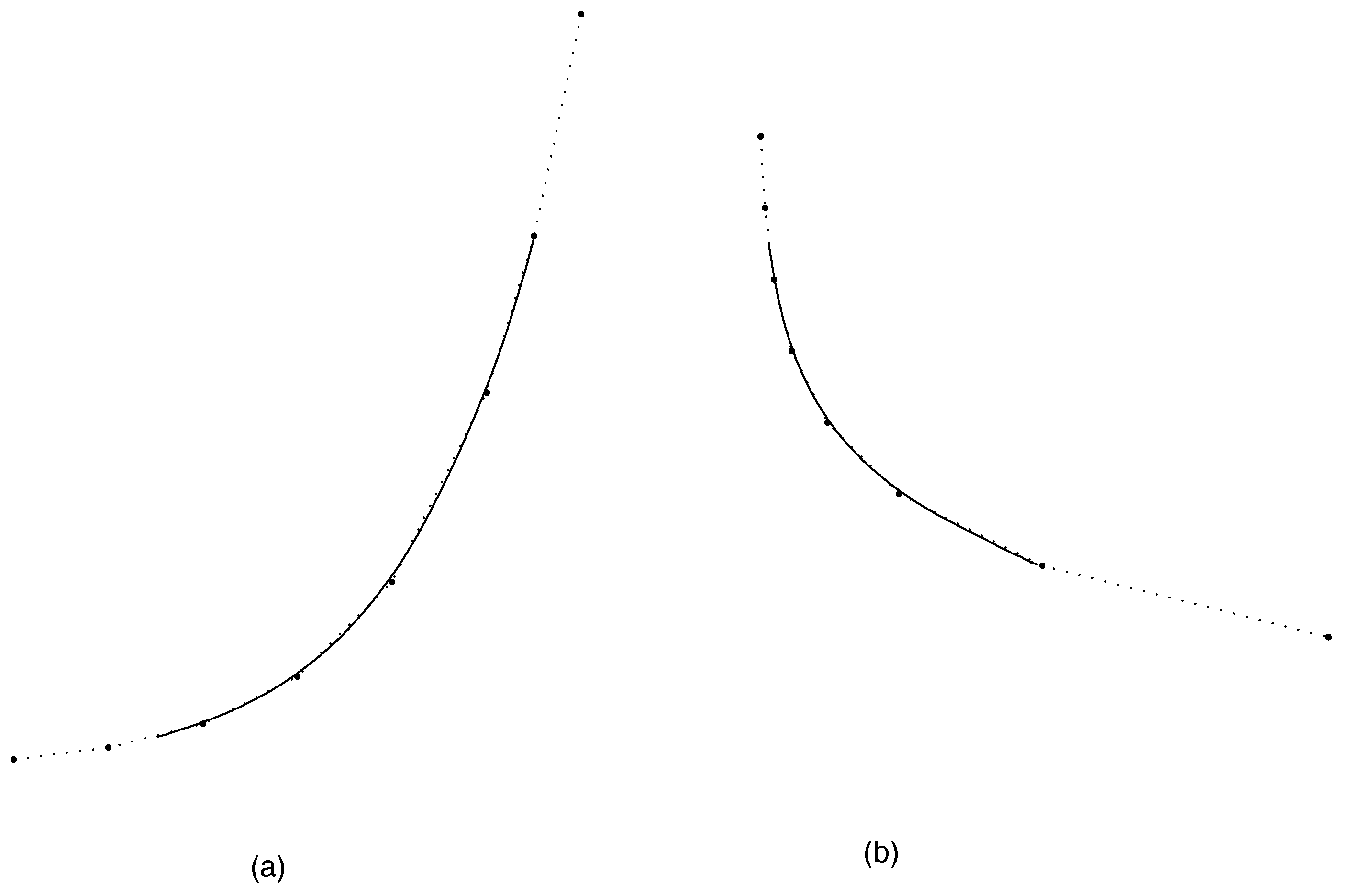
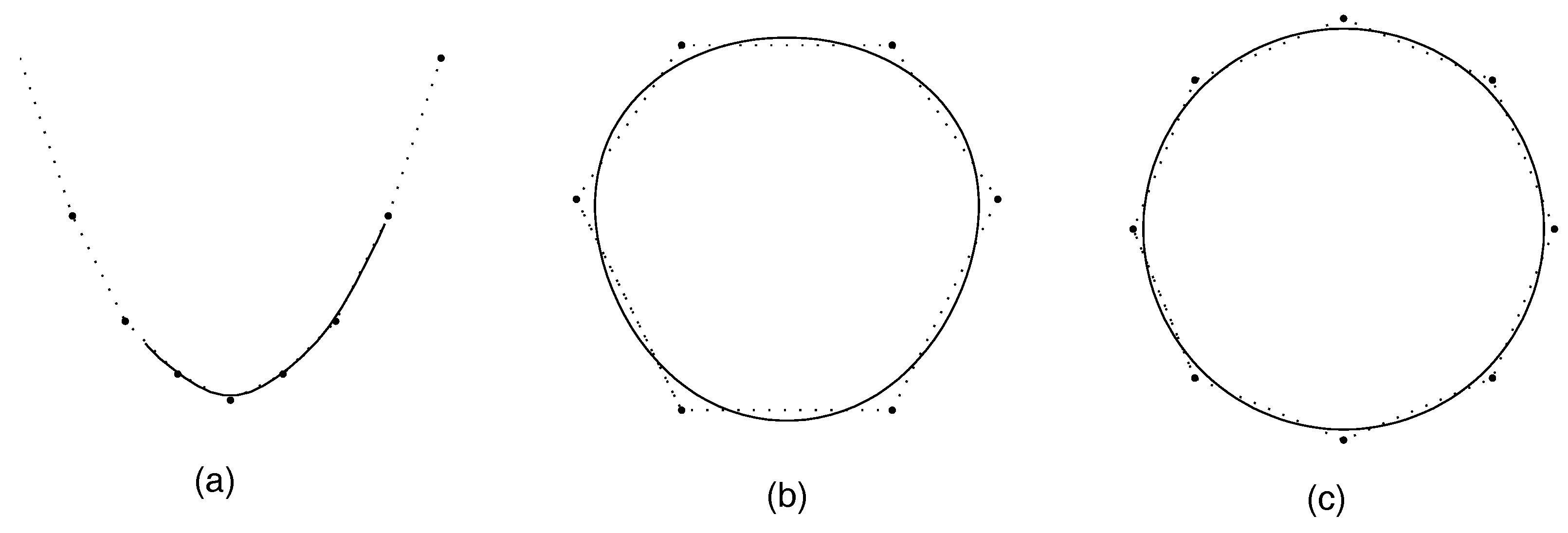
4. A Four-Point Shape-Preserving Subdivision Scheme
4.1. Monotonicity Preservation
4.2. Convexity Preservation
5. Conclusions and Numerical Examples
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Dyn, N.; Levin, D.; Gregory, J.A. A 4-point interpolatory subdivision scheme for curve design. Comput. Aided Geom. Des. 1987, 4, 257–268. [Google Scholar] [CrossRef]
- Dyn, N. Subdivision schemes in CAGD. In Advances in Numerical Analysis II: Wavelets, Subdivision Algorithms, and Radial Basis Functions; Light, W., Ed.; Oxford University Press: Oxford, UK, 1992; pp. 36–104. [Google Scholar]
- Dyn, N.; Levin, D.; Micchelli, C.A. Using parameters to increase smoothness of curves and surfaces generated by subdivision. Comput. Aided Geom. Des. 1990, 7, 129–140. [Google Scholar] [CrossRef]
- Dyn, N.; Kuijt, F.; Levin, D.; Damme, R.V. Convexity preservation of the four-point interpolatory subdivision scheme. Comput. Aided Geom. Des. 1999, 16, 789–792. [Google Scholar] [CrossRef]
- Kuijt, F.; van Damme, R. Monotonicity preserving interpolatory subdivision schemes. J. Comput. Appl. Math. 1999, 101, 203–229. [Google Scholar] [CrossRef]
- Kuijt, F.; van Damme, R. Shape preserving interpolatory subdivision schemes for nonuniform data. J. Approx. Theory 2002, 114, 1–32. [Google Scholar] [CrossRef]
- Dyn, N.; Floater, M.S.; Hormann, K. A C2 four-point subdivision scheme with fourth order accuracy and its extensions. In Mathematical Methods for Curves and Surfaces: Tromsø 2004; Dahlen, M., Morken, K., Schumaker, L.L., Eds.; Nashboro Press: Brentwood, TN, USA, 2005; pp. 145–156. [Google Scholar]
- Zheng, H.; Ye, Z.; Zhao, H. A class of four-point subdivision schemes with two parameters and its properties. J. Comput. Aided Des. Comput. Gr. 2004, 16, 1140–1145. (In Chinese) [Google Scholar]
- Cai, Z. Convergence, error estimation and some properties of four-point interpolation subdivision scheme. Comput. Aided Geom. Des. 1995, 12, 459–468. [Google Scholar]
- Cao, Y. The sufficient and necessary conditions of C2 continuity of the four-point interpolate subdivision scheme for curve and surface. J. Comput. Aided Des. Comput. Gr. 2003, 15, 961–966. (In Chinese) [Google Scholar]
- Siddiqi, S.S.; Ahmad, N. A new five-point approximating subdivision scheme. Int. J. Comput. Math. 2008, 85, 65–72. [Google Scholar] [CrossRef]
- Hao, Y.X.; Wang, R.H.; Li, C.J. Analysis of a 6-point binary subdivision scheme. Appl. Math. Comput. 2011, 218, 3209–3216. [Google Scholar] [CrossRef]
- Cao, H.; Tan, J. A binary five-point relaxation subdivision scheme. J. Inf. Comput. Sci. 2013, 10, 5903–5910. [Google Scholar] [CrossRef]
- Tan, J.; Yao, Y.; Cao, H.; Zhang, L. Convexity preservation of five-point binary subdivision scheme with a parameter. Appl. Math. Comput. 2014, 245, 279–288. [Google Scholar] [CrossRef]
- Tan, J.; Tong, G.; Zhang, L.; Xie, J. Four point interpolatory-corner cutting subdivision. Appl. Math. Comput. 2015, 265, 819–825. [Google Scholar] [CrossRef]
- Rehan, K.; Siddiqi, S.S. A combined binary 6-point subdivision scheme. Appl. Math. Comput. 2015, 270, 130–135. [Google Scholar] [CrossRef]
- Conti, C.; Hormann, K. Polynomial reproduction for univariate subdivision schemes of any arity. J. Approx. Theory 2011, 163, 413–437. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tan, J.; Wang, B.; Shi, J. A Five-Point Subdivision Scheme with Two Parameters and a Four-Point Shape-Preserving Scheme. Math. Comput. Appl. 2017, 22, 22. https://doi.org/10.3390/mca22010022
Tan J, Wang B, Shi J. A Five-Point Subdivision Scheme with Two Parameters and a Four-Point Shape-Preserving Scheme. Mathematical and Computational Applications. 2017; 22(1):22. https://doi.org/10.3390/mca22010022
Chicago/Turabian StyleTan, Jieqing, Bo Wang, and Jun Shi. 2017. "A Five-Point Subdivision Scheme with Two Parameters and a Four-Point Shape-Preserving Scheme" Mathematical and Computational Applications 22, no. 1: 22. https://doi.org/10.3390/mca22010022
APA StyleTan, J., Wang, B., & Shi, J. (2017). A Five-Point Subdivision Scheme with Two Parameters and a Four-Point Shape-Preserving Scheme. Mathematical and Computational Applications, 22(1), 22. https://doi.org/10.3390/mca22010022





