Laplace Transform Homotopy Perturbation Method for the Two Dimensional Black Scholes Model with European Call Option

Abstract

The Black Scholes model is a well-known and useful mathematical model in financial markets. In this paper, the two-dimensional Black Scholes equation with European call option is studied. The explicit solution of this problem is carried out in the form of a Mellin–Ross function by using Laplace transform homotopy perturbation method. The solution example demonstrates that the proposed scheme is effective.

1. Introduction

In the financial market, contracts between buyers and sellers are called options. Generally, options are divided into two types: call option (the right to buy) and put option (the right to sell). In both types, holders can buy or sell the underlying asset before the options’ expiry date at a strike price or a fixed price. Considering only call options, European and American call options are usually concerned. European call options may be brought only on the options’ expiry date, whereas American call options may be brought before that time.

According to the benefit of European option pricing about trade at a discount, we are thus interested in the European option. The European option occurs in the way that holders buy the products from sellers. Before this process can happen, both the buyers and sellers have an agreement about the price and date on which the product will be received and payment will be made. The purchasing process of the products can be considered as the process of buying the underlying asset in the market.

To study the financial derivative in the market, the Black Scholes model proposed by Black and Scholes [1] in 1973 is used. The concept of their model is hedging and eliminating the risk of option pricing for purchasing and selling of underlying assets. The European call option price of this model varies over time and stocks price. In addition, the price of assets is modelled by a geometric Brownian motion with a constant drift and volatility.

In recent years, the Black Scholes equation was used to investigate the behavior of the option pricing. Since the option pricing in a market is dependent on other markets, the multidimensional Black Scholes equation is more efficient than the one dimensional version. There are various methods to find the solution of multidimensional Black Scholes model; for example, a radical basic function (RBF) method [2,3,4,5,6], the Mellin transform method [7], finite different method [8,9,10,11,12], a collection method with the quantic B-spline function [13], and homotopy perturbation method (HPM) [14,15].

One of most commonly used is the homotopy perturbation method [16,17,18,19], which is an alternative method of finding the solution as an infinite series. The solution obtained from HPM converges rapidly to the exact solution. There are many researchers applying HPM to engineering and biological problems [20,21,22,23,24,25,26,27], confirming that HPM has become a potential tool for solving mathematical problems [17]. However, some complicated problems cannot be solved using HPM alone. Therefore, many researchers [28,29,30] proposed Laplace transform homotopy perturbation method (LHPM), which is a combination of Laplace transform and HPM.

In this work, we study the two-dimensional Black Scholes equation with basket option based on European call option. The explicit solution is carried out by using Laplace transformation homotopy perturbation method. The rest of this paper is organized as follows. In Section 2, the mathematical model for two-dimensional Black Scholes equation with basket option based on European call option is presented. In Section 3, the basic ideas of Laplace transform homotopy perturbation method are shown. Moreover, the two dimensional Black Scholes equation with basket option based on European call option is solved by using LHPM as shown in Section 4. The solution example is illustrated in Section 5. Finally, we present a conclusion in Section 6.

2. Two-Dimensional Black Scholes Equation

In this section, we present the two-dimensional option pricing problem with correlation based on the Black Scholes equation [31] as the following equation:

$$\frac{\partial c}{\partial t}+\frac{1}{2}{\sigma }_1^2{S}_1^2\frac{{\partial }^{2}c}{\partial S_1^2}+\frac{1}{2}{\sigma }_2^2{S}_2^2\frac{{\partial }^{2}c}{\partial S_2^2}+\rho {\sigma }_1{\sigma }_2{S}_1{S}_2\frac{\partial c^2}{\partial S_1\partial S_2}+r\left[S_1\frac{\partial c}{\partial S_1}+S_2\frac{\partial c}{\partial S_2}\right]-rc=0,$$

(1)

with the initial condition and terminal condition

$$c(S_1,0,t)=0=c(0,S_2,t),c(S_1,S_2,T)=\max ({\beta }_1{S}_1+{\beta }_2{S}_2-K,0).$$

(2)

We denote by $c(S_1,S_2,t)$ the value of a call option with $S_1$ as the first underlying asset, $S_2$ as the second underlying asset, and t as time. ${\sigma }_1$ and ${\sigma }_2$ are the volatilities of the underlying assets $S_1$ and $S_2$, respectively. r is the risk-free interest rate. K is the strike price. Finally, ${\beta }_1$ and ${\beta }_2$ are the portions of the underlying assets $S_1$ and $S_2$, respectively. Because this equation is regularly augmented with a final time condition, we set the variable $\tau =T-t$. Thus, Equation (1) becomes

$$\frac{\partial c}{\partial \tau }-\frac{1}{2}{\sigma }_1^2{S}_1^2\frac{{\partial }^{2}c}{\partial S_1^2}-\frac{1}{2}{\sigma }_2^2{S}_2^2\frac{{\partial }^{2}c}{\partial S_2^2}-\rho {\sigma }_1{\sigma }_2{S}_1{S}_2\frac{\partial c^2}{\partial S_1\partial S_2}-r\left[S_1\frac{\partial c}{\partial S_1}+S_2\frac{\partial c}{\partial S_2}\right]+rc=0.$$

Without loss of generality , we can consider τ as t, $S_1$ as x, and $S_2$ as y. Hence, this above equation can be written as

$$\frac{\partial c}{\partial t}=\frac{1}{2}{\sigma }_1^2{x}^2\frac{{\partial }^{2}c}{\partial x^2}+\frac{1}{2}{\sigma }_2^2{y}^2\frac{{\partial }^{2}c}{\partial y^2}+\rho {\sigma }_1{\sigma }_{2}xy\frac{\partial c^2}{\partial x\partial y}+r\left[x\frac{\partial c}{\partial x}+y\frac{\partial c}{\partial y}\right]-rc.$$

(3)

The initial condition becomes

$$c(x,y,0)=\max ({\beta }_{1}x+{\beta }_{2}y-K,0).$$

3. Basic Ideas of Laplace Transform Homotopy Perturbation Method

The general form of time-dependent differential equation is investigated to describe the basic ideas of the Laplace transformation Homotopy Perturbation Method as given below:

$$A\left(u\right(x,y,t\left)\right)-f(x,y,t)=0$$

(4)

where A is a differential operator, $u(x,y,t)$ is an unknown function, and $f(x,y,t)$ is a known analytic function. Moreover, A can be separated into two parts:

$$A\left(u(x,y,t)\right)=\frac{\partial }{\partial t}u(x,y,t)+N\left(u(x,y,t)\right),$$

where $\frac{\partial }{\partial t}u(x,y,t)$ is a simple part which is investigated in the problem and N is a the remaining part of A. Then, a general equation on the domain $\mathrm{\Omega }:\{0\le x,y<\infty ;0\le t\le T\}$ can be written as follows:

$$\frac{\partial }{\partial t}u(x,y,t)+N\left(u(x,y,t)\right)=f(x,y,t),(x,y,t)\in \mathrm{\Omega },$$

(5)

with the initial condition

$$u(x,y,0)=h(x,y)\mathrm{for}\mathrm{any}x,y\in [0,\infty )\times [0,\infty ).$$

Now, we apply Laplace transform with respect to t on both sides of Equation (5), and we then get

$$\mathcal{L}\left\{\frac{\partial }{\partial t}u(x,y,t)\right\}+\mathcal{L}\left\{N\left(u\right(x,y,t\left)\right)\right\}=\mathcal{L}\left\{f(x,y,t)\right\}.$$

Using the differentiation property of the Laplace transform, we get

$$\begin{array}{ccc}\hfill \mathcal{L}\left\{u(x,y,t)\right\}& =& s^{-1}h(x,y)-s^{-1}\mathcal{L}\left\{N\left(u\right(x,y,t\left)\right)\right\}+s^{-1}\mathcal{L}\left\{f(x,y,t)\right\}.\hfill \end{array}$$

Taking the inverse Laplace transform on the above equation, we then obtain

$$u(x,y,t)=G(x,y,t)-{\mathcal{L}}^{-1}\left\{s^{-1}\mathcal{L}\left\{N\left(u\right(x,y,t\left)\right)\right\}\right\},$$

where the function $G(x,y,t)$ represents the term arising from the source term and the prescribed initial conditions.

Applying the homotopy perturbation method, He [18,19] constructed the function

$$v(x,y,t;p):\mathrm{\Omega }\times [0,1]\to \mathbb{R},$$

which can be satisfied as follows:

$$\begin{array}{cc}H(v(x,y,t;p),p)=& (1-p)[v(x,y,t;p)-\widetilde{v_0}(x,y,t)]+p[v(x,y,t;p)-G(x,y,t)\\ & +{\mathcal{L}}^{-1}\left\{s^{-1}\mathcal{L}\left\{N\left(v\right(x,y,t;p\left)\right)\right\}\right\}]=0,\end{array}$$

(6)

where $p\in [0,1]$ is an embedding parameter or homotopy parameter and $\widetilde{v_0}(x,y,t)$ is an initial approximation of Equation (6) which can be freely chosen [32] in Equation (5).

Furthermore, Equation (6) is called the homotopy equation, and it can be expressed as follows:

$$\begin{array}{ccc}v(x,y,t;p)\hfill & =\hfill & \widetilde{v_0}(x,y,t)-p[\widetilde{v_0}(x,y,t)-G(x,y,t)\hfill \\ & & +{\mathcal{L}}^{-1}\left\{s^{-1}\mathcal{L}\left\{N\left(v\right(x,y,t;p\left)\right)\right\}\right\}].\hfill \end{array}$$

(7)

From Equations (6) and (7), we can clearly see that

$$\begin{array}{ccc}\hfill p=0\to H\left(v\right(x,y,t;0),0)& =& v(x,y,t;0)-\widetilde{v_0}(x,y,t)=0,\hfill \\ \hfill p=1\to H\left(v\right(x,y,t;1),1)& =& v(x,y,t;1)-G(x,y,t)\hfill \\ & & +{\mathcal{L}}^{-1}\left\{s^{-1}\mathcal{L}\left\{N\left(v\right(x,y,t;1\left)\right)\right\}\right\}=0.\hfill \end{array}$$

By HPM technique, the solution $v(x,y,t;p)$ in Equation (7) is expressed as a sum of components which can be presented by the infinite series

$$\begin{array}{ccc}\hfill v(x,y,t;p)& =& \sum _{i=0}^{\infty }{p}^i{v}_i(x,y,t).\hfill \end{array}$$

(8)

By substituting Equation (8) into Equation (7) and using HPM, it can be expressed as follows:

$$\begin{array}{ccc}\hfill \sum _{i=0}^{\infty }{p}^i{v}_i(x,y,t)& =& \widetilde{v_0}(x,y,t)-p[\widetilde{v_0}(x,y,t)-G(x,y,t)\hfill \\ & & +{\mathcal{L}}^{-1}\left\{s^{-1}\mathcal{L}\left\{N(\sum _{i=0}^{\infty }{p}^i{v}_i(x,y,t;p))\right\}\right\}].\hfill \end{array}$$

To find the approximate solution $v_i,i=0,1,2,\dots$ of this problem, the equating coefficients of corresponding power of p on both sides are utilized. Furthermore, we obtain the recurrence relation as given below:

$$\begin{array}{ccc}\hfill v_0(x,y,t)& =& \widetilde{v_0}(x,y,t)\hfill \\ \hfill v_1(x,y,t)& =& G(x,y,t)-\widetilde{v_0}(x,y,t)\hfill \\ & & -{\mathcal{L}}^{-1}\left\{s^{-1}\mathcal{L}\left\{N\left(\widetilde{v_0}(x,y,t)\right)\right\}\right\}\hfill \\ \hfill v_m(x,y,t)& =& -{\mathcal{L}}^{-1}\left\{s^{-1}\mathcal{L}\left\{N\left(v_{m-1}(x,y,t)\right)\right\}\right\}\mathrm{when}m\ge 2.\hfill \end{array}$$

According to the solution of Equation (8), we obtain

$$v(x,y,t;p)=v_0(x,y,t)+p{v}_1(x,y,t)+p^2{v}_2(x,y,t)+p^3{v}_3(x,y,t)+\dots .$$

From the above equation, p converges to 1, and we obtain the approximate solution in this problem (4) can be expressed

$$u(x,y,t)=v(x,y,t;1)=v_0(x,y,t)+v_1(x,y,t)+v_2(x,y,t)+v_3(x,y,t)+\dots .$$

(9)

Furthermore, the series (9) leads to the explicit solution when infinite series converges.

4. Two-Dimensional Black Scholes Equation with Laplace Transformation Homotopy Perturbation Method

In this section, the two-dimensional Black Scholes model in Equation (3) is considered

$$\begin{array}{ccc}\hfill \frac{\partial c}{\partial t}& =& \frac{1}{2}{\sigma }_1^2{x}^2\frac{{\partial }^{2}c}{\partial x^2}+\frac{1}{2}{\sigma }_2^2{y}^2\frac{{\partial }^{2}c}{\partial y^2}+\rho {\sigma }_1{\sigma }_{2}xy\frac{\partial c^2}{\partial x\partial y}+r\left(x\frac{\partial c}{\partial x}+y\frac{\partial c}{\partial y}\right)-rc\hfill \end{array}$$

(10)

with initial condition

$$\begin{array}{ccc}\hfill c(x,y,0)& =& \max ({\beta }_{1}x+{\beta }_{2}y-K,0).\hfill \end{array}$$

Taking the Laplace transform with respect to t in Equation (10), we get

$$\begin{array}{ccc}\hfill \mathcal{L}\left\{\frac{\partial c}{\partial t}\right\}& =& \mathcal{L}\left\{\frac{1}{2}{\sigma }_1^2{x}^2\frac{{\partial }^{2}c}{\partial x^2}+\frac{1}{2}{\sigma }_2^2{y}^2\frac{{\partial }^{2}c}{\partial y^2}+\rho {\sigma }_1{\sigma }_{2}xy\frac{\partial c^2}{\partial x\partial y}+r\left(x\frac{\partial c}{\partial x}+y\frac{\partial c}{\partial y}\right)-rc\right\}.\hfill \end{array}$$

(11)

Let

$$N\left(c(x,y,t)\right)=\frac{1}{2}{\sigma }_1^2{x}^2\frac{{\partial }^{2}c}{\partial x^2}+\frac{1}{2}{\sigma }_2^2{y}^2\frac{{\partial }^{2}c}{\partial y^2}+\rho {\sigma }_1{\sigma }_{2}xy\frac{\partial c^2}{\partial x\partial y}+r\left(x\frac{\partial c}{\partial x}+y\frac{\partial c}{\partial y}\right)-rc,$$

Equation (11) becomes

$$\begin{array}{ccc}\hfill \mathcal{L}\left\{c(x,y,t)\right\}& =& \frac{1}{s}c(x,y,0)+\frac{1}{s}\mathcal{L}\left\{N\left(c\right(x,y,t\left)\right)\right\}\hfill \\ \hfill \mathcal{L}\left\{c(x,y,t)\right\}& =& \frac{1}{s}\max ({\beta }_{1}x+{\beta }_{2}y-K,0)+\frac{1}{s}\mathcal{L}\left\{N\left(c\right(x,y,t\left)\right)\right\}.\hfill \end{array}$$

Taking the inverse Laplace transform in the above equation, we obtain

$$\begin{array}{ccc}\hfill c(x,y,t)& =& \max ({\beta }_{1}x+{\beta }_{2}y-K,0)+{\mathcal{L}}^{-1}\left\{\frac{1}{s}\mathcal{L}\left\{N\left(c\right(x,y,t\left)\right)\right\}\right\}.\hfill \end{array}$$

Applying the Homotopy Perturbation Method, we construct the following:

$$\begin{array}{cc}\hfill (1-p)\left(c\right(x,y,t;p)& -\widetilde{c_0}(x,y,t))+p[c(x,y,t;p)\hfill \\ & -\max ({\beta }_{1}x+{\beta }_{2}y-K,0)-{\mathcal{L}}^{-1}\left\{\frac{1}{s}\mathcal{L}\left\{N\left(c\right(x,y,t;p\left)\right)\right\}\right]=0\hfill \end{array}$$

or

$$\begin{array}{ccc}\hfill c(x,y,t;p)& =& \widetilde{c_0}(x,y,t)-p\widetilde{c_0}(x,y,t)+p\max ({\beta }_{1}x+{\beta }_{2}y-K,0)\hfill \\ & & +p{\mathcal{L}}^{-1}\left\{\frac{1}{s}\mathcal{L}\left\{N\left(c\right(x,y,t;p\left)\right)\right\}\right\},\hfill \end{array}$$

(12)

where $\widetilde{c_0}(x,y,t)$ can be freely chosen.

We choose $\widetilde{c_0}(x,y,t)=\max ({\beta }_{1}x+{\beta }_{2}y-K,0)+\rho (x^2+y^2)t$ and substitute $\widetilde{c_0}(x,y,t)$ in Equation (12). Thus,

$$\begin{array}{ccc}\hfill c(x,y,t;p)& =& \max ({\beta }_{1}x+{\beta }_{2}y-K,0)+\rho (x^2+y^2)t+p[-(x^2+y^2)t\hfill \\ & & +{\mathcal{L}}^{-1}\left\{\frac{1}{s}\mathcal{L}\left\{N\left(c\right(x,y,t;p\left)\right)\right\}\right\}].\hfill \end{array}$$

(13)

We then assume the solution of problem (13) to be in the form

$$\begin{array}{ccc}\hfill c(x,y,t;p)& =& \sum _{n=0}^{\infty }{p}^n{c}_n(x,y,t).\hfill \end{array}$$

(14)

By substituting the above Equation (14) into Equation (13), we get

$$\begin{array}{ccc}\hfill \sum _{n=0}^{\infty }{p}^n{c}_n(x,y,t)& =& \max ({\beta }_{1}x+{\beta }_{2}y-K,0)+\rho (x^2+y^2)t\hfill \\ & & +p\left(-(x^2+y^2)t+{\mathcal{L}}^{-1}\left\{\frac{1}{s}\mathcal{L}\right\{\frac{1}{2}{\sigma }_1^2{x}^2\sum _{n=0}^{\infty }{p}^n\frac{{\partial }^2{c}_n}{\partial x^2}\right.\hfill \\ & & +\frac{1}{2}{\sigma }_2^2{y}^2\sum _{n=0}^{\infty }{p}^n\frac{{\partial }^2{c}_n}{\partial y^2}+\rho {\sigma }_1{\sigma }_{2}xy\sum _{n=0}^{\infty }{p}^n\frac{\partial c^2}{\partial x\partial y}\hfill \\ & & +r\left(x\sum _{n=0}^{\infty }{p}^n\frac{\partial c_n}{\partial x}+y\sum _{n=0}^{\infty }{p}^n\frac{\partial c_n}{\partial y}\right)\left.-r\sum _{n=0}^{\infty }{p}^n{c}_n\left\}\right\}\right).\hfill \end{array}$$

Equating the corresponding power of p on the both sides in the above equation, we get

$$\begin{array}{cccc}\hfill p^0;& \hfill c_0(x,y,t)& =& \max ({\beta }_{1}x+{\beta }_{2}y-K,0)+\rho (x^2+y^2)t\hfill \\ \hfill p^1;& \hfill c_1(x,y,t)& =& \frac{t^2\rho }{2}\left[({\sigma }_1^2+r)x^2+({\sigma }_2^2+r)y^2\right]-t[{({\sigma }_1^2+r)}^0{x}^2+{({\sigma }_2^2+r)}^0{y}^2\hfill \\ & & & -r(\max ({\beta }_1,0)x+\max ({\beta }_2,0)y)+r\max ({\beta }_{1}x+{\beta }_{2}y-K,0)]\hfill \\ \hfill p^2;& \hfill c_2(x,y,t)& =& \frac{t^3\rho }{6}\left[{({\sigma }_1^2+r)}^2{x}^2+{({\sigma }_2^2+r)}^2{y}^2\right]-\frac{t^2}{2}[{({\sigma }_1^2+r)}^1{x}^2+{({\sigma }_2^2+r)}^1{y}^2\hfill \\ & & & +r^2(\max ({\beta }_1,0)x+\max ({\beta }_2,0)y)-r^2\max ({\beta }_{1}x+{\beta }_{2}y-K,0)]\hfill \\ \hfill p^3;& \hfill c_3(x,y,t)& =& \frac{t^4\rho }{24}\left[{({\sigma }_1^2+r)}^3{x}^2+{({\sigma }_2^2+r)}^3{y}^2\right]-\frac{t^3}{6}[{({\sigma }_1^2+r)}^2{x}^2+{({\sigma }_2^2+r)}^2{y}^2\hfill \\ & & & -r^3(\max ({\beta }_1,0)x+\max ({\beta }_2,0)y)+r^3\max ({\beta }_{1}x+{\beta }_{2}y-K,0)],\hfill \end{array}$$

and so on.

Proceeding in this same manner, we obtain

$$\begin{array}{cccc}\hfill p^0;& \hfill c_0(x,y,t)& =& \max ({\beta }_{1}x+{\beta }_{2}y-K,0)+\rho (x^2+y^2)t\hfill \\ \hfill p^n;& \hfill c_n(x,y,t)& =& \frac{t^{n+1}\rho }{\Gamma (n+2)}\left[{({\sigma }_1^2+r)}^n{x}^2+{({\sigma }_2^2+r)}^n{y}^2\right]-\frac{t^n}{\Gamma (n+1)}[{({\sigma }_1^2+r)}^{n-1}{x}^2\hfill \\ & & & +{({\sigma }_2^2+r)}^{n-1}{y}^2+{(-1)}^n{r}^n(\max ({\beta }_1,0)x+\max ({\beta }_2,0)y)\hfill \\ & & & -{(-1)}^n{r}^n\max ({\beta }_{1}x+{\beta }_{2}y-K,0)]\mathrm{when}n\ge 1.\hfill \end{array}$$

So, the solution $c(x,y,t;p)$ of problem (13) is given by

$$\begin{array}{ccc}\hfill c(x,y,t;p)& =& \sum _{n=0}^{\infty }{p}^n{c}_n(x,y,t)\hfill \\ & =& c_0(x,y,t)+\sum _{n=1}^{\infty }{p}^n\{\frac{t^{n+1}\rho }{\Gamma (n+2)}\left[{({\sigma }_1^2+r)}^n{x}^2+{({\sigma }_2^2+r)}^n{y}^2\right]\hfill \\ & & -\frac{t^n}{\Gamma (n+1)}[{({\sigma }_1^2+r)}^{n-1}{x}^2+{({\sigma }_2^2+r)}^{n-1}{y}^2\hfill \\ & & +{(-1)}^n{r}^n(\max ({\beta }_1,0)x+\max ({\beta }_2,0)y)\hfill \\ & & -{(-1)}^n{r}^n\max ({\beta }_{1}x+{\beta }_{2}y-K,0)\left]\right\}\hfill \\ & =& c_0(x,y,t)+\sum _{n=0}^{\infty }{p}^{n+1}\{\frac{t^{n+2}\rho }{\Gamma (n+3)}\left[{({\sigma }_1^2+r)}^{n+1}{x}^2+{({\sigma }_2^2+r)}^{n+1}{y}^2\right]\hfill \\ & & -\frac{t^{n+1}}{\Gamma (n+2)}[{({\sigma }_1^2+r)}^n{x}^2+{({\sigma }_2^2+r)}^n{y}^2\hfill \\ & & +{(-1)}^{n+1}{r}^{n+1}(\max ({\beta }_1,0)x+\max ({\beta }_2,0)y)\hfill \\ & & -{(-1)}^{n+1}{r}^{n+1}\max ({\beta }_{1}x+{\beta }_{2}y-K,0)\left]\right\}.\hfill \end{array}$$

When p converges to 1, we get

$$\begin{array}{ccc}\hfill c(x,y,t)& =& c_0(x,y,t)+\sum _{n=0}^{\infty }\{\frac{t^{n+2}\rho }{\Gamma (n+3)}\left[{({\sigma }_1^2+r)}^{n+1}{x}^2+{({\sigma }_2^2+r)}^{n+1}{y}^2\right]\hfill \\ & & -\frac{t^{n+1}}{\Gamma (n+2)}[{({\sigma }_1^2+r)}^n{x}^2+{({\sigma }_2^2+r)}^n{y}^2\hfill \\ & & +{(-1)}^{n+1}{r}^{n+1}(\max ({\beta }_1,0)x+\max ({\beta }_2,0)y)\hfill \\ & & -{(-1)}^{n+1}{r}^{n+1}\max ({\beta }_{1}x+{\beta }_{2}y-K,0)\left]\right\}.\hfill \end{array}$$

Hence, we obtain the explicit solution of Equation (10) as:

$$\begin{array}{ccc}\hfill c(x,y,t)& =& \max ({\beta }_{1}x+{\beta }_{2}y-K,0)+x^2\left(\rho ({\sigma }_1^2+r)E_{2,{\sigma }_1^2+r}\left(t\right)-E_{1,{\sigma }_1^2+r}\left(t\right)+\rho t\right)\hfill \\ & & +y^2\left(\rho ({\sigma }_2^2+r)E_{2,{\sigma }_2^2+r}\left(t\right)-E_{1,{\sigma }_2^2+r}\left(t\right)+\rho t\right)\hfill \\ & & -r\left(\max ({\beta }_1,0)x+\max ({\beta }_2,0)y\right)E_{1,-r}\left(t\right)\hfill \\ & & +r\max ({\beta }_{1}x+{\beta }_{2}y-K,0)E_{1,-r}\left(t\right)\hfill \end{array}$$

(15)

where $E_{a,b}\left(t\right)=t^a{\sum }_{k=0}^{\infty }\frac{{\left(bt\right)}^k}{\Gamma (a+k+1)}$ is the Mellin–Ross function [33], in which a and b are constants.

5. Solution Example

In this section, the explicit solution in Equation (15) is implemented to compute the value of European call option by using MATLAB programming (Matlab Release R2016b, The MathWorks Inc., Natick, MA, USA) and the condition as in (2) and ${\beta }_1=2,{\beta }_2=1$,

$$c(S_1,S_2,T)=\max (2S_1+S_2-K,0),$$

with strike price $K=70$. The risk-free interest rate per year is $5\%$, so $r=0.05$, the maturity time is $T=1$ measured in years, and the volatilities of the underlying assets $S_1$ and $S_2$ are ${\sigma }_1=5\%$ and ${\sigma }_2=10\%$, respectively.

In Figure 1, the value surface of European call option with the correlation, $\rho =0.25$, at maturity time is presented over a range of stock prices $0\le S_1\le 200$ and $0\le S_2\le 200$ surrounding at the strike price. The result shows that by increasing the stock prices, $S_1$ and $S_2$, the option value increases significantly. For the set of parameters $K,r,{\sigma }_1,{\sigma }_2$ and T, the different value of European call option of non-negative correlation ${\rho }_0=0$ and ${\rho }_1=0.25$ and non-positive correlation ${\rho }_0=0$ and ${\rho }_2=-0.5$ is plotted over a range of stock prices $0\le S_1\le 200$ and $0\le S_2\le 200$ at the maturity time, as shown in Figure 2. The results as shown in Figure 2 indicate that the correlation has a significant effect on the European call option. Furthermore, increasing both of the stock prices leads to an increase of the different values of European call option.

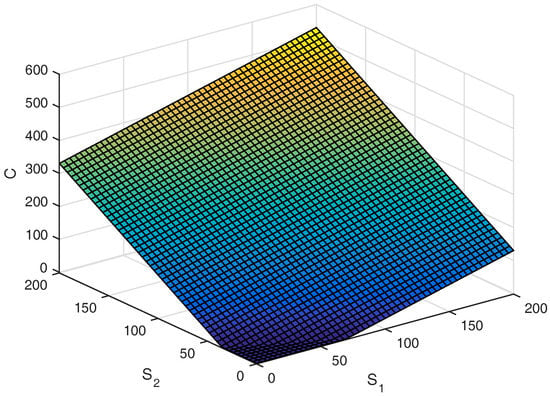
Figure 1. The explicit solution of European call option price obtained from two-dimensional Black Scholes model with stock prices $S_1,S_2$ and correlation $\rho =0.25.$

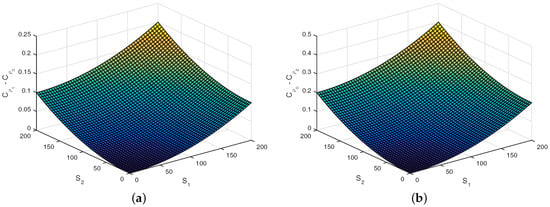
Figure 2. The different value of European call option, $C_{{\rho }_1}-C_{{\rho }_0}$ and $C_{{\rho }_0}-C_{{\rho }_2}$ at the maturity T with stock prices $S_1,S_2$ and correlation ρ each other: (a) ${\rho }_1=0.25$ and ${\rho }_0=0$; (b) ${\rho }_0=0$ and ${\rho }_2=-0.5$.

Before the expiration date, the value of European call option when correlation varies from $-1$ to 1 is investigated as shown in Figure 3. The influence of stock price $S_2$ with fixed stock price $S_1$ and stock price $S_1$ with fixed stock price $S_2$ is shown in Figure 3a,b, respectively. Three different stock prices of $S_1$ and $S_2$ used in this investigation are set to strike price $K=70$ and $K\pm 30$. It is apparent that the relationship between the European call option and the correlation parameter is a linear increasing pattern. The results also indicate that a higher stock price gives a higher rate of change in European call option.

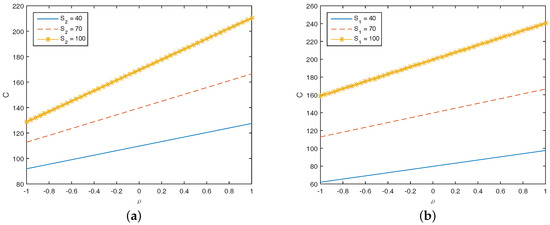
Figure 3. Relationship between the European call option and the correlation ρ at a day before the maturity date: (a) $S_1$ = 70; (b) $S_2$ = 70.

6. Conclusions

One of the most well-known and useful mathematical models in the financial market is the Black Scholes model. In this article, we consider the two-dimensional Black Scholes equation based on European call option. By using the LHPM, we obtain the explicit solution of the problem in the form of a special function, namely the Mellin–Ross function. The advantage of LHPM for this problem is that this explicit solution can be easily implemented to simulate the European call option depending on two stock prices in order to apply in a real life situation for financial markets.