Quasi-Interpolation Operators for Bivariate Quintic Spline Spaces and Their Applications
Abstract
:1. Introduction
2. The Bivariate Spline Space
2.1. The Spaces
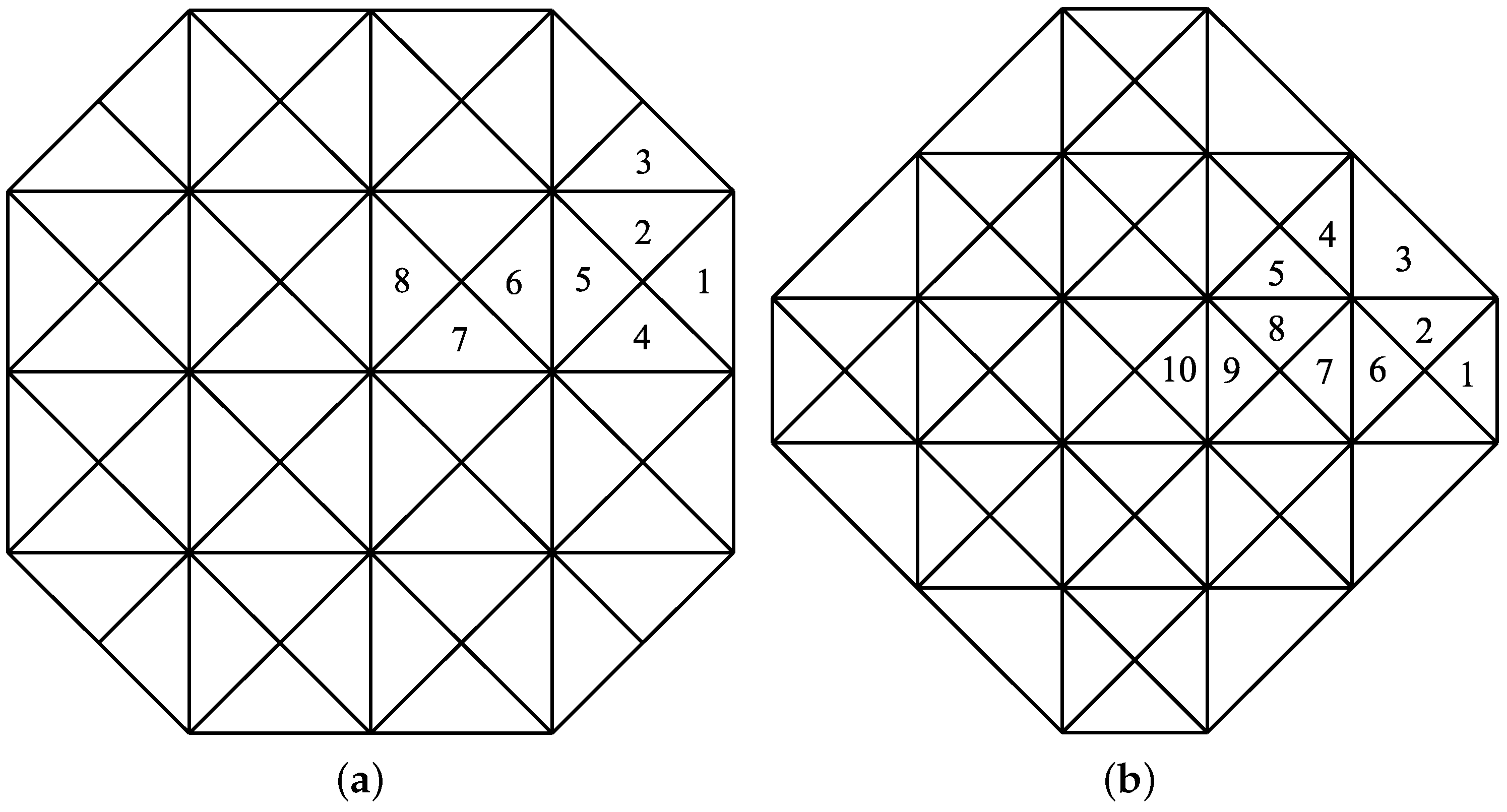
2.2. Basis of
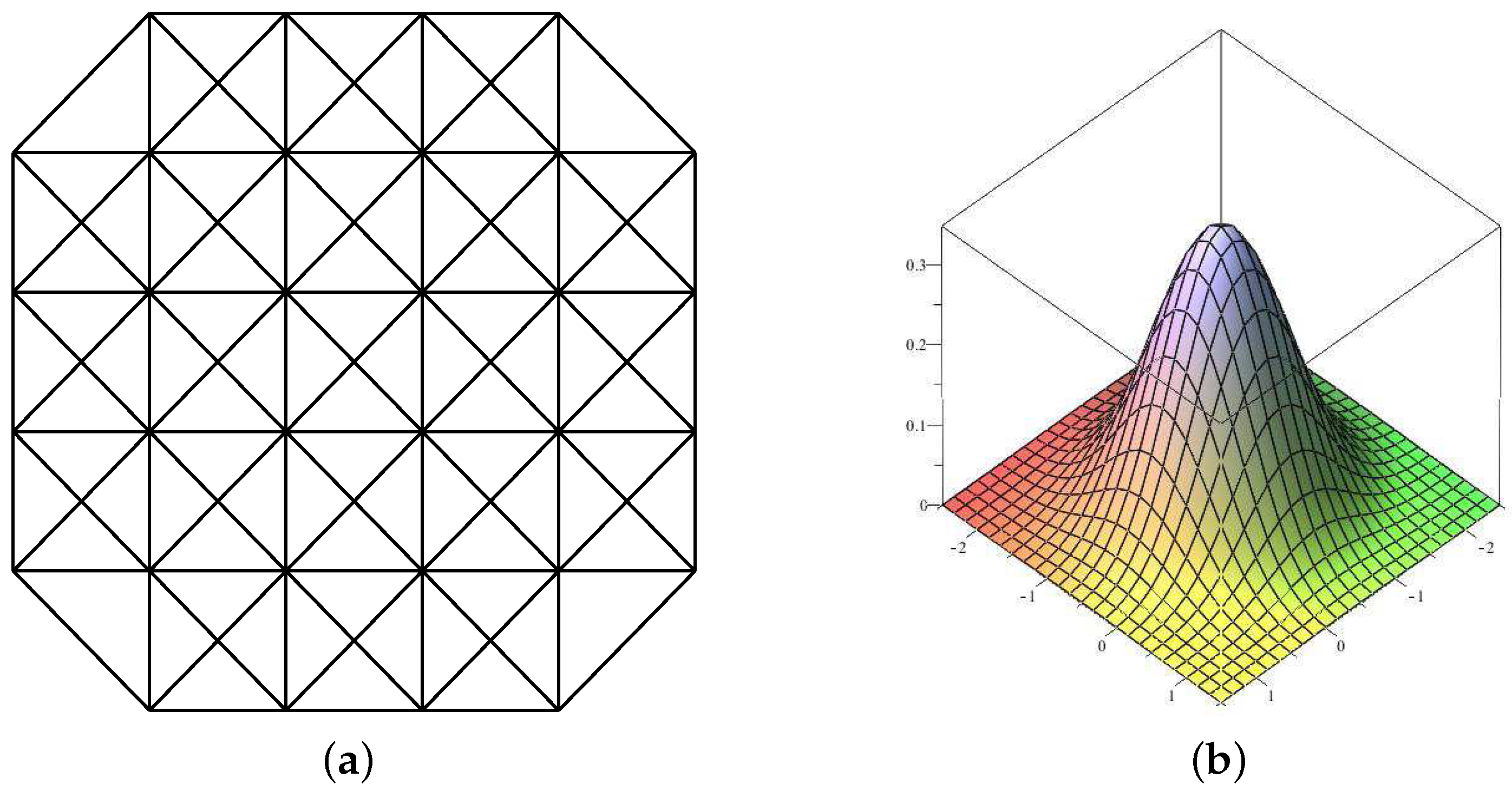
2.3. Quasi-Interpolation Operators for
3. Applications of Quasi-Interpolation Operator
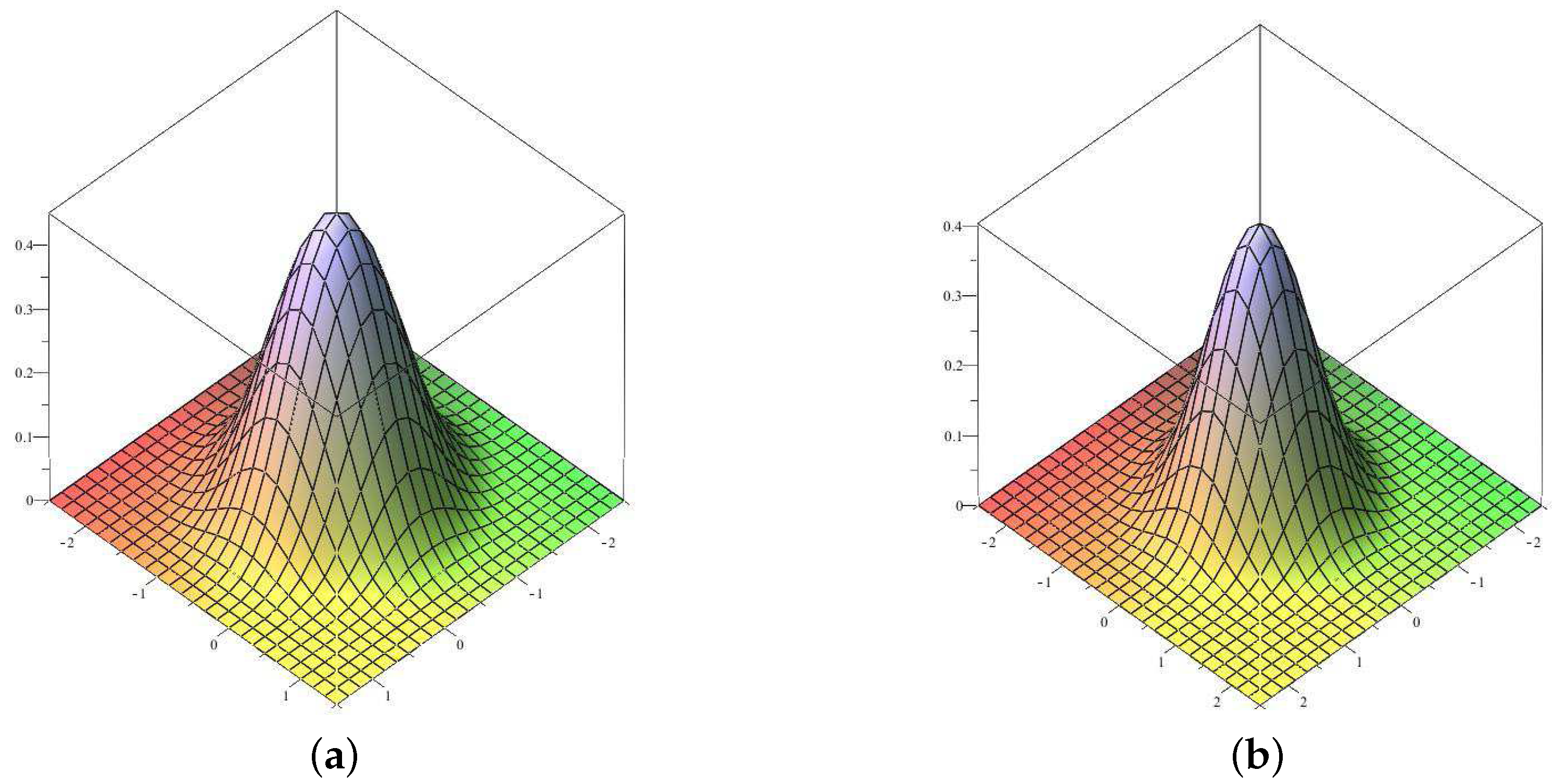
3.1. Solving 2D Burgers’ Equations
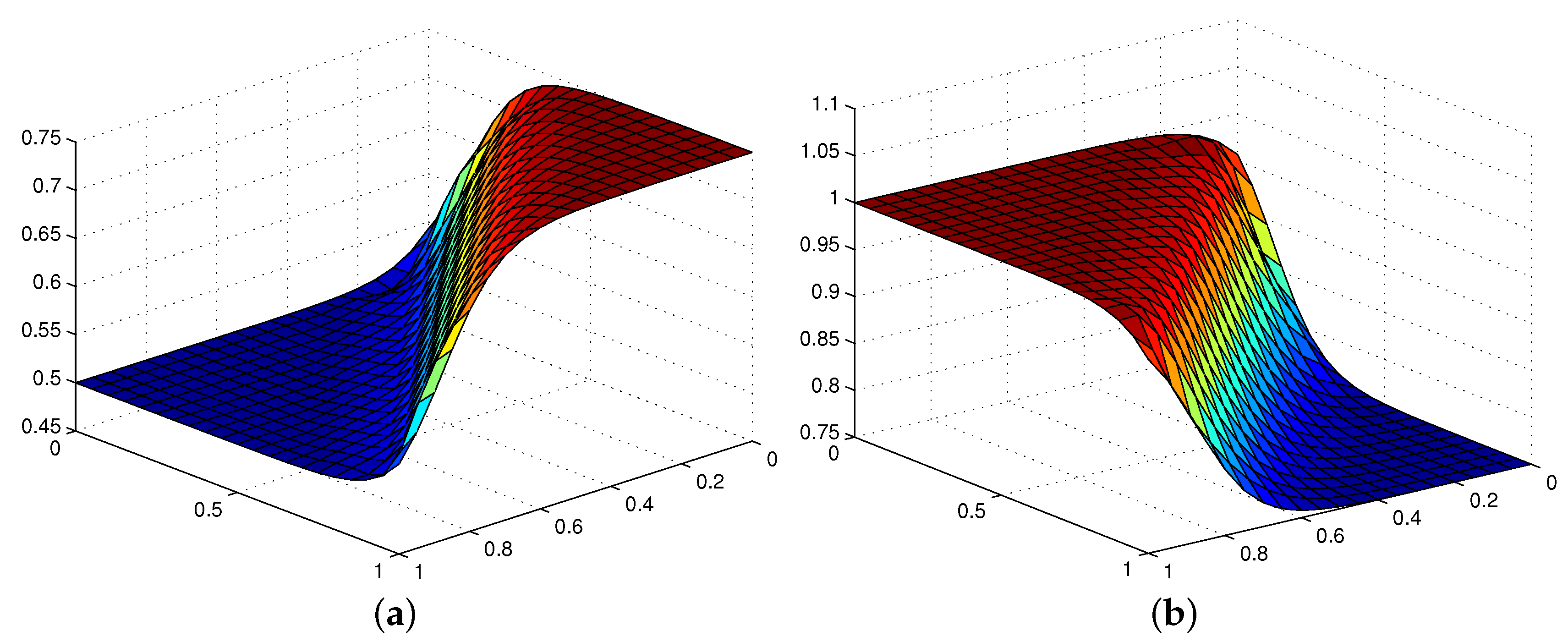
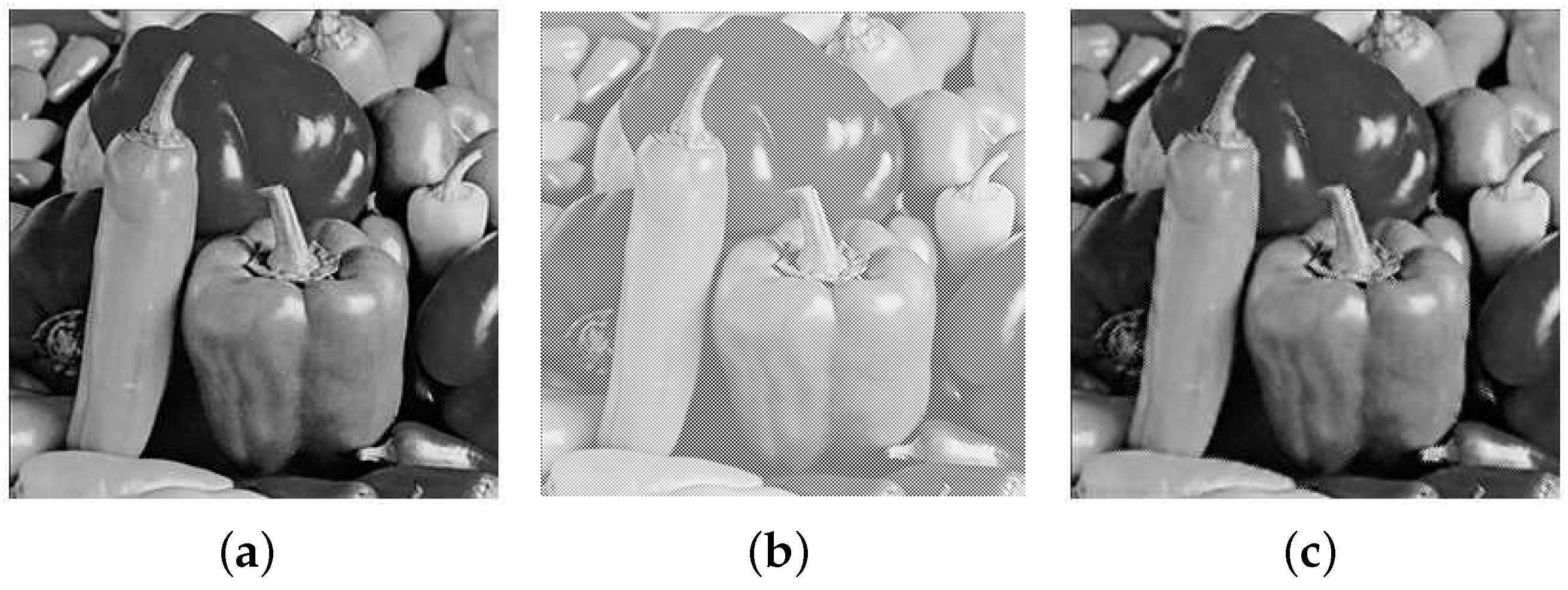
3.2. Image Reconstruction
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Schoenberg, I.J. Contributions to the problem of approximation of equidistant data by analytic functions. Quart. Appl. Math. 1946, 4, 45–99, 112–141. [Google Scholar] [CrossRef]
- De Boor, C. Splines as linear comination of B-splines. In Approximation Theory II; Lorentz, G.G., Chui, C.K., Schumaker, L.L., Eds.; Academy Press: New York, NY, USA, 1976; pp. 1–47. [Google Scholar]
- De Boor, C. Topics in multivariate approximation theory. In Topics in Numerical Analysis; Turner, P.R., Ed.; Lecture Notes Mathematics; Springer: Berlin, Germany, 1982; Volume 965, pp. 39–78. [Google Scholar]
- Dahmen, W.; Micchelli, C.A. Recent progress in multivariate splines, interpolating cardinal splines as their degree tends to infinity; Ward, Israel J., Ed.; Academic press: Cambridge, MA, USA, 1983; pp. 27–121. [Google Scholar]
- Wang, R.H. The structural characterization and interpolation for multivariate splines. Acta Math. Sin. 1975, 18, 91–106. [Google Scholar]
- De Boor, C. A Practical Guide to Splines; Springer: New York, NY, USA, 1978. [Google Scholar]
- Allouch, C.; Sablonnière, P.; Sbibih, D. A collocation method for the numerical solution of a two dimensional integral equation using a quadratic spline quasi-interpolant. Numer. Algorithms 2013, 62, 445–468. [Google Scholar] [CrossRef]
- Dagnino, C.; Remogna, S.; Sablonnière, P. On the solution of Fredholm integral equations based on spline quasi-interpolating projectors. BIT Numer. Math. 2014, 54, 979–1008. [Google Scholar] [CrossRef]
- Dagnino, C.; Lamberti, P.; Remogna, S. Curve network interpolation by C1 quadratic B-spline surfaces. Comput. Aided Geom. Des. 2015, 40, 26–39. [Google Scholar] [CrossRef]
- Wang, R.H. Multivariate Spline Functions and Their Applications; Science Press/Kluwer Academic Publishers: Beijing, China; New York, NY, USA; Dordrecht, The Netherlands; Boston, MA, USA; London, UK, 2001. [Google Scholar]
- Zhu, C.G.; Wang, R.H. Lagrange interpolation by bivariate splines on cross-cut partitions. J. Comp. Appl. Math. 2006, 195, 326–340. [Google Scholar] [CrossRef]
- Zhu, C.G.; Wang, R.H. Numerical solution of Burgers’ equation by cubic B-spline quasi-interpolation. Appl. Math. Comput. 2009, 208, 260–272. [Google Scholar] [CrossRef]
- Basto, M.; Semiao, V.; Calheiros, F. Dynamics and synchronization of numerical solutions of the Burgers equation. J. Comp. Appl. Math. 2009, 231, 793–806. [Google Scholar] [CrossRef]
- Moslem, W.M.; Sabry, R. Zakharov-Kuznetsov-Burgers equation for dust ion acoustic waves. Chaos Solitons Fractals 2008, 36, 628–634. [Google Scholar] [CrossRef]
- Rashidi, M.M.; Erfani, E. New analytical method for solving Burgers’ and nonlinear heat transfer equations and comparison with HAM. Comput. Phys. Commun. 2009, 180, 1539–1544. [Google Scholar] [CrossRef]
- Zhu, H.Q.; Shu, H.Z.; Ding, M.Y. Numerical solutions of two-dimensional Burgers’ equations by discrete Adomian decomposition method. Comput. Math. Appl. 2010, 60, 840–848. [Google Scholar] [CrossRef]
- Abbasbandy, S.; Darvishi, M.T. A numerical solution of Burgers’ equation by modified Adomian’s decomposition method. Appl. Math. Comput. 2005, 163, 1265–1272. [Google Scholar]
- Dehghan, M.; Hamidi, A.; Shakourifar, M. The solution of coupled Burgers’ equation using Adomian-Pade technique. Appl. Math. Comput. 2007, 189, 1034–1047. [Google Scholar] [CrossRef]
- Abbasbandy, S.; Darvishi, M.T. A numerical solution of Burgers’ equation by time discretization of Adomian’s decomposition method. Appl. Math. Comput. 2005, 170, 95–102. [Google Scholar] [CrossRef]
- Zhou, B.; Peng, Y.N.; Ye, C.M.; Tang, J. GPGPU Accelerated Fast Convolution Back-Projection for Radar Image Reconstruction. Tsinghua Sci. Technol. 2011, 16, 256–263. [Google Scholar] [CrossRef]
- Ouaddah, A.; Boughaci, D. Harmony search algorithm for image reconstruction from projections. Appl. Soft Comput. 2016, 46, 924–935. [Google Scholar] [CrossRef]
- U¯ur, S.; Arikan, O. SAR image reconstruction and autofocus by compressed sensing. Digit. Signal Process. 2012, 22, 923–932. [Google Scholar]
- Wang, R.H. The dimension and basis of spaces of multivariate splines. J. Comput. Appl. Math. 1985, 12–13, 163–177. [Google Scholar] [CrossRef]
- Wang, R.H.; Li, C.J. Bivariate quartic spline spaces and quasi-interpolation operators. J. Comp. Appl. Math. 2006, 190, 325–338. [Google Scholar] [CrossRef]
- Foucher, F.; Sablonnière, P. Approximating partial derivatives of first and second order by quadratic spline quasi-interpolants on uniform meshes. Math. Comput. Simul. 2008, 77, 202–208. [Google Scholar] [CrossRef]
- Dagnino, C.; Lamberti, P. On the construction of local quadratic spline quasi-interpolants on bounded rectangular domains. J. Comp. Appl. Math. 2008, 221, 367–375. [Google Scholar] [CrossRef]
- Dagnino, C.; Lamberti, P.; Remogna, S. B-Spline bases for unequally smooth quadratic spline spaces on non-uniform criss-cross triangulations. Numer. Algorithms 2012, 61, 209–222. [Google Scholar] [CrossRef]
- Dagnino, C.; Remogna, S.; Sablonnière, P. Error bounds on the approximation of functions and partial derivatives by quadratic spline quasi-interpolants on non-uniform criss-cross triangulations of a rectangular domain. BIT Numer. Math. 2013, 53, 87–109. [Google Scholar] [CrossRef]
- Chui, C.K.; Wang, R.H. Spaces of bivariate cubic and quartic splines on type-1 triangulation. J. Math. Anal. Appl. 1984, 101, 540–554. [Google Scholar] [CrossRef]
- Li, C.J. Multivariate Splines on Special Triangulations and Their Applications. Ph.D. Thesis, Department of Applied Mathematics, Dalian University of Technology, Dalian, China, 2004. [Google Scholar]
- Song, M.W. Piecewise quintic spline spaces on uniform type-2 triangulation. Master’s Thesis, School of Mathematical Sciences, Dalian University of Technology, Dalian, China, 2007. [Google Scholar]
- Bahadir, A.R. A fully implicit finite-difference scheme for two-dimensional Burgers’ equations. Appl. Math. Comput. 2003, 137, 131–137. [Google Scholar] [CrossRef]
- Biazar, J.; Aminikhah, H. Exact and numerical solutions for non-linear Burgers’ equation by VIM. Math. Comput. Model. 2009, 49, 1394–1400. [Google Scholar] [CrossRef]
- Fletcher, C.A.J. Generating exact solutions of the two-dimensional Burgers’ equation. Int. J. Numer. Meth. Fluids 1983, 3, 213–216. [Google Scholar] [CrossRef]
- Chaikalis, D.; Sgouros, N.P.; Maroulis, D. A real-time FPGA architecture for 3D reconstruction from integral images. J. Vis. Commun. Image Represent. 2010, 21, 9–16. [Google Scholar] [CrossRef]
- Huang, J.Z.; Zhang, S.T.; Metaxas, D. Efficient MR image reconstruction for compressed MR imaging. Med. Image Anal. 2011, 15, 670–679. [Google Scholar] [CrossRef] [PubMed]
- Wakin, M. Standard Test Images. Available online: http://www.ece.rice.edu/wakin/images/ (accessed on 26 March 2016).

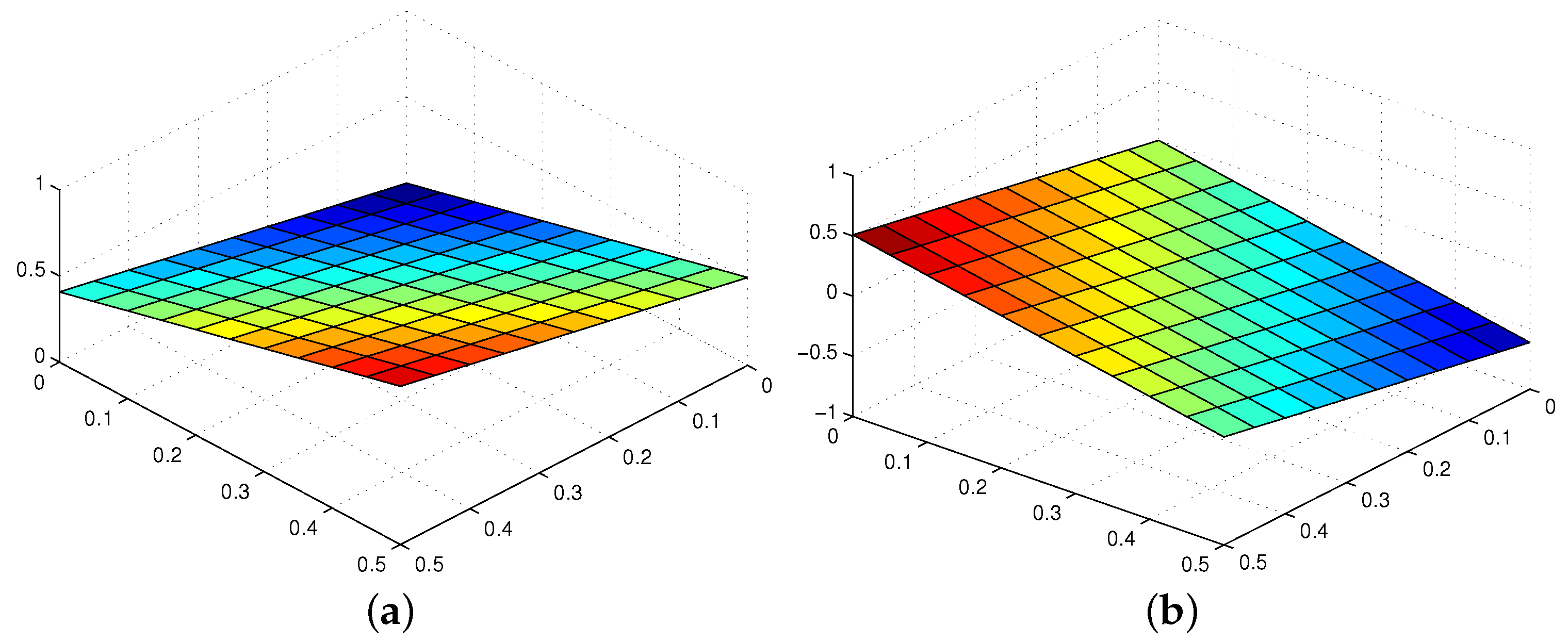



| Mesh Grid | ||||||
|---|---|---|---|---|---|---|
| (0.1, 0.1) | 0.61749 | 0.61720 | 0.59474 | 0.59439 | 0.55564 | 0.55568 |
| (0.9, 0.2) | 0.50021 | 0.50020 | 0.50015 | 0.50014 | 0.50006 | 0.50007 |
| (0.8, 0.3) | 0.50150 | 0.50148 | 0.50108 | 0.50102 | 0.50049 | 0.50048 |
| (0.9, 0.5) | 0.50403 | 0.50398 | 0.50289 | 0.50275 | 0.50155 | 0.50130 |
| (0.8, 0.6) | 0.52640 | 0.52667 | 0.51859 | 0.51896 | 0.50990 | 0.50933 |
| (0.2, 0.8) | 0.74931 | 0.74930 | 0.74900 | 0.74898 | 0.74783 | 0.74786 |
| (0.9, 0.9) | 0.61720 | 0.61720 | 0.59456 | 0.59439 | 0.55369 | 0.55568 |
| Mesh Grid | ||||||
|---|---|---|---|---|---|---|
| (0.1, 0.1) | 0.88251 | 0.88280 | 0.90526 | 0.90561 | 0.94436 | 0.94432 |
| (0.9, 0.2) | 0.99979 | 0.99980 | 0.99985 | 0.99986 | 0.99994 | 0.99993 |
| (0.8, 0.3) | 0.99850 | 0.99852 | 0.99892 | 0.99898 | 0.99951 | 0.99952 |
| (0.9, 0.5) | 0.99597 | 0.99602 | 0.99711 | 0.99725 | 0.99845 | 0.99869 |
| (0.8, 0.6) | 0.97360 | 0.97333 | 0.98141 | 0.98104 | 0.99010 | 0.99067 |
| (0.2, 0.8) | 0.75069 | 0.75070 | 0.75100 | 0.75102 | 0.75217 | 0.75214 |
| (0.9, 0.9) | 0.88250 | 0.88280 | 0.90544 | 0.90561 | 0.94632 | 0.94432 |
| Mesh Grid | ||||||
|---|---|---|---|---|---|---|
| MSQI | Bahadir [32] | Zhu [16] | MSQI | Bahadir [32] | Zhu [16] | |
| (0.1, 0.1) | 1.63803 | 7.24132 | 5.91368 | 6.11973 | 5.13431 | 2.77664 |
| (0.5, 0.1) | 1.85815 | 2.42869 | 4.84030 | 1.73489 | 8.85712 | 4.52081 |
| (0.9, 0.1) | 1.64831 | 8.39751 | 3.41000 | 3.07314 | 6.53372 | 3.37430 |
| (0.3, 0.3) | 1.65880 | 8.25331 | 5.91368 | 6.69829 | 7.31601 | 2.77664 |
| (0.7, 0.3) | 1.94033 | 3.43163 | 4.84030 | 2.16464 | 6.27245 | 4.52081 |
| (0.1, 0.5) | 1.61309 | 5.62014 | 1.64290 | 3.32546 | 4.01942 | 2.86553 |
| Mesh Grid | ||||||
|---|---|---|---|---|---|---|
| MSQI | Bahadir [32] | Zhu [16] | MSQI | Bahadir [32] | Zhu [16] | |
| (0.1, 0.1) | 1.63803 | 8.35601 | 5.91368 | 6.11973 | 6.17325 | 2.77664 |
| (0.5, 0.1) | 1.85815 | 5.13642 | 4.84030 | 1.73489 | 4.67046 | 4.52081 |
| (0.9, 0.1) | 1.64832 | 7.03298 | 3.41000 | 3.07314 | 1.70434 | 3.37400 |
| (0.3, 0.3) | 1.65880 | 6.15201 | 5.91368 | 6.69829 | 6.25402 | 2.77664 |
| (0.7, 0.3) | 1.94033 | 5.41000 | 4.84030 | 2.16464 | 4.66046 | 4.52081 |
| (0.1, 0.5) | 1.61310 | 7.35192 | 1.64290 | 3.32546 | 8.72422 | 2.86553 |
| Mesh Grid | [16] | [16] | ||||
|---|---|---|---|---|---|---|
| (0.1, 0.1) | 0.18367 | 3.29366 | 3.30750 | -0.02041 | 7.46922 | 1.05384 |
| (0.3, 0.1) | 0.34693 | 5.45525 | 5.56160 | 0.18367 | 3.14176 | 3.30770 |
| (0.2, 0.2) | 0.36734 | 6.41938 | 6.61520 | −0.04081 | 1.80110 | 2.10766 |
| (0.4, 0.2) | 0.53060 | 8.79085 | 8.86940 | 0.16326 | 2.16219 | 2.25400 |
| (0.3, 0.3) | 0.55101 | 9.85992 | 9.92330 | −0.06122 | 3.08212 | 3.16150 |
| (0.2, 0.4) | 0.57142 | 1.00279 | 1.09769 | −0.28571 | 7.37580 | 8.57700 |
| (0.5, 0.5) | 0.91835 | 1.65391 | 1.65386 | −0.10204 | 5.26189 | 5.26920 |
| Mesh Grid | [16] | [16] | ||||
|---|---|---|---|---|---|---|
| (0.1, 0.1) | 0.17645 | 1.56636 | 1.01945 | −0.11762 | 2.30003 | 3.54833 |
| (0.3, 0.1) | 0.23529 | 4.91795 | 5.58724 | 0.17646 | 1.53797 | 1.01946 |
| (0.2, 0.2) | 0.35291 | 3.32840 | 2.03891 | −0.23524 | 5.73342 | 7.09666 |
| (0.4, 0.2) | 0.41174 | 2.52872 | 6.60670 | 0.05884 | 1.73085 | 4.56779 |
| (0.3, 0.3) | 0.52936 | 5.66418 | 3.05837 | −0.35284 | 1.04665 | 1.06450 |
| (0.2, 0.4) | 0.64701 | 5.11863 | 4.89963 | −0.76460 | 1.07043 | 1.67222 |
| (0.5, 0.5) | 0.88225 | 1.03951 | 5.09728 | −0.58804 | 1.92169 | 1.77417 |
© 2017 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, R.; Zhu, C.; Hou, X.; Yin, L. Quasi-Interpolation Operators for Bivariate Quintic Spline Spaces and Their Applications. Math. Comput. Appl. 2017, 22, 10. https://doi.org/10.3390/mca22010010
Yu R, Zhu C, Hou X, Yin L. Quasi-Interpolation Operators for Bivariate Quintic Spline Spaces and Their Applications. Mathematical and Computational Applications. 2017; 22(1):10. https://doi.org/10.3390/mca22010010
Chicago/Turabian StyleYu, Rengui, Chungang Zhu, Xianmin Hou, and Li Yin. 2017. "Quasi-Interpolation Operators for Bivariate Quintic Spline Spaces and Their Applications" Mathematical and Computational Applications 22, no. 1: 10. https://doi.org/10.3390/mca22010010
APA StyleYu, R., Zhu, C., Hou, X., & Yin, L. (2017). Quasi-Interpolation Operators for Bivariate Quintic Spline Spaces and Their Applications. Mathematical and Computational Applications, 22(1), 10. https://doi.org/10.3390/mca22010010





