Abstract
The effective purification of corrosive gases at the cathode air stream side is essential for proton exchange membrane fuel cells’ performance in real-world applications. Gas molecular diffusion depth along the pore channel is a sufficient parameter that determines the effectiveness of the porous purification media. The collision between gas molecules and pore surfaces is the crucial determinant of the diffusion depth. An analytical model was developed to predict the gas molecular diffusion depth in the pore channels. Two different crystal sizes of UiO-66 were synthesized to validate against the model result and empirically determine the diffusion depths. The parametric effects of the mean free path, molecular kinetic energy, and molecular polarity on molecular diffusivity were assessed. A smaller molecular mean free path and greater molecular kinetic energy were favorable for larger diffusion depth, owing to the fewer collisions and enhanced bounces after collisions. Greater molecular polarity led to shorter diffusion depth due to the enhanced van der Waals force between molecules and pore surfaces.
1. Introduction
Proton exchange membrane fuel cells (PEMFCs) have become an important alternative electricity source for many applications [1]. Electrodes in PEMFCs, especially cathodes, are susceptible to degradation by the gaseous contaminants in the cathode supply air that is directly extracted from the ambient air [2]. More than 250 airborne contaminants that could lead to cathode degradation are listed by the United States Department of Energy [3], although the concentrations of these pollutants in the ambient air are usually low (<200 μg/m3). Among the major gaseous purification techniques, adsorption has been regarded as a promising measure to remove gaseous pollutants at low concentrations. Porous materials, such as aluminosilicate zeolite, molecular sieves, activated carbon, carbon nanotubes, polymeric resin, and metal–organic frameworks, are used as air purification media owing to their large surface area, high porosity, and hierarchical porous structure (micro-, meso-, and macro-pore) [4,5]. The macro-pores, which are exposed directly to the porous media external surface, provide the transport channels for gas molecules diffusing into the micro-pores. On the other hand, the meso- and micro-pores contribute most adsorptive sites and surface area (≥95%). The adsorption capacity is therefore greatly dependent on the gas molecular diffusion dynamics inside the meso- and micro-pores.
Knudsen diffusion, a result of collisions between gas molecules and pore walls, is the predominant transport mechanism inside the meso- and micro-pores. After a number of collisions, the gas molecules stop rebounding and eventually attach to the pore walls. The maximum depth of a gas molecule’s diffusion along the pore channel, which varies with respect to the pore and gas properties, is defined as “diffusion depth” in this study. Tartakovsky and Dentz (2019) provided a systematic overview of molecular diffusion modeling in the presence of the geometric constraints (e.g., Knudsen and Fick–Jacobs diffusion) that are imposed by the solid matrix of a porous medium [6]. For gaseous molecules with “zero” diameter, the diffusion coefficient DKn is expressed in terms of the Knudsen number, Kn = λ/w, where λ is the mean free path of molecules diffusing in the pore with the characteristic length w. In the Knudsen regime (Kn > 1), the Knudsen diffusion coefficient is calculated as DKn = wv/3, where v is the mean molecular velocity [7]. Previously, most studies have focused on the effect of the pores’ structure and geometry on molecular movements inside the pores [8,9]. There have been many attempts to provide a means for predicting pore diffusivity based on the probability density function. Such studies found that the topology of the pore network and the morphology of the pores affected the molecular movements and accessibility inside the pores [8,9,10,11]. Attempted predictions usually relied upon a “tortuosity factor”, which was typically adopted to describe the motion in longer connecting paths within porous solids relative to that in unconstrained free space [12,13].
Compared to the topology of the pore network and the morphology of the pores, the effect of gas characteristics on molecular diffusivity is also of importance but not yet sufficiently studied. The molecular diffusion depth in pore channels is obviously dependent on gas characteristics (molecule size, molecular mass, geometric shape, molecular mean free path, molecular kinetic energy, molecular polarity, etc.) [12,13]. However, few studies have reported the parametric dependence of molecular diffusivity on these gas characteristics. The analytical calculation of Knudsen diffusion depth along the pore channel as a function of these gas characteristics is limited. Methodologies that can experimentally determine the molecular diffusion depth are even fewer.
The objective of this work is to empirically develop a reliable means for predicting molecule diffusion in a confined long, straight pore channel. Rather than attempting to mathematically calculate molecule movements that have been well studied earlier, here, the impacts of various gas characteristics (molecular mean free path, molecular kinetic energy, and molecular polarity) on the diffusivity were investigated and analytically modeled. The air temperature and pressure were the prevailing parameters that determined molecular mean free path and molecular kinetic energy. Zirconium-based MOF UiO-66 with two crystal sizes (150 nm and 6 μm) were synthesized to experimentally determine the molecular diffusion depth along the pore channels, accordingly. The UiO-66 structure, surface chemical status, and pore structures were characterized by X-ray Diffraction (XRD) patterns, Scanning Electron Microscopy (SEM), Fourier Transform Infrared (FT-IR) spectroscopy, and Brunauer–Emmett–Teller (BET), respectively.
2. Model Postulate
In this study, pores are represented as straight, cylindrical channels to simplify the simulation procedures, as similarly reported in previous work [14,15,16]. For a typical pore channel, the cross-sections of the pore channels are shown in Figure 1. The effect of the pore shape on diffusion has been previously studied with more complicated shapes [8].
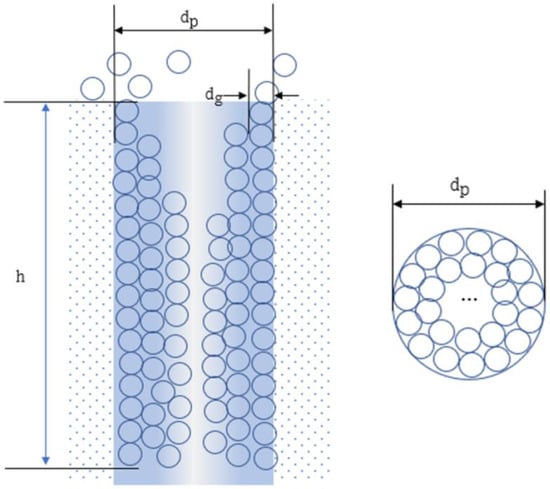
Figure 1.
Geometric diagram of adsorbed gas molecules packing inside a typical straight, cylindrical microchannel. dp is the diameter of the pore, dg is the diameter of the gas molecule, h is the length of the pore channel.
In the Knudsen diffusion regime, a molecule starts from a random position at the entrance of the pore, travels in a straight line until it collides with a pore wall, and changes trajectory in a random way. The time of physical interaction with the surface is neglected compared to the time of the molecule’s flight. Upon collision with the pore channel walls, a molecule is adsorbed for a brief time, loses kinetic energy to some degree, and leaves the surface for the next collision until it is attached to the pore surface when the maximum depth of its diffusion is reached. A longer mean free path and greater molecular kinetic energy lead to more collisions with pore walls and deeper diffusion penetration into pore channels, as shown in Figure S1. As the molecules diffuse and are then saturated in the pores, the number of adsorbed molecules in a single pore channel is calculated by Equation (1):
where Ng is the number of adsorbed molecules, k is a coefficient that represents the void fraction between molecules. When the pore is saturated, k is a constant. h is the saturated diffusion depth, dg is the gas molecule diameter, and dp is the pore diameter.
Then, the mass of adsorbed molecules is calculated by Equation (2):
where M is the molecular weight of the gas and NA is Avogadro’s number.
On the other hand, the diffusion flux is calculated by Knudsen’s equation, as in Equation (3) [17,18]:
where ԑ is the porosity, is the tortuosity factor, , Df is the fractal dimension of the pore wall, is the pore length, R is the universal gas constant, and T is the absolute temperature. The air pressure is calculated as [18]. is Boltzmann constant.
For a specific adsorption tubing, the total mass of adsorbed gas equals the diffusion flux in the pores:
where the adsorption time , is the tubing length, is the tubing diameter, and Q is the gas flow rate.
By substituting Equations (2) and (3) into Equation (4), the saturated diffusion depth can be calculated by Equation (5). The molecular mean free path .
Although it is very difficult to carry out direct measurements of the diffusion depth in confined nano-pores, this modeled diffusion depth was able to be validated with a series of specific adsorption experiments, as described in the next section. The impacts of the molecular mean free path, molecular kinetic energy, and molecular polarity on the diffusivity were also investigated experimentally.
3. Experimental Materials and Methods
In this article, we validated the model results of molecular diffusion depth with the experimental data. Zirconium-based MOF UiO-66 with two crystal sizes (150 nm and 6 μm) were synthesized to experimentally determine the molecular diffusion depth along the pore channels, accordingly. The adsorption experiments for the two sizes of UiO-66 were conducted in the same adsorption tube.
3.1. Material Synthesis
The synthesis of UiO-66 was followed in a previous study [19]. Equimolar amounts of ZrCl4 and H2BDC were dissolved in 50 mL of DMF under ultrasound irradiation. The obtained solution was loaded into a 100 mL Teflon-lined steel autoclave and then placed in a preheated oven at 120 °C for 24 h under static conditions. The produced white powders were collected by centrifugation. The powders were then washed with DMF and methanol several times to remove the extra reactant and dried at 90 °C overnight to remove the solvent. UiO-66 was synthesized with a crystal size of 150 nm. Similar to the above procedure, three equimolar amounts of hydrofluoric acid were added to the solution to repeat the procedure. UiO-66 with a crystal size of 6 μm was then synthesized [20]. The specific amounts of the reactants and hydrofluoric acid modulator in the synthesis are presented in Table 1.

Table 1.
The amounts of reactants and HF modulator in UiO-66 synthesis.
Zirconium tetrachloride (ZrCl4, ≥98%) and terephthalic acid (H2BDC, 98%) were purchased from Aladdin Co., Ltd. (Shanghai, China). N,N-dimethylformamide (DMF), hydrofluoric acid (40%), and all other chemical reagents were purchased from Sinopharm Chemical Reagent Co., Ltd. (Beijing, China). All chemicals were used as received without further purification.
3.2. Characterization
Powder X-ray Diffraction (XRD) patterns were conducted on the X-ray diffractometer (D8 DISCOVER, Bruker AXS, Karlsruhe, Germany) with CuKα X-rays at a scanning rate of 8° min−1 between 5° and 50°. The tube voltage and current were 40 kV and 100 mA, respectively. The crystal size, morphology, and elemental composition of UiO-66 were characterized by field-emission scanning electron microscopy (NOVA Nano SEM 450, FEI Inc., Valley City, ND, USA), and all the samples were coated with chromium prior to measurement. The FT-IR spectra were recorded using a Fourier transform infrared spectrometer (Nicolet 5700, Thermo Electron Scientific Instruments Corp., Waltham, MA, USA) by means of the KBr pellet technique. The BET specific surface area, average pore size, and pore volume of the samples were determined by N2 adsorption/desorption isotherms at 77 K using an automatic surface area and porosity analyzer (Micromeritics ASAP 2020, Micromeritics Instrument Corp., Atlanta, GA, USA). The samples were outgassed overnight at a temperature of 120 °C before the measurement. The surface area was determined through the BET method; the pore volume and pore size were determined through the BJH method.
3.3. Adsorption Experiments
Adsorption experiments on two sizes of UiO-66 were carried out under dry conditions, as schematically presented in Figure 2. In a typical experiment, a 5.0 cm long organic glass column with an inner diameter of 0.5 cm was loaded with 0.2 ± 0.01 g of UiO-66 and placed in a temperature control oven. Prior to the adsorption, N2 (99.99%) flowed into the packed-bed column at a flow rate of 200 mL/min at 80 °C for 2 h to remove any adsorbed compounds. After the purging step, 30 ppm SO2 was introduced into the packed-bed column at a rate of 200 mL/min at 25 °C.
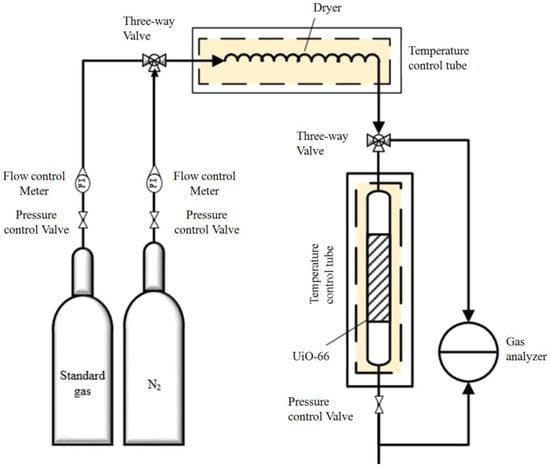
Figure 2.
Apparatus for gas adsorption experiments.
To further investigate the effect of the mean free path on the diffusion depth, the adsorption experiments were conducted at five different air pressures (0.01 MPa, 0.1 MPa, 0.2 MPa, 0.3 MPa, 0.4 MPa). To investigate the effect of molecular kinetic energy on the diffusion depth, the adsorption experiments were conducted at five different temperatures (0 °C, 25 °C, 50 °C, 75 °C, and 100 °C). CO, SO2, and NO2 were used to investigate the effect of molecular polarity on the diffusion depth. The column effluent stream was continuously monitored by a gas analyzer (Ventis MX4, Industrial Scientific Corporation, Pittsburgh, PA, USA). The adsorption bed was considered to be breakthrough and saturated when the effluent concentration reached 5% and 95% of the feed stream concentration, respectively.
4. Results and Discussions
4.1. Characterization
150 nm and 6 μm UiO-66 samples were characterized by XRD, SEM, and a porosity analyzer. Figure 3 shows the two sizes of UiO-66 XRD patterns that corresponded to the typical UiO-66 structure [21], which indicates that the introduction of fluorine did not lead to any destruction or disorder. Furthermore, the 6 μm UiO-66 from fluorine-involved synthesis presented sharper and narrower diffraction peaks than the fluorine-free UiO-66, which illustrates high crystallinity with the formation of larger crystals.
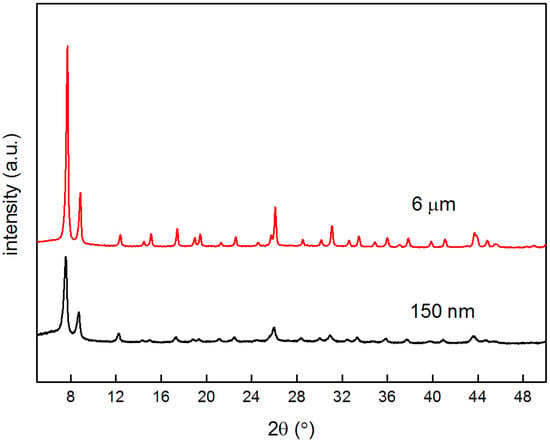
Figure 3.
XRD patterns of UiO-66 with two crystal sizes.
The SEM images of 150 nm and 6 μm UiO-66 samples are shown in Figure 4. As illustrated in Figure 4, the two micron-sized UiO-66 crystals were successfully synthesized in cube-like shapes. The 150 nm crystalline size was synthesized without the addition of hydrofluoric acid and the 6 μm crystalline size with the addition of hydrofluoric acid, respectively.

Figure 4.
SEM images of UiO-66 with two crystal sizes ((a) 150 nm, (b) 6 μm).
The FT-IR spectra of these two sizes of UiO-66 samples exhibited similar characteristic peaks, as shown in Figure S2. At higher frequencies, two intense bands around 1590 and 1395 cm−1 associated with the OCO asymmetric and symmetric stretch vibrations in the carboxylate group in H2BDC are clearly shown for the two sizes of UiO-66 samples. At lower frequencies, the bands around 810 and 710 cm−1 are mixed with the C–H vibration, OH bend, and OCO bend in H2BDC. The band around 556 cm−1 belongs to the Zr–(OC) asymmetric stretch [22]. Thus, the structures of two sizes of UiO-66 were similar and retained in accordance with the XRD analysis.
N2 sorption measurements were conducted to evaluate the porosity of the UiO-66 samples with different crystal sizes. The N2 sorption isotherms and pore size distributions are shown in Figure S3. Both of the samples show a typical Type I sorption isotherm, indicating that they are typical micro-porous materials. Table 2 summarizes the pore characteristics of the two sizes of UiO-66 samples. UiO-66 with a larger crystal size exhibits more N2 adsorption values than the smaller size sample. The pore size distribution shows the existence of micro-pores between 6 and 10 Å. Moreover, the total amounts of micro-pores and the BET surface areas also increase in accordance with the crystal size increase. These porosity enhancement tendencies, owing to the formation of defects by using fluorine as the modulator, are similar to the previous reports [20,23,24].

Table 2.
Pore characteristics of the two sizes of UiO-66 samples.
4.2. Diffusion Depth Validation with Adsorption Experiment
To validate the analytical results from Equation (5), the diffusion depth was empirically determined from the adsorption measurements with two crystal sizes of MOFs. For the same adsorption tube, the cross-sections of the two crystal sizes of the UiO-66 packing schematic diagram are respectively shown in Figure 5. Since the pore sizes of the two UiO-66 crystals were identical, the cubic root of adsorption capacity per pore volume was proportionally related to the molecular diffusion depth inside the pores. Assuming the pores were straight cylinders, the diffusion depth can be calculated by Equation (6):
where r2 = 3000 nm is the radii of the 6 μm UiO-66, Q1 is the adsorption capacity per pore volume of the 150 nm UiO-66, and Q2 is the adsorption capacity per pore volume of 6 μm UiO-66.
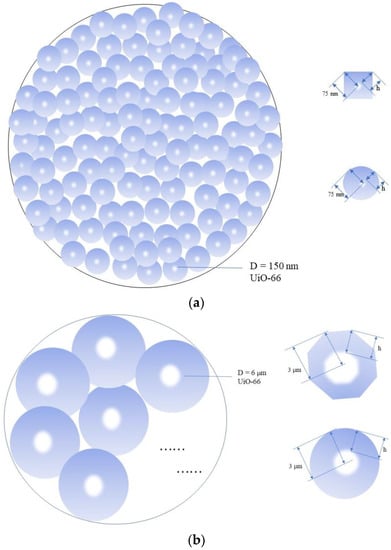
Figure 5.
Cross-sectional view of the two crystal sizes of UiO-66 packing in the adsorption tubes ((a) 6 μm, (b) 150 nm).
It should be noted that Equation (6) is only valid when Q1 < Q2, when the pore volume of 6 μm UiO-66 is not fully filled. In this study, the measured Q1 is always observed to be less than Q2.
Figure 6 shows the diffusion depths calculated from Equation (6) under different air pressures and air temperatures. From Equation (6), it can be seen that the decrease or increase in diffusion depth as a function of air pressure or temperature is the cube root of the quotient of the 6 μm UiO-66 and the 150 nm adsorption capacities. The diffusion depth increase leads to a significant adsorption capacity increase in general. By differentiating Equation (5) with respect to P or T, it was found that the diffusion depth was inversely proportional to the air pressure but proportional to the air temperature. It can be found that the effect of temperature increase (100 K) on the diffusion depth was much greater than the effect of air pressure increase (400 kPa). The empirically measured data agree with the analytical calculation in the same trend.
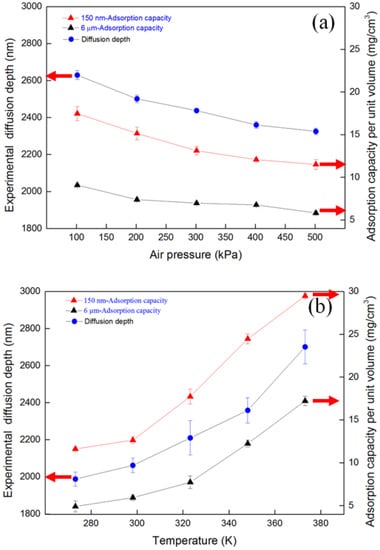
Figure 6.
Calculated diffusion depths from measured data under different (a) air pressures and (b) air temperatures.
Figure 7 compares analytically calculated diffusion depths with empirically measured data under different air pressures and air temperatures. As shown in Figure 7, the trends from the analytical results and empirical data matched very well. It should be noted from Figure 7 that the values from the analytical calculation did not match the empirical data exactly. The empirical diffusion depths were greater and more steady than the analytical calculation across all the air pressures and temperatures. This was likely due to the fact that diffusing molecules in the experiments were not packed homogeneously and strictly in the pores, as shown in the analytical description (Figure 1). For example, after first-layer gas molecule adsorption, more gas molecules may penetrate and diffuse in deep pores because the adsorbed molecules on the pore surfaces are more rigid than the pore surfaces, to some degree. Molecular surface diffusion may also lead to diffusion depth discrepancies between analytical calculations and empirical data. Molecular surface diffusion led to a greater diffusion depth that was not considered in this study and needed further investigation.
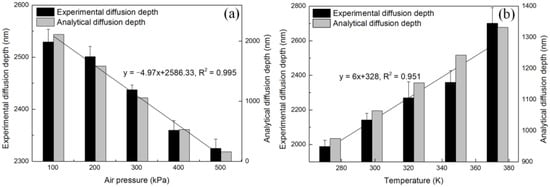
Figure 7.
Experimental and analytical diffusion depths under different (a) air pressures and (b) air temperatures.
4.3. Effect of Mean Free Path, Molecular Kinetic Energy, and Molecular Polarity
Binary or multi-component gases with different above-mentioned characteristics must exhibit different diffusivities during separation or purification. The parametric impacts of these gas characteristics on diffusion depth are empirically measured and discussed in this section.
From Equation (5), it can be seen that diffusion depth is directly determined by the molecular mean free path and molecular kinetic energy. The mean free path was air pressure- and temperature-dependent (). The diffusion depths were calculated as a function of the mean free path by adopting different air pressures and temperatures into the relevant governing equations, as shown in Figure 8a. A larger mean free path led to a greater probability of collisions between molecules and pore surfaces. For the same gas molecule, collisions on the pore surface led to molecular kinetic energy loss to some degree and shorter diffusion depth in the pore.
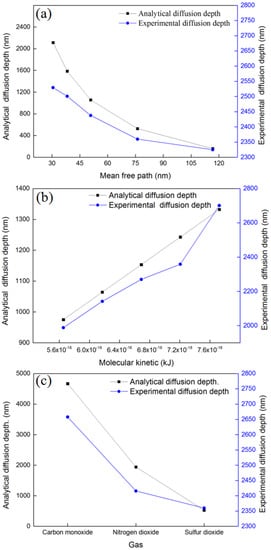
Figure 8.
A comparison of diffusion depths between analytical and empirical data with different (a) mean free paths; (b) molecular kinetic energy; (c) molecular polarities.
Molecular kinetic energy can be calculated by K = 3kBT/2. The diffusion depths were calculated as a function of molecular kinetic energy, as shown in Figure 8b. It can be seen that the diffusion depth is proportional to the molecular kinetic energy. As the molecular kinetic energy increases by 50%, the diffusion depth increases by ~30%. A molecule collides on the pore surface, loses kinetic energy to some degree, and leaves the surface for the next collision until the kinetic energy is not enough. The gas molecules are then captured or absorbed on the pore surface. Larger molecular kinetic energy leads to more collisions and deeper diffusion depth in the pore.
Besides the mean free path and molecular kinetic energy, larger polarization, molecular dipole, and molecular polarity lead to greater electrostatic interaction or van der Waals force between the gas molecule and the pore surface, which results in a shorter diffusion depth [18,19,20]. Adsorption experiments using three gases (CO, NO2, SO2) with different molecular polarities (19.5 × 1025 cm3, 30.2 × 1025 cm3, 40.31 × 1025 cm3) were conducted to determine the effect of molecular polarity on the diffusion depth. It can be seen that CO molecules diffused much deeper than the other two gases because smaller polarity caused less kinetic energy loss during collisions. CO has a linear shape, smaller size and mass, and also a lower polarity than NO2 and SO2, which led to greater diffusivity and diffusion depth.
It should be noted that the analytical results from the theoretical calculation cannot agree with the experimental data precisely due to the different characteristics between modeled and practical pores. The modeled diffusion depth along the ideal straight, cylindrical pores varied more significantly in response to all the studied parameters (molecular mean free path, molecular kinetic energy, and molecular polarity). This was the limitation of this study. Nevertheless, the trends of the diffusion depth as a function of these parameters could be compared and found to be in reasonable agreement. The effects of the molecular mean free path, molecular kinetic energy, and molecular polarity on the gas diffusion depth could be used as a scientific reference to estimate the diffusion depths among multiple mixture gases.
5. Conclusions
In this study, an analytical model was developed to predict the gas molecular diffusion depth in the pore channels. Different crystal sizes of UiO-66 were synthesized to empirically determine the diffusion depths and compare them with modeled results.
The effects of various gas characteristics (molecular mean free path, molecular kinetic energy, and molecular polarity) on the diffusivity were investigated. Significant differences in diffusion depths were found among different gas characteristics. Greater diffusion depth was observed for a smaller mean free path due to fewer collisions between gas molecules and pore surfaces. On the other hand, greater diffusion depth in response to greater molecular kinetic energy with more collisions was observed. Besides the mean free path and molecular kinetic energy, it was found that a larger molecular polarity led to shorter diffusion depth owing to greater van der Waals force between the gas molecule and the pore surface.
The analytical model is able to estimate the purification efficiency and adsorption capacity of porous adsorbents for gaseous contaminants in the cathode supply air that was directly extracted from the ambient air. For a given target adsorbate, the optimal pore structure of porous adsorbent and adsorption conditions could be analytically screened and determined. Although this model cannot precisely calculate the gas molecules’ diffusion in complicated-shaped pores, the results presented in this study provided useful information to facilitate more efficient operation scenarios in major porous diffusion applications such as catalysis, electrochemistry, and separations.
Supplementary Materials
The following supporting information can be found in https://www.mdpi.com/article/10.3390/separations9050130/s1, Figure S1: Schematic diagram of gas molecular diffusion inside pore channels; Figure S2: FT-IR spectra of UiO-66 at two crystal sizes; Figure S3: N2 sorption isotherms of UiO-66 with two crystal sizes.
Author Contributions
Conceptualization, B.X.; methodology, B.X.; validation, H.Q. and B.X.; formal analysis, L.C.; writing—original draft preparation, L.C.; writing—review and editing, H.Q.; visualization, H.Q.; supervision, B.X.; project administration, B.X.; funding acquisition, B.X. All authors have read and agreed to the published version of the manuscript.
Funding
This study was partially sponsored by the National Key R&D Program of China (No. 2019YFC1904001) and the Natural Science Foundation of Shanghai (21ZR1468000).
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
This study was partially sponsored by the National Key R&D Program of China (No. 2019YFC1904001), the Natural Science Foundation of Shanghai (21ZR1468000), the Foundation of State Key Laboratory of Pollution Control and Resource Reuse (Tongji University), China, (No. PCRRE), and the Shanghai Institute of Pollution Control and Ecological Security.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wang, Y.; Diaz, D.F.R.; Chen, K.S.; Wang, Z.; Adroher, X.C. Materials, technological status, and fundamentals of PEM fuel cells—A review. Mater. Today 2020, 32, 178–203. [Google Scholar] [CrossRef]
- Wang, X.X.; Swihart, M.T.; Wu, G. Achievements, challenges and perspectives on cathode catalysts in proton exchange membrane fuel cells for transportation. Nat. Catal. 2019, 2, 578–589. [Google Scholar] [CrossRef]
- St-Pierre, J.; Zhai, Y.; Angelo, M. Quantitative ranking criteria for PEMFC contaminants. Int. J. Hydrog. Energy 2012, 37, 6784–6789. [Google Scholar] [CrossRef]
- Cui, X.; Chen, K.; Xing, H.; Yang, Q.; Krishna, R.; Bao, Z.; Wu, H.; Zhou, W.; Dong, X.; Han, Y.; et al. Pore chemistry and size control in hybrid porous materials for acetylene capture from ethylene. Science 2016, 353, 141–144. [Google Scholar] [CrossRef] [PubMed]
- Cui, X.; Yang, Q.; Yang, L.; Krishna, R.; Zhang, Z.; Bao, Z.; Wu, H.; Ren, Q.; Zhou, W.; Chen, B.; et al. Ultrahigh and Selective SO2 Uptake in Inorganic Anion-Pillared Hybrid Porous Materials. Adv. Mater. 2017, 29, 1606929. [Google Scholar] [CrossRef] [PubMed]
- Tartakovsky, D.M.; Dentz, M. Diffusion in Porous Media: Phenomena and Mechanisms. Transp. Porous Media 2019, 130, 105–127. [Google Scholar] [CrossRef]
- Jacobs, M.H. Diffusion processes. In Ergebnisse der Biologie; Frisch, V.K., Goldschmidt, R., Ruhland, W., Winterstein, H., Eds.; Springer: New York, NY, USA, 1967. [Google Scholar]
- Nakano, Y.; Iwamoto, S.; Yoshinaga, I.; Evans, J.W. The effect of pore necking on Knudsen diffusivity and collision frequency of gas molecules with pore walls. Chem. Eng. Sci. 1987, 42, 1577–1583. [Google Scholar] [CrossRef]
- Burganos, V.N.; Sotirchos, S.V. Knudsen Diffusion in parallel, multidimensional or randomly oriented capillary structures. Chem. Eng. Sci. 1989, 44, 2451–2462. [Google Scholar] [CrossRef]
- Sahimi, M.; Gavalas, G.R.; Tsotsis, T.T. Statistical and continuum models of fluid-solid reactions in porous media. Chem. Eng. Sci. 1990, 45, 1443–1502. [Google Scholar] [CrossRef]
- Keil, F.J. Diffusion and reaction in porous networks. Catal. Today 1999, 53, 245–258. [Google Scholar] [CrossRef]
- Satterfield, C.N. Mass Transfer in Heterogeneous Catalysis; MIT Press: Cambridge, MA, USA, 1970. [Google Scholar]
- Wakao, N.; Smith, J.M. Diffusion in catalyst pellets. Chem. Eng. Sci. 1962, 17, 825–834. [Google Scholar] [CrossRef]
- Froment, G.F.; Bischoff, K.B. Chemical Reactor Analysis and Design, 3rd ed.; Wiley: New York, NY, USA, 1990. [Google Scholar]
- Arbabi, S.; Sahimi, M. Computer simulations of catalyst deactivation—II. The effect of morphological, transport and kinetic parameters on the performance of the catalyst. Chem. Eng. Sci. 1991, 46, 1749–1755. [Google Scholar] [CrossRef]
- Zhang, L.; Seaton, N.A. The application of continuum equations to diffusion and reaction in pore networks. Chem. Eng. Sci. 1994, 49, 41–50. [Google Scholar] [CrossRef]
- Wua, K.; Li, X.; Guo, C.; Chen, Z. Adsorbed Gas Surface Diffusion and Bulk Gas Transport in Nanopores of Shale Reservoirs with Real Gas Effect-Adsorption-Mechanical Coupling. In Proceedings of the Spe Reservoir Simulation Symposium, Houston, TX, USA, 23–25 February 2015. [Google Scholar]
- Evans, J.W.; Abbasi, M.H.; Sarin, A. A Monte Carlo simulation of the diffusion of gases in porous solids. J. Chem. Phys. 1980, 72, 2967–2973. [Google Scholar] [CrossRef]
- Cavka, J.H.; Jakobsen, S.; Olsbye, U.; Guillou, N.; Lamberti, C.; Bordiga, S.; Lillerud, K.P. A new zirconium inorganic building brick forming metal organic frameworks with exceptional stability. J. Am. Chem. Soc. 2008, 130, 13850–13851. [Google Scholar] [CrossRef] [PubMed]
- Han, Y.; Liu, M.; Li, K.; Zuo, Y.; Wei, Y.; Xu, S.; Zhang, G.; Song, C.; Zhang, Z.; Guo, X. Facile synthesis of morphology and size-controlled zirconium metal-organic framework UiO-66: The role of hydrofluoric acid in crystallization. Crystengcomm 2015, 17, 6434–6440. [Google Scholar] [CrossRef]
- Schaate, A.; Roy, P.; Godt, A.; Lippke, J.; Waltz, F.; Wiebcke, M.; Behrens, P. Modulated Synthesis of Zr-Based Metal-Organic Frameworks: From Nano to Single Crystals. Chem. A Eur. J. 2011, 17, 6643–6651. [Google Scholar] [CrossRef] [PubMed]
- Valenzano, L.; Civalleri, B.; Chavan, S.; Bordiga, S.; Nilsen, M.H.; Jakobsen, S.; Lillerud, K.P.; Lamberti, C. Disclosing the Complex Structure of UiO-66 Metal Organic Framework: A Synergic Combination of Experiment and Theory. Chem. Mater. 2011, 23, 1700–1718. [Google Scholar] [CrossRef]
- Wu, H.; Chua, Y.S.; Krungleviciute, V.; Tyagi, M.; Chen, P.; Yildirim, T.; Zhou, W. Unusual and Highly Tunable Missing-Linker Defects in Zirconium Metal-Organic Framework UiO-66 and Their Important Effects on Gas Adsorption. J. Am. Chem. Soc. 2013, 135, 10525–10532. [Google Scholar] [CrossRef] [PubMed]
- Vermoortele, F.; Bueken, B.; Le Bars, G.; Van de Voorde, B.; Vandichel, M.; Houthoofd, K.; Vimont, A.; Daturi, M.; Waroquier, M.; Van Speybroeck, V.; et al. Synthesis Modulation as a Tool To Increase the Catalytic Activity of Metal-Organic Frameworks: The Unique Case of UiO-66(Zr). J. Am. Chem. Soc. 2013, 135, 11465–11468. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).