Optimization of Lactoperoxidase and Lactoferrin Separation on an Ion-Exchange Chromatography Step
Abstract
:1. Introduction
2. Theory
2.1. Response Surface Modeling and Design of Experiments
2.2. Mechanistic Modeling of Chromatography
2.3. Optimization for the ICE Separation of LP and LF
3. Materials and Methods
3.1. Materials, Column and Software
3.2. Experimental Methods
- Final concentration of salt in elution step (M)
- Length of linear elution gradient (CV)
- Superficial velocity (cm/min)
Protein Quantification
3.3. Mathematical Method
3.3.1. Screening Experiments to Determine Importance of Design Factors
3.3.2. SMA Model Calibration and Validation
3.3.3. Optimization Method
4. Results and Discussion
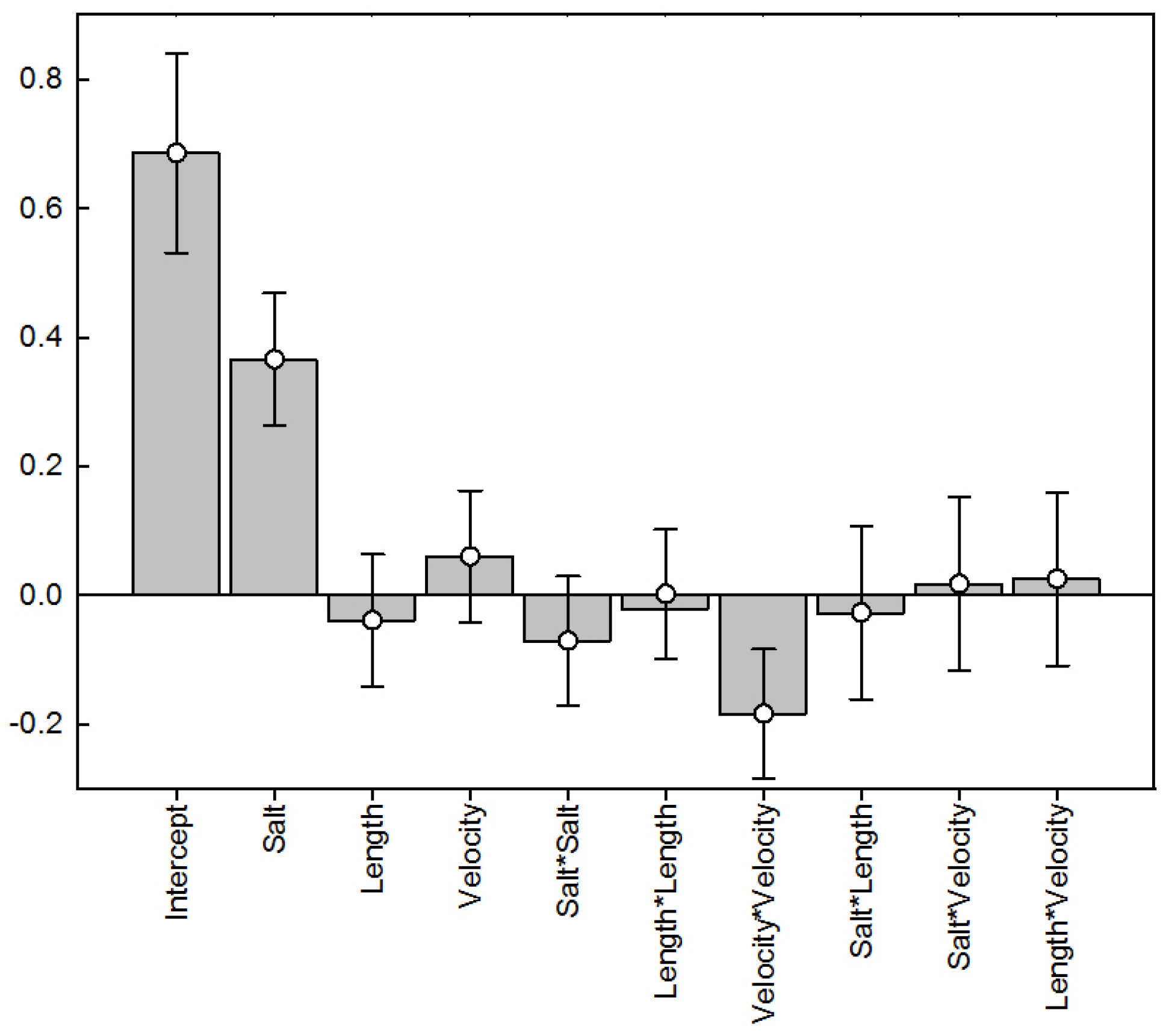
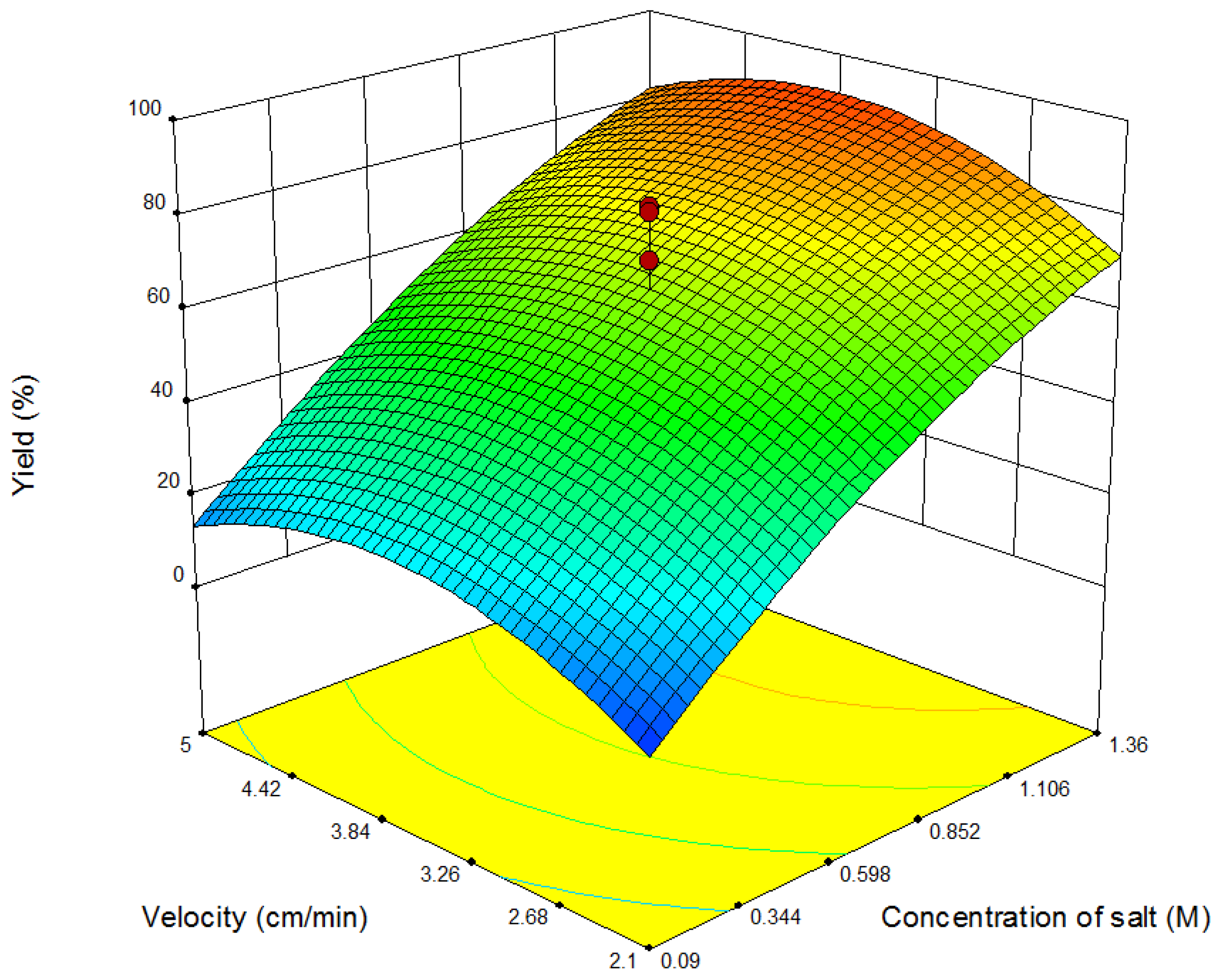
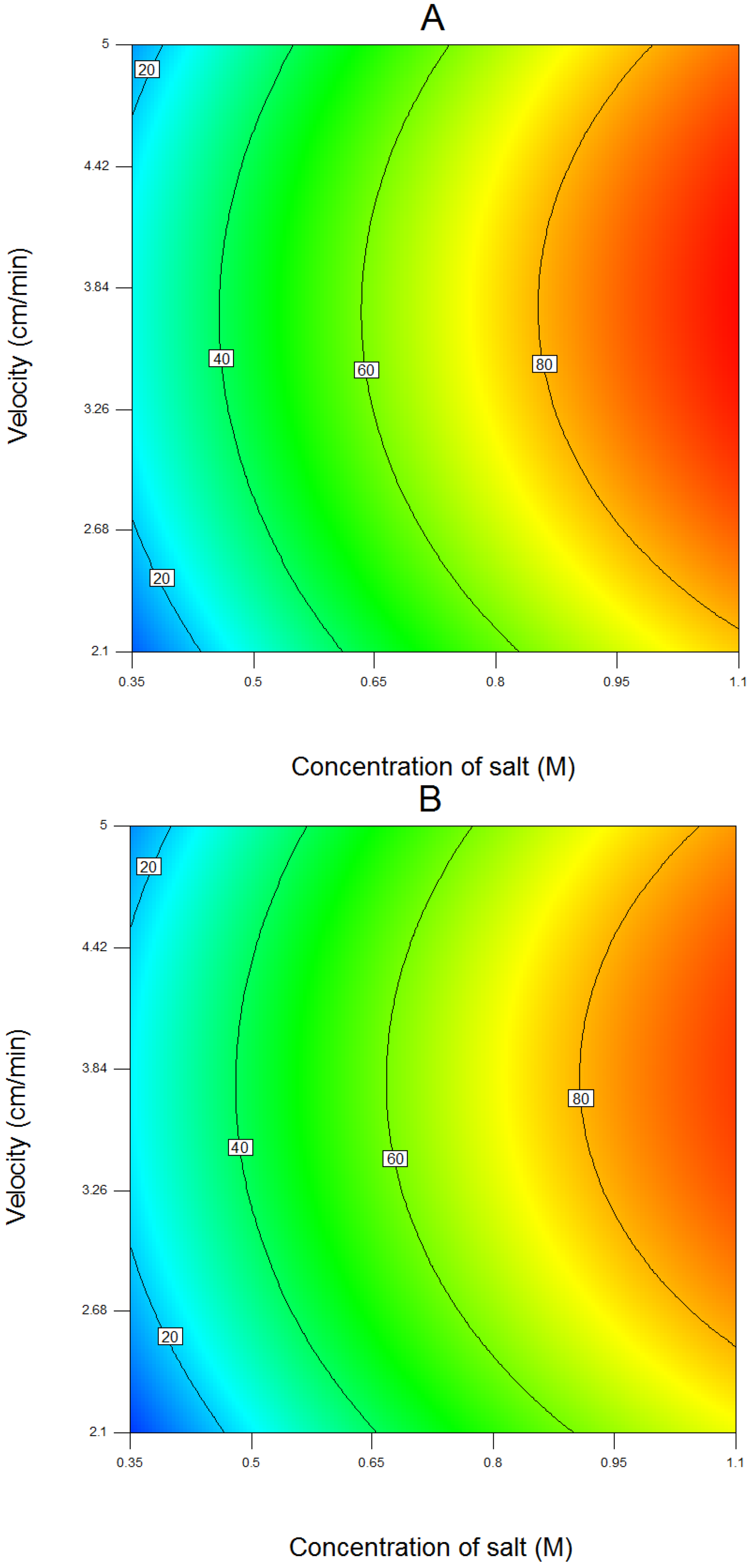
4.1. Results of Response Surface Modeling
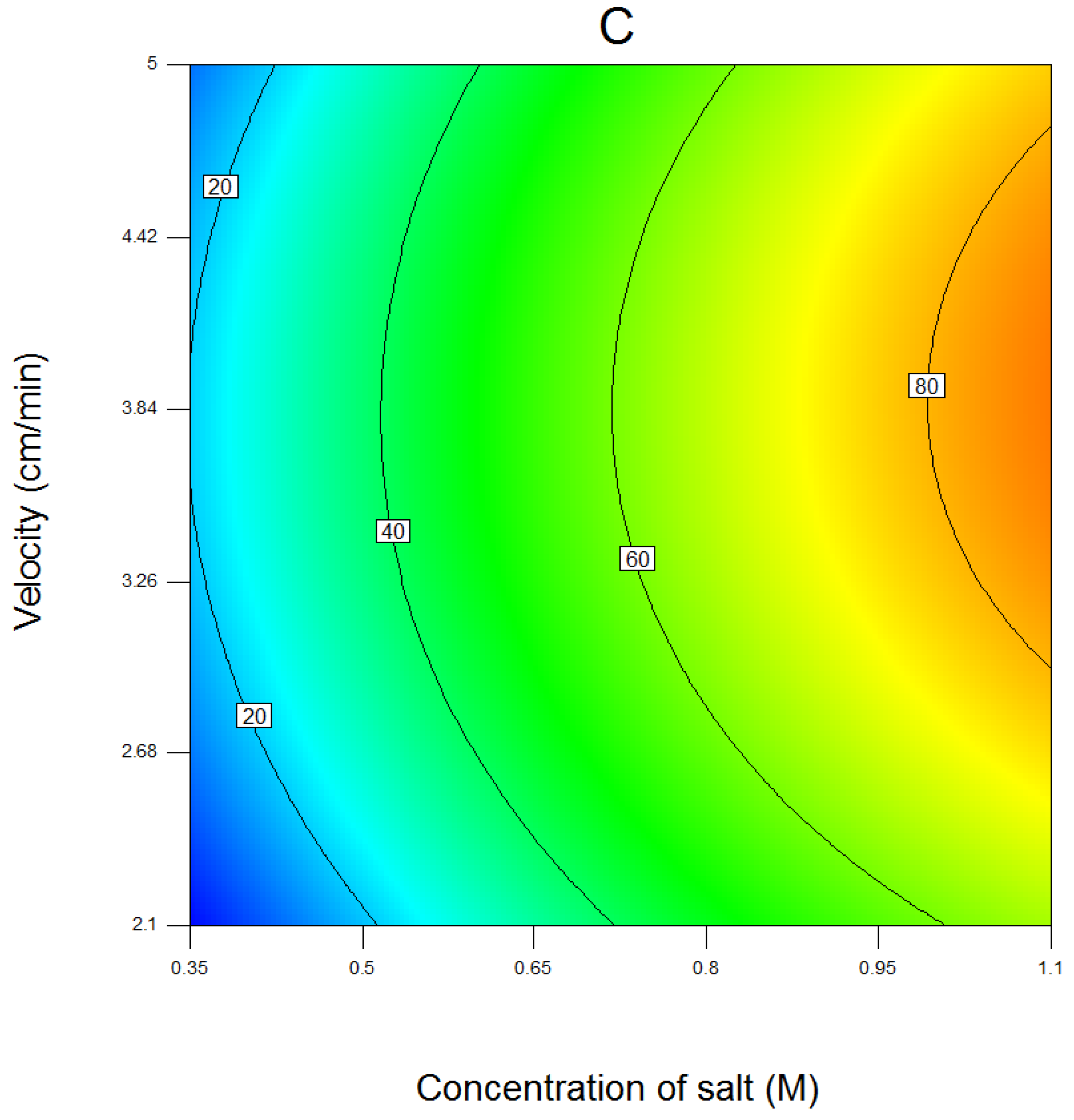
4.2. Results of the Mechanistic Model
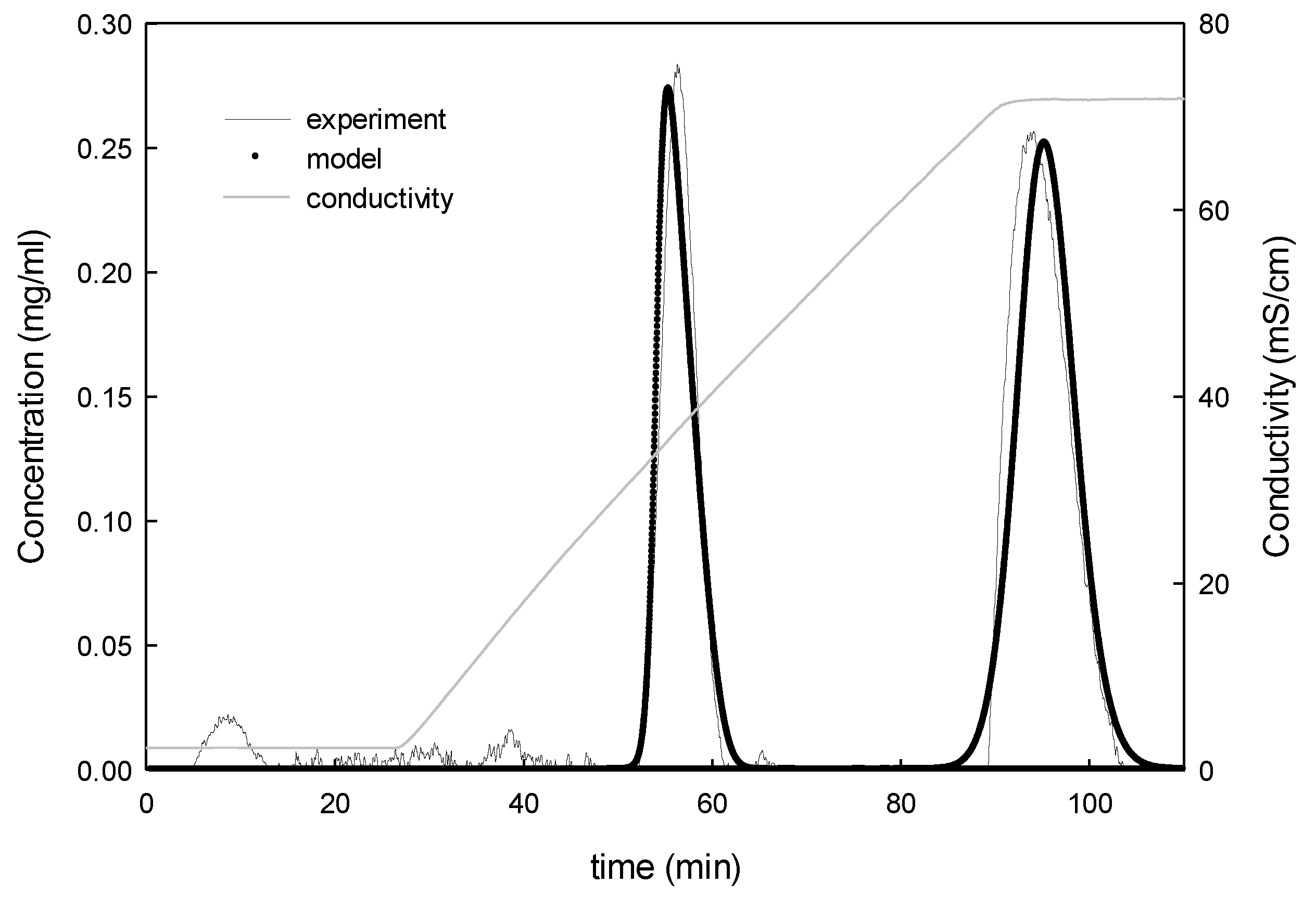
4.2.1. Model Calibration and Validation
4.2.2. Optimization Predictions Based on the Mechanistic Model
5. Conclusions
Author Contributions
Conflicts of Interest
Abbreviation
| cp,i | concentration of protein i in the pores of the adsorbent (M) |
| csalt | salt concentration in the pores of the adsorbent (M) |
| ci | protein concentration i in the mobile phase (M) |
| Dax | axial dispersion coefficient (mm2/s) |
| Dm | molecular diffusivity in mobile phase (mm2/s) |
| keff,i | effective mass transfer coefficient of protein i (mm/s) |
| kads,i | adsorption coefficient of protein i in the SMA isotherm |
| kdes,i | desorption coefficient of protein i in the SMA isotherm |
| keq,i | equilibrium coefficient of protein i |
| L | length of the column (mm) |
| qi | protein concentration i on the adsorbent phase (M) |
| rp | particle radius (mm) |
| uint | interstitial velocity of the fluid (mm/s) |
| Y | recovery yield |
| εc | column voidage |
| εp | particle voidage |
| εt | total voidage |
| 1−εt/εt | phase ratio |
| Λ | total ionic capacity (M) |
| νi | characteristic charge of protein i in SMA isotherm |
| η | mobile phase viscosity (Pa.s) |
| σi | steric factor of protein i in the SMA isotherm |
References
- Ekstrand, B. Antimicrobial factors in milk—A review. Food Biotechnol. 1989, 3, 105–126. [Google Scholar] [CrossRef]
- Dairy Processing Handbook. Available online: http://www.dairyprocessinghandbook.com/chapter/whey-processing (accessed on 10 January 2017).
- Barth, C.A.; Schlimme, E. Milk Proteins: Nutritional, Clinical, Functional and Technological Aspects; Springer International: Darmstadt, Germany, 1988. [Google Scholar]
- Pedersen, L.; Mollerup, J.; Hansen, E.; Jungbauer, A. Whey proteins as a model system for chromatographic separation of proteins. J. Chromatogr. B 2003, 790, 161–173. [Google Scholar] [CrossRef]
- Gerberding, S.; Byers, C. Preparative ion-exchange chromatography of proteins from dairy whey. J. Chromatogr. A 1998, 808, 141–151. [Google Scholar] [CrossRef]
- Hahn, R.; Schulz, P.; Schaupp, C.; Jungbauer, A. Bovine whey fractionation based on cation-exchange chromatography. J. Chromatogr. A 1998, 795, 277–287. [Google Scholar] [CrossRef]
- El-Sayed, M.M.H.; Chase, H.A. Purification of the two major proteins from whey concentrate using a cation-exchange selective adsorption process. Biotechnol. Prog. 2009, 192–199. [Google Scholar] [CrossRef] [PubMed]
- Fee, C.J.; Chand, A. Capture of lactoferrin and lactoperoxidase from raw whole milk by cation exchange chromatography. Sep. Purif. Technol. 2006, 48, 143–149. [Google Scholar] [CrossRef]
- Strohmaier, W. Chromatographic fractionation of whey proteins. IDF Bull. 2004, 389, 29–35. [Google Scholar]
- Tolkach, A.; Kulozik, U. Fractionation of whey proteins and peptides by means of membrane techniques in connection with chemical and physical pretreatments. IDF Bull. 2004, 389, 20–23. [Google Scholar]
- Rombauts, W.A.; Schroeder, W.A.; Morrison, M. Bovine lactoperoxidase. partial characterization of the further purified protein. Biochemistry 1967, 6, 2965–2977. [Google Scholar] [CrossRef] [PubMed]
- Flemmig, J.; Gau, J.; Schlorke, D.; Arnhold, J. Lactoperoxidase as a potential drud tarket. Expert Opin. Ther. Targets 2016, 20, 447–461. [Google Scholar] [CrossRef] [PubMed]
- Yao, X.; Bunt, C.; Cornish, J.; Quek, S.-Y.; Wen, J. Oral delivery of lactoferrin: A review. Int. J. Pept. Res. Ther. 2013, 19, 125–134. [Google Scholar] [CrossRef]
- Noppe, W.; Pliva, F.M.; Galaev, I.Y.; Vanhoorelbeka, K.; Mattiasson, B.; Deckmyn, H. Immobilised peptide displaying phages as affinity ligands purification of lactoferrin from defatted milk. J. Chromatogr. A 2006, 1101, 79–85. [Google Scholar] [CrossRef] [PubMed]
- Andersson, J.; Mattiasson, B. Simulated moving bed technology with a simplified approach for protein purification Separation of lactoperoxidase and lactoferrin from whey protein concentrate. J. Chromatogr. A 2006, 1107, 88–95. [Google Scholar] [CrossRef] [PubMed]
- Korhonen, H.; Pihlanto, A. Technological options for the production of health-promoting proteins and peptides derived from milk and colostrum. Curr. Pharm. Des. 2007, 13, 829–843. [Google Scholar] [CrossRef] [PubMed]
- Fweja, L.W.T.; Lewis, M.J.; Grandison, A.S. Isolation of lactoperoxidase using different cation exchange resins by batch and column prodecures. J. Dairy Res. 2010, 77, 357–367. [Google Scholar] [CrossRef] [PubMed]
- Ahamed, T.; Nfor, B.K.; Verheart, P.D.E.M.; van Dedem, G.W.K.; van der Wielen, L.A.M.; Eppink, M.H.M.; van der Sandt, E.J.A.X.; Ottens, M. pH-gradient ion-exchange chromatography: An analytical tool for design and optimization of protein separations. J. Chromatogr. A 2007, 1164, 181–188. [Google Scholar] [CrossRef] [PubMed]
- Mandenius, C.-F.; Brundin, A. Bioprocess optimization using design-of-experiments methodology. Biotechnol. Prog. 2008, 24, 1191–1203. [Google Scholar] [CrossRef] [PubMed]
- Bezerra, M.A.; Santelli, R.E.; Oliveira, E.P.; Villar, L.S.; Escaleira, L.A. Response surface methodology (RSM) as a tool for optimization in analytical chemistry. Talanta 2008, 76, 965–977. [Google Scholar] [CrossRef] [PubMed]
- Iyer, H.; Tapper, S.; Lester, P.; Wolk, B.; van Reis, R. Use of the steric mass action model in ion-exchange chromatographic process development. J. Chromatogr. A 1999, 832, 1–9. [Google Scholar] [CrossRef]
- Shukla, A.A.; Bae, S.S.; Moore, J.A.; Barnthouse, K.A.; Cramer, S.M. Synthesis and Characterization of High-Affinity, Low Molecular Weight Displacers for Cation-Exchange Chromatography. Ind. Eng. Chem. Res. 1998, 37, 4090–4098. [Google Scholar] [CrossRef]
- Brooks, C.A.; Cramer, S.M. Steric mass-action ion exchange: Displacement profiles and induced salt gradients. AIChE J. 1992, 38, 1969–1978. [Google Scholar] [CrossRef]
- Carlström, A. The heterogeneity of lactoperoxidase. Acta Chem. Scand. 1965, 19, 2387–2394. [Google Scholar] [CrossRef] [PubMed]
- Bardsley, W.G. Steady-state kinetics of lactoperoxidase-catalyzed reactions. Immunol. Ser. 1985, 27, 55–87. [Google Scholar]
- Guiochon, G.; Felinger, A.; Shirazi, D.G.; Katti, A.M. Fundamentals of Preparative and Nonlinear Chromatography; Academic Press: San Diego, CA, USA, 2006. [Google Scholar]
- Davis, M.E. Numerical Methods and Modeling for Chemical Engineers; John Wiley & Sons: New York, NY, USA, 1984. [Google Scholar]
- Danckwerts, P.V. Continuous flow systems. Chem. Eng. Sci. 1953, 2, 1–13. [Google Scholar] [CrossRef]
- Shampine, L.F.; Reichelt, M.W. The MATLAB ODE Suite. SIAM J. Sci. Comput. 1997, 18, 1–22. [Google Scholar] [CrossRef]
- Sherwood, T.K.; Pigford, R.L.; Wilke, C.R. Mass Transfer; McGraw-Hill: New York, NY, USA, 1975. [Google Scholar]
- Gunn, D.J. Axial and radial dispersion in fixed beds. Chem. Eng. Sci. 1987, 42, 363–373. [Google Scholar] [CrossRef]
- Faraji, N.; Zhang, Y.; Ray, A.K. Determination of adsorption isotherm parameters for minor whey proteins by gradient elution preparative liquid chromatography. J. Chromatogr. A 2015, 1412, 67–74. [Google Scholar] [CrossRef] [PubMed]


| Run | Salt | Coded Length of Gradient | Flow Velocity | Salt (M) | Un-Coded Length of Gradient (CV) | Flow Velocity (cm/min) |
|---|---|---|---|---|---|---|
| 1 | −1 | −1 | −1 | 0.35 | 15 | 2.1 |
| 2 | 1 | −1 | −1 | 1.1 | 15 | 2.1 |
| 3 | −1 | 1 | −1 | 0.35 | 30 | 2.1 |
| 4 | 1 | 1 | −1 | 1.1 | 30 | 2.1 |
| 5 | −1 | −1 | 1 | 0.35 | 15 | 4.998 |
| 6 | 1 | −1 | 1 | 1.1 | 15 | 4.998 |
| 7 | −1 | 1 | 1 | 0.35 | 30 | 4.998 |
| 8 | 1 | 1 | 1 | 1.1 | 30 | 4.998 |
| 9 | −1.681 | 0 | 0 | 0.094 | 22.5 | 3.549 |
| 10 | 1.681 | 0 | 0 | 1.355 | 22.5 | 3.549 |
| 11 | 0 | −1.681 | 0 | 0.725 | 9.88 | 3.549 |
| 12 | 0 | 1.681 | 0 | 0.725 | 35.1 | 3.549 |
| 13 | 0 | 0 | −1.681 | 0.725 | 22.5 | 1.112 |
| 14 | 0 | 0 | 1.681 | 0.725 | 22.5 | 5.985 |
| 15 | 0 | 0 | 0 | 0.725 | 22.5 | 3.549 |
| 16 | 0 | 0 | 0 | 0.725 | 22.5 | 3.549 |
| 17 | 0 | 0 | 0 | 0.725 | 22.5 | 3.549 |
| 18 | 0 | 0 | 0 | 0.725 | 22.5 | 3.549 |
| 19 | 0 | 0 | 0 | 0.725 | 22.5 | 3.549 |
| 20 | 0 | 0 | 0 | 0.725 | 22.5 | 3.549 |
| Concentration of Salt (M) | 1.10 |
| Flow velocity (cm/min) | 3.77 |
| Gradient length (CV) | 15 |
| Predicted yield (%) | 96.41 |
| Experimental yield (%) | 78.04 |
| Protein | σ | |||
|---|---|---|---|---|
| lactoperoxidase | 0.22 ± 0.005 | 3.07 ± 0.014 | 19.89 ± 0.071 | 1283 |
| lactoferrin | 11.65 ± 0.003 | 2.73 ± 0.006 | 0.98 ± 0.22 | 0.98 |
| Concentration of Salt (M) | 0.82 |
| Flow velocity (cm/min) | 4.32 |
| Gradient length (CV) | 16.28 |
| Predicted yield (%) | 89.92 |
| Experimental yield (%) | 86.73 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Faraji, N.; Zhang, Y.; Ray, A.K. Optimization of Lactoperoxidase and Lactoferrin Separation on an Ion-Exchange Chromatography Step. Separations 2017, 4, 10. https://doi.org/10.3390/separations4020010
Faraji N, Zhang Y, Ray AK. Optimization of Lactoperoxidase and Lactoferrin Separation on an Ion-Exchange Chromatography Step. Separations. 2017; 4(2):10. https://doi.org/10.3390/separations4020010
Chicago/Turabian StyleFaraji, Naeimeh, Yan Zhang, and Ajay K. Ray. 2017. "Optimization of Lactoperoxidase and Lactoferrin Separation on an Ion-Exchange Chromatography Step" Separations 4, no. 2: 10. https://doi.org/10.3390/separations4020010
APA StyleFaraji, N., Zhang, Y., & Ray, A. K. (2017). Optimization of Lactoperoxidase and Lactoferrin Separation on an Ion-Exchange Chromatography Step. Separations, 4(2), 10. https://doi.org/10.3390/separations4020010







