Next Article in Journal
A Self-Consistent, High-Fidelity Adsorption Model for Chromatographic Process Predictions: Low-to-High Load Density and Charge Variants in a Preparative Cation Exchanger
Previous Article in Journal
Essential Oils as Nature’s Dual Powerhouses for Agroindustry and Medicine: Volatile Composition and Bioactivities—Antioxidant, Antimicrobial, and Cytotoxic
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Separations
Volume 12
Issue 6
10.3390/separations12060146
separations-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Insights into the Adsorptive Separation of Ethylene/Ethane in LTA-Type Zeolites

by
Xiaohui Zhao
1,
Shixue Zhou
2,*,
Magdy Abdelghany Elsayed
1,
Zhongyuan Chen
2,
Chunhui Jiang
1,
Yongli Hu
1 and
Gumawa Windu Manggada
1
1
College of Energy and Mining Engineering, Shandong University of Science and Technology, Qingdao 266590, China
2
College of Chemical and Biological Engineering, Shandong University of Science and Technology, Qingdao 266590, China
*
Author to whom correspondence should be addressed.
Separations 2025, 12(6), 146; https://doi.org/10.3390/separations12060146
Submission received: 22 April 2025 / Revised: 22 May 2025 / Accepted: 28 May 2025 / Published: 1 June 2025
(This article belongs to the Topic Oil, Gas and Water Separation Research)
Browse Figures
Versions Notes

Abstract

:
Understanding the competitive adsorption mechanism is essential for the development of adsorptive separation of ethylene (C2H4) and ethane (C2H6). In this work, density functional theory calculations and molecular dynamics simulations were employed to investigate the adsorption of C2H4 and C2H6 in two LTA-type zeolites, ITQ-29 and 5A. The results show that the adsorption energies of the gas molecules in zeolite 5A are more negative than in ITQ-29, and the difference in adsorption energy between C2H4 and C2H6 in zeolite 5A is significantly larger than in ITQ-29, 13.3 versus 6.2 kJ/mol. Zeolite ITQ-29 demonstrates high C2H4/C2H6 ideal selectivity (43.5 at 5 ns) while exhibiting slow C2H4 uptake efficiency due to the small pore windows, hindering C2H4 diffusion (1.05 × 10−10 m2/s at 298 K). In contrast, zeolite 5A facilitates the faster diffusion of C2H4 molecules (3.25 × 10−9 m2/s at 298 K) and exhibits a modest C2H4/C2H6 selectivity of 1.11 at 5 ns in single-gas adsorption and 2.72 in equimolar binary mixture adsorption. To enhance C2H4/C2H6 selectivity, methyl phosphonic acid is introduced onto zeolite 5A to add a sieving layer that enables the C2H4 molecules to preferentially permeate, and the optimal coverage of methyl phosphonic acid is 50%, yielding a C2H4/C2H6 selectivity of 17.5 at 5 ns in mixture adsorption and preserving the C2H4 uptake efficiency. The insights into the competitive diffusion of molecules in the coating layer and inside the zeolites provide a theoretical basis for the rational design of high-performance adsorbents.

Graphical Abstract

1. Introduction

Light olefins are crucial feedstocks for the manufacture of plastics, rubber, and fibers [1,2]. In industry, the olefins are typically produced through catalytic cracking, steam cracking, and methanol conversion [3,4]. However, the resulting products contain alkanes that need to be separated to yield high-purity olefins for the synthesis of downstream products [5]. The separation of olefins and alkanes is one of the most technologically challenging and energy-intensive processes, with C2H4 and C3H6 separation from gas mixtures accounting for 0.3% of global energy consumption [6]. The cryogenic distillation process, commonly used in industry, necessitates the utilization of large-scale distillation columns of 120–180 trays, high pressures of 1.5–3 MPa, and sub-ambient temperatures of 123–263 K [7]. In contrast, the adsorptive separation process offers significant advantages of minimal energy consumption, high separation efficiency, and straightforward operation [8,9]. With the development of porous materials, such as zeolites [10,11], activated carbon [12,13], metal-organic frameworks [14,15], covalent organic frameworks [16,17], and hydrogen-bonded organic frameworks [18,19], adsorptive separation has become increasingly attractive [20].
The design of porous materials possessing high adsorption selectivity remains a significant challenge in the field of separation of olefins and alkanes with similar molecular sizes and physicochemical properties, which prompts extensive experimental and theoretical studies. Zeolites are widely used in adsorptive separation due to their favorable characteristics, such as well-defined pores, large specific surface area, high chemical and thermal stability, and low cost [21,22,23]. Moreover, the adsorption selectivity in zeolites can be improved by adjusting frameworks, tuning pore structures, varying exchangeable cations, and modifying surfaces. LTA-type zeolite frameworks feature 8-membered ring windows connecting supercages [24], exhibiting a favorable sieving effect for molecules with kinetic diameters in the range of 3.9–4.3 Å [25,26]. Rege et al. [27] employed zeolite 4A for the separation of C3H6 and C3H8 and found that C3H8 is sterically excluded from the pores, whereas C3H6 can readily diffuse through the zeolite, attributing this to the effective pore aperture being the demarcation between the kinetic diameters of C3H6 and C3H8 molecules. Sala et al. [28] synthesized a novel zeolite, designated ITQ-69, with a distinctive tri-directional pore-channel system that is particularly suitable for the kinetic separation of C3H6 and C3H8, and the experimental results demonstrate that the diffusion rate of C3H6 in the zeolite is significantly faster than that of C3H8. Chen et al. [29] reported that the framework Si/Al ratio of MOR-type zeolite regulates the number and distribution of exchangeable cations in the channels, thereby controlling the accessibility of guest molecules and the utilization of space, and an appropriate number of exchangeable cations can enhance the interaction between C2H4 and the zeolite, making the C2H4 molecules more readily access and utilize the space than C2H6. Baamran et al. [30] found that doping ferric oxide nanoparticles into zeolite 13X augments the adsorption capacity by surface electron transfer, which strengthens π–ion interactions between C2H4 molecules and adsorption sites. Additionally, the introduction of ferric oxide results in the formation of nanochannels, thereby enhancing the sieving effect and improving C2H4 selectivity. Ellis et al. [31] demonstrated that surface coating with phosphonic acids of varying alkyl tail length on zeolite 5A enhances the separation of C3H6 and C3H8 through restricting the C3H8 adsorption rate. Zhou et al. [32] found that C3H6/C3H8 kinetic selectivity is improved by increasing phosphonic acids coating density on zeolite 5A and employing phosphonic acids with terminal functional group (amine or carboxylic acid).
Furthermore, with the development of science and technology, molecular simulation has been applied to study adsorptive separation [33]. Mitra et al. [34] simulated the diffusion behavior of C3H6 in zeolites ZSM-5 and Na-Y and found that the molecular diffusion is strongly dependent on pore structure, where zeolite ZSM-5, featuring a network of intersecting channels, restricts the translational diffusion of C3H6 molecules and causes the molecules to orientate along the channels of the zeolite, whereas zeolite Na-Y, having spherical supercages interconnected through windows, enables C3H6 molecules to undergo isotropic rotation freely. Guo et al. [35] simulated the adsorptive separation of N2 and O2 in zeolite Li-LSX incorporated with Ag+ and Ce3+ cations, and they found that Ag+ doping enhances the adsorption of both N2 and O2, whereas Ce3+ doping only increases O2 adsorption. Liu et al. [36] simulated the adsorption of Xe and Kr molecules in CHA-type zeolite with framework Si/Al ratio of 2.5 and Ca2+ as the counter-cations, and they found that the Ca2+ cations act as the primary binding sites for Xe molecules, whereas Kr molecules are stabilized through weak adsorbent–adsorbate interactions with the zeolite framework.
In this work, the adsorption of C2H4 and C2H6 in two LTA-type zeolites, ITQ-29 and 5A, was investigated using first principle calculations based on density functional theory (DFT) and molecular dynamics (MD) simulations based on the molecular force field. The atomic charges, adsorbate structures, and adsorption energies were determined. The adsorption isotherms, molecular diffusion dynamics, and adsorption kinetics were simulated. To improve C2H4/C2H6 adsorption selectivity, methyl phosphonic acid (MPA) was introduced onto the surface of zeolite 5A. A diffusion-mediated competitive adsorption mechanism was demonstrated for the separation of C2H4 and C2H6 in zeolites, providing a new perspective on the separation of olefins and alkanes.

2. Materials and Methods

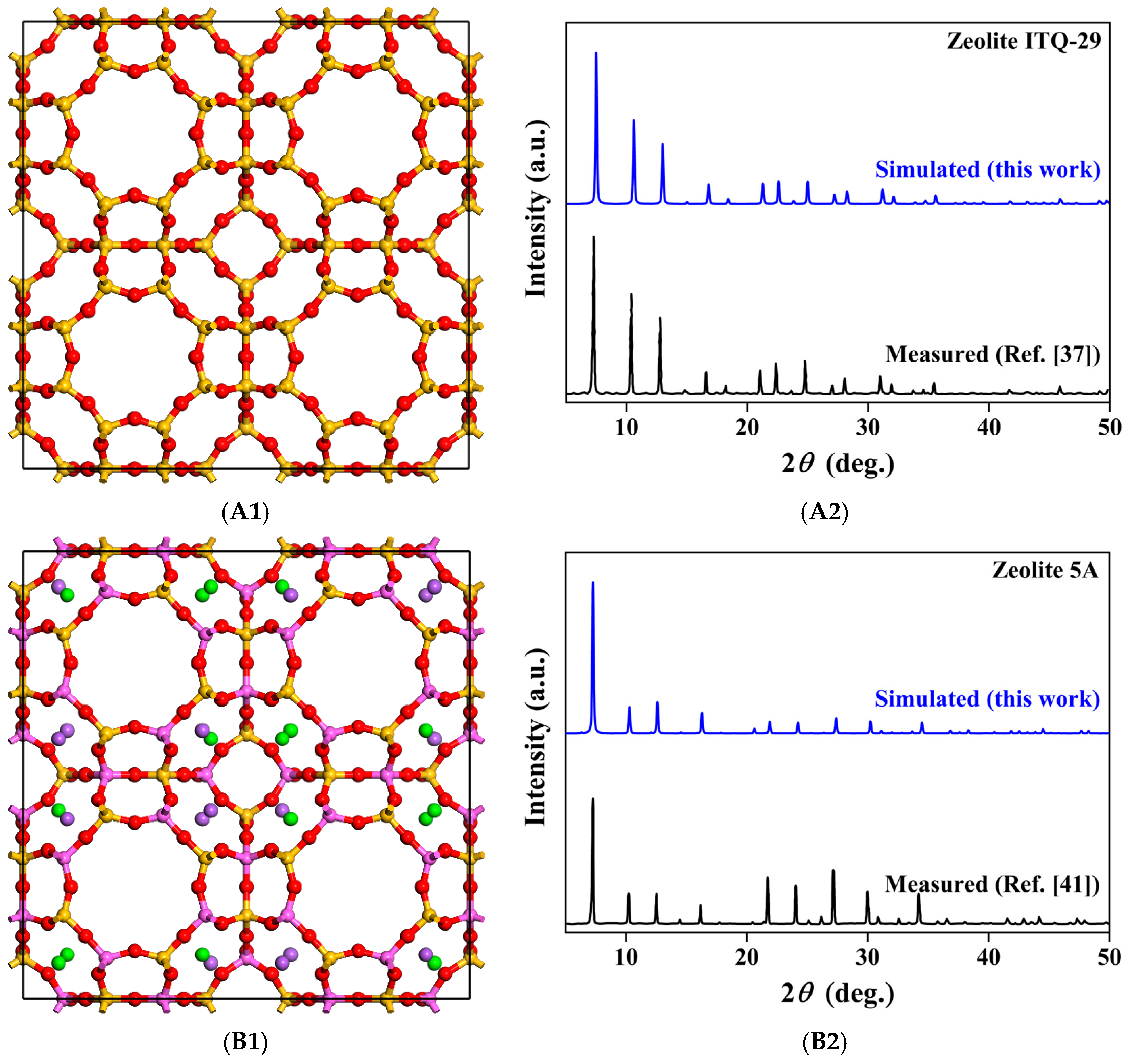
2.1. Structural Models and Density Functional Theory Calculations

Two LTA-type zeolites, ITQ-29 and 5A, were used for the adsorption of C2H4 and C2H6 in this work. The cell model of the zeolite ITQ-29 was built using the atomic coordinates in the literature [37], and the zeolite 5A was built using the atomic coordinates in the literature [38]. Then, the geometries were optimized using the DMol3 module in the Materials Studio 2017 software (Accelrys Software Inc., San Diego, United States) based on DFT calculations. In the calculations, the Perdew–Burke–Ernzerhof (PBE) functional of the generalized gradient approximation (GGA) was adopted to evaluate the nonlocal exchange correlation energy [39]. The electron wave function was based on double numerical plus polarization (DNP) basis set to ensure the calculation accuracy [40], with basis file version 4.4. The self-consistent field tolerance was set at 10−6 Ha. To accelerate the self-consistent field convergence, the direct inversion in an iterative subspace (DIIS), preconditioner, and smearing were enabled, with parameters set at 6, 4.0 a0−1, and 0.005 Ha, respectively. Hexadecapole was chosen for multipolar expansion to describe the electron distribution. The global orbital cutoff scheme was applied with a cutoff distance of 4.8 Å. Gamma point only is used for sampling in the first Brillouin zone, since the system is large enough that the electronic wavefunctions are sufficiently smooth in real space. For geometry optimization, the convergence criteria of the energy, maximum force, and maximum displacement were set at 1.0 × 10−5 Ha, 0.002 Ha Å−1, and 0.005 Å, respectively.
The ITQ-29 and 5A structural models after geometry optimization are shown in Figure 1(A1) and Figure 1(B1), respectively, in which the zeolites consist of three distinct building units: double-4-membered ring (D4R), sodalite cage (β cage), and LTA supercage (α cage). The framework is composed of β cages arranged in simple cubic packing, with adjacent β cages connected by D4R units, and eight β cages surrounding a central α cage. In zeolite 5A, the Na+ and Ca2+ cations are located near the centers of the 6-membered rings of the α cages, as shown in Figure S1. The geometry optimization did not alter the atomic coordinates or cell parameters compared with those in the literature [37,38], as listed in Tables S1 and S2, confirming that the DFT calculation parameters are reliable.
The X-ray diffraction patterns of the cell models were simulated using the powder diffraction task of the Reflex module in the Materials Studio software. To generate the X-ray diffraction patterns, incident radiation of average wavelength 1.541838 Å (Cu Kα radiation) was employed over diffraction angle (2θ) from 5 to 50° at a step size of 0.02°. The peak profile was described using Pseudo-Voigt function with profile parameters NA and NB set at 0.5 and 0.0, and the U, V, and W parameters to calculate instrumental broadening of the peaks were set at 0.02, −0.01, and 0.02°2, respectively. The simulated X-ray diffraction patterns, as shown in Figure 1(A2,B2), are similar to those observed in the experimental measurements [37,41], indicating that the cell models are reliable.
The Hirshfeld population analysis was performed on the DFT-calculated electron densities to determine the atomic charges in the zeolites. The atomic charges are crucial for the simulation accuracy, which govern the electrostatic interactions between adsorbent and adsorbate, thereby affecting the molecular loading in grand canonical Monte Carlo (GCMC) simulations and the molecular diffusion trajectories in molecular dynamics simulations. The average Hirshfeld atomic charges in the zeolites ITQ-29 and 5A are listed in Table S3, which are close to those in the literature [42]. When the Hirshfeld charges were used for adsorption simulation with COMPASSII force field, the resulting isotherm is closer to those experimentally measured [43] than those simulated using Mulliken, ESP, QEq, or Gasteiger charges, as shown in Figure S2 and Table S4.
The geometries of the ITQ-29 and 5A cells with an adsorbed C2H4 or C2H6 molecule near a 6-membered ring were optimized based on DFT calculations. Then, the adsorption energy of the molecule was calculated by subtracting the individual energies of the zeolite and molecule from the total energy of the system.
The supercell surface models of the zeolites used for molecular dynamics simulations were constructed based on the cell models (Figure 1(A1,B1)). First, a p(1 × 1) slab with a thickness of two cells was created through cleaving the cell along the (0 0 1) plane, specifying slab thickness to 2.0 cells, slightly increasing the slab thickness to ensure that the bottom face was terminated only with O atoms, adjusting the distance from the origin to the top face to achieve O atoms only termination, and capping the dangling O atoms at the top and bottom faces with H atoms to maintain chemical stability. Next, a vacuum layer of 500 Å was added above the slab to avoid interactions between periodic images and to serve as a gas reservoir. Finally, geometry optimization based on DFT calculations was performed. The supercell surface model for zeolite ITQ-29 is shown in Figure S3, and that for zeolite 5A is shown in Figure S4. The atomic charges in the supercell surface models were determined through Hirshfeld population analysis.
For zeolite 5A with MPA, the MPA molecules were anchored on the top face of the slab via P-O-Si/Al bonds. After geometry optimization, the fully (100% coverage) MPA-coated supercell surface model is shown in Figure S5. For 25%, 50%, 75%, and 100% coverages of MPA, each pore window has 1, 2, 3, and 4 acid molecules, respectively, as shown in Figure S6.

2.2. Grand Canonical Monte Carlo Simulations

The adsorption isotherms of C2H4 and C2H6 in the ITQ-29 and 5A cells were simulated using the Sorption module in the Materials Studio software with GCMC method based on the molecular force field. The COMPASSII force field was selected for the simulation, which yielded isotherms closer to the experimentally measured (in loading amount and curve shape) ones that are reported in reference [43] than those obtained using the Dreiding, Universal, CVFF or PCFF force fields, as shown in Figure S7. For van der Waals interactions, the atom-based method was used for summation, cubic spline was used for energy truncation, a spline width of 1 Å was used for the truncation, and the cutoff distance was set at 12 Å, which is sufficiently long (validated by testing, as shown in Figure S8) yet remains less than half of the cell edge length to avoid spurious self-interactions. For electrostatic interactions, the Ewald method was used for summation. The Hirshfeld atomic charges derived from DFT calculations for the molecules and zeolites (the average Hirshfeld atomic charges are listed in Tables S3 and S5) were used for the simulation instead of the formal charges in the force field files. The equilibration steps and production steps were both set at 1 × 106, a value sufficiently large to balance computational accuracy and efficiency (validated by testing, as shown in Figures S9 and S10). The β cages of the zeolites were blocked using He atoms in the simulation to prevent unphysical occupation by C2H4 and C2H6 molecules. If using a CVFF forcefield for GCMC simulations, the C2H4 loadings at low pressures or high temperatures were overestimated, and the C2H6 loadings were always overestimated, compared with the experimentally measured data reported in reference [43], as shown in Figure S11.

2.3. Molecular Dynamics Simulations

The molecular dynamics simulations of C2H4 and C2H6 in ITQ-29 and 5A cells were performed using the Large-scale Atomic/Molecular Massively Parallel Simulator (LAMMPS) 2Aug2023 software (Sandia National Laboratories), which provided better computational efficiency than the Forcite module in the Materials Studio software for the large-scale simulation. In the simulations, the CVFF force field, rigorously validated for zeolite systems [44,45], was employed for simulating molecular diffusion in zeolites, and the Hirshfeld atomic charges derived from DFT calculations were used, by which molecular diffusion coefficients comparable to the experimentally measured that reported in reference [44] were derived. The units, atom_style, and time step were set at real, full, and 1 fs, respectively. The boundary was set at p p p. The comm_style was set at tiled, and comm_modify was set at mode single cutoff 14.0. For intramolecular interactions, the bond, angle, and dihedral styles were all set at harmonic. The pair_style was set at lj/cut/coul/long 12.0 12.0, and pair_modify was set at shift yes mix arithmetic. The kspace_style was set at pppm 1.0 × 10−5. The Nosé–Hoover thermostat was employed for the temperature control. After molecular dynamics simulations, the mean square displacement (MSD) versus time was plotted and linear fitting was performed, and then the diffusion coefficient was determined from the slope of the fitted line divided by 6 according to the Einstein relation.
The adsorption kinetics were extracted from the simulations performed on the supercell surface models to plot the time-dependent uptake profiles. The adsorption temperature was set at 298 K (a higher temperature is not favorable for gas uptake (Figure S12)). For single-gas adsorption, 100 molecules were put in the gas reservoir of the supercell surface model (the number of molecules is sufficient, otherwise an insufficient number of molecules results in inefficient uptake (Figure S13)). The simulation timescale was typically set at 5 ns to balance result visualization and computational efficiency (Figure S14). The supercell surface model with a suitable slab thickness of two cells was employed (Figure S15). The ideal selectivity was determined by the ratio of C2H4 to C2H6 uptakes at the same adsorption time in single-gas adsorption, and the mixture selectivity was determined by the uptake ratio of C2H4 to C2H6 in mixed-gas adsorption divided by their content ratio in the feed gas.

3. Results and Discussion

3.1. Adsorption Structures and Adsorption Energies

After geometry optimization based on DFT calculations, the adsorption structures of the C2H4 and C2H6 molecules in zeolites ITQ-29 and 5A are shown in Figure 2. In zeolite ITQ-29, the distances between the C atoms of the C2H4 molecule and the proximal O atoms in host 6-membered ring (3.79–3.87 Å) are shorter than the corresponding distance for the C2H6 molecule (4.36–4.47 Å). This originates from the difference in molecular geometry between C2H4 and C2H6. The C2H4 molecule exhibits a lower steric hindrance than C2H6 to access the 6-membered ring in zeolite ITQ-29. In zeolite 5A, the C2H4 molecule is much closer to the 6-membered ring with a distance of 3.55–3.76 Å, while the C2H6 molecule maintains a larger distance of 4.30–4.56 Å. This is attributed to the presence of Ca2+ cations in zeolite 5A, which exert strong attraction to the C2H4 molecule.
The adsorption energies of the C2H4 and C2H6 molecules in zeolites ITQ-29 and 5A are listed in Table 1 and Table S6. In zeolite ITQ-29, the adsorption energy of C2H4 is more negative than C2H6 (−27.7 vs. −21.5 kJ/mol), which is attributed to the stronger orbital hybridization of the C atoms of C2H4 with the O atoms in host 6-membered ring, as shown in Figure S16. In zeolite 5A, the adsorption energies of C2H4 and C2H6 are −45.6 and −32.3 kJ/mol, respectively, more negative than in zeolite ITQ-29. This enhanced adsorption results from stronger interactions between adsorbate molecules and zeolite 5A with exchangeable cations (Table S7), as evidenced by orbital hybridization (Figure S17) compared with those in zeolite ITQ-29 (Figure S16). Although the adsorption is enhanced for both C2H4 and C2H6 in zeolite 5A, the difference in adsorption energy between C2H4 and C2H6 in zeolite 5A is larger than that in ITQ-29, 13.3 vs. 6.2 kJ/mol, which is responsible for the competitive occupation of adsorption sites by C2H4 over C2H6 in zeolite 5A. The adsorption energies of C2H4 and C2H6 in zeolites ITQ-29 and 5A calculated in this work, without zero-point energy (ZPE) and vibration enthalpy calibration, are comparable to the experimentally measured adsorption enthalpies reported in references [46,47,48], indicating that physisorption dominates the adsorption behavior. The adsorption energies/enthalpies in zeolite 5A in this work and reference [48] are more negative than those in reference [47], since the adsorption enthalpy is influenced by the relative amounts of Ca2+ and Na+ cations and when their amounts are similar, the adsorption enthalpy is more negative [48].

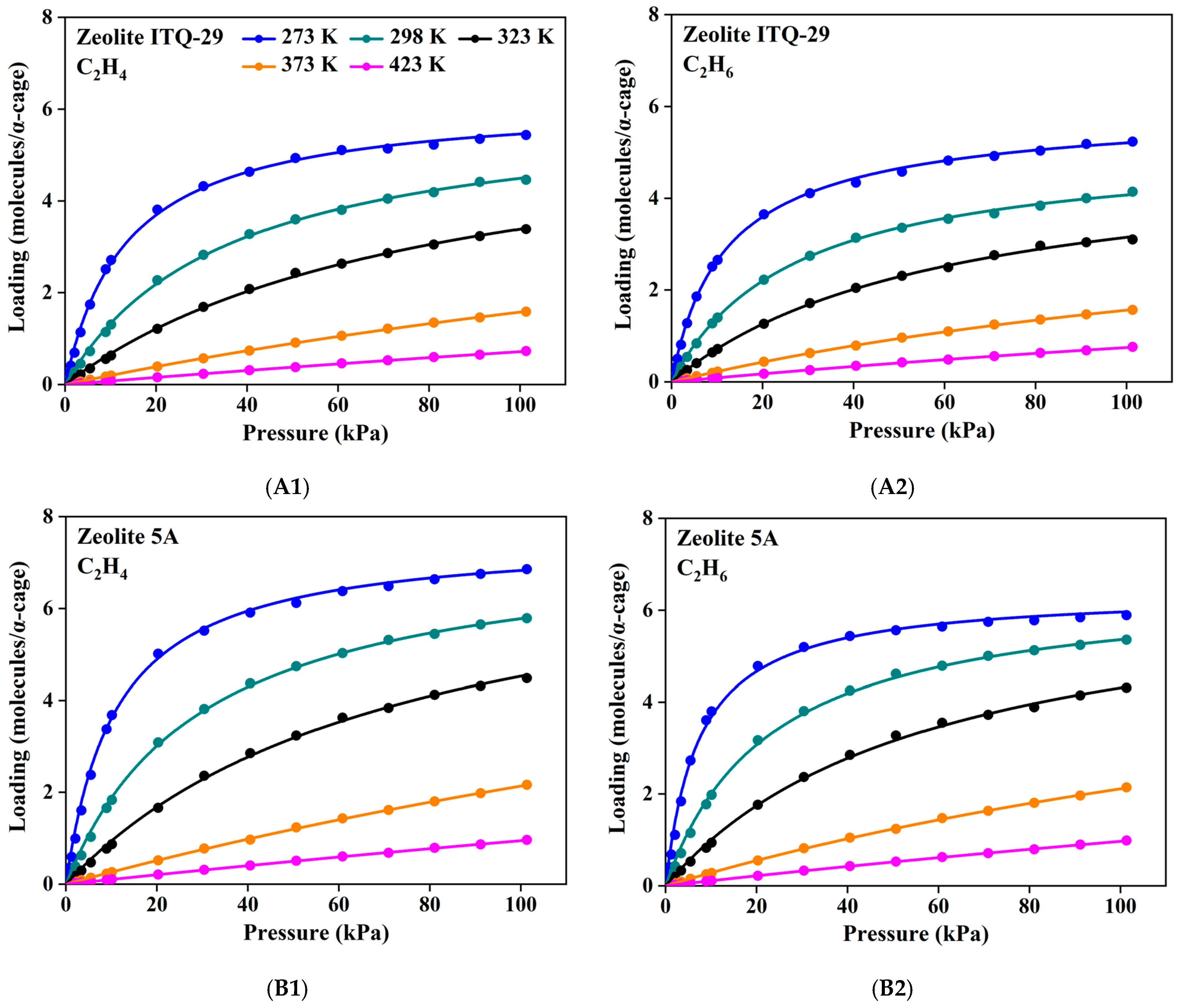
3.2. Adsorption Isotherms

The single-component isotherms of C2H4 and C2H6 adsorption in zeolites ITQ-29 and 5A at different temperatures are shown in Figure 3 and the Langmuir model [49] provides excellent agreement with the adsorption data (Table S8, adj.−R2 > 0.999). As the temperature increases, both loadings of C2H4 and C2H6 in the zeolites decrease sharply, and the loading differences between C2H4 and C2H6 also decrease, which indicates that a low temperature is favorable for the adsorptive separation of C2H4 and C2H6. As pressure increases, both loadings of C2H4 and C2H6 in the zeolites increase rapidly at low pressures owing to abundant adsorption sites, while the loadings approach asymptote at high pressures due to the progressive saturation of adsorption sites. Moreover, the loadings in zeolite 5A are higher than in zeolite ITQ-29. This difference is attributed to their distinct chemical compositions. Zeolite 5A contains Ca2+ and Na+ cations, which enhance the adsorbent–adsorbate interactions through intensifying electrostatic interactions. In contrast, pure silica zeolite ITQ-29 lacks such cations, leading to weaker interactions dominated by van der Waals forces. This indicates that the exchangeable cations play a pivotal role in enhancing adsorption loadings in the zeolite.
The adsorption isotherm for the mixture is affected by the ratio of C2H4 to C2H6, as shown in Figures S18 and S19. The C2H4 loading increases when the C2H4 proportion rises in the mixture. Both loadings of C2H4 and C2H6 are higher in zeolite 5A than in ITQ-29 due to the stronger interactions of gas molecules with zeolite 5A.
The energy distribution profiles for C2H4 and C2H6 adsorption in zeolites ITQ-29 and 5A at different temperatures are shown in Figure 4. The energy distribution exhibits the characteristics of single-site-dominated adsorption. As temperature increases, the curves shift to less negative energies, reflecting the weakening of the adsorption strength. This trend is consistent with the observed temperature-dependent adsorption isotherms, where a low temperature is favorable for gas adsorption. Moreover, the energies are more negative in zeolite 5A than in ITQ-29, as shown in Figure S20, which is attributed to the presence of Ca2+ and Na+ cations in zeolite 5A, enhancing interactions with the molecules through molecular polarization and subsequent electrostatic reinforcement.

3.3. Diffusion Coefficients and Activation Energies

The diffusion coefficient is affected by the molecular loading in zeolite, as shown in Figure S21. With the increase in loading from 0.5 to 2.0 molecules/α-cage in zeolite 5A, the diffusion coefficient significantly decreases, and with a further increase in the loading, the coefficient almost remains constant. Therefore, simulations with 2.0 molecules/α-cage were performed for the further study of molecular diffusion in this section. The diffusion coefficients of C2H4 in zeolite 5A at different temperatures derived from the simulations using the LAMMPS software with CVFF forcefield are similar to the coefficients from the simulations using the Forcite module in the Materials Studio software (COMPASSII and CVFF forcefields), as listed in Table S9. The diffusion coefficients of C2H4 are higher than C2H6 at the same temperatures in both zeolites, as shown in Table S10, which is attributed to the smaller molecular size of C2H4 (minimum cross-section 3.30 × 4.20 Å) than C2H6 (minimum cross-section 3.90 × 4.18 Å) [50]. In zeolite 5A, both diffusion coefficients of C2H4 and C2H6 are much higher than in zeolite ITQ-29 at the same temperatures, which is ascribed to the larger 8-membered ring windows of α-cages in zeolite 5A than in ITQ-29 (4.21 vs. 4.15 Å [51]). As the temperature increases, the diffusion coefficients for C2H4 and C2H6 in zeolites ITQ-29 and 5A all increase.
The Arrhenius plots of the natural logarithm of the diffusion coefficients (ln D) versus inverse temperature (1/T) for C2H4 and C2H6 in zeolites ITQ-29 and 5A are shown in Figure 5. The activation energy of C2H4 diffusion is smaller than that of C2H6 in both zeolites, indicating that C2H4 diffusion is less temperature sensitive. In zeolite 5A, both activation energies of C2H4 and C2H6 are smaller than in zeolite ITQ-29. Moreover, the activation energy presents an inverse relationship with the diffusion coefficient. C2H4 exhibits smaller diffusion activation energy than C2H6 in both zeolites and higher diffusion coefficient in zeolite 5A than in ITQ-29, suggesting that zeolite 5A is a better adsorbent than ITQ-29 for the adsorptive separation of C2H4 over C2H6 at a lower temperature.

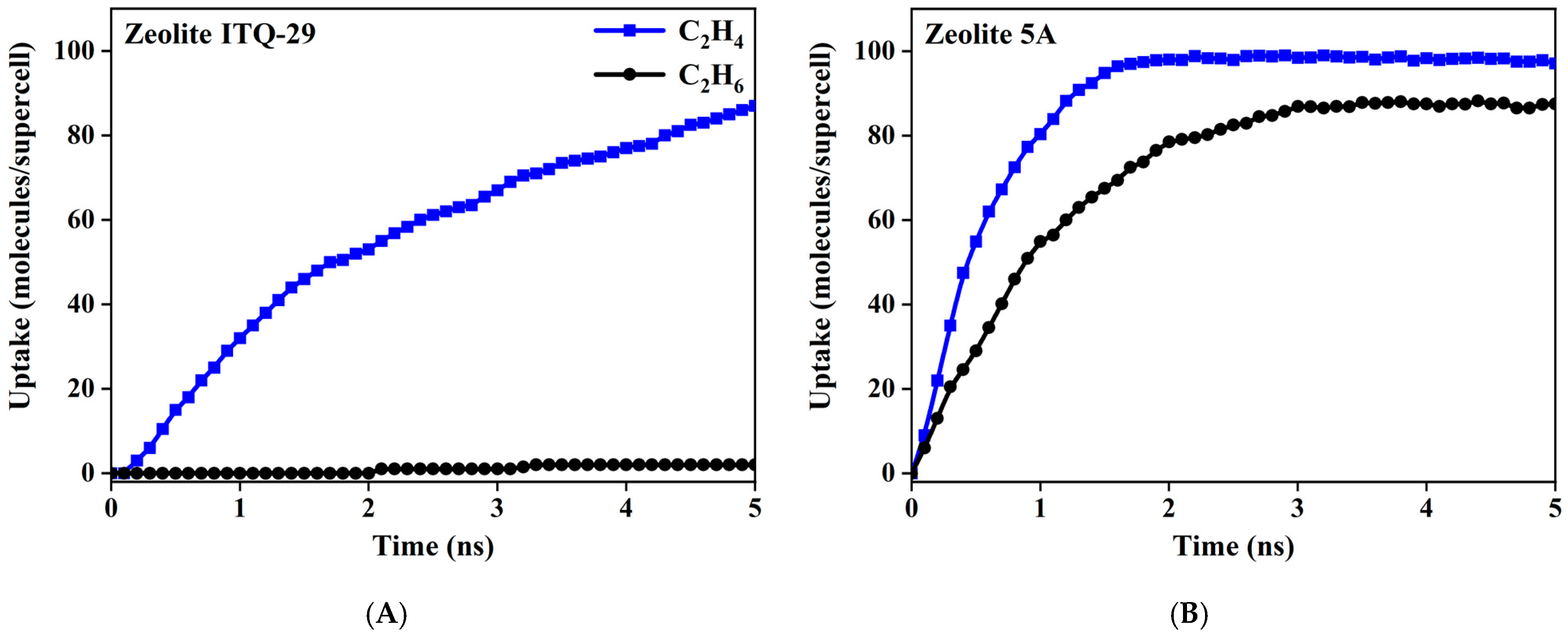
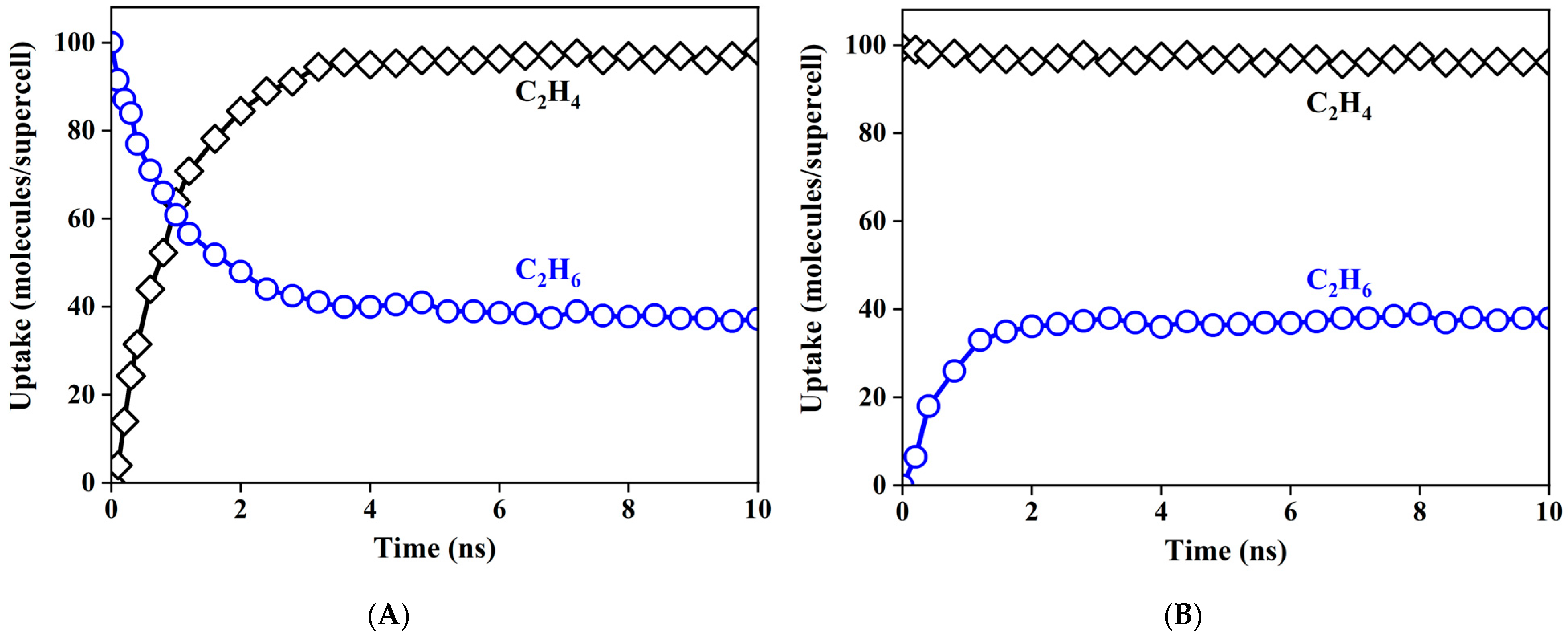
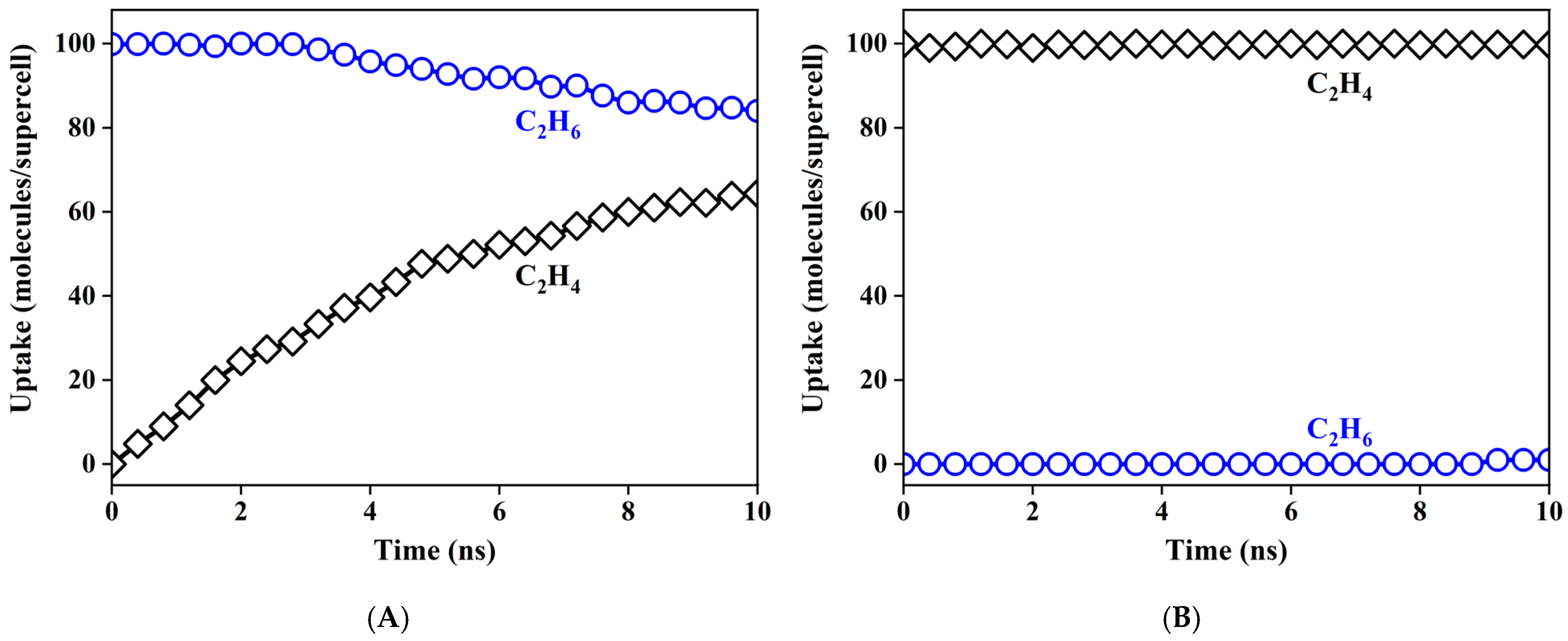
3.4. Adsorption Kinetics

In single-gas adsorption, the uptakes of C2H4 and C2H6 in zeolites ITQ-29 and 5A are shown in Figure 6, based on the simulation of gas molecules diffusing from the gas reservoir into the solid slab of the supercell surface models. In zeolite ITQ-29, the C2H4 uptake increases rapidly until 2 ns, followed by a slow increase due to the depletion of C2H4 molecules in the gas reservoir. Interestingly, the C2H6 uptake remains negligible throughout the simulation, indicating that C2H6 molecules are sterically excluded by the small pore windows of zeolite ITQ-29. In zeolite 5A, the C2H4 uptake increases sharply within 1 ns and achieves equilibrium at 2 ns, while C2H6 uptake increases slowly and achieves equilibrium at 3 ns. At 5 ns, the C2H4 uptake is higher than C2H6 in zeolite 5A (98 vs. 88 molecules per supercell), which is consistent with the adsorption isotherm analysis (Figure 3). In both zeolites, the uptake of C2H4 is faster than C2H6 and zeolite 5A exhibits faster adsorption for both gases than ITQ-29, which is attributed to the smaller molecular size of C2H4 than C2H6 and the larger pore window size of zeolite 5A than ITQ-29; it aligns with the diffusion coefficient trends (Table S10).
The zeolite ITQ-29 exhibits higher ideal selectivity of C2H4/C2H6 (43.5 at 5 ns) than zeolite 5A (1.11). However, its sluggish growth in C2H4 uptake, especially in the internal region (Region 2, Figure S22) of the zeolite, as shown in Figure S23, suggests that zeolite ITQ-29 is not an excellent adsorbent for C2H4/C2H6 separation. Zeolite 5A exhibits a higher C2H4 uptake although its C2H4/C2H6 selectivity is low. Here, the ideal selectivity (1.11 at 298 K) is close to the value in reference (1.41 at 288 K) [52], which also validates the molecular dynamics simulations in this work. To improve the adsorption selectivity in zeolite 5A, the surface of the zeolite was modified with MPA to add a sieving layer that enables C2H4 molecules to preferentially permeate.
In mixture adsorption, the uptakes of C2H4 and C2H6 in zeolite 5A from equimolar binary mixture are shown in Figure 7. In the binary system, the C2H4 uptake is similar to that observed in single-gas adsorption, while the C2H6 uptake is inhibited due to competitive adsorption of C2H4. When the adsorption sites are occupied by C2H4 molecules which processes fast diffusion rate and strong affinity for the zeolite, it is difficult for C2H6 molecules to displace the adsorbed C2H4 molecules although there are still many C2H6 molecules in the gas reservoir, and therefore it results in lower C2H6 uptake. At 5 ns, the C2H4/C2H6 selectivity in the mixture adsorption increases to 2.72, whereas the ideal selectivity in single-gas adsorption is only 1.11, demonstrating the role of competitive adsorption in enhancing selectivity.
The uptakes of C2H4 and C2H6 in zeolite 5A for the 20:80 and 80:20 mixtures are shown in Figure S24. For a 20:80 mixture, 95% of C2H4 molecules are adsorbed in zeolite 5A (Figure S24A), whereas for an 80:20 mixture, only 23% of C2H6 molecules are adsorbed (Figure S24B). This indicates that C2H4 maintains its preferential adsorption over C2H6 across varying feed compositions.
In displacement adsorption, the uptakes of C2H4 and C2H6 in zeolite 5A are shown in Figure 8. When C2H6 molecules are pre-adsorbed in the zeolite, the C2H4 molecules in the gas reservoir rapidly enter the zeolite and displace the pre-adsorbed C2H6 molecules. At 6 ns, 63% of pre-adsorbed C2H6 molecules are displaced by C2H4 molecules, and then the system achieves dynamic equilibrium, as shown in Figure 8A. In reverse, when the C2H4 molecules are pre-adsorbed, the C2H6 uptake increases gradually and stabilizes at 38 molecules per supercell, as shown in Figure 8B, where the C2H6 molecules adsorb on the vacant sites left after C2H4 adsorption while not displacing the pre-adsorbed C2H4 molecules. Moreover, there is no significant C2H4 desorption into the gas reservoir, indicating its stronger affinity for the zeolite as discussed in the adsorption energy calculations and mixture adsorption. The displacement adsorption phenomenon was also observed in experimental measurements [53,54].

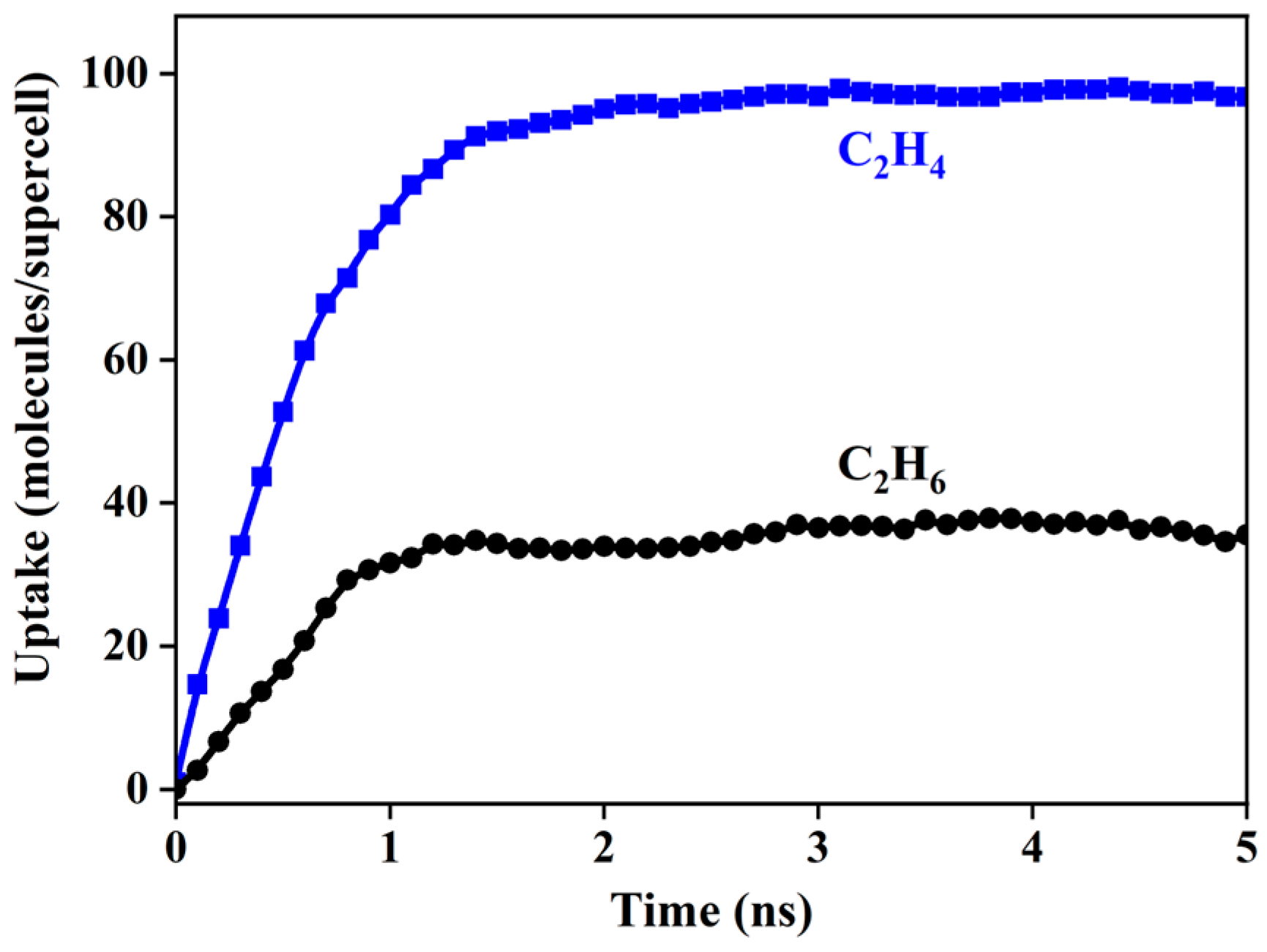
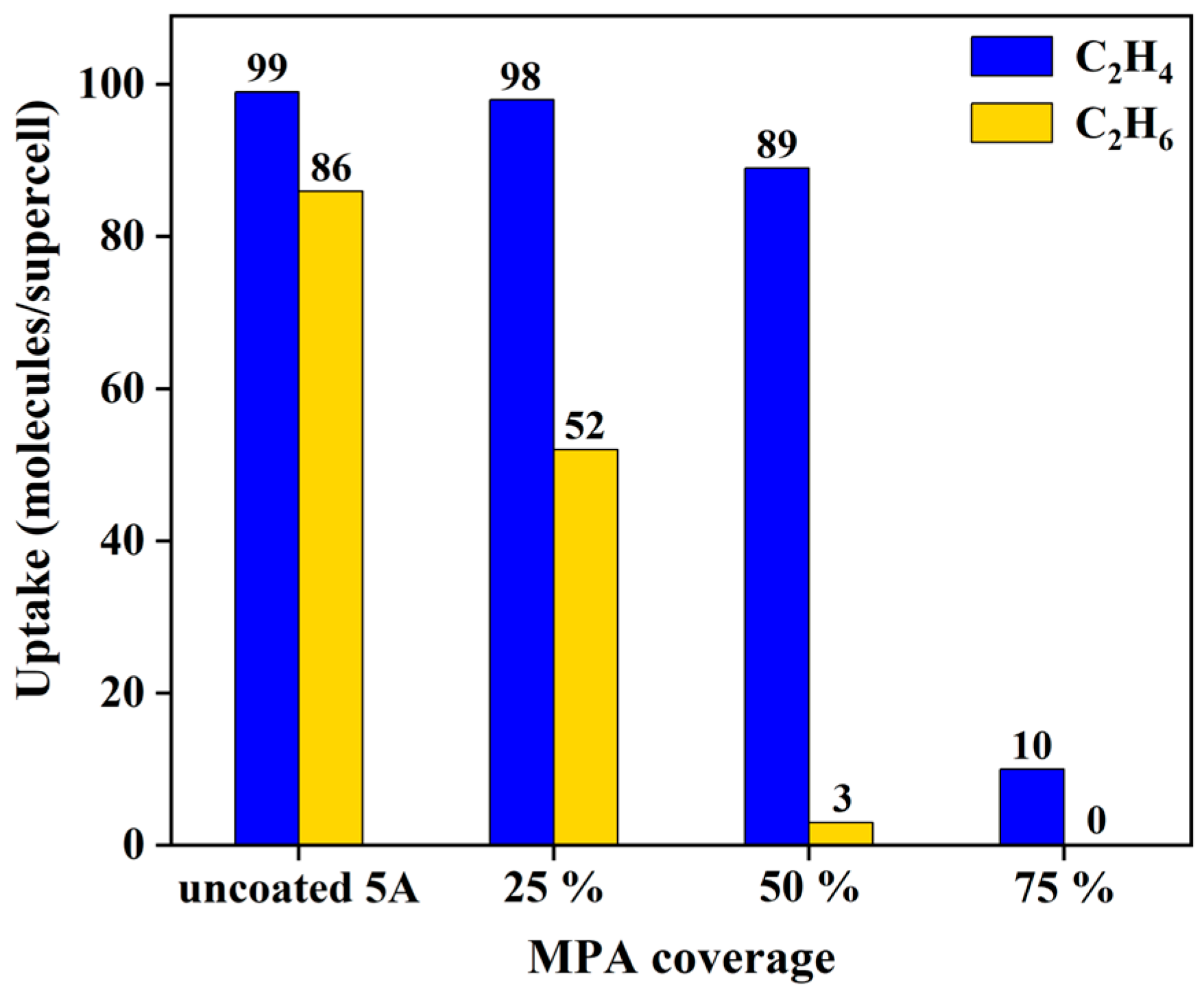
3.5. Surface Modification

In single-gas adsorption, the uptakes of C2H4 and C2H6 in zeolite 5A with different coverages of MPA at 5 ns are shown in Figure 9, and the uptake kinetics curves are presented in Figure S25. With the increase in MPA coverage on the zeolite, the decrease magnitude of C2H6 uptake is larger than C2H4. At 25% coverage, the C2H4 uptake is nearly unaffected compared with the uncoated zeolite, while the C2H6 uptake decreases significantly. This indicates that the diffusion of C2H6 molecules passing through the MPA layer is strongly hindered due to the larger molecular size of C2H6 than C2H4. At 50% coverage, the C2H4 uptake remains nearly unaffected, while the C2H6 molecules are almost sterically excluded, where the MPA layer exhibits a sieving effect on the C2H6 molecules. At 75% coverage, C2H4 uptake is small and C2H6 uptake becomes undetectable. For efficient separation, the optimal MPA coverage on zeolite 5A is 50%, by which the ideal selectivity reaches 29.7 at 5 ns and the C2H4 uptake remains high. This demonstrates the efficacy of surface modification on the zeolites in tuning the separation of C2H4 and C2H6.
In equimolar binary mixture adsorption, the uptakes of C2H4 and C2H6 in zeolite 5A with 50% coverage of MPA are shown in Figure 10. In the binary system, the C2H4 uptake readily increases, similar to that in single-gas adsorption (Figure S25A), while the C2H6 uptake is low although there are many molecules in the gas reservoir. At 5 ns, the C2H4/C2H6 selectivity in mixture adsorption is 17.5. The C2H4 uptake in the central region of the zeolite increases rapidly with the progress of adsorption, as shown in Figure S26, indicating that the MPA coating tunes the diffusion of C2H4 molecules from the gas reservoir into the zeolite while not perturbing the molecular diffusion within the zeolite.
In displacement adsorption, the uptakes of C2H4 and C2H6 in zeolite 5A with 50% coverage of MPA are shown in Figure 11. When C2H6 molecules are pre-adsorbed in the zeolite, the C2H4 molecules in the gas reservoir displace the pre-adsorbed C2H6 molecules progressively although the process is slow compared with that in uncoated zeolite 5A, in which the displacement has not completed even after 10 ns (Figure 11A). In reverse, when the C2H4 molecules are pre-adsorbed, the MPA coating effectively excludes the C2H6 molecules; the C2H4 uptake does not change throughout the simulation, demonstrating that the MPA coating prevents the C2H4 molecules from escaping the solid slab (Figure 11B). This indicates that the MPA coating tunes the molecular diffusion rate across the coating layer while preserving the competitiveness of C2H4 over C2H6 on the adsorption sites, enabling the small molecules to preferentially permeate [55].

4. Conclusions

According to the DFT calculations, the adsorption energies of gas molecules in zeolite 5A are more negative than in ITQ-29, and the difference in adsorption energy between C2H4 and C2H6 in zeolite 5A is significantly larger than that in ITQ-29, which is attributed to the exchangeable cations, facilitating strong interactions with C2H4 molecules through atomic orbital hybridization. According to the molecular dynamics simulations, zeolite ITQ-29 demonstrates high C2H4/C2H6 ideal selectivity (up to 43.5 at 5 ns) while exhibiting slow C2H4 uptake due to its small pore windows, which hinder C2H6 uptake but inadvertently suppress C2H4 uptake. Zeolite 5A facilitates faster diffusion of C2H4 molecules and exhibits a modest C2H4/C2H6 selectivity of 2.72 at 5 ns in binary mixture adsorption. MPA is introduced onto zeolite 5A to add a sieving layer that enables C2H4 molecules to preferentially permeate, by which it reduces the C2H6 uptake significantly while preserving the C2H4 uptake efficiency. The optimal coverage of MPA is 50%, yielding a C2H4/C2H6 selectivity of 17.5 at 5 ns in mixture adsorption. The displacement adsorption demonstrates that C2H4 possesses stronger affinity for the zeolite and readily displaces pre-adsorbed C2H6. These findings provide insights on designing high-performance adsorbents for the separation of olefins and alkanes.

Supplementary Materials

The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/separations12060146/s1. Figure S1: oblique view of the structural model of zeolite 5A; Figure S2: adsorption isotherms of C2H4 at 298 K in zeolite 5A simulated with different atomic charges; Figure S3: top view (A) and front view (B) of the supercell surface model of zeolite ITQ-29; Figure S4: top view (A) and front view (B) of supercell surface model of uncoated zeolite 5A; Figure S5: top view (A) and front view (B) of supercell surface model of zeolite 5A fully coated with MPA; Figure S6: top view of 25% (A), 50% (B), 75% (C), and 100% (D) MPA-coated zeolite 5A; Figure S7: adsorption isotherms of C2H4 at 298 K in zeolite 5A simulated with different force fields; Figure S8: adsorption isotherms of C2H4 at 298 K in zeolite 5A simulated with different cutoff distances for van der Waals interactions; Figure S9: adsorption isotherms of C2H4 at 298 K in zeolite 5A simulated with different equilibrium steps; Figure S10: energy distribution profiles for C2H4 adsorption at 298 K in zeolite 5A simulated with different production steps; Figure S11: adsorption isotherms of C2H4 and C2H6 in zeolite ITQ-29 with CVFF forcefield at different temperatures; Figure S12: uptakes of C2H6 in zeolite 5A simulated at different temperatures; Figure S13: uptakes of C2H6 at 298 K in zeolite 5A simulated with different numbers of molecules in the gas reservoir; Figure S14: uptakes of C2H6 at 298 K in zeolite 5A simulated with different simulation timescales; Figure S15: uptakes of C2H6 at 298 K in zeolite 5A simulated with different supercell surface model thicknesses; Figure S16: partial density of states (PDOS) of the C atoms of C2H4 (A) and C2H6 (B) proximate to the 6-membered ring and the closest O atoms in host 6-membered ring of zeolite ITQ-29; Figure S17: partial density of states (PDOS) of the C atoms of C2H4 (A) and C2H6 (B) proximate to the 6-membered ring, the Ca atom near the 6-membered ring, and the closest O atoms in host 6-membered ring of zeolite 5A; Figure S18: adsorption isotherms for different C2H4/C2H6 mixtures (20:80, 40:60, 60:40, and 80:20) in zeolite ITQ-29 at 298 K; Figure S19: adsorption isotherms for different C2H4/C2H6 mixtures (20:80, 40:60, 60:40, and 80:20) in zeolite 5A at 298 K; Figure S20: energy distribution profiles for C2H4 and C2H6 adsorption in zeolites ITQ-29 (A) and 5A (B) under 101 kPa at 298 K; Figure S21: diffusion coefficients for C2H4 and C2H6 at 298 K in zeolite 5A with different loadings; Figure S22: schematic of the region division of the slab; Figure S23: C2H4 uptakes in different regions of zeolites ITQ-29 (A) and 5A (B) during single-gas adsorption at 298 K; Figure S24: uptakes of C2H4 and C2H6 for mixtures (20:80 and 80:20) in zeolite 5A at 298 K; Figure S25: C2H4 (A) and C2H6 (B) uptakes in zeolite 5A with different coverages of MPA during single-gas adsorption at 298 K; Figure S26: C2H4 uptakes at 298 K in different regions of zeolite 5A with 50% coverage of MPA; Figure S27: front view (A) and top view (B) of adsorption structure of C2H6 molecules in zeolite ITQ-29. Table S1: atomic coordinates of zeolite ITQ-29; Table S2: atomic coordinates of zeolite 5A; Table S3: average Hirshfeld atomic charges of adsorbents derived from DFT calculations; Table S4: electrostatic energies (kJ/mol) and loadings (molecules/α-cage) of C2H4 and C2H6 in zeolite 5A at 298 K and 100 kPa with different charges; Table S5: average Hirshfeld atomic charges of adsorbates derived from DFT calculations; Table S6: adsorption energies of C2H6 molecules in zeolite ITQ-29 with different loadings; Table S7: adsorption energies of light hydrocarbons in zeolite 5A at zero surface coverage; Table S8: adsorption parameters of the Langmuir model* for C2H4 adsorption in zeolite 5A; Table S9: diffusion coefficients (m2/s) of C2H4 in zeolite 5A at different temperatures derived from simulations using different forcefields; Table S10: diffusion coefficients of C2H4 and C2H6 in zeolites ITQ-29 and 5A at different temperatures.

Author Contributions

Conceptualization, S.Z.; methodology, S.Z.; validation, M.A.E.; formal analysis, C.J.; investigation, X.Z.; data curation, X.Z.; writing—original draft preparation, X.Z.; writing—review and editing, S.Z., M.A.E., Z.C., Y.H., and G.W.M.; visualization, Z.C.; supervision, S.Z.; funding acquisition, S.Z. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by National Natural Science Foundation of China (No. 22478229).

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors on request.

Conflicts of Interest

The authors declare no conflicts of interest.

Abbreviations

The following abbreviations are used in this manuscript:
DFTDensity functional theory
MDMolecular dynamics
MPAMethyl phosphonic acid
DDiffusion coefficients

References

  1. Almuqati, N.S.; Aldawsari, A.M.; Alharbi, K.N.; González-Cortés, S.; Alotibi, M.F.; Alzaidi, F.; Dilworth, J.R.; Edwards, P.P. Catalytic production of light olefins: Perspective and prospective. Fuel 2024, 366, 131270. [Google Scholar] [CrossRef]
  2. Siracusa, V.; Blanco, I. Bio-polyethylene (Bio-PE), bio-polypropylene (Bio-PP) and bio-poly (ethylene terephthalate) (Bio-PET): Recent developments in bio-based polymers analogous to petroleum-derived ones for packaging and engineering applications. Polymers 2020, 12, 1641. [Google Scholar] [CrossRef] [PubMed]
  3. Amghizar, I.; Vandewalle, L.A.; Van Geem, K.M.; Marin, G.B. New trends in olefin production. Engineering 2017, 3, 171–178. [Google Scholar] [CrossRef]
  4. Zhao, Z.; Jiang, J.; Wang, F. An economic analysis of twenty light olefin production pathways. J. Energy Chem. 2021, 56, 193–202. [Google Scholar] [CrossRef]
  5. Bereciartua, P.J.; Cantín, Á.; Corma, A.; Jordá, J.L.; Palomino, M.; Rey, F.; Valencia, S.; Corcoran, E.W., Jr.; Kortunov, P.; Ravikovitch, P.I.; et al. Control of zeolite framework flexibility and pore topology for separation of ethane and ethylene. Science 2017, 358, 1068–1071. [Google Scholar] [CrossRef] [PubMed]
  6. Sholl, D.S.; Lively, R.P. Seven chemical separations to change the world. Nature 2016, 532, 435–437. [Google Scholar] [CrossRef]
  7. Ren, T.; Patel, M.; Blok, K. Olefins from conventional and heavy feedstocks: Energy use in steam cracking and alternative processes. Energy 2006, 31, 425–451. [Google Scholar] [CrossRef]
  8. Ruthven, D.M.; Reyes, S.C. Adsorptive separation of light olefins from paraffins. Microporous Mesoporous Mater. 2007, 104, 59–66. [Google Scholar] [CrossRef]
  9. Mersmann, A.; Fill, B.; Hartmann, R.; Maurer, S. The potential of energy saving by gas-phase adsorption processes. Chem. Eng. Technol. 2000, 23, 937–944. [Google Scholar] [CrossRef]
  10. Wang, B.; Li, Q.; Zhang, H.; Zhang, J.; Pan, Q.; Yan, W. Zeolites for the separation of ethylene, ethane, and ethyne. Front. Chem. Sci. Eng. 2024, 18, 108. [Google Scholar] [CrossRef]
  11. Sun, Z.; Shu, Q.; Zhang, Q.; Li, S.; Zhu, G.; Wang, C.; Zhang, J.; Li, H.; Huang, Z. A hydrothermal synthesis process of ZSM-5 zeolite for VOCs adsorption using desilication solution. Separations 2024, 11, 39. [Google Scholar] [CrossRef]
  12. Xing, J.; Jing, F.; Chu, W.; Sun, H.; Yu, L.; Zhang, H.; Luo, S. Improvement of adsorptive separation performance for C2H4/C2H6 mixture by CeO2 promoted CuCl/activated carbon adsorbents. Acta Phys.-Chim. Sin. 2015, 31, 2158–2164. [Google Scholar] [CrossRef]
  13. Sircai, S.; Golden, T.C.; Rao, M.B. Activated carbon for gas separation and storage. Carbon 1996, 34, 1–12. [Google Scholar] [CrossRef]
  14. Cadiau, A.; Adil, K.; Bhatt, P.M.; Belmabkhout, Y.; Eddaoudi, M. A metal-organic framework-based splitter for separating propylene from propane. Science 2016, 353, 137–140. [Google Scholar] [CrossRef] [PubMed]
  15. Zheng, S.; Xu, Y.; Yao, X.; Wang, C.; Liu, P.; Zhao, H.; Lu, J.; Ju, J. Efficient removal of tetracycline by metal-organic framework ZIF-67 and its mechanism. Separations 2024, 11, 63. [Google Scholar] [CrossRef]
  16. Kan, X.; Wang, J.; Dong, Y. COFs as porous organic materials for the separation and purification of ethylene from C2 hydrocarbons. Chem. Commun. 2024, 60, 13984–13997. [Google Scholar] [CrossRef] [PubMed]
  17. Cao, X.; Zhang, Z.; He, Y.; Xue, W.; Huang, H.; Zhong, C. Machine-learning-aided computational study of covalent organic frameworks for reversed C2H6/C2H4 separation. Ind. Eng. Chem. Res. 2022, 61, 11116–11123. [Google Scholar] [CrossRef]
  18. Zhang, X.; Li, L.; Wang, J.; Wen, H.; Krishna, R.; Wu, H.; Zhou, W.; Chen, Z.; Li, B.; Qin, G.; et al. Selective ethane/ethylene separation in a robust microporous hydrogen-bonded organic framework. J. Am. Chem. Soc. 2020, 142, 633–640. [Google Scholar] [CrossRef]
  19. Zhang, X.; Wang, J.; Li, L.; Pei, J.; Krishna, R.; Wu, H.; Zhou, W.; Qin, G.; Chen, B.; Li, B. A rod-packing hydrogen-bonded organic framework with suitable pore confinement for benchmark ethane/ethylene separation. Angew. Chem. Int. Ed. 2021, 60, 10304–10310. [Google Scholar] [CrossRef]
  20. Saha, D.; Kim, M.B.; Robinson, A.J.; Babarao, R.; Thallapally, P.K. Elucidating the mechanisms of paraffin-olefin separations using nanoporous adsorbents: An overview. iScience 2021, 24, 103042. [Google Scholar] [CrossRef]
  21. Li, J.; Corma, A.; Yu, J. Synthesis of new zeolite structures. Chem. Soc. Rev. 2015, 44, 7112–7127. [Google Scholar] [CrossRef]
  22. Feng, C.; E, J.; Han, W.; Deng, Y.; Zhang, B.; Zhao, X.; Han, D. Key technology and application analysis of zeolite adsorption for energy storage and heat-mass transfer process: A review. Renew. Sustain. Energy Rev. 2021, 144, 110954. [Google Scholar] [CrossRef]
  23. Khaleque, A.; Alam, M.M.; Hoque, M.; Mondal, S.; Haider, J.B.; Xu, B.; Johir, M.A.H.; Karmakar, A.K.; Zhou, J.L.; Ahmed, M.B.; et al. Zeolite synthesis from low-cost materials and environmental applications: A review. Environ. Adv. 2020, 2, 100019. [Google Scholar] [CrossRef]
  24. Treacy, M.M.J.; Foster, M.D. Packing sticky hard spheres into rigid zeolite framework. Microporous Mesoporous Mater. 2009, 118, 106–114. [Google Scholar] [CrossRef]
  25. Padin, J.; Rege, S.U.; Yang, R.T.; Cheng, L.S. Molecular sieve sorbents for kinetic separation of propane/propylene. Chem. Eng. Sci. 2000, 55, 4525–4535. [Google Scholar] [CrossRef]
  26. Liu, J.; Goss, J.; Calverley, T.; Liu, Y.; Broomall, C.; Kang, J.; Golombeski, R.; Anaya, D.; Moe, B.; Mabe, K.; et al. Carbon molecular sieve fiber with 3.4–4.9 angstrom effective micropores for propylene/propane and other gas separations. Microporous Mesoporous Mater. 2020, 305, 110341. [Google Scholar] [CrossRef]
  27. Rege, S.U.; Padin, J.; Yang, R.T. Olefin/paraffin separations by adsorption: π-complexation vs. kinetic separation. AIChE J. 1998, 44, 799–809. [Google Scholar] [CrossRef]
  28. Sala, A.; Pérez-Botella, E.; Jordá, J.L.; Cantin, A.; Rey, F.; Valencia, S. ITQ-69: A germanium-containing zeolite and its synthesis, structure determination, and adsorption properties. Angew. Chem. Int. Ed. 2021, 60, 11745–11750. [Google Scholar] [CrossRef]
  29. Chen, H.; Wang, B.; Zhang, B.; Ren, Y.; Chen, J.; Gui, J.; Shi, X.; Yan, W.; Li, J.; Li, L. Enhancing the separation of C2H4/C2H6 in customized MOR zeolites. Inorg. Chem. Front. 2024, 11, 2427–2435. [Google Scholar] [CrossRef]
  30. Baamran, K.; Moreno, J.D.L.; Rownaghi, A.A.; Rezaei, F. Kinetic assessment of light hydrocarbons separation over Fe-doped 13X composite sorbents under multicomponent feed conditions. Ind. Eng. Chem. Res. 2023, 62, 11917–11929. [Google Scholar] [CrossRef]
  31. Ellis, L.D.; Parker, S.T.; Hu, J.; Zaccarine, S.F.; Stellato, M.J.; Funke, H.H.; Sievers, C.; Pylypenko, S.; Falconer, J.L.; Medlin, J.W. Tuning gas adsorption selectivity and diffusion rates in zeolites with phosphonic acid monolayers. Cell Rep. Phys. Sci. 2020, 1, 100036. [Google Scholar] [CrossRef]
  32. Zhou, X.; Falconer, J.L.; Medlin, J.W. Organic-coated zeolites for selective gas adsorption: Effect of functional group identity and coating density. Sep. Purif. Technol. 2025, 363, 132040. [Google Scholar] [CrossRef]
  33. Abdelrasoul, A.; Zhang, H.; Cheng, C.; Doan, H. Applications of molecular simulations for separation and adsorption in zeolites. Microporous Mesoporous Mater. 2017, 242, 294–348. [Google Scholar] [CrossRef]
  34. Mitra, S.; Sharma, V.K.; Chaplot, S.L.; Mukhopadhyay, R. Diffusion of hydrocarbon in zeolite and effect due to pore topology: Neutron scattering and MD simulation studies. Chem. Phys. 2014, 430, 69–77. [Google Scholar] [CrossRef]
  35. Guo, C.; Guan, Z.; Zhou, J.; Tang, S.; Zhang, C.; Zhao, K. Molecular insights into improved oxygen adsorption: Ag+ and Ce3+ doping in Li-LSX for air separation. Appl. Surf. Sci. 2024, 663, 160186. [Google Scholar] [CrossRef]
  36. Liu, S.; Lian, X.; Yue, B.; Xu, S.; Wu, G.; Chai, Y.; Zhang, Y.; Li, L. Control of zeolite local polarity toward efficient xenon/krypton separation. J. Am. Chem. Soc. 2024, 146, 8335–8342. [Google Scholar] [CrossRef]
  37. Carey, T.; Corma, A.; Rey, F.; Tang, C.C.; Hriljac, J.A.; Anderson, P.A. The effect of extra framework species on the intrinsic negative thermal expansion property of zeolites with the LTA topology. Chem. Commun. 2012, 48, 5829–5831. [Google Scholar] [CrossRef]
  38. Seff, K.; Shoemaker, D.P. The structures of zeolite sorption complexes. I. The structures of dehydrated zeolite 5A and its iodine sorption complex. Acta Crystallogr. 1967, 22, 162–170. [Google Scholar] [CrossRef]
  39. Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
  40. Seminario, J.M. Energetics using DFT: Comparions to precise ab initio and experiment. Chem. Phys. Lett. 1993, 206, 547–554. [Google Scholar] [CrossRef]
  41. Ghosh, A.; Ma, L.; Gao, C. Zeolite molecular sieve 5A acts as a reinforcing filler, altering the morphological, mechanical, and thermal properties of chitosan. J. Mater. Sci. 2013, 48, 3926–3935. [Google Scholar] [CrossRef]
  42. Ozturk, Z. Hydrogen storage on lithium modified silica based chabazite type zeolite, A computational study. Int. J. Hydrogen Energy 2018, 43, 22365–22376. [Google Scholar] [CrossRef]
  43. Nam, G.M.; Jeong, B.M.; Kang, S.H.; Lee, B.K.; Choi, D.K. Equilibrium isotherms of CH4, C2H6, C2H4, N2, and H2 on zeolite 5A using a static volumetric method. J. Chem. Eng. Data 2005, 50, 72–76. [Google Scholar] [CrossRef]
  44. Gulianta, V.V.; Huth, A.J. Force fields for classical atomistic simulations of small gas molecules in silicalite-1 for energy-related gas separations at high temperatures. J. Porous Mater. 2013, 20, 741–751. [Google Scholar] [CrossRef]
  45. Luca, G.D.; Pullumbi, P.; Barbieri, G.; Famà, A.D.; Bernardo, P.; Drioli, E. Gusev and Suter calculation of the diffusion coefficients of light gases in silicalite-1 membrane and silica-sodalite zeolite. Sep. Purif. Technol. 2004, 36, 215–228. [Google Scholar] [CrossRef]
  46. Witte, N.D.; Robijins, S.; Denayer, J.F.M.; Dusselier, M.; Assche, T.R.C.V. Inverse gas chromatography study of n-alkane and 1-alkene adsorption on pure-silica LTA (ITQ-29) and CHA. J. Phys. Chem. C 2023, 127, 24393–24402. [Google Scholar] [CrossRef]
  47. Derrah, R.I.; Loughlin, K.F.; Ruthven, D.M. Sorption of ethylene, propylene and cyclopropane in 5A zeolite. J. Chem. Soc. 1972, 68, 1947–1955. [Google Scholar] [CrossRef]
  48. Bläker, C.; Mauer, V.; Pasel, C.; Dreisbach, F.; Bathen, D. Adsorption mechanisms of ethane, ethene and ethyne on calcium exchanged LTA and FAU zeolites. Adsorption 2024, 30, 1547–1564. [Google Scholar] [CrossRef]
  49. Ghosal, P.S.; Gupta, A.K. Determination of thermodynamic parameters from Langmuir isotherm constant-revisited. J. Mol. Liq. 2017, 225, 137–146. [Google Scholar] [CrossRef]
  50. Xu, Y.; Xu, J.; Yang, C. Molecule design of effective C2H4/C2H6 separation membranes: From 2D nanoporous graphene to 3D AHT zeolite. J. Membr. Sci. 2020, 604, 118033. [Google Scholar] [CrossRef]
  51. Foster, M.D.; Rivin, I.; Treacy, M.M.J.; Delgado Friedrichs, O. A geometric solution to the largest-free-sphere problem in zeolite framework. Microporous Mesoporous Mater. 2006, 90, 32–38. [Google Scholar] [CrossRef]
  52. Golipour, H.; Mokhtarani, B.; Mafi, M.; Moradi, A.; Godini, H.R. Experimental measurement for adsorption of ethylene and ethane gases on copper-exchanged zeolites 13X and 5A. J. Chem. Eng. Data 2020, 65, 3920–3932. [Google Scholar] [CrossRef]
  53. Zhou, X.; Falconer, J.L.; Medlin, J.W. Competitive adsorption between propylene and propane on zeolite 5A and the influence of organic phosphonic acid coatings. Sep. Purif. Technol. 2024, 346, 127435. [Google Scholar] [CrossRef]
  54. Li, X.; Yang, X.; Shang, H.; Liu, J.; Jin, X.; Wang, X.; Wang, Y.; Li, J.; Yang, J. Critical role of zeolite adsorbents in a displacement-adsorption separation process of methane-nitrogen gas. Ind. Eng. Chem. Res. 2025, 64, 2966–2976. [Google Scholar] [CrossRef]
  55. Zhou, X.; Falconer, J.L.; Medlin, J.W. Mechanism of selectivity control for zeolites modified with organic monolayers. Microporous Mesoporous Mater 2022, 337, 111913. [Google Scholar] [CrossRef]
Separations 12 00146 g001
Figure 1. Structural models and X-ray diffraction patterns of the zeolites ITQ-29 (A1,A2) and 5A (B1,B2). Spheres: yellow (Si), red (O), pink (Al), purple (Na), and green (Ca). The lattice parameters for zeolite ITQ-29 are a = b = c = 23.70 Å, and for zeolite 5A, a = b = c = 24.84 Å. The chemical formula of the structural model for zeolite ITQ-29 is Si192O384, and that for zeolite 5A is Ca32Na32Si96Al96O384.
Figure 1. Structural models and X-ray diffraction patterns of the zeolites ITQ-29 (A1,A2) and 5A (B1,B2). Spheres: yellow (Si), red (O), pink (Al), purple (Na), and green (Ca). The lattice parameters for zeolite ITQ-29 are a = b = c = 23.70 Å, and for zeolite 5A, a = b = c = 24.84 Å. The chemical formula of the structural model for zeolite ITQ-29 is Si192O384, and that for zeolite 5A is Ca32Na32Si96Al96O384.
Separations 12 00146 g001
Separations 12 00146 g002
Figure 2. Adsorption structures of C2H4 and C2H6 molecules in zeolites ITQ-29 (A1,A2) and 5A (B1,B2). Spheres: yellow (Si), red (O), pink (Al), green (Ca), gray (C), and white (H). Only the 6-membered rings near the adsorbate molecules in the zeolite cells are shown in the figure, and the distances between each C atom of the molecules and its proximal O atom in host 6-membered ring of zeolite ITQ-29 or 5A and the minimal distances between C and Ca atoms in zeolite 5A are shown.
Figure 2. Adsorption structures of C2H4 and C2H6 molecules in zeolites ITQ-29 (A1,A2) and 5A (B1,B2). Spheres: yellow (Si), red (O), pink (Al), green (Ca), gray (C), and white (H). Only the 6-membered rings near the adsorbate molecules in the zeolite cells are shown in the figure, and the distances between each C atom of the molecules and its proximal O atom in host 6-membered ring of zeolite ITQ-29 or 5A and the minimal distances between C and Ca atoms in zeolite 5A are shown.
Separations 12 00146 g002
Separations 12 00146 g003
Figure 3. Adsorption isotherms of C2H4 and C2H6 in zeolites ITQ-29 (A1,A2) and 5A (B1,B2) at different temperatures. The data points are from GCMC simulations, and the solid lines represents the fittings of the data using the Langmuir model.
Figure 3. Adsorption isotherms of C2H4 and C2H6 in zeolites ITQ-29 (A1,A2) and 5A (B1,B2) at different temperatures. The data points are from GCMC simulations, and the solid lines represents the fittings of the data using the Langmuir model.
Separations 12 00146 g003
Separations 12 00146 g004
Figure 4. Energy distribution profiles for C2H4 and C2H6 adsorption in zeolites ITQ-29 (A1,A2) and 5A (B1,B2) under 101 kPa at different temperatures. The y-axis represents the probability density, P (E) (a.u.), which is normalized to unity. More negative energies represent stronger adsorbent–adsorbate interactions.
Figure 4. Energy distribution profiles for C2H4 and C2H6 adsorption in zeolites ITQ-29 (A1,A2) and 5A (B1,B2) under 101 kPa at different temperatures. The y-axis represents the probability density, P (E) (a.u.), which is normalized to unity. More negative energies represent stronger adsorbent–adsorbate interactions.
Separations 12 00146 g004
Separations 12 00146 g005
Figure 5. Arrhenius plots of ln D versus 1/T for C2H4 and C2H6 in zeolites ITQ-29 (A) and 5A (B). The data points are derived from simulations, and the dashed line represents the linear fit of the data. The linear fittings yield high adj.−R2 values, indicating a strong correlation between the ln D and 1/T. The activation energy Ea equals the slope of the fitted line multiplied by the negative value of the universal gas constant.
Figure 5. Arrhenius plots of ln D versus 1/T for C2H4 and C2H6 in zeolites ITQ-29 (A) and 5A (B). The data points are derived from simulations, and the dashed line represents the linear fit of the data. The linear fittings yield high adj.−R2 values, indicating a strong correlation between the ln D and 1/T. The activation energy Ea equals the slope of the fitted line multiplied by the negative value of the universal gas constant.
Separations 12 00146 g005
Separations 12 00146 g006
Figure 6. Uptakes of C2H4 and C2H6 in zeolites ITQ-29 (A) and 5A (B) during single-gas adsorption at 298 K. In the simulation, initially there are 100 C2H4 or C2H6 molecules in the gas reservoir of the supercell surface model before adsorption starts. Following the simulation, the molecules that enter the solid slab are counted as uptake. At 5 ns, the ideal selectivity (uptake ratio) of C2H4/C2H6 in zeolite ITQ-29 is 43.2, and that in zeolite 5A is 1.11.
Figure 6. Uptakes of C2H4 and C2H6 in zeolites ITQ-29 (A) and 5A (B) during single-gas adsorption at 298 K. In the simulation, initially there are 100 C2H4 or C2H6 molecules in the gas reservoir of the supercell surface model before adsorption starts. Following the simulation, the molecules that enter the solid slab are counted as uptake. At 5 ns, the ideal selectivity (uptake ratio) of C2H4/C2H6 in zeolite ITQ-29 is 43.2, and that in zeolite 5A is 1.11.
Separations 12 00146 g006
Separations 12 00146 g007
Figure 7. Uptakes of C2H4 and C2H6 in zeolite 5A during equimolar binary mixture adsorption at 298 K. In the simulation, initially there are 100 C2H4 and 100 C2H6 molecules in the reservoir of the supercell surface model before the adsorption starts. Following the simulation, the molecules that enter the solid slab are counted as uptake. At 5 ns, the C2H4/C2H6 adsorption selectivity in zeolite 5A is 2.72 for the equimolar binary mixture.
Figure 7. Uptakes of C2H4 and C2H6 in zeolite 5A during equimolar binary mixture adsorption at 298 K. In the simulation, initially there are 100 C2H4 and 100 C2H6 molecules in the reservoir of the supercell surface model before the adsorption starts. Following the simulation, the molecules that enter the solid slab are counted as uptake. At 5 ns, the C2H4/C2H6 adsorption selectivity in zeolite 5A is 2.72 for the equimolar binary mixture.
Separations 12 00146 g007
Separations 12 00146 g008
Figure 8. Uptakes of C2H4 and C2H6 in zeolite 5A during displacement adsorption at 298 K. In the simulation, initially there are 100 C2H6 molecules in the slab and 100 C2H4 molecules in the gas reservoir of the supercell surface model (A) or 100 C2H4 molecules in the slab and 100 C2H6 molecules in the gas reservoir (B) before the adsorption starts. Following the simulation, the molecules in the gas reservoir may displace the molecules pre-adsorbed in the solid slab.
Figure 8. Uptakes of C2H4 and C2H6 in zeolite 5A during displacement adsorption at 298 K. In the simulation, initially there are 100 C2H6 molecules in the slab and 100 C2H4 molecules in the gas reservoir of the supercell surface model (A) or 100 C2H4 molecules in the slab and 100 C2H6 molecules in the gas reservoir (B) before the adsorption starts. Following the simulation, the molecules in the gas reservoir may displace the molecules pre-adsorbed in the solid slab.
Separations 12 00146 g008
Separations 12 00146 g009
Figure 9. Uptakes of C2H4 and C2H6 in zeolite 5A with different coverages of MPA in single-gas adsorption at 5 ns and 298 K.
Figure 9. Uptakes of C2H4 and C2H6 in zeolite 5A with different coverages of MPA in single-gas adsorption at 5 ns and 298 K.
Separations 12 00146 g009
Separations 12 00146 g010
Figure 10. Uptakes of C2H4 and C2H6 in zeolite 5A with 50% coverage of MPA during equimolar binary mixture adsorption at 298 K. In the simulation, initially there are 100 C2H4 and 100 C2H6 molecules in the reservoir of the supercell surface model before the adsorption starts. At 5 ns, the C2H4/C2H6 adsorption selectivity in zeolite 5A with 50% coverage of MPA is 17.5 for the equimolar binary mixture.
Figure 10. Uptakes of C2H4 and C2H6 in zeolite 5A with 50% coverage of MPA during equimolar binary mixture adsorption at 298 K. In the simulation, initially there are 100 C2H4 and 100 C2H6 molecules in the reservoir of the supercell surface model before the adsorption starts. At 5 ns, the C2H4/C2H6 adsorption selectivity in zeolite 5A with 50% coverage of MPA is 17.5 for the equimolar binary mixture.
Separations 12 00146 g010
Separations 12 00146 g011
Figure 11. Uptakes of C2H4 and C2H6 in zeolite 5A with 50% coverage of MPA during displacement adsorption at 298 K. In the simulation, initially there are 100 C2H6 molecules in the slab and 100 C2H4 molecules in the gas reservoir (A) or 100 C2H4 molecules in the slab and 100 C2H6 molecules in the gas reservoir (B) before the adsorption starts.
Figure 11. Uptakes of C2H4 and C2H6 in zeolite 5A with 50% coverage of MPA during displacement adsorption at 298 K. In the simulation, initially there are 100 C2H6 molecules in the slab and 100 C2H4 molecules in the gas reservoir (A) or 100 C2H4 molecules in the slab and 100 C2H6 molecules in the gas reservoir (B) before the adsorption starts.
Separations 12 00146 g011
Table 1. Adsorption energies/enthalpies of C2H4 and C2H6 in zeolites ITQ-29 and 5A.
Table 1. Adsorption energies/enthalpies of C2H4 and C2H6 in zeolites ITQ-29 and 5A.
AdsorbentAdsorbateAdsorption Energy/Enthalpy (kJ/mol)Source
ITQ-29C2H4−27.7This work
ITQ-29C2H6−21.5This work
5AC2H4−45.6This work
5AC2H6−32.3This work
ITQ-29C2H4−25.7[46]
ITQ-29C2H6−23.0[46]
5AC2H4−33.5[47]
5AC2H6−27.6[47]
5AC2H4−59.0[48]
5AC2H6−37.0[48]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Zhao, X.; Zhou, S.; Elsayed, M.A.; Chen, Z.; Jiang, C.; Hu, Y.; Manggada, G.W. Insights into the Adsorptive Separation of Ethylene/Ethane in LTA-Type Zeolites. Separations 2025, 12, 146. https://doi.org/10.3390/separations12060146

AMA Style

Zhao X, Zhou S, Elsayed MA, Chen Z, Jiang C, Hu Y, Manggada GW. Insights into the Adsorptive Separation of Ethylene/Ethane in LTA-Type Zeolites. Separations. 2025; 12(6):146. https://doi.org/10.3390/separations12060146

Chicago/Turabian Style

Zhao, Xiaohui, Shixue Zhou, Magdy Abdelghany Elsayed, Zhongyuan Chen, Chunhui Jiang, Yongli Hu, and Gumawa Windu Manggada. 2025. "Insights into the Adsorptive Separation of Ethylene/Ethane in LTA-Type Zeolites" Separations 12, no. 6: 146. https://doi.org/10.3390/separations12060146

APA Style

Zhao, X., Zhou, S., Elsayed, M. A., Chen, Z., Jiang, C., Hu, Y., & Manggada, G. W. (2025). Insights into the Adsorptive Separation of Ethylene/Ethane in LTA-Type Zeolites. Separations, 12(6), 146. https://doi.org/10.3390/separations12060146

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop