Influence of the Filtration Velocity on the Local Oil Distribution of Oleophilic Coalescence Filter Media
Abstract
1. Introduction
2. Material and Methods
2.1. Thin Porous Filter Media
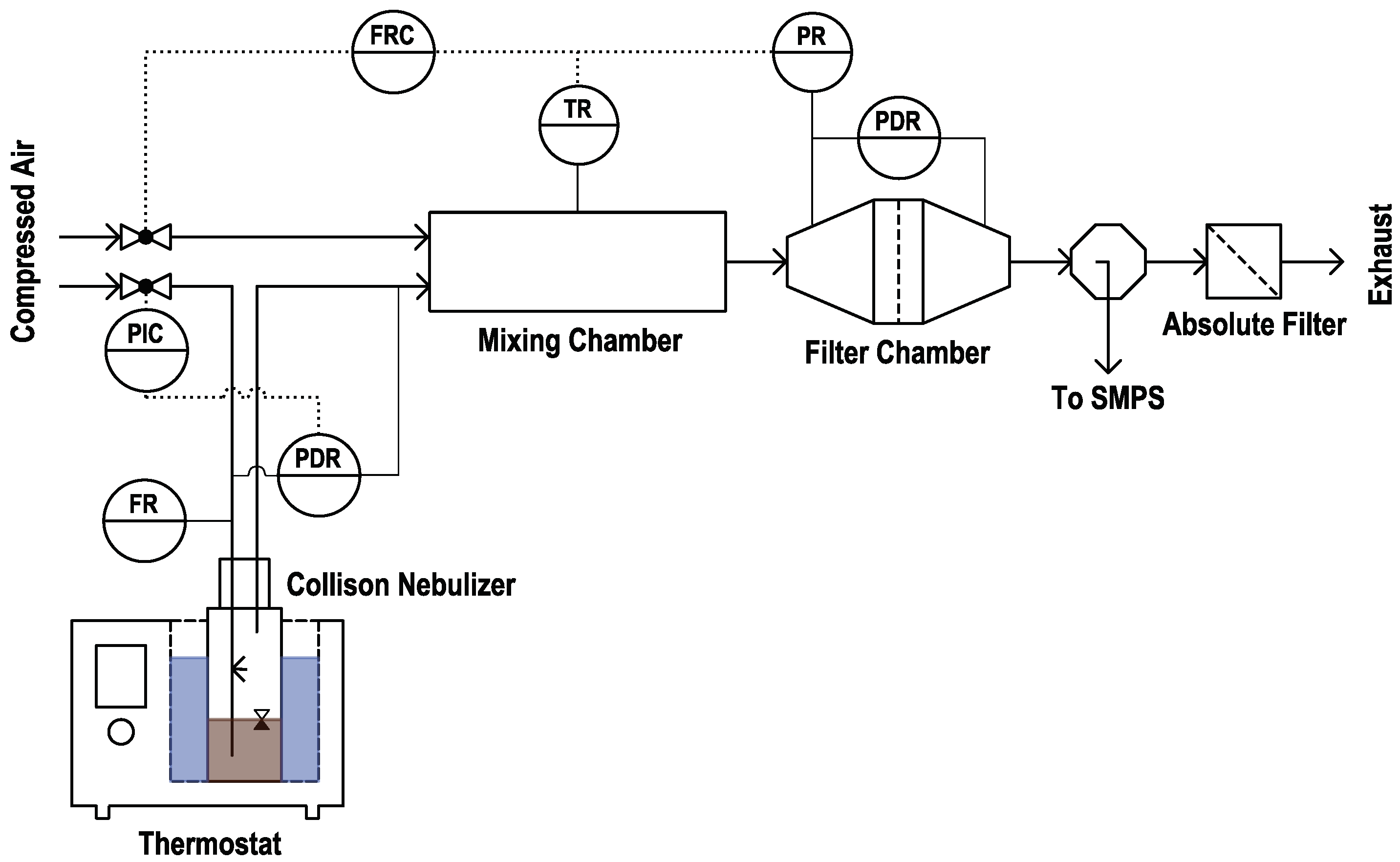
2.2. Experimental Set-Up
2.3. µ-CT Scanning
2.4. Segmentation of the µ-CT Scan
3. Results and Discussion
3.1. Local Porosity and Saturation
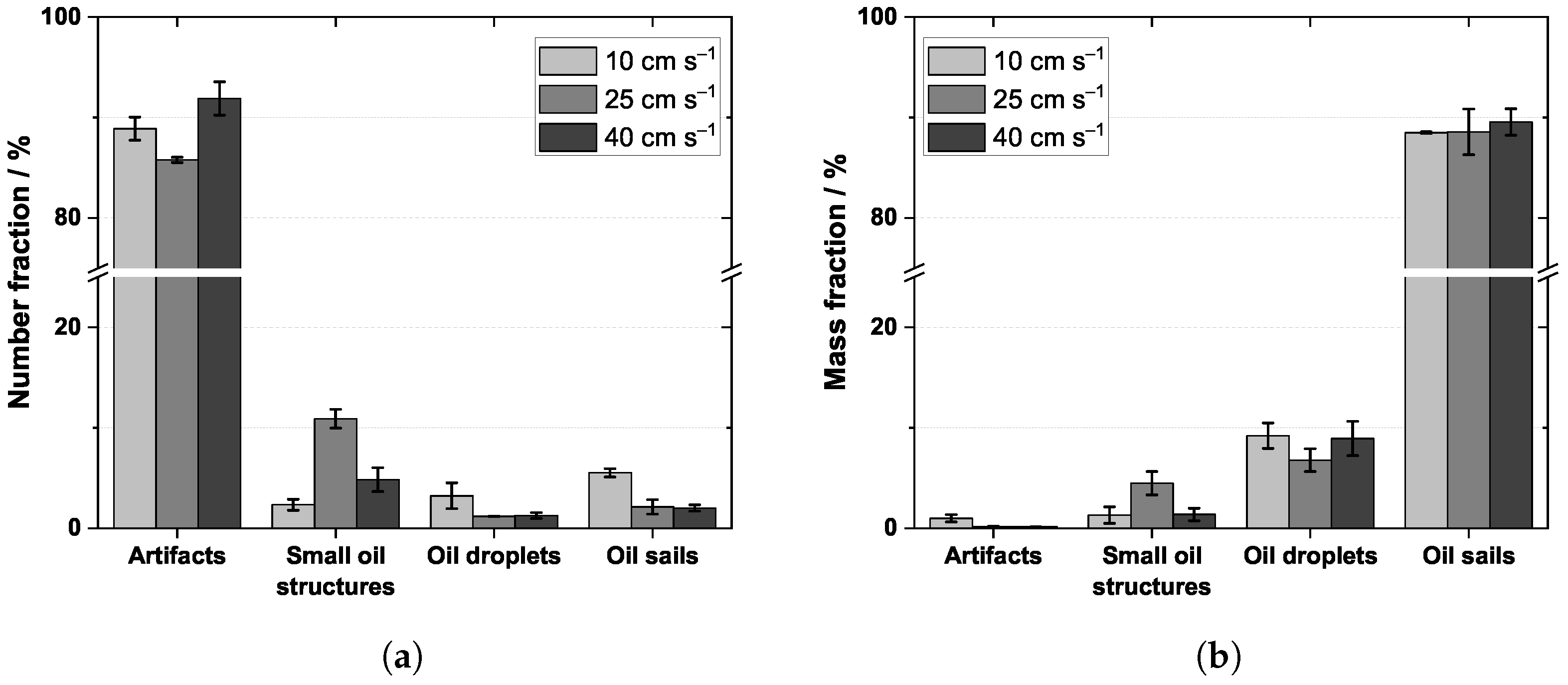
3.2. Identification of Deposited Oil Structures
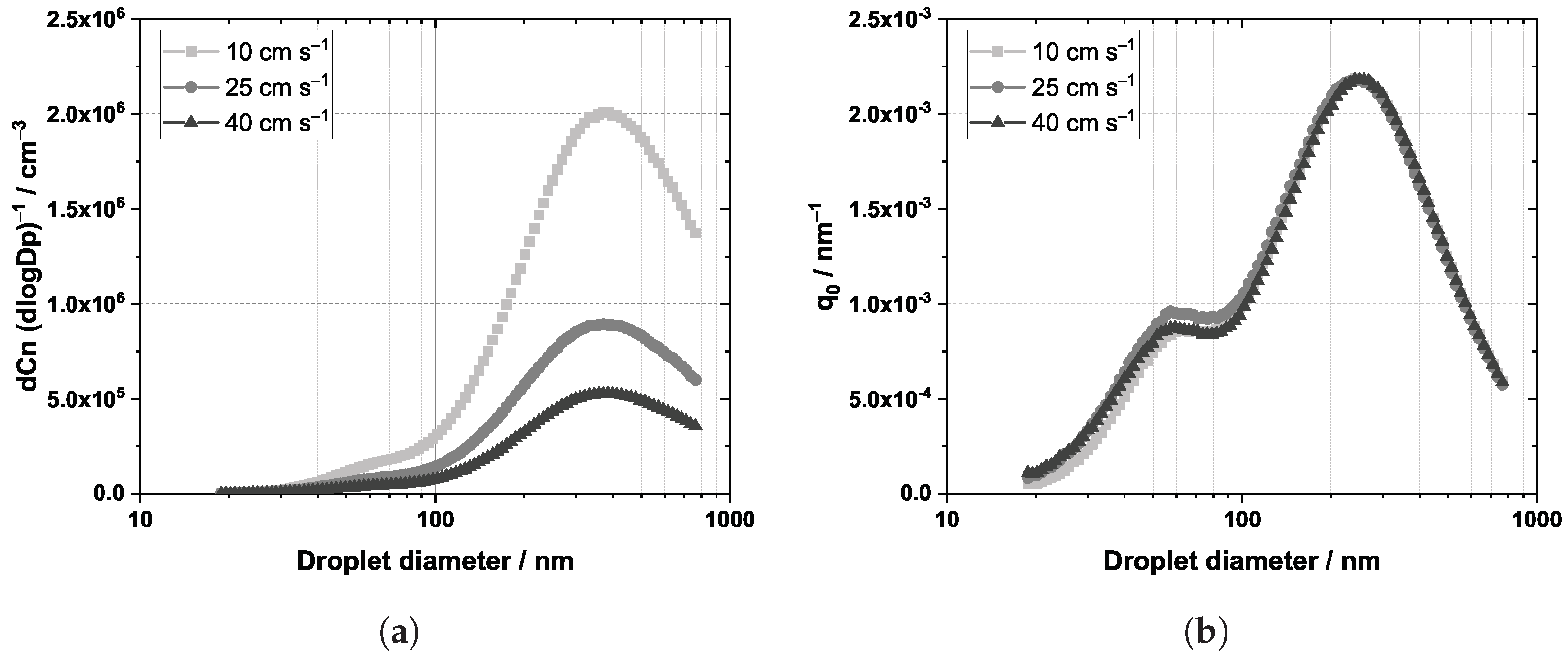
3.3. Oil Droplet Concentrations and Distributions
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| FOV | Field of view |
| µ-CT | X-ray microtomography |
| PET | Polyethylene terephthalate |
References
- Mead-Hunter, R.; King, A.J.; Mullins, B.J. Aerosol-mist coalescing filters—A review. Sep. Purif. Technol. 2014, 133, 484–506. [Google Scholar] [CrossRef]
- Kazerouni, N.; Thomas, T.L.; Petralia, S.A.; Hayes, R.B. Mortality among workers exposed to cutting oil mist: Update of previous reports. Am. J. Ind. Med. 2000, 38, 410–416. [Google Scholar] [CrossRef] [PubMed]
- Penner, T.; Meyer, J.; Kasper, G.; Dittler, A. Impact of operating conditions on the evolution of droplet penetration in oil mist filters. Sep. Purif. Technol. 2019, 211, 697–703. [Google Scholar] [CrossRef]
- Straube, C.; Yang, G.; Voll, D.; Meyer, J.; Théato, P.; Dittler, A. Influence of 3D printed downstream support structures on pressure drop and entrainment of oleophilic and oleophobic oil mist filters. Sep. Purif. Technol. 2022, 290, 120802. [Google Scholar] [CrossRef]
- Agranovski, I.E.; Braddock, R.D.; Crozier, S.; Whittaker, A.; Minty, S.; Myojo, T. Study of wet porous filtration. Sep. Purif. Technol. 2003, 30, 129–137. [Google Scholar] [CrossRef]
- Kampa, D.; Wurster, S.; Buzengeiger, J.; Meyer, J.; Kasper, G. Pressure drop and liquid transport through coalescence filter media used for oil mist filtration. Int. J. Multiph. Flow 2014, 58, 313–324. [Google Scholar] [CrossRef]
- Kampa, D.; Wurster, S.; Meyer, J.; Kasper, G. Validation of a new phenomenological “jump-and-channel” model for the wet pressure drop of oil mist filters. Chem. Eng. Sci. 2015, 122, 150–160. [Google Scholar] [CrossRef]
- Frising, T.; Thomas, D.; Bémer, D.; Contal, P. Clogging of fibrous filters by liquid aerosol particles: Experimental and phenomenological modelling study. Chem. Eng. Sci. 2005, 60, 2751–2762. [Google Scholar] [CrossRef]
- Charvet, A.; Gonthier, Y.; Gonze, E.; Bernis, A. Experimental and modelled efficiencies during the filtration of a liquid aerosol with a fibrous medium. Chem. Eng. Sci. 2010, 65, 1875–1886. [Google Scholar] [CrossRef]
- Contal, P.; Simao, J.; Thomas, D.; Frising, T.; Callé, S.; Appert-Collin, J.; Bémer, D. Clogging of fibre filters by submicron droplets. Phenomena and influence of operating conditions. J. Aerosol Sci. 2004, 35, 263–278. [Google Scholar] [CrossRef]
- Kolb, H.E.; Schmitt, R.; Dittler, A.; Kasper, G. On the accuracy of capillary flow porometry for fibrous filter media. Sep. Purif. Technol. 2018, 199, 198–205. [Google Scholar] [CrossRef]
- Kolb, E.; Kasper, G. On the functioning of coalescence filters with a drainage layer—A comment on several papers by Chang et al. Sep. Purif. Technol. 2019, 225, 54–59. [Google Scholar] [CrossRef]
- Penner, T.; Meyer, J.; Dittler, A. Oleophilic and oleophobic media combinations—Influence on oil mist filter operating performance. Sep. Purif. Technol. 2021, 261, 118255. [Google Scholar] [CrossRef]
- Penner, T.; Meyer, J.; Dittler, A. Characterization of mesoscale inhomogeneity in nonwovens and its relevance in the filtration of fine mists. J. Aerosol Sci. 2021, 151, 105674. [Google Scholar] [CrossRef]
- Azarafza, A.; King, A.; Mead-Hunter, R.; Schuler, J.; Abishek, S.; Mullins, B.J. The influence of layer separation on multilayer mist coalescing filter performance. Sep. Purif. Technol. 2021, 273, 118752. [Google Scholar] [CrossRef]
- Kolb, H.E.; Kasper, G. Mist filters: How steady is their “steady state”? Chem. Eng. Sci. 2019, 204, 118–127. [Google Scholar] [CrossRef]
- Conder, J.R.; Liew, T.P. Fine mist filtration by wet filters—II: Efficiency of fibrous filters. J. Aerosol Sci. 1989, 20, 45–57. [Google Scholar] [CrossRef]
- Davies, C.N. Filtration of aerosols. J. Aerosol Sci. 1983, 14, 147–161. [Google Scholar] [CrossRef]
- Raynor, P.C.; Leith, D. The Influence of Accumulated Liquid on Fibrous Filter Performance. J. Aerosol Sci. 2000, 31, 19–34. [Google Scholar] [CrossRef]
- Gougeon, R.; Boulaud, D.; Renoux, A. 15.P.01 Theoretical and experimental study of fibrous filters loading with liquid aerosols in the inertial regime. J. Aerosol Sci. 1994, 25, 189–190. [Google Scholar] [CrossRef]
- Payet, S.; Boulaud, D.; Madelaine, G.; Renoux, A. Penetration and pressure drop of a HEPA filter during loading with submicron liquid particles. J. Aerosol Sci. 1992, 23, 723–735. [Google Scholar] [CrossRef]
- Mullins, B.J.; Braddock, R.D.; Agranovski, I.E.; Cropp, R.A.; O’Leary, R.A. Observation and modelling of clamshell droplets on vertical fibres subjected to gravitational and drag forces. J. Colloid Interface Sci. 2005, 284, 245–254. [Google Scholar] [CrossRef]
- Mullins, B.J.; Braddock, R.D.; Agranovski, I.E.; Cropp, R.A. Observation and modelling of barrel droplets on vertical fibres subjected to gravitational and drag forces. J. Colloid Interface Sci. 2006, 300, 704–712. [Google Scholar] [CrossRef]
- Straube, C.; Meyer, J.; Dittler, A. Investigation of the local oil distribution on oleophilic mist filters applying X-ray micro-computed tomography. Sep. Purif. Technol. 2023, 311, 123279. [Google Scholar] [CrossRef]
- Charvet, A.; Du Rolland Roscoat, S.; Peralba, M.; Bloch, J.F.; Gonthier, Y. Contribution of synchrotron X-ray holotomography to the understanding of liquid distribution in a medium during liquid aerosol filtration. Chem. Eng. Sci. 2011, 66, 624–631. [Google Scholar] [CrossRef]
- Chaudhuri, J.; Boettcher, K.; Ehrhard, P. Optical investigations into wetted commercial coalescence filter using 3D micro-computer-tomography. Chem. Eng. Sci. 2022, 248, 117096. [Google Scholar] [CrossRef]
- Agranovski, I.E.; Myojo, T.; Braddock, R.D.; Jarvis, D. Combined Wettable/Non-wettable Filter for Mist Purification. Chem. Eng. Technol. 2001, 24, 287–292. [Google Scholar] [CrossRef]
- Charvet, A.; Gonthier, Y.; Bernis, A.; Gonze, E. Filtration of liquid aerosols with a horizontal fibrous filter. Chem. Eng. Res. Des. 2008, 86, 569–576. [Google Scholar] [CrossRef]
- Straube, C.; Meyer, J.; Dittler, A. Identification of Deposited Oil Structures on Thin Porous Oil Mist Filter Media Applying µ-CT Imaging Technique. Separations 2021, 8, 193. [Google Scholar] [CrossRef]
- Latief, F.D.E.; Fauzi, U.; Irayani, Z.; Dougherty, G. The effect of X-ray micro computed tomography image resolution on flow properties of porous rocks. J. Microsc. 2017, 266, 69–88. [Google Scholar] [CrossRef]
- Mead-Hunter, R.; Mullins, B.J.; Becker, T.; Braddock, R.D. Evaluation of the force required to move a coalesced liquid droplet along a fiber. Langmuir: ACS J. Surf. Colloids 2011, 27, 227–232. [Google Scholar] [CrossRef] [PubMed]
- Patel, S.U.; Kulkarni, P.S.; Patel, S.U.; Chase, G.G. The effect of surface energy of woven drainage channels in coalescing filters. Sep. Purif. Technol. 2012, 87, 54–61. [Google Scholar] [CrossRef]
- Fang, J.; Davoudi, M.; Chase, G.G. Drop movement along a fiber axis due to pressure driven air flow in a thin slit. Sep. Purif. Technol. 2015, 140, 77–83. [Google Scholar] [CrossRef]

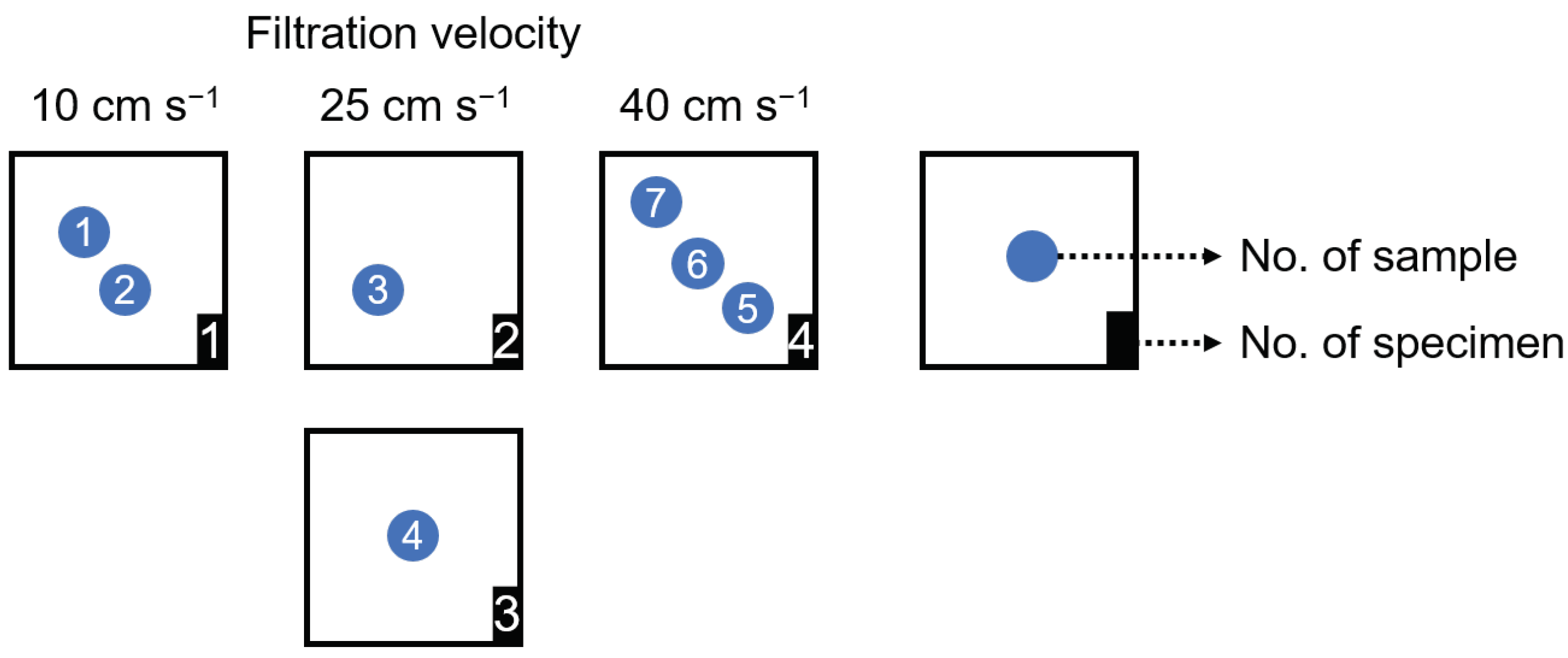


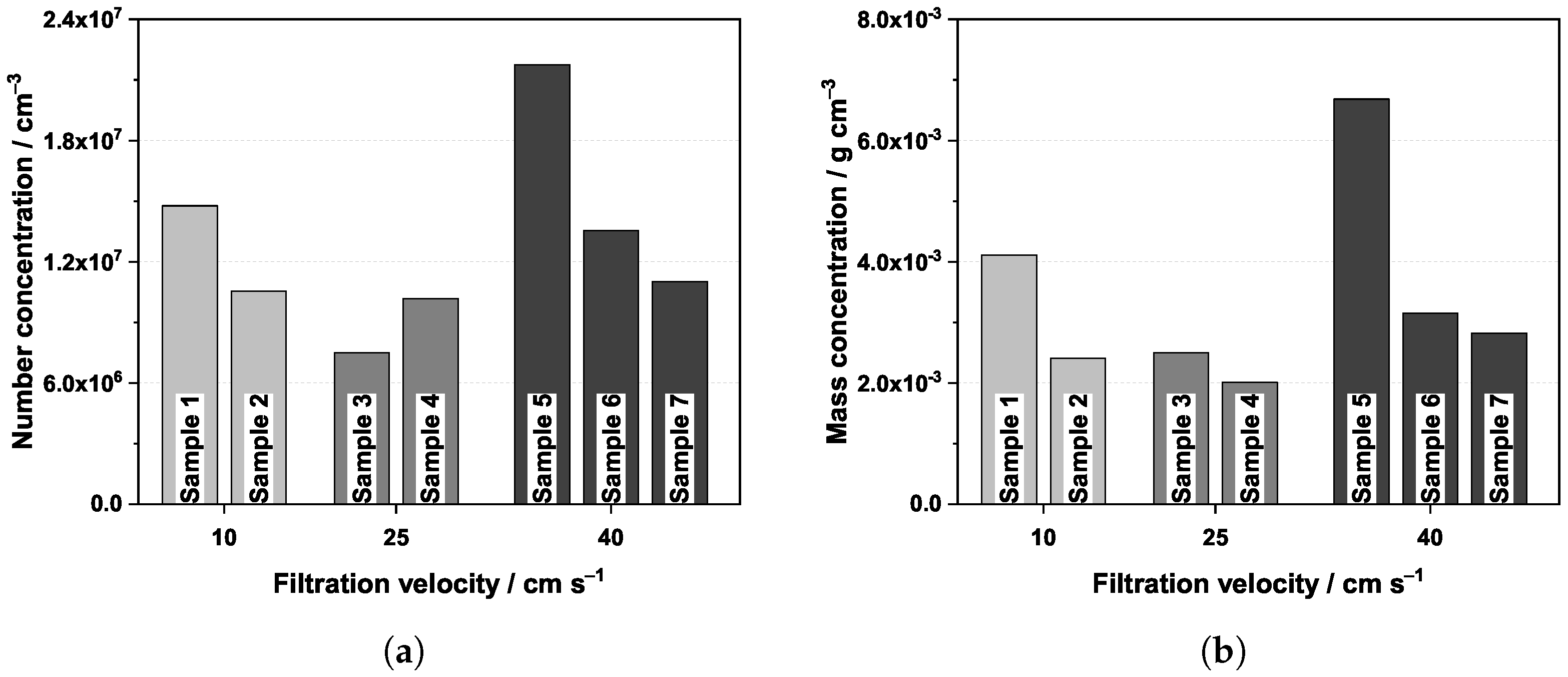
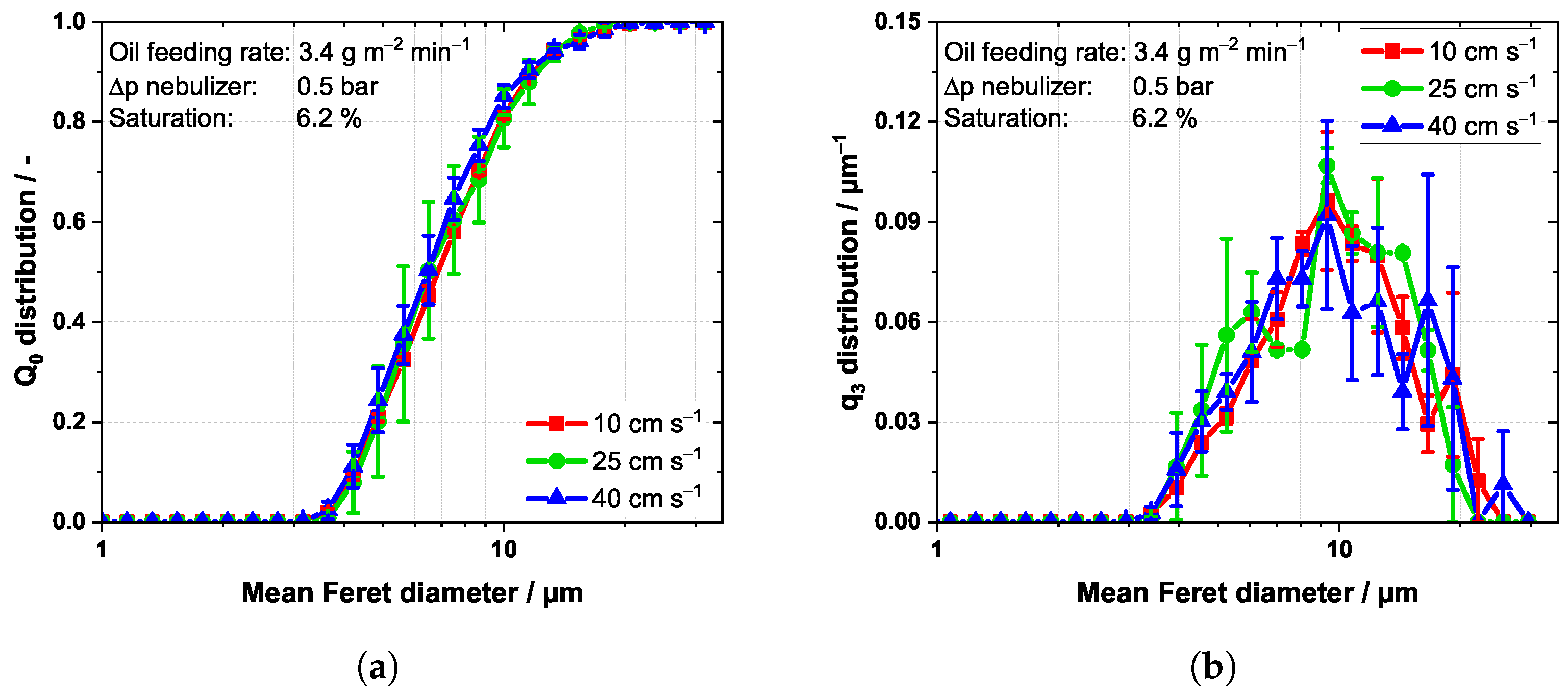
| Sample | Binning | Flow Velocity | Pixel Size | Local Porosity | Local Saturation |
|---|---|---|---|---|---|
| [-] | [-] | [cm s] | [nm] | [%] | [%] |
| 1 | 2 | 10 | 399.2 | 95.0 | 4.0 |
| 2 | 2 | 10 | 399.2 | 97.7 | 3.0 |
| 3 | 1 | 25 | 193.5 | 97.1 | 2.5 |
| 4 | 1 | 25 | 186.7 | 96.7 | 3.7 |
| 5 | 1 | 40 | 186.6 | 96.9 | 5.8 |
| 6 | 1 | 40 | 186.6 | 96.1 | 4.3 |
| 7 | 1 | 40 | 186.6 | 97.0 | 3.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Straube, C.; Meyer, J.; Dittler, A. Influence of the Filtration Velocity on the Local Oil Distribution of Oleophilic Coalescence Filter Media. Separations 2023, 10, 254. https://doi.org/10.3390/separations10040254
Straube C, Meyer J, Dittler A. Influence of the Filtration Velocity on the Local Oil Distribution of Oleophilic Coalescence Filter Media. Separations. 2023; 10(4):254. https://doi.org/10.3390/separations10040254
Chicago/Turabian StyleStraube, Christian, Jörg Meyer, and Achim Dittler. 2023. "Influence of the Filtration Velocity on the Local Oil Distribution of Oleophilic Coalescence Filter Media" Separations 10, no. 4: 254. https://doi.org/10.3390/separations10040254
APA StyleStraube, C., Meyer, J., & Dittler, A. (2023). Influence of the Filtration Velocity on the Local Oil Distribution of Oleophilic Coalescence Filter Media. Separations, 10(4), 254. https://doi.org/10.3390/separations10040254






