Experimental Investigations of the Detachment of Different Particle Structures from a Magnetizable Fiber in the Gas Phase
Abstract
:1. Introduction
2. Materials and Methods
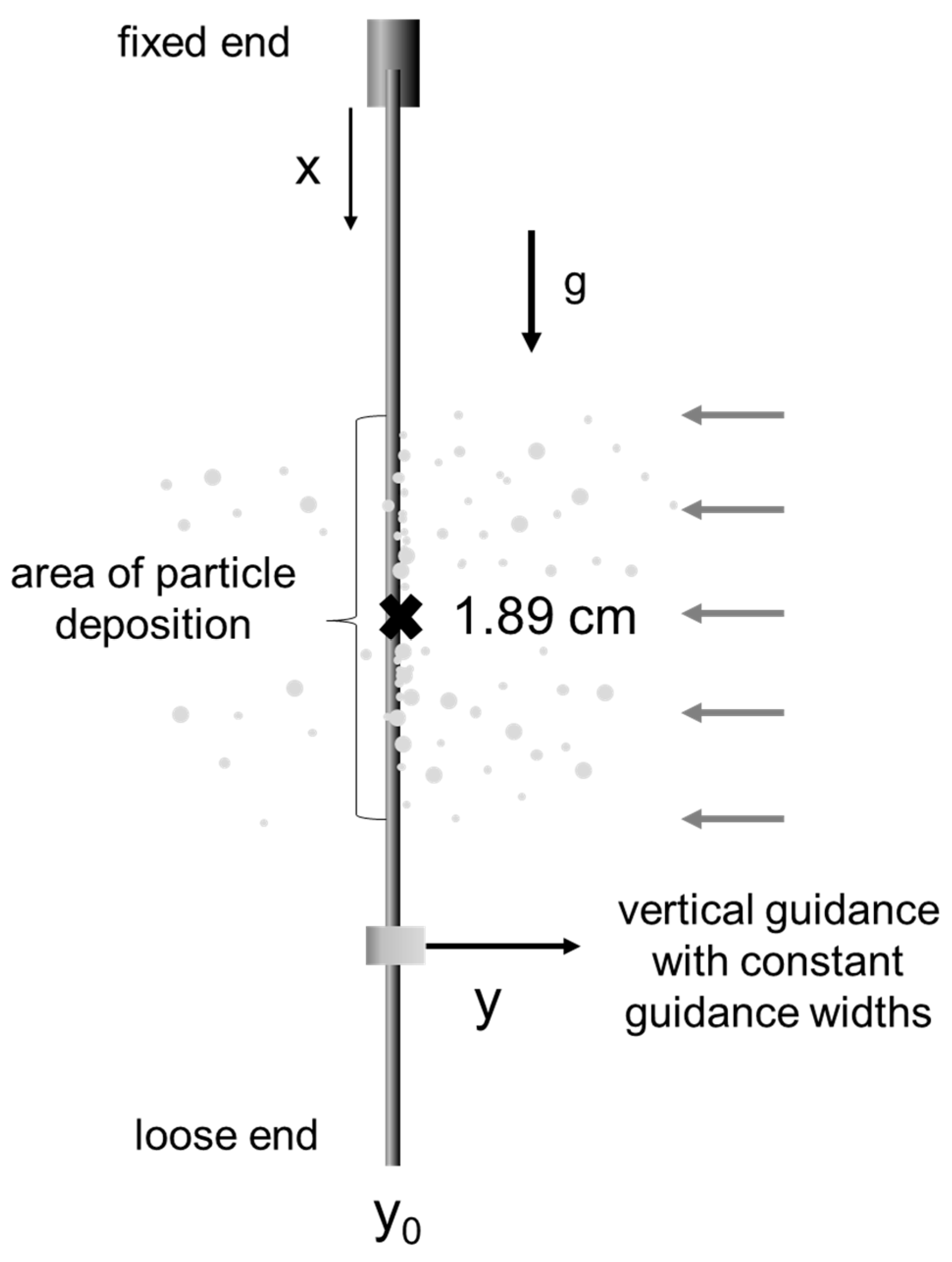
2.1. Fiber
2.2. Particulate Matter
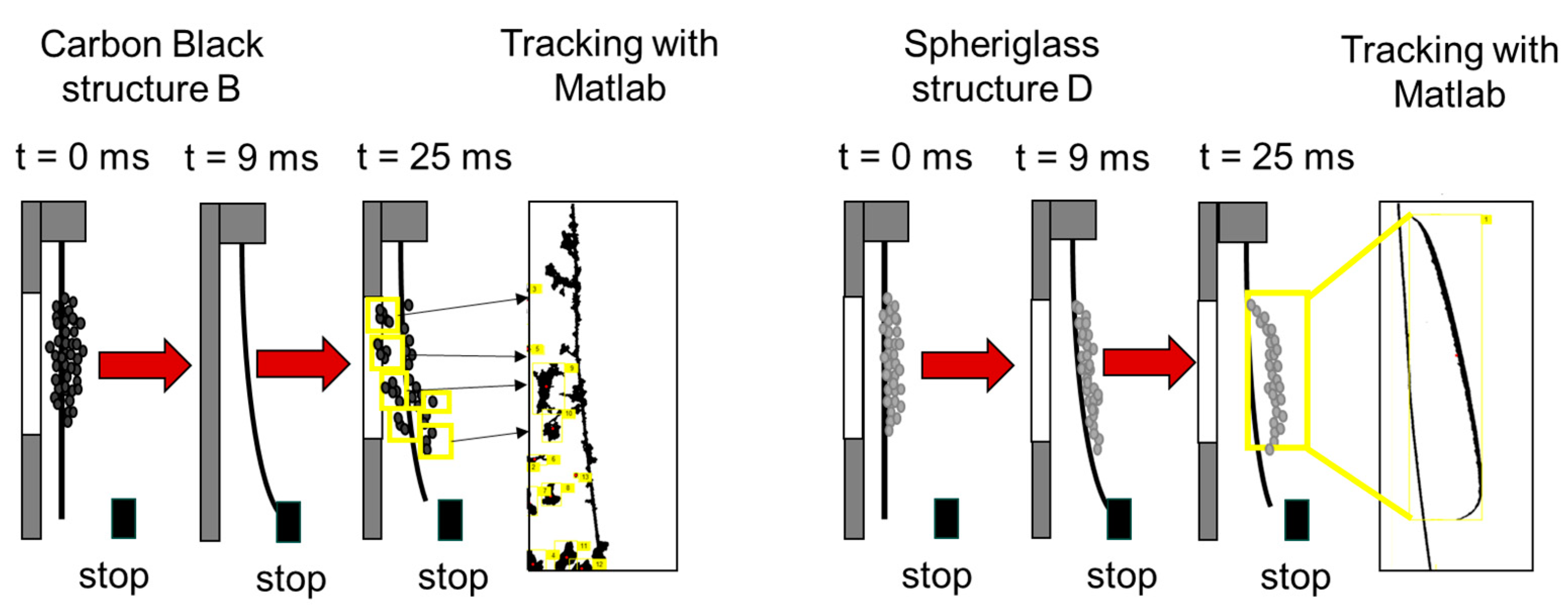
2.3. Particle Deposition and Magnetic-Induced Detachment
- The particle structure was generated on the fiber with a steady-state flow.
- The external magnetic field was switched on and the fiber was magnetized and deflected. Regeneration was performed both with and without additional flow.
- The magnetic field was switched off.
- The regeneration (step 2–3) was repeated two more times.
2.4. Investigated Particle Structures on a Single Fiber
2.5. Determination of the Degree of Regeneration
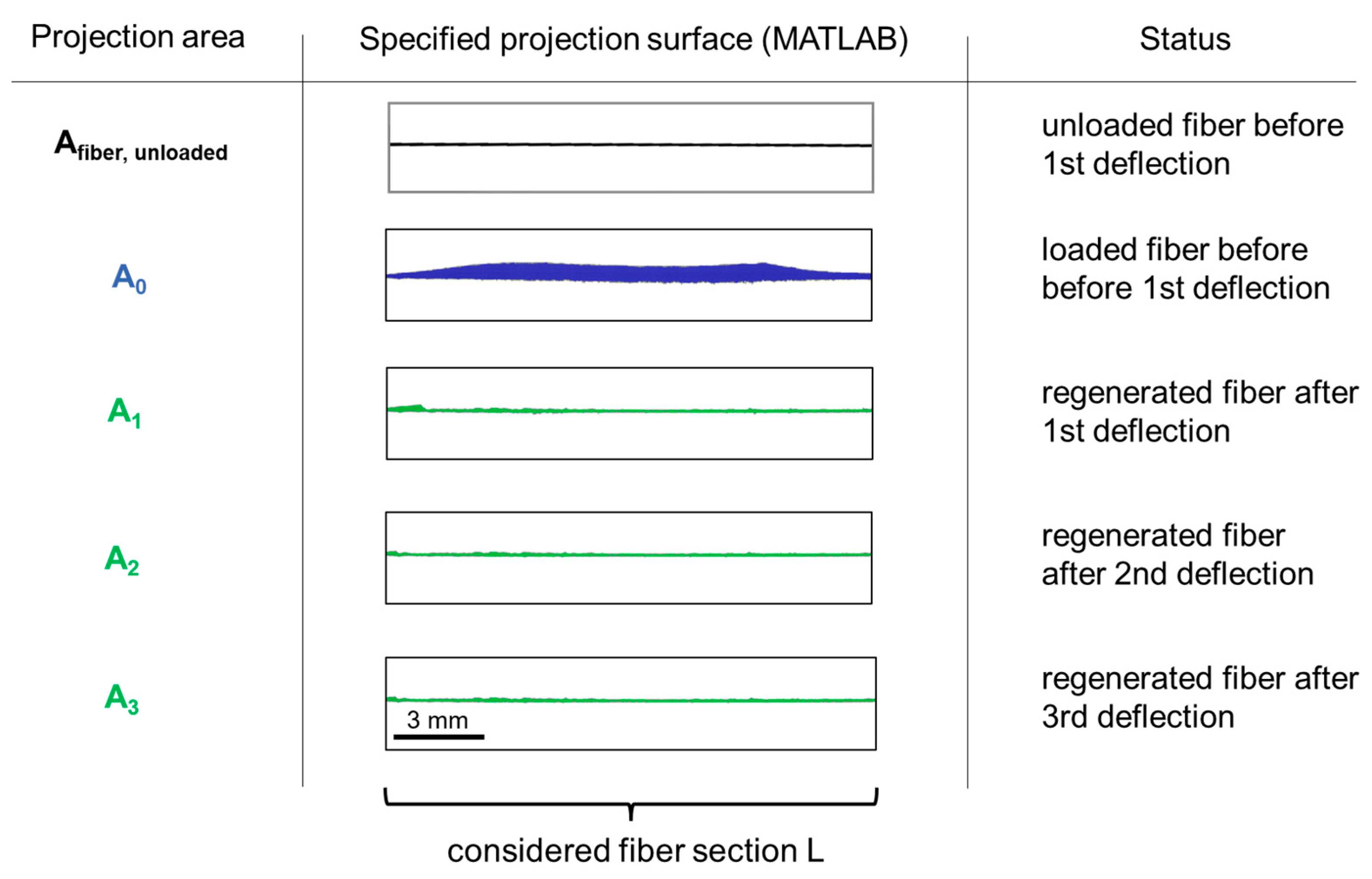
2.6. Determination of the Projection Area of Detached Agglomerates
2.7. Determination of the Acceleration for Particle Detachment
3. Results
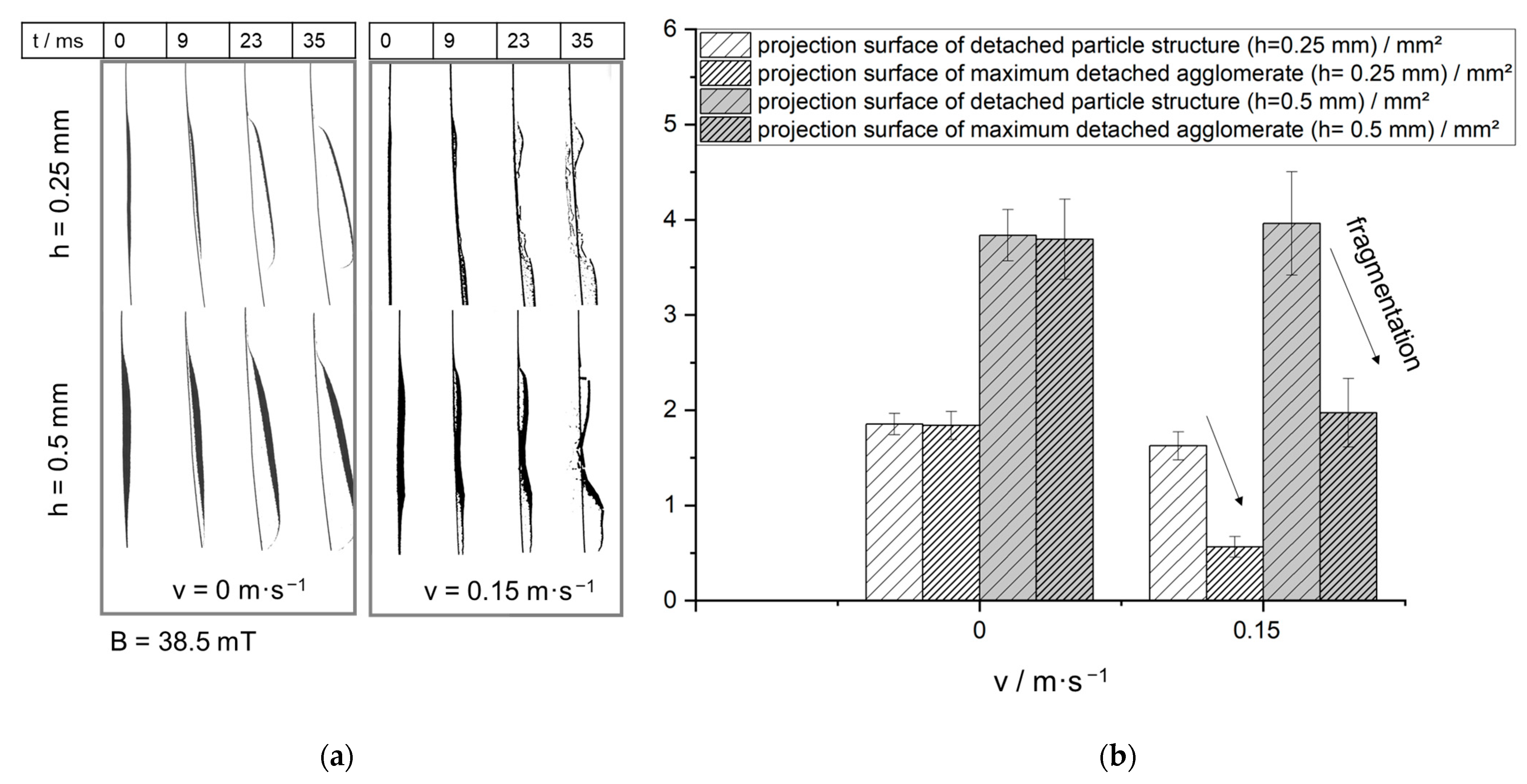
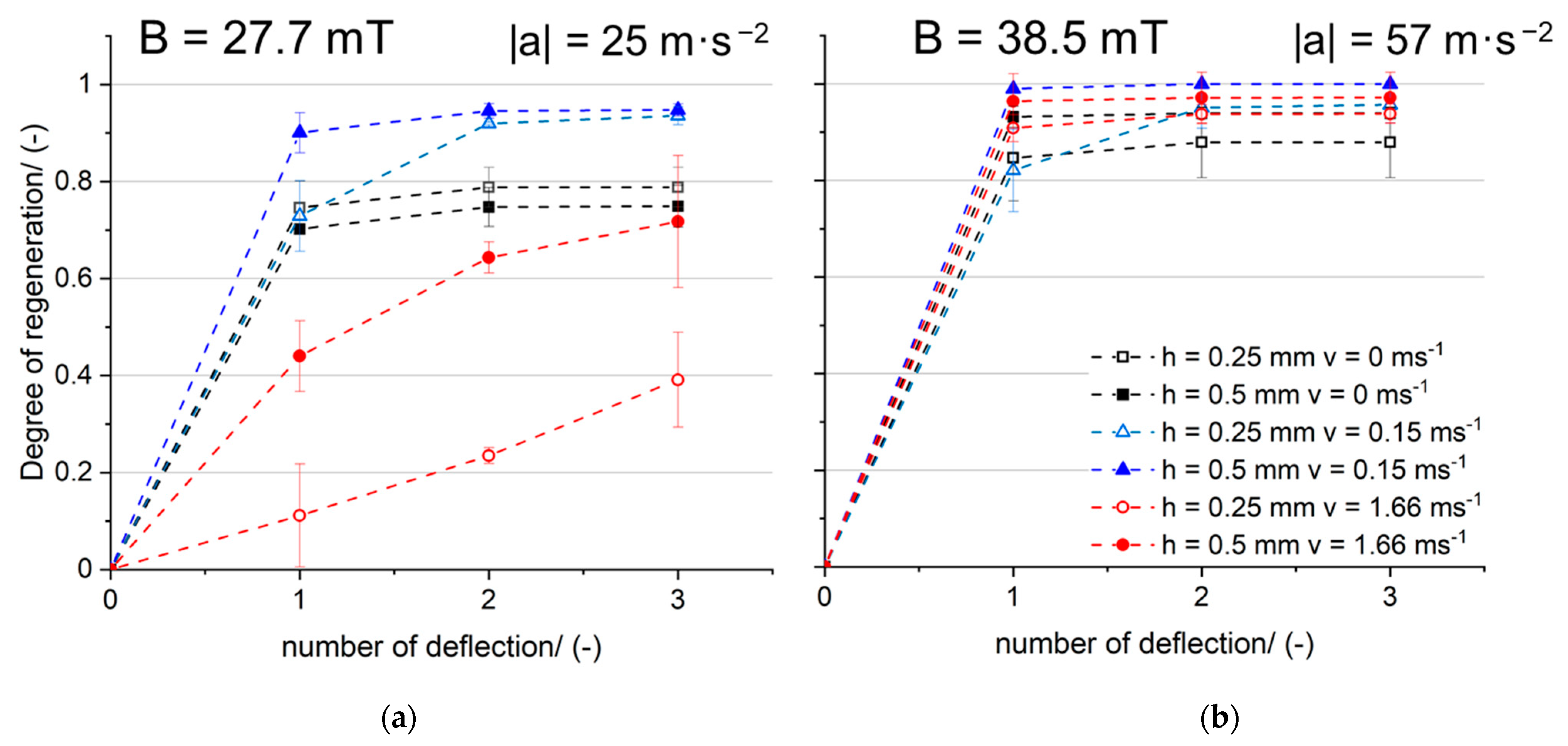
3.1. Single Deflection of the Fiber
3.2. Repeated Deflections of the Single Fiber
4. Conclusions and Outlook
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Langguth, F. Handbuch der Elektrochemie Elektromagnetische Aufbereitung. Verlag von Wilhelm Knapp: Halle, Germany, 1903. [Google Scholar]
- Korda, D. La Séparation Électromagnétique et Électrostatique des Minerais; L’Eclairage Electrique; Cornell University: Ithaca, NY, USA, 1905. [Google Scholar]
- Gunther, C.G. Electro-Magnetic Ore Separation; McGraw-Hill Publishing Co.: New York, NY, USA, 1909. [Google Scholar]
- Farsi, C.; Amroune, S.; Moussaoui, M.; Mohamad, B.; Benkherbache, H. High-Gradient Magnetic Separation Method for Weakly Magnetic Particles: An Industrial Application. Metallofiz. Novejsie Tehnol. 2019, 41, 1103–1119. [Google Scholar] [CrossRef]
- Svoboda, J. Magnetic Techniques for the Treatment of Materials; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2004. [Google Scholar]
- Li, Y.; Zhou, B.; Xu, F.; Jiang, H.; Zhang, W. The advantages of a superconducting magnetic intensity greater than 1T for phosphate–ferric flocs separation in HGMS. Sep. Purif. Technol. 2015, 141, 331–338. [Google Scholar] [CrossRef]
- Oberteuffer, J. Magnetic separation: A review of principles, devices, and applications. IEEE Trans. Magn. 1974, 10, 223–238. [Google Scholar] [CrossRef]
- Ge, W.; Encinas, A.; Araujo, E.; Song, S. Magnetic matrices used in high gradient magnetic separation (HGMS): A review. Results Phys. 2017, 7, 4278–4286. [Google Scholar] [CrossRef]
- Miltenyi, S.; Müller, W.; Weichel, W.; Radbruch, A. High gradient magnetic cell separation with MACS. Cytom. J. Int. Soc. Anal. Cytol. 1990, 11, 231–238. [Google Scholar] [CrossRef]
- Yavuz, C.T.; Mayo, J.T.; Yu, W.W.; Prakash, A.; Falkner, J.C.; Yean, S.; Cong, L.; Shipley, H.J.; Kan, A.; Tomson, M.; et al. Low-field magnetic separation of monodisperse Fe3O4 nanocrystals. Science 2006, 314, 964–967. [Google Scholar] [CrossRef]
- Hubbuch, J.J.; Matthiesen, D.B.; Hobley, T.J.; Thomas, O.R. High gradient magnetic separation versus expanded bed adsorption: A first principle comparison. Bioseparation 2001, 10, 99–112. [Google Scholar] [CrossRef]
- Svoboda, J.; Fujita, T. Recent developments in magnetic methods of material separation. Miner. Eng. 2003, 16, 785–792. [Google Scholar] [CrossRef]
- Dauer, R.R.; Dunlop, E.H. High gradient magnetic separation of yeast. Biotechnol. Bioeng. 1991, 37, 1021–1028. [Google Scholar] [CrossRef]
- Luo, L.; Nguyen, A.V. A review of principles and applications of magnetic flocculation to separate ultrafine magnetic particles. Sep. Purif. Technol. 2017, 172, 85–99. [Google Scholar] [CrossRef]
- Ebner, A.D.; Ritter, J.A.; Ploehn, H.J. Magnetic Hetero-flocculation of Paramagnetic Colloidal Particles. J. Colloid Interface Sci. 2000, 225, 39–46. [Google Scholar] [CrossRef] [PubMed]
- Bilad, M.R.; Mezohegyi, G.; Declerck, P.; Vankelecom, I.F.J. Novel magnetically induced membrane vibration (MMV) for fouling control in membrane bioreactors. Water Res. 2012, 46, 63–72. [Google Scholar] [CrossRef]
- Yang, F.-R.; Chen, Y.-F.; Lin, S.-A. Vibration Filter. U.S. Patent #20060138037, 29 June 2006. Available online: https://patents.justia.com/patent/20060138037 (accessed on 19 November 2023).
- Zhou, F.; Diao, Y.; Wang, R.; Yang, B.; Zhang, T. Experimental study on PM2.5 removal by magnetic polyimide loaded with cobalt ferrate. Energy Built Environ. 2020, 1, 404–409. [Google Scholar] [CrossRef]
- Binnig, J.; Meyer, J.; Kasper, G. Origin and mechanisms of dust emission from pulse-jet cleaned filter media. Powder Technol. 2009, 189, 108–114. [Google Scholar] [CrossRef]
- Simon, X.; Bémer, D.; Chazelet, S.; Thomas, D.; Régnier, R. Consequences of high transitory airflows generated by segmented pulse-jet cleaning of dust collector filter bags. Powder Technol. 2010, 201, 37–48. [Google Scholar] [CrossRef]
- Levy, G.K.; Birch, M.A.; Brooks, R.A.; Neelakantan, S.; Markaki, A.E. Stimulation of Human Osteoblast Differentiation in Magneto-Mechanically Actuated Ferromagnetic Fiber Networks. J. Clin. Med. 2019, 8, 1522. [Google Scholar] [CrossRef]
- Iranmanesh, M.; Hulliger, J. Magnetic separation: Its application in mining, waste purification, medicine, biochemistry and chemistry. Chem. Soc. Rev. 2017, 46, 5925–5934. [Google Scholar] [CrossRef]
- Chung, C.Y.; Chen, S.C.; Lin, K.J. Effect of Magnetic Field on the Fiber Orientation during the Filling Process in Injection Molding, Part 1: Simulation and Mold Design. Mater. Sci. Forum 2018, 936, 126–135. [Google Scholar] [CrossRef]
- Künzel, K.; Papež, V.; Carrera, K.; Konrád, P.; Mára, M.; Kheml, P.; Sovják, R. Electromagnetic Properties of Steel Fibres for Use in Cementitious Composites, Fibre Detection and Non-Destructive Testing. Materials 2021, 14, 2131. [Google Scholar] [CrossRef]
- Gerbal, F.; Wang, Y.; Lyonnet, F.; Bacri, J.-C.; Hocquet, T.; Devaud, M. A refined theory of magnetoelastic buckling matches experiments with ferromagnetic and superparamagnetic rods. Proc. Natl. Acad. Sci. USA 2015, 112, 7135–7140. [Google Scholar] [CrossRef]
- Szabadi, J.; Meyer, J.; Dittler, A. Particulate Matter Detachment from a Magnetizable Single Fiber Applying Magnetic Forces in Ambient Air. Separations 2023, 10, 297. [Google Scholar] [CrossRef]
- Szabadi, J.; Meyer, J.; Dittler, A. In situ characterization of particle structures generated at different flow velocities on a single fiber in the gas phase. J. Aerosol Sci. 2023, 173, 106197. [Google Scholar] [CrossRef]
- Zoller, J.; Zargaran, A.; Braschke, K.; Meyer, J.; Janoske, U.; Dittler, A. Morphology of particulate deposits formed on a single filter fibre by exposure to mixed aerosol flow. J. Aerosol Sci. 2021, 152, 105718. [Google Scholar] [CrossRef]
- Franzreb, M. Magnettechnologie in der Verfahrenstechnik Wässriger Medien; University of Karlsruhe: Karlsruhe, Germany, 2003. [Google Scholar]
- Kanaoka, C.; Emi, G.; Hiragi, S.; Myojo, T. Morphology of particulate agglomerates on a cylindrical fiber and a collection efficiency of a dust loaded fiber. In Proceedings of the Second International Aerosol Conference, Berlin, Germany, 22–26 September 1986; pp. 674–677. [Google Scholar]
- Löffler, F. Abblasen von an Filterfasern Abgeschiedenen Feststoffteilchen. Verfahrenstechnik 1972, 6, 3–7. [Google Scholar]
- Kasper, G.; Schollmeier, S.; Meyer, J. Structure and density of deposits formed on filter fibers by inertial particle deposition and bounce. J. Aerosol Sci. 2010, 41, 1167–1182. [Google Scholar] [CrossRef]
- Otsu, N. A Threshold Selection Method from Gray-Level Histograms. IEEE Trans. Syst. Man Cybern. 1979, 9, 62–66. [Google Scholar] [CrossRef]
- Mathworks. Motion-Based Multiple Object Tracking. Available online: https://de.mathworks.com/help/vision/ug/motion-based-multiple-object-tracking.html (accessed on 4 November 2023).

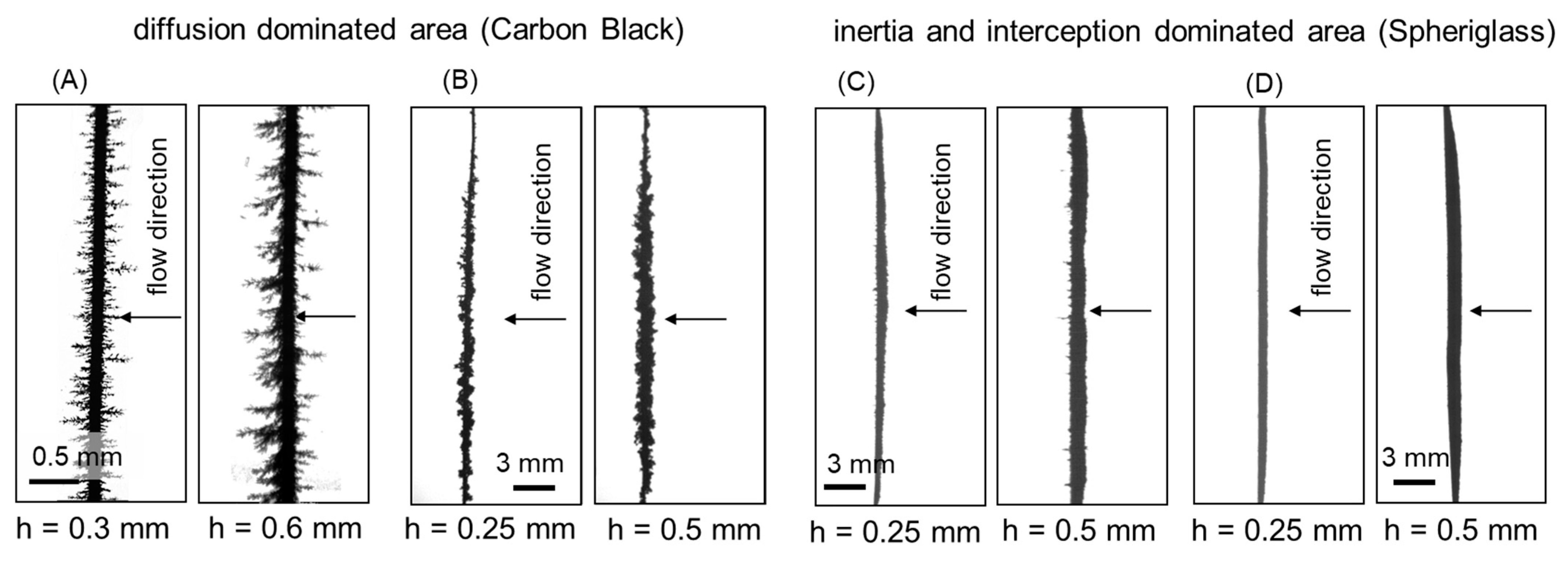
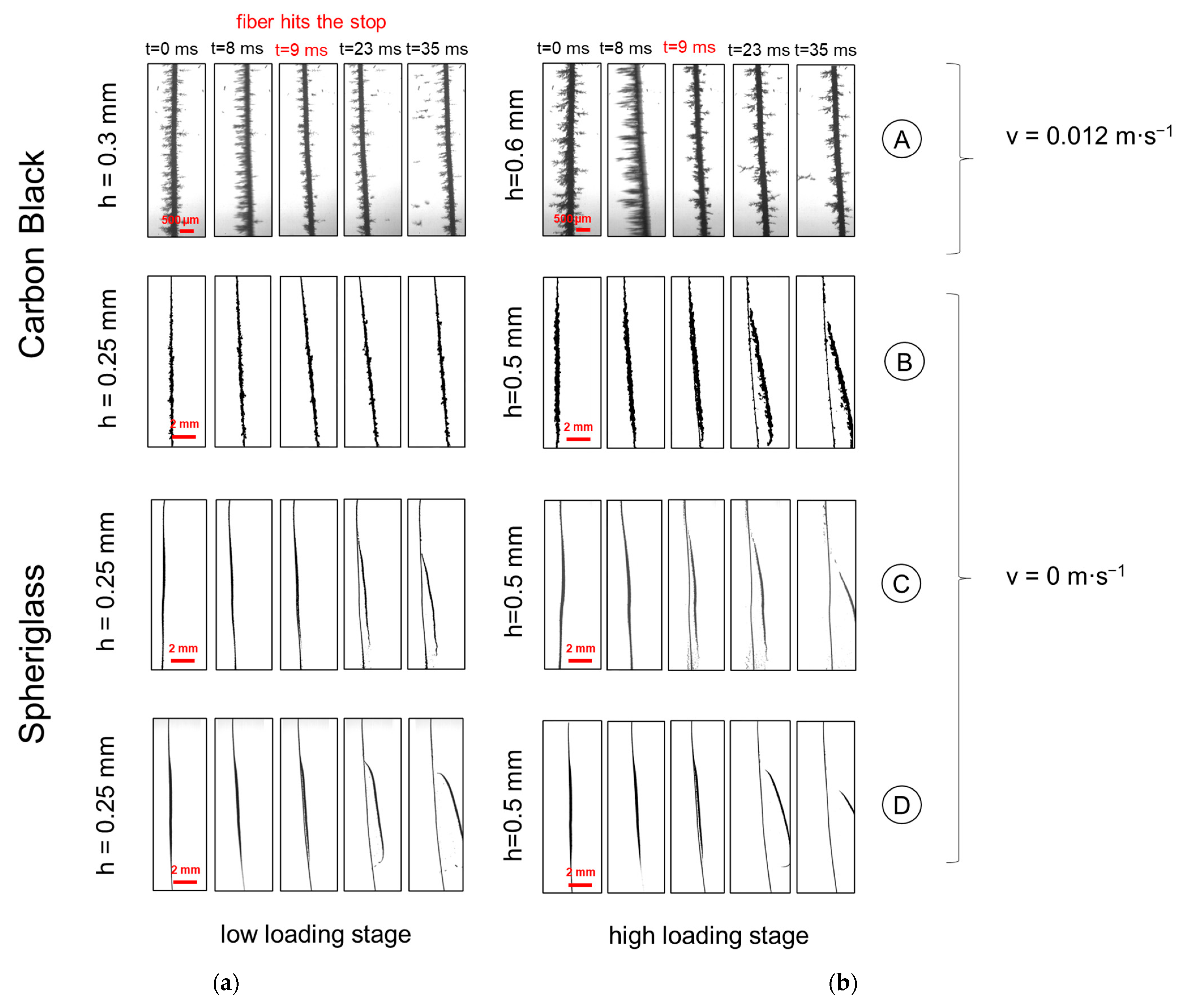
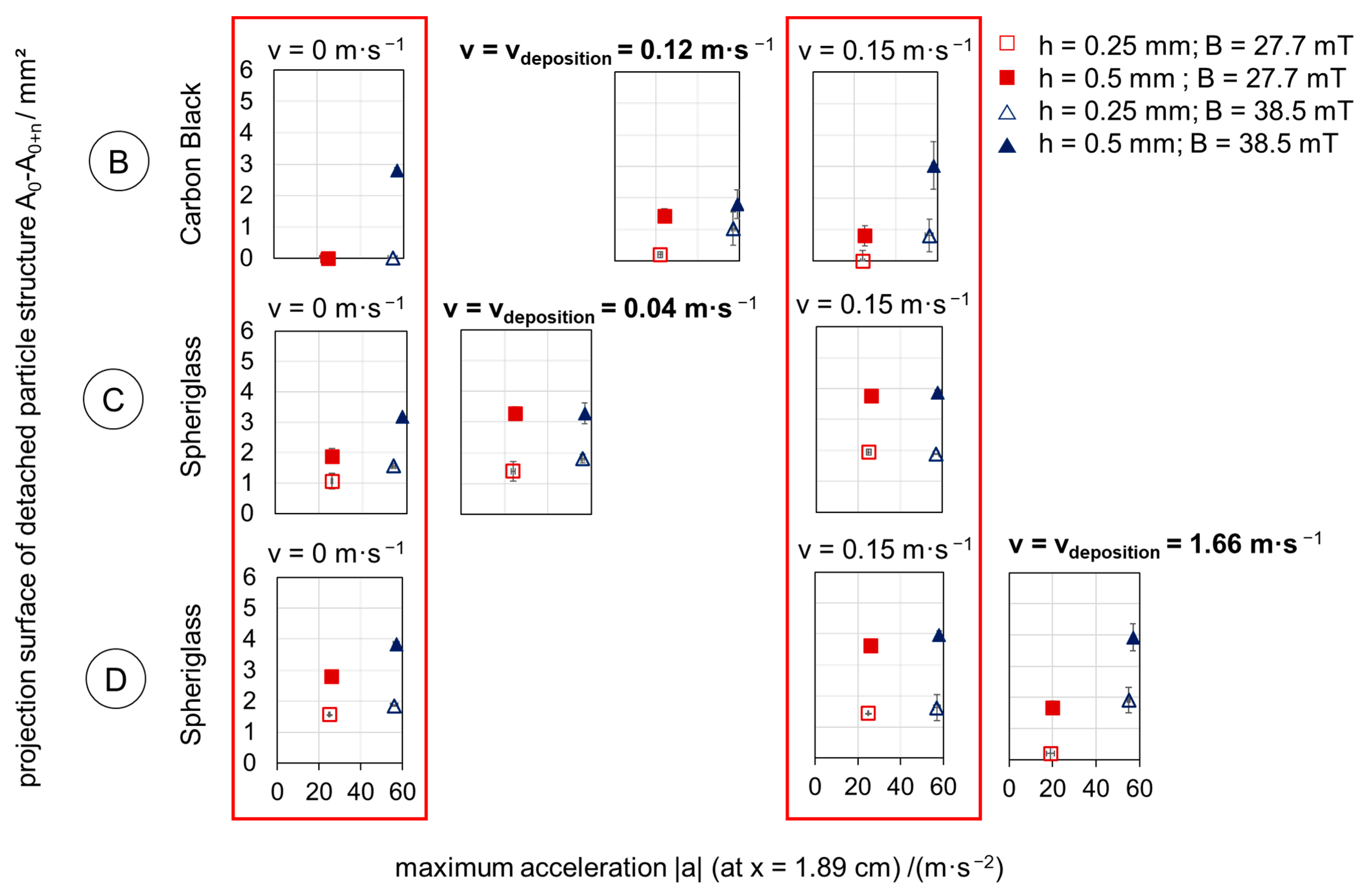
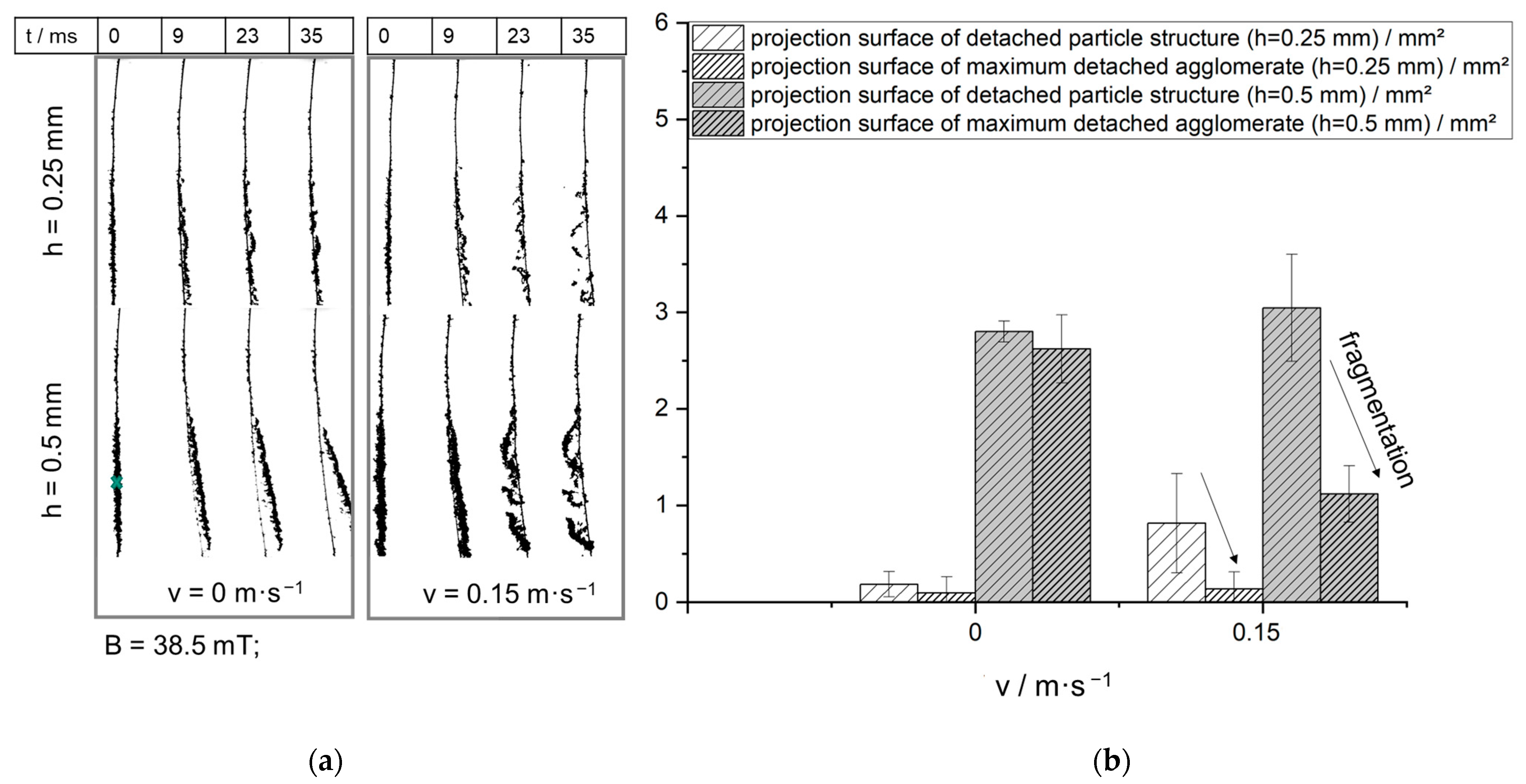
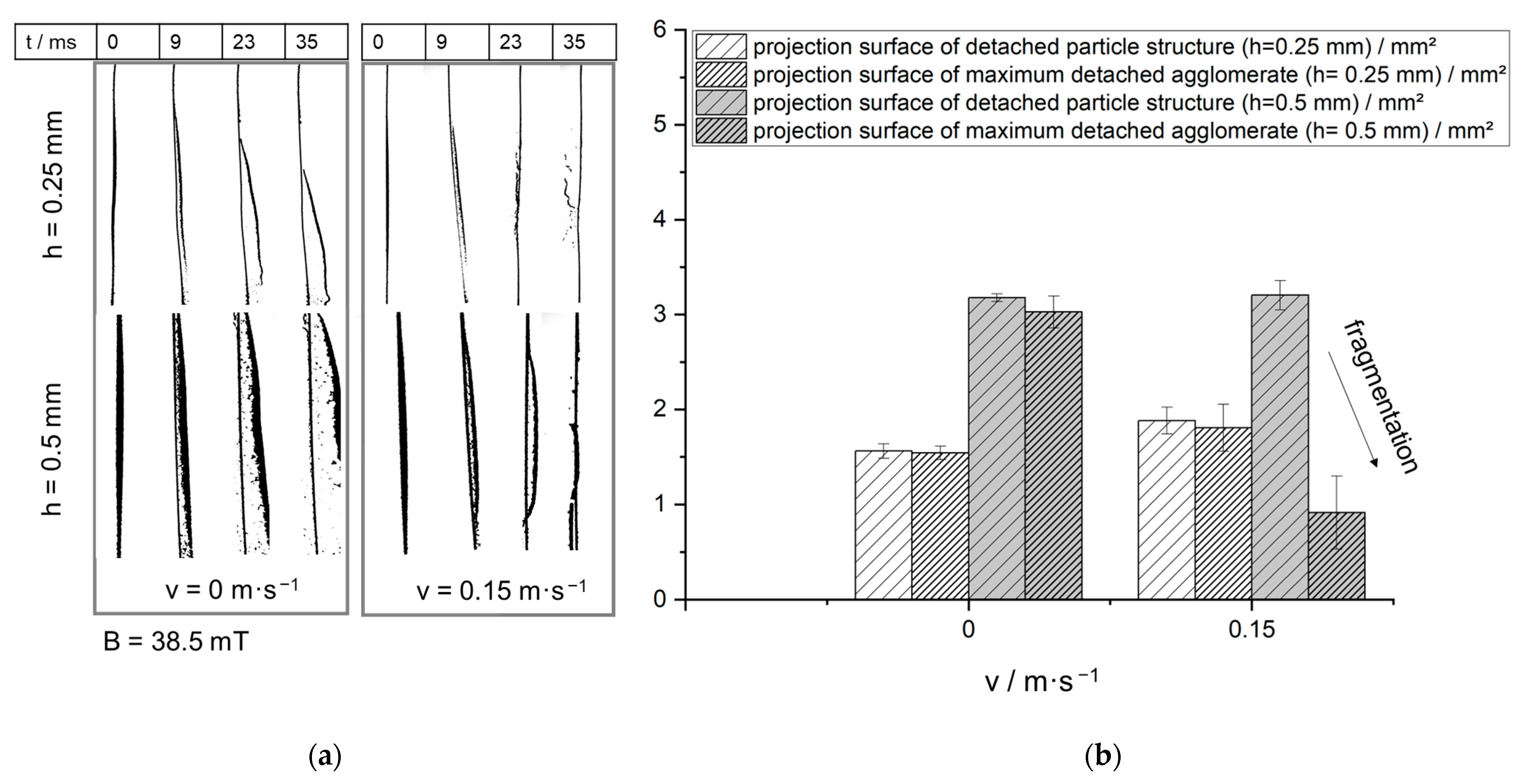


| Carbon Black A | Carbon Black B | Spheriglass C | Spheriglass D | |
|---|---|---|---|---|
| Péclet number, Stokes number/- | Pe = 2.6 × 104 | Pe = 2.6 × 105 | St = 0.15 | St = 6.5 |
| Loading heights/mm | h1 = 0.3 ± 0.02 h2 = 0.6 ± 0.05 | h1 = 0.25 ± 0.05 h2 = 0.5 ± 0.07 | h1 = 0.25 ± 0.03 h2 = 0.5 ± 0.04 | h1 = 0.25 ± 0.01 h2 = 0.5 ± 0.02 |
| /L·min−1 | 9.73 | 9.73 | 9.73 | 9.73 |
| /L·min−1 | - | - | 15.17 | 15.17 |
| /L·min−1 | 9.58 | 8.23 | 24.41 | 4.9 |
| /L·min−1 | 0.15 | 1.5 | 0.5 | 20 |
| /mg∙h−1 | 2.48 | 24.8 | 14 | 566 |
| /m·s−1 | 0.012 | 0.12 | 0.04 | 1.66 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Szabadi-Fuchs, J.; Meyer, J.; Dittler, A. Experimental Investigations of the Detachment of Different Particle Structures from a Magnetizable Fiber in the Gas Phase. Separations 2023, 10, 579. https://doi.org/10.3390/separations10120579
Szabadi-Fuchs J, Meyer J, Dittler A. Experimental Investigations of the Detachment of Different Particle Structures from a Magnetizable Fiber in the Gas Phase. Separations. 2023; 10(12):579. https://doi.org/10.3390/separations10120579
Chicago/Turabian StyleSzabadi-Fuchs, Julia, Jörg Meyer, and Achim Dittler. 2023. "Experimental Investigations of the Detachment of Different Particle Structures from a Magnetizable Fiber in the Gas Phase" Separations 10, no. 12: 579. https://doi.org/10.3390/separations10120579
APA StyleSzabadi-Fuchs, J., Meyer, J., & Dittler, A. (2023). Experimental Investigations of the Detachment of Different Particle Structures from a Magnetizable Fiber in the Gas Phase. Separations, 10(12), 579. https://doi.org/10.3390/separations10120579






