Computational Experience with Piecewise Linear Relaxations for Petroleum Refinery Planning
Abstract
:1. Introduction
2. Problem Description on Refinery Planning Model
3. Computational Experiments
3.1. Reformulation as Relaxation Models
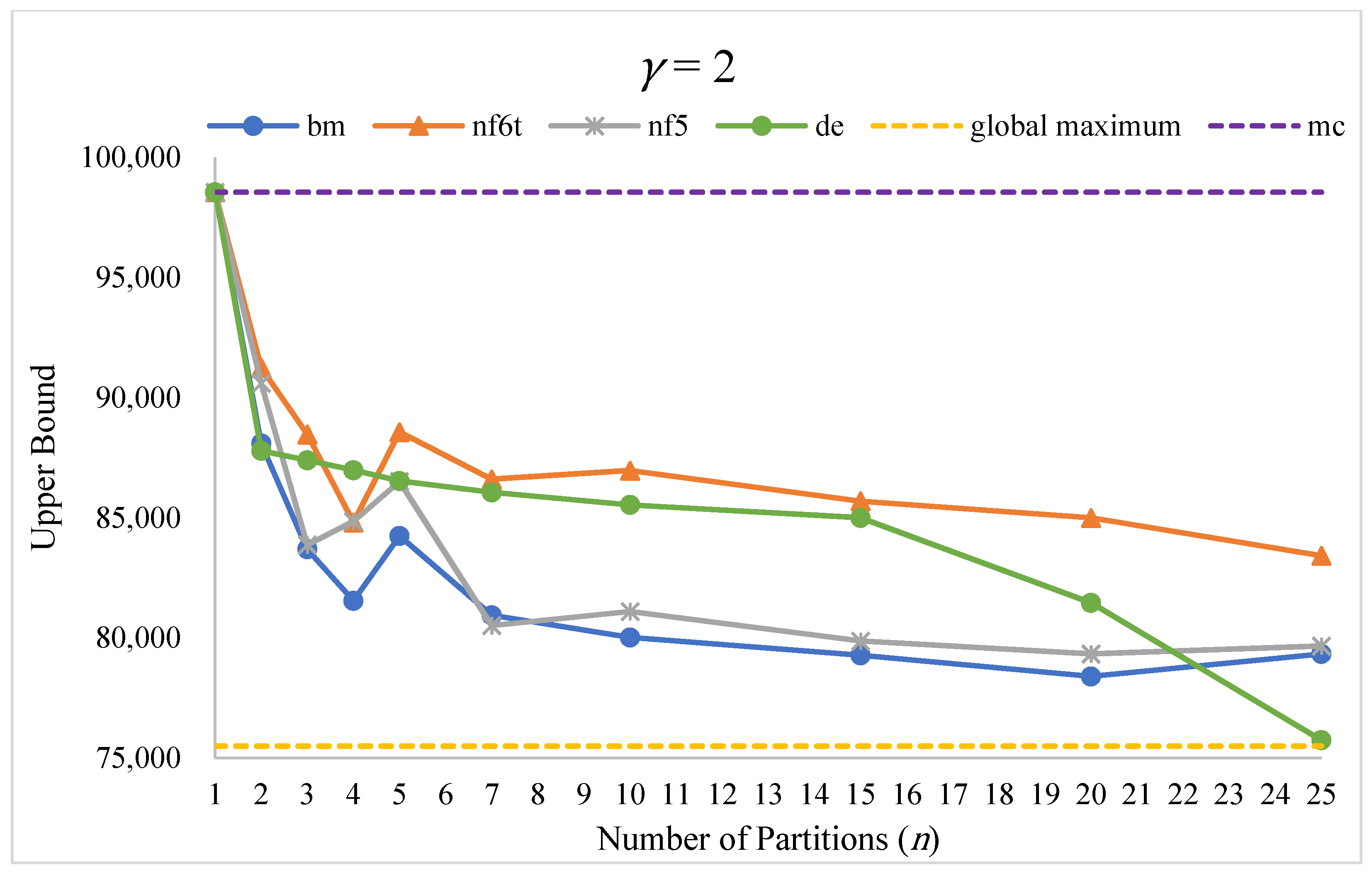
3.2. Computational Results
4. Concluding Remarks
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| Sets and indices | |
| Set of process unit u | |
| Set of CDU fraction p | |
| Set of gridpoints for segment n | |
| Parameters | |
| Segment size (i.e., length) | |
| M | Big-M parameter |
| Gridpoint for segment n | |
| qn | Length of segment n |
| Continuous variables | |
| Load of process unit u | |
| Weight transfer ratio of fraction p (for CDU) | |
| Deviation of partitioned variables in bilinear term from lower bound | |
| Auxiliary variable for relaxation | |
| Variable for reformulation to replace bilinear terms | |
| Binary variables | |
| Disjunction in bm scheme | |
| Disjunction in nf5 and nf6t formulations | |
References
- Aspen Technology. Aspen PIMS and Aspen PIMS-AO. 2013. Available online: http://www.aspentech.com/brochures/aspen_pims_ao.pdf (accessed on 15 August 2013).
- Honeywell. Symphonite RPMS (Refining and Petrochemical Modeling System); Honeywell: Toronto, ON, Canada, 2020. [Google Scholar]
- Haverly Systems. GRTMPS. 2012. Available online: http://www.haverly.com/main-products/13-products/9-grtmps (accessed on 9 August 2012).
- Barsamian, A. Fundamentals of Supply Chain Management for Refining. In IBC Asia Oil & Gas SCM Conference Proceedings; 2001. [Google Scholar]
- Andrade, T.; Ribas, G.; Oliveira, F. A Strategy Based on Convex Relaxation for Solving the Oil Refinery Operations Planning Problem. Ind. Eng. Chem. Res. 2016, 55, 144–155. [Google Scholar] [CrossRef]
- Rigby, B.; Lasdon, L.S.; Waren, A.D. The Evolution of Texaco’s Blending Systems: From OMEGA to StarBlend. Interfaces 1995, 25, 64–83. [Google Scholar] [CrossRef]
- Moro, L.F.L.; Zanin, A.C.; Pinto, J.M. A planning model for refinery diesel production. Comput. Chem. Eng. 1998, 22, S1039–S1042. [Google Scholar] [CrossRef]
- Steinschorn, D.; Hofferl, F. Refinery Scheduling Using Mixed Integer LP and Dynamic Recursion. In National Petroleum Refiners Association—Publications—All Series; National Petroleum Refiners Association: Houston, TX, USA, 1997. [Google Scholar]
- Khor, C.S.; Varvarezos, D. Petroleum refinery optimization. Optim. Eng. 2016, 18, 943–989. [Google Scholar] [CrossRef]
- Khor, C.S.; Elkamel, A. Roles of Computers in Petroleum Refineries. In Handbook of Petroleum Refining and Natural Gas Processing; Riazi, M.R., Eser, S., Diez, J.L.P., Agrawal, S.S., Eds.; ASTM International: Conshohocken, PA, USA, 2013; pp. 685–700. [Google Scholar]
- Watkins, R.N. Petroleum Refinery Distillation; Houston (Tex.), Book Division; Gulf Publishing Company: London, UK; Paris, France, 1979. [Google Scholar]
- Hasan, M.M.F.; Karimi, I. Exergy analysis of multi-stage crude distillation units. Front. Chem. Sci. Eng. 2013, 7, 437–446. [Google Scholar]
- Li, J.; Misener, R.; Floudas, C.A. Scheduling of crude oil operations under demand uncertainty: A robust optimization framework coupled with global optimization. AIChE J. 2012, 58, 2373–2396. [Google Scholar] [CrossRef]
- Li, J.; Misener, R.; Floudas, C.A. Continuous-time modeling and global optimization approach for scheduling of crude oil operations. AIChE J. 2012, 58, 205–226. [Google Scholar] [CrossRef]
- Geddes, R.L. A general index of fractional distillation power for hydrocarbon mixtures. AIChE J. 1958, 4, 389–392. [Google Scholar] [CrossRef]
- Menezes, B.C.; Kelly, J.D.; Grossmann, I.E. Improved Swing-Cut Modeling for Planning and Scheduling of Oil-Refinery Distillation Units. Ind. Eng. Chem. Res. 2013, 52, 18324–18333. [Google Scholar] [CrossRef]
- Lee, S.; Grossmann, I.E. Cutpoint Temperature Surrogate Modeling for Distillation Yields and Properties. Ind. Eng. Chem. Res. 2020, 59, 18616–18628. [Google Scholar]
- Brooks, R.; Walsem, F.D.; Drury, J. Choosing cutpoints to optimize product yields. Hydrocarb. Process. 1999, 78, 53–60. [Google Scholar]
- Uribe-Rodriguez, A.; Castro, P.M.; Gonzalo, G.-G.; Chachuat, B. Two-stage stochastic programming with fixed recourse via scenario planning with economic and operational risk management for petroleum refinery planning under uncertainty. Chem. Eng. Process. Process Intensif. 2008, 47, 1744–1764. [Google Scholar]
- Pinto, J.M.; Joly, M.; Moro, L.F.L. Planning and scheduling models for refinery operations. Comput. Chem. Eng. 2000, 24, 2259–2276. [Google Scholar] [CrossRef]
- Alattas, A.M.; Grossmann, I.E.; Palou-Rivera, I. Integration of Nonlinear Crude Distillation Unit Models in Refinery Planning Optimization. Ind. Eng. Chem. Res. 2011, 50, 6860–6870. [Google Scholar] [CrossRef]
- Trierwiler, Advances in Crude Oil LP Modeling; National Petrochemical & Refiners Association: Houston, TX, USA, 2001.
- Salhi, A.; Horst, R.; Tuy, H. A nonlinear programming model for refinery planning and optimisation with rigorous process models and product quality specifications. Int. J. Oil Gas Coal Technol. 2008, 1, 283–307. [Google Scholar]
- Williams, H.P.; Nemhauser, G.L.; Wolsey, L.A. Overall integration of the management of H2 and CO2 within refinery planning using rigorous process models. Chem. Eng. Commun. 2013, 200, 139–161. [Google Scholar]
- Zhang, J.; Zhu, X.; Towler, G. A Level-by-Level Debottlenecking Approach in Refinery Operation. Ind. Eng. Chem. Res. Ind. Eng. Chem. Res. 2001, 40, 1528–1540. [Google Scholar] [CrossRef]
- Li, W.; Hui, C.-W.; Li, A. Integrating CDU, FCC and product blending models into refinery planning. Comput. Chem. Eng. 2005, 29, 2010–2028. [Google Scholar] [CrossRef]
- Menezes, B.C.; Moro, L.F.; Lin, W.O.; Medronho, R.A.; Pessoa, F.L. Nonlinear Production Planning of Oil-Refinery Units for the Future Fuel Market in Brazil: Process Design Scenario-Based Model. Ind. Eng. Chem. Res. 2014, 53, 4352–4365. [Google Scholar] [CrossRef]
- Guerra, O.J.; Le Roux, G.A.C. Improvements in Petroleum Refinery Planning: 1. Formulation of Process Models. Ind. Eng. Chem. Res. 2011, 50, 13403–13418. [Google Scholar] [CrossRef]
- Guerra, O.J.; Le Roux, G.A.C. Improvements in Petroleum Refinery Planning: 2. Case Studies. Ind. Eng. Chem. Res. 2011, 50, 13419–13426. [Google Scholar] [CrossRef]
- Li, J.; Xiao, X.; Boukouvala, F.; Floudas, C.A.; Zhao, B.; Du, G.; Su, X.; Liu, H. Data-Driven Mathematical Modeling and Global Optimization Framework for Entire Petrochemical Planning Operations. AIChE J. 2016, 62, 3020–3040. [Google Scholar] [CrossRef]
- Alattas, A.M.; Grossmann, I.E.; Palou-Rivera, I. Refinery Production Planning: Multiperiod MINLP with Nonlinear CDU Model. Ind. Eng. Chem. Res. 2012, 51, 12852–12861. [Google Scholar] [CrossRef] [Green Version]
- Castillo Castillo, P.; Castro, P.M.; Mahalec, V. Global Optimization Algorithm for Large-Scale Refinery Planning Models with Bilinear Terms. Ind. Eng. Chem. Res. 2017, 56, 530–548. [Google Scholar] [CrossRef]
- McCormick, G.P. Computability of global solutions to factorable nonconvex programs: Part I—Convex underestimating problems. Math. Program. 1976, 10, 147–175. [Google Scholar] [CrossRef]
- Al-Khayyal, F.A.; Falk, J.E. Jointly constrained biconvex programming. Math. Oper. Res. 1983, 8, 273–286. [Google Scholar] [CrossRef]
- Misener, R.; Floudas, C.A. ANTIGONE: Algorithms for coNTinuous/Integer Global Optimization of Nonlinear Equations. J. Glob. Optim. 2014, 59, 503–526. [Google Scholar] [CrossRef]
- Meyer, C.A.; Floudas, C.A. Global optimization of a combinatorially complex generalized pooling problem. AIChE J. 2006, 52, 1027–1037. [Google Scholar] [CrossRef]
- Karuppiah, R.; Grossmann, I.E. Global optimization for the synthesis of integrated water systems in chemical processes. Comput. Chem. Eng. 2006, 30, 650–673. [Google Scholar] [CrossRef] [Green Version]
- Wicaksono, D.S.; Karimi, I.A. Piecewise MILP under- and overestimators for global optimization of bilinear programs. AIChE J. 2008, 54, 991–1008. [Google Scholar] [CrossRef]
- Gounaris, C.E.; Misener, R.; Floudas, C.A. Computational Comparison of Piecewise−Linear Relaxations for Pooling Problems. Ind. Eng. Chem. Res. 2009, 48, 5742–5766. [Google Scholar] [CrossRef]
- Hasan, M.M.F.; Karimi, I.A. Piecewise linear relaxation of bilinear programs using bivariate partitioning. AIChE J. 2009, 56, 1880–1893. [Google Scholar] [CrossRef]
- Misener, R.; Floudas, C.A. Advances for the pooling problem: Modeling, global optimization, and computational studies. Appl. Comput. Math. 2009, 8, 3–22. [Google Scholar]
- Nagarajan, H.; Lu, M.; Wang, S.; Bent, R.; Sundar, K. An adaptive, multivariate partitioning algorithm for global optimization of nonconvex programs. J. Glob. Optim. 2019, 74, 639–675. [Google Scholar] [CrossRef] [Green Version]
- Tawarmalani, M.; Ahmed, S.; Sahinidis, N.V. Global optimization of 0–1 hyperbolic programs. J. Glob. Optim. 2002, 24, 385–416. [Google Scholar] [CrossRef]
- Tawarmalani, M.; Sahinidis, N.V. Convexification and Global Optimization in Continuous and Mixed-Integer Nonlinear Programming: Theory, Algorithms, Software, and Applications. Nonconvex Optimization and Its Applications; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2002; Volume 65, p. 504. [Google Scholar]
- Grossmann, I.E.; Lee, S. Global optimization of nonlinear generalized disjunctive programming with bilinear equality constraints: Applications to process networks. Comput. Chem. Eng. 2003, 27, 1557–1575. [Google Scholar]
- Uribe-Rodriguez, A.; Castro, P.M.; Gonzalo, G.G.; Chachuat, B. Global optimization of large-scale MIQCQPs via cluster decomposition: Application to short-term planning of an integrated refinery-petrochemical complex. Comput. Chem. Eng. 2020, 140, 106883. [Google Scholar] [CrossRef]
- Yang, H.; Bernal, D.E.; Franzoi, R.E.; Engineer, F.G.; Kwon, K.; Lee, S.; Grossmann, I.E. Integration of crude-oil scheduling and refinery planning by Lagrangean Decomposition. Comput. Chem. Eng. 2020, 138, 106812. [Google Scholar] [CrossRef]
- Sergeyev, Y.D. Global one-dimensional optimization using smooth auxiliary functions. Math. Program. 1998, 81, 127–146. [Google Scholar] [CrossRef]
- Sergeyev, Y.D. On convergence of “Divide the Best” global optimization algorithms. Optimization 1998, 44, 303–325. [Google Scholar] [CrossRef]
- Horst, R.; Tuy, H. Global Optimization: Deterministic Approaches, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 1996. [Google Scholar]
- Nemhauser, G.; Wolsey, L. Integer and Combinatorial Optimization; Wiley: New York, NY, USA, 1988. [Google Scholar]
- Tawarmalani, M.; Sahinidis, N.V. Global optimization of mixed-integer nonlinear programs: A theoretical and computational study. Math. Program. 2004, 99, 563–591. [Google Scholar] [CrossRef]
- Tawarmalani, M.; Sahinidis, N.V. A polyhedral branch-and-cut approach to global optimization. Math. Program. 2005, 103, 225–249. [Google Scholar] [CrossRef]
- Sahinidis, N.V.; Tawarmalani, M. BARON 7.2.5: Global Optimization of Mixed-Integer Nonlinear Programs, User’s Manual. 2005. Available online: http://www.gams.com/dd/docs/solvers/baron.pdf (accessed on 1 July 2021).
- Zamora, J.M.; Grossmann, I.E. Continuous global optimization of structured process systems models. Comput. Chem. Eng. 1998, 22, 1749–1770. [Google Scholar] [CrossRef]
- Misener, R.; Floudas, C. GloMIQO: Global mixed-integer quadratic optimizer. J. Glob. Optim. 2013, 57, 3–50. [Google Scholar] [CrossRef] [Green Version]
- Neumaier, A. Complete search in continuous global optimization and constraint satisfaction. Acta Numer. 2004, 13, 271–369. [Google Scholar] [CrossRef] [Green Version]
- Smith, E.M.B.; Pantelides, C.C. A symbolic reformulation/spatial branch-and-bound algorithm for the global optimisation of nonconvex MINLPs. Comput. Chem. Eng. 1999, 23, 457–478. [Google Scholar] [CrossRef]
- Faria, D.C.; Bagajewicz, M.J. Global Optimization of Water Management Problems Using Linear Relaxation and Bound Contraction Methods. Ind. Eng. Chem. Res. 2011, 50, 3738–3753. [Google Scholar] [CrossRef]
- Faria, D.C.; Bagajewicz, M.J. Novel bound contraction procedure for global optimization of bilinear MINLP problems with applications to water management problems. Comput. Chem. Eng. 2011, 35, 446–455. [Google Scholar] [CrossRef]
- Faria, D.C.; Bagajewicz, M.J. A new approach for global optimization of a class of MINLP problems with applications to water management and pooling problems. AIChE J. 2012, 58, 2320–2335. [Google Scholar] [CrossRef]
- Faria, D.C.; Bagajewicz, M.J. Global optimization based on subspaces elimination: Applications to generalized pooling and water management problems. AIChE J. 2012, 58, 2336–2345. [Google Scholar] [CrossRef]
- Rote, G. The convergence rate of the sandwich algorithm for approximating convex functions. Computing 1992, 48, 337–361. [Google Scholar] [CrossRef]










| Method | Relation Type | Feature | Application |
|---|---|---|---|
| Fixed yield | Linear | Simple; amenable to large-scale models (especially LP); can cater for different operating modes | Simulation [18], planning optimization (LP [18], NLP [7,19], MINLP [20]), and scheduling optimization (MILP [8]) |
| Swing cut | Linear or nonlinear | More accurate than fixed yield; can represent multiple operating modes [21] | Planning optimization (LP [22], MILP, NLP [16,23,24,25,26,27,28,29], and MINLP [30]) |
| Fractionation index | Nonlinear | High accuracy (considers relative volatility and phase equilibrium) | Planning optimization (NLP [21] and MINLP) [31,32] |
| Computing platform | GAMS 30.3.0/CPLEX 12; 1.9 GHz (speed, Intel Core i3); 8192 MB (RAM) |
| No. of continuous variables | 49 |
| No. of nonlinear variables | 42 |
| No. of constraints | 61 |
| No. of nonconvex terms | 21 (bilinear) |
| Bilinear Term | Count |
|---|---|
| 5 | |
| 4 | |
| 4 | |
| 4 | |
| 4 | |
| Total | 21 |
| Convergence Indicator for | Convergence Indicator (%) for | |||||||
|---|---|---|---|---|---|---|---|---|
| bm | nf6t | nf5 | de | bm | nf6t | nf5 | de | |
| 0.25 | 0.89 | 0.95 | 0.90 | 0.71 | 0.11 | 0.50 | 0.10 | 0.29 |
| 0.5 | 0.84 | 0.97 | 0.97 | 0.69 | 0.16 | 0.03 | 0.03 | 0.31 |
| 1 | 0.92 | 0.90 | 0.89 | 0.68 | 0.08 | 0.10 | 0.11 | 0.32 |
| 1.5 | 0.93 | 0.96 | 0.85 | 0.59 | 0.07 | 0.04 | 0.15 | 0.41 |
| 2 | 0.97 | 0.77 | 0.92 | 0.56 | 0.03 | 0.23 | 0.08 | 0.44 |
| 3 | 0.95 | 0.85 | 0.99 | 0.89 | 0.05 | 0.15 | 0.01 | 0.11 |
| 4 | 0.91 | 0.70 | 0.80 | 0.91 | 0.09 | 0.30 | 0.20 | 0.09 |
| Relative Difference (%) | ||||
|---|---|---|---|---|
| bm | nf6t | nf5 | de | |
| 0.25 | 0.642 | 0.493 | 0.465 | 0.530 |
| 0.5 | 0.450 | 0.298 | 0.259 | 0.458 |
| 1 | 0.320 | 0.255 | 0.251 | 0.472 |
| 1.5 | 0.290 | 0.405 | 0.295 | 0.395 |
| 2 | 0.267 | 0.480 | 0.318 | 0.375 |
| 3 | 0.360 | 0.566 | 0.400 | 0.341 |
| 4 | 0.490 | 0.652 | 0.455 | 0.250 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rana, Z.A.; Khor, C.S.; Zabiri, H. Computational Experience with Piecewise Linear Relaxations for Petroleum Refinery Planning. Processes 2021, 9, 1624. https://doi.org/10.3390/pr9091624
Rana ZA, Khor CS, Zabiri H. Computational Experience with Piecewise Linear Relaxations for Petroleum Refinery Planning. Processes. 2021; 9(9):1624. https://doi.org/10.3390/pr9091624
Chicago/Turabian StyleRana, Zaid Ashraf, Cheng Seong Khor, and Haslinda Zabiri. 2021. "Computational Experience with Piecewise Linear Relaxations for Petroleum Refinery Planning" Processes 9, no. 9: 1624. https://doi.org/10.3390/pr9091624
APA StyleRana, Z. A., Khor, C. S., & Zabiri, H. (2021). Computational Experience with Piecewise Linear Relaxations for Petroleum Refinery Planning. Processes, 9(9), 1624. https://doi.org/10.3390/pr9091624