Abstract
This comparative study inspects the MHD three-dimensional revolving flow and temperature transmission of a radiative stretching surface. The flow of nanofluid is modeled using the Tiwari and Das model. Water is the base fluid, and the nanoparticles are composed of two different types of nanoparticle, i.e., gold and silver ( and ). The non-radiative heat flow notion is examined in a temperature field that results in a nonlinear energy equation. Conformist transformations are used to generate a self-similar arrangement of the leading differential system. The resulting system has an intriguing temperature ratio constraint, which shows whether the flow has a little or significant temperature differential. By using a powerful mathematical technique, numerical results are obtained. The solutions are influenced by both stretching and rotation. The difference in velocity constituents with the elements’ volume fraction is non-monotonic. Results for the rotating nanofluid flow and heat transfer properties for both types of nanoparticles are highlighted with graphs. The impact of physical concentrations, such as heat flux rates and skin friction constants, are examined at the linear extending surface and clarified graphically.-water nanofluid has a high-temperature transfer constant compared to -water nanofluid. The velocity profile was also discovered to have a parabolic distribution shape.
1. Introduction
Problems associated with pouring in a spinning setting occur in many fields, such as engineering and geophysics. The movement of volcanic emissions near the Earth’s crust’s mantle, as well as its rotation, is a prominent geophysical application. The engineering applications of pouring in a spinning setting occur in a large range of chemical industries, the processing of food, centrifugal filtration processes, the design of the multi-pore supplier in the gas-solid liquidized bed, rotating machinery, and in manufacturing processes. Wang [1]. Conducted innovative research on three-dimensional revolving viscid flow, created by a widening surface. First, the problem was addressed with a constraint that denotes the ratio of the revolution to the surface broadening rate. Then, by using a regular perturbation approach, he found a series of solutions. He concluded that the velocity of fluid decays as the parameter increases. Rajeswari and Nath [2], and Nazar et al. [3] furthered Wang’s efforts concerning unstable flow problems. Their outcomes specify a seamless alteration from the initial unstable flow to the end smooth state flow. Vajravelu and Kumar [4] conducted a noteworthy exploration of the arithmetical and consistent clarifications of a nonlinear scheme caused by a three-dimensional rotational flow. Hayat et al. [5] provided the homotopic solution of succeeding-grade non-Newtonian rotating flow. They found that velocity has a direct relationship with material parameters. Zaimi et al. [6] and Hayat et al. [7] calculated the rotating flow of viscid fluid and proved that frontier layer viscosity is an accumulative function of the viscid fluid parameter. Entropy generation in steady fluid, due to a rotating disk, was investigated by Rashidi et al. [8].
The poor temperature conductivity of traditional coolants such as water, crude oil, and mineral oil limits their ability to cool heat transfer devices. As it is widely known, metals have a relatively high heat conductivity as compared to liquids. Thus, scattering nanometer-sized metallic particles in liquids is one of the most effective ways to improve heat transfer performance. Choi and Eastman [9] conceived the concept of nanofluid. During the last few decades, nanofluid convective heat transfer has been a popular research topic [10,11,12,13,14,15]. Turkyilmazoglu [16] studied the different types of water-based nanofluids. He used the spectral Chebyshev collocation technique to represent numerical results.
Magnetic nanofluids are colloidal solutions of magnetizable nanoparticles with fluid, magnetic, and thermal characteristics. They are beneficial in a variety of applications. High-temperature plasmas, nuclear reactor cooling, MHD accelerators, power-generating systems, and liquid–metal fluids are the major industrial and geothermal uses of the magnetohydrodynamic (MHD) flow. Cobalt, magnetite, hematite, and other iron-based nanoparticles can be found in them. Such types of nanoparticles can be used for MRI, hyperthermia, and magnetic cell separation. Sheikholeslami and Ganji [17] considered ferro- and magnetohydrodynamic fluid. They estimated the electrical and thermal conductivity using Maxwell’s model. Moraveji and Hejazian [18] considered the natural convection of magnetite–water nanofluid via a rectangular container. Aydin and Kaya [19] examined mixed convection MHD flow over an inclined plate. They found that increasing the angle of inclination is a decreasing function of skin friction and heat flux. Ellahi [20] provided the analytical solutions of MHD non-Newtonian nanofluids passing through a pipe by considering the temperature-dependent viscosity. Sheikholeslami et al. [21] presented the numerical outcomes of nanofluid flow and temperature transmission in the presence of a magnetic field. Takhar and Nath [22] conducted a statistical study of MHD spinning flow above an unsteady enlarging pane. The combined impact of slip circumstances and Joule heating on the MHD peristaltic flows of a hyperbolic curvature nanofluid in a tending planar channel was investigated by Hayat et al. [23]. Rizwana et al. [24] studied the MHD oblique immobility point flow of a nanofluid. Ahmed et al. [25] described the carbon nanotube magneto-hydrodynamics of nanofluid flow on a stretching surface. Hybrid nanofluid entropy generation and temperature-dependent viscosity were discussed by Ahmad et al. [26]. Shahid et al. [27] conducted a numerical examination of stimulation energy on MHD nanofluid flow. Bahireal et al. [28] examined a manganese-zinc ferrite water nanofluid under a nonuniform magnetic field. Recently, many researchers have determined the effects of heat transfer and magnetism on nanofluids [29,30,31]. Mahian et al. [32] contributed to this research area by reviewing recent advances in the modeling of nanofluid flow in three dimensions for single-phase and two-phase nanofluids. Waqas et al. [33] examined the MHD flow of a hybrid nanofluid over a spinning disc with nonlinear thermal radiation and found favorable agreement in their results. Yasin et al. [34] investigated the impact of several factors on the 2D MHD frontier layer movement of an electoral conducting fluid above a stretchy surface, including the heat sink and suction parameter.
Thermal radiation has a critical part of a variety of industrial uses, including glass manufacturing and heating system design, as well as cosmos technology uses such as aeronautical aerodynamic rockets. In recent years, some research on nonlinear radiative heat transport has been published [35,36,37]. Imtiaz et al. [38] considered radiation effects on the movement of carbon nanotubes amongst stretchy rotational disks. Over a nonlinear stretched sheet, Cortell [39] investigated the properties of viscous degeneration and heat radiation. In the presence of thermal radiation from a nanofluid, Hady et al. [40] examined the impact of heat transmission across a nonlinear expanding sheet. Hussain et al. [41] examined the Carreau–Yasuda temperature convention near a stagnation point. Benos et al. [42] conducted analytical research in the presence of radiation, the Lorentz force, the Navier slip boundary condition, and the heat source. Alsani et al. [43] deliberated the joint effects of the inclined applied magnetic field, the permeable enlarging surface, mass transportation, and radiative warming on micropolar flow. Hussain et al. [44] discussed the MHD for viscid nanofluid with radiative effects. Mousavi et al. [45] presented a dual solution for Casson hybrid nanofluid flow above a widening surface. Mikhailenko et al. [46,47] computationally examined the convective nanofluid circulation and heat transmission within a rotating square chamber with a local isothermal element using a wide range of Rayleigh numbers, nanoparticle concentrations, and Taylor numbers. Mustafa et al. [48] considered boundary layer flow with the existence of nonlinear radiative temperature transmission. They concluded that the heat and temperature frontier layer width increase as the thermophoretic effects and Brownian motion intensify.
To the best of our knowledge, no one has ever described the rotating flow of a nanofluid generated by a broadening surface. Therefore, this comparative study addresses this gap in the current research. Interesting aspects of nonlinear radiative heat transmission for Ag- and Au-water-based nanofluid are also discussed. This research enables the reader to investigate the issue of both large and small temperature variations between the enlarging surface and the fluid. The leading nonlinear differential coordination is dealt with by using the powerful bvp4c technique. The Tiwari and Das [49] model is employed to discuss the problem. The effects of different constraints on velocity and temperature are emphasized. The impact of the surface radiative parameter , the magnetic parameter , and the rotation parameter on temperature, velocity, and skin friction coefficients are calculated, visually confirmed, and discussed for Ag0 and -water-based nanofluids.
2. Materials and Methods
Consider the rotating flow of -water and -water ferrofluid that is generated by a radiative surface parallel to the plane. The surface is stretched uniformly in the direction at constant rate . The temperature beyond the thermal boundary layer is , whereas denotes the temperature on the surface of the sheet. Geometry of the problem is shown in Figure 1. The Tiwari and Das model [49] equations symbolizing the preservation of mass, energy, and momentum are expressed as:
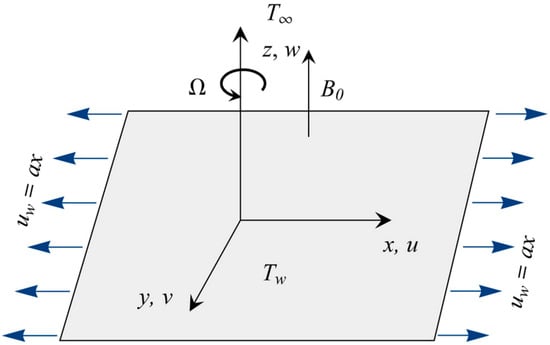
Figure 1.
Geometry of the problem.
With the following boundary conditions:
where is the component, is the component, and is the component of angular velocity ; is the fluid’s dynamic viscosity; is the density of the nanofluid; is the thermal diffusivity of the nanofluid; is the nanofluid’s temperature; is the wall temperature; is the ambient fluid temperature; is the volumetric heat capacity of the nanofluid; is the volumetric heat capability of the base fluid; is the volumetric heat capacity of the solid nanoparticles; and is a consistent magnetic field applied normally to the sheet. is the Rosseland radiative temperature fluidity, where is the Stefan–Boltzmann coefficient and is the mean immersion coefficient. As shown below, all these are connected to the particle volume fraction of the nanoparticles [50].
Furthermore, Maxwell [51] describes the electrical conductivity of nanofluid as:
The volume fraction of the nanoparticles is denoted by in Equations (6)–(10), and subscripts and refer to solid and fluid, respectively. Table 1 shows the thermophysical characteristics of the base fluid and solid nanoparticles.

Table 1.
Thermophysical characteristics of the base fluid and solid nanoparticles.
In the following equations, we seek a similarity solution [6] for Equations (1)–(4),
The steadiness Equation (1) is identically satisfied in the preceding equations, whereas Equations (1)–(5) become:
with conditions as follows:
represents the Prandtl number of base fluid, is the radiation constraint, is the magnetic field constraint, is the proportion of rotation to the enlarging surface rate, and is the temperature ratio parameter [52].
The skin friction coefficients , and Nusselt number are of physical relevance, and are defined as follows:
The wall shear stress is supplied by and , and is the wall temperature flux given by:
where is the Reynold’s number.
The rotational flow and temperature transmission of -water and -water ferrofluid, generated by a linear enlarging surface, were investigated in this research using the Tiwari and Das model [49]. The numerical results of Equations (12)–(14), under the conditions of Equation (15), were calculated in MATLAB using the bvp4c method. The volume portion was assumed to be in the range of in all findings (as above from 0.2 is not feasible due to aggregation), and the Prandtl number used for water was Pr = 6.2. We associated pure base fluid using Wang’s [1] and Nazar et al.’s [3] studies and found an extremely high agreement with them (Table 2).

Table 2.
For specific situations (, the present results are compared to prior research.
3. Results and Discussion
A numerical calculation for steady three-dimensional flow was executed to analyze the outcomes of the current problem. The numerical values of the local Nusselt number for some values of the parameters are computed in Table 3 and Table 4. The magnitude of decays severely with the volume fraction when a large wall-to-ambient temperature ratio is considered. When the magnetic parameter value rises, the Lorentz force acts perpendicularly on the surface, resulting in the decay in the Nusselt number in the absence of radiation, and it grows when radiation exists. Similar behavior can be noted from the tables for rotation parameters. As rotation rises, the Nusselt number decreases for the absence and increases for the existence of radiation. Moreover, has an inverse and nonlinear relation with the radiation parameter . This outcome is true for both linear and nonlinear cases and holds in linear and non-linear situations.

Table 3.
Values of the local Nusselt number (for -water nanofluid) for different values of embedded constraints.

Table 4.
Values of the Nusselt number (for -water nanofluid) for changed values of embedded constraints.
The impact of the magnetic field constraint on the dimensionless component and component of velocity is shown in Figure 2 and Figure 3. The function has a parabolic profile with a negative value, indicating flow in the negative direction. The flow loses speed in both the x and y directions as increases. In both types of nanofluid, the existence of magnetic field limits fluid mobility, resulting in a smaller boundary layer and increased magnetic field intensity.
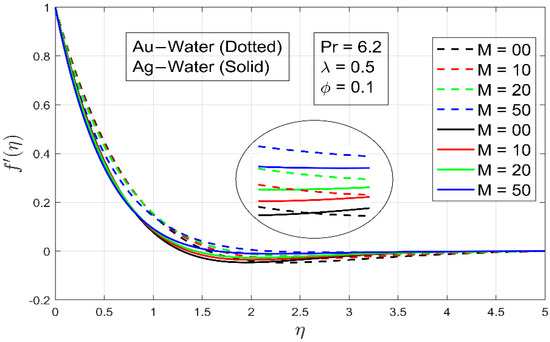
Figure 2.
The effect of parameter on .
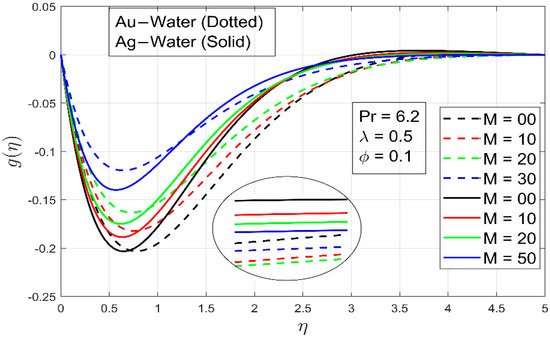
Figure 3.
The effect of parameter on .
The influence of ratio on the and components of velocity is shown in Figure 4 and Figure 5. When compared to the rotation rate, a larger value of implies lesser stretching rates (along the x axis). As a result, when increases, the component of velocity is inversely proportional to and the strength of the component of velocity rises. The behavior is similar for both nanofluids.
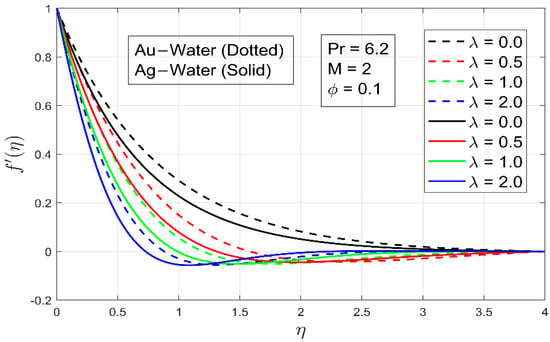
Figure 4.
The effect of parameter on .
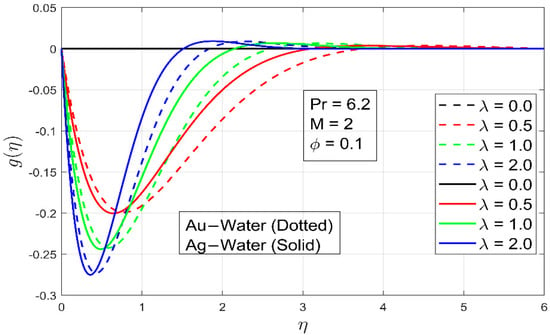
Figure 5.
The effect of parameter on .
The skin friction coefficients and are shown in Figure 6 and Figure 7 for varying values of and volume fraction , respectively. Because fluid exerts stress on the stretched wall, the values of skin friction and are negative. The magnitudes of and diminish as increases because a transverse magnetic field has a propensity to produce a Lorentz force, which opposes transference. For both types of nanofluid, this results in a decrease in flow speed and an increase in surface shear stress. Figure 8 depicts the effect of volume fraction on the temperature. Due to the consideration of a large , the high viscous force creates a thicker thermal barrier, as predicted. This can also be noted as the wall temperature gradient increases.
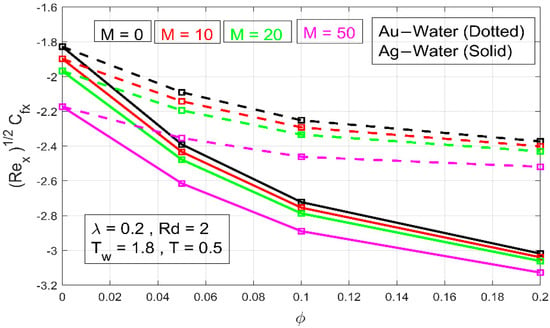
Figure 6.
The effect of parameter on .
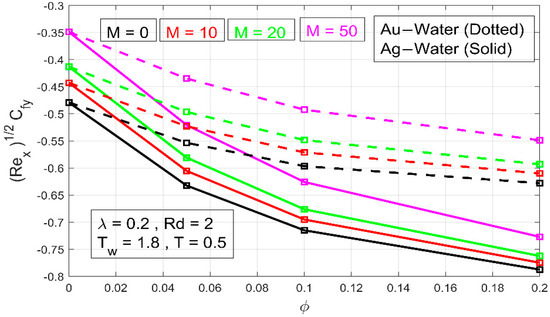
Figure 7.
The effect of parameter on .
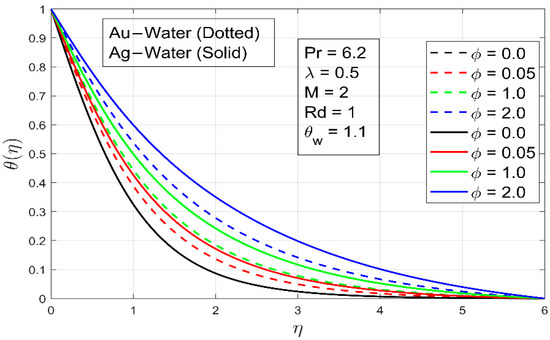
Figure 8.
The effect of parameter on .
The effect of the magnetic field M on temperature is shown in Figure 9. The temperature rises due to the resistance linked with the Lorentz force caused by the applied magnetic field. As a result, as increases, the temperature increases and the thermal boundary layer thickens. On a thermal boundary layer, the behavior of ratio is qualitatively comparable to that of M (Figure 10). When it changes, however, the consequences are more noticeable.
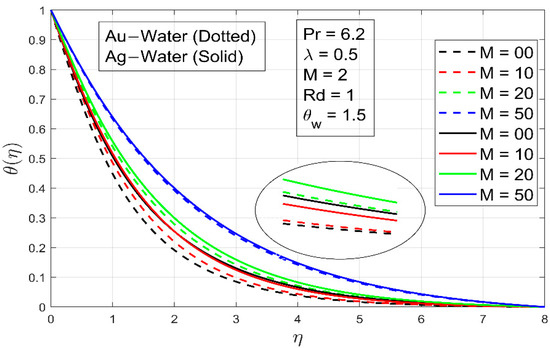
Figure 9.
The effect of parameter on .
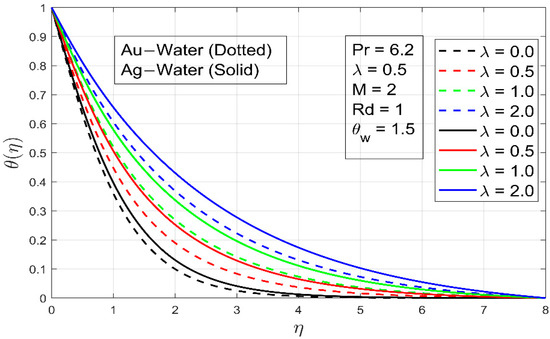
Figure 10.
The effect of parameter on .
Figure 11 depicts the temperature profile for different values of the temperature ratio parameter . When increases, unlike the linear radiation scenario, the profile changes from a regular form to an S-shaped thicker profile. The thermal diffusivity is a function of temperature and controls the enlarging of the thermal boundary layer. Because the sheet is warmer than the fluid, is higher adjacent to the sheet than at the fluid layer. As a result, increasing the wall-to-ambient temperature ratio parameter tends to lower the temperature gradient at the surface, resulting in the inflection point. When is sufficient enough, the concavity of temperature functionality changes in [0, 1). In the case of linear radiation heat transmission, however, the concavity has been retained. As becomes greater, the temperature gradient between the wall and the environment increases, resulting in a thicker thermal frontier layer. These findings are consistent with those in the literature.
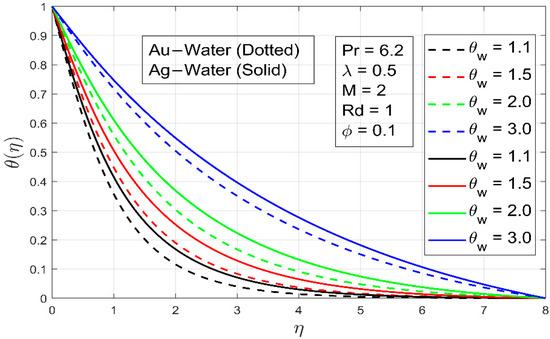
Figure 11.
The effect of parameter on .
The effects of the radiation parameter are shown in Figure 12 and Figure 13 for both linear and nonlinear radiative heat flows. When the radiation parameter increases in the linear radiation scenario, the temperature wall slope approaches a constant finite value. In the event of nonlinear radiation, this effect is not retained. When a larger radiation parameter is considered, the temperature seems to be higher. Furthermore, compared to linear radiation, temperature increases gradually with nonlinear radiation. We may deduce from Figure 12 that the outcomes of linear and nonlinear radiation are equal only when small and is near the unit. As the radiation parameter steadily raises, the variation between linear and nonlinear radiation grows.
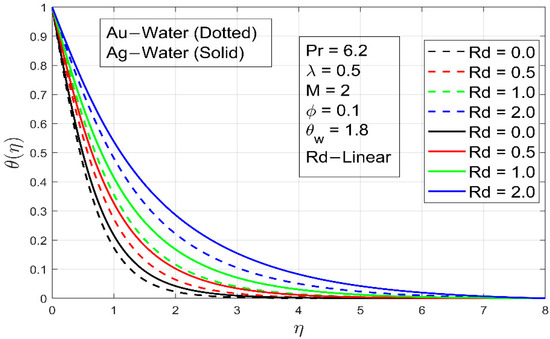
Figure 12.
The effect of parameter linear on .
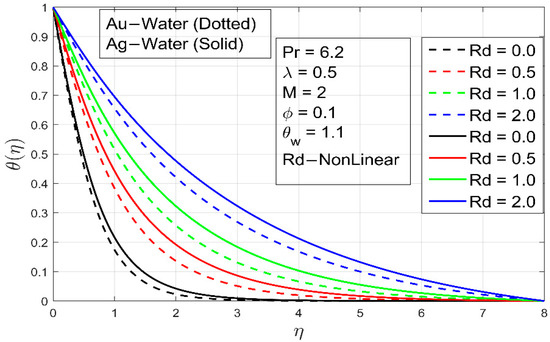
Figure 13.
The effect of parameter nonlinear on .
Figure 14 demonstrates that when the volume fraction is raised, the local Nusselt number exhibits an inverse relationship. Notably, the temperature transmission rate from the sheet changes substantially with M.
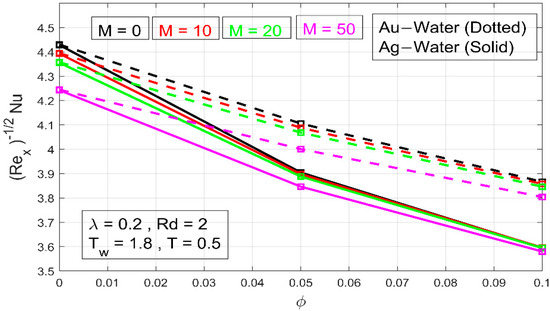
Figure 14.
The effect of on .
4. Conclusions
In this study, we investigated the magnetic and radiative effects on three-dimensional rotating nanofluid flow. The Tiwari and Das [49] model was used to investigate the rotational flow and temperature transmission of -water and -water ferrofluids across a deformable surface. A numerical technique was used in MATLAB to solve the proposed nonlinear boundary value problem. The following are some of the most important findings of this study:
- The local Nusselt number increases as magnetic field increases;
- The y component of velocity is negative for both types of nanofluids, and the velocity distribution is parabolic;
- The parameter has fundamentally different impacts on the and components of velocity;
- The velocity distributions and both decay when a large magnetic field is applied;
- The magnetic field and the volume fraction have inverse relationships with the skin friction coefficient and local Nusselt numbers, respectively;
- The parameter enhances the local Nusselt number as it increases;
- -water nanofluid has a high-temperature transfer constant compared to -water nanofluid.
Author Contributions
Conceptualization, A.H. (Azad Hussain) and M.A.; methodology, A.R.; software, M.A.; validation, M.A.E., A.H. (Ali Hassan) and C.A.S.; formal analysis, A.R.; investigation, A.R., A.H. (Ali Hassan); resources, M.A.; data curation, K.S.N.; writing—original draft preparation, M.A., writing—review and editing, A.H. (Ali Hassan).; visualization, M.A.E. and C.A.S.; supervision, A.H. (Azad Hussaian).; project administration, K.S.N.; funding acquisition, M.A.E. All authors have read and agreed to the published version of the manuscript.
Funding
The authors extend their appreciation to the Deanship of Scientific Research at King Khalid University, Saudi Arabia, for funding this work through the Research Group Program under grant no.: RGP. 2/108/42.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding authors.
Acknowledgments
The authors extend their appreciation to the Deanship of Scientific Research at King Khalid University, Saudi Arabia, for funding this work through the Research Group Program under grant no.: RGP. 2/108/42.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wang, C.Y. Stretching a surface in a rotating fluid. Z. Angew. Math. Und Phys. 1988, 39, 177–185. [Google Scholar] [CrossRef]
- Rajeswari, V.; Nath, G. Unsteady flow over a stretching surface in a rotating fluid. Int. J. Eng. Sci. 1992, 30, 747–756. [Google Scholar] [CrossRef]
- Nazar, R.; Amin, N.; Pop, I. Unsteady boundary layer flow due to a stretching surface in a rotating fluid. Mech. Res. Commun. 2004, 31, 121–128. [Google Scholar] [CrossRef]
- Vajravelu, K.; Kumar, B. Analytical and numerical solutions of a coupled non-linear system arising in a three-dimensional rotating flow. Int. J. Non-Linear Mech. 2004, 39, 13–24. [Google Scholar] [CrossRef]
- Hayat, T.; Javed, T.; Sajid, M. Analytic solution for MHD rotating flow of a second grade fluid over a shrinking surface. Phys. Lett. A 2008, 372, 3264–3273. [Google Scholar] [CrossRef]
- Zaimi, K.; Ishak, A.; Pop, I. Stretching surface in rotating viscoelastic fluid. Appl. Math. Mech. 2013, 34, 945–952. [Google Scholar] [CrossRef]
- Hayat, T.; Farooq, M.; Alsaedi, A.; Al-Solamy, F. Impact of Cattaneo-Christov heat flux in the flow over a stretching sheet with variable thickness. AIP Adv. 2015, 5, 087159. [Google Scholar] [CrossRef]
- Rashidi, M.M.; Abelman, S.; Mehr, N.F. Entropy generation in steady MHD flow due to a rotating porous disk in a nanofluid. Int. J. Heat Mass Transf. 2013, 62, 515–525. [Google Scholar] [CrossRef]
- Choi, S.U.; Eastman, J.A. Enhancing Thermal Conductivity of Fluids with Nanoparticles; No. ANL/MSD/CP-84938; CONF-951135-29; Argonne National Lab.: Lemont, IL, USA, 1995. [Google Scholar]
- Kuznetsov, A.; Nield, D. Natural convective boundary-layer flow of a nanofluid past a vertical plate. Int. J. Therm. Sci. 2010, 49, 243–247. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Sheykholeslami, F.B.; Khoshhal, S.; Mola-Abasia, H.; Ganji, D.D.; Rokni, H.B. Effect of magnetic field on Cu–water nanofluid heat transfer using GMDH-type neural network. Neural Comput. Appl. 2014, 25, 171–178. [Google Scholar] [CrossRef]
- Nield, D.; Kuznetsov, A. Forced convection in a parallel-plate channel occupied by a nanofluid or a porous medium saturated by a nanofluid. Int. J. Heat Mass Transf. 2014, 70, 430–433. [Google Scholar] [CrossRef]
- Khan, J.A.; Mustafa, M.; Hayat, T.; Sheikholeslami, M.; Alsaedi, A. Three-Dimensional Flow of Nanofluid Induced by an Exponentially Stretching Sheet: An Application to Solar Energy. PLoS ONE 2015, 10, e0116603. [Google Scholar] [CrossRef]
- Mustafa, M.; Khan, J.A. Model for flow of Casson nanofluid past a non-linearly stretching sheet considering magnetic field effects. AIP Adv. 2015, 5, 077148. [Google Scholar] [CrossRef] [Green Version]
- Rashidi, M.M.; Freidoonimehr, N.; Hosseini, A.; Bég, O.A.; Hung, T.K. Homotopy simulation of nanofluid dynamics from a non-linearly stretching isothermal permeable sheet with transpiration. Meccanica 2014, 49, 469–482. [Google Scholar] [CrossRef]
- Turkyilmazoglu, M. Nanofluid flow and heat transfer due to a rotating disk. Comput. Fluids 2014, 94, 139–146. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Ganji, D.D. Ferrohydrodynamic and magnetohydrodynamic effects on ferrofluid flow and convective heat transfer. Energy 2014, 75, 400–410. [Google Scholar] [CrossRef]
- Moraveji, M.K.; Hejazian, M. Natural convection in a rectangular enclosure containing an oval-shaped heat source and filled with Fe3O4/water nanofluid. Int. Commun. Heat Mass Transf. 2013, 44, 135–146. [Google Scholar] [CrossRef]
- Aydın, O.; Kaya, A. MHD mixed convective heat transfer flow about an inclined plate. Heat Mass Transf. 2009, 46, 129–136. [Google Scholar] [CrossRef]
- Ellahi, R. The effects of MHD and temperature dependent viscosity on the flow of non-Newtonian nanofluid in a pipe: Analytical solutions. Appl. Math. Model. 2013, 37, 1451–1467. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Hatami, M.; Ganji, D.D. Nanofluid flow and heat transfer in a rotating system in the presence of a magnetic field. J. Mol. Liq. 2014, 190, 112–120. [Google Scholar] [CrossRef]
- Takhar, H.S.; Nath, G. Unsteady flow over a stretching surface with a magnetic field in a rotating fluid. Z. Für Angew. Math. Und Phys. 1998, 49, 989–1001. [Google Scholar] [CrossRef]
- Hayat, T.; Shafique, M.; Tanveer, A.; Alsaedi, A. Magnetohydrodynamic effects on peristaltic flow of hyperbolic tangent nanofluid with slip conditions and Joule heating in an inclined channel. Int. J. Heat Mass Transf. 2016, 102, 54–63. [Google Scholar] [CrossRef]
- Rizwana, R.; Hussain, A.; Nadeem, S. Mix convection non-boundary layer flow of unsteady MHD oblique stagnation point flow of nanofluid. Int. Commun. Heat Mass Transf. 2021, 124, 105285. [Google Scholar] [CrossRef]
- Ahmed, Z.; Nadeem, S.; Saleem, S.; Ellahi, R. Numerical study of unsteady flow and heat transfer CNT-based MHD nanofluid with variable viscosity over a permeable shrinking surface. Int. J. Numer. Methods Heat Fluid Flow 2019, 29, 4607–4623. [Google Scholar] [CrossRef]
- Ahmad, S.; Nadeem, S.; Ullah, N. Entropy generation and temperature-dependent viscosity in the study of SWCNT–MWCNT hybrid nanofluid. Appl. Nanosci. 2020, 10, 5107–5119. [Google Scholar] [CrossRef]
- Shahid, A.; Huang, H.L.; Khalique, C.M.; Bhatti, M.M. Numerical analysis of activation energy on MHD nanofluid flow with exponential temperature-dependent viscosity past a porous plate. J. Ther. Anal. Calorim. 2021, 143, 2585–2596. [Google Scholar] [CrossRef]
- Bahiraei, M.; Hosseinalipour, S.M.; Hangi, M. Numerical study and optimization of hydrothermal characteristics of Mn–Zn ferrite nanofluid within annulus in the presence of magnetic field. J. Supercond. Novel Magn. 2014, 27, 527–534. [Google Scholar] [CrossRef]
- Zhang, X.; Huang, H. Effect of magnetic obstacle on fluid flow and heat transfer in a rectangular duct. Int. Commun. Heat Mass Transf. 2014, 51, 31–38. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Bandpy, M.G.; Ellahi, R.; Zeeshan, A. Simulation of MHD CuO–water nanofluid flow and convective heat transfer considering Lorentz forces. J. Magn. Magn. Mater. 2014, 369, 69–80. [Google Scholar] [CrossRef]
- Bahiraei, M.; Hangi, M. Flow and heat transfer characteristics of magnetic nanofluids: A review. J. Magn. Magn. Mater. 2015, 374, 125–138. [Google Scholar] [CrossRef]
- Mahian, O.; Kolsi, L.; Amani, M.; Estellé, P.; Ahmadi, G.; Kleinstreuer, C.; Pop, I. Recent advances in modeling and simulation of nanofluid flows-Part I: Fundamentals and theory. Phys. Rep. 2019, 790, 1–48. [Google Scholar] [CrossRef]
- Waqas, H.; Farooq, U.; Naseem, R.; Hussain, S.; Alghamdi, M. Impact of MHD radiative flow of hybrid nanofluid over a rotating disk. Case Stud. Ther. Eng. 2021, 26, 101015. [Google Scholar] [CrossRef]
- Yasin, M.H.M.; Ishak, A.; Pop, I. MHD heat and mass transfer flow over a permeable stretching/shrinking sheet with radiation effect. J. Magn. Magn. Mater. 2016, 407, 235–240. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Rashidi, M.M.; Ganji, D.D. Effect of non-uniform magnetic field on forced convection heat transfer of Fe3O4–water nanofluid. Comput. Methods Appl. Mech. Eng. 2015, 294, 299–312. [Google Scholar] [CrossRef]
- Pantokratoras, A.; Fang, T. Blasius flow with non-linear Rosseland thermal radiation. Meccanica 2014, 49, 1539–1545. [Google Scholar] [CrossRef]
- Mushtaq, A.; Mustafa, M.; Hayat, T.; Alsaedi, A. Effects of thermal radiation on the stagnation-point flow of upper-convected Maxwell fluid over a stretching sheet. J. Aerosp. Eng. 2014, 27, 04014015. [Google Scholar] [CrossRef]
- Imtiaz, M.; Hayat, T.; Alsaedi, A.; Ahmad, B. Convective flow of carbon nanotubes between rotating stretchable disks with thermal radiation effects. Int. J. Heat Mass Transf. 2016, 101, 948–957. [Google Scholar] [CrossRef]
- Cortell, R. Effects of viscous dissipation and radiation on the thermal boundary layer over a nonlinearly stretching sheet. Phys. Lett. A 2008, 372, 631–636. [Google Scholar] [CrossRef]
- Hady, F.M.; Ibrahim, F.S.; Abdel-Gaied, S.M.; Eid, M.R. Radiation effect on viscous flow of a nanofluid and heat transfer over a nonlinearly stretching sheet. Nanoscale Res. Lett. 2012, 7, 229. [Google Scholar] [CrossRef] [Green Version]
- Hussain, A.; Rehman, A.; Nadeem, S.; Malik, M.Y.; Issakhov, A.; Sarwar, L.; Hussain, S. A combined convection Carreau–Yasuda nanofluid model over a convective heated surface near a stagnation point: A numerical study. Math. Prob. Eng. 2021, 2021, 6665743. [Google Scholar] [CrossRef]
- Benos, L.T.; Mahabaleshwar, U.S.; Sakanaka, P.H.; Sarris, I.E. Thermal analysis of the unsteady sheet stretching subject to slip and magnetohydrodynamic effects. Ther. Sci. Eng. Prog. 2019, 13, 100367. [Google Scholar] [CrossRef]
- Aslani, K.E.; Mahabaleshwar, U.S.; Singh, J.; Sarris, I.E. Combined Effect of Radiation and Inclined MHD Flow of a Micropolar Fluid Over a Porous Stretching/Shrinking Sheet with Mass Transpiration. Int. J. Appl. Comput. Math. 2021, 7, 60. [Google Scholar] [CrossRef]
- Hussain, A.; Sarwar, L.; Akbar, S.; Malik, M.Y.; Ghafoor, S. Model for MHD viscoelastic nanofluid flow with prominence effects of radiation. Heat Transf. Asian Res. 2019, 48, 463–482. [Google Scholar] [CrossRef]
- Mousavi, S.M.; Rostami, M.N.; Yousefi, M.; Dinarvand, S.; Pop, I.; Sheremet, M.A. Dual solutions for Casson hybrid nanofluid flow due to a stretching/shrinking sheet: A new combination of theoretical and experimental models. Chin. J. Phys. 2021, 71, 574–588. [Google Scholar] [CrossRef]
- Mikhailenko, S.A.; Sheremet, M.A.; Oztop, H.F.; Abu-Hamdeh, N. Thermal convection in Al2O3–water nanoliquid rotating chamber with a local isothermal heater. Int. J. Mech. Sci. 2019, 156, 137–145. [Google Scholar] [CrossRef]
- Mikhailenko, S.A.; Sheremet, M.A.; Pop, I. Convective heat transfer in a rotating nanofluid cavity with sinusoidal temperature boundary condition. J. Ther. Anal. Calorim. 2019, 137, 799–809. [Google Scholar] [CrossRef]
- Mustafa, M.; Mushtaq, A.; Hayat, T.; Ahmad, B. Nonlinear radiation heat transfer effects in the natural convective boundary layer flow of nanofluid past a vertical plate: A numerical study. PLoS ONE 2014, 9, e103946. [Google Scholar] [CrossRef]
- Tiwari, R.K.; Das, M.K. Heat transfer augmentation in a two-sided lid-driven differentially heated square cavity utilizing nanofluids. Int. J. Heat Mass Transf. 2007, 50, 2002–2018. [Google Scholar] [CrossRef]
- Nadeem, S.; Ur Rehman, A.; Mehmood, R.; Adil Sadiq, M. Partial Slip effects on a rotating flow of two phase nanofluid over a stretching surface. Curr. Nanosci. 2014, 10, 846–854. [Google Scholar] [CrossRef]
- Maxwell, J.C. A Treatise on Electricity and Magnetism; Clarendon Press: Oxford, UK, 1873; Volume 1. [Google Scholar]
- Mushtaq, A.; Mustafa, M.; Hayat, T.; Alsaedi, A. On the numerical solution of the nonlinear radiation heat transfer problem in a three-dimensional flow. Z. Nat. A 2014, 69, 705–713. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).