Abstract
Advancements in internal combustion technology, such as efficiency improvements and the usage of new complex fuels, are often coupled with developments of suitable numerical tools for predicting the complex dynamic behavior of sprays. Therefore, this work presents a Eulerian multi-fluid model specialized for the dynamic behavior of dense evaporating liquid fuel sprays. The introduced model was implemented within the open-source OpenFOAM library, which is constantly gaining popularity in both industrial and academic settings. Therefore, it represents an ideal framework for such development. The presented model employs the classes method and advanced interfacial momentum transfer models. The droplet breakup is considered using the enhanced WAVE breakup model, where the mass taken from the parent droplets is distributed among child classes using a triangular distribution. Furthermore, the complex thermal behavior within the moving droplets is considered using a parabolic temperature profile and an effective thermal conductivity approach. This work includes an uncertainty estimation analysis (for both spatial and temporal resolutions) for the developed solver. Furthermore, the solver was validated against two ECN Spray A conditions (evaporating and non-evaporating). Overall, the presented results show the capability of the implemented model to successfully predict the complex dynamic behavior of dense liquid sprays for the selected operating conditions.
1. Introduction
Although fuel spray modeling is not a new or unknown problem, continuous advancements in efficiency improvements and new fuels require new modeling solutions with improved functionality and accuracy. Therefore, numerical tools for predicting the complex, dynamic behavior of sprays impact the development of improved internal combustion (IC) engines. The utilization of numerical simulations greatly affects the development and improvement of multiple other complex engineering challenges, e.g., furnaces [1], fluidized beds [2], fuel cells [3], and carbon capture and storage [4].
As previously mentioned, the two primary development efforts in IC technology are improving the efficiency of engines and developments regarding new fuels and engines which can run on them. Efficiency improvements are mainly related to the compression ignition regime and increasing the compression ratio [5], which often contributes to an increase in nitrogen oxide emissions. The partially premixed combustion approach [6] is one of the various strategies that should allow high efficiencies and minimize emissions. Even the spark-ignited engines have several methods for reducing emissions and increasing efficiencies, e.g., the corona ignition condition [7], where the electron dissociation reaction replaces the classic hydrocarbon oxidation, and partial fuel stratification combustion strategies [8]. Optimal fuel–air mixing is a prerequisite for emissions reduction, and is directly coupled to the flow conditions occurring in the nozzle. Injection velocity controls the atomization and droplet breakup, directly affecting the liquid core penetration and evaporation rate.
Complex in-nozzle flow properties, such as cavitation, initial turbulent fluctuations, and high injection pressures, promote the liquid core’s atomization [9,10,11,12]. Another approach is to employ extreme pressure and temperature conditions, which contribute to diffusive mixing at supercritical states [13,14,15,16,17,18]. Predicting and controlling these complex phenomena is vital for increasing the efficiency of modern IC engines.
Modern engines are also required to operate on a broad range of different fuels, for example, biofuels [19], solar fuels [20] (where solar energy is stored as synthetic chemical fuels, i.e., methanol or ethanol), and “smart” fuels which have additives for improving the properties of the fuel (e.g., ignition control [21] and reduction of emissions [22]). Furthermore, surrogate fuels [23,24] are developed to mimic the selected properties of targeted real fuels. Increasing demand in the heavy-duty market resulted in the utilization of naphtha and heavy fuel oils as alternative fuels [25,26].
Computational fluid dynamics (CFD) proposes numerous multiphase approaches which are suitable for modeling liquid sprays. The most detailed and computationally most expensive is the direct numerical simulation (DNS) method [27,28,29,30]. DNS does not need any sub-models to reproduce detailed spray behavior, such as atomization, secondary breakup, and turbulence coupling between the liquid and gas phases. DNS is still not viable for standard engineering calculations, but it is constantly gaining popularity due to the increasing HPC resource availability.
The most popular approach is the Lagrangian method, where the group of droplets (parcels) are traced in a Lagrangian manner. In contrast, the continuous phase is represented as a continuum in the Eulerian coordinates. Despite its popularity and multiple benefits, this approach has some disadvantages, e.g., problems with modeling the near-nozzle region where the spray is denser [27,31], pronounced sensitivity to cell resolution [32], and problems with numerical instabilities [33]. Furthermore, the droplet phase and the continuous phase are calculated in a decoupled manner.
The third approach—the Euler–Euler approach—describes both the droplet disperse phase and the continuous phase as interpenetrating continua in the Eulerian coordinates. Therein, all phases are described using properly derived conservation equations [34,35], but some of the small-scale phenomena are neglected due to the averaging procedure. This method has various formulations, but this study focuses on the Eulerian multi-fluid model. This approach couples the population balance equation (PBE) [36] with the averaged momentum and continuity equations, which allows modeling of polydisperse flows. For the discretization of the PBE, a classes method is employed. The PBE is divided into an arbitrary number of droplet classes with predefined diameters. Consequently, all droplet classes have their phase continuity and momentum equations, which introduce higher precision due to the allowed spatial and temporal variance in velocity and interfacial momentum transfer models (highly dependent on the dispersed element size). The mixture continuity equation is used to derive the mixture pressure equation, and all phases, including the single continuous phase, share the same mixture pressure. The higher precision and resolution of the results come at a price. The numbers of equations and calculations that need to be executed are directly coupled to the selected number of droplet classes.
Particular problems encountered by the engineering and academic communities require different levels of accuracy and execution speed. Therefore, all three aforementioned approaches are actively used and developed [27,28,37,38,39,40,41,42,43,44].
This research presents the upgrade of the previously developed and published Eulerian multi-fluid model (specialized for dense spray applications) with evaporation capability. The developed opensource framework can now successfully predict the dynamic behavior of dense evaporating liquid fuel sprays, i.e., the atomization and secondary breakup in the dense near-nozzle region, and the evaporation and mixing phenomena which dominantly occur in the dilute part of the spray. This work is a significant upgrade to the previously developed and published model [45,46,47]. The addition of an energy conservation equation, species transfer, and density variance allow the implementation of an evaporation model. Furthermore, to capture the finite thermal conductivity of droplets, the model also includes a parabolic temperature profile within droplets, and to account for the internal flow within the droplets, an effective thermal conductivity approach is employed. The developed model was tested and validated with the ECN Spray A experimental measurements [48,49,50]. The development was done within the OpenFOAM library. To the authors’ knowledge, such a detailed modeling approach has not yet been applied with the Eulerian method using the multi-fluid formulation. The proposed model allows straightforward upgrades in the future, allowing simulation of even more complex fuel behavior (e.g., pronounced multi-component behavior).
The remainder of the paper is organized into four sections. Section 2 gives a detailed description of the mathematical model, i.e., updates and new implementations performed within the previously developed model. Section 3 presents the employed numerical procedure. Section 4 introduces the selected test cases and presents the numerical results, including uncertainty analysis and two validation cases for evaporating and non-evaporating conditions. Section 5 provides a conclusion and comments regarding the implemented model.
2. Mathematical Model
This work is a significant upgrade to the previously developed and published model, which was employed to predict the dynamic behavior of bubbly flows and non-evaporating dense sprays [45,46,47].
In this work, the model is further upgraded with evaporation handling, which requires implementing a species transfer equation and energy equations for all phases. Due to evaporation, the continuous phase exhibits significant changes in chemical composition, which directly influence the thermophysical properties. Substantial temperature differences also impact the thermophysical properties of the liquid fuel. Therefore, the phase continuity equations and momentum equations were re-implemented into a compressible formulation. Furthermore, the mass transfer due to droplet breakup is distributed among multiple child classes using a triangular distribution. The previously developed turbulence model is updated with an algebraic model, which improves the coupling of the droplet turbulence variables with the continuous phase turbulence.
This section presents the Eulerian multi-fluid model, which is specialized for high-speed evaporating sprays. The following sub-sections emphasize the updates and new developments within the described solver. The details regarding the employed averaging procedures, pressure-velocity coupling, and phase-intensive continuity and momentum equations can be found in [35,45,46,47,51,52]. The following sub-sections use the finite volume notation of Weller [51].
2.1. The Phase-Intensive Momentum Equation
Following the approach presented by [51], the compressible phase-intensive momentum equation can be generalized for a multi-fluid formulation:
where is the density-weighted ensemble averaged phase velocity (for phase ), gives the mixture pressure shared by all phases, is the phase density, is the phase fraction, gives the viscous and turbulent stress, and g denotes the gravitational acceleration. Vectors and denote the averaged interfacial momentum transfer term and net momentum source term due to mass transfer caused by droplet breakup and evaporation.
The interfacial momentum transfer term is responsible for exchanging momentum between the continuous gas phase and droplet classes. The momentum exchange is taken into account using the turbulent dispersion and drag. The momentum exchange term for the i-th droplet class reads:
In Equation (2), the subscript c denotes the continuous phase, and the subscript d, i signifies the i-th droplet phase. The term denotes the relative velocity, is the droplet diameter, is turbulence kinetic energy of the continuous phase, and gives the turbulent dispersion coefficient, which is calculated using the approach described by [53,54]. The droplet drag coefficient is implemented following the procedure described by [55], which takes into account large deformations of droplets:
where the droplet drag is blended between the drag of an ideal sphere and a disc, which has a 3.6 times larger drag. The blending factor , i.e., the normalized distortion parameter, is evaluated using the Taylor–Analogy (TAB) model [56]. The drag of an ideal sphere is evaluated using the correlation given by [57], which takes into account the local phase fraction correction for dense spray regions:
where gives the Reynolds number for the i-th droplet class.
The total interfacial momentum transfer to the continuous phase is given by:
where is the selected number of droplet classes.
2.2. Phase Continuity Equation
Following the approach presented by [51], the compressible phase continuity equation is generalized for a multi-fluid formulation:
where gives the relative velocity between phases i and j, and denotes the ensemble averaged mixture velocity:
and is given by:
In Equation (6), the net source term describes the mass transfer between the phases. In this work, the mass exchange between phases is taken into account using the breakup and evaporation model. The net mass exchange term for the i-th droplet class is given by:
where gives the droplet birth rate, and denotes the droplet death rate due to breakup. The term gives the droplet death rate due to evaporation. The net source term for the continuous phase is given by:
2.3. Breakup Model
Using the previously developed functionality [46], the aerodynamic interaction between the gas and high-speed liquid phases is taken into account using the WAVE breakup model [58,59,60,61,62]. The interaction develops and increases disturbances on the droplet’s surface, which eventually lead to the breakup of parent droplets into smaller child droplets. The size of child droplets (predicted stable radius) is directly proportional to the wavelength :
In this work, the proportionality coefficient is taken to be 0.61. The mass loss per unit volume (death rate) of the parent class i due to the breakup process is given by:
where the rate of change of the i-th class radius is evaluated as:
In Equation (13), denotes the breakup time of the i-th phase:
where is a model constant and denotes the estimated wavelength. Further details regarding the numerical implementation of the WAVE model for the multi-fluid formulation are given in [46].
In this work, the WAVE model is further upgraded by adding a probability distribution for the mass transfer to the child droplet classes. The implementation was done following the procedure described by [63]. In [63], the authors presented that this approach prevents the Eulerian multi-fluid model from overestimating the generation of small droplets. The distribution function smears the transfer of mass to multiple child droplet classes. This work employs the triangular distribution function, which is straightforward to implement because all parameters are directly available. Figure 1 gives an example of the approach employed for distributing mass transfer calculated with the WAVE breakup model. The mass taken from the parent class is distributed among the smaller droplet classes using a triangular distribution. The parent class’s lower boundary gives the upper limit b, and the lower limit a is given by the lower boundary of the smallest class. The distribution’s mode value c is given by the target diameter, estimated by the WAVE model . In Figure 1 the area given by the blue bars represents the weighting factors of individual child classes. To satisfy the mass conservation criterion, the sum of all weighting factors must be unity. In Figure 1 the red bar is given only to represent the location and bounds of the parent droplet class.
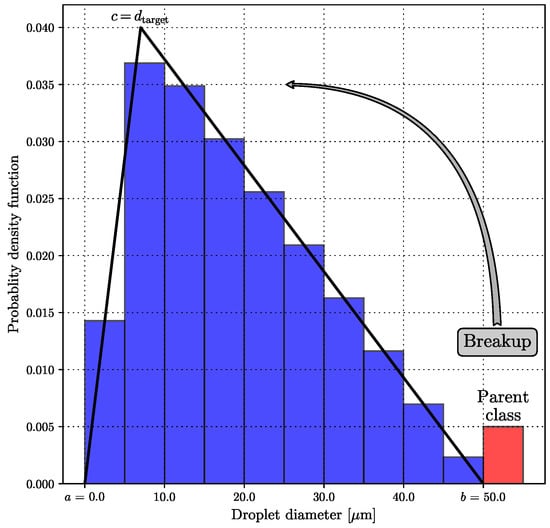
Figure 1.
Employed triangular distribution function for child droplets. The given example shows the triangular distribution for ten (uniform) child classes, when a = 0, b = 50, and c = 7 m.
The probability density function (PDF) of the selected triangular distribution is given by:
2.4. Turbulence Model
Due to the relatively low computation cost and reasonable accuracy, the standard k– model [64] is employed to account for turbulence effects within the simulation. To improve the model’s predictive capabilities for spray applications, the model utilizes the round jet correction of Pope [65], where . The droplet phase turbulence is coupled to the continuous phase turbulence values using an algebraic model [66,67]:
where is the turbulent kinetic energy of the droplet phase, and the frequency is given by:
and the relaxation time :
where denotes the kinematic viscosity of the continuous phase. The characteristic macroscopic length scale can be written as:
where is the turbulence model constant, and denotes the rate of dissipation of turbulent kinetic energy (of the continuous phase). Furthermore, the droplet phase eddy viscosity is evaluated using the following expression:
where is the eddy viscosity of the continuous phase.
2.5. Species Transfer
The fuel vapor species transfer equation is given by:
where is the mass fraction of the fuel vapor in the continuous phase, is the binary diffusion coefficient of fuel vapor, is the turbulent Schmidt number, and gives the source term due to the evaporation of droplet classes.
2.6. Energy Equation
Following the approach given by [67], the energy equation for the continuous phase is given by:
where denotes the static enthalpy of the continuous phase, is the specific heat capacity, and is the effective thermal conductivity. The net enthalpy source term describes the heat rate supplied to the gas phase, including both the convective heat transfer and evaporation. The droplet phase energy equation is given by:
where accounts for the energy transfer due to droplet breakup, convective heat transfer, and evaporation. Equation (23) does not include the energy diffusion term because a parabolic temperature profile model [68] considers the finite thermal conductivity within the droplet classes. Following the guidelines described in [68], the droplet surface temperature is calculated as:
where is the derivative of the droplet radius (with respect to time), is the latent heat of vaporization, and is given by:
, and is defined as:
In Equation (25), Nu is the Nusselt number. Furthermore, to take into account the intensive recirculation occurring inside the moving droplets, which is caused by the surface friction, an effective conductivity approach is adopted. Abramzon and Sirignano [69] suggested a practical approach where the droplet thermal conductivity is replaced by effective conductivity:
where the factor is calculated as:
In Equation (27), denotes the Peclet number of the i-th droplet phase.
The implemented parabolic temperature profile and effective conductivity model allow a more accurate prediction of the droplet thermal behavior [70]. Better prediction of the droplet temperature improves the evaluation of droplet surface properties that directly influence the phenomena occurring on the droplet’s surface, e.g., evaporation.
The temperature-dependent thermophysical properties of the liquid fuel and vapor were evaluated using the expressions available in [71,72].
2.7. Evaporation Model
For modeling the droplet evaporation process, a hydrodynamic approach is employed. This approach assumes that the fuel vapor near the droplet surface is saturated all the time. Therefore, the droplet evaporation rate is equal to the rate of the vapor diffusion going from the droplet surface to the surrounding gas [73]. This approach focuses more on modeling the diffusion process than the detachment process of molecules from the droplet surface, which is much more challenging. This work utilizes the Abramzon and Sirignano hydrodynamic model [69]. The authors employed the film theory to consider the convective transport caused by the relative velocity between the droplet and ambient gas. Furthermore, the model is applicable for non-unitary Lewis number (in the gas film) cases.
The proposed model gives the following relations for the instantaneous rate of droplet evaporation:
and
In this model, the averaged variables, i.e., the ones with overlines, are evaluated at a reference fuel vapor concentration and temperature using the “1/3 rule” [69]. In Equation (29), Sh denotes the dimensionless Sherwood number and gives the Spalding mass transfer number:
In Equation (30), is the average specific heat capacity of vapor in the film and denotes the Spalding heat transfer number:
The non-dimensional parameters are defined as [69]:
and
where the correction factors and are given by:
and
The non-dimensional parameters for non-evaporating droplets ( and ) are implemented as [69,74]:
and
where:
Assuming ideal mixing and by applying Raoult’s law, the mass fuel vapor fraction at the droplet surface is evaluated as [71,73]:
where and give the molar masses of vapor and surrounding gas. However, neglecting real gas behavior (at high temperatures and pressures) introduces deviations because the ideal behavior assumption does not consider molecular interactions (attractive and repulsive forces) [15,73,75]. In Equation (40), the term denotes the saturation vapor pressure, and for n-dodecane, it can be estimated using the following expression [73]:
During the execution of the solution procedure for the implemented evaporation model, is estimated using the old (from the previous iteration or time-step) value. The new value is evaluated using:
where is given by:
In Equation (43), indicates the dimensionless Lewis number. Both and are re-evaluated until the difference is below the desired accuracy [69]. The heat penetrating into the droplet is calculated as:
The droplet death rate due to evaporation can be evaluated using the following expression [76]:
and similarly, the heat penetrating the droplet class is given by:
3. Numerical Approach
The described model was implemented in foam-extend, a community-driven fork of OpenFOAM. Hence, the implemented equations were discretized using a collocated cell-centered finite volume method (FVM) [77,78]. The developed solution algorithm employs the PISO loop [79] and the selected solution procedure for each time step is presented in Algorithm 1.
| Algorithm 1 Employed solution procedure for each time step. |
| Evaluate the breakup and evaporation model. |
| Solve the phase continuity equations. |
| Evaluate the momentum transfer models. |
| Construct the phase momentum equations and predict fluxes. |
| Solve the energy equations. |
| Solve the mixture pressure equation. |
| Correct fluxes and reconstruct the velocity fields. |
| Solve the turbulence model. |
| Solve the species transfer equation. |
In this work, the mass fraction, turbulence variables, phase fraction variables, and energy variables were advected using a linear upwind-biased approximation. The momentum variables used the gamma scheme [80]. Time derivatives employed the first-order implicit Euler scheme. Laplacians, gradients, and cell-to-face interpolations were calculated using a linear interpolation. The solution of the pressure equation employed the selection algebraic multigrid algorithm [81] and the Gauss–Seidel smoother [82]. The solution procedure for the energy equations, phase continuity equations, turbulence model, and species transfer used the bi-conjugate gradient method, which was preconditioned by DILU [83].
4. Results and Discussion
This section presents the performed uncertainty estimation analysis (both grid and time step sensitivity) of the developed solver. Furthermore, the solver was tested for two ECN Spray A conditions (evaporating and non-evaporating) and compared to available experimental measurements [48,50].
The ECN Spray A test case included a fuel injector with a nominal nozzle outlet diameter of 0.09 mm, and n-dodecane as the injected fuel. In this work, the injection process was modeled using the blob injection model [62]—i.e., large droplets with a diameter similar to the nozzle size were injected into the domain. The velocity of the blobs was estimated from the fuel injection rate. The selected fuel injection curve [84] is given in Figure 2.
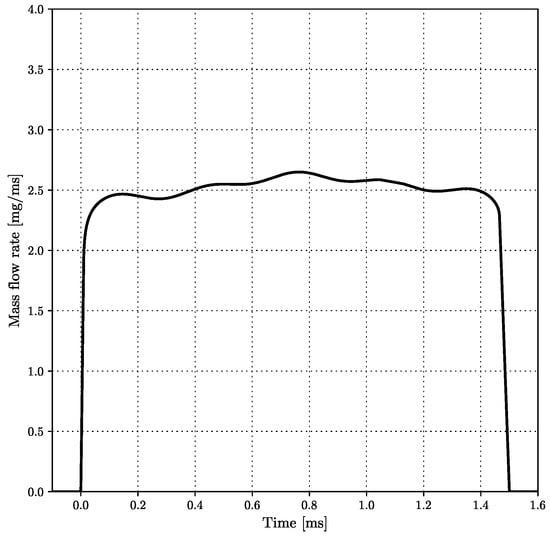
Figure 2.
Employed rate of fuel injection [84].
The employed two-dimensional wedge domain is presented in Figure 3. The inlet is located on the left side and has the same size as the selected nozzle. The remaining surfaces (except the axisymmetric wedge planes) were treated as open boundaries. Furthermore, the inlet side of the geometry is scaled down, compared to the outlet side, to increase the grid density in the radial direction in the near nozzle region. The domain size is selected to be sufficiently large to reduce the influence of boundary conditions on the numerical results.
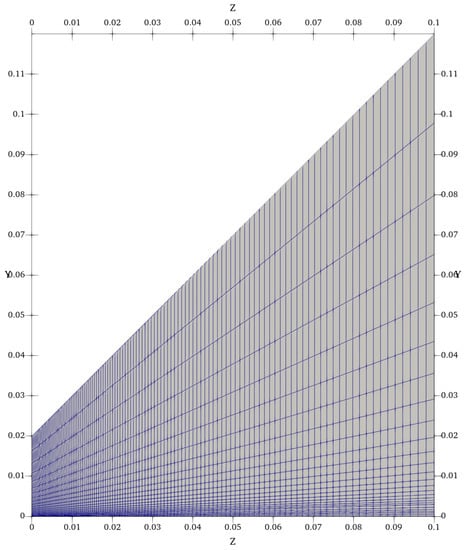
Figure 3.
Streamwise and radial cell density of the finest grid.
All presented results use the same set of non-uniform droplet classes (0.75, 2.25, 4.0, 6.0, 8.5, 20.0, 40.0, 60.0, and 80.0 m). The employed droplet classes have significantly greater resolution towards the smaller droplets, which agrees with the experimental measurements for the Spray A conditions [50].
4.1. Uncertainty Analysis
The employed uncertainty analysis followed the procedures for unsteady flows described in [85] and was performed using the ReFRESCO application [86]. To quantify the uncertainty of the implemented solver, multiple simulations were carried out for the same flow conditions by systematically varying the density of the employed computational grid and the selected time step.
The initial grid was defined to have two cells per nozzle radius in the radial direction. With increasing distance from the nozzle location, the refinement was progressively decreased, which resulted in 26 radial cells in total. In the streamwise direction, the first cell (near the nozzle exit) had a width of 0.25 mm, and it was gradually increased to 2 mm over a length of 0.1 m (total length of the domain), resulting in 118 cells. The initial grid is presented in Figure 3. The remaining three coarser grids were obtained by uniformly decreasing the number of cells in the streamwise direction, but the number and distribution of radial cells remained the same. However, references [32,87] suggest that even finer grids are required to resolve the near-nozzle and mixing layer accurately.
The uncertainty analysis was performed for the liquid penetration length. The penetration length was calculated as the streamwise distance from the nozzle outlet, where the cumulative liquid fuel mass reached 98.5% of the total liquid mass located in the computational domain. The uncertainty analysis employed the evaporation conditions for the Spray A test case, which will be described in a more detailed manner in Section 4.2.2. The input data for the analysis are presented in Table 1.

Table 1.
Input data for the uncertainty estimation analysis. The values give the liquid spray penetration length (in millimeters) at 0.2 ms (after start of injection) for various grids and time steps.
Table 2 presents the output of the analysis following the notation given by [85]. gives the input value of the most refined level, is the extrapolated value, and denotes the uncertainty estimate. The p and q variables present the achieved accuracy in space and time.

Table 2.
Output from the uncertainty estimation analysis.
Considering the previously described numerical settings in Section 3, the achieved second-order accuracy in space and the first-order accuracy in time were expected. The relatively high uncertainty value suggests that the liquid penetration length (for high threshold values) is sensitive to the employed spatial and temporal resolution. However, similar behavior was observed with various codes and models presented during the ECN Workshop [88].
4.2. Validation
The implemented model was tested and validated for evaporating and non-evaporating Spray A conditions. Both cases employed the finest computational grid and smallest time step from the previous section.
4.2.1. Non-Evaporating Conditions
This section demonstrates the predictive capability of the implemented breakup model by comparing the resulting droplet population in the dense part of the spray at non-evaporating conditions. The liquid fuel (n-dodecane) was injected into a vessel at 2.0 MPa and 300 K [50]. The resulting Sauter mean diameter (SMD) curve is compared to the available experimental measurements [50]. The comparison is shown in Figure 4. The given SMD curve was calculated as in [67]:
where and .
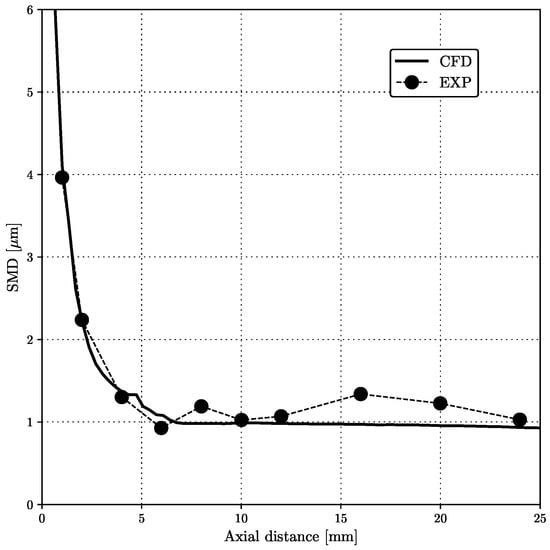
Figure 4.
Axial SMD profile.
The SMD data were extracted using an axial sampling line after the SMD profile reached a steady state. The numerical results are in good agreement with the experimentally measured SMD curve, especially in the near-nozzle region where the SMD curve undergoes a rapid decline. However, the numerical results failed to predict the slight increase in the more stable part of the spray, but similar behavior was also reproduced with the Lagrangian solvers [89]. Overall, the implemented breakup model successfully predicted the rapid decline of the SMD curve and the stable droplet size in the farther part of the spray.
The obtained penetration plot for the liquid phase is shown in Figure 5. Following the approach presented in [89], the non-evaporating liquid penetration profile is compared to the experimental measurements given by [49,88]. As the comparison in Figure 5 indicates, the numerical results are in good agreement with the experimental measurements.
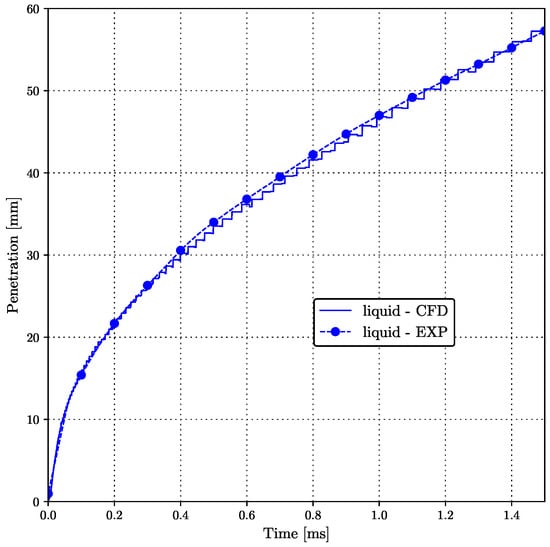
Figure 5.
Liquid penetration profile.
The visual representation of the liquid spray (at t = 1.4 ms) is given in Figure 6.
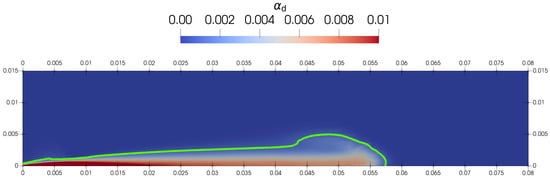
Figure 6.
Liquid spray at t = 1.4 ms. The green line gives the iso-contour = 0.1%.
4.2.2. Evaporating Conditions
In this test case, the liquid fuel at 363 K was injected into a vessel at 6.0 MPa and 900 K with 0% oxygen (non-reacting condition) [48]. These conditions, coupled with the previously described breakup regime, caused intense evaporation of the liquid phase. Therefore, the experimental measurements predicted the liquid penetration around 10 mm, which meant that practically all injected liquid mass evaporated in the first 10 mm in the axial direction.
The obtained penetration plot for the liquid phase and fuel vapor is shown in Figure 7. Here, the fuel vapor penetration is defined as the maximum streamwise distance from the nozzle outlet, where the mass fraction of the fuel vapor is 0.1%.
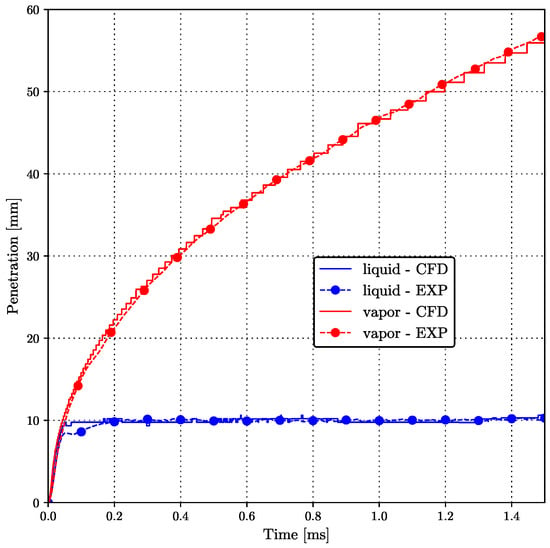
Figure 7.
Liquid and vapor penetration profiles.
As seen in Figure 7, the numerical results are in very good agreement with experimental measurements for both penetration curves. The model could successfully predict the fuel vapor penetration during the whole duration of fuel injection. Furthermore, the implemented model effectively predicted stable liquid penetration around 10 mm, but it gave a slight overprediction during the initial stabilization period.
The visual representation of the vapor penetration and liquid spray (at t = 1.4 ms) is given in Figure 8.
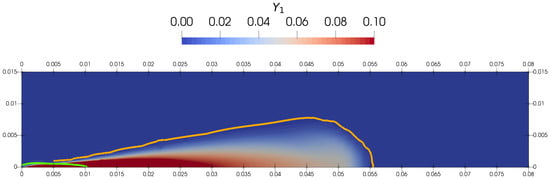
Figure 8.
Vapor penetration at t = 1.4 ms. The green line gives the iso-contour = 0.1%, and the orange line denotes = 0.1%.
The comparison of mixture fraction profiles at two different radial positions is given by Figure 9 and Figure 10. Figure 9 gives the comparison at the streamwise location mm in the radial direction. The “Gaussian” mixture fraction profile was predicted well, especially the peak value, but there was a slight underprediction for the outer part of the jet.
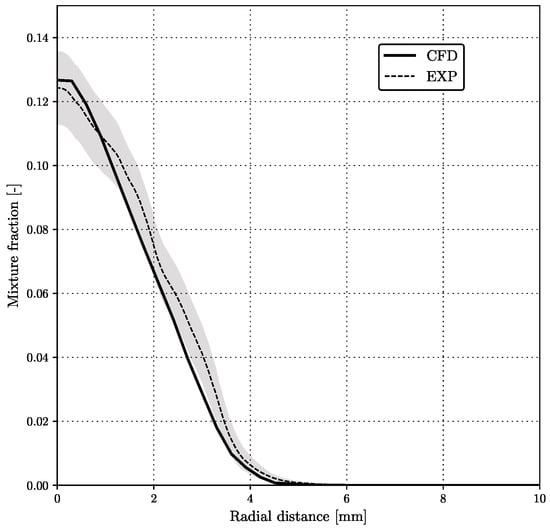
Figure 9.
Radial mixture fraction distribution at mm.
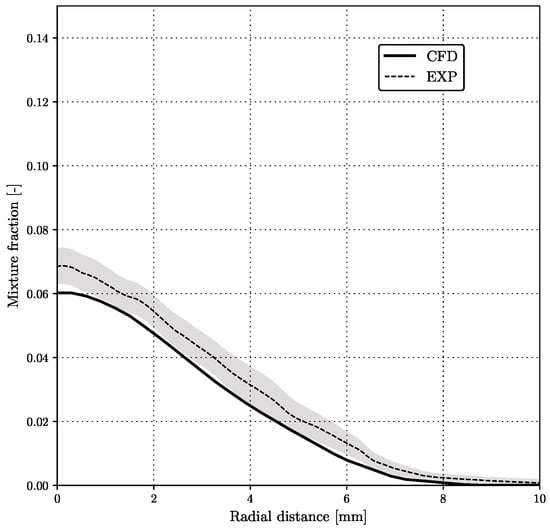
Figure 10.
Radial mixture fraction distribution at mm.
Figure 10 gives the comparison at the location mm. Again, the shape of the “Gaussian” mixture fraction profile is in good agreement with the measurements, but there was a slight underprediction over the entire sampling radius.
Overall, the implemented model successfully predicted the dynamic behavior of dense liquid sprays for the selected operating conditions.
The presented results were obtained on a desktop workstation with the AMD EPYC 7302 CPU. The validation case (finest computational grid and smallest time step) took approximately 4.5 h using five CPU cores. Since the solver is still in the development phase, there is a lot of potential for enhancing the performance of the implemented model.
5. Conclusions
The development of an advanced simulation framework for the dynamic behavior of dense evaporating liquid fuel sprays was presented. This work gave a detailed description of upgrades performed on the previously developed and published model, including updating the solver to a compressible formulation, implementing energy equations for all phases, and adding species transfer and evaporation functionality. Special attention was given to modeling the thermal phenomena occurring inside the moving droplets. The presented Eulerian multi-fluid model was implemented within the open-source foam-extend library, a community-driven fork of OpenFOAM.
The validation section showed that the implemented solver could accurately predict the atomization process and secondary breakup in the dense region of the spray. Furthermore, it also correctly predicted the evaporation and mixing phenomena, which are more pronounced in the dilute part of the spray. The validation was performed for evaporating and non-evaporating ECN Spray conditions. The verification analysis proved that the solver behaves consistently, provided our numerical settings and computational grids. Therefore, the developed solver represents a stable foundation for further development. The solver is planned to be upgraded with multi-component functionality in future work, which should enable simulations of even more complex fuels.
Author Contributions
Conceptualization, R.K. and M.B.; methodology, R.K. and M.B.; software, R.K. and H.J.; validation, R.K. and M.B.; formal analysis, R.K.; investigation, R.K.; resources, R.K. and H.J.; data curation, R.K.; writing—original draft preparation, R.K.; writing—review and editing, R.K. and M.B.; visualization, R.K.; supervision, H.G.I. and H.J.; project administration, H.G.I.; funding acquisition, M.B., H.G.I. and H.J. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the King Abdullah University of Science and Technology within the OSR-2017-CRG6-3409.03 research grant, and the Croatian Science Foundation (project number DOK-01-2018).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zhou, Z.; Wang, R.; Yi, Q.; Wang, G.; Ma, C. Combustion Enhancement of Pulverized Coal with Targeted Oxygen-Enrichment in an Ironmaking Blast Furnace. Processes 2021, 9, 440. [Google Scholar] [CrossRef]
- Di Renzo, A.; Napolitano, E.S.; Di Maio, F.P. Coarse-Grain DEM Modelling in Fluidized Bed Simulation: A Review. Processes 2021, 9, 279. [Google Scholar] [CrossRef]
- D’Adamo, A.; Riccardi, M.; Borghi, M.; Fontanesi, S. CFD Modelling of a Hydrogen/Air PEM Fuel Cell with a Serpentine Gas Distributor. Processes 2021, 9, 564. [Google Scholar] [CrossRef]
- Sacomano Filho, F.L.; de Albuquerque Paixão e Freire de Carvalho, L.E.; van Oijen, J.A.; Krieger Filho, G.C. Effects of Reaction Mechanisms and Differential Diffusion in Oxy-Fuel Combustion Including Liquid Water Dilution. Fluids 2021, 6, 47. [Google Scholar] [CrossRef]
- Kalghatgi, G.T. Developments in internal combustion engines and implications for combustion science and future transport fuels. Proc. Combust. Inst. 2015, 35, 101–115. [Google Scholar] [CrossRef]
- Manente, V.; Johansson, B.; Cannella, W. Gasoline partially premixed combustion, the future of internal combustion engines? Int. J. Engine Res. 2011, 12, 194–208. [Google Scholar] [CrossRef]
- La Civita, G.; Orlandi, F.; Mariani, V.; Cazzoli, G.; Ghedini, E. Numerical Characterization of Corona Spark Plugs and Its Effects on Radicals Production. Energies 2021, 14, 381. [Google Scholar] [CrossRef]
- Tornatore, C.; Sjöberg, M. Optical Investigation of a Partial Fuel Stratification Strategy to Stabilize Overall Lean Operation of a DISI Engine Fueled with Gasoline and E30. Energies 2021, 14, 396. [Google Scholar] [CrossRef]
- Badock, C.; Wirth, R.; Fath, A.; Leipertz, A. Investigation of cavitation in real size diesel injection nozzles. Int. J. Heat Fluid Flow 1999, 20, 538–544. [Google Scholar] [CrossRef]
- Desantes, J.M.; Payri, R.; Salvador, F.J.; De La Morena, J. Influence of cavitation phenomenon on primary break-up and spray behavior at stationary conditions. Fuel 2010, 89, 3033–3041. [Google Scholar] [CrossRef]
- Weigand, A.; Atzler, F.; Kastner, O.; Rotondi, R.; Schwarte, A. The Effect of Closely Coupled Pilot Injections On Diesel Engine Emissions; IMechE: London, UK, 2011; pp. 111–124. [Google Scholar] [CrossRef]
- Johnson, J.E.; Yoon, S.; Naber, J.; Lee, S.; Hunter, G.; Truemner, R.; Harcombe, T. Characteristics of 3000 bar Diesel Spray Injection under Non-Vaporizing and Vaporizing Conditions. In Proceedings of the ICLASS 2012, 12th Triennial International Conference on Liquid Atomization and Spray Systems, Heidelberg, Germany, 2–6 September 2012. [Google Scholar]
- Ningegowda, B.M.; Rahantamialisoa, F.; Zembi, J.; Pandal, A.; Im, H.G.; Battistoni, M. Large Eddy Simulations of Supercritical and Transcritical Jet Flows Using Real Fluid Thermophysical Properties; SAE International: Warren Dale, PA, USA, 2020. [Google Scholar] [CrossRef]
- Manin, J.; Bardi, M.; Pickett, L.M.; Dahms, R.N.; Oefelein, J.C. Microscopic investigation of the atomization and mixing processes of diesel sprays injected into high pressure and temperature environments. Fuel 2014, 134, 531–543. [Google Scholar] [CrossRef]
- Dahms, R.N.; Oefelein, J.C. Liquid jet breakup regimes at supercritical pressures. Combust. Flame 2014, 162. [Google Scholar] [CrossRef]
- Chehroudi, B. Recent experimental efforts on high-pressure supercritical injection for liquid rockets and their implications. Int. J. Aerosp. Eng. 2012, 2012, 121802. [Google Scholar] [CrossRef]
- Gopal, J.M.; Tretola, G.; Morgan, R.; de Sercey, G.; Atkins, A.; Vogiatzaki, K. Understanding Sub and Supercritical Cryogenic Fluid Dynamics in Conditions Relevant to Novel Ultra Low Emission Engines. Energies 2020, 13, 3038. [Google Scholar] [CrossRef]
- Ningegowda, B.M.; Rahantamialisoa, F.N.; Pandal, A.; Jasak, H.; Im, H.G.; Battistoni, M. Numerical Modeling of Transcritical and Supercritical Fuel Injections Using a Multi-Component Two-Phase Flow Model. Energies 2020, 13, 5676. [Google Scholar] [CrossRef]
- Hamid, M.F.; Idroas, M.Y.; Mohamed, M.; Sa’ad, S.; Yew Heng, T.; Che Mat, S.; Miskam, M.A.; Abdullah, M.K. Numerical Investigation of the Characteristics of the In-Cylinder Air Flow in a Compression-Ignition Engine for the Application of Emulsified Biofuels. Processes 2020, 8, 1517. [Google Scholar] [CrossRef]
- Sivasankaralingam, V.; Raman, V.; Mubarak Ali, M.J.; Alfazazi, A.; Lu, T.; Im, H.; Sarathy, S.M.; Dibble, R. Experimental and Numerical Investigation of Ethanol/Diethyl Ether Mixtures in a CI Engine; SAE International: Warrendale, PA, USA, 2016; Volume 1. [Google Scholar] [CrossRef]
- Emberson, D.; Sandquist, J.; Løvås, T.; Schönborn, A.; Saanum, I. Varying Ignition Quality of a Fuel for a HCCI Engine Using a Photochemically-Controlled Additive: The Development of a ‘Smart’ Fuel. Energies 2021, 5, 1470. [Google Scholar] [CrossRef]
- Palazzo, N.; Zigan, L.; Huber, F.J.T.; Will, S. Impact of Oxygenated Additives on Soot Properties during Diesel Combustion. Energies 2021, 14, 147. [Google Scholar] [CrossRef]
- Sarathy, S.M.; Kukkadapu, G.; Mehl, M.; Javed, T.; Ahmed, A.; Naser, N.; Tekawade, A.; Kosiba, G.; AlAbbad, M.; Singh, E.; et al. Compositional effects on the ignition of FACE gasolines. Combust. Flame 2016, 169, 171–193. [Google Scholar] [CrossRef]
- Elwardany, A.E.; Sazhin, S.S.; Im, H.G. A new formulation of physical surrogates of FACE A gasoline fuel based on heating and evaporation characteristics. Fuel 2016, 176, 56–62. [Google Scholar] [CrossRef]
- Badra, J.A.; Sim, J.; Elwardany, A.; Jaasim, M.; Viollet, Y.; Chang, J.; Amer, A.; Im, H.G. Numerical Simulations of Hollow-Cone Injection and Gasoline Compression Ignition Combustion With Naphtha Fuels. J. Energy Resour. Technol. 2016, 138, 052202. [Google Scholar] [CrossRef]
- Elbaz, A.M.; Gani, A.; Hourani, N.; Emwas, A.H.; Sarathy, S.M.; Roberts, W.L. TG/DTG, FT-ICR Mass Spectrometry, and NMR Spectroscopy Study of Heavy Fuel Oil. Energy Fuels 2015, 29, 7825–7835. [Google Scholar] [CrossRef]
- Shinjo, J. Recent Advances in Computational Modeling of Primary Atomization of Liquid Fuel Sprays. Energies 2018, 11, 2971. [Google Scholar] [CrossRef]
- Vukcevic, V.; Keser, R.; Jasak, H.; Battistoni, M.; Im, H.; Roenby, J. Development of a CFD Solver for Primary Diesel Jet Atomization in FOAM-Extend; SAE International: Warren Dale, PA, USA, 2019. [Google Scholar] [CrossRef]
- Holz, S.; Braun, S.; Chaussonnet, G.; Koch, R.; Bauer, H.J. Close Nozzle Spray Characteristics of a Prefilming Airblast Atomizer. Energies 2019, 12, 2835. [Google Scholar] [CrossRef]
- Ries, F.; Li, Y.; Klingenberg, D.; Nishad, K.; Janicka, J.; Sadiki, A. Near-Wall Thermal Processes in an Inclined Impinging Jet: Analysis of Heat Transport and Entropy Generation Mechanisms. Energies 2018, 11, 1354. [Google Scholar] [CrossRef]
- Hoyas, S.; Gil, A.; Margot, X.; Khuong-Anh, D.; Ravet, F. Evaluation of the Eulerian-Lagrangian Spray Atomization (ELSA) model in spray simulations: 2D cases. Math. Comput. Model. 2013, 57, 1686–1693. [Google Scholar] [CrossRef]
- IYER, V.; ABRAHAM, J. Penetration and Dispersion of Transient Gas Jets and Sprays. Combust. Sci. Technol. 1997, 130, 315–334. [Google Scholar] [CrossRef]
- Abraham, J. What is Adequate Resolution in the Numerical Computations of Transient Jets? SAE International: Warrendale, PA, USA, 1997. [Google Scholar] [CrossRef]
- Crowe, C.; Schwarzkopf, J.; Sommerfeld, M.; Tsuji, Y. Multiphase Flows with Droplets and Particles, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2011. [Google Scholar] [CrossRef]
- Hill, D.P. The Computer Simulation of Dispersed Two-phase Flows. Ph.D Thesis, Imperial College London, London, UK, 1998. [Google Scholar]
- Marchisio, D.L.; Fox, R.O. Computational Models for Polydisperse Particulate and Multiphase Systems; Cambridge University Press: Cambridge, UK, 2013; p. 498. [Google Scholar] [CrossRef]
- Zembi, J.; Battistoni, M.; Ranuzzi, F.; Cavina, N.; De Cesare, M. CFD Analysis of Port Water Injection in a GDI Engine under Incipient Knock Conditions. Energies 2019, 12, 3409. [Google Scholar] [CrossRef]
- Sparacino, S.; Berni, F.; D’Adamo, A.; Krastev, V.K.; Cavicchi, A.; Postrioti, L. Impact of the Primary Break-Up Strategy on the Morphology of GDI Sprays in 3D-CFD Simulations of Multi-Hole Injectors. Energies 2019, 12, 2890. [Google Scholar] [CrossRef]
- Gadalla, M.; Kannan, J.; Tekgül, B.; Karimkashi, S.; Kaario, O.; Vuorinen, V. Large-Eddy Simulation of ECN Spray A: Sensitivity Study on Modeling Assumptions. Energies 2020, 13, 3360. [Google Scholar] [CrossRef]
- Ishak, M.; Ismail, F.; Che Mat, S.; Abdullah, M.; Abdul Aziz, M.; Idroas, M. Numerical Analysis of Nozzle Flow and Spray Characteristics from Different Nozzles Using Diesel and Biofuel Blends. Energies 2019, 12, 281. [Google Scholar] [CrossRef]
- Petranović, Z.; Edelbauer, W.; Vujanović, M.; Duić, N. Modelling of spray and combustion processes by using the Eulerian multiphase approach and detailed chemical kinetics. Fuel 2017, 191, 25–35. [Google Scholar] [CrossRef]
- Vujanović, M.; Petranović, Z.; Edelbauer, W.; Baleta, J.; Duić, N. Numerical modelling of diesel spray using the Eulerian multiphase approach. Energy Convers. Manag. 2015, 104, 160–169. [Google Scholar] [CrossRef]
- Ganti, H.; Kamin, M.; Khare, P. Design Space Exploration of Turbulent Multiphase Flows Using Machine Learning-Based Surrogate Model. Energies 2020, 13, 4565. [Google Scholar] [CrossRef]
- Dauch, T.F.; Ates, C.; Rapp, T.; Keller, M.C.; Chaussonnet, G.; Kaden, J.; Okraschevski, M.; Koch, R.; Dachsbacher, C.; Bauer, H.J. Analyzing the Interaction of Vortex and Gas–Liquid Interface Dynamics in Fuel Spray Nozzles by Means of Lagrangian-Coherent Structures (2D). Energies 2019, 12, 2552. [Google Scholar] [CrossRef]
- Keser, R.; Vukčević, V.; Battistoni, M.; Im, H.; Jasak, H. Implicitly coupled phase fraction equations for the Eulerian multi-fluid model. Comput. Fluids 2019, 192, 104277. [Google Scholar] [CrossRef]
- Keser, R.; Ceschin, A.; Battistoni, M.; Im, H.G.; Jasak, H. Development of a Eulerian Multi-Fluid Solver for Dense Spray Applications in OpenFOAM. Energies 2020, 13, 4740. [Google Scholar] [CrossRef]
- Keser, R.; Ceschin, A.; Battistoni, M.; Im, H.G.; Jasak, H. Implicitly coupled phase fraction equations for polydisperse flows. Int. J. Numer. Methods Fluids 2021, 93, 1627–1644. [Google Scholar] [CrossRef]
- Pickett, L.M.; Abraham, J.P. Computed And Measured Fuel Vapor Distribution In A Diesel Spray. At. Sprays 2010, 20, 241–250. [Google Scholar] [CrossRef]
- Pickett, L.M.; Genzale, C.L.; Bruneaux, G.; Malbec, L.M.; Hermant, L.; Christiansen, C.; Schramm, J. Comparison of Diesel Spray Combustion in Different High-Temperature, High-Pressure Facilities. SAE Int. J. Engines 2010, 3, 156–181. [Google Scholar] [CrossRef]
- Kastengren, A.; Ilavsky, J.; Viera, J.P.; Payri, R.; Duke, D.J.; Swantek, A.; Tilocco, F.Z.; Sovis, N.; Powell, C.F. Measurements of droplet size in shear-driven atomization using ultra-small angle x-ray scattering. Int. J. Multiph. Flow 2017, 92, 131–139. [Google Scholar] [CrossRef]
- Weller, H.G. Derivation Modelling and Solution of the Conditionally Averaged Two-Phase Flow Equations; Technical Report Tech. Rep.; Nabla Ltd., 2002. [Google Scholar]
- Rusche, H. Computational Fluid Dynamics of Dispersed Two-Phase Flows at High Phase Fractions. Ph.D. Thesis, Imperial College London, London, UK, 2002. [Google Scholar]
- Reeks, M.W. On the continuum equations for dispersed particles in nonuniform flows. Phys. Fluids A Fluid Dyn. 1992, 4, 1290–1303. [Google Scholar] [CrossRef]
- Lopez de Bertodano, M.A. Two fluid model for two-phase turbulent jets. Nucl. Eng. Des. 1998, 179, 65–74. [Google Scholar] [CrossRef]
- Liu, A.B.; Mather, D.; Reitz, R.D. Modeling the Effects of Drop Drag and Breakup on Fuel Sprays; SAE Technical Paper; SAE International: Warrendale, PA, USA, 1993. [Google Scholar] [CrossRef]
- O’Rourke, P.J.; Amsden, A.A. The Tab Method for Numerical Calculation of Spray Droplet Breakup; SAE International: Warren Dale, PA, USA, 1987. [Google Scholar] [CrossRef]
- O’Rourke, P.J.; Bracco, F.V. Modeling of drop interactions in thick sprays and a comparison with experiments. Proc. Inst. Mech. Eng. 1980. [Google Scholar] [CrossRef]
- Reitz, R.D. Atomization and Other Breakup Regimes of a Liquid Jet. Ph.D. Thesis, Princeton University, Princeton, NJ, USA, 1978. [Google Scholar]
- Reitz, R.D.; Bracco, F.V. Mechanism of atomization of a liquid jet. Phys. Fluids 1982, 25, 1730–1742. [Google Scholar] [CrossRef]
- Reitz, R.D.; Bracco, F.V. Mechanisms of Breakup of Round Liquid Jets. Encycl. Fluid Mech. 1986, 3, 223–249. [Google Scholar]
- Stiesch, G. Modeling Engine Spray and Combustion Processes; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar] [CrossRef]
- Reitz, R.D. Modeling atomization processes in high-pressure vaporizing sprays. At. Spray Technol. 1987, 3, 309–337. [Google Scholar]
- Pađen, I.; Petranović, Z.; Edelbauer, W.; Vujanović, M. Numerical modeling of spray secondary atomization with the Euler-Eulerian multi-fluid approach. Comput. Fluids 2021, 222, 104919. [Google Scholar] [CrossRef]
- Gosman, A.D.; Lekakou, C.; Politis, S.; Issa, R.I.; Looney, M.K. Multidimensional modeling of turbulent two-phase flows in stirred vessels. AIChE J. 1992, 38, 1946–1956. [Google Scholar] [CrossRef]
- Pope, S.B. An explanation of the turbulent round-jet/plane-jet anomaly. AIAA J. 1978, 16, 279–281. [Google Scholar] [CrossRef]
- Melville, W.K.; Bray, K.N. A model of the two-phase turbulent jet. Int. J. Heat Mass Transf. 1979, 22, 647–656. [Google Scholar] [CrossRef]
- Moukalled, F.; Darwish, M. Mixing and evaporation of liquid droplets injected into an air stream flowing at all speeds. Phys. Fluids 2008, 20, 040804. [Google Scholar] [CrossRef]
- Dombrovsky, L.A.; Sazhin, S.S. A Parabolic Temperature Profile Model for Heating of Droplets. J. Heat Transf. 2003, 125, 535–537. [Google Scholar] [CrossRef]
- Abramzon, B.; Sirignano, W.A. Droplet vaporization model for spray combustion calculations. Int. J. Heat Mass Transf. 1989, 32, 1605–1618. [Google Scholar] [CrossRef]
- Sazhin, S.S. Modelling of fuel droplet heating and evaporation: Recent results and unsolved problems. Fuel 2017, 196, 69–101. [Google Scholar] [CrossRef]
- Abramzon, B.; Sazhin, S.S. Convective vaporization of a fuel droplet with thermal radiation absorption. Fuel 2006, 85, 32–46. [Google Scholar] [CrossRef]
- Sazhin, S.S. Advanced models of fuel droplet heating and evaporation. Prog. Energy Combust. Sci. 2006, 32, 162–214. [Google Scholar] [CrossRef]
- Sazhin, S.S. Droplets and Sprays, 1st ed.; Springer: London, UK, 2014; p. 345. [Google Scholar] [CrossRef]
- Clift, R.; Grace, J.; Weber, M. Bubbles, Drops, and Particles; Academic Press: New York, NY, USA, 1978. [Google Scholar]
- Hohmann, S.; Renz, U. Numerical simulation of fuel sprays at high ambient pressure: The influence of real gas effects and gas solubility on droplet vaporisation. Int. J. Heat Mass Transf. 2003, 46, 3017–3028. [Google Scholar] [CrossRef]
- Vujanović, M. Numerical Modelling of Multiphase Flow in Combustion of Liquid Fuel. Ph.D. Thesis, University of Zagreb, Zagreb, Croatia, 2010. [Google Scholar]
- Jasak, H. Error Analysis and Estimation for the Finite Volume Method with Applications to Fluid Flows. Ph.D. Thesis, Imperial College London, London, UK, 1996. [Google Scholar]
- Ferziger, J.H.; Peric, M.; Leonard, A. Computational Methods for Fluid Dynamics. Phys. Today 1997. [Google Scholar] [CrossRef]
- Issa, R.I. Solution of the implicitly discretised fluid flow equations by operator-splitting. J. Comput. Phys. 1986, 62, 40–65. [Google Scholar] [CrossRef]
- Jasak, H.; Weller, H.G.; Gosman, A.D. High resolution NVD differencing scheme for arbitrarily unstructured meshes. Int. J. Numer. Methods Fluids 1999, 31, 431–449. [Google Scholar] [CrossRef]
- Uroić, T.; Jasak, H. Parallelisation of selective algebraic multigrid for block–pressure–velocity system in OpenFOAM. Comput. Phys. Commun. 2021, 258, 107529. [Google Scholar] [CrossRef]
- Uroić, T.; Jasak, H. Block-selective algebraic multigrid for implicitly coupled pressure-velocity system. Comput. Fluids 2018, 167, 100–110. [Google Scholar] [CrossRef]
- Saad, Y. Iterative Methods for Sparse Linear Systems, 2nd ed.; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2003. [Google Scholar]
- Pickett, L.M.; Manin, J.; Payri, R.; Bardi, M.; Gimeno, J. Transient Rate of Injection Effects on Spray Development. In Proceedings of the 11th International Conference on Engines & Vehicles, Capri, Italy, 15–19 September 2013; pp. 1–2013. [Google Scholar] [CrossRef]
- Eça, L.; Hoekstra, M. A procedure for the estimation of the numerical uncertainty of CFD calculations based on grid refinement studies. J. Comput. Phys. 2014, 262, 104–130. [Google Scholar] [CrossRef]
- ReFRESCO. A Community Based Open-Usage and Open-Source CFD Code for the MARITIME World; ReFRESCO: Rotterdam, The Netherlands, 2018. [Google Scholar]
- Doisneau, F.; Arienti, M.; Oefelein, J. On Multi-Fluid models for spray-resolved les of reacting jets. Proc. Combust. Inst. 2017, 36, 2441–2450. [Google Scholar] [CrossRef]
- ECN. ECN1 Proceedings—Engine Combustion Network. Available online: https://ecn.sandia.gov/ecn-workshop/ecn1-proceedings/ (accessed on 7 May 2021).
- Magnotti, G.M.; Genzale, C.L. Detailed assessment of diesel spray atomization models using visible and X-ray extinction measurements. Int. J. Multiph. Flow 2017, 97, 33–45. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).