Optimization of Methanol Synthesis under Forced Periodic Operation
Abstract
1. Introduction
2. Kinetic Model
- i
- : ⊙ for oxidized surface centers, also assumed as active center for CO hydrogenation;
- ii
- : * for reduced surface centers, also assumed as active center for CO2 hydrogenation;
- iii
- : ⊗ as active surface centers for heterolytic decomposition of hydrogen.
3. Reactor Model
4. Methods
4.1. Steady State Optimization
4.2. Optimization of Forced Periodic Operation
4.3. Multi-Objective Optimization
5. Results
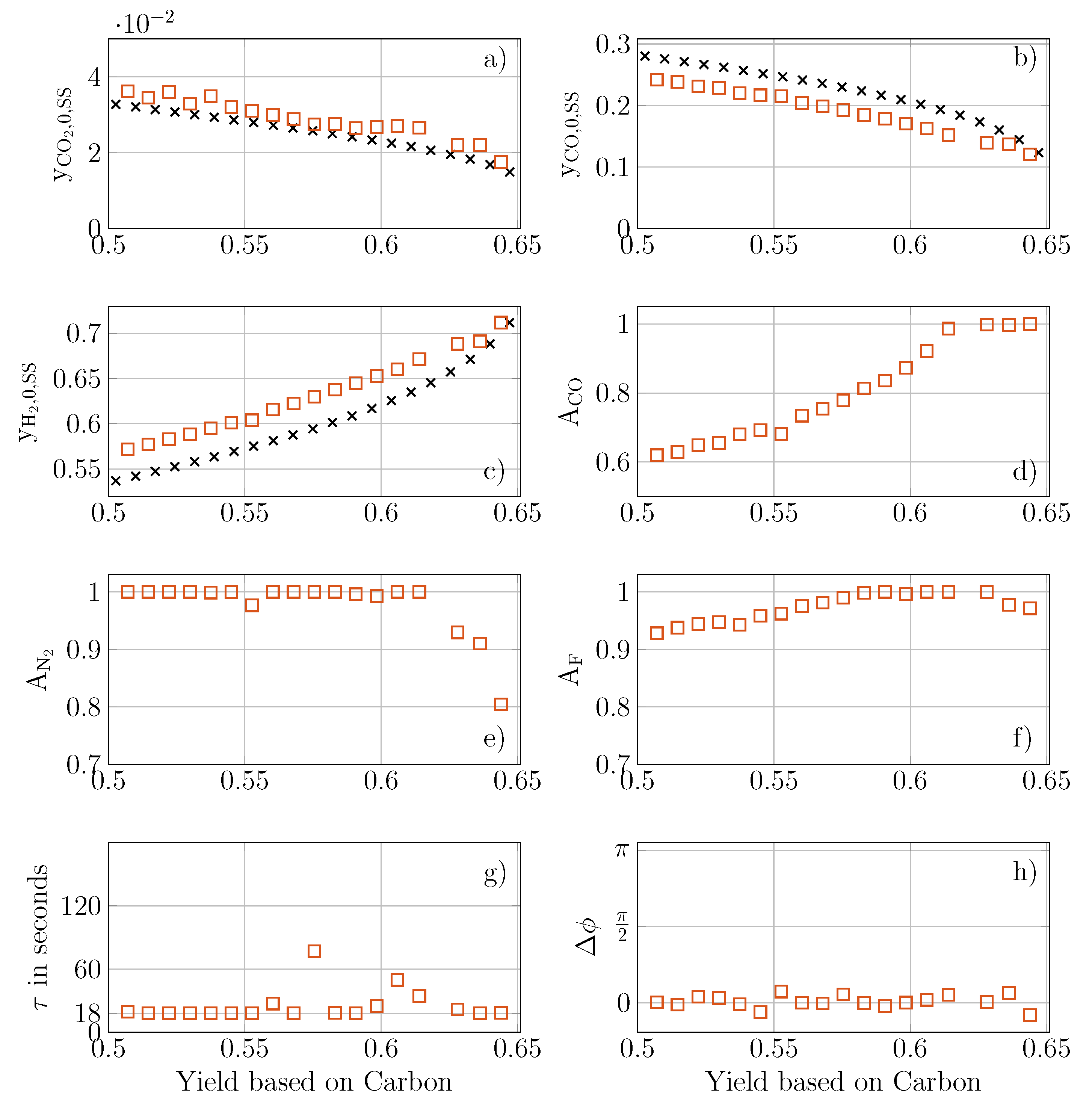
5.1. Steady State Multi-Objective Optimization
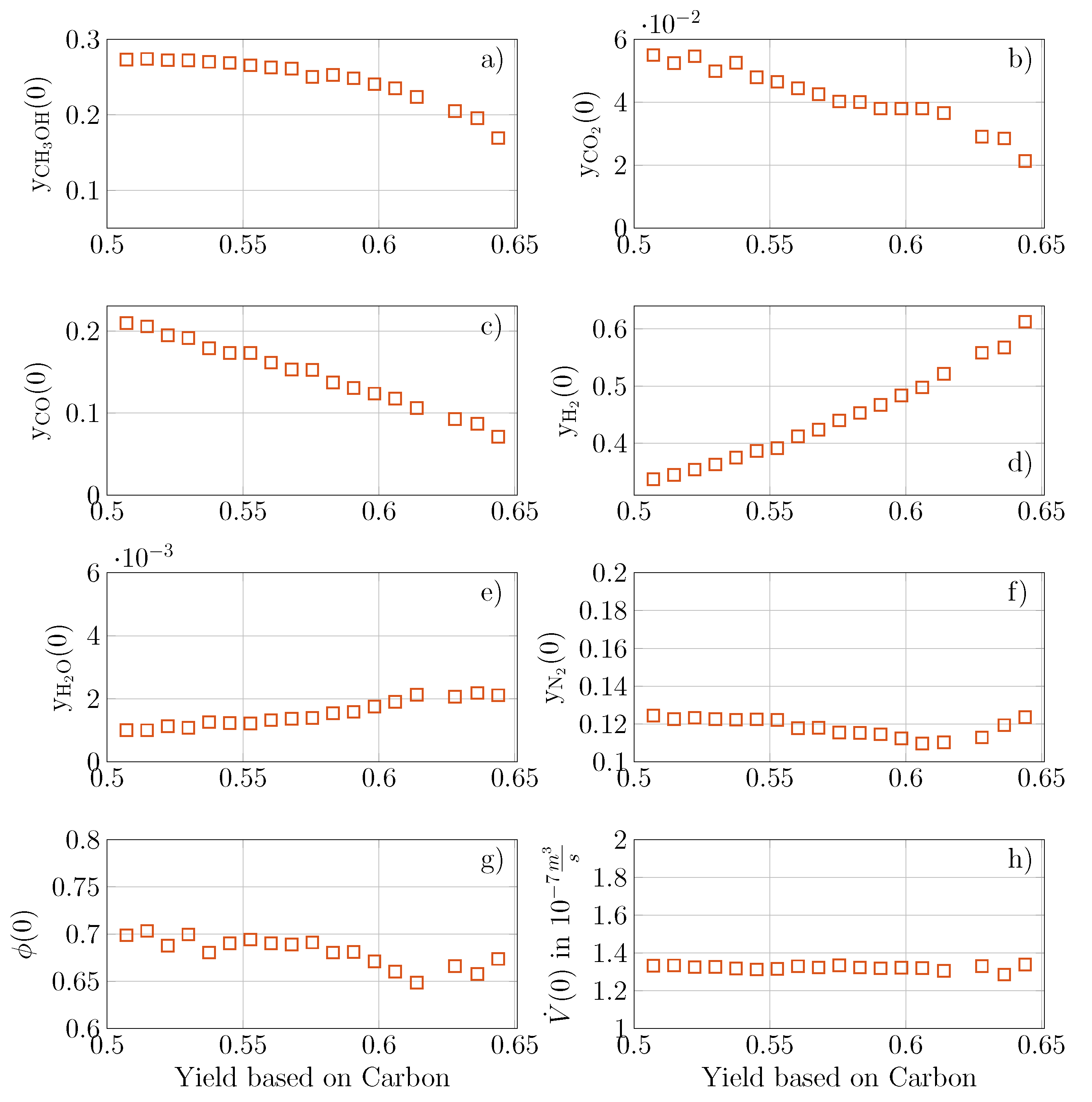
5.2. Multi-Objective Optimization of Forced Periodic Operation
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| amplitude of input CO, N2 or volumetric flow rate | |
| [J/mol] | Gibbs free energy |
| J | objective function |
| [mol/s/kgcat/bar3] | reaction rate constant for |
| [mol/s/kgcat/bar] | reaction rate constant for |
| [1/s] | reaction rate constant for oxidation and reduction of the catalyst |
| adsorption constant | |
| [1/bar2] | equilibrium constant for |
| equilibrium constant for | |
| equilibrium constant for oxidation and reduction of the catalyst | |
| [mol/s] | molar flow rate |
| [mol/s] | molar flow rate of component i |
| p [bar] | pressure |
| [bar] | partial pressure of compenent i |
| [mol/kgcat] | specific number of surface centers |
| R [J/K/mol] | gas constant |
| [mol/s/kgcat] | rate of reaction j |
| T [K] | temperature |
| u | general input |
| [m3] | volume of the gas phase in the reactor |
| [m3/s] | volumetric flow rate |
| x | optimization variables |
| y | general output variables |
| mole fraction of component i | |
| yield of methanol based on total carbon in the feed | |
| Greek letters | |
| relative number of free surface centers | |
| [s] | period time |
| maximum fraction of reduced centers on the catalyst surface | |
| fraction of reduced centers on the catalyst surface | |
| phase shift | |
| [1/s] | frequency |
| Subscripts | |
| periodic | forced periodic feed stream |
| steady state | |
| 0 | feed stream |
| i | component ( CH3OH, CO2, CO, H2, |
| H2O, N) | |
| j | reaction ( CO hydrogenation, CO2 hydrogenation, |
| RWGS) | |
| Superscripts | |
| G | gas phase |
| S | solid phase |
| * | reduced surface center |
| ⊙ | oxidized surface center |
| ⊗ | reduced surface center |
| Abbreviations | |
| OP | Operating point |
Appendix A. Partial Derivatives of the Isotherms of the Adsorbed Species
- (i)
- ⊙ oxidized surface centers: CH3OH, CO2, CO
- (ii)
- * reduced surface centers: CH3OH, CO2, H2, H2O
- (iii)
- ⊗ surface centers for heterolytic decomposition of hydrogen: H2
References
- Asinger, F. Methanol—Chemie und Energierohstoff; Springer: Berlin/Heidelberg, Germany, 1986. [Google Scholar]
- Kalz, K.F.; Kraehnert, R.; Dvoyashkin, M.; Dittmeyer, R.; Gläser, R.; Krewer, U.; Reuter, K.; Grunwaldt, J.D. Future challenges in heterogeneous catalysis: Understanding catalysts under dynamic reaction conditions. ChemCatChem 2017, 9, 17–29. [Google Scholar] [CrossRef]
- Olah, G.A. Beyond oil and gas: The methanol economy. Angew. Chem. 2005, 44, 2636–2639. [Google Scholar] [CrossRef]
- Martín, M. Methodology for solar and wind energy chemical storage facilities design under uncertainty: Methanol production from CO2 and hydrogen. Comput. Chem. Eng. 2016, 92, 43–54. [Google Scholar] [CrossRef]
- Raeuchle, K.; Plass, L.; Wernicke, H.J.; Bertau, M. Methanol for renewable energy storage and utilization. Energy Technol. 2016, 4, 193–200. [Google Scholar] [CrossRef]
- Petkovska, M.; Nikolić, D.; Seidel-Morgenstern, A. Nonlinear frequency response method for evaluating forced periodic operations of chemical reactors. Isr. J. Chem. 2018, 58, 663–681. [Google Scholar] [CrossRef]
- Douglas, J.M.; Rippin, D.W.T. Unsteady state process operation. Chem. Eng. Sci. 1966, 21, 305–315. [Google Scholar] [CrossRef]
- Horn, F.J.M. Periodic countercurrent processes. Ind. Eng. Chem. Process Des. Dev. 1967, 6, 20–30. [Google Scholar] [CrossRef]
- Baily, J.E. Periodic operation of chemical reactors: A review. Chem. Eng. Commun. 1973, 1, 111–124. [Google Scholar] [CrossRef]
- Silveston, P.L. Periodic operation of chemical reactors—A review of the experimental literature. Sadhana 1987, 10, 217–246. [Google Scholar] [CrossRef]
- Silveston, P.L.; Hudgins, R.R. Periodic Operation of Reactors; Elsevier: Amsterdam, The Netherlands, 2013. [Google Scholar]
- Nappi, A.O.; Fabbricino, L.; Hudgins, R.R.; Silveston, P.L. Influence of forced feed composition cycling on catalytic methanol synthesis. Can. J. Chem. Eng. 1994, 72, 657–671. [Google Scholar] [CrossRef]
- Chanchlani, K.G.; Hudgins, R.R.; Silveston, P.L. Methanol synthesis under periodic operation: An experimental investigation. Can. J. Chem. Eng. 1985, 63, 963–970. [Google Scholar] [CrossRef]
- Seidel, C.; Jörke, A.; Vollbrecht, B.; Seidel-Morgenstern, A.; Kienle, A. Kinetic modelling of methanol synthesis from renweable resources. Chem. Eng. Sci. 2018, 175, 130–138. [Google Scholar] [CrossRef]
- Seidel, C.; Jörke, A.; Vollbrecht, B.; Seidel-Morgenstern, A.; Kienle, A. Corrigendum to ’Kinetic modeling of methanol synthesis from renewable resources’ (Chem. Eng. Sci. 175 (2018) 130-138). Chem. Eng. Sci. 2020, 223, 115724. [Google Scholar] [CrossRef]
- Vollbrecht, B. Zur Kinetik der Methanolsynthese an einem technischen Cu/ZnO/Al2O3-Katalysator. Ph.D. Thesis, Otto-von-Guericke Universität Magdeburg, Magdeburg, Germany, 2007. [Google Scholar]
- Skrzypek, J.; Sloczyński, J.; Ledakowicz, S. Methanol Synthesis: Science and Engineering; Polish Scientific Publishers: Warsaw, Poland, 1994. [Google Scholar]
- Slotboom, Y.; Bos, M.J.; Pieper, J.; Vrieswijk, V.; Likozar, B.; Kersten, S.R.; Brilman, D. Critical assessment of steady-state kinetic models for the synthesis of methanol over an industrial Cu/ZnO/Al2O3 catalyst. Chem. Eng. J. 2020, 389. [Google Scholar] [CrossRef]
- Horst, R.; Tuy, H. Global Optimization; Springer: Berlin, Germany, 1993. [Google Scholar]
- Nikolić, D.; Seidel-Morgenstern, A.; Petkovska, M. Nonlinear frequency response analysis of forced periodic operation of non-isothermal CSTR with simultaneous modulation of inlet concentration and inlet temperature. Chem. Eng. Sci. 2015, 137, 40–58. [Google Scholar] [CrossRef][Green Version]
- Nikolić, D.; Seidel-Morgenstern, A.; Petkovska, M. Periodic operation with modulation of inlet concentration and flow rate. Part I: Nonisothermal continuous stirred-tank reactor. Chem. Eng. Technol. 2016, 39, 2020–2028. [Google Scholar] [CrossRef]
- Nikolić, D.; Seidel-Morgenstern, A.; Petkovska, M. Periodic operation with modulation of inlet concentration and flow rate. Part II: Adiabatic continuous stirred-tank reactor. Chem. Eng. Technol. 2016, 39, 2126–2134. [Google Scholar] [CrossRef]
- Felischak, M.; Kaps, L.; Hamel, C.; Nikolić, D.; Petkovska, M.; Seidel-Morgenstern, A. Analysis and experimental demonstration of forced periodic operation of an adiabatic stirred tank reactor: Simultaneous modulation of inlet concentration and total flow-rate. Chem. Eng. J. 2021, 410, 128197. [Google Scholar] [CrossRef]
- Cervantes, A.; Biegler, L.T. Optimization Strategies for Dynamic Systems. In Encyclopedia of Optimization; Springer: Boston, MA, USA, 2008; pp. 2847–2858. [Google Scholar] [CrossRef]
- Das, I.; Dennis, J.E. A closer look at drawbacks of minimizing weighted sums of objectives for Pareto set generation in multicriteria optimization problems. Struct. Optim. 1997, 14, 63–69. [Google Scholar] [CrossRef]
- Marler, R.T.; Arora, J.S. The weighted sum method for multi-objective optimization: New insights. In Structural and Multidisciplinary Optimization; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar] [CrossRef]
- Haimes, Y.V. On a bicriterion formation of the problems of integrated system identification and system optimization. IEEE Transact. Syst. Man Cybern. 1971. [Google Scholar] [CrossRef]
- Ehrgott, M. Multicriteria Optimization: Second Edition; Springer Science & Media: Berlin/Heidelberg, Germany, 2005; pp. 1–323. [Google Scholar] [CrossRef]
- Maußner, J. Single- and Multi-Objective Reactor Design Under Uncertainty. Ph.D. Thesis, Friedrich-Alexander-Universität Erlangen-Nürnberg (FAU), Erlangen, Germany, 2020. [Google Scholar]
- Nikolić, D.; Seidel, C.; Felischak, M.; Milicić, T.; Kienle, A.; Seidel-Morgenstern, A.; Petkovska, M. Forced periodic operations of a chemical reactor for methanol synthesis—The search for the best scenario based on the nonlinear frequency response method. Part I Single input modulations. 2021. In preparation. [Google Scholar]
- Nikolić, D.; Seidel, C.; Felischak, M.; Milicić, T.; Kienle, A.; Seidel-Morgenstern, A.; Petkovska, M. Forced periodic operations of a chemical reactor for methanol synthesis—The search for the best scenario based on the nonlinear frequency response method. Part II Simultaneous modulation of two inputs. 2021. In preparation. [Google Scholar]

| Parameter | Value | Units |
|---|---|---|
| 0.00673 | mol/kgcat/s/bar3 | |
| 26.4549 | - | |
| 0.0430 | mol/kgcat/s/bar3 | |
| 1.5308 | - | |
| 0.0117 | mol/kgcat/s/bar3 | |
| 15.6154 | - | |
| 1.1064 | ||
| 0 | 1/bar | |
| 0 | 1/bar | |
| 0 | - | |
| 0.1497 | 1/bar | |
| 0 | 1/bar | |
| 0.0629 | 1/bar | |
| 0 | 1/bar | |
| 0.3357 × 103 | J/mol | |
| 21.8414 ×103 | J/mol | |
| 7.9174 × 10 −3 | 1/s | |
| 0.188 × 10−4 | 1/s | |
| 0.9 | - |
| Parameter | Value | Units |
|---|---|---|
| p | 60 | bar |
| T | 473 | K |
| 0.15 | - | |
| 1.14 × 10−7 | m3/s | |
| 1.03 × 10−4 | m3 | |
| 0.00395 | kg | |
| 0.98 | mol/kg |
| OP | A | A | A | in s | ||||
|---|---|---|---|---|---|---|---|---|
| OP1 | - | - | - | - | - | |||
| OP2 | 1 | 1 | 34 | |||||
| OP3 | 1 | |||||||
| OP4 | - | - | - | - | - | |||
| OP5 | 1 | 18 | ||||||
| OP6 | 1 | 1 | 34 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Seidel, C.; Nikolić, D.; Felischak, M.; Petkovska, M.; Seidel-Morgenstern, A.; Kienle, A. Optimization of Methanol Synthesis under Forced Periodic Operation. Processes 2021, 9, 872. https://doi.org/10.3390/pr9050872
Seidel C, Nikolić D, Felischak M, Petkovska M, Seidel-Morgenstern A, Kienle A. Optimization of Methanol Synthesis under Forced Periodic Operation. Processes. 2021; 9(5):872. https://doi.org/10.3390/pr9050872
Chicago/Turabian StyleSeidel, Carsten, Daliborka Nikolić, Matthias Felischak, Menka Petkovska, Andreas Seidel-Morgenstern, and Achim Kienle. 2021. "Optimization of Methanol Synthesis under Forced Periodic Operation" Processes 9, no. 5: 872. https://doi.org/10.3390/pr9050872
APA StyleSeidel, C., Nikolić, D., Felischak, M., Petkovska, M., Seidel-Morgenstern, A., & Kienle, A. (2021). Optimization of Methanol Synthesis under Forced Periodic Operation. Processes, 9(5), 872. https://doi.org/10.3390/pr9050872








