Conceptual Design of a Negative Emissions Polygeneration Plant for Multiperiod Operations Using P-Graph
Abstract
1. Introduction
2. Problem Statement
3. Methodology
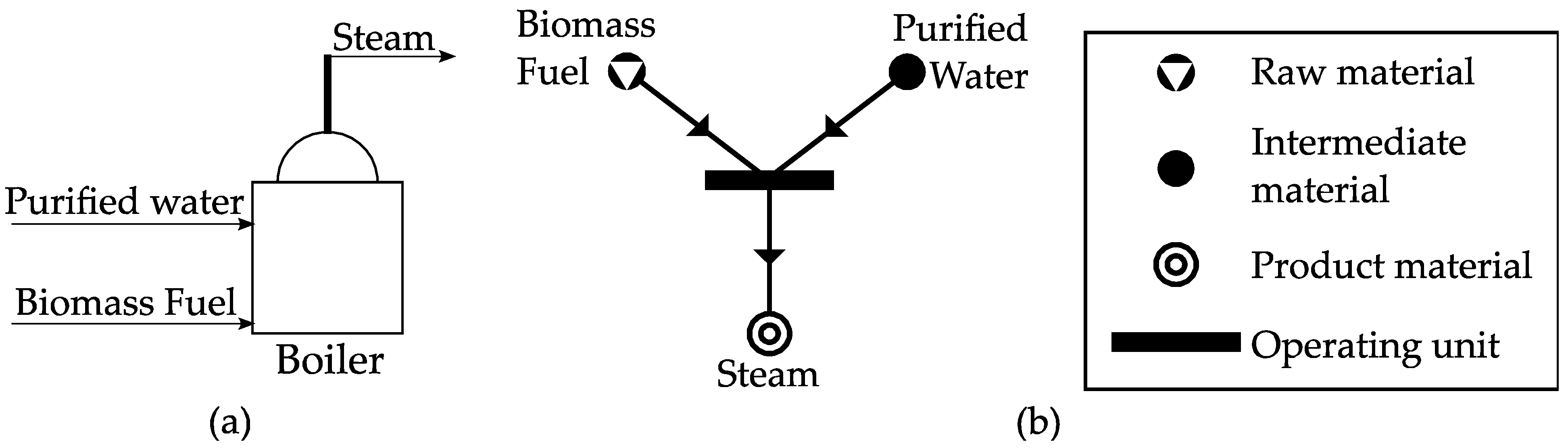
3.1. P-Graph Framework
3.2. Illustrative Example
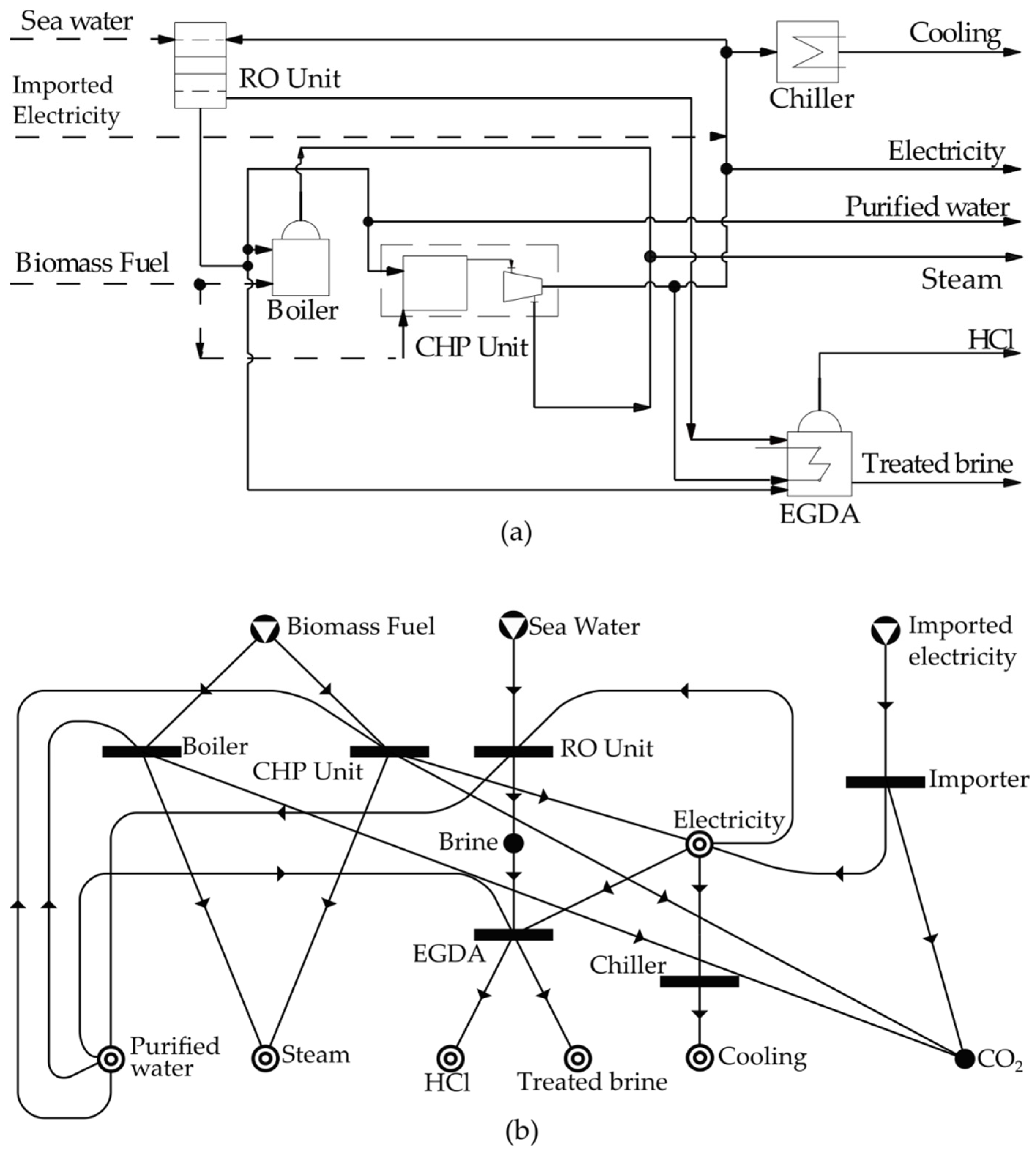
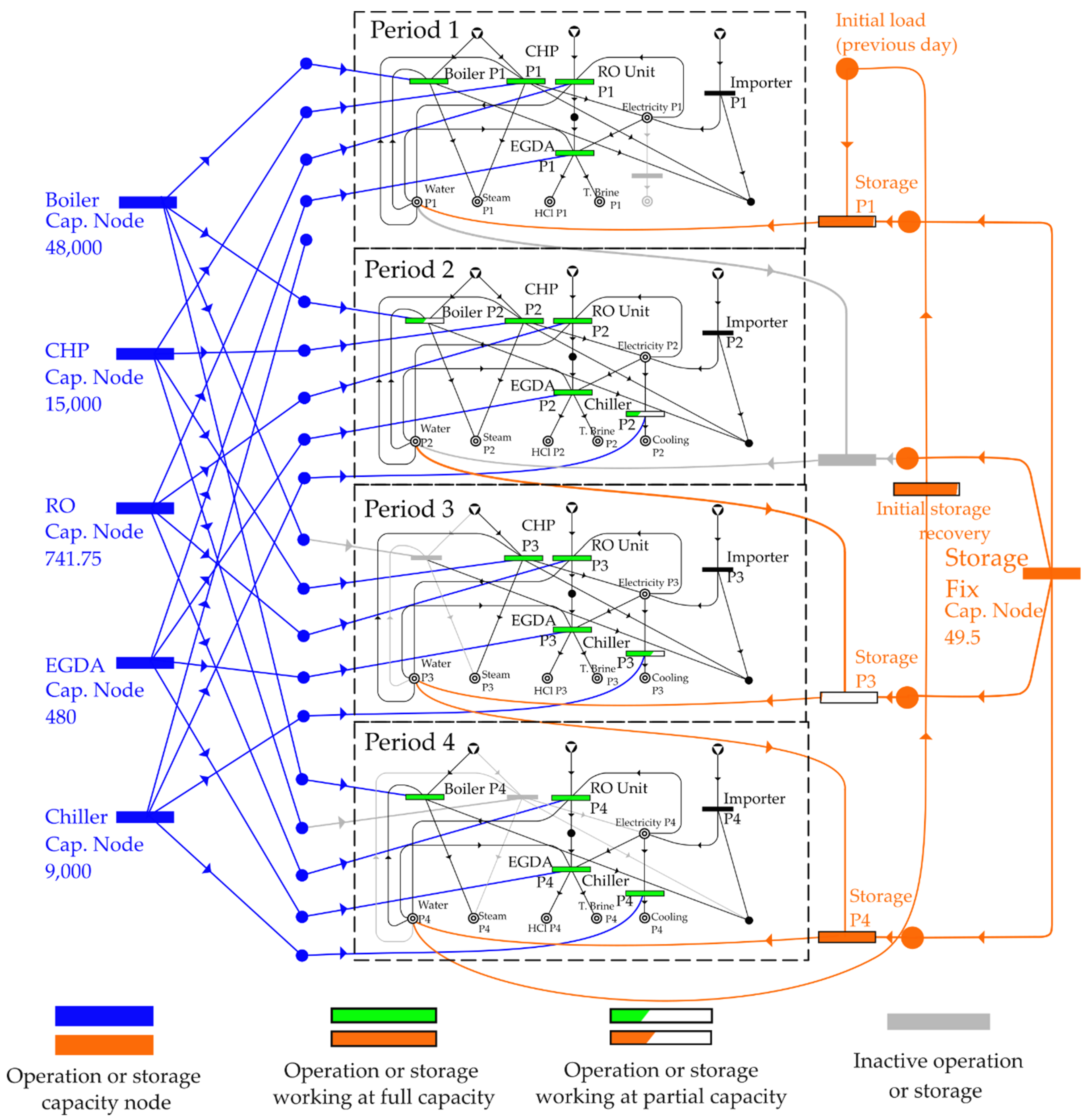
4. Case Study
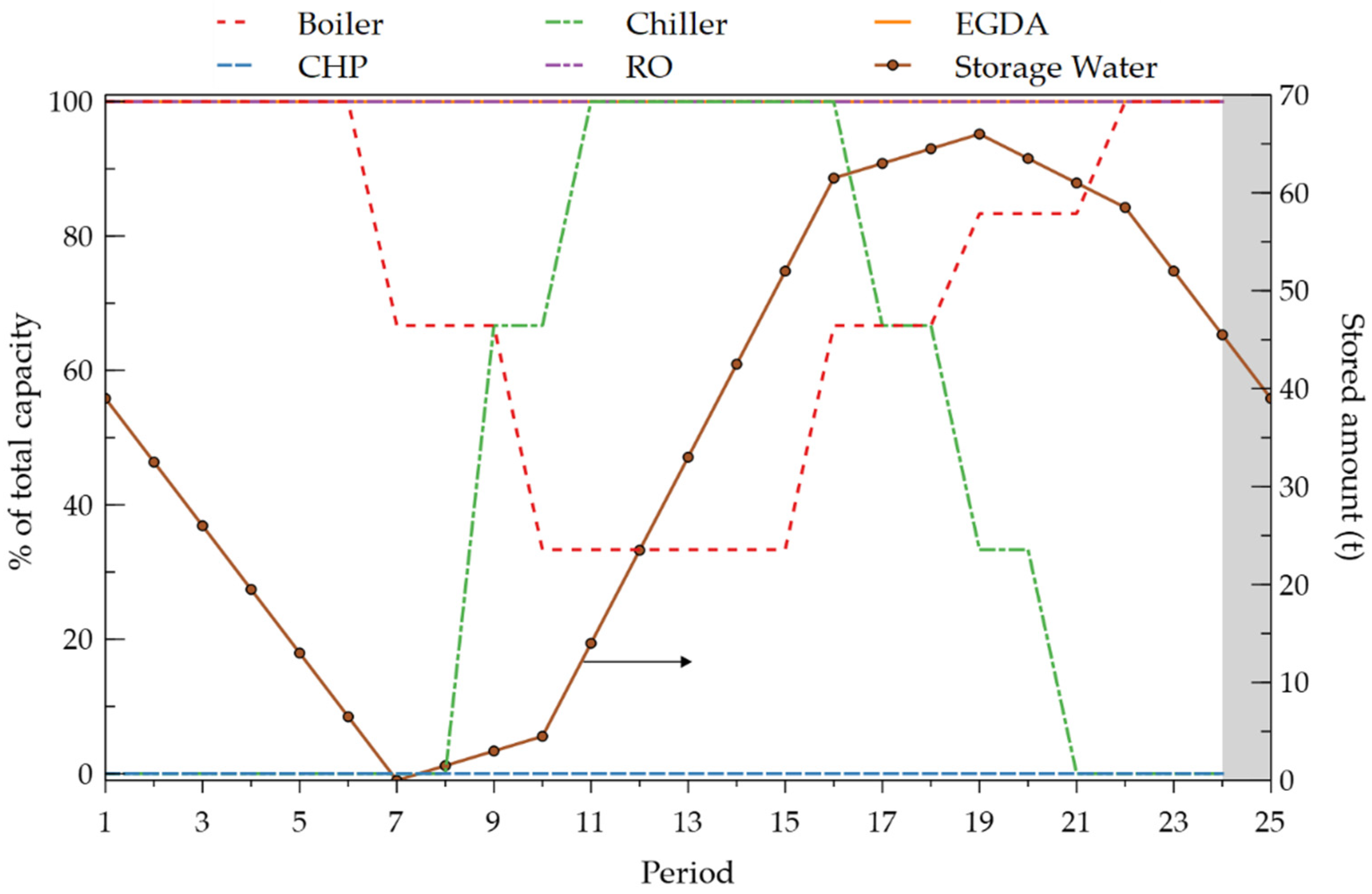
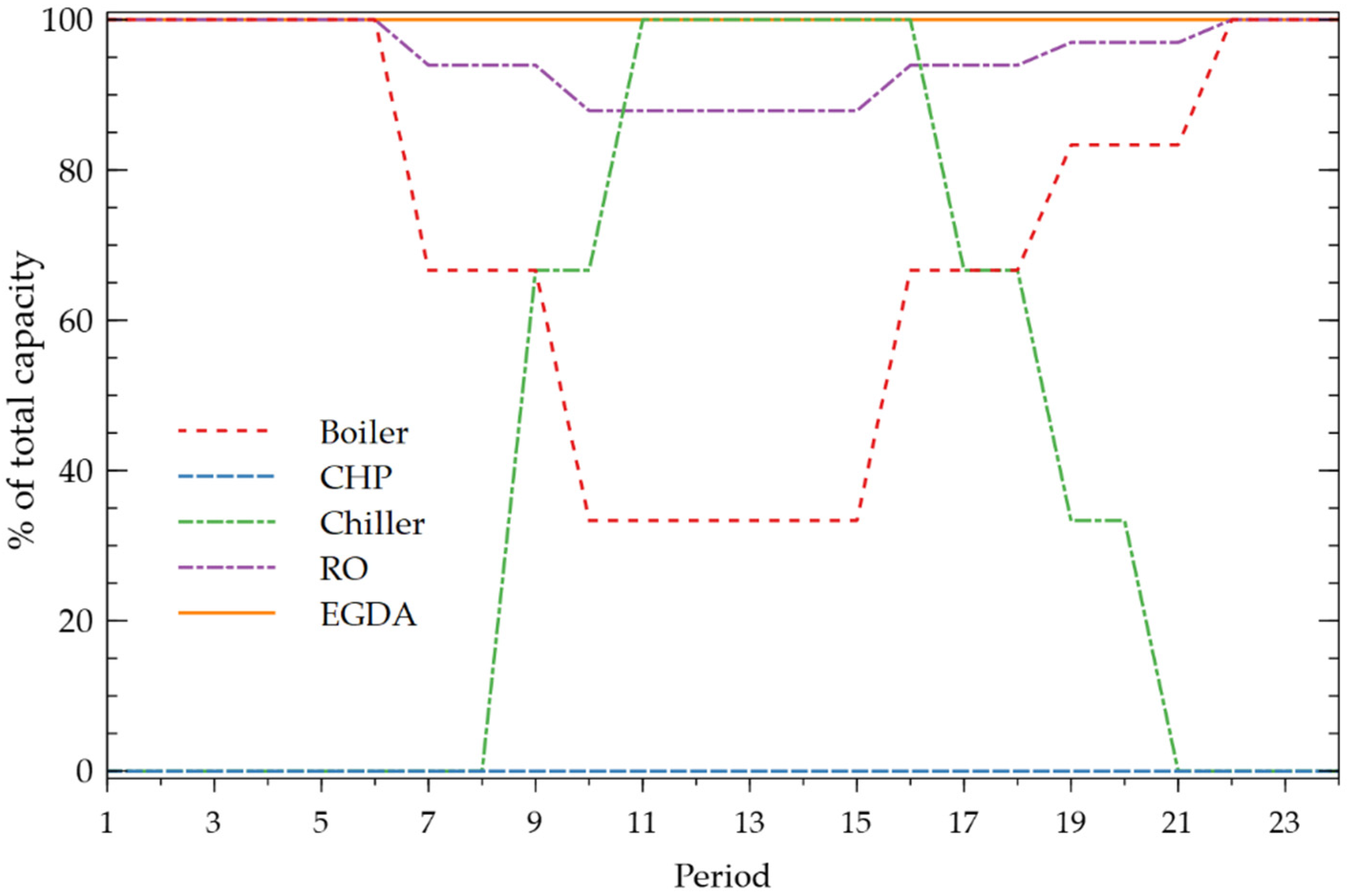
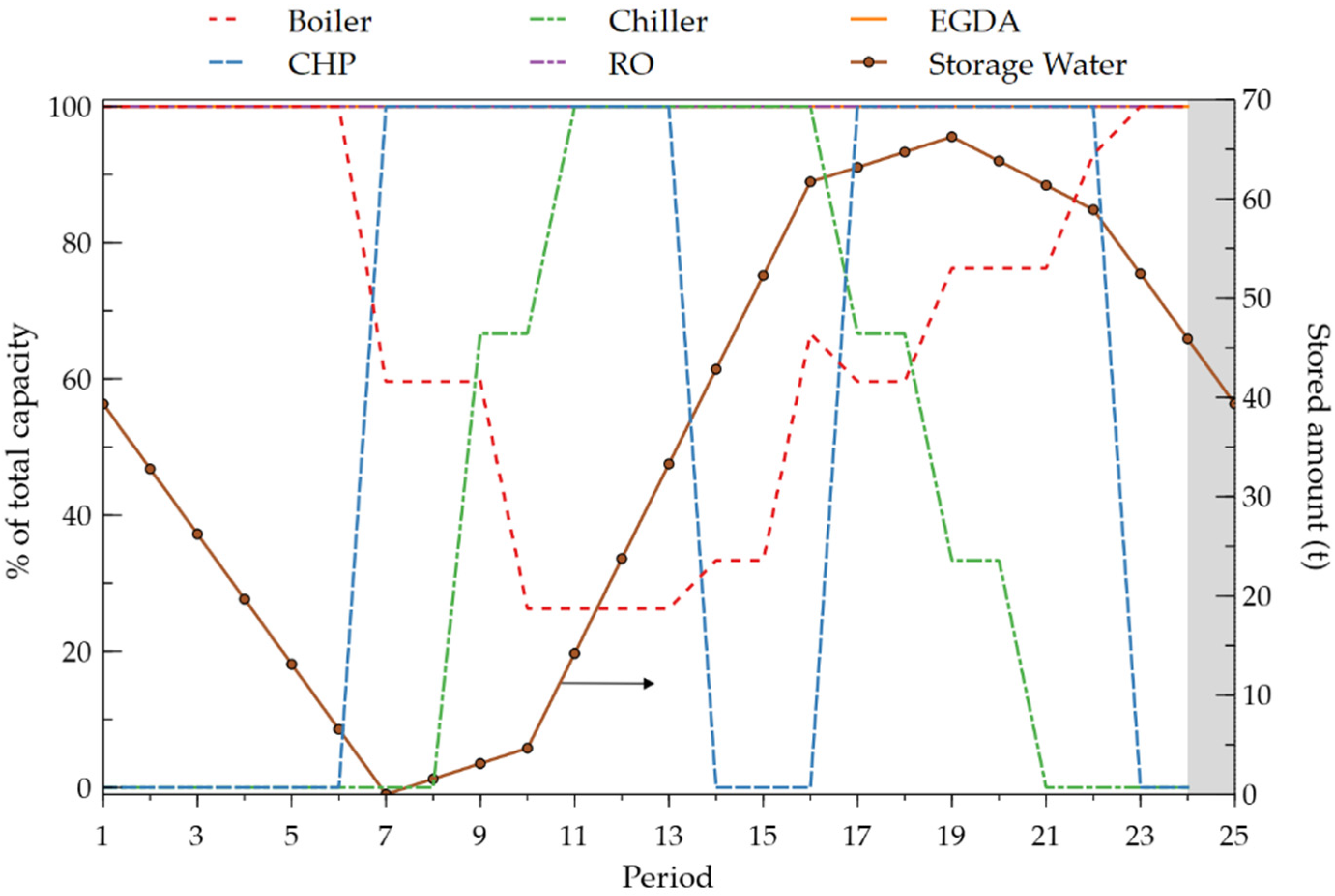
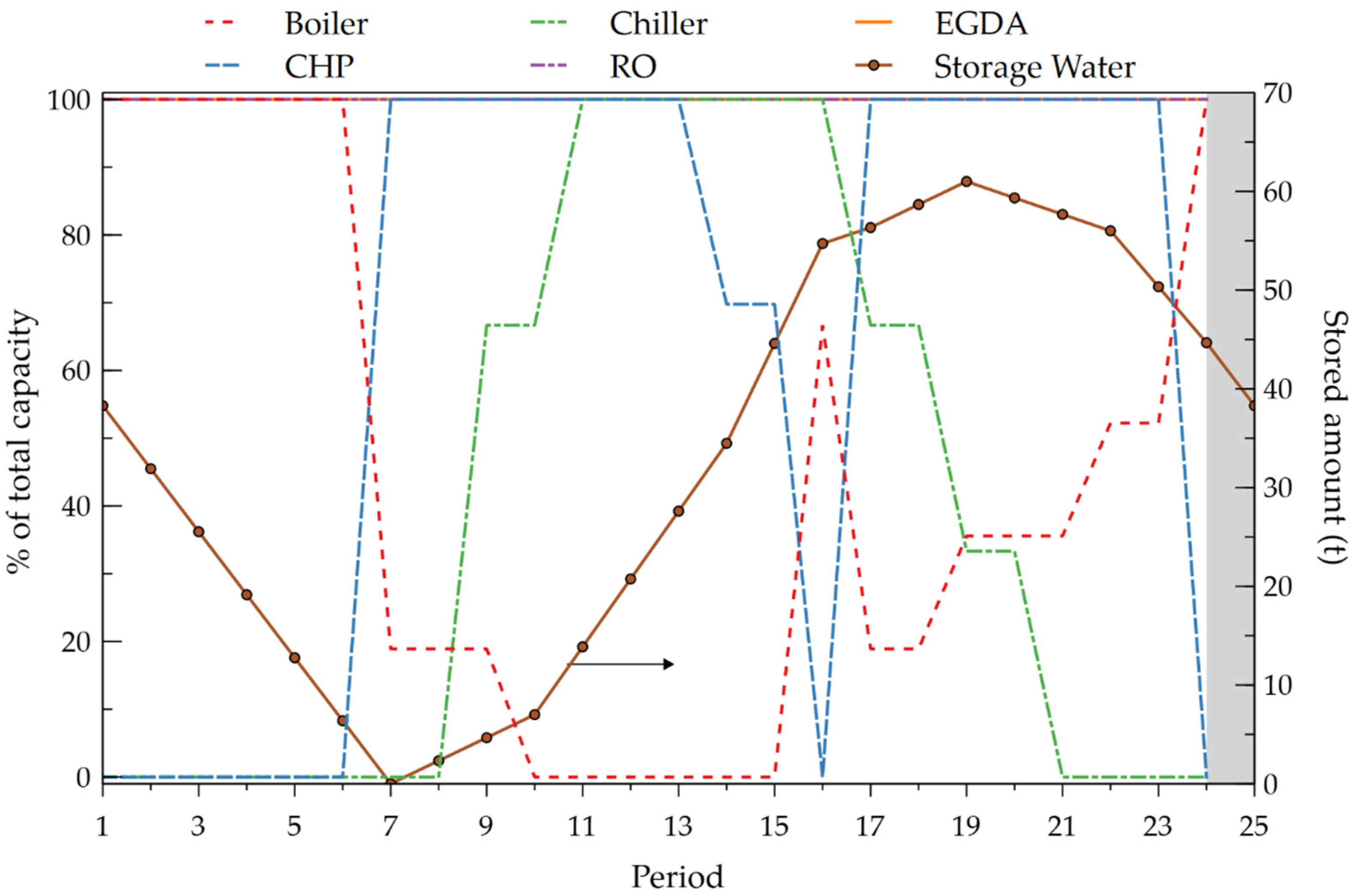
4.1. Case 1. No Limitation of CO2 Emissions
4.2. Cases 2 to 4. Variation of Footprint Limit
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Intergovernmental Panel on Climate Change. Climate Change 2014 Mitigation of Climate Change; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- Adams, T.A.; Ghouse, J.H. Polygeneration of fuels and chemicals. Curr. Opin. Chem. Eng. 2015, 10, 87–93. [Google Scholar] [CrossRef]
- McLaren, D. A comparative global assessment of potential negative emissions technologies. Process Saf. Environ. Prot. 2012, 90, 489–500. [Google Scholar] [CrossRef]
- Haszeldine, R.S.; Flude, S.; Johnson, G.; Scott, V. Negative emissions technologies and carbon capture and storage to achieve the Paris Agreement commitments. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2018, 376, 20160447. [Google Scholar] [CrossRef] [PubMed]
- Hilaire, J.; Minx, J.C.; Callaghan, M.W.; Edmonds, J.; Luderer, G.; Nemet, G.F.; Rogelj, J.; del Mar Zamora, M. Negative emissions and international climate goals—learning from and about mitigation scenarios. Clim. Chang. 2019, 157, 189–219. [Google Scholar] [CrossRef]
- Davies, P.A.; Yuan, Q.; De Richter, R. Desalination as a negative emissions technology. Environ. Sci. Water Res. Technol. 2018, 4, 839–850. [Google Scholar] [CrossRef]
- Tan, R.R.; Aviso, K.B.; Foo, D.C.Y.; Lee, J.Y.; Ubando, A.T. Optimal synthesis of negative emissions polygeneration systems with desalination. Energy 2019, 187, 115953. [Google Scholar] [CrossRef]
- Guo, X.; Sun, H.; Wu, J.; Jin, J.; Zhou, J.; Gao, Z. Multiperiod-based timetable optimization for metro transit networks. Transp. Res. Part B Methodol. 2017, 96, 46–67. [Google Scholar] [CrossRef]
- Wang, B.; Yuan, M.; Zhang, H.; Zhao, W.J.; Liang, Y. An MILP model for optimal design of multi-period natural gas transmission network. Chem. Eng. Res. Des. 2018, 129, 122–131. [Google Scholar] [CrossRef]
- Mirdar Harijani, A.; Mansour, S.; Karimi, B.; Lee, C.G. Multi-period sustainable and integrated recycling network for municipal solid waste—A case study in Tehran. J. Clean. Prod. 2017, 151, 96–108. [Google Scholar] [CrossRef]
- Li, T.; Liu, P.; Li, Z. A multi-period and multi-regional modeling and optimization approach to energy infrastructure planning at a transient stage: A case study of China. Comput. Chem. Eng. 2020, 133, 106673. [Google Scholar] [CrossRef]
- Torkaman, S.; Fatemi Ghomi, S.M.T.; Karimi, B. Multi-stage multi-product multi-period production planning with sequence-dependent setups in closed-loop supply chain. Comput. Ind. Eng. 2017, 113, 602–613. [Google Scholar] [CrossRef]
- Voll, P.; Jennings, M.; Hennen, M.; Shah, N.; Bardow, A. The optimum is not enough: A near-optimal solution paradigm for energy systems synthesis. Energy 2015, 82, 446–456. [Google Scholar] [CrossRef]
- Orosz, Á.; Friedler, F. Multiple-solution heat exchanger network synthesis for enabling the best industrial implementation. Energy 2020, 208, 118330. [Google Scholar] [CrossRef]
- Friedler, F.; Aviso, K.B.; Bertok, B.; Foo, D.C.Y.; Tan, R.R. Prospects and challenges for chemical process synthesis with P-graph. Curr. Opin. Chem. Eng. 2019, 26, 58–64. [Google Scholar] [CrossRef]
- Friedler, F.; Tarján, K.; Huang, Y.W.; Fan, L.T. Combinatorial algorithms for process synthesis. Chem. Eng. Sci. 1992, 16, S313–S320. [Google Scholar] [CrossRef]
- Friedler, F.; Tarján, K.; Huang, Y.W.; Fan, L.T. Graph-theoretic approach to process synthesis: Polynomial algorithm for maximal structure generation. Comput. Chem. Eng. 1993, 17, 929–942. [Google Scholar] [CrossRef]
- Friedler, F.; Varga, J.B.; Fan, L.T. Decision-mapping: A tool for consistent and complete decisions in process synthesis. Chem. Eng. Sci. 1995, 50, 1755–1768. [Google Scholar] [CrossRef]
- Friedler, F.; Varga, J.B.; Feher, E.; Fan, L.T. Combinatorially Accelerated Branch-and-Bound Method for Solving the MIP Model of Process Network Synthesis. In State of the Art in Global Optimization; Floudas, C.A., Pardalos, P.M., Eds.; Springer: Boston, MA, USA, 1996; pp. 609–626. ISBN 978-1-4613-3439-2. [Google Scholar]
- Heckl, I.; Halász, L.; Szlama, A.; Cabezas, H.; Friedler, F. Process synthesis involving multi-period operations by the P-graph framework. Comput. Chem. Eng. 2015, 83, 157–164. [Google Scholar] [CrossRef]
- Aviso, K.B.; Lee, J.Y.; Dulatre, J.C.; Madria, V.R.; Okusa, J.; Tan, R.R. A P-graph model for multi-period optimization of sustainable energy systems. J. Clean. Prod. 2017, 161, 1338–1351. [Google Scholar] [CrossRef]
- P-Graph Community P-Graph Web Page. Available online: http://p-graph.org (accessed on 13 June 2020).
- Bertok, B.; Bartos, A. Algorithmic process synthesis and optimisation for multiple time periods including waste treatment: Latest developments in p-graph studio software. Chem. Eng. Trans. 2018, 70, 97–102. [Google Scholar] [CrossRef]
- Bertok, B.; Bartos, A. Renewable energy storage and distribution scheduling for microgrids by exploiting recent developments in process network synthesis. J. Clean. Prod. 2020, 244, 118520. [Google Scholar] [CrossRef]
- del Rosario, A.; Aiken, P.; Ailleret, F. Comparison of Energy Systems Using Life Cycle Assessment; World Energy Council: London, UK, 2004. [Google Scholar]
- Tan, R.R.; Aviso, K.B. An extended P-graph approach to process network synthesis for multi-period operations. Comput. Chem. Eng. 2016, 85, 40–42. [Google Scholar] [CrossRef]
- P-Graph Community Multi-Periodic Processes with P-Graph. Available online: http://p-graph.org/multiperiodic-processes/ (accessed on 16 January 2021).
- Tzeng, G.-H.; Huang, J.-J. Multiple Attribute Decision Making: Methods and Applications; CRC Press: Boca Raton, FL, USA, 2011. [Google Scholar]




| Period Name | Electricity | Steam | Cooling | Purified Water | ||||
|---|---|---|---|---|---|---|---|---|
| Price (EUR/kwh) | Demand (kwh) | Price (EUR/kwh) | Demand (kwh) | Price (EUR/kwh) | Demand (kwh) | Price (EUR/t) | Demand (t) | |
| 1 | 0.08 | 36,000 | 0.04 | 72,000 | 0.06 | 0 | 1.2 | 600 |
| 2 | 0.12 | 60,000 | 0.04 | 48,000 | 0.06 | 3000 | 1.2 | 600 |
| 3 | 0.09 | 48,000 | 0.04 | 24,000 | 0.06 | 6000 | 1.2 | 600 |
| 4 | 0.04 | 24,000 | 0.04 | 48,000 | 0.06 | 9000 | 1.2 | 600 |
| Materials/Operations | Boiler | CHP Unit | Chiller | RO Unit | EGDA | Importer |
|---|---|---|---|---|---|---|
| Biomass fuel (t/h) | −0.25 | −0.8 | ||||
| Imported electricity (kWe) * | −1 | |||||
| Electricity (kWe) * | 1 | −0.2 | −3 | −0.013 | 1 | |
| Steam (kWh) * | 1 | 1.6 | ||||
| Cooling (kWc) * | 1 | |||||
| Purified water (t/h) | −0.002 | −0.003 | 1 | −0.1 | ||
| HCl (t/h) | 0.1 | |||||
| Seawater (t/h) | −2 | |||||
| Brine (t/h) | 1 | −1 | ||||
| Treated brine (t/h) | 1 | |||||
| CO2 emissions (kg eq./kWh) | 0.0168 | 0.038 | 0.2 | |||
| Fixed investment cost | 45,000 | 380,000 | 44,000 | 0 | 0 | 0 |
| Proportional investment cost | 175 | 950 | 268 | 15,000 | 350 | 0 |
| Stored Material | Fixed Investment Cost (EUR) | Proportional Investment Cost (EUR/t) | Maximum Storage |
|---|---|---|---|
| Purified Water | 16,000 | 150 | - |
| HCl | 40,000 | 375 | 25 t |
| Period | Electricity | Steam | Cooling | Purified Water | ||||
|---|---|---|---|---|---|---|---|---|
| Price (EUR/kWh) | Demand (kWh) | Price (EUR/kWh) | Demand (kWh) | Price (EUR/kWh) | Demand (kWh) | Price (EUR/t) | Demand (t) | |
| 1 | 0.05 | 4000 | 0.04 | 12,000 | 0.06 | 0 | 1.2 | 100 |
| 2 | 0.03 | 4000 | 0.04 | 12,000 | 0.06 | 0 | 1.2 | 100 |
| 3 | 0.02 | 4000 | 0.04 | 12,000 | 0.06 | 0 | 1.2 | 100 |
| 4 | 0.04 | 4000 | 0.04 | 12,000 | 0.06 | 0 | 1.2 | 100 |
| 5 | 0.05 | 6000 | 0.04 | 12,000 | 0.06 | 0 | 1.2 | 100 |
| 6 | 0.05 | 6000 | 0.04 | 12,000 | 0.06 | 0 | 1.2 | 100 |
| 7 | 0.08 | 6000 | 0.04 | 8000 | 0.06 | 0 | 1.2 | 100 |
| 8 | 0.08 | 8000 | 0.04 | 8000 | 0.06 | 0 | 1.2 | 100 |
| 9 | 0.10 | 8000 | 0.04 | 8000 | 0.06 | 1000 | 1.2 | 100 |
| 10 | 0.12 | 10,000 | 0.04 | 4000 | 0.06 | 1000 | 1.2 | 100 |
| 11 | 0.12 | 10,000 | 0.04 | 4000 | 0.06 | 1500 | 1.2 | 100 |
| 12 | 0.10 | 10,000 | 0.04 | 4000 | 0.06 | 1500 | 1.2 | 100 |
| 13 | 0.09 | 10,000 | 0.04 | 4000 | 0.06 | 1500 | 1.2 | 100 |
| 14 | 0.07 | 8000 | 0.04 | 4000 | 0.06 | 1500 | 1.2 | 100 |
| 15 | 0.07 | 8000 | 0.04 | 4000 | 0.06 | 1500 | 1.2 | 100 |
| 16 | 0.06 | 8000 | 0.04 | 8000 | 0.06 | 1500 | 1.2 | 100 |
| 17 | 0.08 | 8000 | 0.04 | 8000 | 0.06 | 1000 | 1.2 | 100 |
| 18 | 0.08 | 8000 | 0.04 | 8000 | 0.06 | 1000 | 1.2 | 100 |
| 19 | 0.09 | 10,000 | 0.04 | 10,000 | 0.06 | 500 | 1.2 | 100 |
| 20 | 0.10 | 10,000 | 0.04 | 10,000 | 0.06 | 500 | 1.2 | 100 |
| 21 | 0.11 | 10,000 | 0.04 | 10,000 | 0.06 | 0 | 1.2 | 100 |
| 22 | 0.08 | 4000 | 0.04 | 12,000 | 0.06 | 0 | 1.2 | 100 |
| 23 | 0.07 | 4000 | 0.04 | 12,000 | 0.06 | 0 | 1.2 | 100 |
| 24 | 0.06 | 4000 | 0.04 | 12,000 | 0.06 | 0 | 1.2 | 100 |
| Characteristic | Units | Reference Stream | Case 1 | Case 2 | Case 3 | Case 4 | Case 5 |
|---|---|---|---|---|---|---|---|
| CO2 emission | kg/day | CO2 eq. | 40,300 | 39,000 | 30,000 | 25,340 | 20,000 |
| Profit | EUR/day | 853.64 | 712.88 | 341.72 | 0.26 | −668.00 | |
| Boiler capacity | kWh | Steam | 12,000 | 12,000 | 12,000 | 12,000 | 9031.3 |
| CHP capacity | kWe | Electricity | 0 | 529.2 | 3582.7 | 5000 | 6383.9 |
| Chiller | kWc | Cooling | 1500 | 1500 | 1500 | 1500 | 1500 |
| RO unit capacity | t/h | Purified water | 125.5 | 125.45 | 125.6 | 126.16 | 127.62 |
| EGDA | t/h | Treated brine | 80 | 80 | 80 | 80 | 82 |
| Imported electricity | MWh/day | Electricity | 183.6 | 176.97 | 128.71 | 103.23 | 73.12 |
| Water storage tank | t | 66 | 66.2 | 61 | 52.4 | 34.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pimentel, J.; Orosz, Á.; Aviso, K.B.; Tan, R.R.; Friedler, F. Conceptual Design of a Negative Emissions Polygeneration Plant for Multiperiod Operations Using P-Graph. Processes 2021, 9, 233. https://doi.org/10.3390/pr9020233
Pimentel J, Orosz Á, Aviso KB, Tan RR, Friedler F. Conceptual Design of a Negative Emissions Polygeneration Plant for Multiperiod Operations Using P-Graph. Processes. 2021; 9(2):233. https://doi.org/10.3390/pr9020233
Chicago/Turabian StylePimentel, Jean, Ákos Orosz, Kathleen B. Aviso, Raymond R. Tan, and Ferenc Friedler. 2021. "Conceptual Design of a Negative Emissions Polygeneration Plant for Multiperiod Operations Using P-Graph" Processes 9, no. 2: 233. https://doi.org/10.3390/pr9020233
APA StylePimentel, J., Orosz, Á., Aviso, K. B., Tan, R. R., & Friedler, F. (2021). Conceptual Design of a Negative Emissions Polygeneration Plant for Multiperiod Operations Using P-Graph. Processes, 9(2), 233. https://doi.org/10.3390/pr9020233








