Evaluation of Energy Performance and Thermal Comfort Considering the Heat Storage Capacity and Thermal Conductivity of Biocomposite Phase Change Materials
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials and Preparation
2.2. Characterization Techniques
2.3. Building Energy Simulation Modeling
3. Results
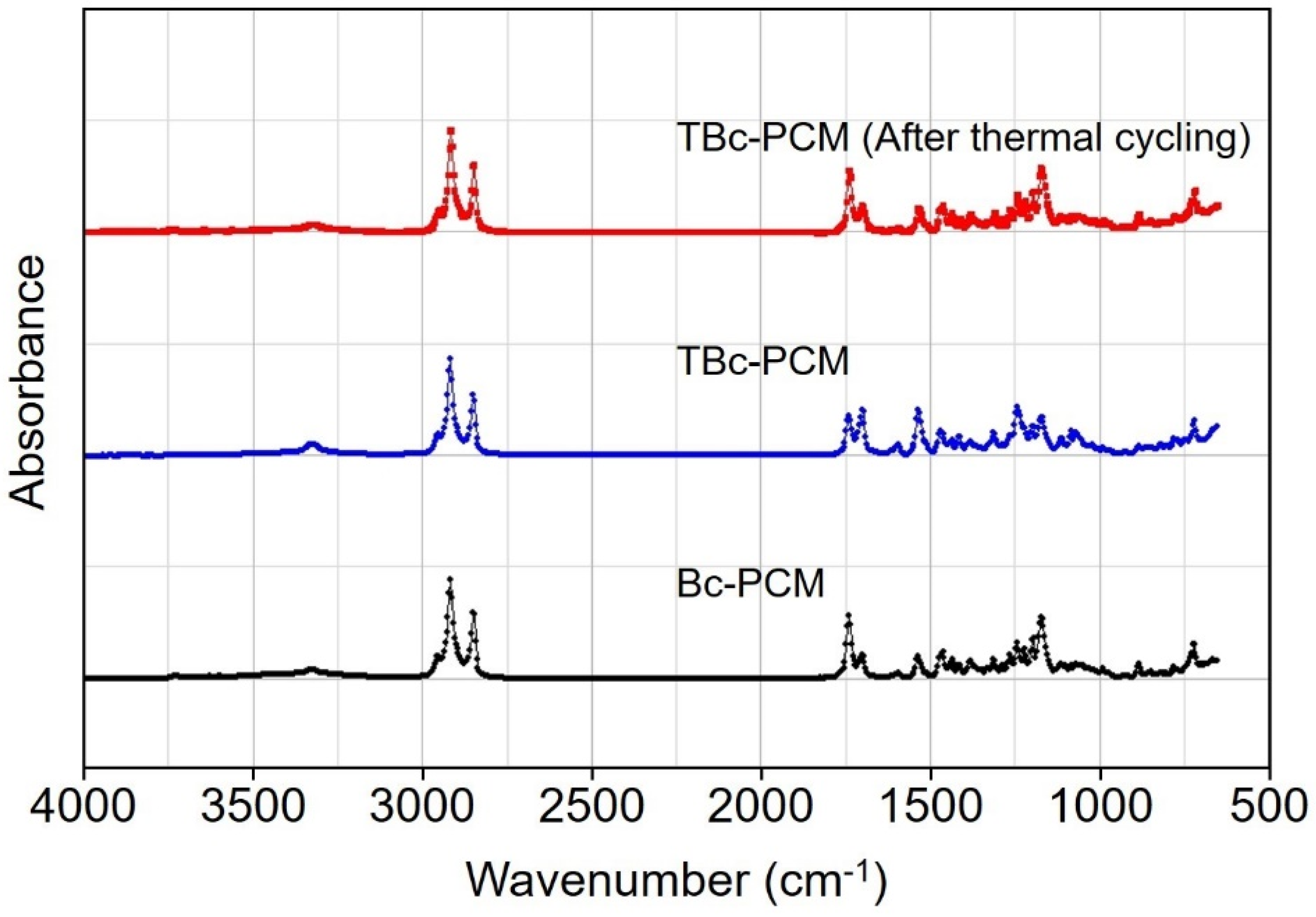
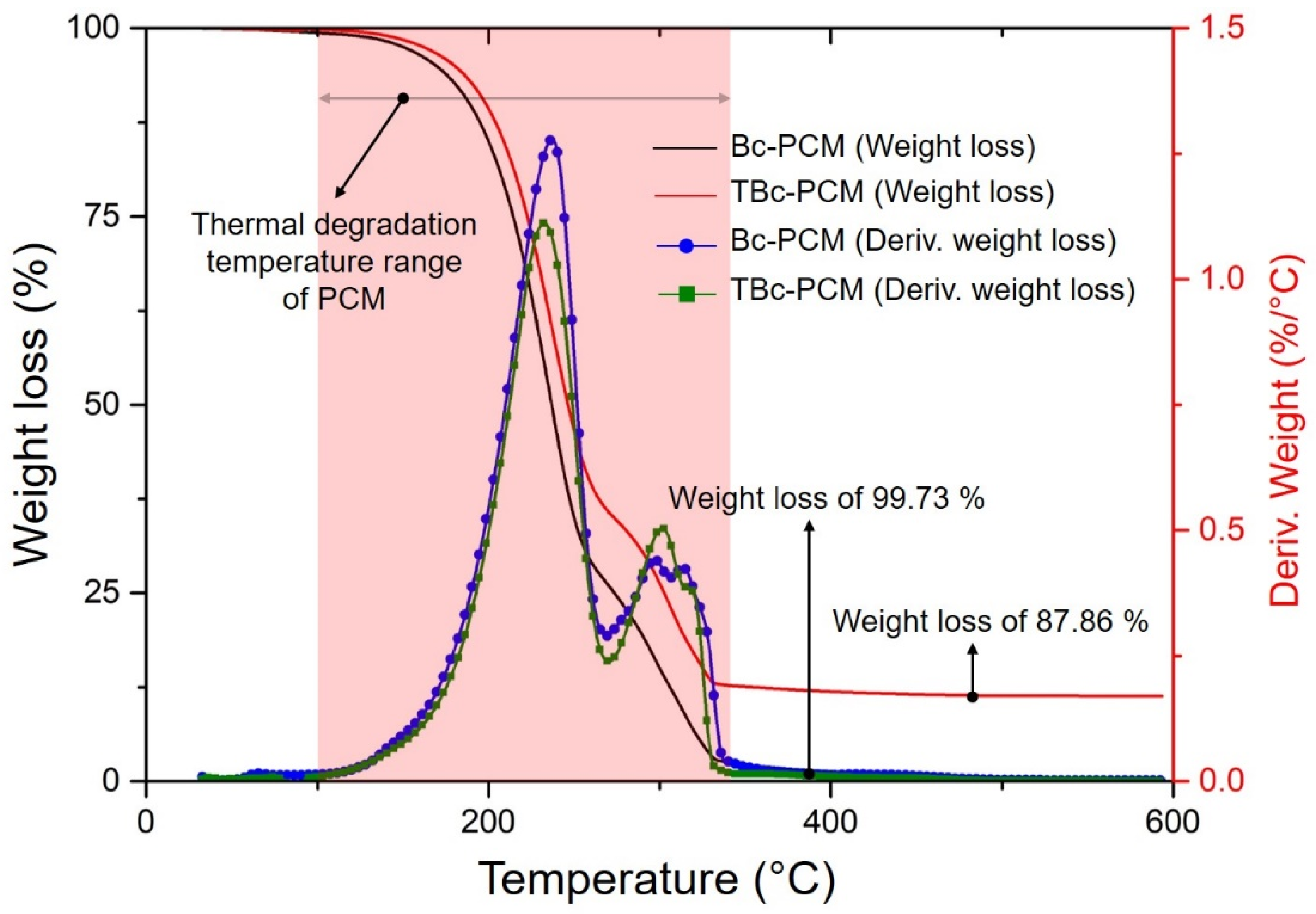
3.1. Chemical Stability Analysis of Bc-PCM and TBc-PCM
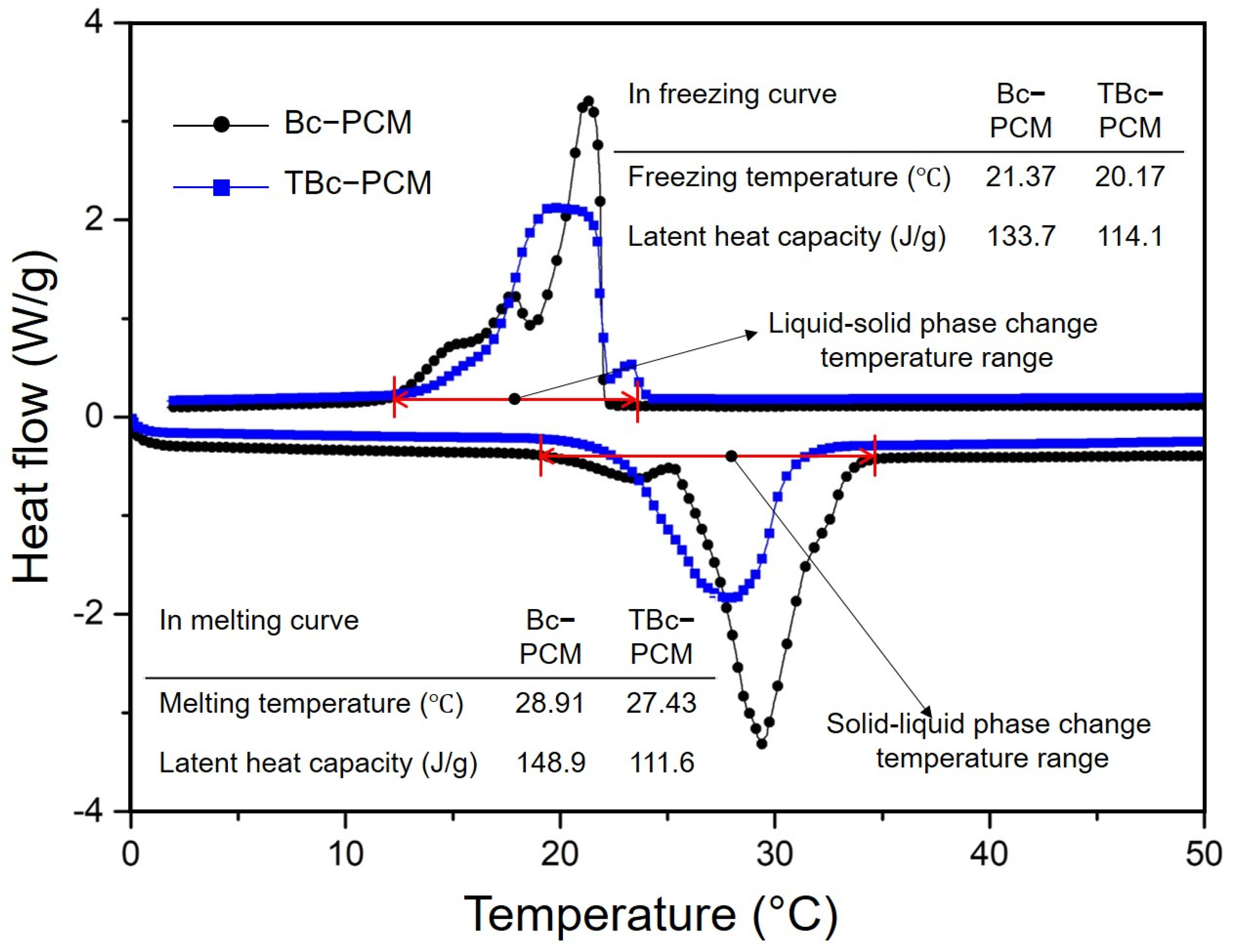
3.2. Thermal Properties of Bc-PCM and TBc-PCM
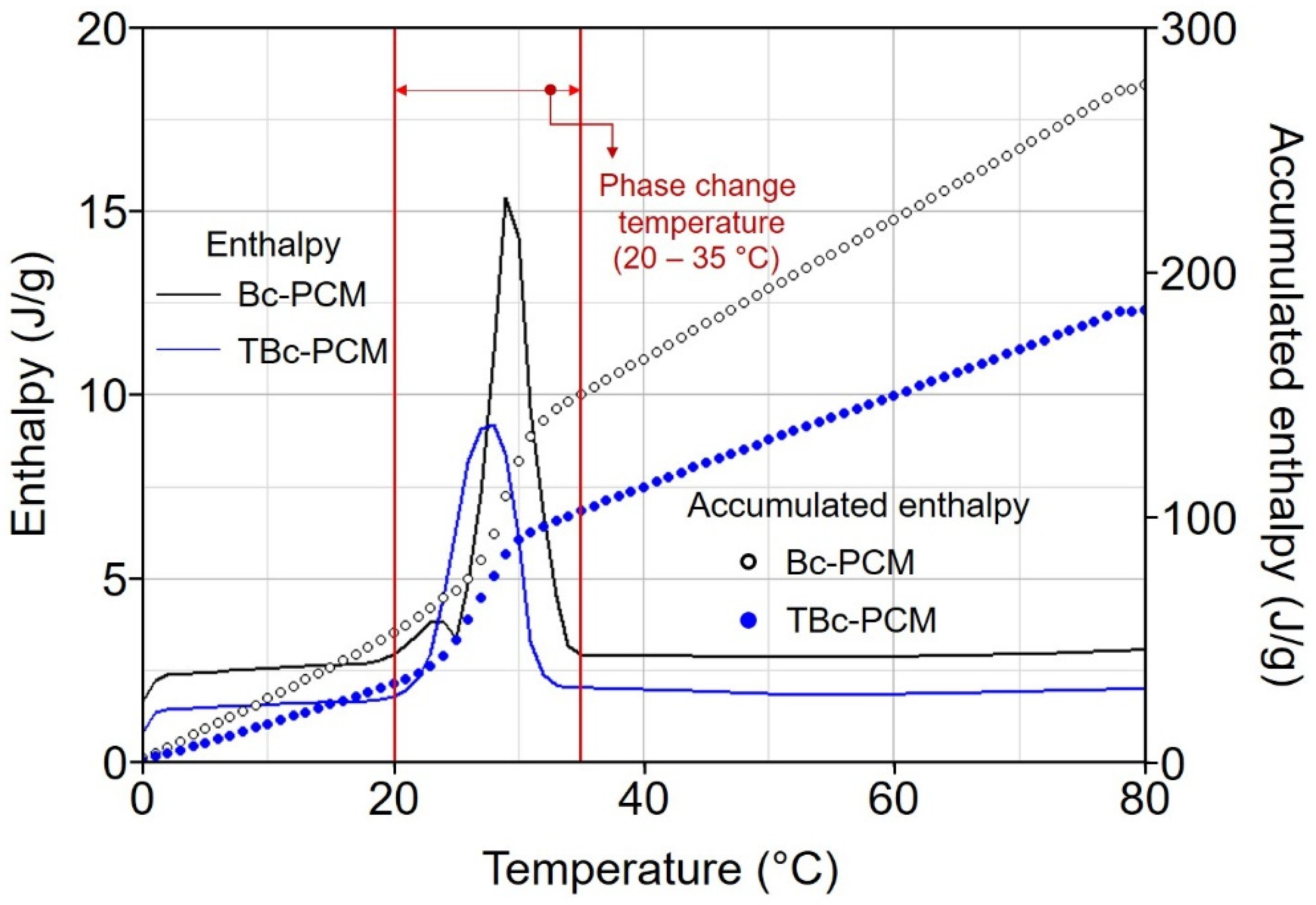
3.2.1. Heat Storage Analysis and Enthalpy Analyses
3.2.2. Thermal Durability and Thermal Conductivity Analyses
3.3. Energy Simulation Analysis
3.3.1. Annual Heating and Cooling Load Reduction
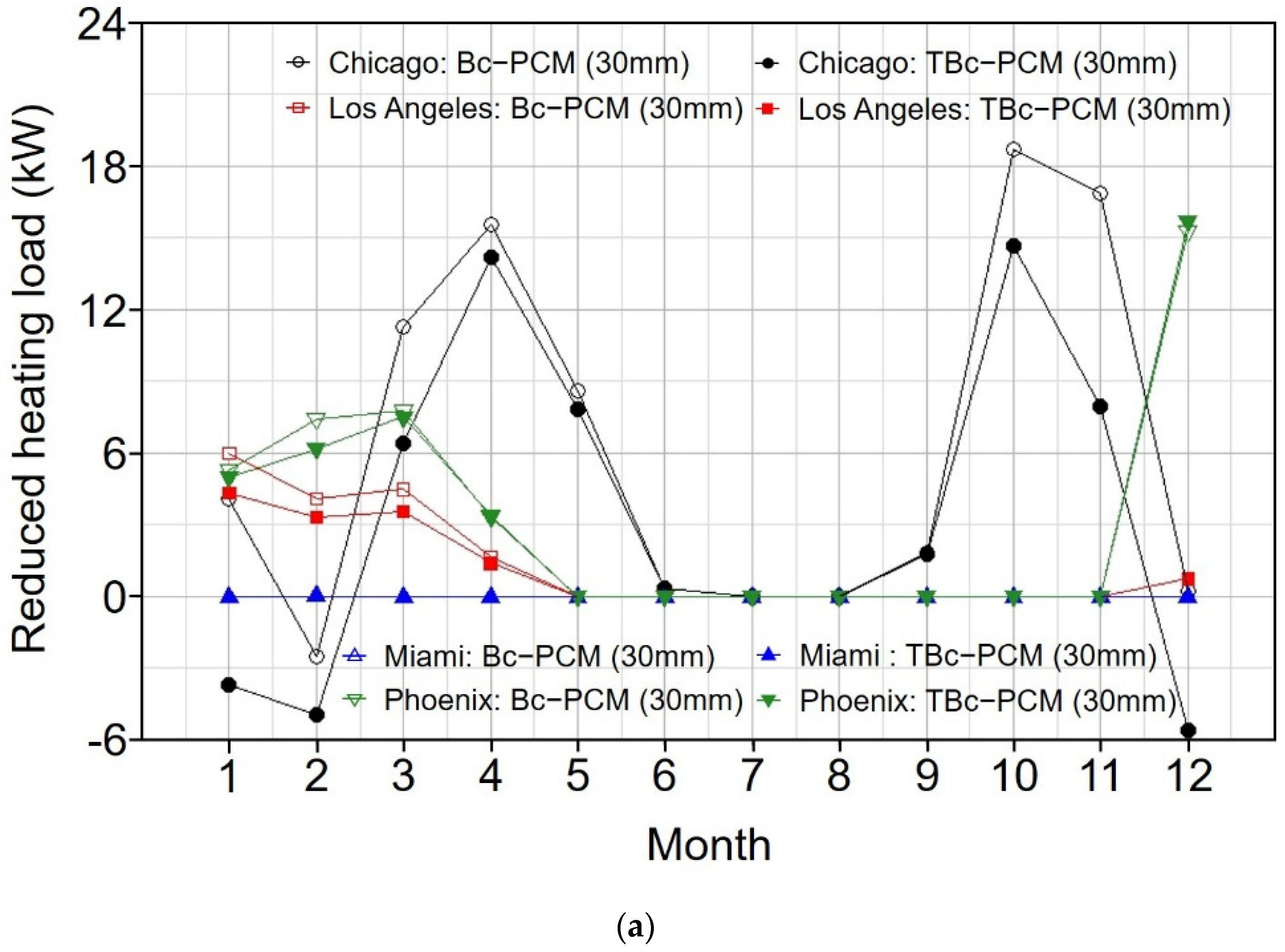
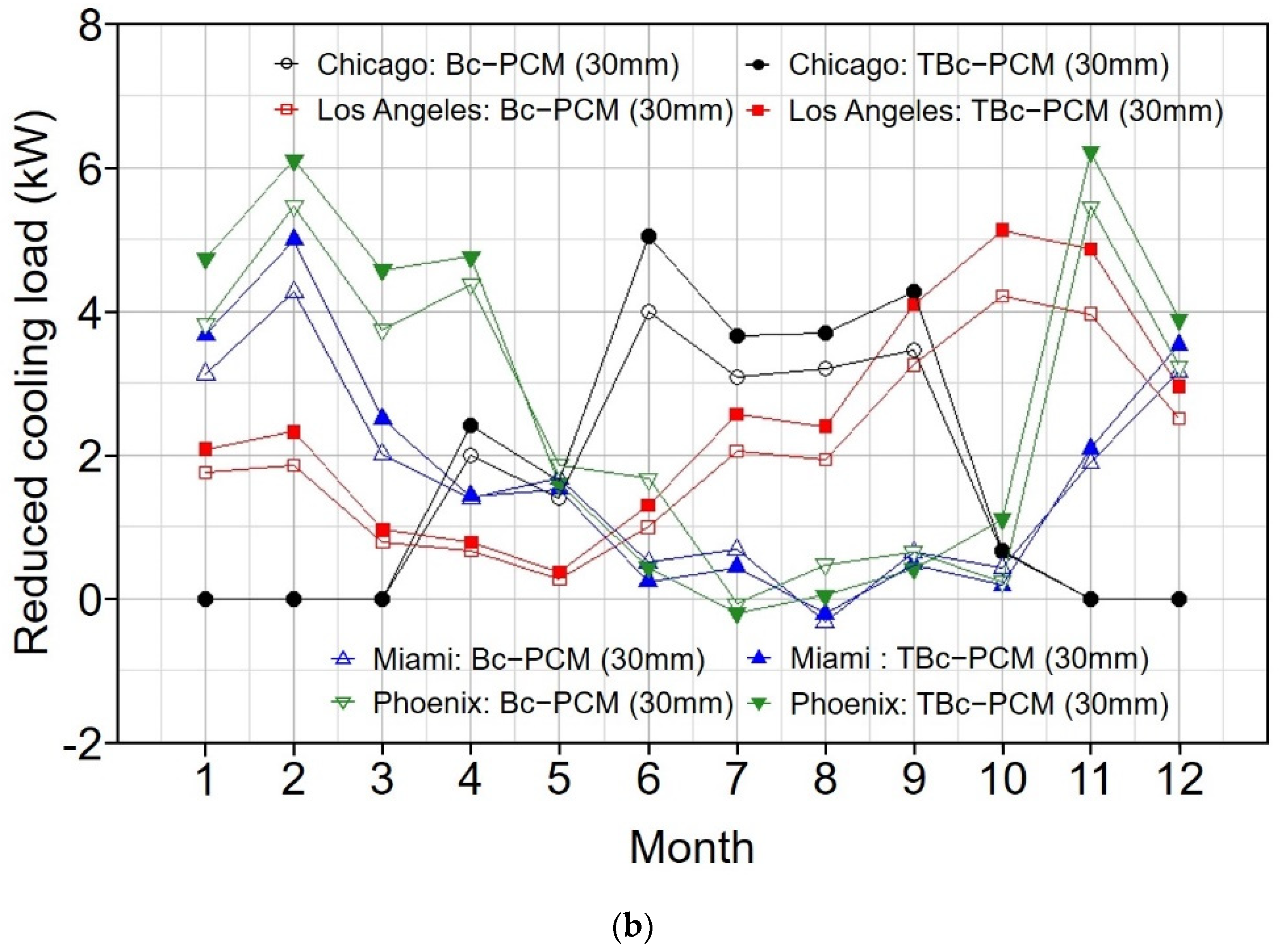
3.3.2. Monthly Heating and Cooling Load Reduction
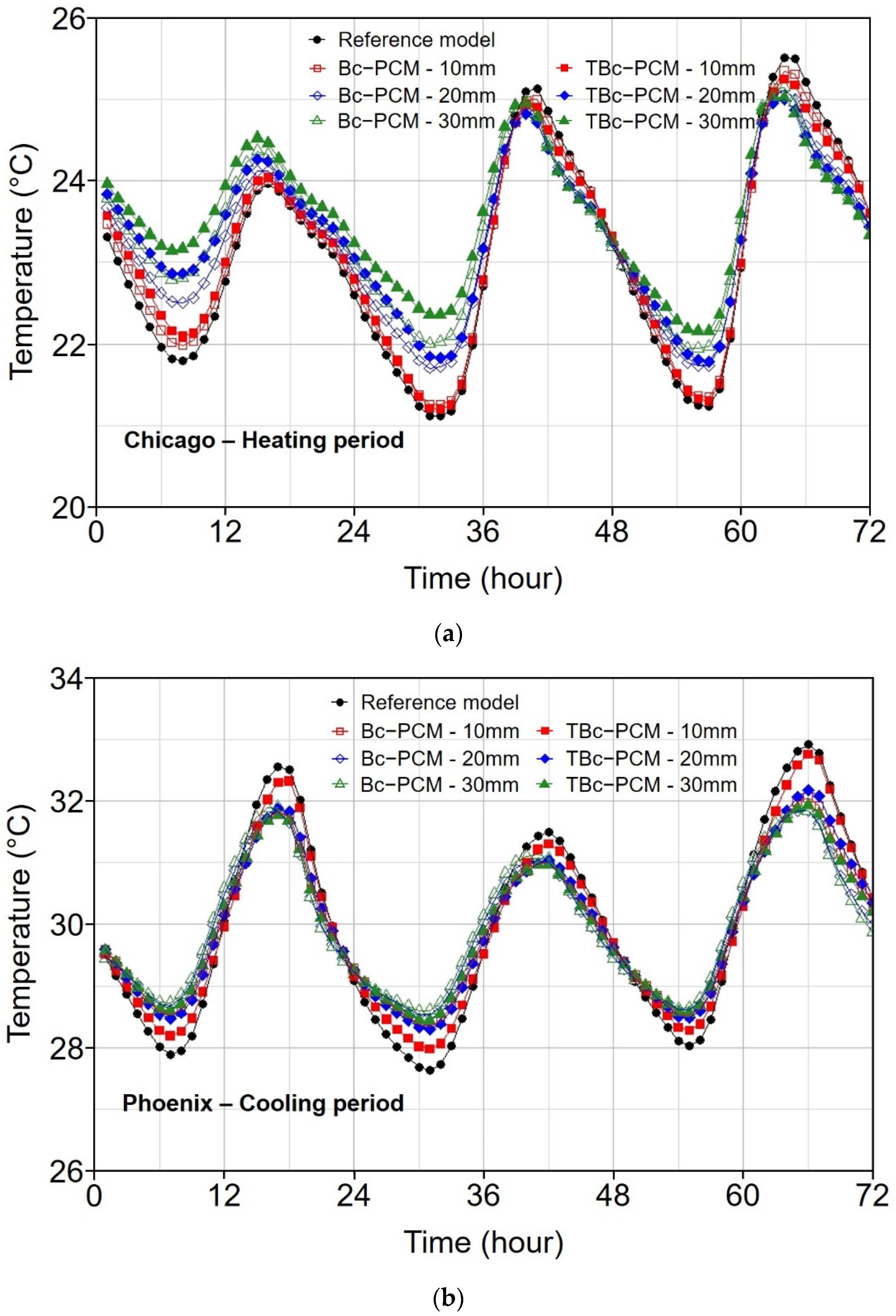
3.3.3. Surface Temperature Change Analysis
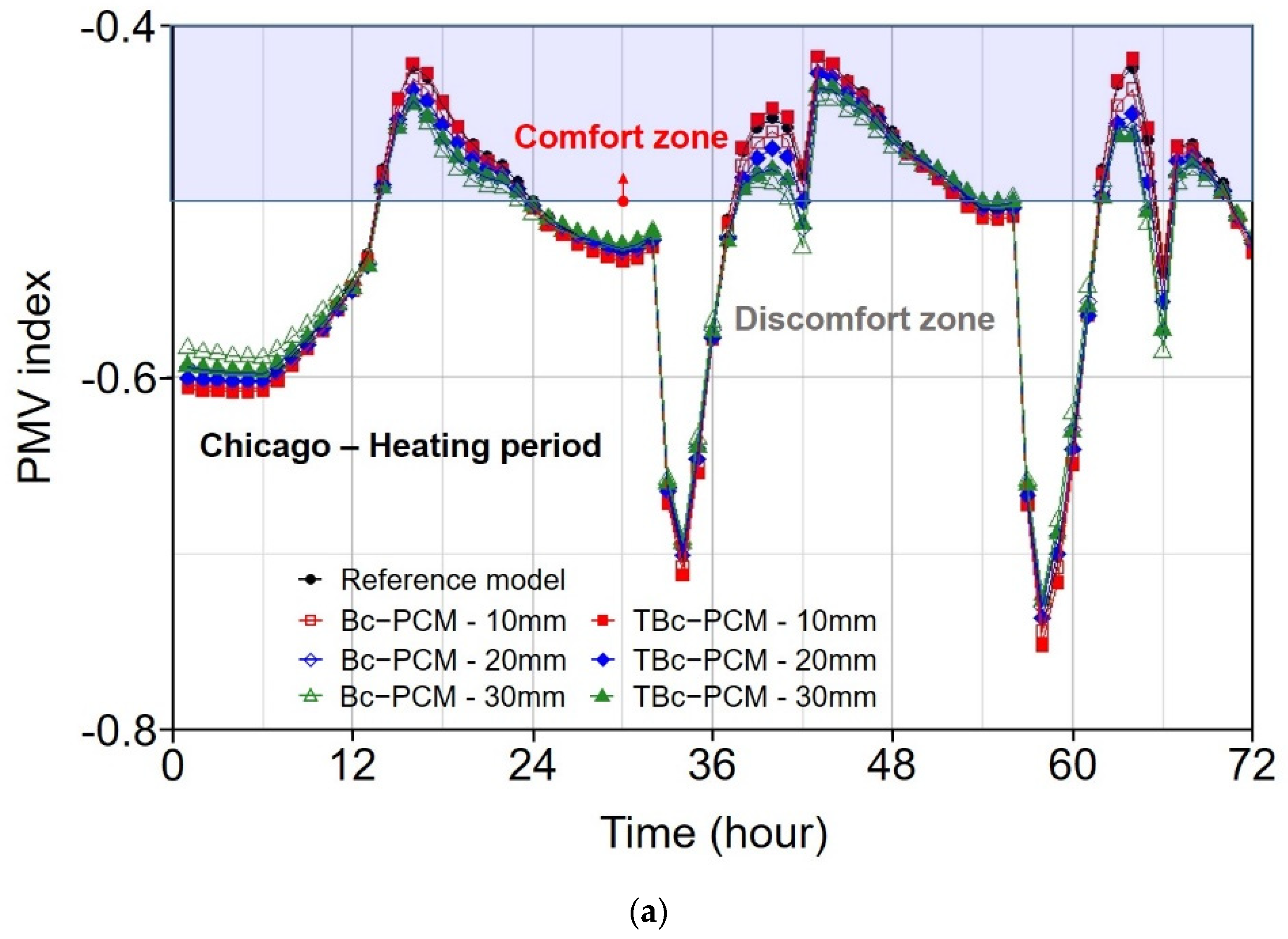
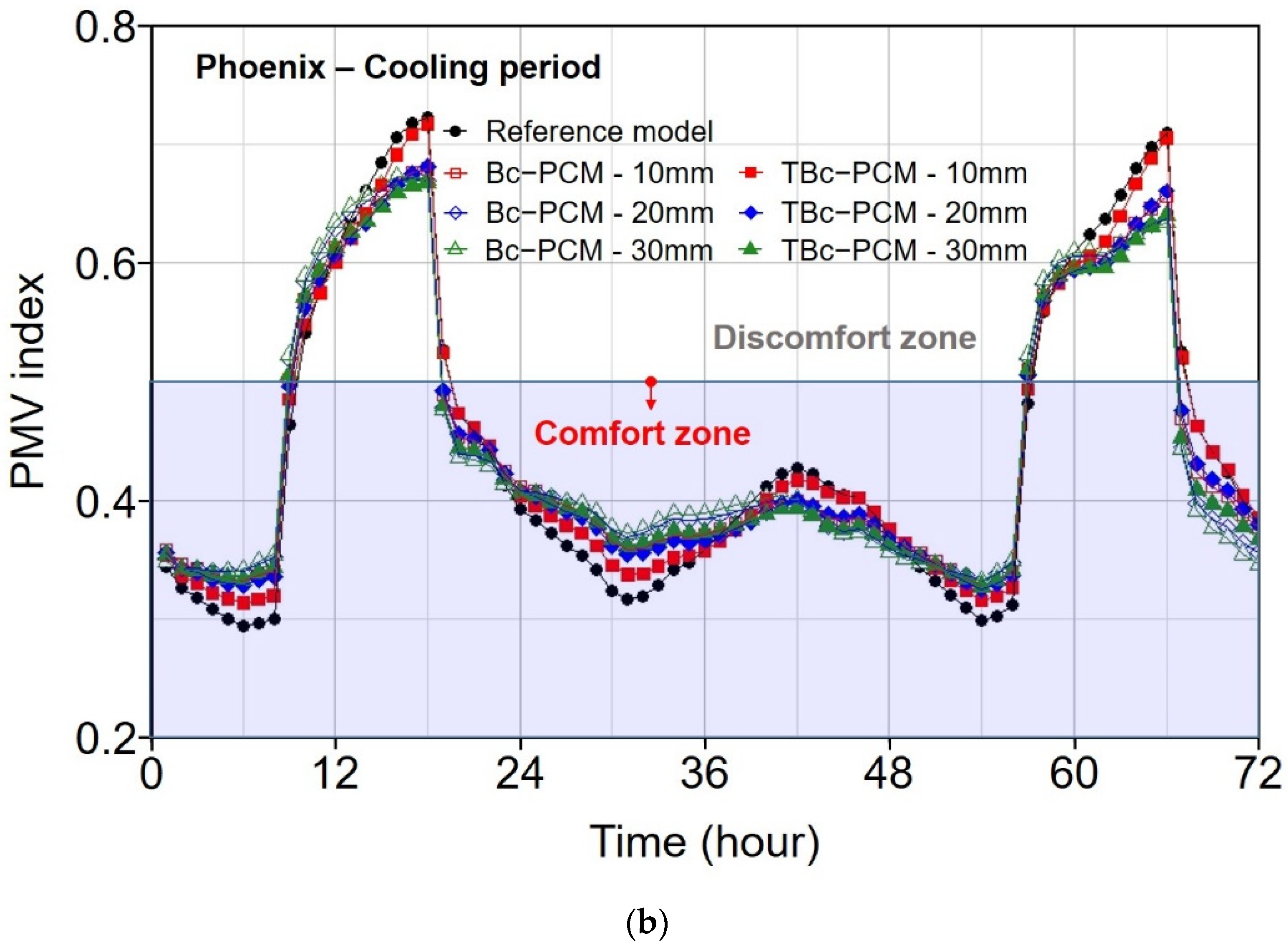
3.3.4. Thermal Comfort Evaluation through PMV Index
4. Conclusions
- In the FTIR-analysis shows that the characteristics of Bc-PCM in TBc-PCM were not changed after impregnation process. Thermal property analyses revealed that Bc-PCM showed a higher heat capacity and enthalpy value compared to TBc-PCM. Thermal conductivity analysis showed that TBc-PCM exhibited a 378% increase in the thermal conductivity compared to Bc-PCM.
- In the building energy simulation results, when the temperature difference between room temperature and the phase change temperature was large (heating period), the PCM stored energy as sensible heat, so Bc-PCM with a larger PCM capacity is more effective in terms of energy consumption reduction. On the other hand, because PCM stores more heat energy in the form of latent heat during the cooling period, the cooling energy reduction effect was higher when TBc-PCM with high thermal conductivity was applied owing to the high heat transfer.
- In the monthly heating and cooling load reduction analysis, the highest energy reduction effect was observed when the TBc-PCM with high thermal conductivity was applied under the condition that the latent heat performance could be maximized. In conclusion, when applying biocomposite PCM (28–30 °C of phase change temperature range), it is effective to apply TBc-PCM (High thermal conductivity) in the cooling season, and it is advantageous in terms of energy reduction by applying Bc-PCM (High latent heat capacity) to the heating season.
- In the surface temperature change analysis, the temperature change decreased as the thickness of the PCM increased. In addition, under the condition that the PCM can maximize the latent heat storage, the Bc-PCM with a large amount of PCM showed a smaller temperature difference.
- In the thermal comfort evaluation through the PMV index, the high thermal conductivity and the small amount of heat storage caused a sudden change in the surface temperature, which had an effect on the mean radiant temperature, resulting in a more rapid PMV change. We also found that the PMV index was closer to the comfort zone in the discomfort zone when PCM was applied. In conclusion, the application of PCM is advantageous in terms of energy reduction and thermal comfort. However, to maximize these performances, it is necessary to understand the heat storage capacity and thermal conductivity of PCMs.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Memon, S.A. Phase change materials integrated in building walls: A state of the art review. Renew. Sustain. Energy Rev. 2014, 31, 870–906. [Google Scholar] [CrossRef]
- Pérez-Lombard, L.; Ortiz, J.; Pout, C. A review on buildings energy consumption information. Energy Build. 2008, 40, 394–398. [Google Scholar] [CrossRef]
- Ramakrishnan, S.; Wang, X.; Sanjayan, J.; Wilson, J. Thermal performance of buildings integrated with phase change materials to reduce heat stress risks during extreme heatwave events. Appl. Energy 2017, 194, 410–421. [Google Scholar] [CrossRef]
- Pigliautile, I.; Chàfer, M.; Pisello, A.L.; Pérez, G.; Cabeza, L.F. Inter-building assessment of urban heat island mitigation strategies: Field tests and numerical modelling in a simplified-geometry experimental set-up. Renew. Energy 2020, 147, 1663–1675. [Google Scholar] [CrossRef]
- Piselli, C.; Prabhakar, M.; de Gracia, A.; Saffari, M.; Pisello, A.L.; Cabeza, L.F. Optimal control of natural ventilation as passive cooling strategy for improving the energy performance of building envelope with PCM integration. Renew. Energy 2020, 162, 171–181. [Google Scholar] [CrossRef]
- Diaconu, B.M. Thermal energy savings in buildings with PCM-enhanced envelope: Influence of occupancy pattern and ventilation. Energy Build. 2011, 43, 101–107. [Google Scholar] [CrossRef]
- Iten, M.; Liu, S.; Shukla, A. A review on the air-PCM-TES application for free cooling and heating in the buildings. Renew. Sustain. Energy Rev. 2016, 61, 175–186. [Google Scholar] [CrossRef]
- Jeon, J.; Lee, J.H.; Seo, J.; Jeong, S.-G.; Kim, S. Application of PCM thermal energy storage system to reduce building energy consumption. J. Therm. Anal. Calorim. 2010, 111, 279–288. [Google Scholar] [CrossRef]
- Cabeza, L.F.; Castell, A.; Barreneche, C.d.; De Gracia, A.; Fernández, A. Materials used as PCM in thermal energy storage in buildings: A review. Renew. Sustain. Energy Rev. 2011, 15, 1675–1695. [Google Scholar] [CrossRef]
- Pandey, B.; Banerjee, R.; Sharma, A. Coupled EnergyPlus and CFD analysis of PCM for thermal management of buildings. Energy Build. 2021, 231, 110598. [Google Scholar] [CrossRef]
- Baetens, R.; Jelle, B.P.; Gustavsen, A. Phase change materials for building applications: A state-of-the-art review. Energy Build. 2010, 42, 1361–1368. [Google Scholar] [CrossRef] [Green Version]
- Sharma, V.; Rai, A.C. Performance assessment of residential building envelopes enhanced with phase change materials. Energy Build. 2020, 208, 109664. [Google Scholar] [CrossRef]
- Tyagi, V.V.; Buddhi, D. PCM thermal storage in buildings: A state of art. Renew. Sustain. Energy Rev. 2007, 11, 1146–1166. [Google Scholar] [CrossRef]
- Jeong, S.-G.; Cha, J.; Kim, S.; Seo, J.; Lee, J.-H.; Kim, S. Preparation of thermal-enhanced epoxy resin adhesive with organic PCM for applying wood flooring. J. Therm. Anal. Calorim. 2014, 117, 1027–1034. [Google Scholar] [CrossRef]
- Sharma, R.; Ganesan, P.; Tyagi, V.; Metselaar, H.; Sandaran, S. Developments in organic solid–liquid phase change materials and their applications in thermal energy storage. Energy Convers. Manag. 2015, 95, 193–228. [Google Scholar] [CrossRef] [Green Version]
- Keshteli, A.N.; Sheikholeslami, M. Nanoparticle enhanced PCM applications for intensification of thermal performance in building: A review. J. Mol. Liq. 2019, 274, 516–533. [Google Scholar] [CrossRef]
- Wi, S.; Chang, S.J.; Kim, S. Improvement of thermal inertia effect in buildings using shape stabilized PCM wallboard based on the enthalpy-temperature function. Sustain. Cities Soc. 2020, 56, 102067. [Google Scholar] [CrossRef]
- Noël, J.A.; Kahwaji, S.; Desgrosseilliers, L.; Groulx, D.; White, M.A. Phase change materials. Storing Energy 2016, 2, 249–272. [Google Scholar]
- de Albuquerque Landi, F.F.; Fabiani, C.; Pisello, A.L. Palm oil for seasonal thermal energy storage applications in buildings: The potential of multiple melting ranges in blends of bio-based fatty acids. J. Energy Storage 2020, 29, 101431. [Google Scholar] [CrossRef]
- Fabiani, C.; Pisello, A.L.; Barbanera, M.; Cabeza, L.F. Palm oil-based bio-PCM for energy efficient building applications: Multipurpose thermal investigation and life cycle assessment. J. Energy Storage 2020, 28, 101129. [Google Scholar] [CrossRef]
- Yu, S.; Jeong, S.-G.; Chung, O.; Kim, S. Bio-based PCM/carbon nanomaterials composites with enhanced thermal conductivity. Sol. Energy Mater. Sol. Cells 2014, 120, 549–554. [Google Scholar] [CrossRef]
- Wen, R.; Zhang, X.; Huang, Z.; Fang, M.; Liu, Y.; Wu, X.; Min, X.; Gao, W.; Huang, S. Preparation and thermal properties of fatty acid/diatomite form-stable composite phase change material for thermal energy storage. Sol. Energy Mater. Sol. Cells. 2018, 178, 273–279. [Google Scholar] [CrossRef]
- Wan, Y.-C.; Chen, Y.; Cui, Z.-X.; Ding, H.; Gao, S.-F.; Han, Z.; Gao, J.-K. A promising form-stable phase change material prepared using cost effective pinecone biochar as the matrix of palmitic acid for thermal energy storage. Sci. Rep. 2019, 9, 1–10. [Google Scholar]
- Wu, S.; Li, T.; Yan, T.; Dai, Y.; Wang, R. High performance form-stable expanded graphite/stearic acid composite phase change material for modular thermal energy storage. Int. J. Heat Mass Transf. 2016, 102, 733–744. [Google Scholar] [CrossRef]
- Amin, M.; Putra, N.; Kosasih, E.A.; Prawiro, E.; Luanto, R.A.; Mahlia, T. Thermal properties of beeswax/graphene phase change material as energy storage for building applications. Appl. Therm. Eng. 2017, 112, 273–280. [Google Scholar] [CrossRef]
- Fang, X.; Zhang, Z. A novel montmorillonite-based composite phase change material and its applications in thermal storage building materials. Energy Build. 2006, 38, 377–380. [Google Scholar] [CrossRef]
- Fang, X.; Zhang, Z.; Chen, Z. Study on preparation of montmorillonite-based composite phase change materials and their applications in thermal storage building materials. Energy Convers. Manag. 2008, 49, 718–723. [Google Scholar] [CrossRef]
- Zhang, D.; Zhou, J.; Wu, K.; Li, Z. Granular phase changing composites for thermal energy storage. Sol. Energy 2005, 78, 471–480. [Google Scholar] [CrossRef]
- Jeong, S.-G.; Jeon, J.; Seo, J.; Lee, J.-H.; Kim, S. Performance evaluation of the microencapsulated PCM for wood-based flooring application. Energy Convers. Manag. 2012, 64, 516–521. [Google Scholar] [CrossRef]
- Cha, J.; Seo, J.; Kim, S. Building materials thermal conductivity measurement and correlation with heat flow meter, laser flash analysis and TCi. J. Therm. Anal. Calorim. 2012, 109, 295–300. [Google Scholar] [CrossRef]
- Zhang, A.; Bokel, R.; van den Dobbelsteen, A.; Sun, Y.; Huang, Q.; Zhang, Q. An integrated school and schoolyard design method for summer thermal comfort and energy efficiency in Northern China. Build. Environ. 2017, 124, 369–387. [Google Scholar] [CrossRef]
- Park, J.H.; Berardi, U.; Chang, S.J.; Wi, S.; Kang, Y.; Kim, S. Energy retrofit of PCM-applied apartment buildings considering building orientation and height. Energy 2021, 222, 119877. [Google Scholar] [CrossRef]
- Fanger, P.O.; Melikov, A.K.; Hanzawa, H.; Ring, J. Turbulence and draft. The turbulence of airflow has a significant impact on the sensation of draft. ASHRAE J. 1989, 31, 18–25. [Google Scholar]
- Fanger, P. Moderate Thermal Environments Determination of the PMV and PPD Indices and Specification of the Conditions for Thermal Comfort; ISO 7730 1984; International Organization for Standardization: Geneva, Switzerland, 1984. [Google Scholar]
- Chowdhury, A.A.; Rasul, M.; Khan, M.M.K. Thermal-comfort analysis and simulation for various low-energy cooling-technologies applied to an office building in a subtropical climate. Appl. Energy 2008, 85, 449–462. [Google Scholar] [CrossRef]
- Ekici, C. Measurement uncertainty budget of the PMV thermal comfort equation. Int. J. Thermophys. 2016, 37, 48. [Google Scholar] [CrossRef]
- International Organization for Standardization. ISO 7730: Ergonomics of the Thermal Environment: Analytical Determination and Interpretation of Thermal Comfort Using Calculation of the PMV and PPD Indices and Local Thermal Comfort Criteria; International Organization for Standardization: Geneva, Switzerland, 2005. [Google Scholar]
- Jeong, S.-G.; Chang, S.J.; We, S.; Kim, S. Energy efficient thermal storage montmorillonite with phase change material containing exfoliated graphite nanoplatelets. Sol. Energy Mater. Sol. Cells 2015, 139, 65–70. [Google Scholar] [CrossRef]
- Evola, G.; Marletta, L.; Sicurella, F. A methodology for investigating the effectiveness of PCM wallboards for summer thermal comfort in buildings. Build. Environ. 2013, 59, 517–527. [Google Scholar] [CrossRef]
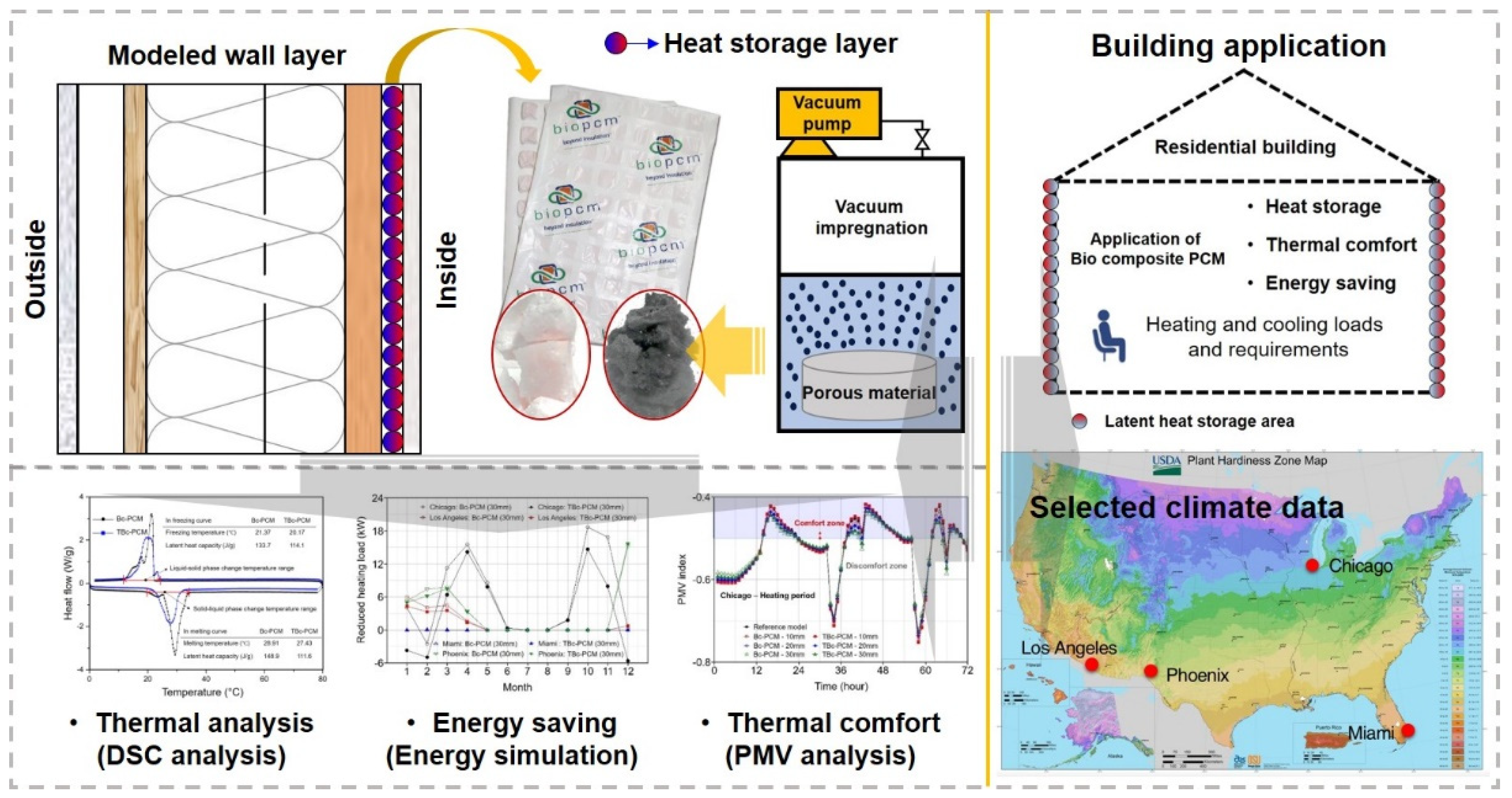
| City | Latitude (°) | Longitude (°) | Elevation (m) | Average Temperature (°C) | Average Relative Humidity (%) | Average Wind Speed (m/s) | Köppen Climate Classification |
|---|---|---|---|---|---|---|---|
| Chicago | 41.99 | −87.91 | 205 | 16.66 | 69.98 | 3.58 | Dfa |
| Los Angeles | 33.94 | −118.41 | 99 | 9.98 | 70.33 | 4.56 | Csb |
| Miami | 25.82 | −80.30 | 9 | 24.31 | 72.54 | 4.34 | Aw |
| Phoenix | 33.44 | −111.99 | 337 | 22.52 | 36.31 | 2.98 | BWh |
| Thickness (m) | Thermal Conductivity (W/mK) | Specific Heat (J/kgK) | Density (kg/m3) | Thermal Resistance (m2∙K/W) | |
|---|---|---|---|---|---|
| Exterior wall | |||||
| Plaster board | 0.03 | 0.25 | 1000 | 900 | |
| PCM composite layer | Variable | ||||
| EPS (Expanded Polystyrene) | 0.03 | 0.04 | 1500 | 15 | |
| Glass fiber insulation | 0.155 | 0.035 | 840 | 12 | |
| OSB (Oriented standard board) | 0.012 | 0.13 | 1700 | 650 | |
| Air gap | 0.038 | 0.18 | |||
| Cement board | 0.009 | 0.255 | 2040 | 520.00 | |
| Partition | |||||
| Plaster board | 0.0095 | 0.25 | 1000 | 900 | |
| Air gap | 0.012 | 0.18 | |||
| Plaster board | 0.0095 | 0.25 | 1000 | 900 | |
| Roof | |||||
| Plywood | 0.005 | 0.15 | 2500 | 560 | |
| PCM layer | Variable | ||||
| EPS | 0.075 | 0.04 | 1500 | 15 | |
| Glass fiber insulation | 0.159 | 0.035 | 840 | 12 | |
| OSB | 0.012 | 0.13 | 1700 | 650 | |
| Asphalt | 0.003 | 0.7 | 1000 | 2100 | |
| Thickness (m) | Thermal Conductivity (W/mK) | Specific Heat (J/kgK) | Density (kg/m3) | |
|---|---|---|---|---|
| Bc-PCM | 0.01 | 0.150 | Variable | 860 |
| 0.02 | ||||
| 0.03 | ||||
| TBc-PCM | 0.01 | 0.568 | Variable | 860 |
| 0.02 | ||||
| 0.03 |
| Heating Load (kW) | |||||||
| Reference | Bc-PCM | TBc-PCM | |||||
| 10 mm | 20 mm | 30 mm | 10 mm | 20 mm | 30 mm | ||
| Chicago | 4497.49 | 4495.67 (1.82) | 4441.73 (55.76) | 4404.51 (92.98) | 4518.26 (−20.77) 1 | 4474.12 (23.37) | 4440.48 (57.01) |
| Los Angeles | 44.01 | 41.16 (2.85) | 31.78 (12.23) | 26.96 (17.05) | 45.22 (−1.21) 1 | 35.83 (8.18) | 30.63 (13.38) |
| Miami | 0.02 | 0 (0.02) | 0 (0.02) | 0 (0.02) | 0 (0.02) | 0 (0.02) | 0 (0.02) |
| Phoenix | 83.85 | 77.58 (6.27) | 57.48 (26.37) | 44.73 (39.12) | 81.57 (2.28) | 60.35 (23.50) | 46.13 (37.72) |
| Cooling Load (kW) | |||||||
| Reference | Bc-PCM | TBc-PCM | |||||
| 10 mm | 20 mm | 30 mm | 10 mm | 20 mm | 30 mm | ||
| Chicago | 101.51 | 96.30 (5.21) | 88.12 (13.39) | 83.71 (17.80) | 94.12 (7.39) | 85.42 (16.09) | 80.10 (21.41) |
| Los Angeles | 70.27 | 61.10 (9.17) | 50.06 (20.21) | 45.96 (24.31) | 56.29 (13.98) | 45.04 (25.23) | 40.39 (29.88) |
| Miami | 587.29 | 585.39 (1.9) | 574.78 (12.51) | 567.77 (19.52) | 584.38 (2.91) | 573.45 (13.84) | 566.37 (20.92) |
| Phoenix | 737.74 | 729.83 (7.91) | 714.55 (23.19) | 706.78 (30.96) | 728.57 (9.17) | 713.26 (24.48) | 704.03 (33.71) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jeong, S.-G.; Lee, T.; Lee, J. Evaluation of Energy Performance and Thermal Comfort Considering the Heat Storage Capacity and Thermal Conductivity of Biocomposite Phase Change Materials. Processes 2021, 9, 2191. https://doi.org/10.3390/pr9122191
Jeong S-G, Lee T, Lee J. Evaluation of Energy Performance and Thermal Comfort Considering the Heat Storage Capacity and Thermal Conductivity of Biocomposite Phase Change Materials. Processes. 2021; 9(12):2191. https://doi.org/10.3390/pr9122191
Chicago/Turabian StyleJeong, Su-Gwang, Taemin Lee, and Jeonghun Lee. 2021. "Evaluation of Energy Performance and Thermal Comfort Considering the Heat Storage Capacity and Thermal Conductivity of Biocomposite Phase Change Materials" Processes 9, no. 12: 2191. https://doi.org/10.3390/pr9122191
APA StyleJeong, S.-G., Lee, T., & Lee, J. (2021). Evaluation of Energy Performance and Thermal Comfort Considering the Heat Storage Capacity and Thermal Conductivity of Biocomposite Phase Change Materials. Processes, 9(12), 2191. https://doi.org/10.3390/pr9122191







