Multi-Rate Data Fusion for State and Parameter Estimation in (Bio-)Chemical Process Engineering
Abstract
:1. Introduction
2. Methods
2.1. Unscented Kalman Filtering
- Calculate the Sigma-Points
- Propagate each SP using the model equations
- Using weightsdetermine , , , and by averaging over weighted SP
2.2. UKF for Delayed and Multi-Rate Measurements
3. Results and Discussion
3.1. Exothermal Chemical Reactor
3.1.1. Model Formulation
3.1.2. Scenario I: State Estimation
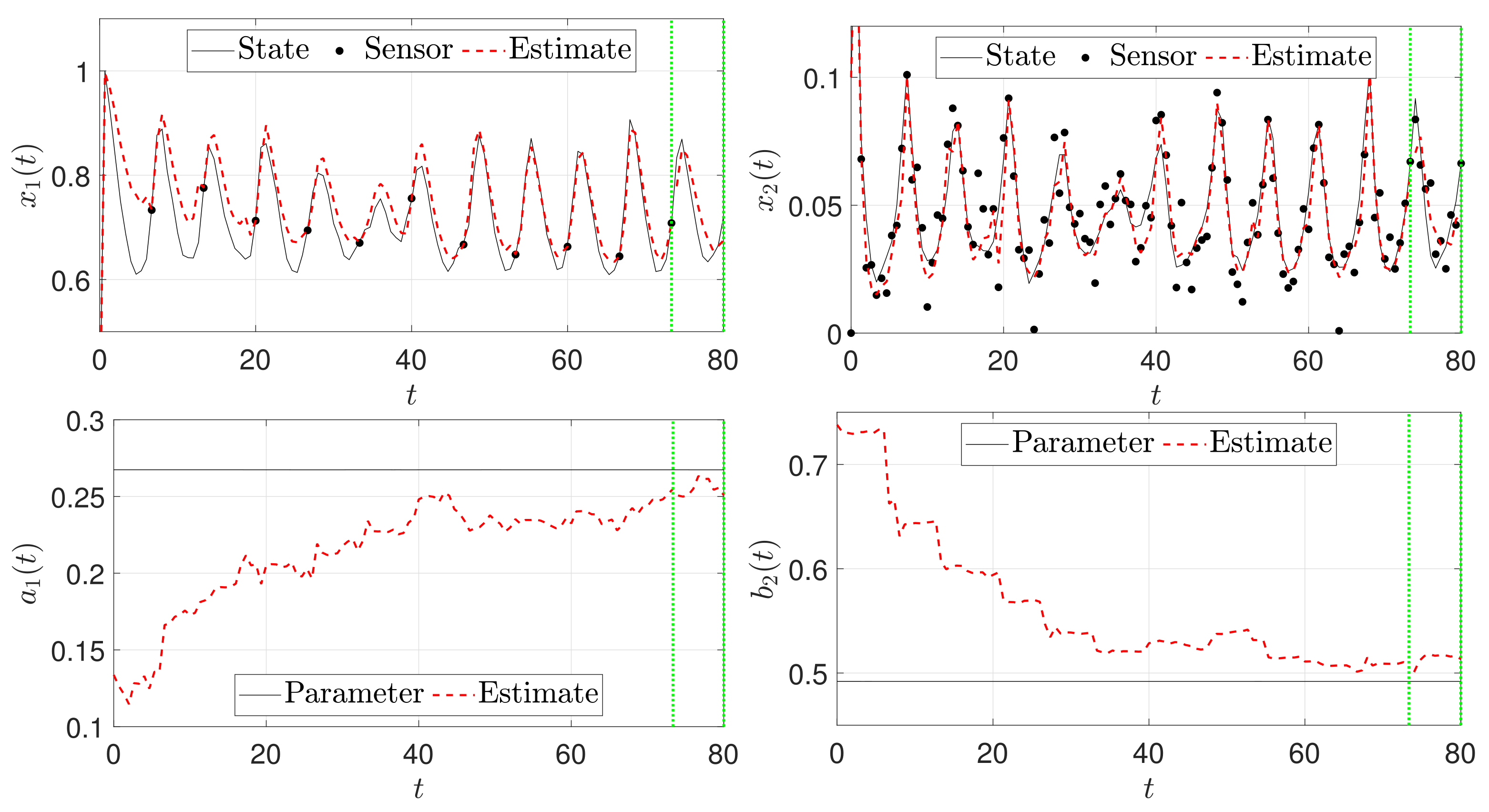
3.1.3. Scenario II: Simultaneous State and Parameter Estimation
3.2. Microbial PHA Production
3.2.1. Model Formulation
3.2.2. State Estimation
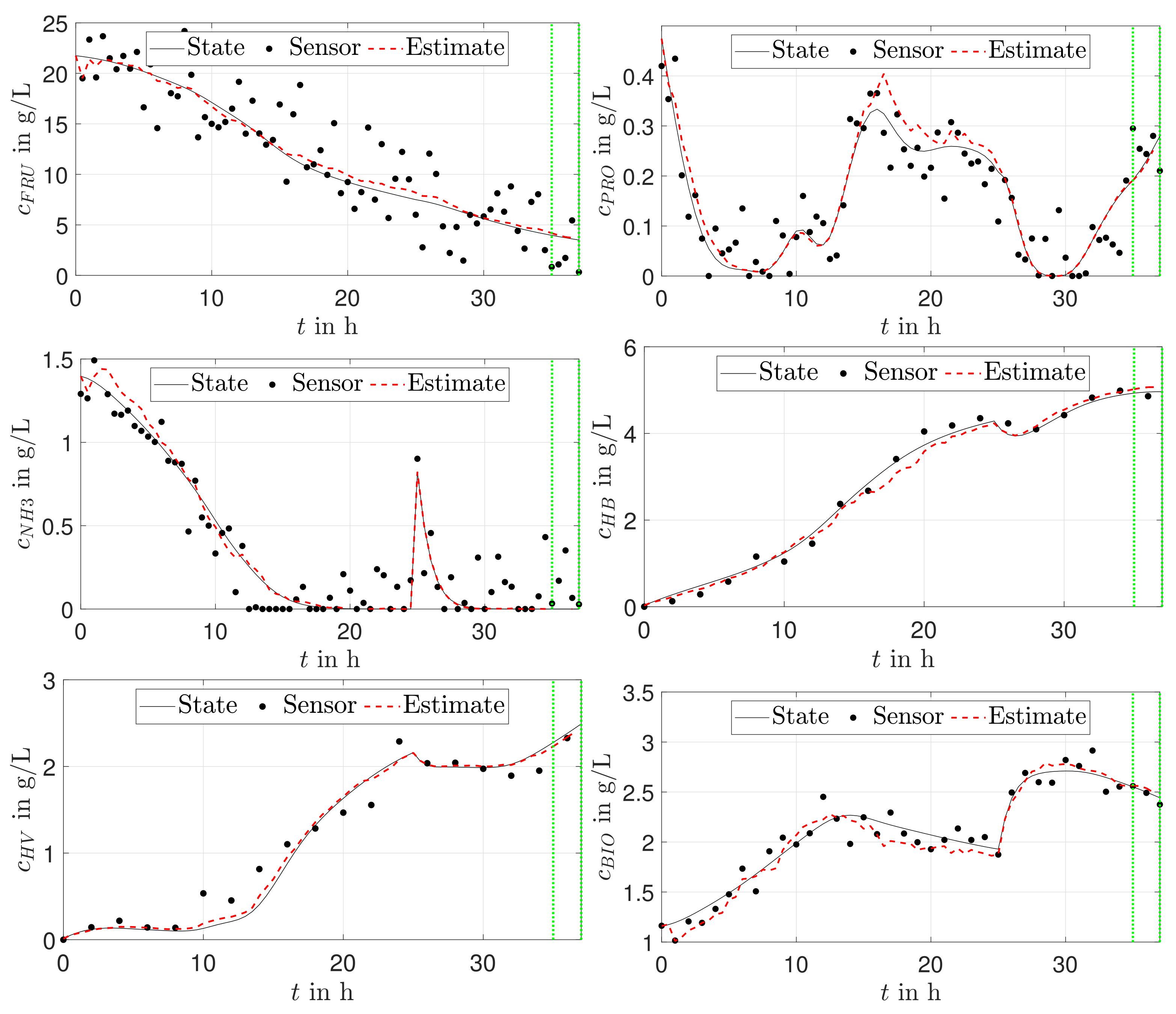
3.2.3. Simultaneous State and Parameter Estimation
4. Conclusions and Outlook
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| HB | Hydroxybutyrate |
| HV | Hydroxyvalerate |
| KF | Kalman Filter |
| MR | Multi-rate |
| ODE | Ordinary Differential Equation |
| PHA | Polyhydroxyalkaonate |
| PHB | poly(3-hydroxybutyrate) |
| PHBV | poly(3-hydroxybutyrate-co-3-hydroxyvalerate) |
| UKF | Unscented Kalman Filter |
| UT | Unscented Transformation |
Appendix A. Reactor Model for Biopolymer Production

| Parameter | Unit | Description | Value |
|---|---|---|---|
| [L/g h] | consumption of fructose | ||
| and ammonium for growth | 4.34 × 10 | ||
| [L/g h] | consumption of propionic acid | ||
| and ammonium for growth | 0.0048 | ||
| [L/g h] | HA consumption | 0.0713 | |
| [L/g h] | consumption of fructose | ||
| for HB accumulation | 0.0563 | ||
| [L/g h] | consumption of propionic acid | ||
| for HB accumulation | 0.6803 | ||
| [L/g h] | consumption of propionic acid | ||
| for HV accumulation | 2.0208 | ||
| [L/g h] | fructose consumption | ||
| for maintenance | 3.4184 × 10 | ||
| [L/g h] | propionic acid consumption | ||
| for maintenance | 0.0125 | ||
| [g/L] | inhibitory propionic acid concentration | 1.5 | |
| [g/L] | Michalis-Menten rate for ammonium | 0.2 | |
| [g/L] | propionic acid concentration in the feed | 20 | |
| (0) | [g/L] | initial fructose concentration | |
| data set 1 | 21.75 | ||
| (0) | [g/L] | initial propionic acid concentration | |
| data set 2 | 0.48 | ||
| (0) | [g/L] | initial ammonium concentration | |
| data set 2 | 1.40 | ||
| (0) | [g/L] | initial residual biomass concentration | |
| data set 2 | 1.16 | ||
| (0) | [g/L] | initial HB concentration | |
| data set 2 | 0.03 | ||
| (0) | [g/L] | initial HV concentration | |
| data set 2 | 0.01 | ||
| [g/L] | HA (HB + HV) concentration | time-dependent | |
| [%] | exhaust CO | artificial | |
| measurement | |||
| [%] | inlet CO | artificial | |
| measurement | |||
| [-] | CO dependent metabolic activity | time-dependent | |
| D | [-] | dilution rate | time-dependent |
| [%] | feed rate for propionic acid | pH-controlled | |
| [g/L] | maximum concentration of PHA | 0.89 |
References
- Ge, Z. Review on data-driven modeling and monitoring for plant-wide industrial processes. Chemom. Intell. Lab. Syst. 2017, 171, 16–25. [Google Scholar] [CrossRef]
- Ge, Z. Process Data Analytics via Probabilistic Latent Variable Models: A Tutorial Review. Ind. Eng. Chem. Res. 2018, 57, 12646–12661. [Google Scholar] [CrossRef]
- Mohd Ali, J.; Ha Hoang, N.; Hussain, M.; Dochain, D. Review and classification of recent observers applied in chemical process systems. Comput. Chem. Eng. 2015, 76, 27–41. [Google Scholar] [CrossRef] [Green Version]
- Haug, A. Bayesian estimation for target tracking, Part I: General concepts. Wiley Interdiscip. Rev. Comput. Stat. 2012, 4, 375–383. [Google Scholar] [CrossRef]
- Haug, A. Bayesian estimation for target tracking, Part II: The Gaussian sigma-point Kalman filters. Wiley Interdiscip. Rev. Comput. Stat. 2012, 4, 489–497. [Google Scholar] [CrossRef]
- Haug, A. Bayesian estimation for target tracking, Part III: Monte Carlo filters. Wiley Interdiscip. Rev. Comput. Stat. 2012, 4, 498–512. [Google Scholar] [CrossRef]
- Khatibisepehr, S.; Huang, B.; Khare, S. Design of inferential sensors in the process industry: A review of Bayesian methods. J. Process. Control 2013, 23, 1575–1596. [Google Scholar] [CrossRef]
- Patwardhan, S.C.; Narasimhan, S.; Jagadeesan, P.; Gopaluni, B.; Shah, S.L. Nonlinear Bayesian state estimation: A review of recent developments. Control Eng. Pract. 2012, 20, 933–953. [Google Scholar] [CrossRef]
- Robertson, D.G.; Lee, J.H.; Rawlings, J.B. A moving horizon-based approach for least-squares estimation. AIChE J. 1996, 42, 2209–2224. [Google Scholar] [CrossRef]
- Rao, C.V.; Rawlings, J.B.; Mayne, D.Q. Constrained state estimation for nonlinear discrete-time systems: Stability and moving horizon approximations. IEEE Trans. Autom. Control 2003, 48, 246–258. [Google Scholar] [CrossRef] [Green Version]
- Valluru, J.; Patwardhan, S.C.; Biegler, L.T. Development of robust extended Kalman filter and moving window estimator for simultaneous state and parameter/disturbance estimation. J. Process. Control 2018, 69, 158–178. [Google Scholar] [CrossRef]
- Simon, D. Optimal State Estimation: Kalman, H-Infinity, and Nonlinear Approaches; John Wiley and Sons, Inc.: Hoboken, NJ, USA, 2006. [Google Scholar] [CrossRef]
- Särkkä, S. Bayesian Filtering and Smoothing; Number 3; Cambridge University Press: New York, NY, USA, 2013. [Google Scholar]
- Gao, B.; Hu, G.; Gao, S.; Zhong, Y.; Gu, C. Multi-sensor optimal data fusion based on the adaptive fading unscented Kalman filter. Sensors 2018, 18, 488. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kager, J.; Herwig, C.; Stelzer, I.V. State estimation for a penicillin fed-batch process combining particle filtering methods with online and time delayed offline measurements. Chem. Eng. Sci. 2018, 177, 234–244. [Google Scholar] [CrossRef]
- Tatiraju, S.; Soroush, M.; Ogunnaike, B.A. Multirate nonlinear state estimation with application to a polymerization reactor. AIChE J. 1999, 45, 769–780. [Google Scholar] [CrossRef]
- Zambare, N.; Soroush, M.; Grady, M.C. Real-time multirate state estimation in a pilot-scale polymerization reactor. AIChE J. 2002, 48, 1022–1033. [Google Scholar] [CrossRef]
- Lathrop, P.M.; Duan, Z.; Ling, C.; Elabd, Y.A.; Kravaris, C. Modeling and Observer-Based Monitoring of RAFT Homopolymerization Reactions. Processes 2019, 7, 768. [Google Scholar] [CrossRef] [Green Version]
- Van der Merwe, R. Sigma-Point Kalman Filters for Probablilistic Inference in Dynamic State-Space Models. Ph.D. Thesis, Oregon Health & Science University, Portland, OR, USA, 2004. [Google Scholar]
- Kalman, R.E. A new approach to linear filtering and prediction problems. J. Basic Eng. 1960, 82, 35–45. [Google Scholar] [CrossRef] [Green Version]
- Li, T.; Corchado, J.M.; Bajo, J.; Sun, S.; De Paz, J.F. Effectiveness of Bayesian filters: An information fusion perspective. Inf. Sci. 2016, 329, 670–689. [Google Scholar] [CrossRef]
- Schaffner, J.; Zeitz, M. Entwurf nichtlinearer Beobachter. In Entwurf Nichtlinearer Regelungen; Engell, S., Ed.; Oldenbourg Wissenschaftsverlag: Münich, Germany, 1995. [Google Scholar]
- Duvigneau, S.; Dürr, R.; Behrens, J.; Kienle, A. Advanced Kinetic Modeling of Bio-co-polymer Poly(3-hydroxybutyrate-co-3-hydroxyvalerate) Production Using Fructose and Propionate as Carbon Sources. Processes 2021, 9, 1260. [Google Scholar] [CrossRef]
- Higham, D.J. An algorithmic introduction to numerical simulation of stochastic differential equations. SIAM Rev. 2001, 43, 525–546. [Google Scholar] [CrossRef]
- Strong, P.; Laycock, B.; Mahamud, S.; Jensen, P.; Lant, P.; Tyson, G.; Pratt, S. The Opportunity for High-Performance Biomaterials from Methane. Microorganisms 2016, 4, 11. [Google Scholar] [CrossRef] [PubMed]
- Dahman, Y.; Ugwu, C.U. Production of green biodegradable plastics of poly (3-hydroxybutyrate) from renewable resources of agricultural residues. Bioprocess Biosyst. Eng. 2014, 37, 1561–1568. [Google Scholar] [CrossRef] [PubMed]
- Koller, M.; Braunegg, G. Advanced approaches to produce polyhydroxyalkanoate (PHA) biopolyesters in a sustainable and economic fashion. EuroBiotech J. 2018, 2, 89–103. [Google Scholar] [CrossRef] [Green Version]
- Tsang, Y.F.; Kumar, V.; Samadar, P.; Yang, Y.; Lee, J.; Ok, Y.S.; Song, H.; Kim, K.H.; Kwon, E.E.; Jeon, Y.J. Production of bioplastic through food waste valorization. Environ. Int. 2019, 127, 625–644. [Google Scholar] [CrossRef] [PubMed]
- Bück, A.; Seidel, C.; Dürr, R.; Neugebauer, C. Robust feedback control of convective drying of particulate solids. J. Process. Control 2018, 69, 86–96. [Google Scholar] [CrossRef]
- Dürr, R.; Bück, A. Influence of moisture control on activity in continuous fluized bed drying of baker’s yeast pellets. Dry. Technol. 2020, 1–6. [Google Scholar] [CrossRef]
- Dürr, R.; Seidel, C.; Neugebauer, C.; Bück, A. Self-tuning control of continuous fluidized bed drying of baker’s yeast pellets. Dry. Technol. 2020, 38, 646–654. [Google Scholar] [CrossRef]
- Dürr, R.; Waldherr, S. A Novel Framework for Parameter and State Estimation of Multicellular Systems Using Gaussian Mixture Approximations. Processes 2018, 6, 187. [Google Scholar] [CrossRef] [Green Version]
- Bück, A.; Peglow, M.; Tsotsas, E.; Mangold, M.; Kienle, A. Model-based measurement of particle size distributions in layering granulation processes. AIChE J. 2011, 57, 929–941. [Google Scholar] [CrossRef]
- Mangold, M. Use of a Kalman filter to reconstruct particle size distributions from FBRM measurements. Chem. Eng. Sci. 2012, 70, 99–108. [Google Scholar] [CrossRef]
- Geyyer, R.; Dürr, R.; Temmel, E.; Li, T.; Lorenz, H.; Palis, S.; Seidel-Morgenstern, A.; Kienle, A. Control of continuous mixed solution mixed product removal crystallization processes. Chem. Eng. Technol. 2017, 40, 1362–1369. [Google Scholar] [CrossRef] [Green Version]
- Müller, T.; Dürr, R.; Isken, B.; Schulze-Horsel, J.; Reichl, U.; Kienle, A. Distributed modeling of human influenza a virus–host cell interactions during vaccine production. Biotechnol. Bioeng. 2013, 110, 2252–2266. [Google Scholar] [CrossRef] [PubMed]
- Dürr, R.; Müller, T.; Duvigneau, S.; Kienle, A. An efficient approximate moment method for multi-dimensional population balance models—Application to virus replication in multi-cellular systems. Chem. Eng. Sci. 2017, 160, 321–334. [Google Scholar] [CrossRef] [Green Version]
- Duvigneau, S.; Dürr, R.; Laske, T.; Bachmann, M.; Dostert, M.; Kienle, A. Model-based approach for predicting the impact of genetic modifications on product yield in biopharmaceutical manufacturing—Application to influenza vaccine production. PLoS Comput. Biol. 2020, 16, 1–22. [Google Scholar] [CrossRef] [PubMed]



| Parameter | Value | Parameter | Value |
|---|---|---|---|
| g | E | ||
| u | |||
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| 10 | 1 | ||
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| 10 | 0 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dürr, R.; Duvigneau, S.; Seidel, C.; Kienle, A.; Bück, A. Multi-Rate Data Fusion for State and Parameter Estimation in (Bio-)Chemical Process Engineering. Processes 2021, 9, 1990. https://doi.org/10.3390/pr9111990
Dürr R, Duvigneau S, Seidel C, Kienle A, Bück A. Multi-Rate Data Fusion for State and Parameter Estimation in (Bio-)Chemical Process Engineering. Processes. 2021; 9(11):1990. https://doi.org/10.3390/pr9111990
Chicago/Turabian StyleDürr, Robert, Stefanie Duvigneau, Carsten Seidel, Achim Kienle, and Andreas Bück. 2021. "Multi-Rate Data Fusion for State and Parameter Estimation in (Bio-)Chemical Process Engineering" Processes 9, no. 11: 1990. https://doi.org/10.3390/pr9111990
APA StyleDürr, R., Duvigneau, S., Seidel, C., Kienle, A., & Bück, A. (2021). Multi-Rate Data Fusion for State and Parameter Estimation in (Bio-)Chemical Process Engineering. Processes, 9(11), 1990. https://doi.org/10.3390/pr9111990









