A Multi-Scale Model for the Spread of HIV in a Population Considering the Immune Status of People
Abstract
1. Introduction
2. Materials and Methods
2.1. Population Model: Sexual Contact Network
- 1.
- Infection dynamics by the virus in the immunological scale.
- 2.
- Defines the virus propagation in the population scale, considering aspects from the immunological scale.
2.2. Model for HIV Infection in the Immunological Scale
3. Results
3.1. Local Stability Analysis of the Immunological Model
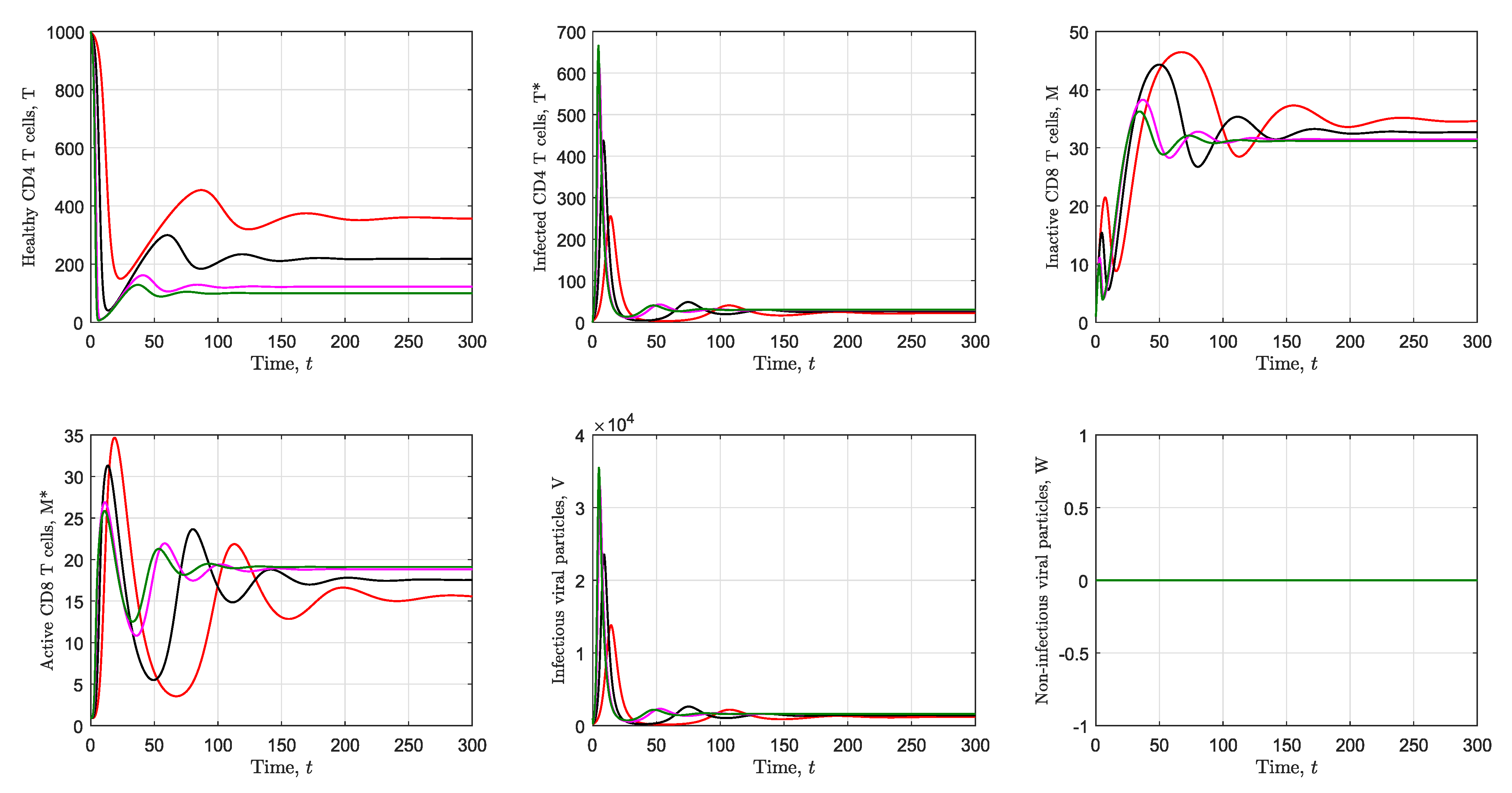
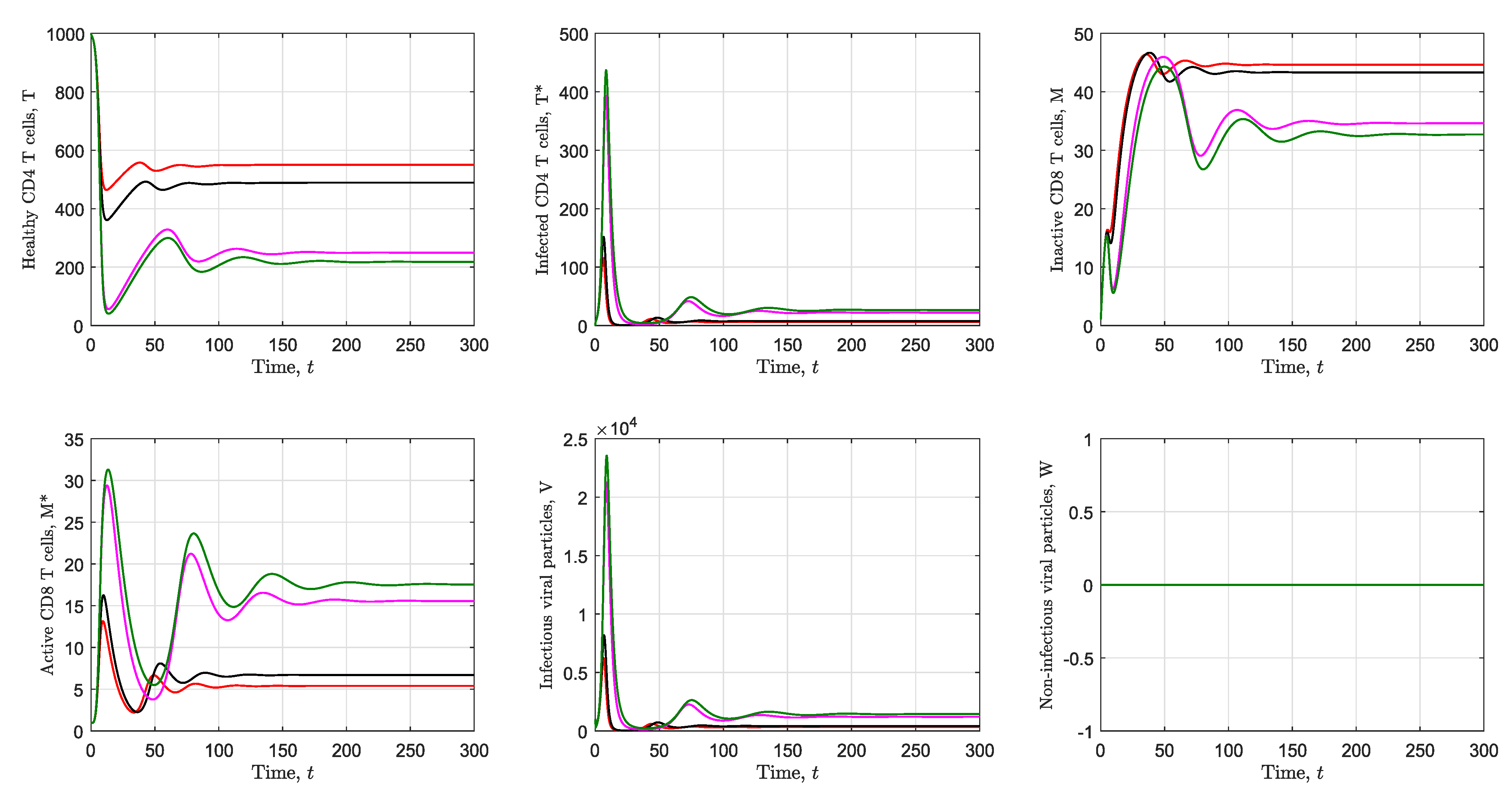
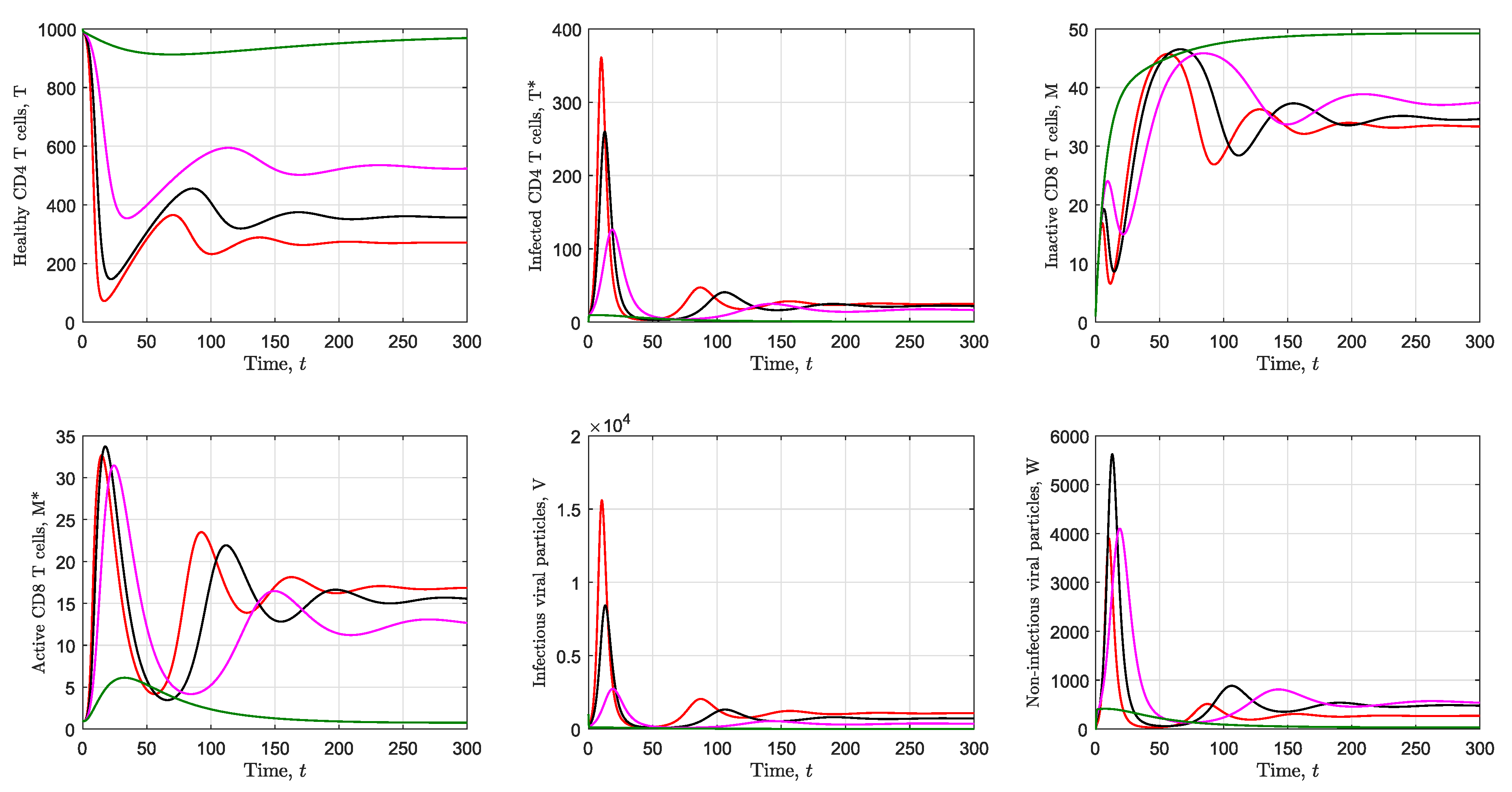
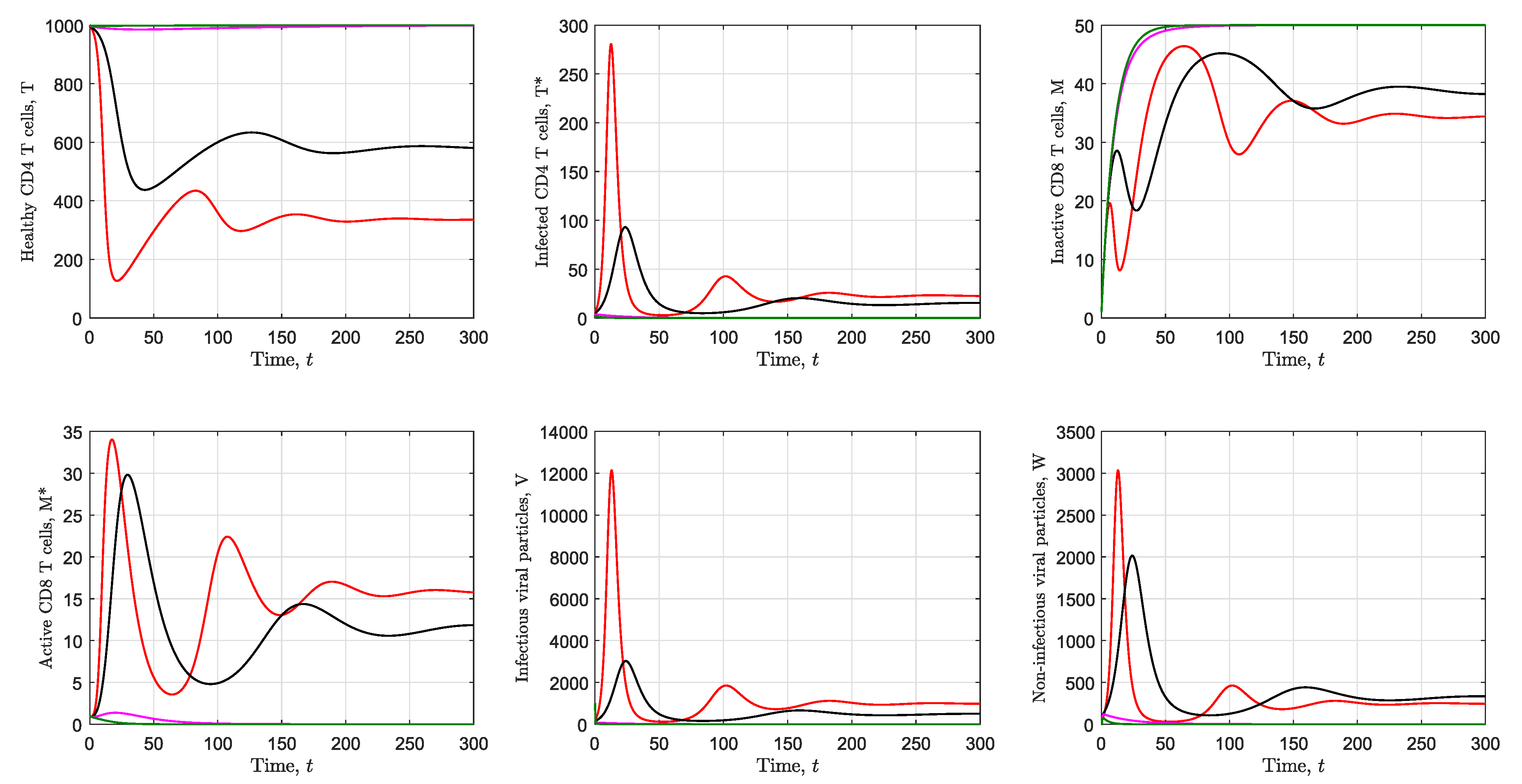
3.2. Simulation of the Immunological Model
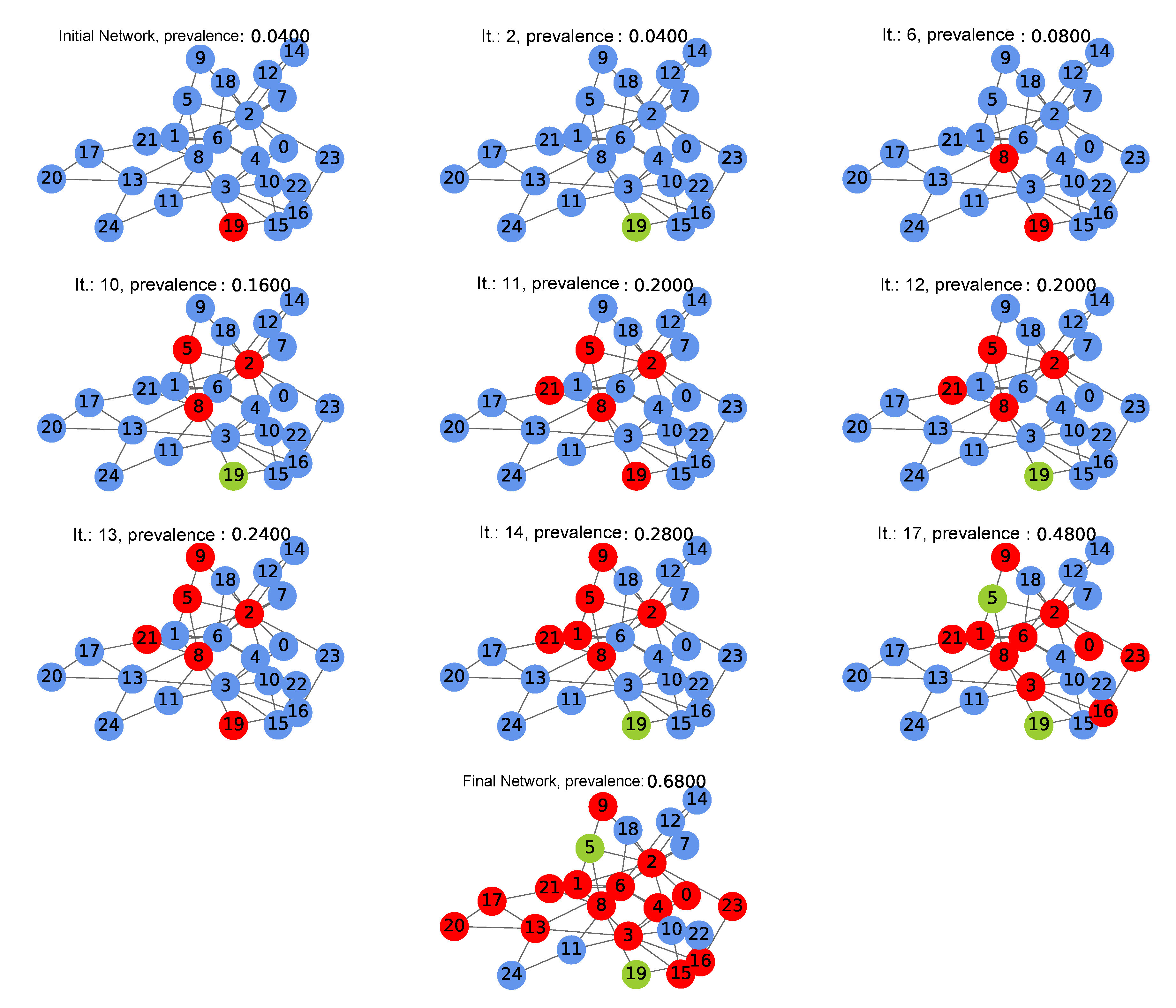
3.3. Coupling Algorithm of the Immunological and Population Scales
- 1.
- The network was constructed by beginning with the random values [38,39,40] shown in the following, which seeks for each individual i, for , from the network to have a different immune system. Additionally, for the values of the other parameters used in the system of differential equations that describe the immunological scale, those described in Table 2 were used.
- (a)
- Initial number of healthy CD4 T cells in the i-th person per mm: .
- (b)
- Initial number of inactive CD8 T cells in the i-th person per mm: .
- (c)
- Values of infected CD4 T cells, active CD8 T cells, infectious and non-infectious viral particles will be null, given that it is considered that the th person is still not infected by the virus, that is, .
- (d)
- Production rate of healthy cells of the i-th person: .
- (e)
- Infection probability of the healthy cells of the i-th person: .
- (f)
- Production rate of viral particles of the i-th person: .
Then, a vertex from the network is chosen randomly as the first infected and is assigned a random viral load between 1 and 1000 vir/mm[41]. With the aforementioned, the network is created, obtaining the initial state at . - 2.
- From the corresponding initial condition, we solve the system of differential equations of the immunological system (7) for each vertex i during one unit of time, saving the numerical solutions , , , , and ; therefore, we have the immunological status of each individual in the population during that unit of time. Additionally, the final value of each of the numerical solutions will be used as the initial condition in the following iteration. Furthermore, we saved the number of susceptible subjects, carriers with ART and carriers without ART at the end of the iteration.
- 3.
- Based on the numerical solutions, the following decisions were made:
- (a)
- If the i-th person is an HIV carrier and presents a number of healthy CD4 T cells below 350 cell/mm, a random probability of accessing to ART is assigned, if it is >, it is established to use ART, so that a random value is assigned for and between .
- (b)
- If the i-th person is an HIV carrier already using ART, a random probability of therapy abandonment is assigned, if it is <, it is established that the individual leaves ART, that is .
This is why in the simulations that will be presented ahead in different iterations, the state of the vertices will vary from carriers with therapy to carriers without therapy, and vice versa. - 4.
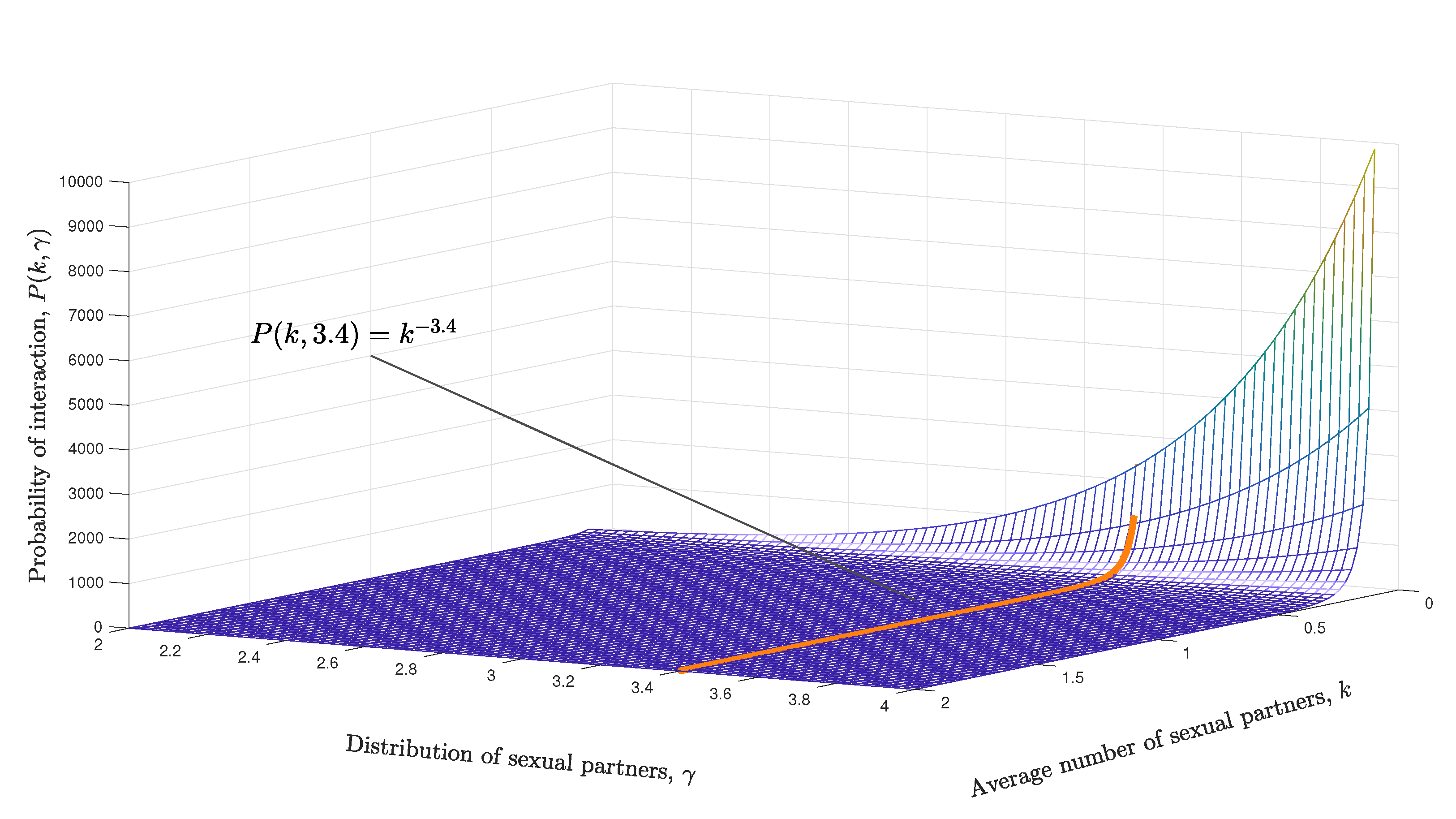
- The transmission process considers different factors. If the i-th person is an HIV carrier, the decision is made randomly whether to have a sexual encounter with only one of their susceptible “neighbors” (another susceptible vertex sharing an edge). If the random decision was affirmative, the infected person is partnered with one of their susceptible sex partners, then, the probability of transmitting the infection from the infected person i to the susceptible person j is given by (taken from [16]), where represents the average degree (associated with the potential number of sex partners) and is the infection probability through sexual contact; the probability is taken from [40] and is shown in Table 3 according to the values of vir/mm.Finally, if person j becomes infected, an initial viral load is assigned with 10% of the load owned by the person i who caused the infection.
- 5.
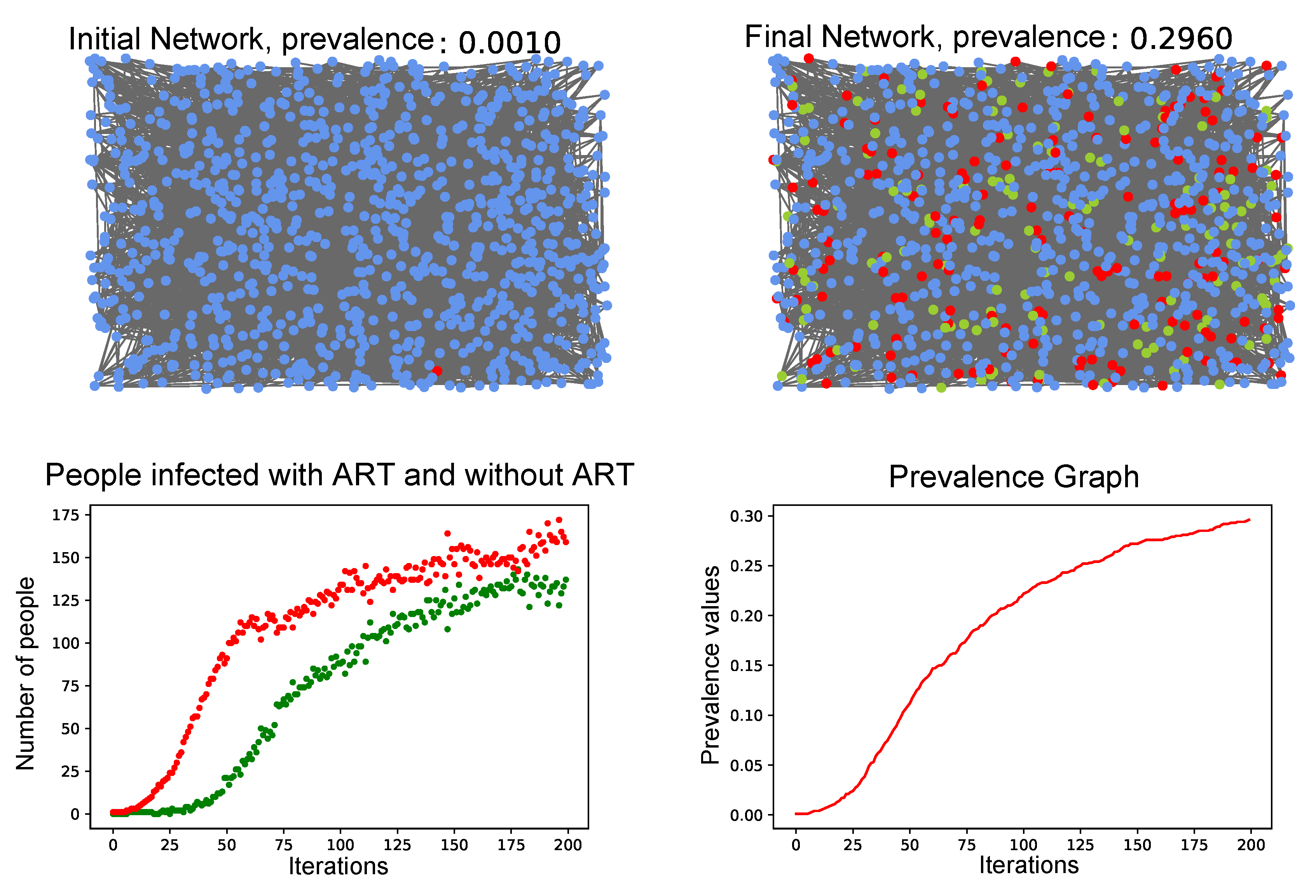
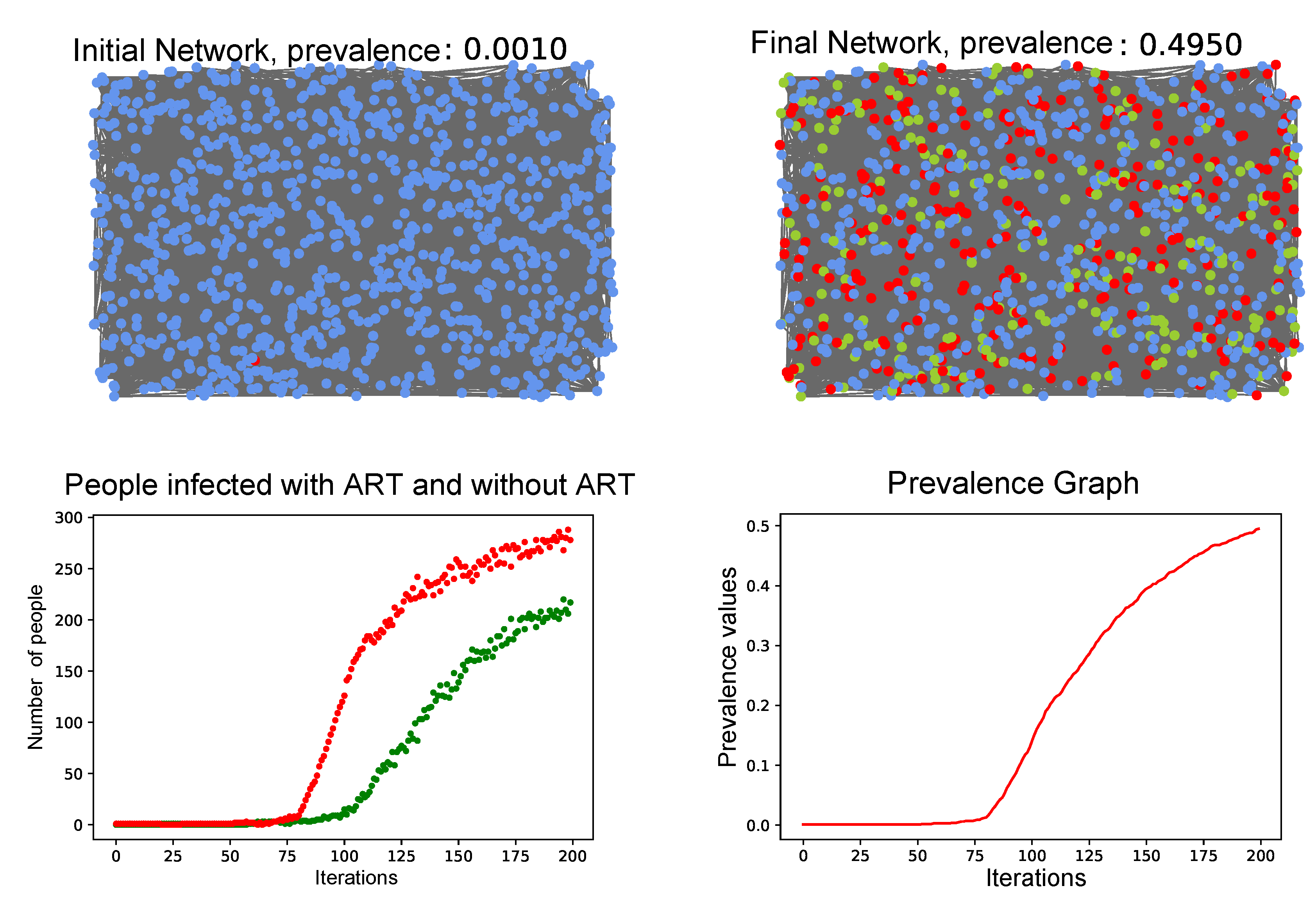
- At the end of each iteration, the prevalence was calculated, as the rate between the number of HIV carriers with or without therapy and the total number of people from the network, that is,
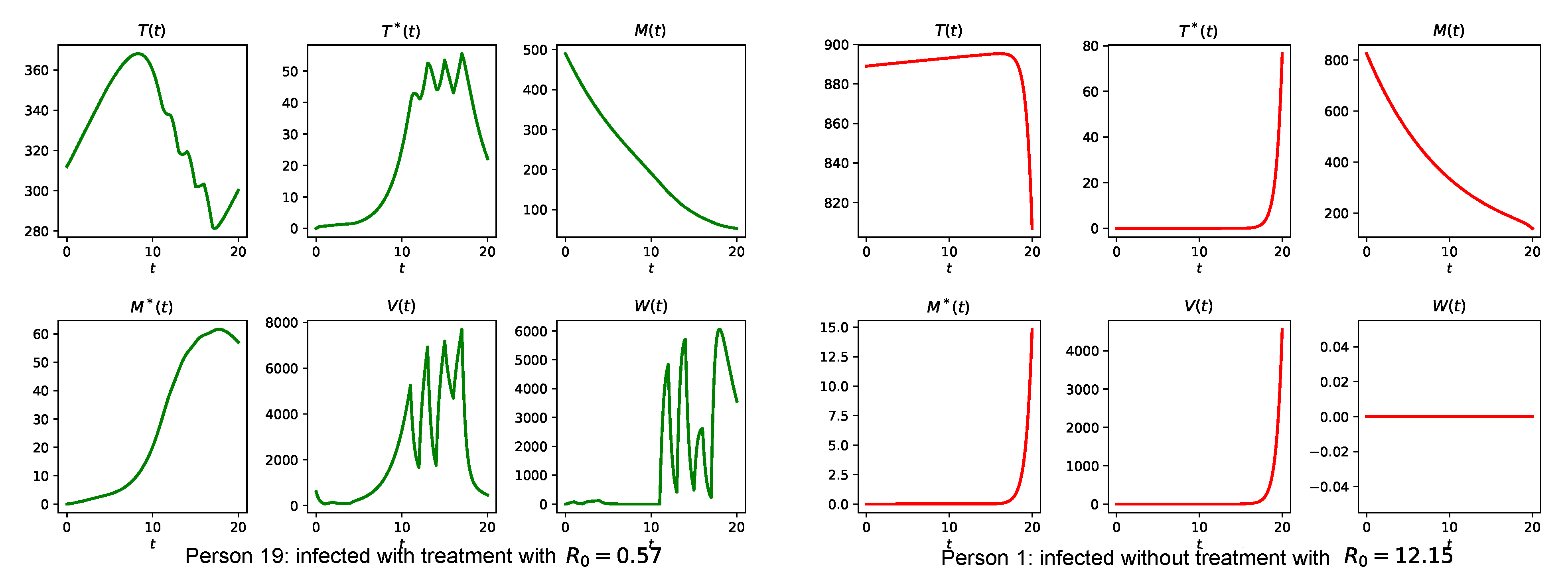
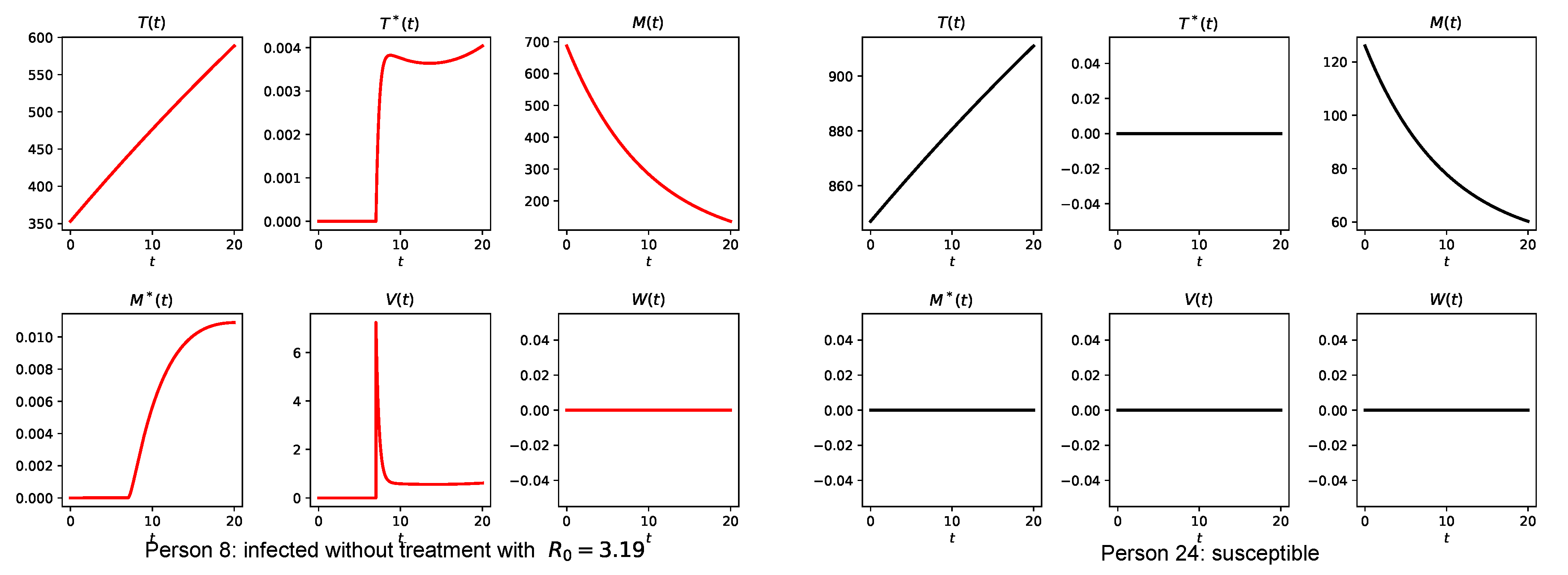
3.4. Simulation of the Coupled Model
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| HIV | Human Immunodeficiency Virus |
| AIDS | Acquired immune deficiency syndrome |
| ART | Antiretroviral therapy |
| RTI | Reverse transcriptase inhibitors |
| PI | Protease Inhibitors |
| LAE | locally asymptotically stable |
| Sym | Symbol |
Appendix A. Demonstration of Propositions and Basic Reproduction Number
- 1.
- There are two positive solutions, that is, two endemic equilibriums if and satisfy the conditions to obtain (see (8)); that is:
- 2.
- There are no positive solutions, that is, there is no endemic equilibrium if and fulfill:
- 3.
- There is a single endemic equilibrium point if and fulfill:
References
- AIDS InfoNet. Available online: http://www.aidsinfonet.org/uploaded/factsheets/204_spa_485.pdf (accessed on 22 May 2018).
- Organización Mundial de la Salud. Available online: https://www.who.int/features/factfiles/hiv/es/ (accessed on 14 February 2019).
- UNAIDS. Available online: https://www.unaids.org/es/resources/documents/2021/UNAIDS_FactSheet (accessed on 23 August 2021).
- InfoSIDA. Available online: https://www.infosida.es//que-es-el-vih (accessed on 26 March 2018).
- Planas, G. La infección por el virus de la inmunodeficiencia humana. In Farmacia Hospitalaria Tomo II, 3rd ed.; Fundación Española de Farmacia Hospitalaria: Madrid, Spain, 2002; pp. 1493–1516. [Google Scholar]
- Dirección general de comunicación por los derechos humanos de la CDHDF. VIH un llamado a la acción positiva. Dfensor 2014, 2, 5–19. [Google Scholar]
- Velasquez, S.; Bedoya, B. Los jóvenes: Población vulnerable del VIH/SIDA. Med. UPB 2010, 29, 144–154. [Google Scholar]
- UNAIDS. Available online: http://data.unaids.org/topics/young-people/youngpeoplehivaids_es.pdf (accessed on 25 May 2018).
- Comisión Nacional de los Derechos Humanos México. Available online: https://www.cndh.org.mx/sites/default/files/doc/Programas/VIH/Divulgacion/cartillas/Cartilla-DH-Jovenes-VIH-Sida.pdf (accessed on 14 April 2018).
- Instituto Nacional de Salud. Boletín Epidemilógico Semanal, Semana epidemiológica 47, 17 al 23 de Noviembre de 2019. Available online: https://www.ins.gov.co/buscador-eventos/BoletinEpidemiologico/2019_Boletin_epidemiologico_semana_47.pdf (accessed on 29 September 2020).
- CATIE. Available online: https://www.catie.ca/en/fact-sheets/transmission/hiv-viral-load-hiv-treatment-and-sexual-hiv-transmission (accessed on 23 August 2021).
- UNAIDS. Available online: https://www.unaids.org/sites/default/files/media_asset/JC2484_therapy-2015_es_1.pdf (accessed on 7 January 2018).
- Toro-Zapata, H.D.; Vasquez-Roa, E.M.; Mesa-Mazo, M.J. Modelo estocástico para la infección con VIH de las células CD4 T+ del sistema inmune. Rev. Mat. Teor. Apl. 2017, 24, 287–313. [Google Scholar] [CrossRef][Green Version]
- Toro-Zapata, H.D.; Rodríguez-Osorio, A.J.; Medellín-Prieto, D.A. Modelo para el acceso efectivo al tratamiento antirretroviral en relación con el fracaso terapéutico de la infección por VIH. Rev. EIA 2019, 16, 115–130. [Google Scholar] [CrossRef]
- Barabási, A.L.; Albert, R. Emergence of scaling in random networks. Science 1999, 286, 509–512. [Google Scholar] [CrossRef]
- May, R.M.; Lloyd, A.L. Infection dynamics on scale-free networks. Phys. Rev. E 2001, 64, 066112. [Google Scholar] [CrossRef] [PubMed]
- Newman, M.E.; Barabási, A.L.E.; Watts, D.J. The Structure and Dynamics of Networks; Princeton University Press: Princeton, NJ, USA, 2006; pp. 1–8. [Google Scholar]
- Sloot, P.M.; Ivanov, S.V.; Boukhanovsky, A.V.; van de Vijver, D.A.; Boucher, C.A. Stochastic simulation of HIV population dynamics through complex network modelling. Int. J. Comput. Math. 2008, 85, 1175–1187. [Google Scholar] [CrossRef]
- Mei, S.; Sloot, P.M.; Quax, R.; Zhu, Y.; Wang, W. Complex agent networks explaining the HIV epidemic among homosexual men in Amsterdam. Math. Comput. Simul. 2010, 80, 1018–1030. [Google Scholar] [CrossRef][Green Version]
- Maximino, A. Redes complejas: Estructura, dinámica y evolución. Soc. Netw. 2011, 14, 121–135. [Google Scholar]
- Li, W.; Zhang, S.-M.; Bi, G.-M. Analysis and simulation of the HIV transmission among homosexual based on agent dynamical small world network. Procedia Eng. 2011, 15, 541–548. [Google Scholar]
- Leonardo Rafael, L. Modelado de Epidemias Utilizando Sistemas Auto-Organizados; Universidad Nacional del Litoral: Santa Fe, Argentina, 2017. [Google Scholar]
- Toro-Zapata, H.D.; Caicedo-Casso, A.; Lee, S. The Role of Immune Response in Optimal HIV therapy Interventions. Processes 2018, 6, 102. [Google Scholar] [CrossRef]
- Networkx. Available online: https://networkx.org/documentation/networkx-1.10/reference/generated/networkx.generators.random_graphs.powerlaw_cluster_graph.html#networkx.generators.random_graphs.powerlaw_cluster_graph (accessed on 2 September 2019).
- García-Valdecasas, J.I. La estructura compleja de las redes sociales. Rev. Esp. Sociol. 2015, 24, 65–84. [Google Scholar]
- Sancho Caparrini, F.; Introducción a las Redes Aleatorias. Departamento Ciencias de la Computación e Inteligencia Artificial, Universidad de Sevilla. 2016. Available online: http://www.cs.us.es/~fsancho/?e=80 (accessed on 10 May 2021).
- Instituto de Ciencias Físicas (ICF) de la UNAM. Available online: https://www.fis.unam.mx/~max/English/notasredes.pdf (accessed on 20 March 2019).
- Chen, G.; Wang, X.; Li, X. Introduction to Complex Networks: Models Structures and Dynamics; Higher Education Press: Beijing, China, 2012. [Google Scholar]
- Uruguay Ministerio de Salud Pública; Dirección General de la Salud; Departamento de Programación Estratégica en Salud. Infección por virus de la Inmunodeficiencia Humana (VIH): Pautas para diagnóstico, monitorización y tratamiento antirretroviral; Área Salud Sexual y Reproductiva. Programa Nacional ITS-VIH/Sida; Uruguay Ministerio de Salud Pública: Montevideo, Uruguay, 2017. [Google Scholar]
- InfoSIDA. Glosario del VIH Términos Relacionados con el VIH/SIDA. NLM 9a Ed. 2018. Available online: https://clinicalinfo.hiv.gov/themes/custom/aidsinfo/documents/spanishglossary_sp.pdf (accessed on 20 October 2021).
- Bubnoff, A. Juego de clones. VAX 2013, 11, 2–5. [Google Scholar]
- Culshaw, R.; Ruan, S.; Spiteri, R. Optimal hiv therapy by maximising immune response. J. Math. Biol. 2004, 48, 545–562. [Google Scholar] [CrossRef]
- Orellana, J.M. Optimal drug scheduling for HIV therapy efficiency improvement. Biomed. Signal Process. Control 2011, 6, 379–386. [Google Scholar] [CrossRef]
- Toro-Zapata, H.D.; Caicedo-Casso, A.; Bichara, D.; Lee, S. Role of active and inactive cytotoxic immune response in human immunodeficiency virus dynamics. Osong Public Health Res. Perspect. 2014, 5, 3–8. [Google Scholar] [CrossRef] [PubMed]
- Toro-Zapata, H.D.; Trujillo-Salazar, C.A.; Prieto-Medellín, D.A. Evaluación teórica de estrategias óptimas y sub-óptimas de terapia antirretroviral para el control de la infección por VIH. Rev. Salud Pública 2018, 20, 117–125. [Google Scholar] [CrossRef]
- Ramírez, C.; Muñoz, A.; García, M. Modelos Biomatemáticos II; Universidad del Quindío: Armenia, Colombia, 2008. [Google Scholar]
- Londoño-González, C.A.; Toro-Zapata, H.D.; Trujillo-Salazar, C.A. Modelo de simulación para la infección por VIH y su interacción con la respuesta inmune citotóxica. Rev. Salud Pública 2014, 16, 103–115. [Google Scholar]
- Noda Albelo, A.L.; Vidal Tallet, L.A.; Pérez Lastre, J.E.; Cañete, Villafranca, R. Interpretación clínica del conteo de linfocitos CD4 T positivos en la infección por VIH. Rev. Cuba. Med. 2013, 52, 118–127. [Google Scholar]
- Avila, L.M.; Gómez, C.P.; Ríos, R.S.; Laverde, E. Estandarización de valores normales de linfocitos CD3, CD4, CD8 y relación CD4/CD8 por citometría de flujo en individuos sanos colombianos. Acta Méd. Colomb. 1996, 21, 158–161. [Google Scholar]
- Lasry, A.; Sansom, S.L.; Wolitski, R.J.; Green, T.A.; Borkowf, C.B.; Patel, P.; Mermin, J. HIV sexual transmission risk among serodiscordant couples: Assessing the effects of combining prevention strategies. Aids 2014, 28, 1521–1529. [Google Scholar] [CrossRef] [PubMed]
- GeoSalud. Available online: https://www.geosalud.com/vih-sida/analisis_sangre_pg5.htm (accessed on 10 August 2019).
- Worldometer. Población Mundial. Available online: https://www.worldometers.info/es/ (accessed on 2 November 2020).
- Wiggins, S. Introduction to Applied Nonlinear Dynamical Systems and Chaos, 2nd ed.; Springer: New York, NY, USA, 2003. [Google Scholar]

| Sym. | Description | Value |
|---|---|---|
| k | Average number of sex partners | 2, 4 and 10 |
| Distribution of sex partners | 3.4 | |
| Number of susceptible young people, carriers with ART, and carriers without ART | 25 and 1000 | |
| Discrete simulation time in weeks | 200 | |
| Number of iterations on the network | Varies | |
| Number of young people susceptible of acquiring the virus | Varies | |
| Number of young people carriers of the virus with ART | Varies | |
| Number of young people carriers of the virus without ART | Varies |
| Sym. | Description | Value | Ref. |
|---|---|---|---|
| Production rate of healthy CD4 T cells | 10 mm d | [32,33] | |
| CD4 T cells infection probability | 2.5 × 10 mm d | [33] | |
| Death rate of the uninfected CD4 T cells | 1 × 10 d | [32] | |
| Death rate of infected CD4 T cells | 0.26 d | [32,33] | |
| N | Production rate of viral particles | 500 d | [32] |
| c | Rate of virus elimination | 2.4 d | [33] |
| Activation probability of CD8 T cells | 2 × 10 mm d | - | |
| Replication probability of the active CD8 T cells | 5 × 10 mm d | [33] | |
| Death rate of CD8 T cells | 0.1 mm d | [32,33] | |
| Probability of the active CD8 T cells eliminating the infected CD4 T cells | 2 × 10 mm d | [33] | |
| Production rate of inactive CD8 T cells | 5 mm d | [33] | |
| Effectiveness of RTI | - | - | |
| Effectiveness of PI | - | - | |
| Initial value of the healthy CD4 T cells | 1000 mm | [33] | |
| Initial value of infected CD4 T cells | 0 mm | [33] | |
| Initial value of inactive CD8 T cells | 0 mm | [33] | |
| Initial value of active CD8 T cells | 1 mm | [33] | |
| Initial infectious viral load | 1 × 10 mm | [33] | |
| Initial non-infectious viral load | - | - |
| Type of Risk | Viral Load Range | Infection Probability |
|---|---|---|
| Low risk | ||
| Medium risk | ||
| High risk |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vásquez-Quintero, S.d.A.; Toro-Zapata, H.D.; Prieto-Medellín, D.A. A Multi-Scale Model for the Spread of HIV in a Population Considering the Immune Status of People. Processes 2021, 9, 1924. https://doi.org/10.3390/pr9111924
Vásquez-Quintero SdA, Toro-Zapata HD, Prieto-Medellín DA. A Multi-Scale Model for the Spread of HIV in a Population Considering the Immune Status of People. Processes. 2021; 9(11):1924. https://doi.org/10.3390/pr9111924
Chicago/Turabian StyleVásquez-Quintero, Sol de Amor, Hernán Darío Toro-Zapata, and Dennis Alexánder Prieto-Medellín. 2021. "A Multi-Scale Model for the Spread of HIV in a Population Considering the Immune Status of People" Processes 9, no. 11: 1924. https://doi.org/10.3390/pr9111924
APA StyleVásquez-Quintero, S. d. A., Toro-Zapata, H. D., & Prieto-Medellín, D. A. (2021). A Multi-Scale Model for the Spread of HIV in a Population Considering the Immune Status of People. Processes, 9(11), 1924. https://doi.org/10.3390/pr9111924







