A Model of Transport of Particulate Biomass in a Stream of Fluid
Abstract
1. Introduction
- The particles are spheres of a diameter d;
- The fluid fills unlimited space;
- The stream flows along straight lines.
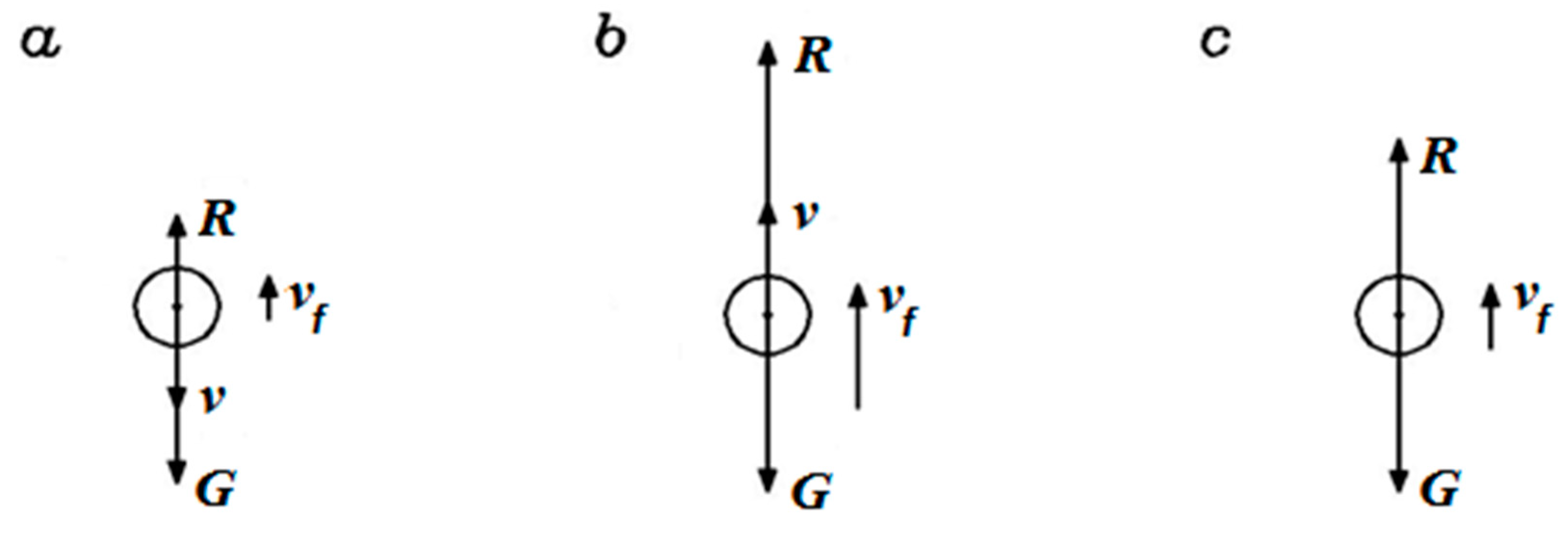
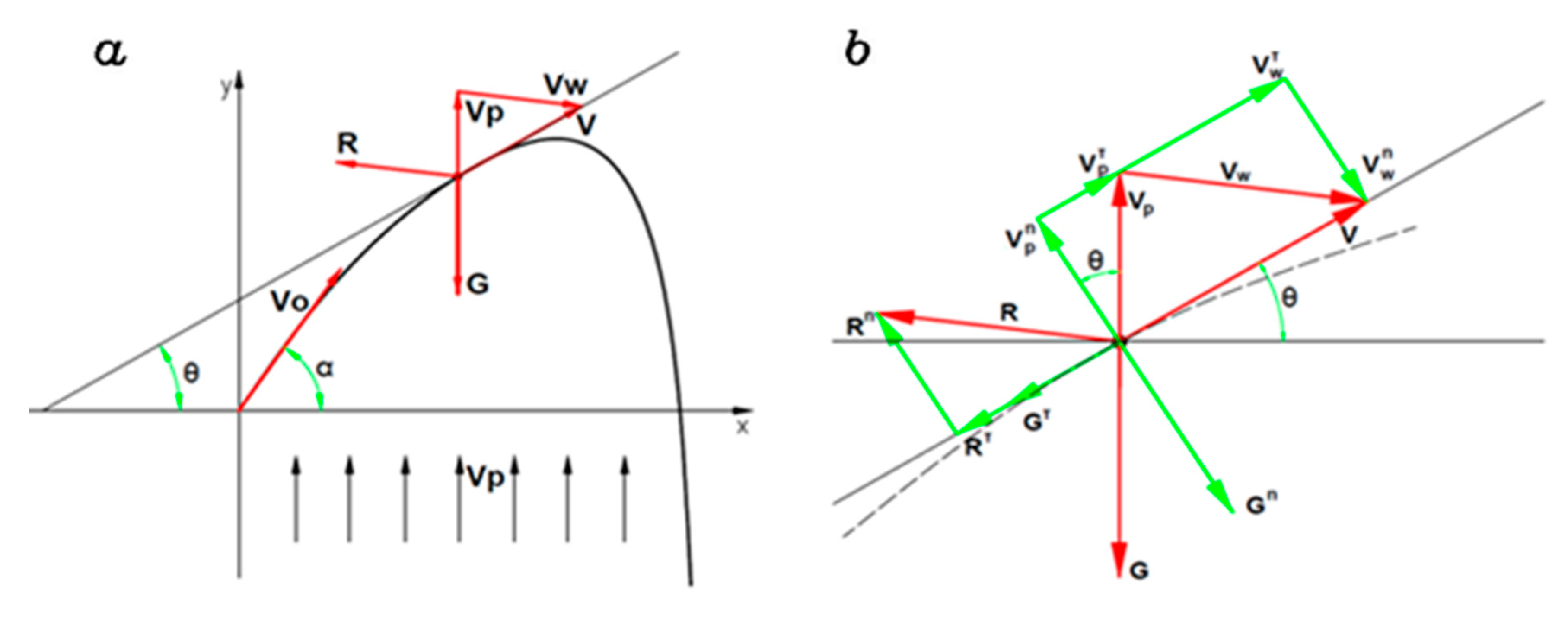
- Drag force R;
- Apparent weight G (weight minus buoyancy);
- Inertial force F.
− g/(kv2w0 cos2θ0) }−1/2 dθ
− g/(kv2w0 cos2θ0) }−1 dθ
− g/(kv2w0 cos2θ0) }−1 dθ
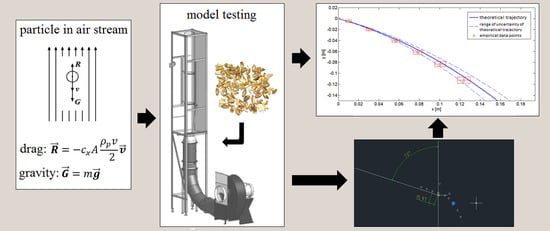
2. Materials and Methods
- The density and dynamic viscosity of the air are constant;
- The air velocity distribution is flat along a given cross-section of the pneumatic channel;
- The fluctuating component of the velocity is negligible;
- The solid particle is spherical, with a diameter d, mass m, and drag coefficient cx;
- The solid particle does not rotate along its axis and remains in thermodynamic equilibrium with the air;
- The drag coefficient is constant;
- The mass of the layer of air accompanying the particle and the buoyant force are negligibly small;
- The boundary effects pertaining to the walls of the pneumatic channel have no influence on the particle;
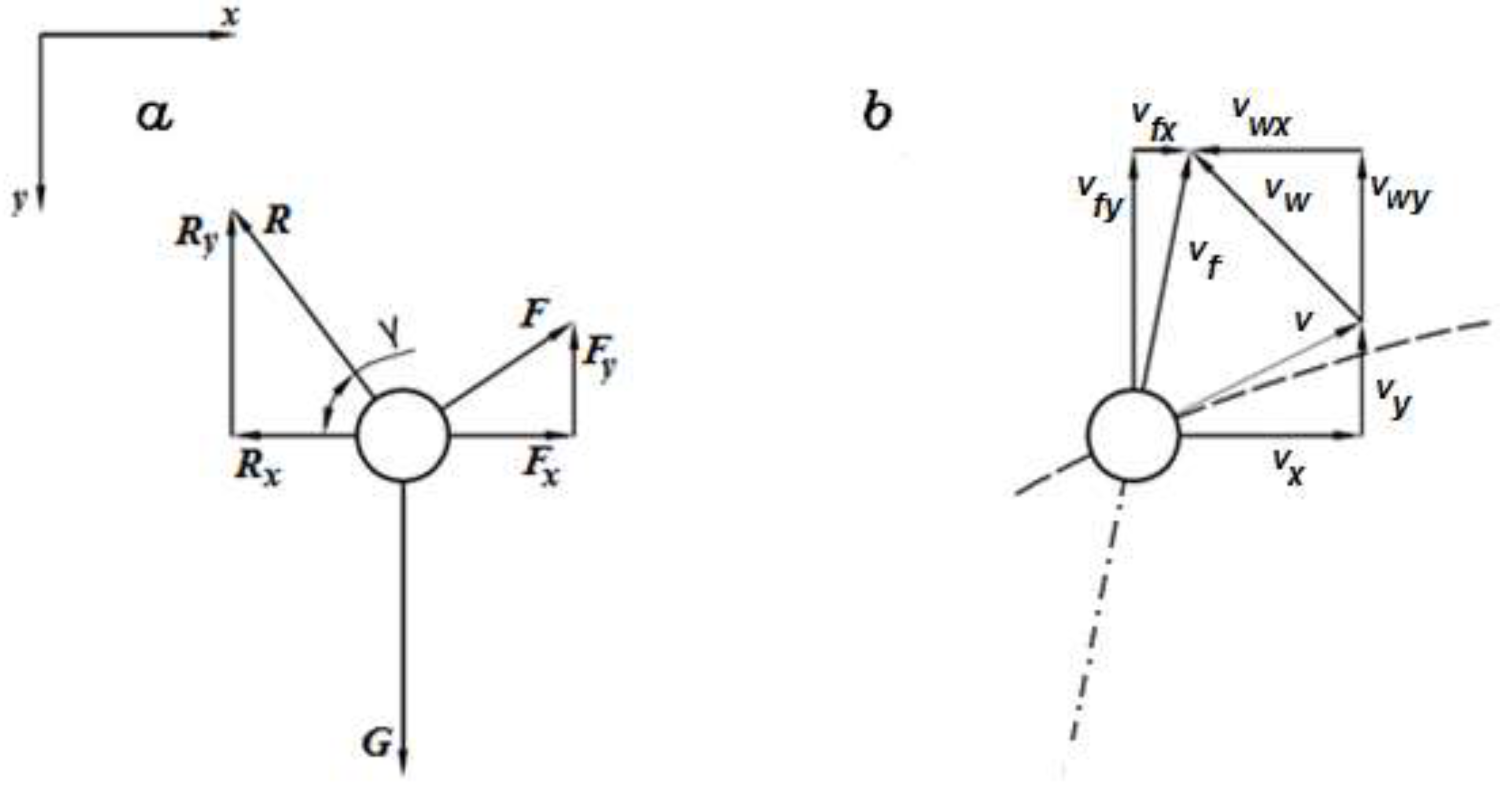
- The particle is introduced into the pneumatic channel with a velocity of a known value v0 at an angle α in respect to the horizontal level (Figure 4a);
- The particle’s movement, determined by gravity and drag, occurs on a single plane.
{vc2 cosθ − vf cos(θ + β)][vf2 + v2 − 2vfvsin(θ + β)]1/2}
- For a vertical stream (β = 0):
- θeq = π/2, for vf > vc;
- θeq = 0, for vf = vc;
- θeq = −π/2, for vf < vc.
- For a horizontal stream (β = π/2): θeq = arctan(−vc/vf);
- For a tilted stream (0 < β < π/2): θeq = arctan[(vf cosθ − vc)/(vf sinβ)].
{vc2 cosθ − vf cos(θ + β)][vf2 + v2 − 2vfvsin(θ + β)]1/2}
v = v(θ), v(α) = v0, α ≤ θ ≤ θeq
3. Results
3.1. Numerical Calculations
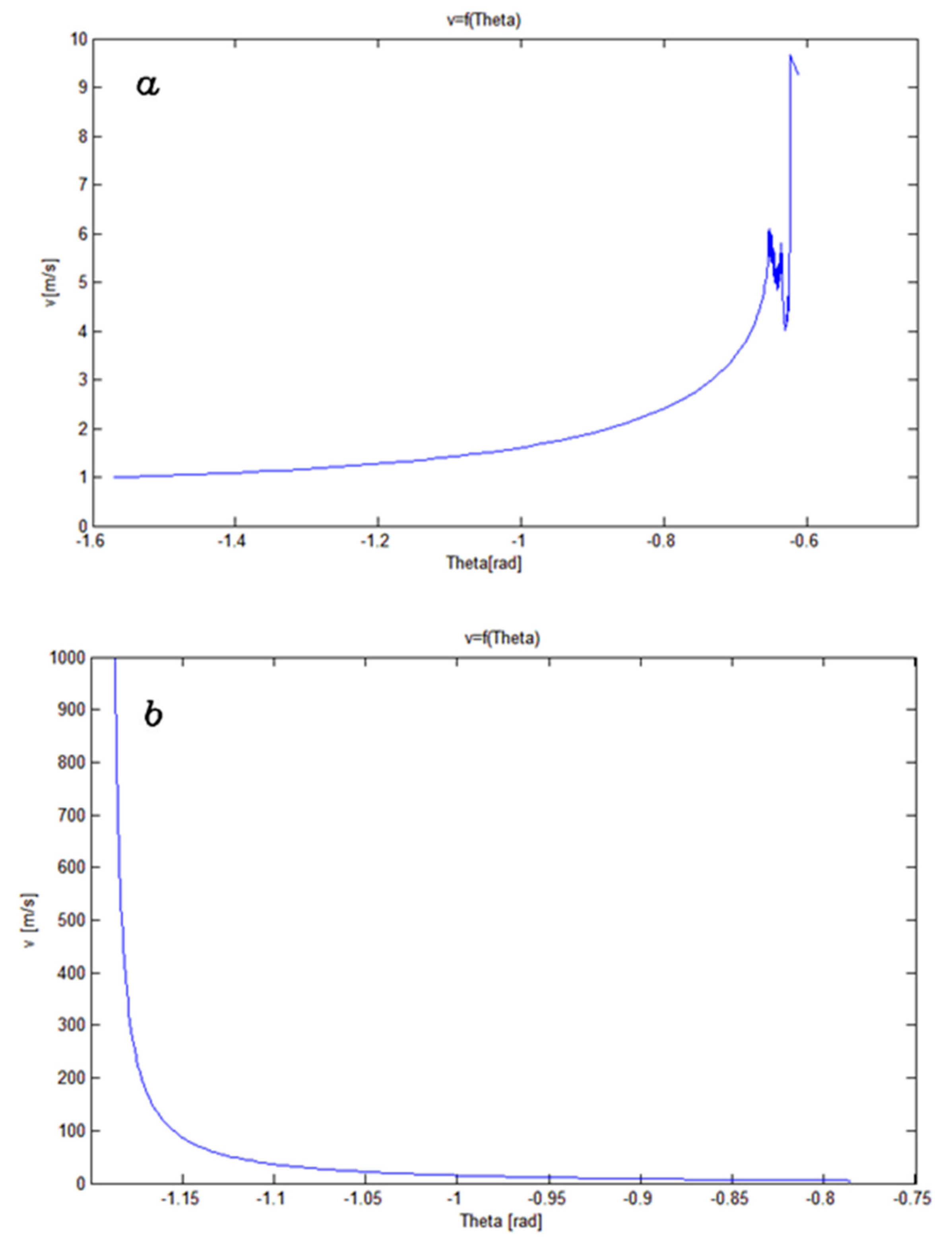
- The loss of absolute stability of a solution before reaching the boundary angle θ (Figure 5a). This problem appears when very small increases of the angle θ are accompanied by comparatively large changes in the value of the function v(θ). Bjorck and Dahlquist [28] called this problem “stiff.” It is then advisable to use methods dedicated to stiff problems. An attempt at using one, the multi-step NDFs method as realized by solverode15s, ended in failure. The algorithm for the NDFs method ends where oscillations previously began. The impossibility to reduce the length of the integration step appears to be the cause of the problem. Similar behavior characterizes other algorithms intended to solve stiff systems. Therefore, there may be a cause beyond stiffness for the observed difficulties.
- The impossibility of solving problems where the initial value of the angle θ equals its final value (i.e., particles are introduced into the stream at an angle equal to the boundary angle). For obvious reasons, Equation (24) has only a single point as a solution, which is also a known initial point. This problem concerns, for example, the horizontal introduction of a particle into a vertical stream of a velocity equal to the terminal velocity (when α = θeq = 0).
{vc2 sinθ + [v − vf sin(θ + β)][vf2 + v2 − 2vfvsin(θ + β)]1/2}
θ = θ(v), θ(v0) = α, v0 ≤ v ≤ veq
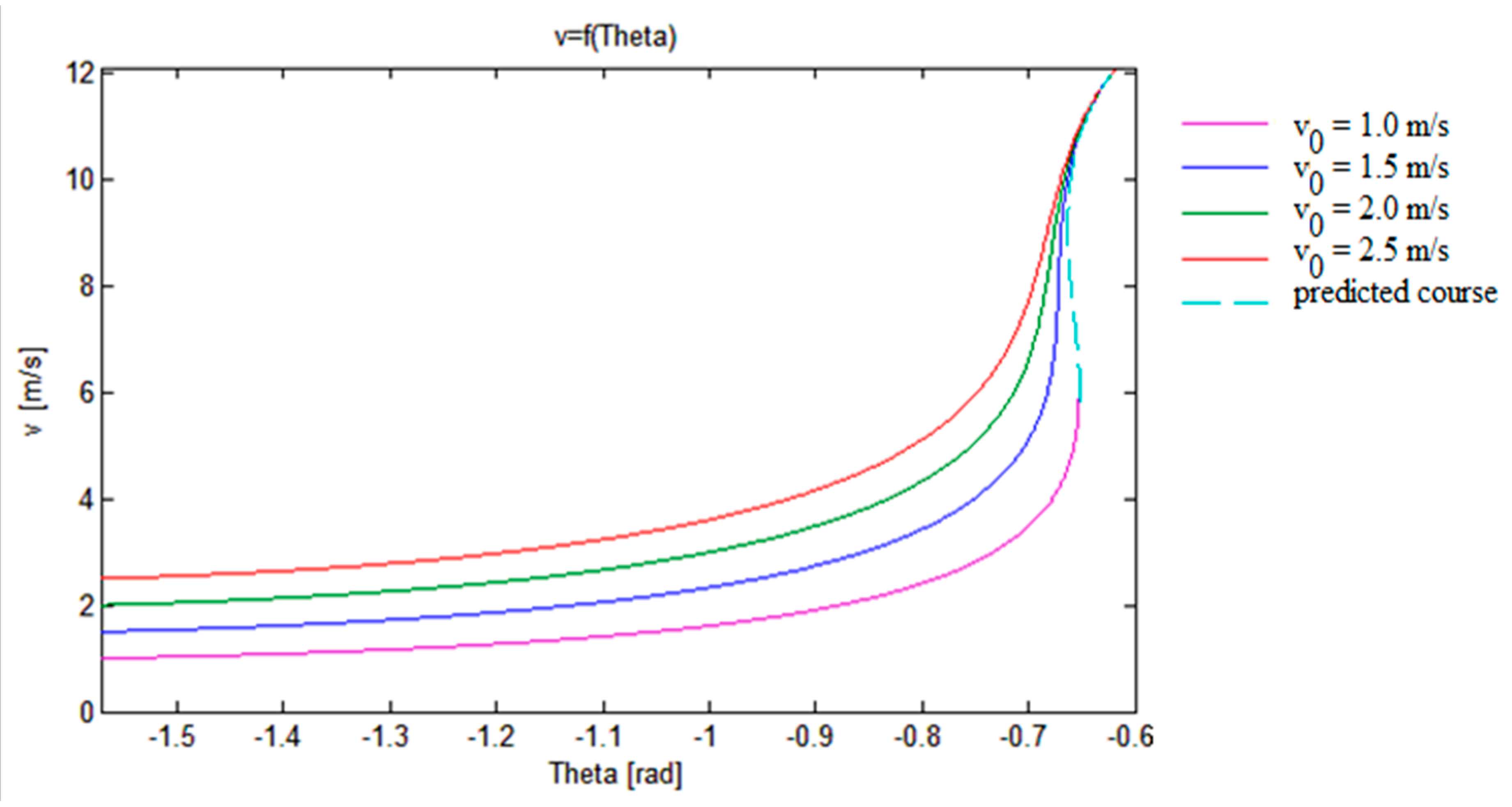
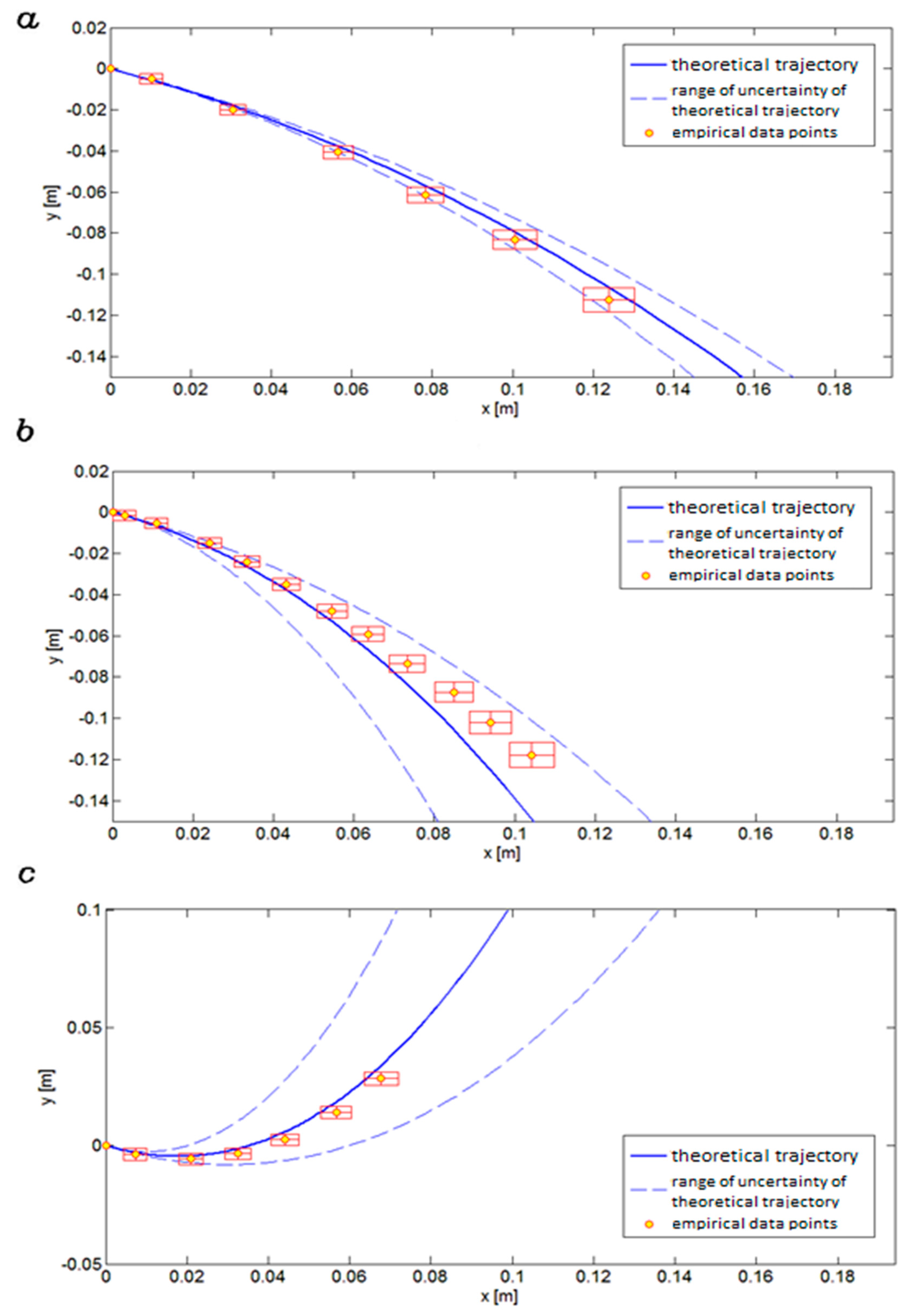
3.2. Model Verification
- The angle α was measured using an electronic goniometer with an accuracy of 0.1°;
- The air velocity was measured with an EE65-VB5-D02 air velocity transmitter with an accuracy of ± (0.3 + 3%);
- The initial velocity of the particle v0 was assessed by computer-assisted image analysis, tracing the path of the particle within a side vessel over a given time Δt (±0.0002 s). This resulted in the value of path length uncertainty Δs = 0.002 m. Thus, the uncertainty of the initial velocity v0 was calculated on this basis, using the exact differentiation formula:
- For x: ±(0.0023 + 0.001%);
- For y: ±(0.0067 + 0.001%).
4. Discussion
5. Conclusions
- The trajectory of particles in unsteady motion in a stream of air can be described with parametric equations of the following form:x = ∫θα (f2(θ)cosθ/g) {(vf/vc2) cos(θ + β) [vf2 + f2(θ) − 2vfvsin(θ + β)f(θ)]1/2 − cosθ}−1 dθwhere f(θ) is the absolute particle velocity hodograph function, equal to the solution of the following differential equation:y = ∫θα (f2(θ)sinθ/g) {(vf/vc2) cos(θ + β) [vf2 + f2(θ) − 2vfvsin(θ + β)f(θ)]1/2 − cosθ}−1 dθdv/dθ = v {vc2 sinθ + [v − vf sin(θ + β)][vf2 + v2 − 2vfvsin(θ + β)]1/2}/
{vc2 cosθ − vf cos(θ + β)][vf2 + v2 − 2vfvsin(θ + β)]1/2} - To solve the proposed equations of motion, it is necessary to use numerical methods for solving differential equations and integration with additional control over the possible matching of several hodograph function values to a single argument.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Forces | |
| R | force of aerodynamic drag (N); |
| G | force of gravity (N), apparent force of gravity (N); |
| W | buoyant force (when not subsumed into the apparent force of gravity) (N); |
| F | inertial force (N). |
| Particle Characteristics | |
| m | mass of the particle (kg); |
| V | volume of the particle (m3); |
| ρ | density of the particle (kg/m3); |
| A | projected area of the particle along the direction of movement (m2); |
| d | diameter of the particle (m); |
| a, b, c | a non-spherical particle’s dimensions along each axis (c > a, b) (m). |
| Kinematic Quantities | |
| ˆx, ˆy | unit vectors (m); |
| x | particle position in the horizontal direction (m); |
| y | particle position in the vertical direction (m); |
| x0, y0 | coordinates of the particle’s location upon reaching equilibrium (m); |
| vf | velocity of the fluid stream (m/s); |
| v | velocity of the particle (m/s); |
| v{x,y} | velocity of the particle in the direction {x, y} (m/s); |
| vf {x,y} | velocity of the fluid in the direction {x, y} (m/s); |
| vc | critical (terminal) velocity of the particle in a stream (m/s); |
| vw | relative velocity of the particle in respect to the stream (m/s); |
| v0 | initial velocity of the particle (m/s); |
| vw0 | initial relative velocity of the particle in respect to the stream (m/s); |
| veq | absolute velocity of the particle upon reaching the equilibrium state (m/s); |
| vwN | relative normal velocity of the particle (m/s); |
| vwT | relative tangential velocity of the particle (particle’s change in position over time) (m/s); |
| vfN | fluid velocity in the normal direction of particle movement (m/s); |
| vfT | fluid velocity in the tangential direction of particle movement (m/s); |
| aN | normal acceleration of the particle (m/s2); |
| aT | tangential acceleration of the particle (m/s2); |
| t | time (s). |
| Angular Parameters | |
| θ | the angle between the tangent and the horizontal axis (rd); |
| θ0, α | initial angle (i.e., angle between the initial particle velocity and the horizontal axis) (rd); |
| θeq | the equilibrium angle (of the particle in equilibrium with the stream) (rd); |
| β | the tilt angle of the pneumatic channel (rd); |
| γ | the angle between the drag force vector and the horizontal axis (rd); |
| r | local radius of the trajectory (m). |
| Aerodynamic and Other Important Parameters | |
| cx | aerodynamic drag coefficient (-); |
| νf | kinematic viscosity of the fluid (s/m2); |
| ρf | density of the fluid (air) (kg/m3); |
| Re | the Reynolds number (-); |
| k | inverse volatility parameter of the particle (m); |
| k0 | volatility parameter of the particle (1/m); |
| ϕ | an empirical parameter denoting the amount of fluid moving along with the particle (-); |
| Ψ | Mohsenin’s sphericity parameter (-); |
| g | Earth’s gravity (m/s2). |
References
- Klinzing, G.E. A review of pneumatic conveying status, advances and projections. Powder Technol. 2018, 333, 78–90. [Google Scholar] [CrossRef]
- Lourenço, G.A.; Gomes, T.L.C.; Duarte, C.R.; Ataíde, C.H. Experimental study of efficiency in pneumatic conveying system’s feeding rate. Powder Technol. 2019, 343, 262–269. [Google Scholar] [CrossRef]
- Zheng, K.; Du, C.; Li, J.; Qiu, B.; Yang, D. Underground pneumatic separation of coal and gangue with large size (≥50 mm) in green mining based on the machine vision system. Powder Technol. 2015, 278, 223–233. [Google Scholar] [CrossRef]
- Bi, H.; Zhu, H.; Zu, L.; He, S.; Gao, Y.; Gao, S. Pneumatic separation and recycling of anode and cathode materials from spent lithium iron phosphate batteries. Waste Manag. Res. 2019, 37, 374–385. [Google Scholar] [CrossRef] [PubMed]
- Grandison, A.S.; Lewis, M.J. (Eds.) Separation Process in the Food and Biotechnology Industries; Woodhead Publishing: Cambridge, UK, 1996. [Google Scholar]
- Innocentini, M.D.M.; Barizan, W.S.; Alves, M.N.O.; Pisani, R., Jr. Pneumatic separation of hulls and meats from cracked soybeans. Food Bioprod. Process. 2009, 87, 237–246. [Google Scholar] [CrossRef]
- Güner, M. Pneumatic conveying characteristics of some agricultural seeds. J. Food Eng. 2007, 80, 904–913. [Google Scholar] [CrossRef]
- Panasiewicz, M. Analysis of the pneumatic separation process of agricultural materials. Int. Agrophys. 1999, 13, 233–239. [Google Scholar]
- Panasiewicz, M.; Sobczak, P.; Mazur, J.; Zawiślak, K.; Andrejko, D. The technique and analysis of the process of separation and cleaning grain materials. J. Food Eng. 2012, 109, 603–608. [Google Scholar] [CrossRef]
- Anantharaman, A.; Cahyadi, A.; Hadinoto, K.; Chew, J.W. Impact of particle diameter, density and sphericity on minimum pickup velocity of binary mixtures in gas-solid pneumatic conveying. Powder Technol. 2016, 297, 311–319. [Google Scholar] [CrossRef]
- Markowski, M.; Żuk-Gołaszewska, K.; Kwiatkowski, D. Influence of variety on selected physical and mechanical properties of wheat. Ind. Crop. Prod. 2013, 47, 113–117. [Google Scholar] [CrossRef]
- Łukaszuk, J.; Molenda, M.; Horabik, J.; Szot, B.; Montross, M.D. Airflow resistance of wheat bedding as influenced by the filling method. Res. Agric. Eng. 2008, 54, 50–57. [Google Scholar] [CrossRef]
- Komarnicki, P.; Banasiak, J.; Bieniek, J. Rozkład aerodynamicznych parametrów stanu równowagi procesowej czyszczenia ziarna. Inż. Rol. 2008, 4, 389–396. [Google Scholar]
- Klinzing, G.E.; Basha, O.M. A correlation for particle velocities in pneumatic conveying. Powder Technol. 2017, 310, 201–204. [Google Scholar] [CrossRef]
- Sun, S.; Yuan, Z.; Peng, Z.; Moghtaderi, B.; Doroodchi, E. Computational investigation of particle flow characteristics in pressurised dense phase pneumatic conveying systems. Powder Technol. 2018, 329, 241–251. [Google Scholar] [CrossRef]
- Nesterenko, A.V.; Leshchenko, S.M.; Vasylkovskyi, O.M.; Petrenko, D.I. Analytical assessment of the pneumatic separation quality in the process of grain multilayer feeding. INMATEH Agric. Eng. 2017, 53, 65–70. [Google Scholar]
- Tobias, E.; Gaudet, C.; Viator, H.; Aragon, D.; Ehrenhauser, F. Leaf and panicle separator for sweet sorghum. Sugar Tech. 2018, 20, 252–260. [Google Scholar] [CrossRef]
- Badretdinov, I.; Mudarisov, S.; Tuktarov, M.; Arslanbekova, S. Mathematical modeling of the grain material separation in the pneumatic system of the grain-cleaning machine. J. Appl. Eng. Sci. 2019, 641, 529–534. [Google Scholar] [CrossRef]
- Stepanenko, S.P.; Kotov, B.I. Pneumonitis fractionation of grain materials in air streams of variable structure. Mach. Energ. J. Rural Prod. Res. 2020, 11, 127–132. [Google Scholar]
- Kryszak, D.; Bartoszewicz, A.; Szufa, S.; Piersa, P.; Obraniak, A.; Olejnik, T.P. Modeling of transport of loose products with the use of the non-grid method of discrete elements (DEM). Processes 2020, 8, 1489. [Google Scholar] [CrossRef]
- Lift, R.; Grace, J.R.; Weber, M.E. Bubbles, Drops and Particles; Academic Press: New York, NY, USA, 1978. [Google Scholar]
- Orzechowski, Z. Przepływy Dwufazowe, Jednowymiarowe, Ustalone, Adiabatyczne; PWN: Warszawa, Poland, 1990. [Google Scholar]
- Orzechowski, Z.; Prywer, J.; Zarzycki, R. Mechanika Płynów w Inżynierii i Ochronie Środowiska; WNT: Warszawa, Poland, 2008. [Google Scholar]
- Mohsenin, N.N. Physical Properties of Plant and Animal Materials; Gordon and Breach Science Public: New York, NY, USA, 1986. [Google Scholar]
- Frączek, J.; Reguła, T. Metodyczne aspekty pomiaru właściwości aerodynamicznych cząstek stałych pochodzenia roślinnego. Acta Agrophys. 2012, 19, 515–525. [Google Scholar]
- Grochowicz, J. Machines for Cleaning and Sorting of Seeds; PWRiL: Warsaw, Poland, 1980. [Google Scholar]
- Frączek, J.; Wróbel, M. Metodyczne aspekty oceny kształtu nasion. Inż. Rol. 2006, 87, 155–163. [Google Scholar]
- Dahlquist, G.; Bjorck, A. Numerical Methods in Scientific Computing; SIAM: Philadelphia, PA, USA, 2008; Volume 1. [Google Scholar]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Reguła, T.; Frączek, J.; Fitas, J. A Model of Transport of Particulate Biomass in a Stream of Fluid. Processes 2021, 9, 5. https://doi.org/10.3390/pr9010005
Reguła T, Frączek J, Fitas J. A Model of Transport of Particulate Biomass in a Stream of Fluid. Processes. 2021; 9(1):5. https://doi.org/10.3390/pr9010005
Chicago/Turabian StyleReguła, Tomasz, Jarosław Frączek, and Jakub Fitas. 2021. "A Model of Transport of Particulate Biomass in a Stream of Fluid" Processes 9, no. 1: 5. https://doi.org/10.3390/pr9010005
APA StyleReguła, T., Frączek, J., & Fitas, J. (2021). A Model of Transport of Particulate Biomass in a Stream of Fluid. Processes, 9(1), 5. https://doi.org/10.3390/pr9010005