Abstract
A coupled surface response optimization method with a three-dimensional finite volume method is adopted in this study to identify five independent geometric variables of the die interior that provides a design with the lowest velocity variance at the exit of the coat-hanger extrusion die. Two of these five geometric variables represent the manifold dimension while the other three variables represent the die profile. In this method, B-spline fitting with four points was used to represent the die profile. A comparison of the optimized die obtained in our study and the die with a geometry derived by a previous theoretical work shows a 20.07% improvement in the velocity distribution at the exit of the die.
1. Introduction
Extrusion process is one of the important processes deployed for polymer processing. One of the associated applications of polymer extrusion is extruding a polymer flat sheet. The coat-hanger die is designed to distribute the polymer melt uniformly through the die lip. Non-uniform thickness across the width of the extrudate results in low quality yield. To prevent this adverse effect, non-uniform velocity at the exit and deflection across the lips of the die should be avoided. Coat-hanger die is a commonly used die in the extrusion industry [1,2,3]. A complex relationship between the rheological behavior, flow distribution, and temperature field makes it extremely difficult to develop a universal die model that can be used easily for every fluid property and process condition. Therefore, industries are heavily dependent on a trial-and-error approach for designing an effective die. A more prudent approach is to incorporate an optimization method along with a model that defines and regulates flow as well as heat transfer in the die flow manifold and in the slit.
Several different manifolds for sheeting die have been developed over time. The most common ones are the T-manifold [4], the fishtail [5], and the coat-hanger manifold, with the latter being extensively used in industry. Two major methods are used for dies analysis: analytical and numerical. Due to their oversimplifications, analytical methods are used for determining the overall geometry of the die. With the advancement in computational power, numerical methods have become a more common method for the analysis of dies. Michaeli et al. [5] reviewed most of the analytical methods developed during the last decades. Most of these methods are developed based on the assumption of a power-law model for describing the rheological behavior of the polymer flowing inside the cavity of the die.
Winter and Fritz [6], based on the pressure gradient at the intersection of the manifold and the slit, have modelled a coat-hanger die that results in a constant shear rate on the die interior walls and a uniform velocity at die exit. Although their results have been experimentally tested, these are restricted to power-law fluids and have not taken into account the effect of temperature and die lip deflections.
Based on the finite element method, Wang et al. [7] studied the flow distribution of power-law fluid in coat-hanger die. Their study examined different geometries and concluded that dog bone geometry gives a relatively flatter exit velocity distribution. Huang et al. [8] analyzed flow distribution of polymer melt in the coat-hanger extrusion die for the purpose of understanding flow behavior, such as dead spots in the die cavity. Wu et al. [9] also studied the flow and temperature fields of the coat-hanger die. They concluded that the highest temperature, which is important for temperature-sensitive polymers, occurs at the center of the manifold. Na and Kim [10] studied the effect of the manifold angle on the flow rate distribution. They also reported that the power-law index significantly affects the flow distribution. Catherine [11] studied the flow and temperature fields of polymer melt in the extrusion die cavity and analyzed rheology, temperature dependency, and residence time distribution.
In all previous studies, the die profile is derived either based on the models with many simplified assumptions, such as the constant shear rate in the manifold and slit, or based on the simplest rheological models such as the power-law model. In this paper, the die profile is approximated with a spline curve. In addition, a more elaborate rheological model with temperature dependency is used. An optimization algorithm based on the response surface method is utilized for optimizing five distinct independent variables representing the manifold and the die profile for uniform velocity output along the die lip. In this way, applicability of die curve relation can be tested.
2. Modelling and Simulation
To optimize the die cavity geometry, the flow field needs to be simulated. For this purpose, the generalized Newtonian incompressible viscous model is solved by the finite volume method. Here, the steady-state continuity equation, Navier–Stokes equations, and energy equations are solved. Simulations are performed on the commercially available software package, Ansys Fluent 19.1. Fluent is a computational fluid dynamics (CFD) package that numerically solves flow equations via the finite volume method.
2.1. Governing Equations
In the model presented in this study, polymer melt flow is considered as steady state. Conversion of mass and momentum equations for a fluid flow of density with no external body force is given as follows:
where is the stress tensor and is defined as
where η( is the apparent viscosity and is the shear rate, while γ is the strain tensor satisfying
Since rheological properties of the fluid is temperature dependent, a conversion of energy is required to solve for the temperature field:
where k is the thermal conductivity and cp is the specific heat. Due to temperature rise as a result of viscous dissipation [12], Φ is added as a source term in the energy equation and is given by:
In 3D Cartesian coordinates, it becomes the following [13]:
From the continuity equation, the last term in the equation can be set to zero. The generalized Newtonian models are widely used in industry and academia for modelling the rheological behavior of polymers. While in a Newtonian model the shear stress is directly proportional to the strain rate, generalized Newtonian models give more flexibility. In this paper, a temperature-dependent Carreau–Yasuda viscosity model was selected:
in which , η0 is a near-zero shear rate viscosity, λ is the time constant, n is the power-law index, a is the Carreau–Yasuda constant, αT is the Arrhenius expression, E0 is activation energy, T is temperature, and T0 is absolute reference temperature. The values of these parameters for polypropylene are shown in Table 1. Table 2 shows the other thermo-physical properties of polypropylene. A user-defined function in C code was written for adapting the Carreau–Yasuda equation into the simulation.

Table 1.
Carreau–Yasuda parameters for polypropylene [14].

Table 2.
Thermo-physical of polypropylene [15,16].
2.2. Boundary Conditions
As mentioned above, due to symmetry, only one quarter of the internal cavity of the extrusion die was considered for the simulation. The computational domain is shown in Figure 1. Boundary conditions are as follows.
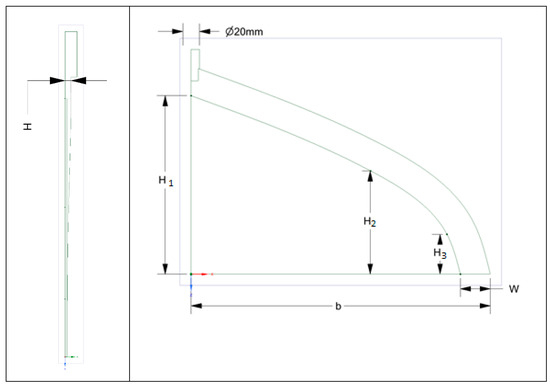
Figure 1.
Schematic of the extrusion die in this analysis.
Inflow boundary condition: The inlet is a fully developed profile with a volumetric flow rate of 5 × 10−3 m3/s. Velocity is calculated based on the method given by Kim [17].Velocity and temperature profiles are adapted from Wei and Michaeli [5,18,19]. In this method, velocity is given as follows:
where:
In these equations, shear rate and shear stress are substituted by the Carreau–Yasuda viscosity in Equation (8) as mentioned in the study by Kim [17]. Integrations of Equations (10) and (11) are solved numerically by the trapezoidal method. Temperature profile is calculated by solving the following energy equation:
where r0 is the entrance radius, Tw is the wall temperature, and k is the thermal conductivity of the medium. Wall temperature Tw is considered to be 220 °C. A user-defined function (UDF) program in C was written for the velocity and temperature profiles at the inlet of the die.
A numerical method of the Runge–Kutta 4th order is used to solve this equation. Due to the dependency of velocity on temperature in Equation (8), velocity and temperature are calculated iteratively until convergence is achieved.
Pressure outflow boundary condition: Gauge pressure at the exit of the die equals to zero.
Non-slip boundary condition: At the internal boundaries of die where the fluid meets the solid, a no-slip boundary condition is assumed. In addition, the temperature at the internal surface of the die is 220 °C.
Symmetry boundary condition: Since the geometry of a die is symmetric in two directions, symmetry boundary conditions are considered for the boundaries Γ4 and Γ5.
The velocity and temperature profiles based on the temperature-dependent Carreau–Yasuda equation at the entrance of the die are shown in Figure 2.
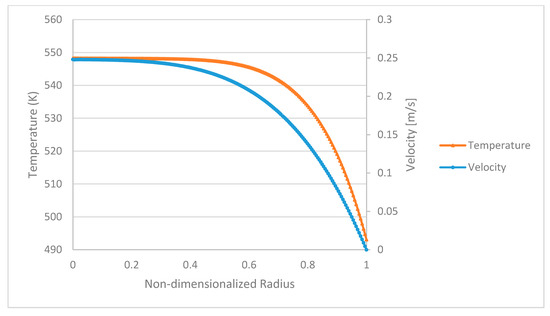
Figure 2.
Velocity and temperature profiles at the entry of the die.
3. Design Variables and Objective Function of Optimization
In this paper, the surface response method is utilized for optimization purposes. The goal of the optimization process is to minimize velocity distribution at the exit of the die. As a result, the following objective function is defined to represent the non-uniformity of velocity at the die exit:
where vi is the velocity at node I, is the average velocity, and N is number of nodes at exit. Five different independent variables were selected to represent the geometry of the die. These five variables are shown in Figure 1. H and W are the depth and the width of the die, respectively, while H1, H2, and H3 are the nodes the spline curve is based on. Under the assumptions given in a study by Winter [6], the change of y with x is given by the following equation:
In this paper, three more variables are assigned to represent this curvature, namely H1, H2, and H3. After a preliminary evaluation, it was found that three nodes are sufficient for accurately representing the y-x curve.
3.1. Mesh Independency
Due to symmetry, only one quarter of the die cavity geometry was selected. Different meshes with different numbers of elements were constructed. For every mesh, simulation was performed and compared. As shown in Figure 3, meshes with 500,000 elements and higher show negligible change in both velocity disparity and pressure drop. As a result, these mesh elements are selected for the next simulations. Figure 4 shows the mesh grid for the independent variables of H = 5 mm, W = 36 mm, H1 = 216 mm, H2 = 124.6 mm, and H3 = 48.3 mm. The radius of the pipe that connects from the extruder to the die is 10 mm.
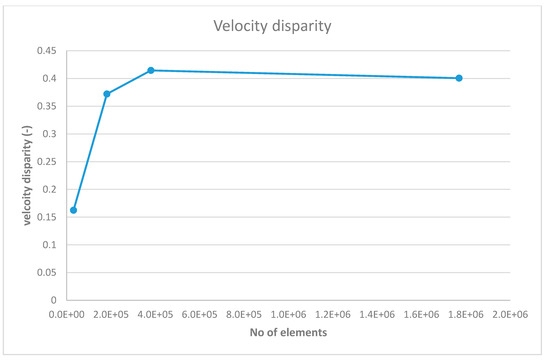
Figure 3.
Mesh independency.

Figure 4.
Sample grid used for the simulation.
3.2. Validation
To the knowledge of the authors, there are no experimental data of flat sheeting extrusion die for validation. Therefore, the data provided by Wei and Leo [18] for the non-isothermal flow of polymer melt in a pipe were considered for validation. Figure 5 shows the comparison of temperature profiles for both the simulation and Wei and Leo’s analytical equation. An average error of 1.54 °C suggests the validity of the computational fluid dynamics model that is used for next sections.
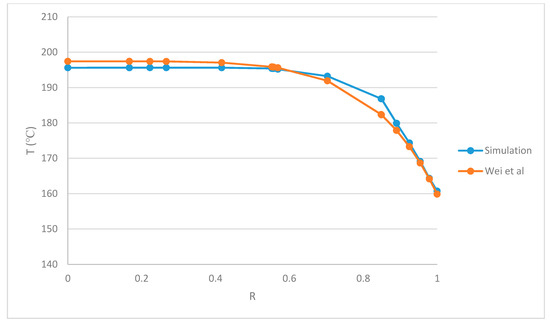
Figure 5.
Temperature profile comparison of simulation and analytical results.
4. Results and Discussion
Fluid Low and Heat Transfer Analysis
The main objective of the optimization process is to reach a global minimum for objective variables, i.e., velocity variance at the exit of the die. For this purpose, the surface response method with a central composite design of experiment was adapted. For five independent variables, the central composite design (CCD) gives 52 experiments or simulations [20]. The default values of these parameters were based on the theoretical analysis of Winter [6]. A range of 10% was assumed for the variation of these values. Values of independent variables and their variation around central node in CCD are shown in Table 3. It is worth noting that the central values were adapted from an equation given by Winter. Lower and upper values are 10% higher and lower than the central values.

Table 3.
Central composite design for five geometrical variables.
In the surface response method, the dependency of the independent variable variance is usually approximated by a quadratic function:
When a good fit between the data and the quadratic function is obtained, by minimizing the quadratic function and the corresponding independent variable, the optimal point where there is least velocity disparity or in other words maximum uniformity of velocity at the exit of die can be attained.
As mentioned above, the data of 52 simulations, which are needed for the fitting of the quadratic function, are shown in Table 4. Figure 6 shows the main effects plot for velocity disparity. From these plots, it is clear that the manifold dimensions (i.e., H and W) have the highest impacts on reduction in velocity disparity, while H1, which represents the first point in the spline of the die curve, has the lowest effect. A Python program was developed to generate the geometry for each case. The polymer melt in this study is polypropylene with a flow rate of 5 × 10−3 m3/s.

Table 4.
Design of experiment and simulation results.
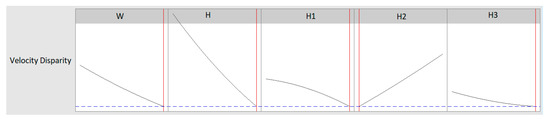
Figure 6.
Main effects plots for velocity disparity.
After a quadratic regression of the data, an equation that shows the relation between the dependent variable and independent variables is derived as follows:
Based on this equation, W has the highest effect on velocity disparity. Basically, an extrusion die is a fluid distribution system, and the most important factor in a distribution system is the manifold. Therefore, clearly the manifold dimensions (i.e., H and W) show the most effect on the velocity distribution. Among the variables H1, H2, and H3, which represent the die profiles, the velocity disparity depends mostly on H3 and with slightly lower dependence on H2. This can be explained by considering that H3 and to some extent H2 determine the angle that the manifold reaches at the end of the die. A higher H3 gives a wider angle, while a greater H2 leads to a wider angle.
By minimizing this equation, an optimal point where velocity disparity is minimum is obtained. At the optimal point, these parameters (H, W, H1, H2, and H3) are found to be 6.19, 44.56, 204.63, 95.27, and 59.7, respectively.
A simulation with the obtained values for the independent variables was performed.
Figure 7 and Figure 8 show the velocity distribution in the cavity and across the die exit, respectively. The velocity disparity values for the default design (Winter type) and the optimal design are found to be 0.68861 and 0.55035, respectively. This shows a 20.07% improvement in the velocity distribution at the exit of the extrusion die compared to the default die. Near the edge of the die, where the manifold reaches the slit, there is a spike in the velocity before it falls to zero at the wall of the die. As it can be seen, maximum velocity occurs at a little bit further distance from the entry of die. This demonstrates the insufficiency of the power law.
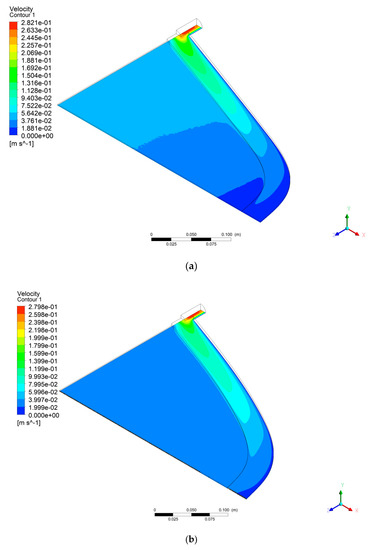
Figure 7.
Velocity distribution in (a) the initial die and (b) optimized die.
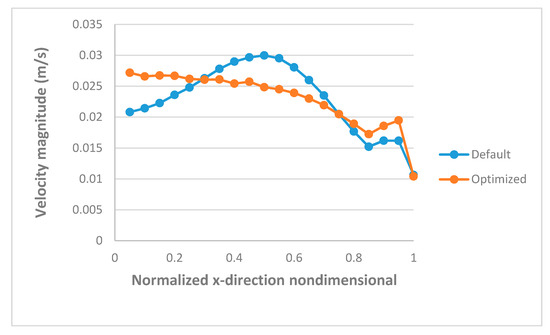
Figure 8.
Comparison of velocity distribution in the initial and optimized dies.
Figure 8 shows the velocity distribution at the exit of the die for both the initial and optimized dies.
Figure 9 shows the pressure distribution comparison for the initial and optimized dies. Pressure drops for the initial and optimized dies appears to be 6.723 and 6.628 MPa, respectively. This shows a 1.4% reduction in the pressure drop. A lower pressure drop leads to a lower energy consumption.
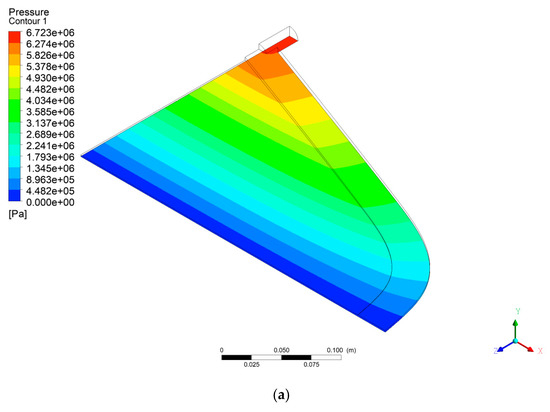
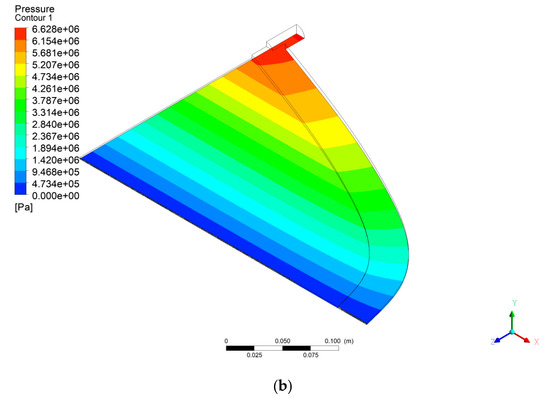
Figure 9.
Pressure distribution for (a) the initial die and (b) optimized die.
Figure 10 shows the temperature distributions for the initial and optimized dies. Both contours look similar. A comparison of temperature distributions at the outlet of the die for the initial and optimized dies is depicted in Figure 11. As it is shown, the optimized die has more uniform temperature at the outlet. As discussed before, the optimized die gives more uniform velocity. Uniform velocity results in a more uniform temperature profile at the exit of the die. Since polymers are susceptible to degradation due to the high temperatures, an optimized die with more uniform velocity is more desirable.
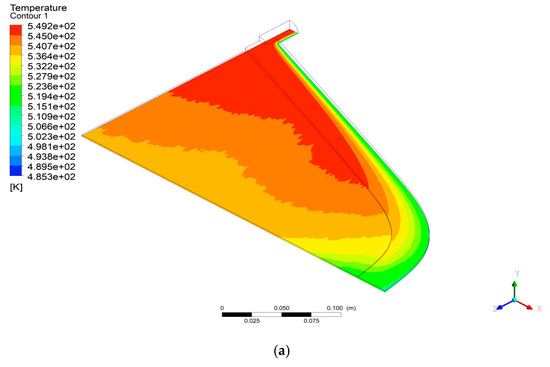
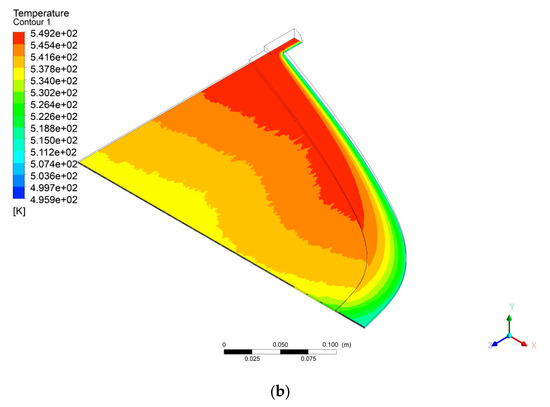
Figure 10.
Temperature distribution for (a) the initial die and (b) optimized die.
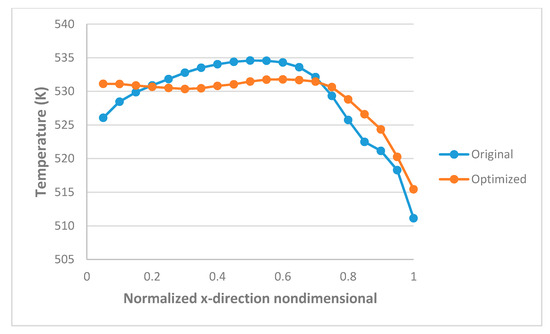
Figure 11.
Temperature distribution comparison at the outlet.
5. Conclusions
This article presented a geometric optimization algorithm involving an integration with computational fluid dynamics. Temperature-dependent rheological properties along with viscous dissipation are considered in the CFD model. A Carreau–Yasuda model with Arrhenius temperature dependency was used for the viscosity model. Fully developed velocity and temperature profiles were utilized at the inlet of the die. The die profile was approximated by a spline curve with three points. Based on the response surface method and the central composite experiment design, a relation between velocity disparity at the exit of the die and five independent geometric variables was derived. The obtained optimized geometry shows a 20.07% improvement in the distribution of velocity at die exit.
Author Contributions
A.P. and D.W. conceived the idea of this research; A.R. developed the framework of the paper, performed numerical simulations, and prepared the manuscript under the supervision of A.P., D.W. and D.Z. All authors have read and agreed to the published version of the manuscript.
A.P. and D.W. conceived the idea of this research; A.R. developed the framework of the paper, performed numerical simulations, and prepared the manuscript under the supervision of A.P., D.W. and D.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded under the target program No. AP05134166 “Development and Prototyping of Extrusion Dies for Advanced Plastic Sheets and Thin Film Production” from the Ministry of Education and Science of the Republic of Kazakhstan.
Acknowledgments
The authors would like to express their deepest gratitude to Otilia Nuta for checking the English of this paper
Conflicts of Interest
The authors declare no conflict of interest.
References
- Michaeli, W. Extrusion Dies for Plastics and Rubber: Design and Engineering Computations; Hanser: Munich, Germany, 2003. [Google Scholar]
- Michaeli, W.; Kaul, S. Approach of an Automatic Extrusion die Optimization. J. Polym. Eng. 2004, 24, 1–3. [Google Scholar] [CrossRef]
- Puissant, S.; Vergnes, B.; Agassant, J.F.; Demay, Y.; Labaig, J.J. Two-dimensional multilayer coextrusion flow in a flat coat-hanger die. Part 2: Experiments and theoretical validation. Polym. Eng. Sci. 1996, 36, 936–942. [Google Scholar] [CrossRef]
- Matsubara, Y. Flat die geometry—A note. Polym. Eng. Sci. 1988, 28, 1275. [Google Scholar] [CrossRef]
- Hopmann, C.; Michaeli, W. Extrusion Dies for Plastics and Rubber. In Extrusion Dies for Plastics and Rubber, 4th ed.; Hopmann, C., Michaeli, W., Eds.; Hanser Publisher: Munich, Germany, 2016; pp. 1–18. [Google Scholar]
- Winter, H.H.; Fritz, H.G. Design of dies for the extrusion of sheets and annular parisons: The distribution problem. Polym. Eng. Sci. 1986, 26, 543–553. [Google Scholar] [CrossRef]
- Wang, Y. The flow distribution of molten polymers in slit dies and coathanger dies through three-dimensional finite element analysis. Polym. Eng. Sci. 1991, 31, 204–212. [Google Scholar]
- Huang, Y.; Gentle, C.R.; Hull, J.B. A comprehensive 3-D analysis of polymer melt flow in slit extrusion dies. Adv. Polym. Technol. 2004, 23, 111–124. [Google Scholar] [CrossRef]
- Wu, T.; Jiang, B.; Xu, S.; Bi, C. Nonisothermal comprehensive 3D analysis of polymer melt flow in a coat-hanger die. Polym. Eng. Sci. 2006, 46, 406–415. [Google Scholar]
- Na, S.Y.; Kim, D.H. Three-dimensional modelling of Non-Newtonian fluid flow in a coat-hanger die. Korean J. Chem. Eng. 1995, 12, 236–243. [Google Scholar] [CrossRef]
- Catherine, O. Polymer melt rheology and flow simulations applied to cast film extrusion die design: An industrial perspective. AIP Conf. Proc. 2017, 1843, 30009. [Google Scholar]
- Benkreira, H. Step-change in Enhancing Extrusion as a Unit Operation. In Proceedings of the 7th World Congress of Chemical Engineering, Glasgow, Scortland, 10 July 2005. [Google Scholar]
- Bird, R.B.; Stewart, W.E.; Lightfoot, E.N. Transport Phenomena; Wiley: Hoboken, NJ, USA, 2006. [Google Scholar]
- Osswald, T.A.; Rudolph, N. Polymer Rheology: Fundamentals and Applications; Hanser Publisher: Munich, Germany, 2015. [Google Scholar]
- Çengel, Y.A.; Ghajar, A.J. Heat and Mass Transfer: Fundamentals & Applications; McGraw-Hill Education: NewYork, NY, USA, 2011. [Google Scholar]
- Mark, J.E. Physical Properties of Polymers Handbook; Springer: New York, NY, USA, 2007. [Google Scholar]
- Kim, K.S. Flow-rate based method for velocity of fully developed laminar flow in tubes. J. Rheol. 2018, 62, 1397–1407. [Google Scholar] [CrossRef]
- Wei, D.; Zhang, Z. Decay estimates of heat transfer to molten polymer flow in pipes with viscous dissipation. Electron. J. Differ. Equ. 2001, 39, 1–14. [Google Scholar]
- Wei, D.; Luo, H. Finite element solutions of heat transfer in molten polymer flow in tubes with viscous dissipation. Int. J. Heat Mass Transf. 2003, 46, 3097–3108. [Google Scholar] [CrossRef]
- Cavazzuti, M. Optimization Methods: From Theory to Design Scientific and Technological Aspects in Mechanics. Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).