Viscous Loss Analysis of the Flooded Electro-Hydrostatic Actuator Motor under Laminar and Turbulent Flow States
Abstract
:1. Introduction
2. Method for Judging Cooling Fluid Flow State
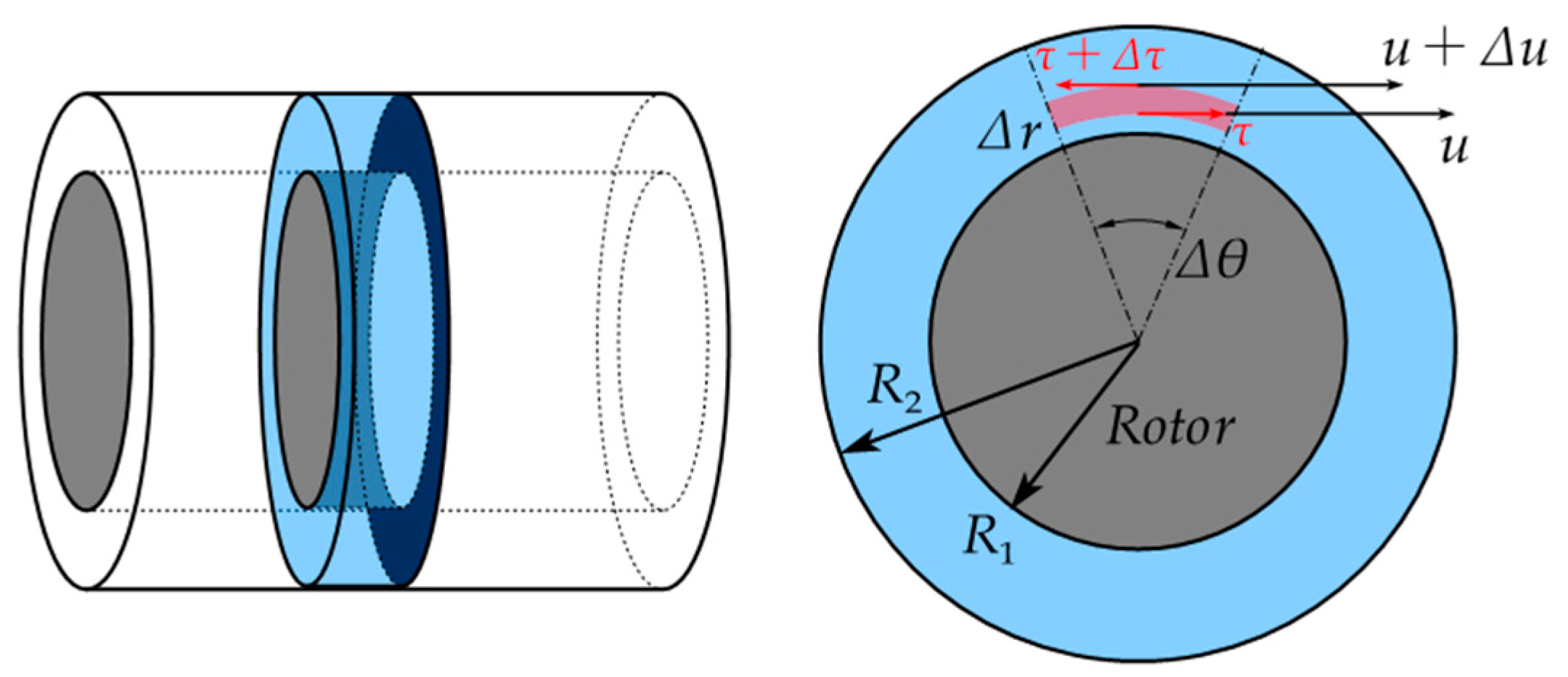
3. Theoretical Analysis of Air Gap Viscous Loss
3.1. Calculation Method of Viscous Loss in Laminar State
3.2. Calculation Method of Viscous Loss in Turbulent State
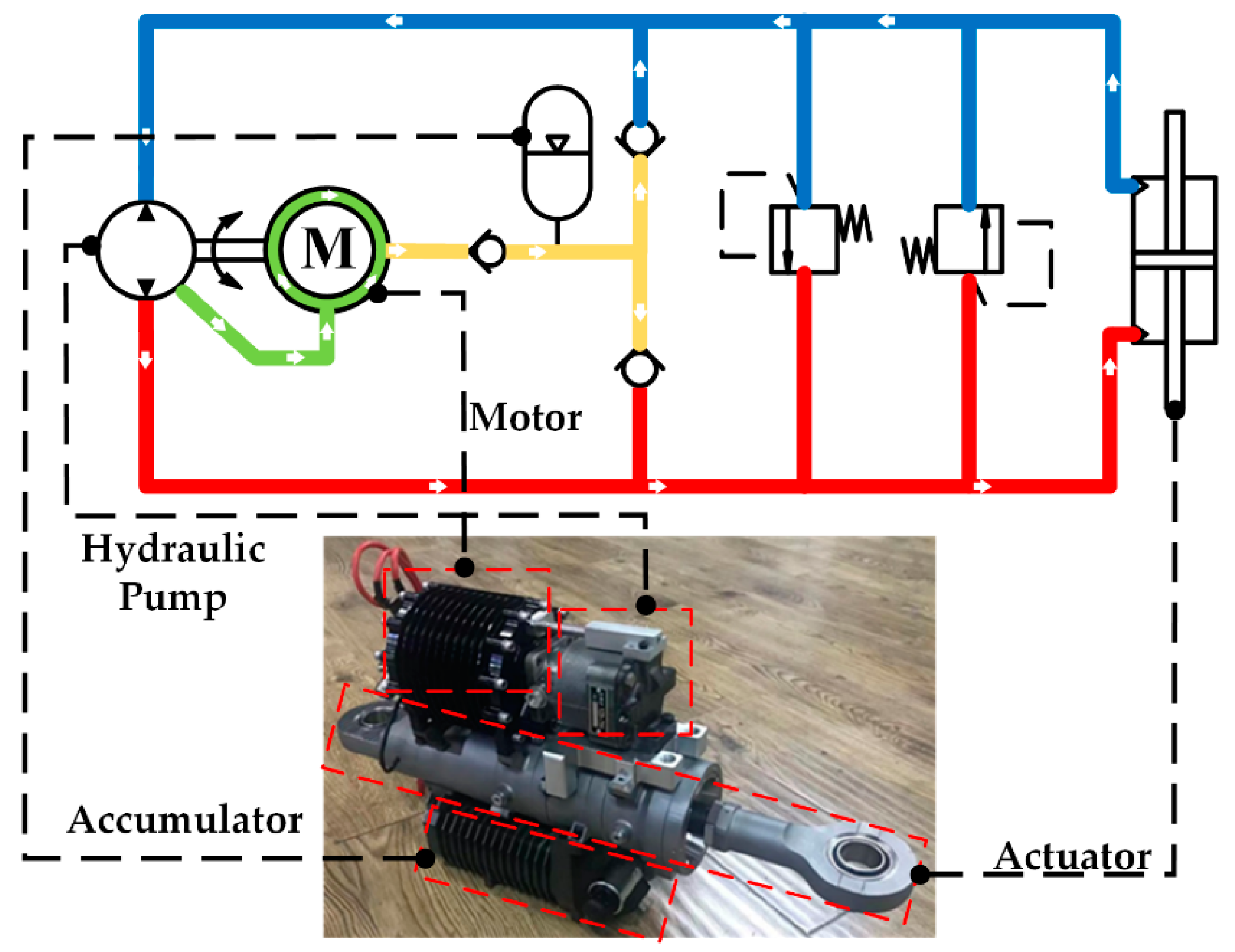
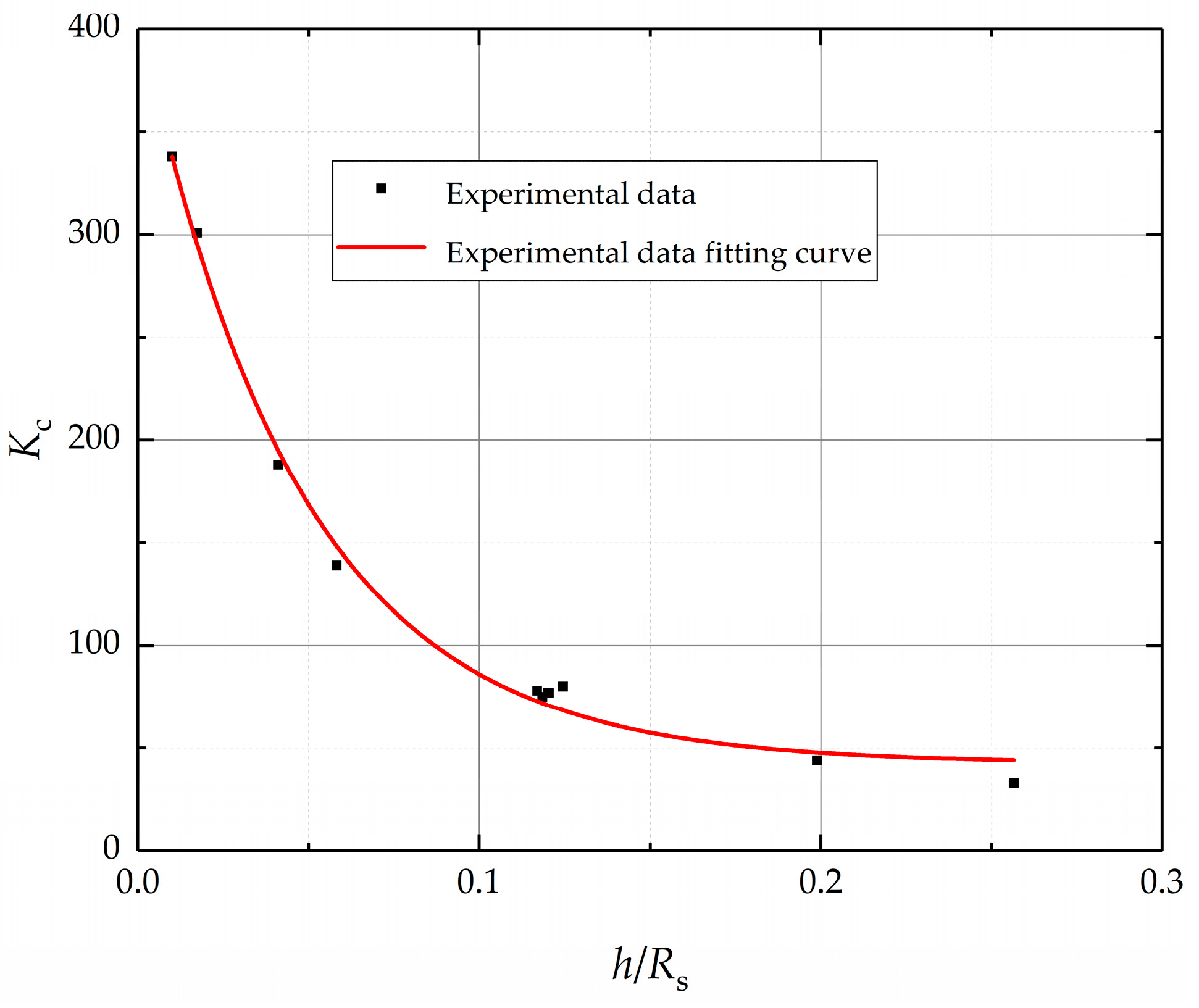
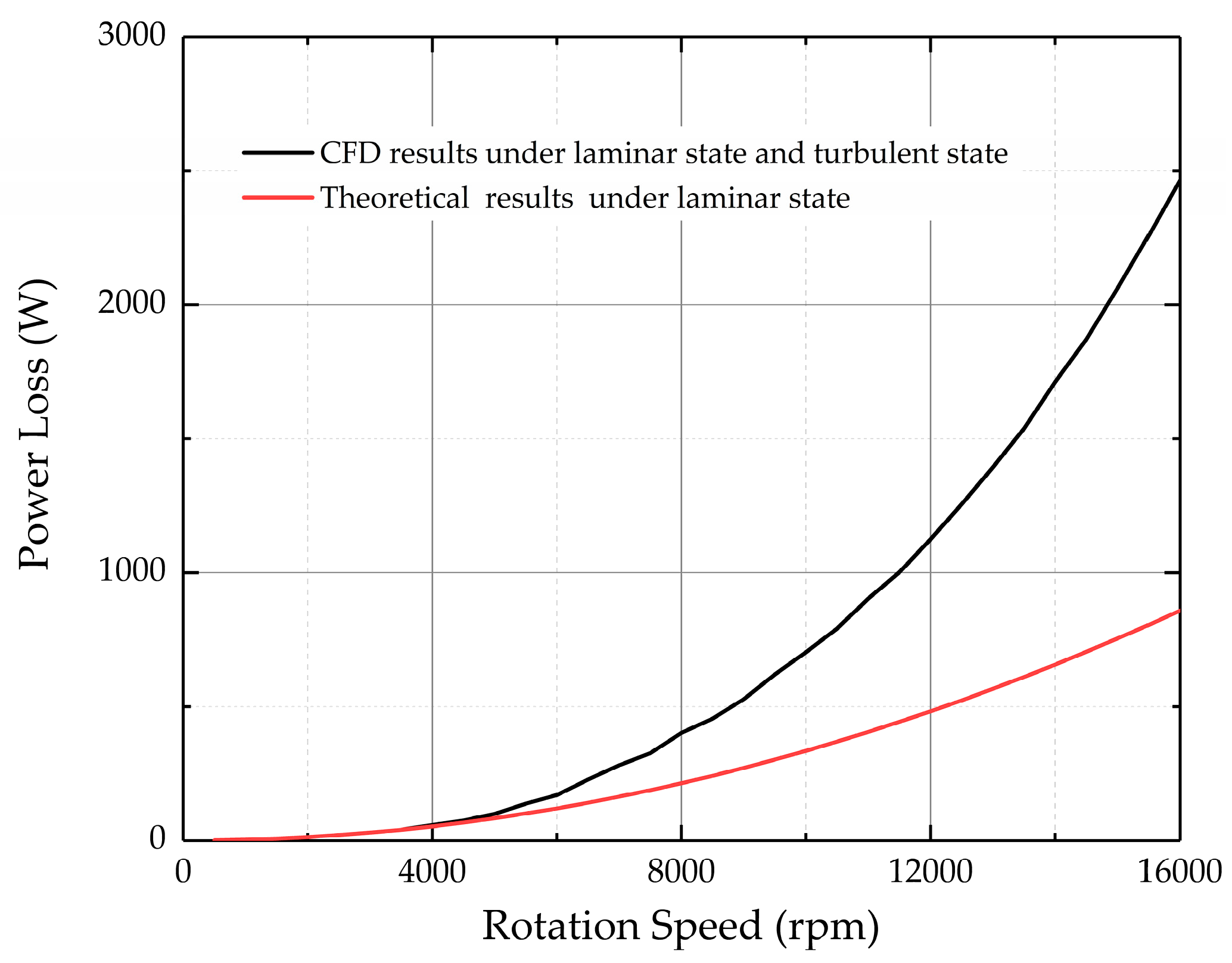
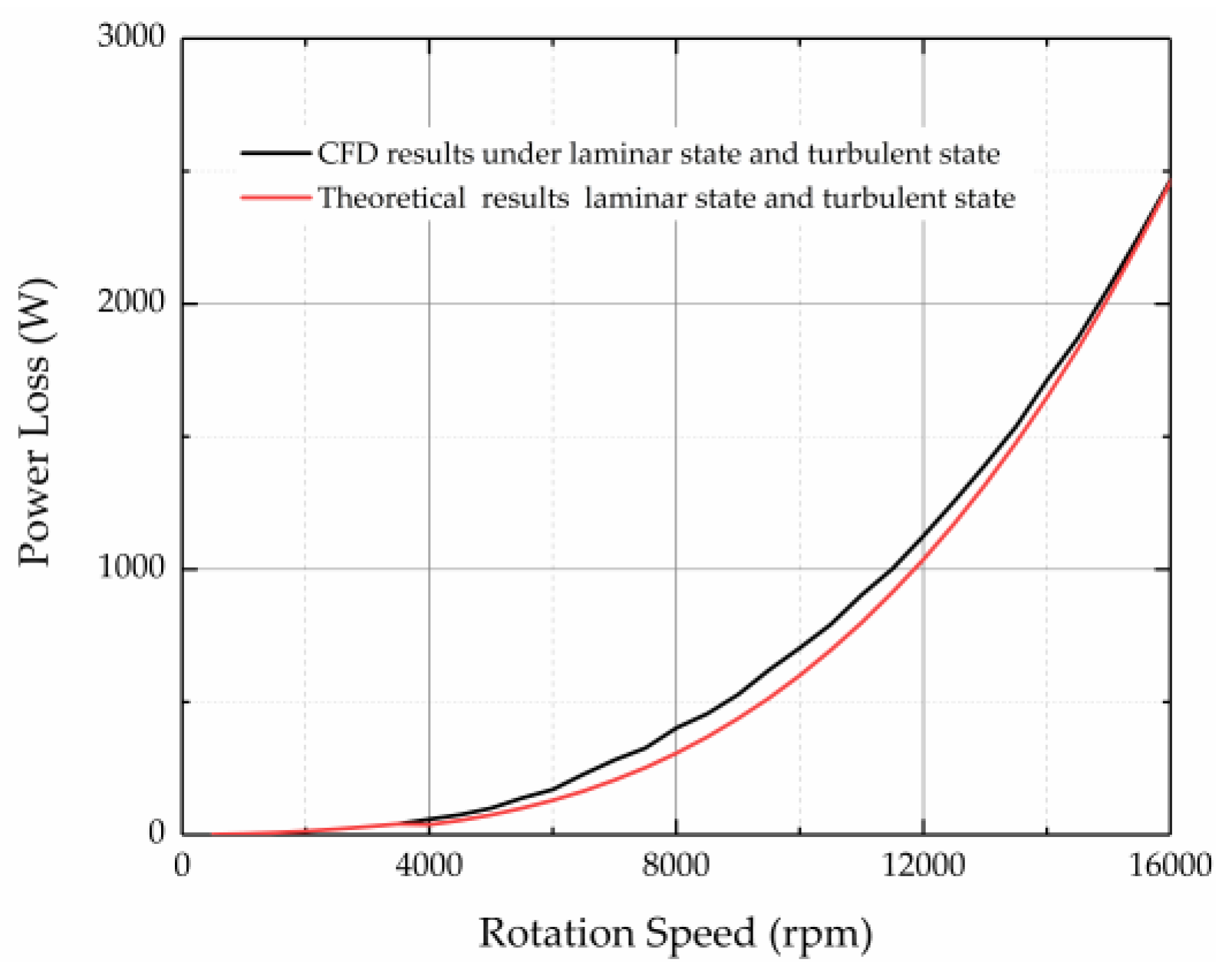
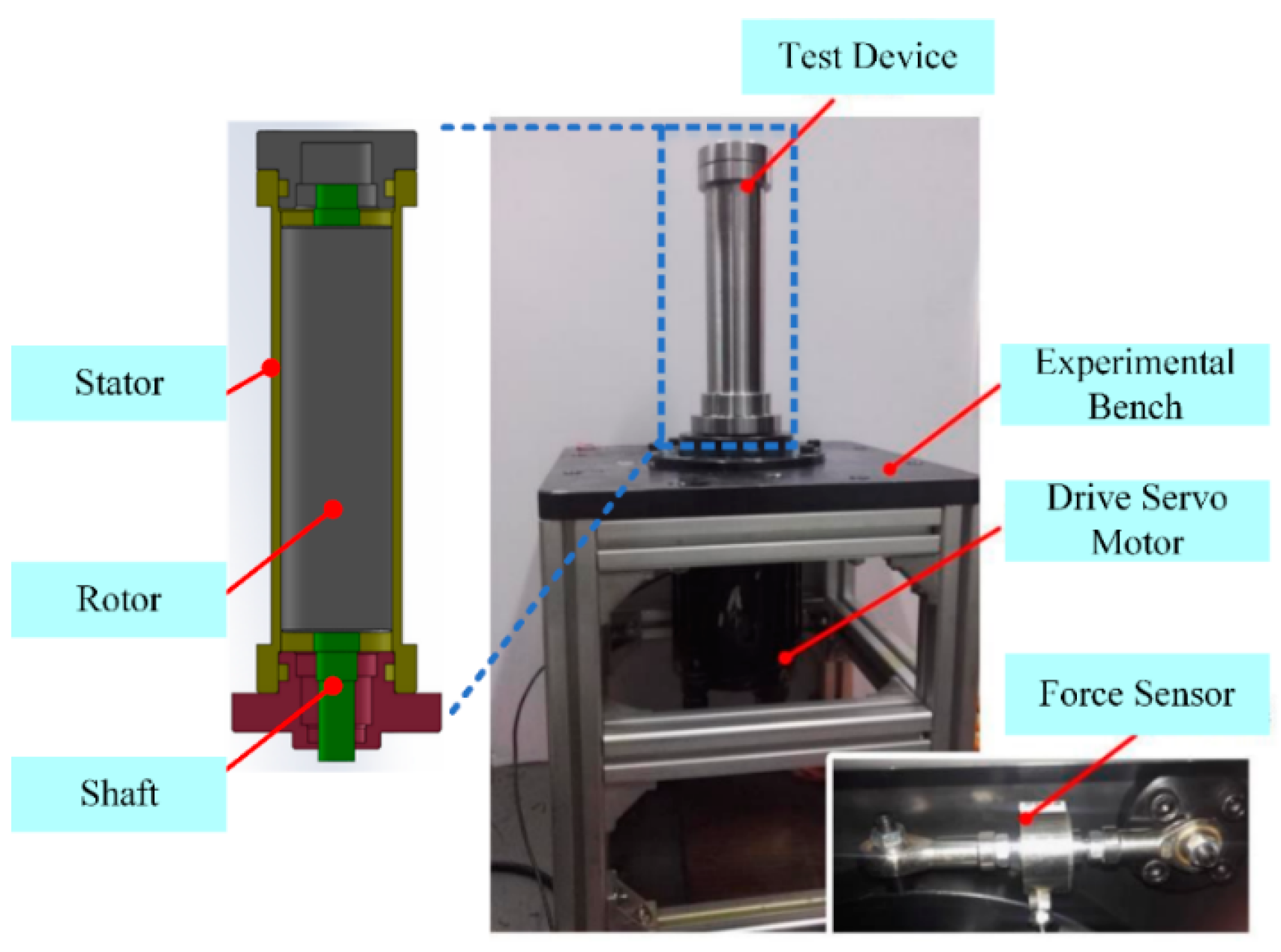
4. Experimental Results
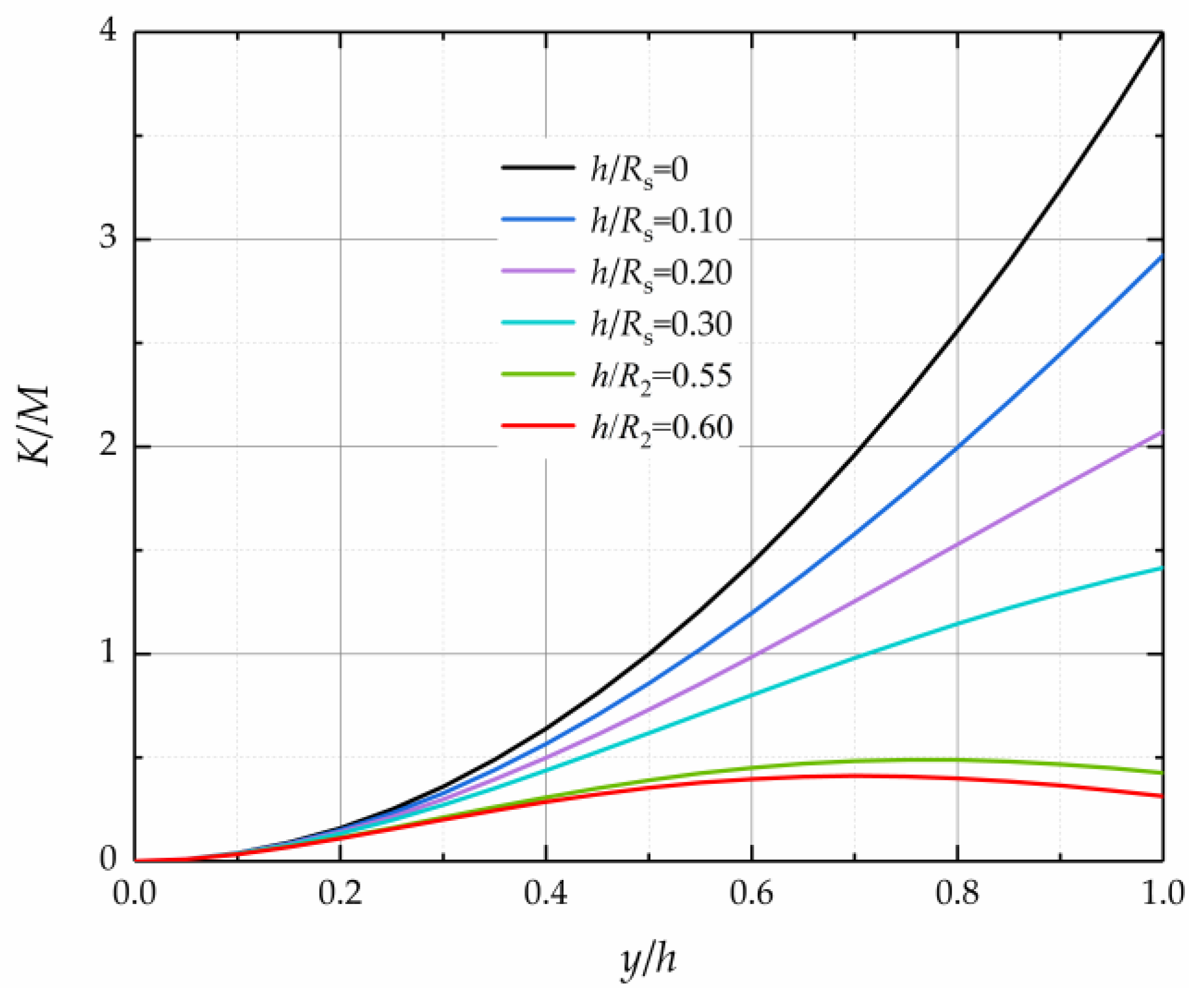
5. Discussion
Author Contributions
Funding
Conflicts of Interest
Appendix A
References
- Song, B.; Lee, D.; Park, S.Y.; Baek, Y.S. Design and Performance of Nonlinear Control for an Electro-Hydraulic Actuator Considering a Wearable Robot. Processes 2019, 7, 389. [Google Scholar] [CrossRef] [Green Version]
- Xue, L.; Wu, S.; Xu, Y.; Ma, D. A Simulation-Based Multi-Objective Optimization Design Method for Pump-Driven Electro-Hydrostatic Actuators. Processes 2019, 7, 274. [Google Scholar] [CrossRef] [Green Version]
- Kargov, A.; Werner, T.; Pylatiuk, C.; Schulz, S. Development of a miniaturized hydraulic actuation system for artificial hands. Sens. Actuators A Phys. 2008, 141, 548–557. [Google Scholar] [CrossRef]
- Samer, A.; Fethi, B.O.; Faycal, N.; Gordon, G. High performance Integrated Electro-Hydraulic Actuator for robotics. Part II: Theoretical modelling, simulation, control & comparisons with real measurement. Sens. Actuators A Phys. 2001, 169, 124–132. [Google Scholar]
- Jose, V.C.; Adrian, B. Integrative thermodynamic optimization of the environmental control system of an aircraft. Int. J. Heat Mass Transf. 2001, 44, 3907–3917. [Google Scholar]
- Ponomarev, P.; Polikarpova, M.; Pyrhönen, J. Thermal modeling of directly-oil-cooled permanent magnet synchronous machine. In Proceedings of the 2012 XXth International Conference on Electrical Machines, Marseille, France, 2–5 September 2012; pp. 1882–1887. [Google Scholar]
- Maré, J.C. Aerospace Actuators 2, Single-by-Wire and Power-by-Wire; Great Britain and the United States by ISTE Ltd.: London, UK; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2017; pp. 134–169. [Google Scholar]
- Shang, Y.; Li, X.; Qian, H.; Wu, S.; Pan, Q.; Huang, L. A Novel Electro Hydrostatic Actuator System with Energy Recovery Module for More Electric Aircraft. IEEE Trans. Ind. Electron. 2020, 67, 2991–2999. [Google Scholar] [CrossRef]
- Zhang, J.; Li, Y.; Xu, B.; Chen, X.; Pan, M. Churning losses analysis on the thermal-hydraulic model of a high-speed electro-hydrostatic actuator pump. Int. J. Heat Mass Transf. 2018, 127, 1023–1030. [Google Scholar] [CrossRef]
- Chandrasekhar, S. Hydrodynamics and Hydromagnetic Stability; Courier Corporation: Dover, UK, 1961; pp. 272–381. [Google Scholar]
- Drazin, P.G.; Reid, W.H. Hydrodynamic Stability, 2nd ed.; Cambridge University Press: Cambridge, UK, 2004; pp. 69–123. [Google Scholar]
- Chossat, P.; Iooss, G. The Couette–Taylor Problem; Springer: Berlin, Germany, 1994. [Google Scholar]
- Schlichting, H. Boundary Layer Theory, 7th ed.; Springer: Berlin/Heidelberg, Germany, 1979; pp. 83–111, 449–554. [Google Scholar]
- Andereck, C.D.; Liu, S.S.; Swinney, H.L. Flow regimes in a circular Couette system with independently rotating cylinders. J. Fluid Mech. 1986, 164, 155–183. [Google Scholar] [CrossRef] [Green Version]
- Marcus, P.S. Simulation of Taylor-Couette flow. Part 2. Numerical results for wave-vortex flow with one travelling wave. J. Fluid Mech. 1984, 146, 65–113. [Google Scholar] [CrossRef] [Green Version]
- Taylor, G.I. Stability of a viscous liquid contained between two rotating cylinders. Philos. Trans. R. Soc. Lond. Ser. A 1923, 223, 289–343. [Google Scholar]
- Dou, H.S.; Khoo, B.C.; Yeo, K.S. Instability of Taylor–Couette flow between concentric rotating cylinders. Int. J. Therm. Sci. 2008, 47, 1422–1435. [Google Scholar] [CrossRef] [Green Version]
- Sangha, P.S.; Sawata, T.; Yon, J.; Mellor, P.H. Assessment of fluid drag loss in a flooded rotor electro-hydrostatic actuator motor. In Proceedings of the 2015 IEEE International Electric Machines & Drives Conference (IEMDC), Coeur d’Alene, ID, USA, 10–13 May 2015; pp. 139–142. [Google Scholar]
- Qi, W.; Zou, J.; Li, J. Numerical calculation of viscous drag loss of oil-filled BLDC motor for underwater applications. In Proceedings of the 2010 International Conference on Electrical Machines and Systems, Incheon, Korea, 10–13 October 2010; pp. 1739–1742. [Google Scholar]
- Nerg, J.; Rilla, M.; Pyrhonen, J. Thermal Analysis of Radial-Flux Electrical Machines with a High Power Density. IEEE Trans. Ind. Electron. 2008, 55, 3543–3554. [Google Scholar] [CrossRef]
- Wendt, F. Turbulent Stromungen zwischen zwei rotierenden konaxialen Zylindern. Ing. Arch. 1933, 9, 577–595. [Google Scholar] [CrossRef]
- Yamada, Y. Torque resistance of a flow between rotating co-axial cylinders having axial flow. Bullentin JSME 1962, 5, 634–642. [Google Scholar] [CrossRef] [Green Version]
- Dou, H.S. Mechanism of flow instability and transition to turbulence. Int. J. Non Linear Mech. 2006, 41, 512–517. [Google Scholar] [CrossRef]
- Dou, H.S. Physics of Flow Instability and Turbulent Transition in Shear Flows; National University of Singapore: Singapore, 2006. [Google Scholar]
- Dou, H.S.; Khoo, B.C.; Yeo, K.S. Turbulent transition in plane Couette flows. In New Trends in Fluid Mechanics Research; Zhuang, F.G., Li, J.C., Eds.; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar] [CrossRef] [Green Version]
- Dou, H.S. Three important theorems for flow stability. In New Trends in Fluid Mechanics Research; Zhuang, F.G., Li, J.C., Eds.; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar] [CrossRef]
- Dou, H.S. Energy Gradient Theory of Hydrodynamic Instability. In Proceedings of the Third International Conference on Nonlinear Science, Singapore, 30 June–2 July 2004; Available online: http://arxiv.org/abs/nlin.CD/0501049 (accessed on 11 August 2020).
- Dou, H.S.; Khoo, B.C.; Yeo, K.S. Energy loss distribution in the plane Couette flow and the Taylor–Couette flow between concentric rotating cylinders. Int. J. Therm. Sci. 2007, 46, 262–275. [Google Scholar] [CrossRef] [Green Version]
- Coles, D. Transition in circular Couette flow. J. Fluid Mech. 1965, 21, 385–425. [Google Scholar] [CrossRef] [Green Version]
- Snyder, H.A. Stability of rotating Couette flow. II. Comparisons with numerical results. Phys. Fluids 1968, 11, 1599–1605. [Google Scholar] [CrossRef]
- Gollub, J.P.; Swinney, H.L. Onset of turbulence in a rotating fluid. Phys. Rev. Lett. 1975, 35, 927–930. [Google Scholar] [CrossRef]
- Hinko, K.A. Transitions in the Small Gap Limit of Taylor-Couette Flow; The Ohio State University Physics Summer Institute, REU Summer: Columbus, OH, USA, 2003. [Google Scholar]
- Zhang, J.; Li, Y.; Xu, B.; Pan, M.; Lv, F. Experimental Study on the Influence of the Rotating Cylinder Block and Pistons on Churning Losses in Axial Piston Pumps. Energies 2017, 10, 662. [Google Scholar] [CrossRef] [Green Version]



| Parameters | Value | Unit |
|---|---|---|
| Radius of the rotor | m | |
| Radius of the stator | m | |
| Length of the air gap L | m | |
| Density of the oil | kg/m3 | |
| Dynamic viscosity of the oil | N s/m2 | |
| Kinematic viscosity of the oil | m2/s |
| Simulation Settings | Setup | |
|---|---|---|
| General | Solver Type | Pressure-Based |
| Velocity Formulation | Absolute | |
| Time | Steady | |
| Models | Viscous | Laminar/Standard k-epsilon and Standard Wall Functions |
| Boundary | End Face 1 | Symmetry |
| End Face 2 | Symmetry | |
| Rotor | Moving Wall (Rotation Speed can be set) | |
| Stator | Wall (No Slip) | |
| Method | Schema | SIMPLEC |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Jiao, Z.; Yu, T.; Shang, Y. Viscous Loss Analysis of the Flooded Electro-Hydrostatic Actuator Motor under Laminar and Turbulent Flow States. Processes 2020, 8, 975. https://doi.org/10.3390/pr8080975
Li Y, Jiao Z, Yu T, Shang Y. Viscous Loss Analysis of the Flooded Electro-Hydrostatic Actuator Motor under Laminar and Turbulent Flow States. Processes. 2020; 8(8):975. https://doi.org/10.3390/pr8080975
Chicago/Turabian StyleLi, Yanpeng, Zongxia Jiao, Tian Yu, and Yaoxing Shang. 2020. "Viscous Loss Analysis of the Flooded Electro-Hydrostatic Actuator Motor under Laminar and Turbulent Flow States" Processes 8, no. 8: 975. https://doi.org/10.3390/pr8080975
APA StyleLi, Y., Jiao, Z., Yu, T., & Shang, Y. (2020). Viscous Loss Analysis of the Flooded Electro-Hydrostatic Actuator Motor under Laminar and Turbulent Flow States. Processes, 8(8), 975. https://doi.org/10.3390/pr8080975




