Study on Clearance-Rubbing Dynamic Behavior of 2-DOF Supporting System of Magnetic-Liquid Double Suspension Bearing
Abstract
:1. Introduction
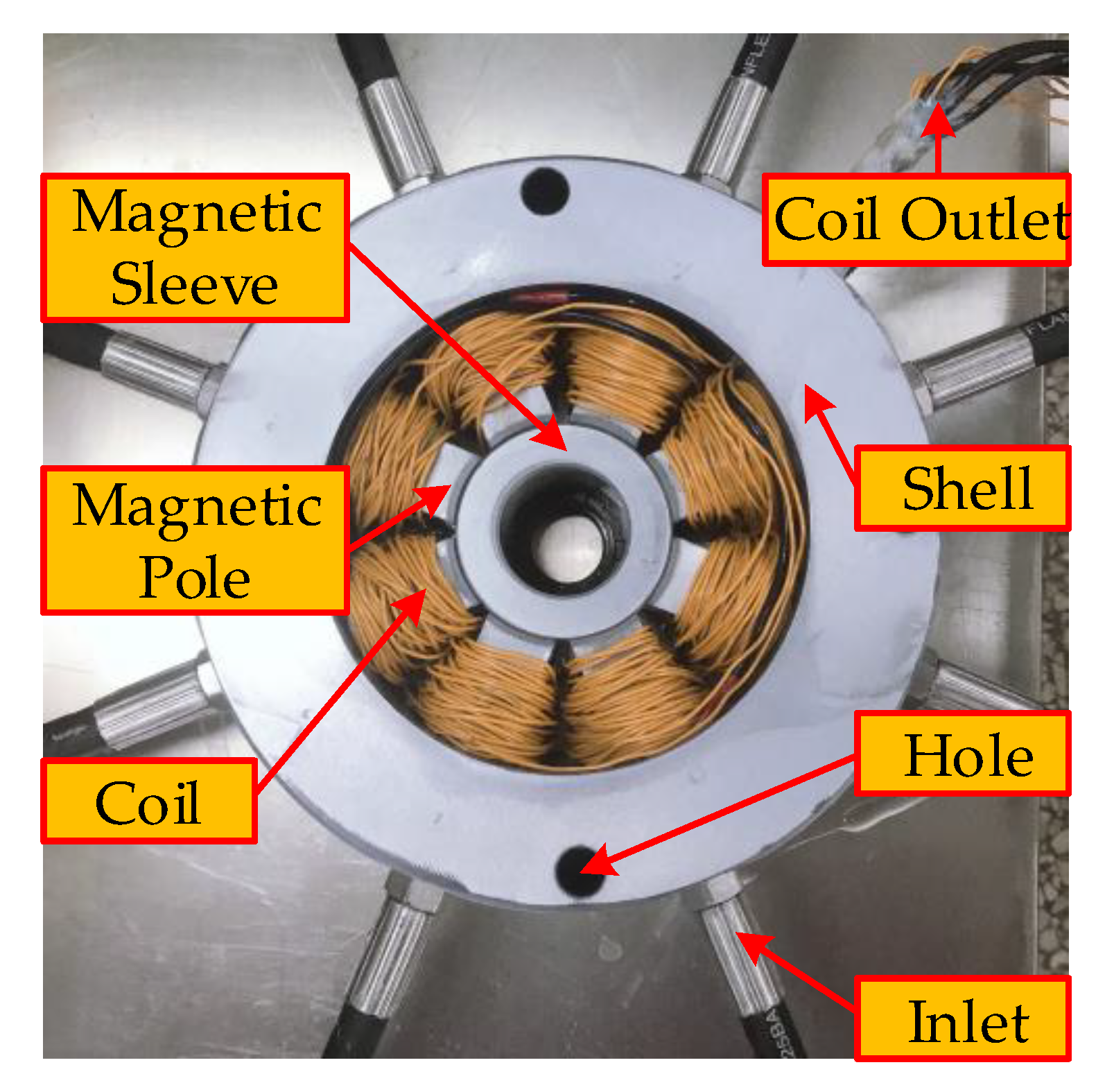
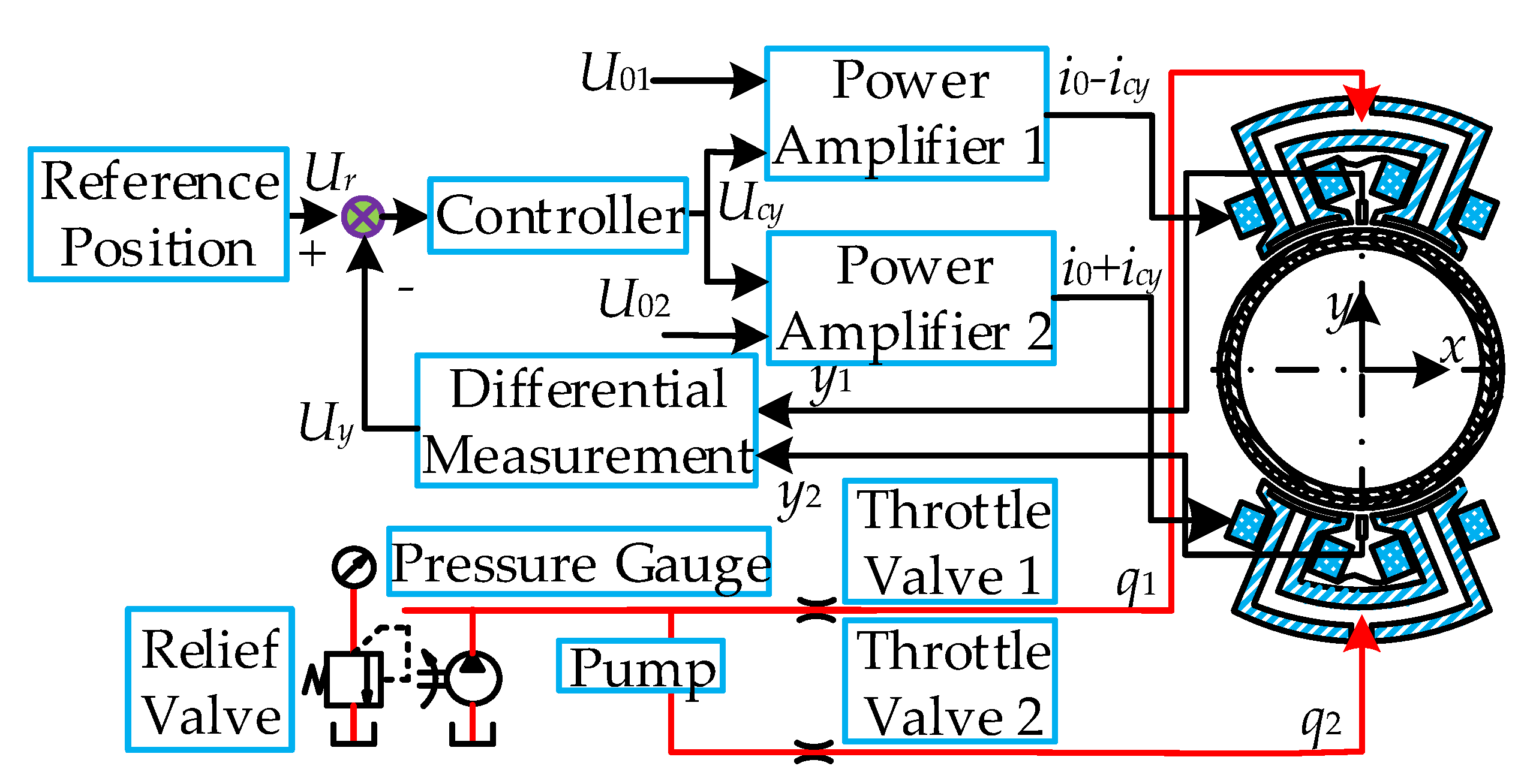
2. Rubbing Dynamic Model of 2-DOF Supporting System
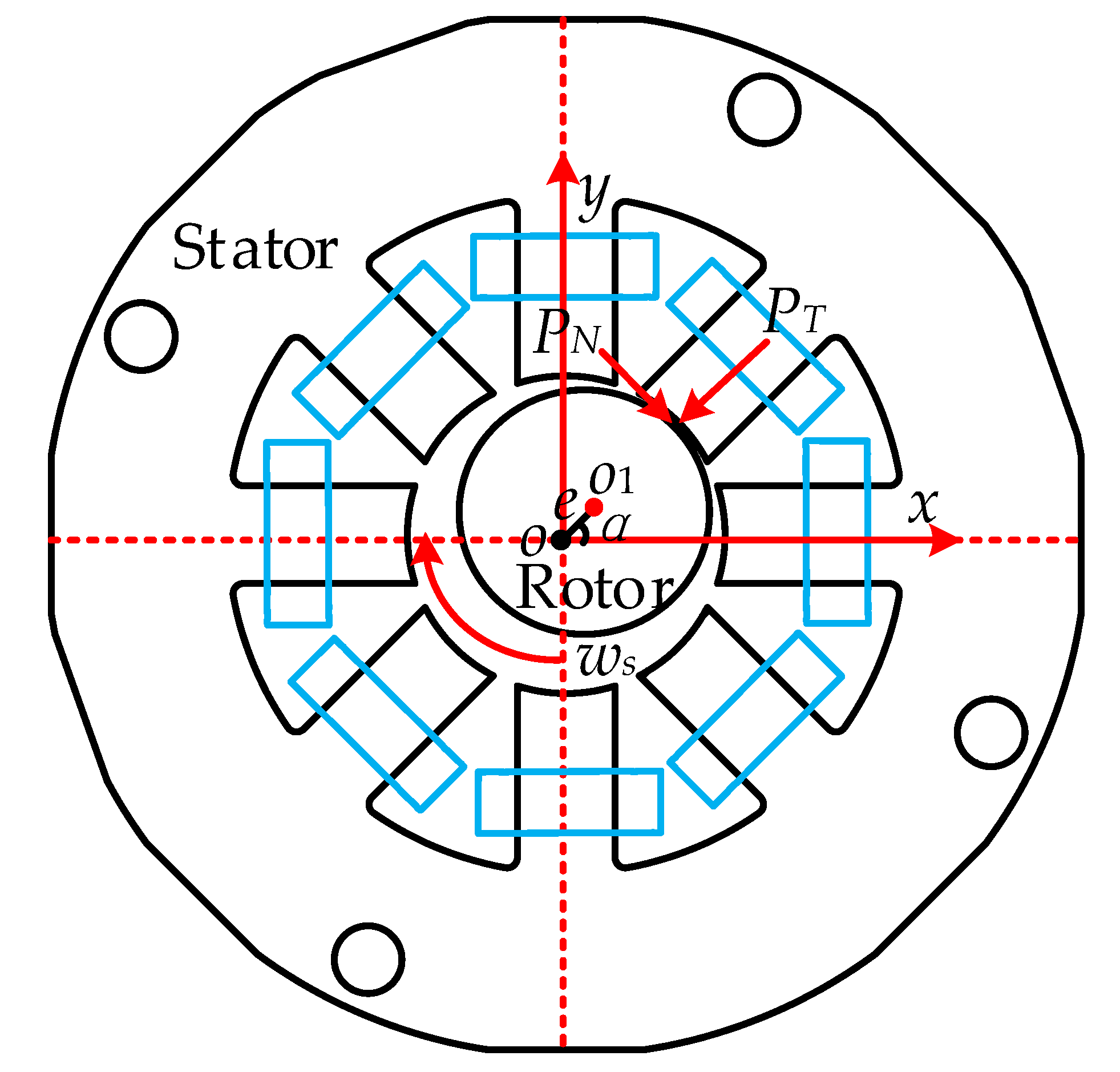
2.1. Rubbing Force Model
- (1)
- There is local Elastic Collision and Coulomb Friction between magnetic pole and magnetic sleeve;
- (2)
- The small gap between two magnetic poles can be ignored;
- (3)
- The frictional thermal effect between magnetic pole and magnetic sleeve can be ignored;
- (4)
- The winding leakage, marginal magnetic flux, vortex loss, magnetic material saturation, coupling effect between magnetic poles can be ignored;
- (5)
- The inertial force and viscous pressure characteristics of the liquid are ignored.
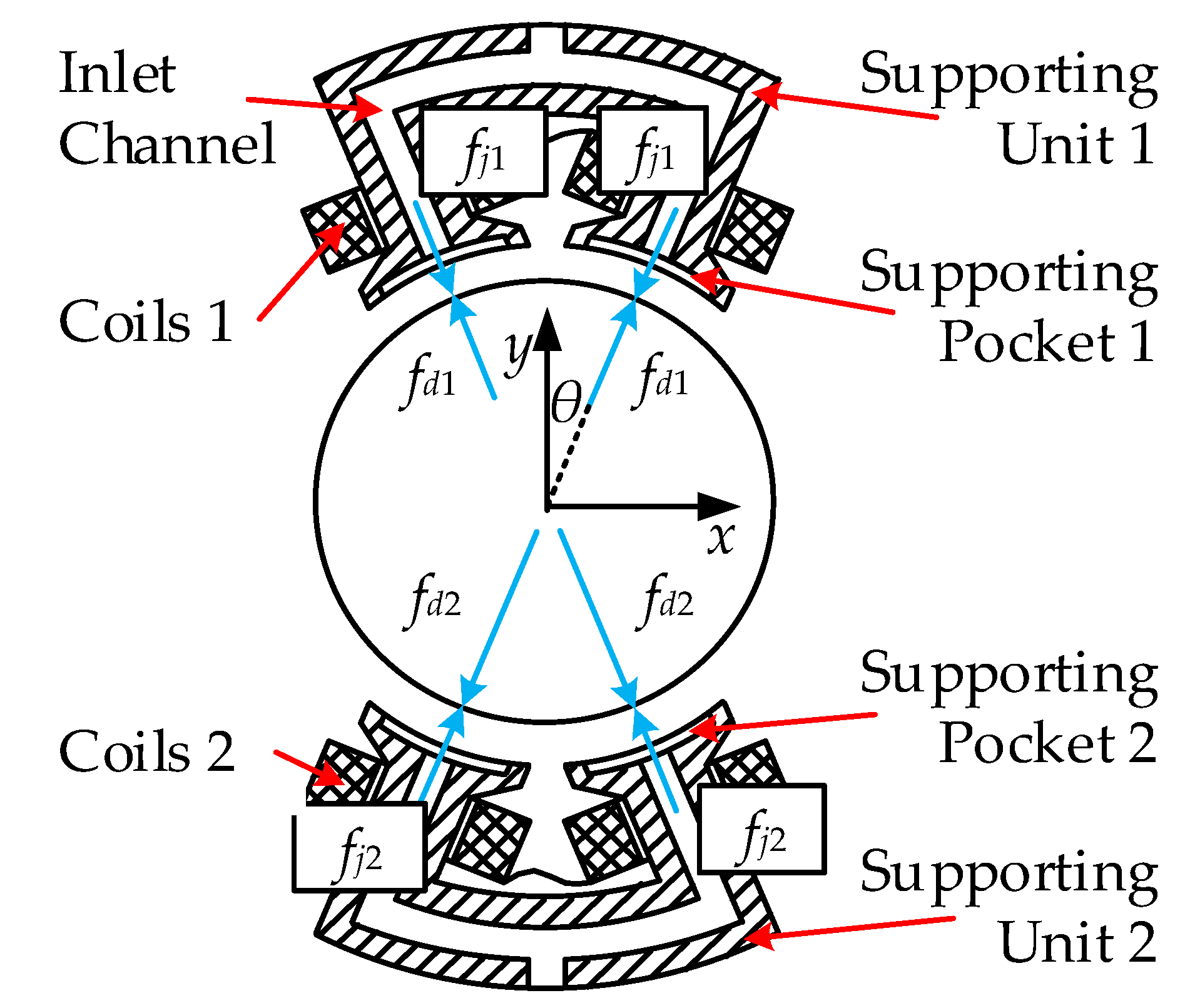
2.2. Dynamic Equation of 2-DOF Supporting System
3. Simulation of Clearance-Rubbing of 2-DOF Supporting System
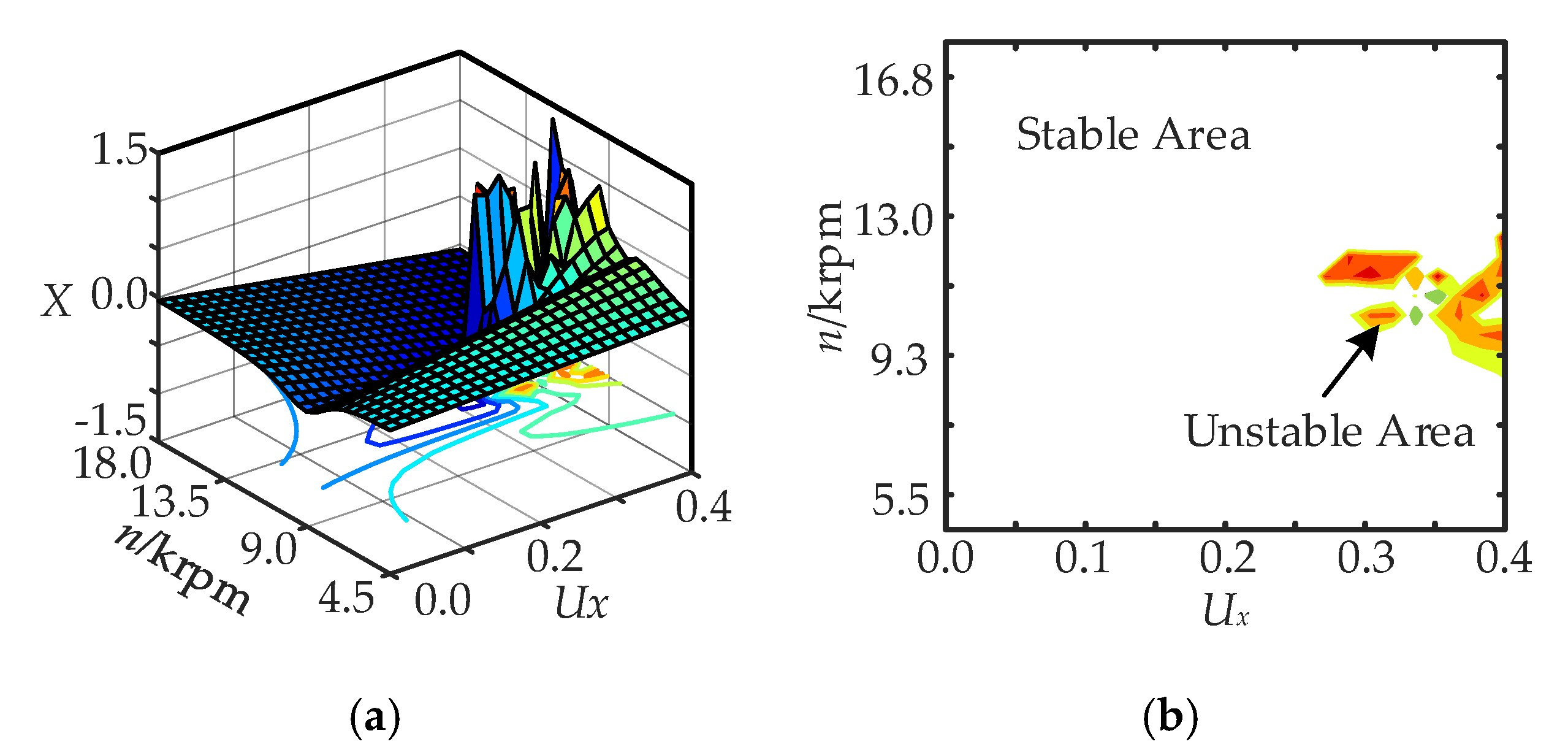
3.1. Influence of Ux on Rotor Displacement
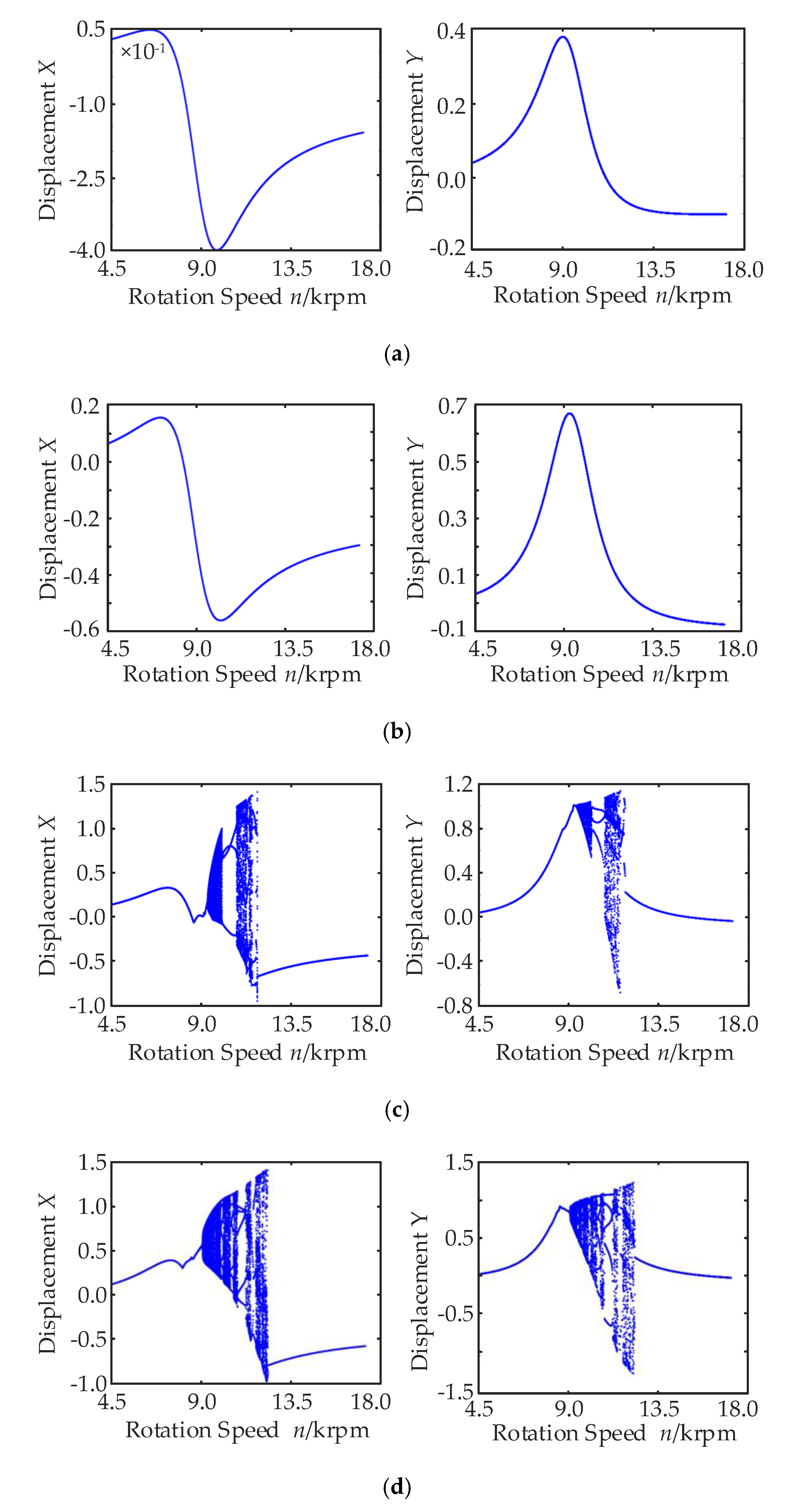
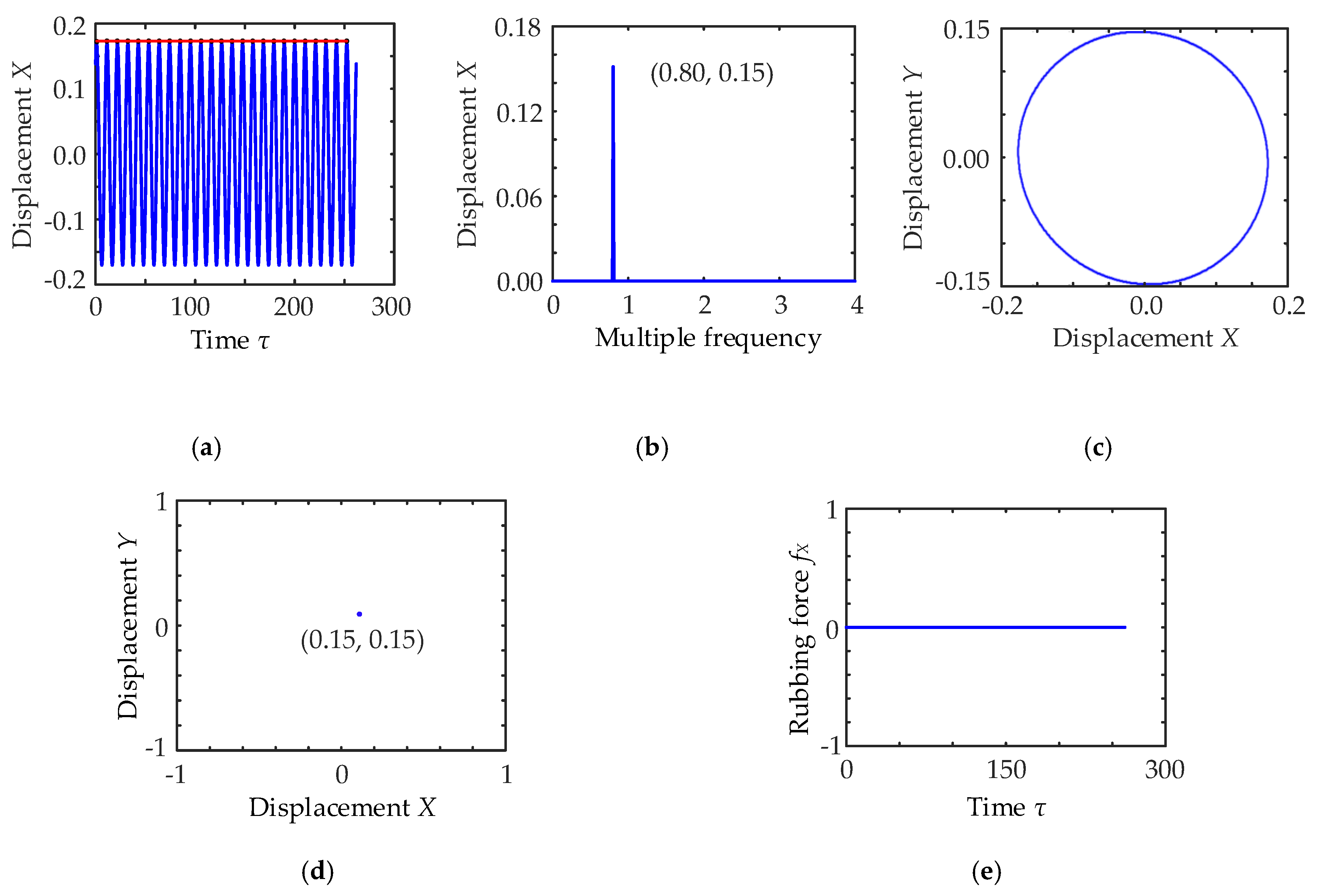
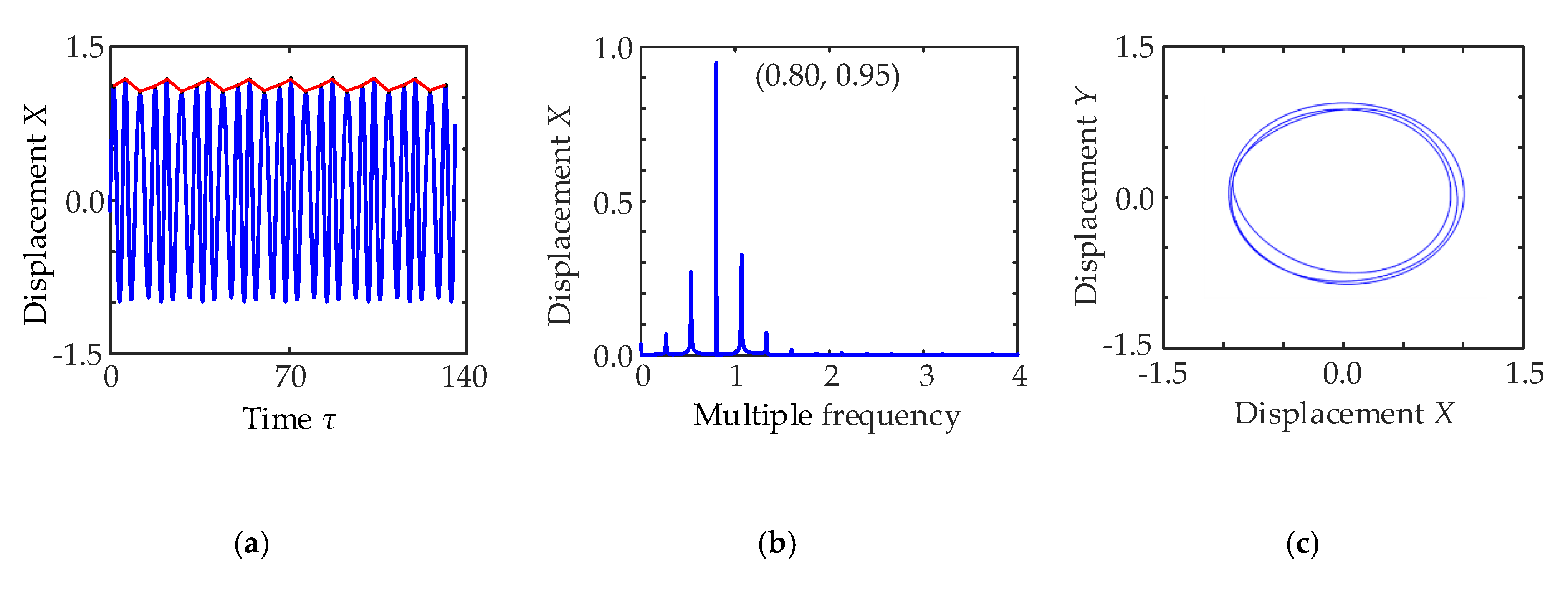
3.2. Influence of Rotation Speed on Rotor Displacement
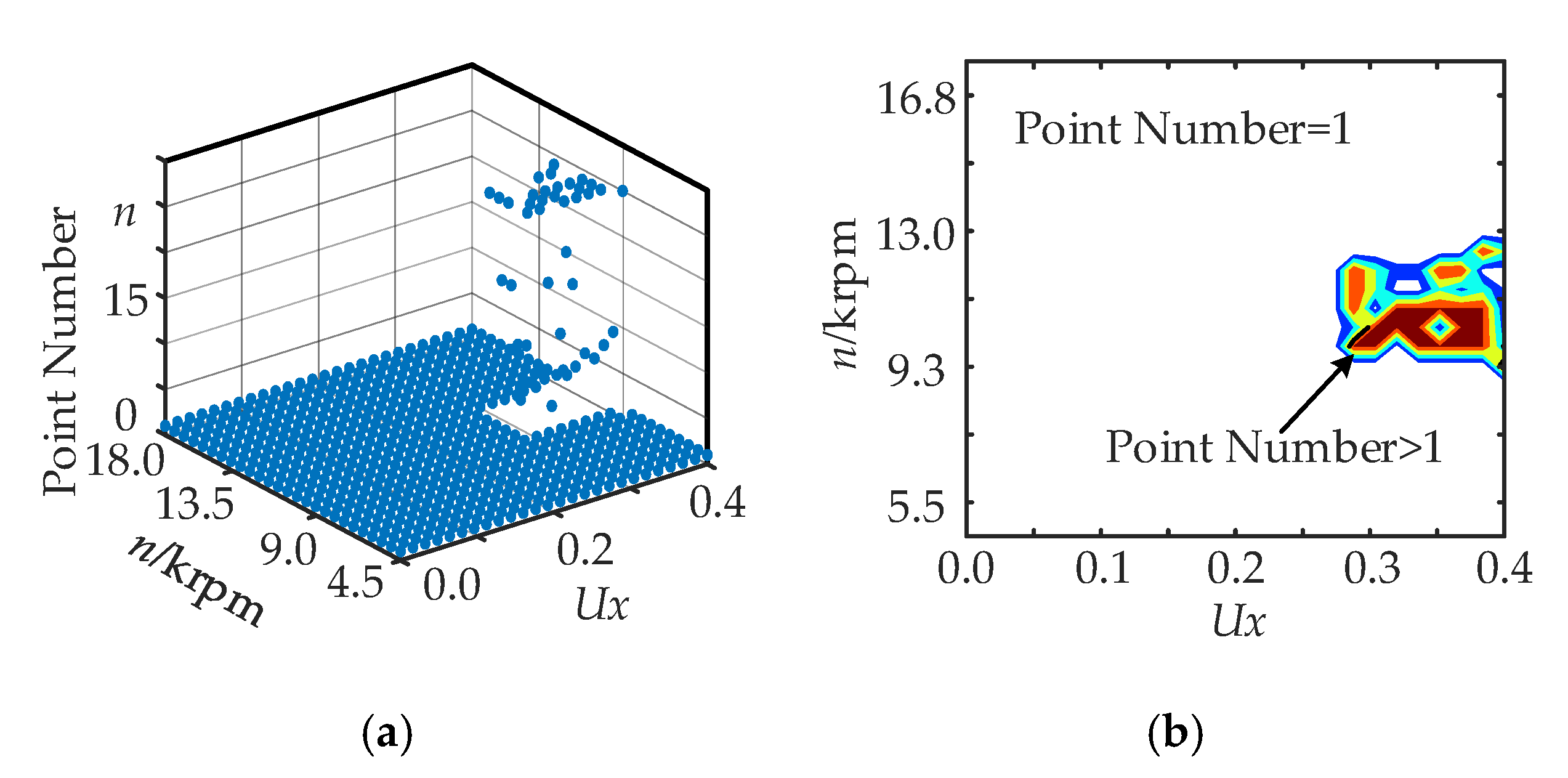
3.3. Influence of Rotor Displacement on Eccentricity Ratio and Rotation Speed
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Wu, O.Y.; Qian, J.; Fan, Z.; Yuan, X.Y.; Meng, Q.F. Lubrication model and dynamic characteristics of distributed liquid film for hydrodynamic bearing. Adv. Mat. Res. 2013, 744, 194–198. [Google Scholar] [CrossRef]
- Burak, G.; Liang, L.D.; Arash, A.; Huatian, H.; Petre, N.; Naomi, J.H. Monolithic metal dimer-on-film structure: New plasmonic properties introduced by the underlying metal. Nano Lett. 2020, 20, 2087–2093. [Google Scholar]
- Mo, N.; Liu, X.N.; Zhou, Y.; Yang, G.J.; Shi, Z.G. Vibration transmission characteristics of active magnetic bearings. J. Vib. Shock 2015, 34, 79–83. [Google Scholar]
- Burak, G.; Arash, A.; Mustafa, K.; Raju, S.; Nezih, P. VO2-based reconfigurable antenna platform with addressable microheater matrix. Adv. Electron. Mater. 2017, 3, 1700170. [Google Scholar]
- Zhang, W.Y.; Cheng, L.; Zhu, H.Q. Suspension force error source analysis and multidimensional dynamic model for a centripetal force type-magnetic bearing. IEEE Trans. Ind. Electron. 2020, 67, 7617–7628. [Google Scholar] [CrossRef]
- Wang, N.; Jiang, D.; Behdinan, K. Vibration response analysis of rubbing faults on a dual-rotor bearing system. Arch. Appl. Mech. 2017, 87, 1891–1907. [Google Scholar] [CrossRef]
- Zhang, W.Y.; Yang, H.K.; Cheng, L.; Zhu, H.Q. Modeling based on exact segmentation of magnetic field for a centripetal force type-magnetic bearing. IEEE Trans. Ind. Electron. 2020, 67, 7691–7701. [Google Scholar] [CrossRef]
- Ishida, Y.; Inagaki, M.; Ejima, R.; Hayashi, A. Nonlinear resonances and self-excited oscillations of a rotor caused by radial clearance and collision. Nonlinear Dyn. 2009, 57, 593–605. [Google Scholar] [CrossRef]
- Xiong, W.L.; Hu, C.; Lv, L.; Zheng, L.G. Research on the influence of controllable restrictor parameters on the characteristics of hydrostatic journal bearing. Chin. J. Mech. Eng. 2018, 54, 63–71. [Google Scholar] [CrossRef]
- Hoshi, H.; Tadahiko, S.; Setsuo, T. Third generation blood pumps with mechanical non-contact magnetic bearing. Artif. Organs 2006, 30, 324–338. [Google Scholar] [CrossRef]
- Zhang, W.; Zu, J.W.; Wang, F.X. Global bifurcations and chaos for a rotor-active magnetic bearing system with time-varying stiffness. Chaos Soliton Fract. 2008, 35, 586–608. [Google Scholar] [CrossRef]
- Wang, H.; Liu, J. Stability and bifurcation analysis in a magnetic bearing system with time delays. Chaos Soliton Fract. 2005, 26, 813–825. [Google Scholar] [CrossRef]
- Zhao, Y.; Liu, Q.; Ma, L.; Wang, K. Novel lorentz force-type magnetic bearing with flux congregating rings for magnetically suspended gyrowheel. IEEE Trans. Magn. 2019, 55, 1–8. [Google Scholar] [CrossRef]
- Braut, S.; Zigulic, R.; Skoblar, A.; Stimac-Roncevic, G. Partial rub detection based on instantaneous angular speed measurement and variational mode decomposition. J. Vib. Eng. Technol. 2020, 8, 351–364. [Google Scholar] [CrossRef]
- Bulgarevich, S.B.; Boiko, M.V.; Lebedinskii, K.S. Adsorption separation of components of liquid lubricant on rubbing surfaces under sliding friction. J. Frict. Wear. 2015, 36, 534–541. [Google Scholar] [CrossRef]
- Kostyuk, A.G.; Shatokhin, V.F.; Volokhovskaya, O.A. Specific features relating to the motion of a rotor with rubbing against the stator. Therm. Eng. 2013, 60, 628–634. [Google Scholar] [CrossRef]
- Zhang, G.; Yin, Q.Z.; Jiang, D.D.; Liang, S.P. Research on nonlinear dynamics of five-DOF active magnetic bearings-rotor system. Chin. J. Mech. Eng. 2010, 46, 15–21. [Google Scholar] [CrossRef]
- Zhu, C.S. Nonlinear dynamics of rotor drop on rolling element backup bearings after active magnetic bearings failure. Chin. J. Mech. Eng. 2006, 42, 200–206. [Google Scholar] [CrossRef]
- Cansiz, A.; Yildizer, İ.; McGuiness, D.T. Rotor optimization in a superconducting magnetic bearing by using frozen image model and Amperian current approximation. Cryogenics 2019, 98, 60–66. [Google Scholar] [CrossRef]
- Guo, C.; Li, C.G.; Wang, D.Y. Nonlinear dynamic analysis and experiment verification of rubbing faults of rotor-ball bearing-support-stator coupling system for aero-engine. J. Aerosp. Power. 2008, 23, 1304–1311. [Google Scholar]
- Dai, X.; Zhang, X.; Jin, X. The partial and full rubbing of a flywheel rotor–bearing–stop system. Int. J. Mech. Sci. 2001, 43, 505–519. [Google Scholar] [CrossRef]
- Peng, G.; Li, C.; Cao, C.; Hong, J. Dynamic response and safety design of rotor system with impact excitation. J. Propul. Technol. 2018, 39, 1111–1121. [Google Scholar]
- Kankar, P.K.; Sharma, S.C.; Harsha, S.P. Fault diagnosis of ball bearings using machine learning methods. Expert Syst. Appl. 2011, 38, 1876–1886. [Google Scholar] [CrossRef]
- Zhang, G.Y.; Huang, H.Z.; Zhou, M.; Chen, Y.; Wei, J.C. A nonlinear dynamic model and its stability for the generator rotor with coupling the unbalanced electromagnetic force and the oil film force. Proc. Chin. Soc. Electr. Eng. 2014, 34, 2406–2413. [Google Scholar]
- Yu, H.; Chen, Y.S.; Cao, Q.J. Nonlinear dynamic behavior analysis for a cracked multi-DOF rotor system. J. Vib. Shock 2014, 33, 92–98. [Google Scholar]
- Shatokhin, V.F. Patterns of the rotor-over-stator rolling under change in the damping components. Therm. Eng. 2018, 65, 143–150. [Google Scholar] [CrossRef]
- Jin, X.; Zhao, M.; Chow, T.W.; Pecht, M. Motor bearing fault diagnosis using trace ratio linear discriminant analysis. IEEE Trans. Ind. Electron. 2013, 61, 2441–2451. [Google Scholar] [CrossRef]
- Hua, C.; Ta, N.; Rao, Z. Dynamic characteristics analysis of a rub-impact rubber bearing-shaft system. J. Vib. Control 2015, 21, 388–401. [Google Scholar] [CrossRef]
- Ji, X.; Chen, Y. Tribological behavior of babbitt alloy rubbing against Si3N4 and steel under dry friction condition. J. Mater. Eng. Perform. 2016, 25, 750–755. [Google Scholar] [CrossRef]
- Xie, Z.Y.; Mou, W.X.; Zhou, H.K.; Wang, X. Variable parameter control of active magnetic bearing rotor system based on rotation speed. J. Vib. Eng. 2012, 25, 739–744. [Google Scholar]
- Liu, Y.; Li, Y.; Shi, T.; Ma, H.; Wen, B.C. Study on misalignment-rubbing coupling fault of rotor system supported by oil film force. J. Mech. Eng. 2016, 52, 79–86. [Google Scholar] [CrossRef]
- Shang, Y.J.; Lin, J.Z.; Liu, X.j.; Xin, X.W. Impact of hydrostatic bearings on the dynamic performance of electric spindle rotor device. Mech. Sci. Technol. Aeronaut. Eng. 2015, 34, 688–693. [Google Scholar]
- Gunerkar, R.S.; Jalan, A.K.; Belgamwar, S.U. Fault diagnosis of rolling element bearing based on artificial neural network. J. Mech. Sci. Technol. 2019, 33, 505–511. [Google Scholar] [CrossRef]








| Parameters | Value | Parameters | Value |
|---|---|---|---|
| Bias current i0 | 1 A | Film thickness h0 | 50 μm |
| System pressure ps | 0.1 Mpa | Angle θ | 22.5° |
| Throttle ratio β | 2 Dimensionless | Flow coefficient | 0.7 Dimensionless |
| Lubricants viscosity μ | 1.3 × 10−3 pa·s | Area of magnetic pole S | 1080 mm2 |
| Mass of rotor m | 4 kg | Number of coil N | 50 Dimensionless |
| Air permeability μ0 | 4π × 10−7 H/m | Hydraulic resistor Rh0 | 1.5 × 10−10 N·s/m |
| Supporting area Ae | 416 mm2 | Friction coefficient f | 0.2 Dimensionless |
| Extrusion area Ab | 56 mm2 | Stiffness of rotor kc | 6 × 107 N/m |
| Bearing bore diameter | 61 mm | Bearing length | 71 mm |
| Eccentricity Ratio Ux | Stable Scope 1 | Unstable Scope 2 | Stable Scope 3 |
|---|---|---|---|
| 0.30 | (4.5, 9.5) krpm | (4.5, 9) krpm | (12.5, 18) krpm |
| 0.40 | (4.5, 9) krpm | (9, 13) krpm | (13, 18) krpm |
| Rotation Speed n | Motion Rule | Rotation Speed Test n |
|---|---|---|
| (4.5, 9.5) krpm | Single Period | 5.5 krpm |
| (9.5, 10.5) krpm | Quasi Period | 10 krpm |
| (10.5, 11) krpm | Double Period | 10.7 krpm |
| (11, 12.5) krpm | Chaos | 11.5 krpm |
| (12.5, 18) krpm | Single Period | 13.5 krpm |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, J.; Yan, W.; Wang, Z.; Gao, D.; Du, G. Study on Clearance-Rubbing Dynamic Behavior of 2-DOF Supporting System of Magnetic-Liquid Double Suspension Bearing. Processes 2020, 8, 973. https://doi.org/10.3390/pr8080973
Zhao J, Yan W, Wang Z, Gao D, Du G. Study on Clearance-Rubbing Dynamic Behavior of 2-DOF Supporting System of Magnetic-Liquid Double Suspension Bearing. Processes. 2020; 8(8):973. https://doi.org/10.3390/pr8080973
Chicago/Turabian StyleZhao, Jianhua, Weidong Yan, Ziqi Wang, Dianrong Gao, and Guojun Du. 2020. "Study on Clearance-Rubbing Dynamic Behavior of 2-DOF Supporting System of Magnetic-Liquid Double Suspension Bearing" Processes 8, no. 8: 973. https://doi.org/10.3390/pr8080973
APA StyleZhao, J., Yan, W., Wang, Z., Gao, D., & Du, G. (2020). Study on Clearance-Rubbing Dynamic Behavior of 2-DOF Supporting System of Magnetic-Liquid Double Suspension Bearing. Processes, 8(8), 973. https://doi.org/10.3390/pr8080973




