Robust Multi-Stage Nonlinear Model Predictive Control Using Sigma Points
Abstract
1. Introduction
2. Preliminaries
3. Robust Multi-Stage NMPC
3.1. Standard Multi-Stage NMPC
3.1.1. Multi-Stage NMPC (MS NMPC)
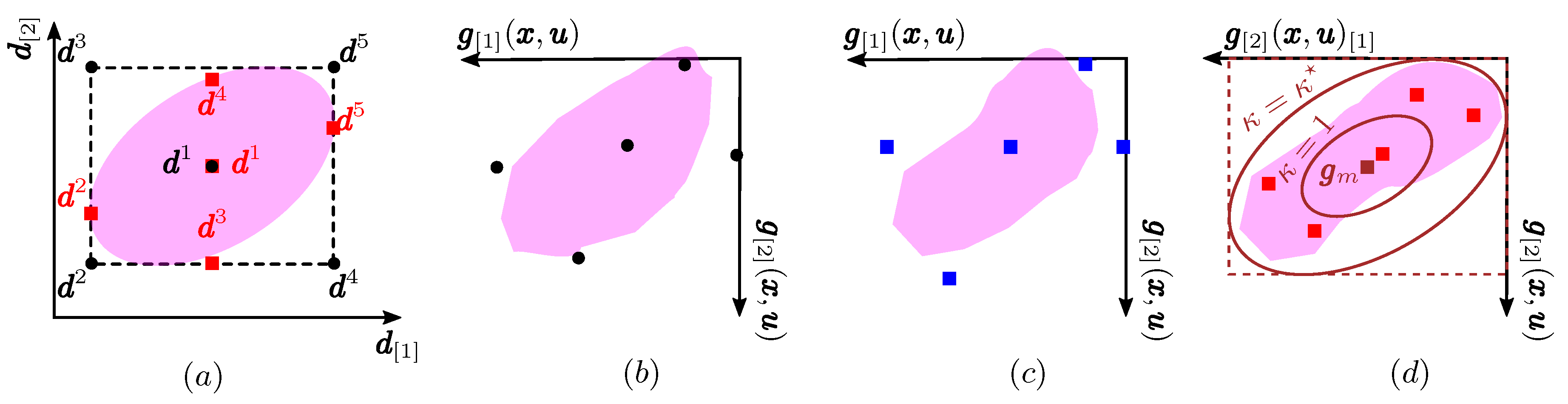
3.1.2. Multi-Stage NMPC Based on the Vertex Over-Approximation (MS-VA NMPC)
3.2. Multi-Stage NMPC Using Sigma Points
3.2.1. Multi-Stage NMPC Based on the Box Over-Approximation of the Reachable Set of States (MS-SB NMPC)
Tuning of the Scaling Factor
3.2.2. Multi-Stage NMPC Based on the Box Over-Approximation of the Reachable Set of the Constraint Function (MS-CB NMPC)
Tuning of the Scaling Factor
4. Adaptive Robust Multi-Stage NMPC
4.1. Adaptive Standard Multi-Stage NMPC
4.2. Adaptive Multi-Stage NMPC Using Sigma Points
5. Case Studies
5.1. Case Study 1: Benchmark Semi-Batch Reactor
5.1.1. Formulation of the Optimal Control Problem
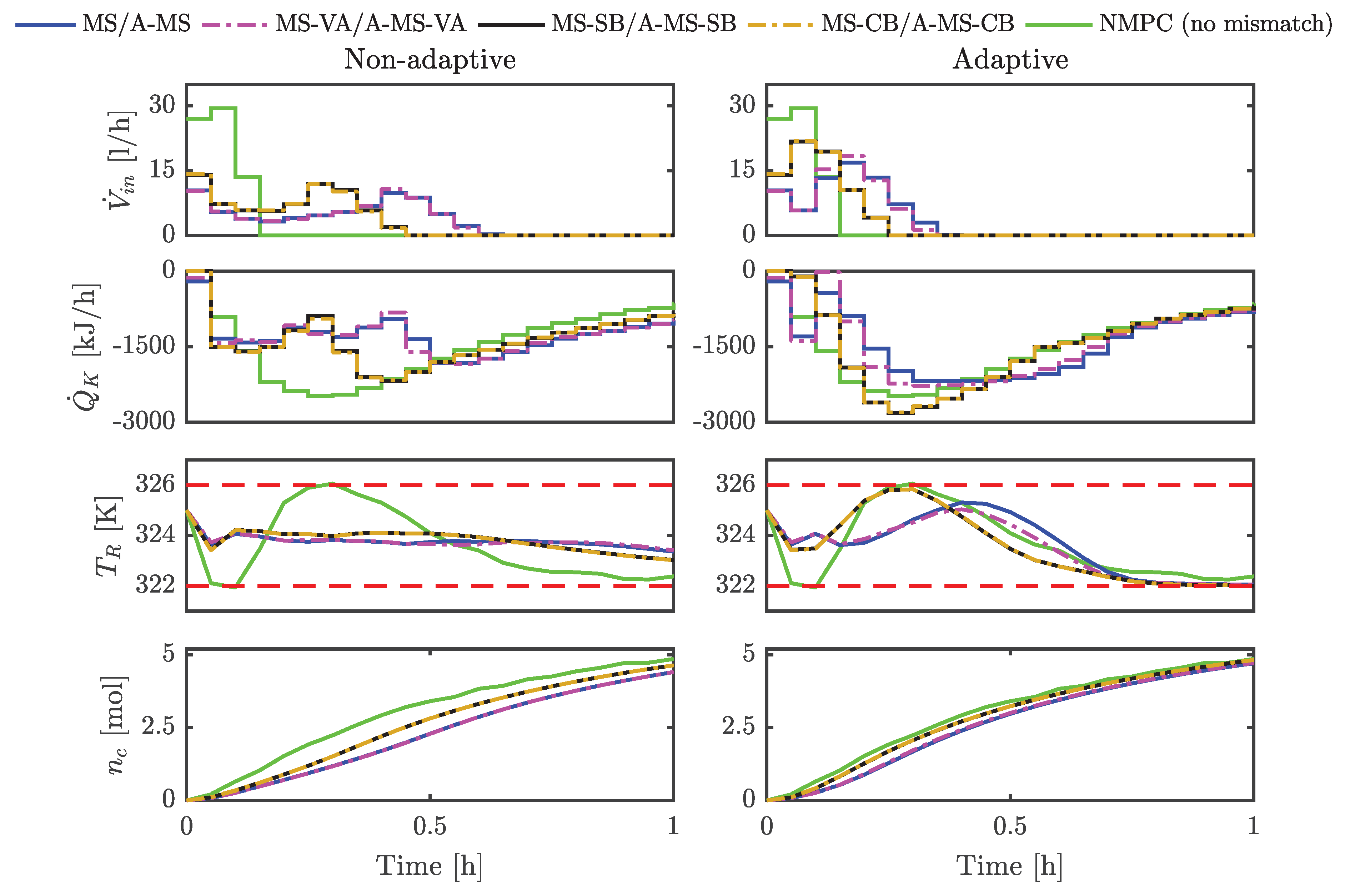
5.1.2. Results Obtained Using the Non-Adaptive and the Adaptive Controllers for One Set of Parameters
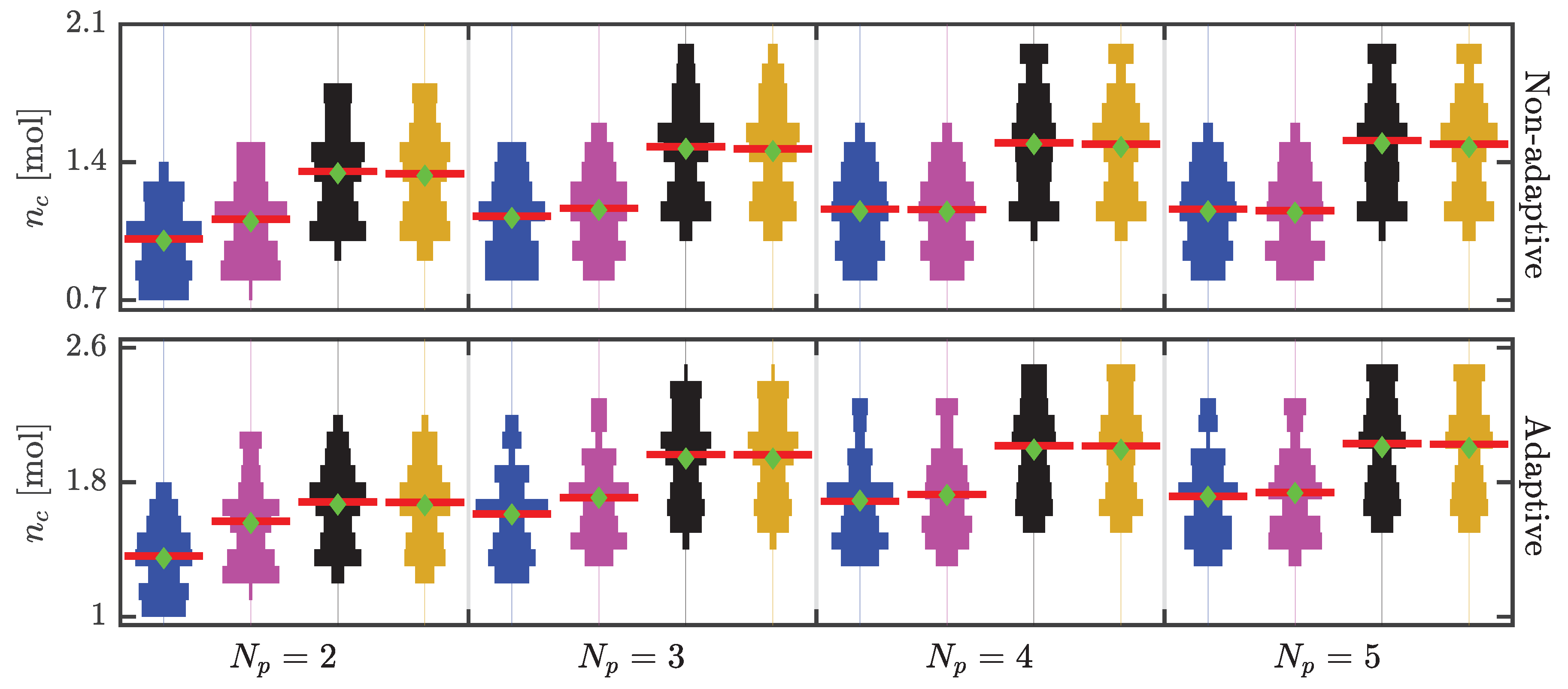
5.1.3. Controller Performance Analysis for Different Values of the Tuning Parameters
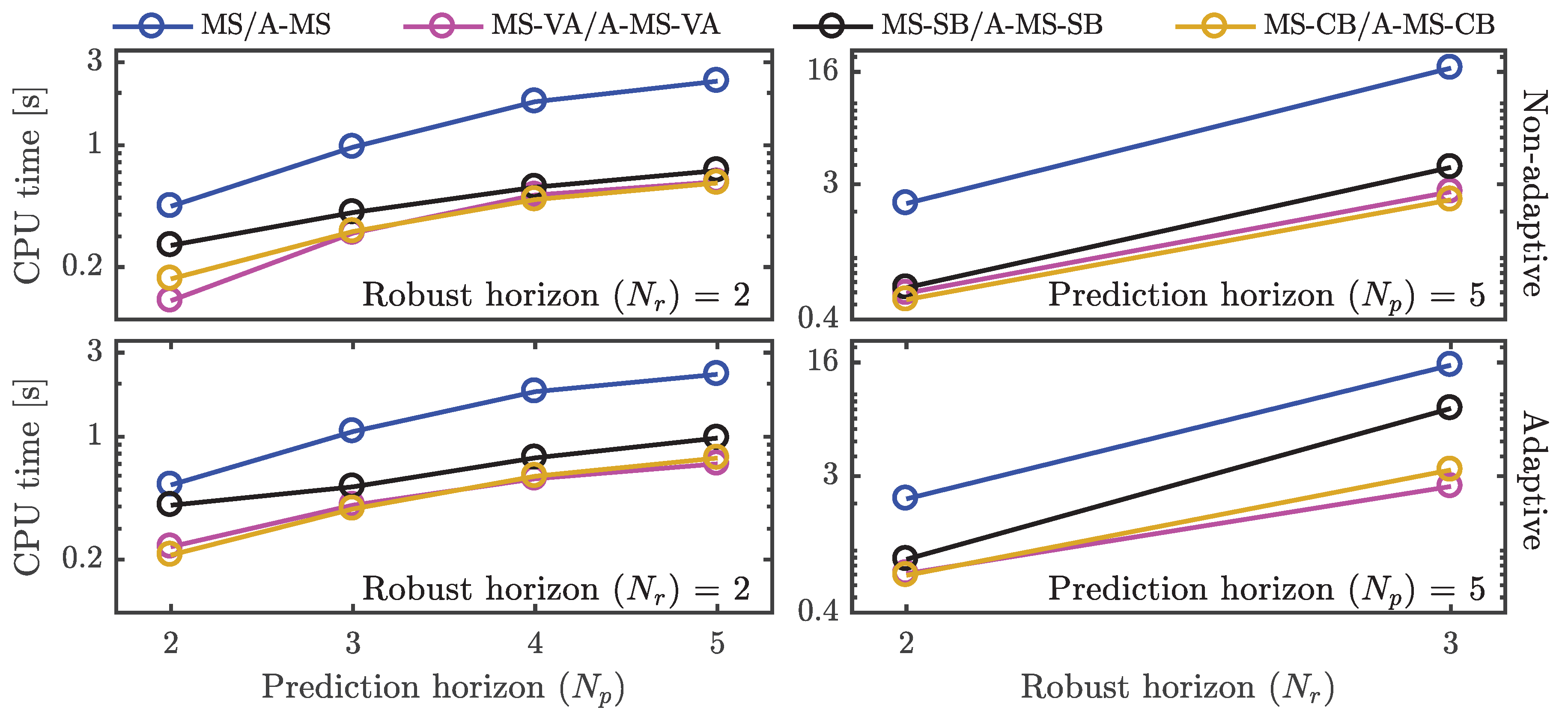
Effect of the Length of the Prediction Horizon
Effect of the Length of the Robust Horizon
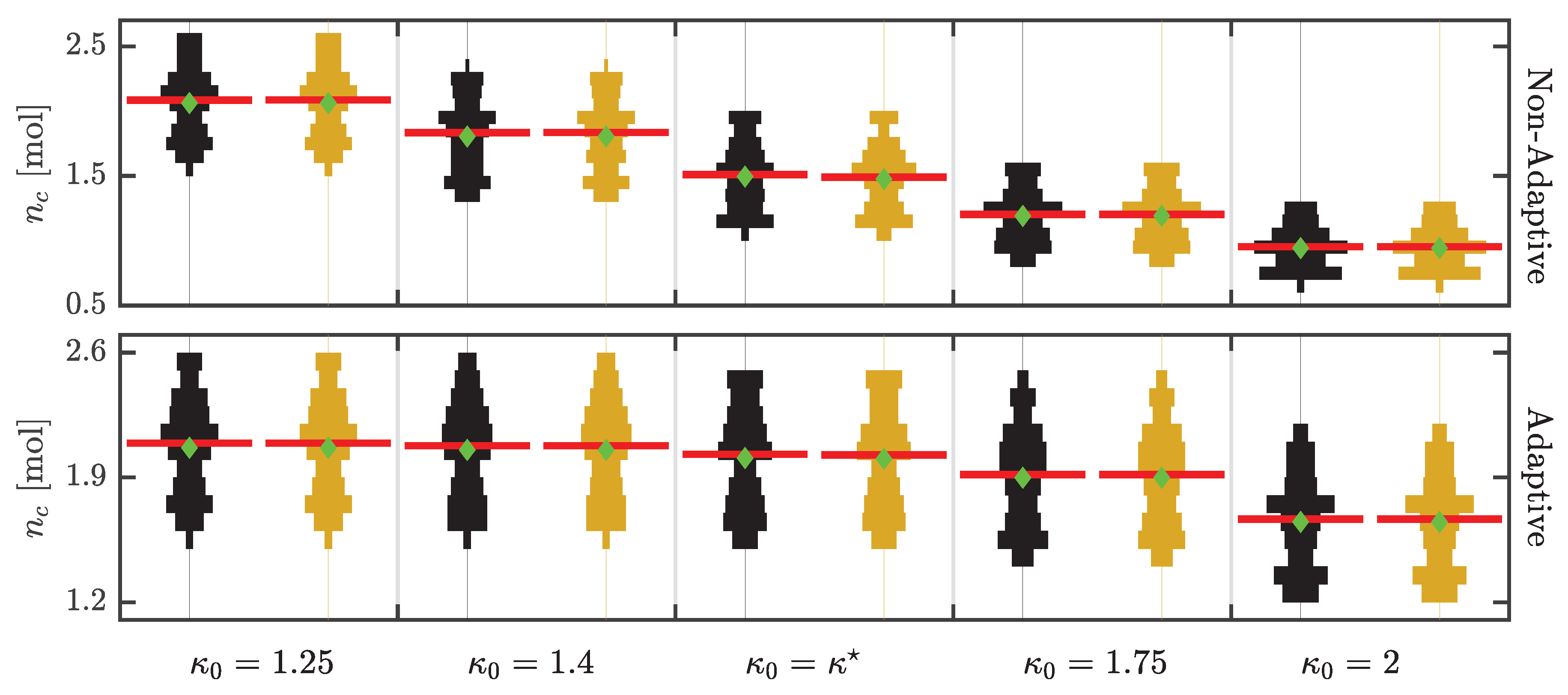
Effect of the Scaling Factor
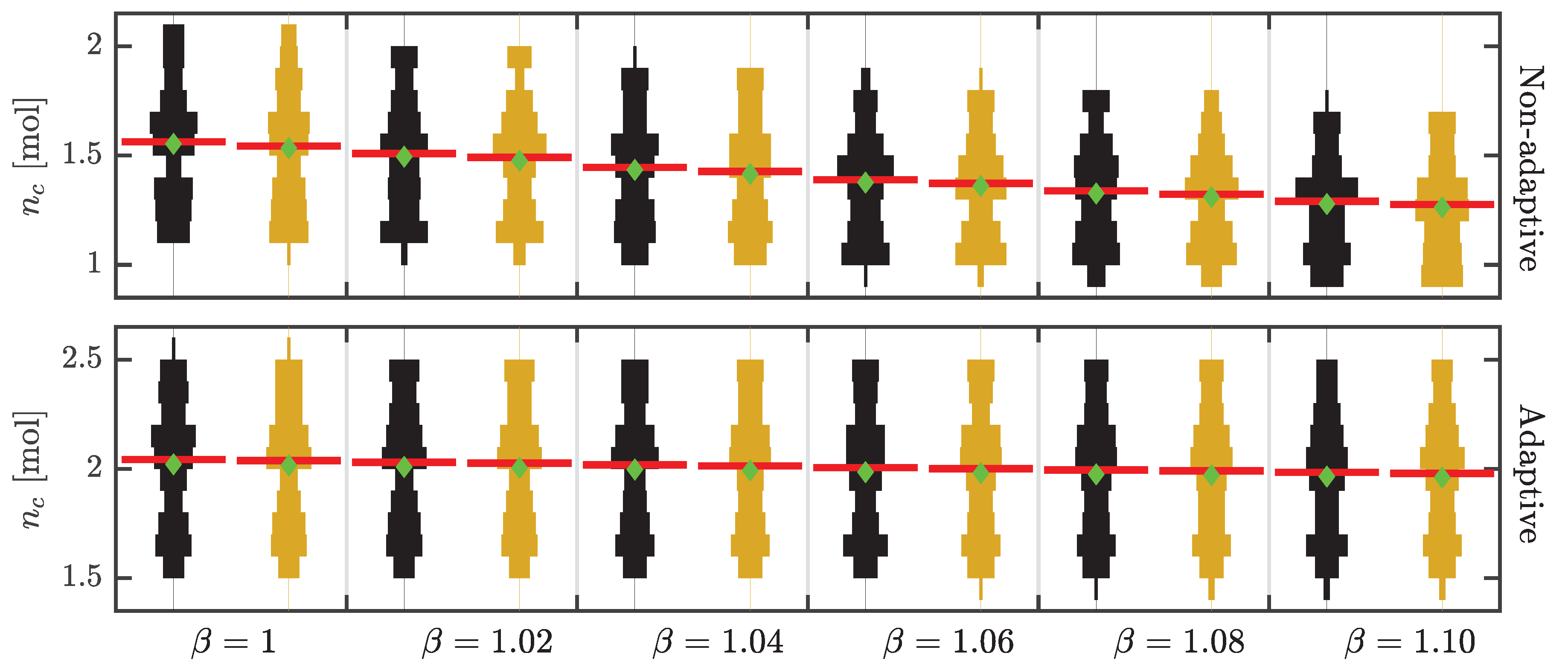
Effect of Change in the Scaling Factor
Effect of change in scaling increase factor
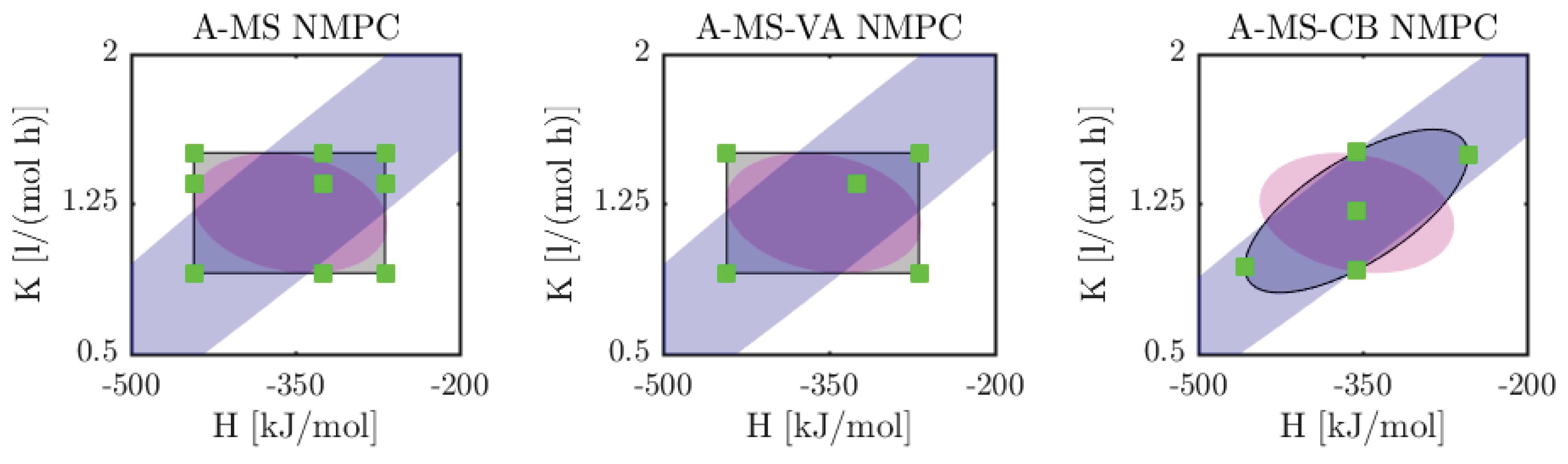
5.2. Case Study 2: Industrial Semi-Batch Polymerization Reactor
5.2.1. Formulation of the Optimal Control Problem
5.2.2. Results
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| A-MS | Adaptive multi-stage NMPC |
| A-MS-VA | Adaptive multi-stage NMPC based on the vertex over-approximation |
| A-MS-SB | Adaptive multi-stage NMPC based on the box over-approximation of the reachable set of states |
| A-MS-CB | Adaptive multi-stage NMPC based on the box over-approximation of the reachable set of the |
| constraint function | |
| EHE | External Heat Exchanger |
| FC | Flow control |
| MPC | Model predictive control |
| NMPC | Nonlinear model predictive control |
| MS | Multi-stage NMPC |
| MS-VA | Multi-stage NMPC based on the vertex over-approximation |
| MS-SB | Multi-stage NMPC based on the box over-approximation of the reachable set of states |
| MS-CB | Multi-stage NMPC based on the box over-approximation of the reachable set of the |
| constraint function | |
| TC | Temperature control |
References
- Qin, S.; Badgwell, T.A. A survey of industrial model predictive control technology. Control Eng. Pract. 2003, 11, 733–764. [Google Scholar] [CrossRef]
- García, C.E.; Prett, D.M.; Morari, M. Model predictive control: Theory and practice—A survey. Automatica 1989, 25, 335–348. [Google Scholar] [CrossRef]
- Grüne, L.; Pannek, J. Nonlinear Model Predictive Control: Theory and Algorithms; Springer Publishing Company, Incorporated: London, UK, 2013. [Google Scholar]
- Rawlings, J.B.; Mayne, D.Q.; Diehl, M.M. Model Predictive Control: Theory, Computation, and Design, 2nd ed.; Nob Hill Publishing, LLC: Madison, WI, USA, 2017. [Google Scholar]
- Mayne, D.Q. Model predictive control: Recent developments and future promise. Automatica 2014, 50, 2967–2986. [Google Scholar] [CrossRef]
- Campo, P.J.; Morari, M. Robust Model Predictive Control. In Proceedings of the 1987 American Control Conference, Minneapolis, MN, USA, 10–12 June 1987; pp. 1021–1026. [Google Scholar]
- Scokaert, P.O.M.; Mayne, D.Q. Min-max feedback model predictive control for constrained linear systems. IEEE Trans. Autom. Control 1998, 43, 1136–1142. [Google Scholar] [CrossRef]
- Mayne, D.; Seron, M.; Rakovic, S. Robust model predictive control of constrained linear systems with bounded disturbances. Automatica 2005, 41, 219–224. [Google Scholar] [CrossRef]
- Bemporad, A.; Morari, M. Robust Model Predictive Control: A Survey; Springer: London, UK, 2007; Volume 245, pp. 207–226. [Google Scholar] [CrossRef]
- Lucia, S.; Finkler, T.; Basak, D.; Engell, S. A new Robust NMPC Scheme and its Application to a Semi-batch Reactor Example. IFAC Proc. Vol. 2012, 45, 69–74. [Google Scholar] [CrossRef]
- Witsenhausen, H. A minimax control problem for sampled linear systems. IEEE Trans. Autom. Control 1968, 13, 5–21. [Google Scholar] [CrossRef]
- Lee, J.H.; Yu, Z.H. Worst-case formulations of model predictive control for systems with bounded parameters. Automatica 1997, 33, 763–781. [Google Scholar] [CrossRef]
- Mayne, D. Control of Constrained Dynamic Systems. Eur. J. Control 2001, 7, 87–99. [Google Scholar] [CrossRef]
- Mayne, D.; Kerrigan, E. Tube-based Robust Nonlinear Model Predictive Control. In Proceedings of the 7th IFAC Symposium on Nonlinear Control Systems, Pretoria, South Africa, 22–24 August 2007; pp. 110–115. [Google Scholar]
- Yu, S.; Maier, C.; Chen, H.; Allgöwer, F. Tube MPC scheme based on robust control invariant set with application to Lipschitz nonlinear systems. Syst. Control Lett. 2013, 62, 194–200. [Google Scholar] [CrossRef]
- Rawlings, J.B.; Amrit, R. Optimizing Process Economic Performance Using Model Predictive Control. In Nonlinear Model Predictive Control; Springer: Berlin/Heidelberg, Germany, 2009; pp. 119–138. [Google Scholar] [CrossRef]
- Mayne, D.Q.; Kerrigan, E.C.; van Wyk, E.J.; Falugi, P. Tube-based robust nonlinear model predictive control. Int. J. Robust Nonlinear Control 2011, 21, 1341–1353. [Google Scholar] [CrossRef]
- Rakovivć, S.V.; Kouvaritakis, B.; Cannon, M.; Panos, C.; Findeisen, R. Fully Parameterized Tube MPC. IFAC Proc. Vol. 2011, 44, 197–202. [Google Scholar] [CrossRef]
- Kouvaritakis, B.; Cannon, M. Model Predictive Control: Classical, Robust and Stochastic; Springer International Publishing: Cham, Switzerland, 2016. [Google Scholar] [CrossRef]
- Villanueva, M.E.; Quirynen, R.; Diehl, M.; Chachuat, B.; Houska, B. Robust MPC via min–max differential inequalities. Automatica 2017, 77, 311–321. [Google Scholar] [CrossRef]
- Lucia, S.; Finkler, T.; Engell, S. Multi-stage nonlinear model predictive control applied to a semi-batch polymerization reactor under uncertainty. J. Process Control 2013, 23, 1306–1319. [Google Scholar] [CrossRef]
- Thangavel, S.; Lucia, S.; Paulen, R.; Engell, S. Dual robust nonlinear model predictive control: A multi-stage approach. J. Process Control 2018, 72, 39–51. [Google Scholar] [CrossRef]
- Bargiela, A. Interval and Ellipsoidal Uncertainty Models. In Granular Computing: An Emerging Paradigm; Physica-Verlag HD: Heidelberg, Germany, 2001; pp. 23–57. [Google Scholar] [CrossRef]
- Franceschini, G.; Macchietto, S. Model-based design of experiments for parameter precision: State of the art. Chem. Eng. Sci. 2008, 63, 4846–4872. [Google Scholar] [CrossRef]
- Wan, E.A.; Van Der Merwe, R. The unscented Kalman filter for nonlinear estimation. In Proceedings of the IEEE 2000 Adaptive Systems for Signal Processing, Communications, and Control Symposium, Lake Louise, AB, Canada, 4 October 2000; pp. 153–158. [Google Scholar] [CrossRef]
- Julier, S.J.; Uhlmann, J.K. New extension of the Kalman filter to nonlinear systems. In Signal Processing, Sensor Fusion, and Target Recognition VI; Kadar, I., Ed.; International Society for Optics and Photonics, SPIE: Bellingham, WA, USA, 1997; Volume 3068, pp. 182–193. [Google Scholar] [CrossRef]
- Kandepu, R.; Foss, B.; Imsland, L. Applying the unscented Kalman filter for nonlinear state estimation. J. Process Control 2008, 18, 753–768. [Google Scholar] [CrossRef]
- Gustafsson, F.; Hendeby, G. Some Relations Between Extended and Unscented Kalman Filters. IEEE Trans. Signal Process. 2012, 60, 545–555. [Google Scholar] [CrossRef]
- Yan, J.; Bitmead, R.R. Incorporating state estimation into model predictive control and its application to network traffic control. Automatica 2005, 41, 595–604. [Google Scholar] [CrossRef]
- Heine, T.; Kawohl, M.; King, R. Robust model predictive control using the unscented transformation. In Proceedings of the 2006 IEEE Conference on Computer Aided Control System Design, Munich, Germany, 4–6 October 2006; pp. 224–230. [Google Scholar] [CrossRef]
- Recker, S.; Kühl, P.; Diehl, M.; Bock, H.G. Sigmapoint Approach for Robust Optimization of Nonlinear Dynamic Systems. In Proceedings of the 2nd International Conference on Simulation and Modeling Methodologies, Technologies and Applications—Volume 1: SIMULTECH; INSTICC, SciTePress: Setúbal, Portugal, 2012; pp. 199–207. [Google Scholar] [CrossRef]
- Völz, A.; Graichen, K. Stochastic model predictive control of nonlinear continuous-time systems using the unscented transformation. In Proceedings of the 2015 European Control Conference (ECC), Linz, Austria, 15–17 July 2015; pp. 3365–3370. [Google Scholar]
- Subramanian, S.; Lucia, S.; Engell, S. Economic Multi-stage Output Feedback NMPC using the Unscented Kalman Filter. IFAC-PapersOnLine 2015, 48, 38–43. [Google Scholar] [CrossRef]
- Farrokhsiar, M.; Najjaran, H. An unscented model predictive control approach to the formation control of nonholonomic mobile robots. In Proceedings of the 2012 IEEE International Conference on Robotics and Automation, Saint Paul, MN, USA, 14–18 May 2012; pp. 1576–1582. [Google Scholar] [CrossRef]
- Prakash, J.; Patwardhan, S.C.; Shah, S.L. State estimation and nonlinear predictive control of autonomous hybrid system using derivative free state estimators. J. Process Control 2010, 20, 787–799. [Google Scholar] [CrossRef]
- Bradford, E.; Imsland, L. Economic Stochastic Model Predictive Control Using the Unscented Kalman Filter. IFAC-PapersOnLine 2018, 51, 417–422. [Google Scholar] [CrossRef]
- Thangavel, S.; Paulen, R.; Engell, S. Adaptive multi-stage NMPC using sigma point principles. In Proceedings of the IFAC Conference on Advances in Control & Optimization of Dynamical Systems (ACODS), Chennai, India, 16–19 February 2020. [Google Scholar]
- Thangavel, S.; Paulen, R.; Engell, S. Adaptive multi-stage NMPC using sigma point principles. In Proceedings of the 2020 European Control Conference (ECC), Saint-Petersburg, Russia, 12–15 May 2020. [Google Scholar]
- Lee, J.H.; Ricker, N.L. Extended Kalman Filter Based Nonlinear Model Predictive Control. Ind. Eng. Chem. Res. 1994, 33, 1530–1541. [Google Scholar] [CrossRef]
- Findeisen, R.; Imsland, L.; Allgöwer, F.; Foss, B.A. Output feedback stabilization of constrained systems with nonlinear predictive control. Int. J. Robust Nonlinear Control 2003, 13, 211–227. [Google Scholar] [CrossRef]
- Subramanian, S.; Lucia, S.; Engell, S. A Synergistic Approach to Robust Output Feedback Control: Tube-based Multi-stage NMPC. IFAC PapersOnLine 2018, 51, 500–505. [Google Scholar] [CrossRef]
- Åström, K.; Wittenmark, B. Problems of identification and control. J. Math. Anal. Appl. 1971, 34, 90–113. [Google Scholar] [CrossRef]
- Wittenmark, B. Adaptive Dual Control Methods: An Overview. IFAC Proc. Vol. 1995, 28, 67–72. [Google Scholar] [CrossRef]
- Adetola, V.; DeHaan, D.; Guay, M. Adaptive model predictive control for constrained nonlinear systems. Syst. Control Lett. 2009, 58, 320–326. [Google Scholar] [CrossRef]
- Swarnkar, P.; Jain, S.K.; Nema, R. Adaptive Control Schemes for Improving the Control System Dynamics: A Review. IETE Tech. Rev. 2014, 31, 17–33. [Google Scholar] [CrossRef]
- Uhlmann, J.K. Simultaneous Map Building and Localization for Real Time Applications; Technical Report; University of Oxford: Oxford, UK, 1994. [Google Scholar]
- Julier, S.J. The scaled unscented transformation. In Proceedings of the 2002 American Control Conference, Anchorage, AK, USA, 8–10 May 2002; Volume 6, pp. 4555–4559. [Google Scholar]
- Lucia, S.; Andersson, J.A.; Brandt, H.; Diehl, M.; Engell, S. Handling uncertainty in economic nonlinear model predictive control: A comparative case study. J. Process Control 2014, 24, 1247–1259. [Google Scholar] [CrossRef]
- De la Penad, D.M.; Bemporad, A.; Alamo, T. Stochastic Programming Applied to Model Predictive Control. In Proceedings of the 44th IEEE Conference on Decision and Control, Seville, Spain, 15 December 2005; pp. 1361–1366. [Google Scholar] [CrossRef]
- Bernardini, D.; Bemporad, A. Scenario-based model predictive control of stochastic constrained linear systems. In Proceedings of the 48th IEEE Conference on Decision and Control (CDC), Shanghai, China, 15–18 December 2009; pp. 6333–6338. [Google Scholar] [CrossRef]
- Lucia, S. Robust Multi-Stage Nonlinear Model Predictive Control; Shaker Verlag: Herzogenrath, Germany, 2015. [Google Scholar] [CrossRef]
- Subramanian, S.; Lucia, S.; Baradaran Birjandi, S.A.; Paulen, R.; Engell, S. A Combined Multi-stage and Tube-based MPC Scheme for Constrained Linear Systems. IFAC-PapersOnLine 2018, 51, 481–486. [Google Scholar] [CrossRef]
- Mayne, D.; Rawlings, J.; Rao, C.; Scokaert, P. Constrained model predictive control: Stability and optimality. Automatica 2000, 36, 789–814. [Google Scholar] [CrossRef]
- Huang, R.; Harinath, E.; Biegler, L.T. Lyapunov stability of economically oriented NMPC for cyclic processes. J. Process Control 2011, 21, 501–509. [Google Scholar] [CrossRef]
- Angeli, D.; Amrit, R.; Rawlings, J. On Average Performance and Stability of Economic Model Predictive Control. IEEE Trans. Autom. Control 2012, 57, 1615–1626. [Google Scholar] [CrossRef]
- Holtorf, F.; Mitsos, A.; Biegler, L.T. Multistage NMPC with on-line generated scenario trees: Application to a semi-batch polymerization process. J. Process Control 2019, 80, 167–179. [Google Scholar] [CrossRef]
- Lucia, S.; Paulen, R.; Engell, S. Multi-stage Nonlinear Model Predictive Control with verified robust constraint satisfaction. In Proceedings of the 53rd IEEE Conference on Decision and Control, Los Angeles, CA, USA, 15–17 December 2014; pp. 2816–2821. [Google Scholar] [CrossRef]
- Puschke, J.; Mitsos, A. Robust feasible control based on multi-stage eNMPC considering worst-case scenarios. J. Process Control 2018, 69, 8–15. [Google Scholar] [CrossRef]
- Lopez, B.T.; Slotine, J.J.E.; How, J.P. Dynamic Tube MPC for Nonlinear Systems. In Proceedings of the 2019 American Control Conference (ACC), Philadelphia, PA, USA, 10–12 July 2019; pp. 1655–1662. [Google Scholar]
- Houska, B. Robust Optimization of Dynamic Systems. Ph.D. Thesis, Arenberg Doctoral School for Science, Engineering & Technology, Katholieke Universiteit Leuven, Leuven, Belgium, 2011. [Google Scholar]
- Tawarmalani, M.; Sahinidis, N.V. A polyhedral branch-and-cut approach to global optimization. Math. Program. 2005, 103, 225–249. [Google Scholar] [CrossRef]
- Ugray, Z.; Lasdon, L.; Plummer, J.; Glover, F.; Kelly, J.; Marti, R. Scatter Search and Local NLP Solvers: A Multistart Framework for Global Optimization. INFORMS J. Comput. 2007, 19, 328–340. [Google Scholar] [CrossRef]
- Rao, C.V.; Rawlings, J.B.; Lee, J.H. Constrained linear state estimation—A moving horizon approach. Automatica 2001, 37, 1619–1628. [Google Scholar] [CrossRef]
- Thangavel, S.; Aboelnour, M.; Lucia, S.; Paulen, R.; Engell, S. Robust Dual Multi-stage NMPC using Guaranteed Parameter Estimation. IFAC-PapersOnLine 2018, 51, 72–77. [Google Scholar] [CrossRef]
- Kurzhanskiy, A.A.; Varaiya, P. Ellipsoidal Toolbox (ET). In Proceedings of the 45th IEEE Conference on Decision and Control, San Diego, CA, USA, 13–15 December 2006; pp. 1498–1503. [Google Scholar]
- Srinivasan, B.; Palanki, S.; Bonvin, D. Dynamic optimization of batch processes: I. Characterization of the nominal solution. Comput. Chem. Eng. 2003, 27, 1–26. [Google Scholar] [CrossRef]
- EMBOCON EU Project. 2014. Available online: http://www.embocon.org (accessed on 14 July 2013).
- Lynn, L.L.; Parkin, E.S.; Zahradnik, R.L. Near-Optimal Control by Trajectory Approximation. Tubular Reactors with Axial Dispersion. Ind. Eng. Chem. Fundam. 1970, 9, 58–63. [Google Scholar] [CrossRef]
- Lynn, L.L.; Parkin, E.S.; Zahradnik, R.L. The use of orthogonal polynomials in the near-optimal control of distributed systems by trajectory approximation. Ind. Eng. Chem. Fundam. 1970, 9, 58–63. [Google Scholar] [CrossRef]
- Elrod, H.G. Efficient numerical method for computation of the thermohydrodynamics of laminar lubricating films. ASME J. Tribol. 1991, 113, 506–511. [Google Scholar] [CrossRef]
- Hintze, J.L.; Nelson, R.D. Violin Plots: A Box Plot-Density Trace Synergism. Am. Stat. 1998, 52, 181–184. [Google Scholar] [CrossRef]
- Hairer, E.; Wanner, G. Solving Ordinary Differential Equations II: Stiff and Differential-Algebraic Problems; Springer: Berlin/Heidelberg, Germany, 1996. [Google Scholar] [CrossRef]









| Number of | MS | MS-VA | MS-SB | MS-CB | |
|---|---|---|---|---|---|
| Samples in Set | |||||
| OV | model equations | ||||
| control inputs | |||||
| unscented transformation | − | − | |||
| constraints | model equations | ||||
| control bounds | |||||
| non-anticipativity constraints | |||||
| additional constraint | |||||
| unscented transformation | − | − | |||
| enforcing for reachable set | − | − | |||
| Parameter | Description | Value | Unit |
|---|---|---|---|
| heat-transfer coefficient between the reactor and jacket | 1700 | ||
| r | radius of the cross-section of the inner part | m | |
| density of the reactor contents | 1000 | ||
| specific heat capacity of the reactor contents | |||
| input concentration of reactant B | 3 | ||
| volume of the contents inside the cooling jacket | L | ||
| temperature of the flows entering the reactor | 300 | K | |
| initial concentration of the product C | 0 |
| Control | Lower Bound | Upper Bound | Unit |
|---|---|---|---|
| 0 | |||
| 0 |
| State | Initial Condition | Lower Bound | Upper Bound | Unit |
|---|---|---|---|---|
| 0 | 8 | L | ||
| 2 | 0 | 5 | ||
| 0 | 0 | 5 | ||
| 325 | 273 | 350 | K | |
| 325 | 273 | 350 | K |
| Robust | Non-Adaptive | Adaptive | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Horizon | MS | MS-VA | MS-SB | MS-CB | A-MS | A-MS-VA | A-MS-SB | A-MS-CB | |
| min | 2 | ||||||||
| 3 | |||||||||
| mean | 2 | ||||||||
| 3 | |||||||||
| max | 2 | ||||||||
| 3 | |||||||||
| Control | Lower Bound | Upper Bound | Unit |
|---|---|---|---|
| 0 | 30,000 | ||
| 60 | 100 | ||
| 60 | 100 |
| Parameter | Description | Value | Unit |
|---|---|---|---|
| R | Universal gas constant | ||
| Specific heat capacity of the water (coolant) | |||
| Specific heat capacity of the steel | |||
| Specific heat capacity of the feed | 3 | ||
| Specific heat capacity of the contents inside reactor | 5 | ||
| Heat-transfer coefficient between water and steel | 17,280 | ||
| Feed temperature | 25 | ||
| A | Heat-transfer surface of the jacket | 65 | |
| Mass of coolant in the jacket | 5000 | ||
| Mass of the reactor (steel) | 39,000 | ||
| Mass of the product in external heat exchanger | 200 | ||
| Mass of the coolant in external heat exchanger | 1000 | ||
| Mass of the coolant flow into the jacket | 300,000 | ||
| Mass of the coolant flow into the external heat exchanger | |||
| Mass of the product flow into the external heat exchanger | |||
| Activation energy | 8500 | ||
| Reaction parameter 1 | 32 | − | |
| Reaction parameter 2 | 4 | − | |
| Mass fraction of coolant water in the feed | − | ||
| Mass fraction of monomer A in the feed | − | ||
| Heat-transfer coefficient between monomer and steel | 3600 | ||
| Heat-transfer coefficient between product and steel | 360 | ||
| Experimental coefficient | 3,600,000 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Thangavel, S.; Paulen, R.; Engell, S. Robust Multi-Stage Nonlinear Model Predictive Control Using Sigma Points. Processes 2020, 8, 851. https://doi.org/10.3390/pr8070851
Thangavel S, Paulen R, Engell S. Robust Multi-Stage Nonlinear Model Predictive Control Using Sigma Points. Processes. 2020; 8(7):851. https://doi.org/10.3390/pr8070851
Chicago/Turabian StyleThangavel, Sakthi, Radoslav Paulen, and Sebastian Engell. 2020. "Robust Multi-Stage Nonlinear Model Predictive Control Using Sigma Points" Processes 8, no. 7: 851. https://doi.org/10.3390/pr8070851
APA StyleThangavel, S., Paulen, R., & Engell, S. (2020). Robust Multi-Stage Nonlinear Model Predictive Control Using Sigma Points. Processes, 8(7), 851. https://doi.org/10.3390/pr8070851





