Understanding the Effect of Granulation and Milling Process Parameters on the Quality Attributes of Milled Granules
Abstract
1. Introduction
Motivation and Objectives
2. Materials and Methods
2.1. Materials
2.2. Methods
2.3. Particle Size Distribution
2.4. Bulk and Tapped Density
2.5. Friability
2.6. Porosity
3. Results and Discussion
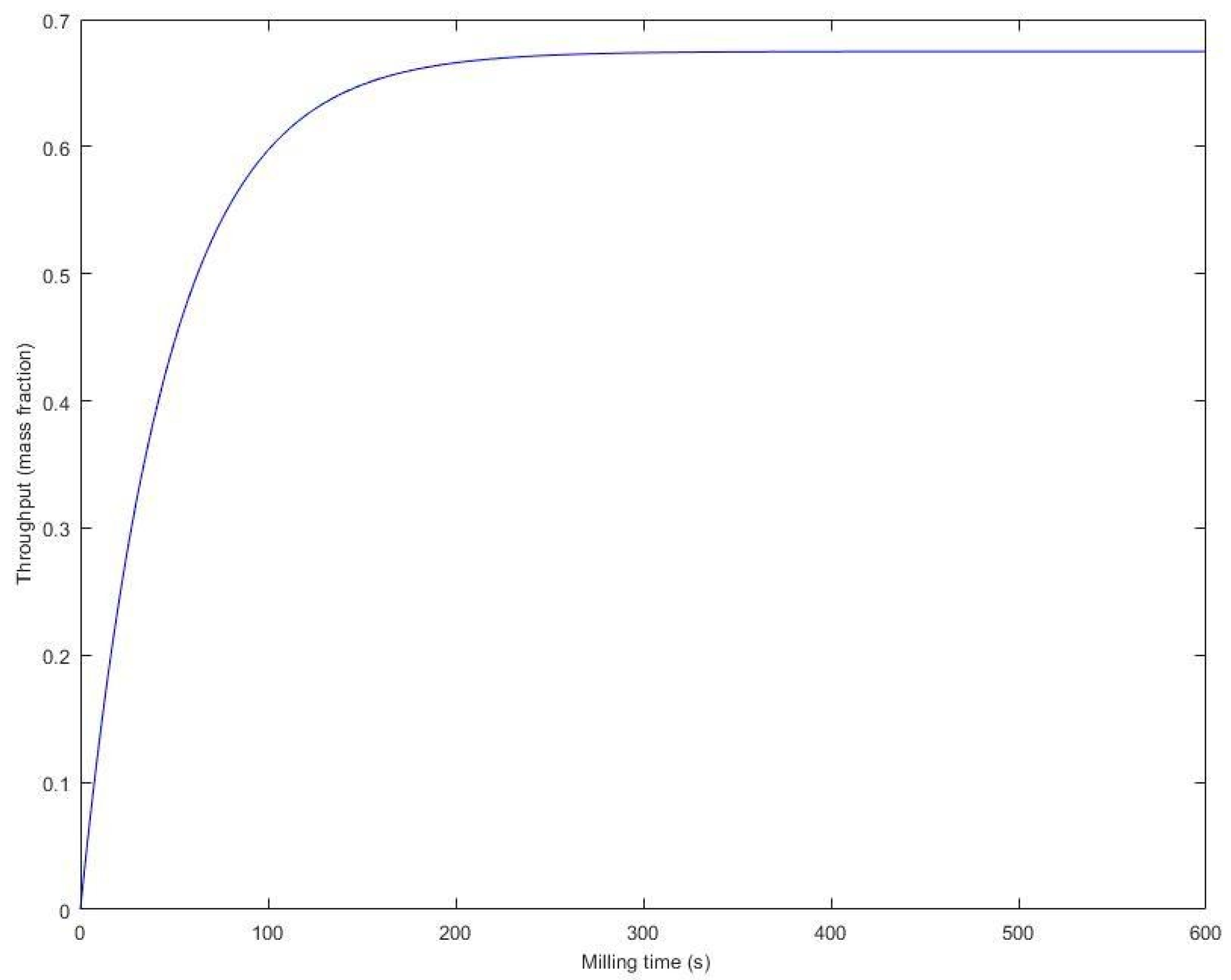
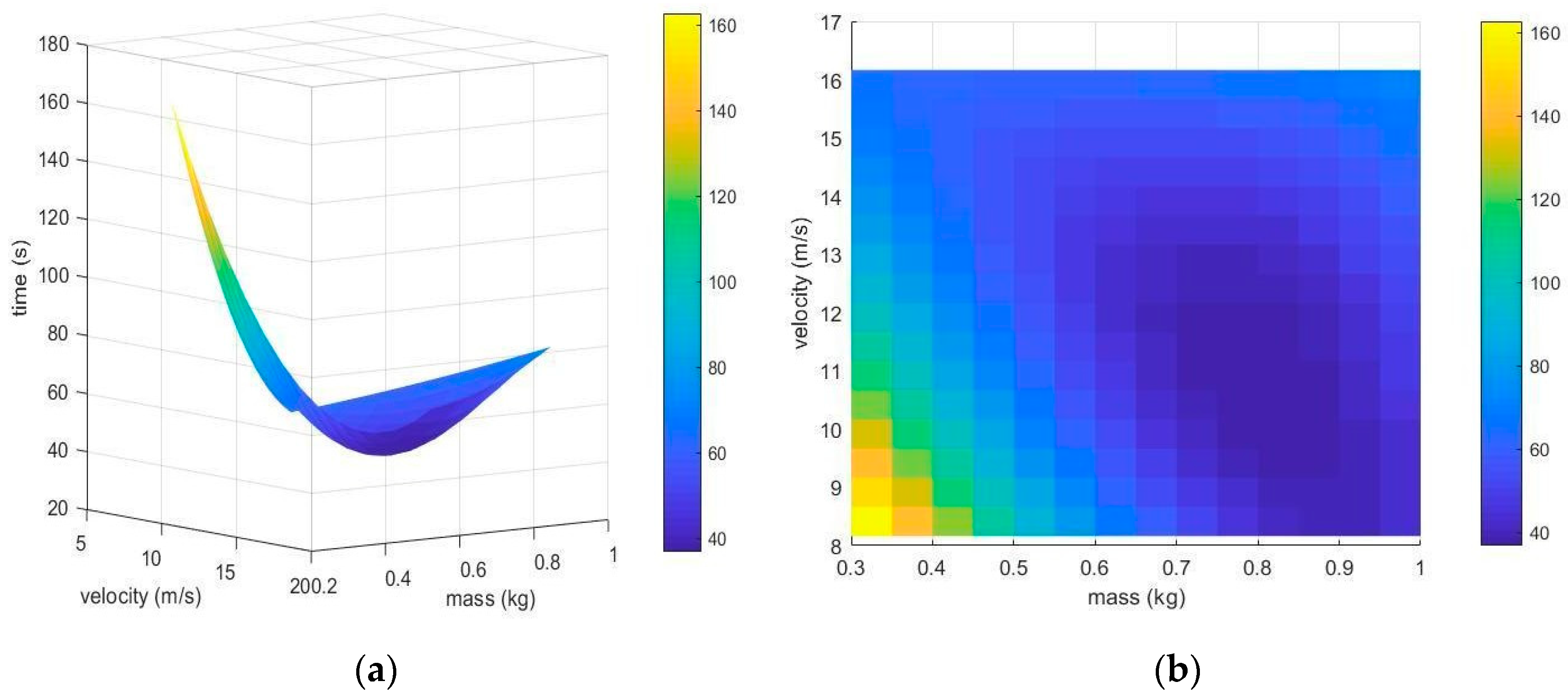
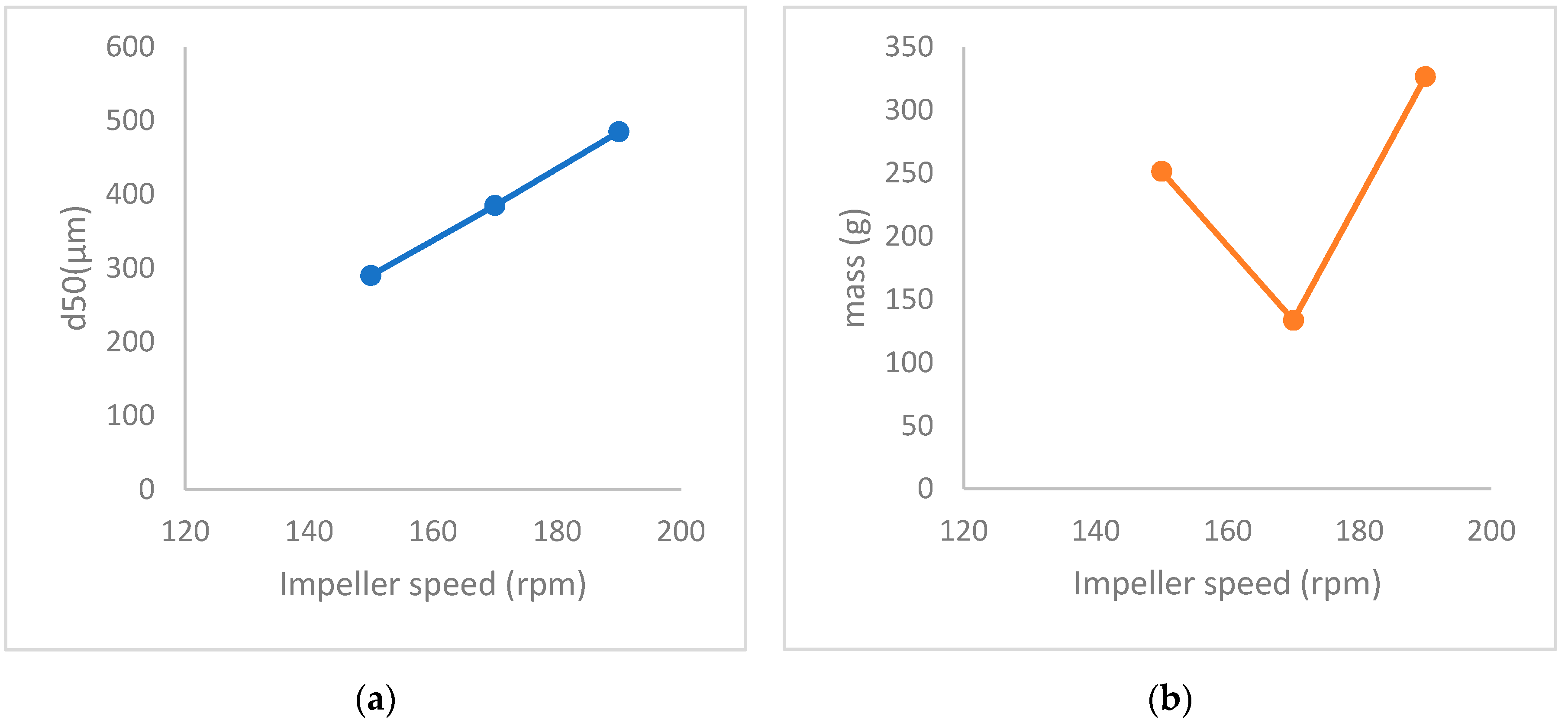
3.1. Effect of Impeller Speed and Batch Loading on Mass Throughput of the Mill
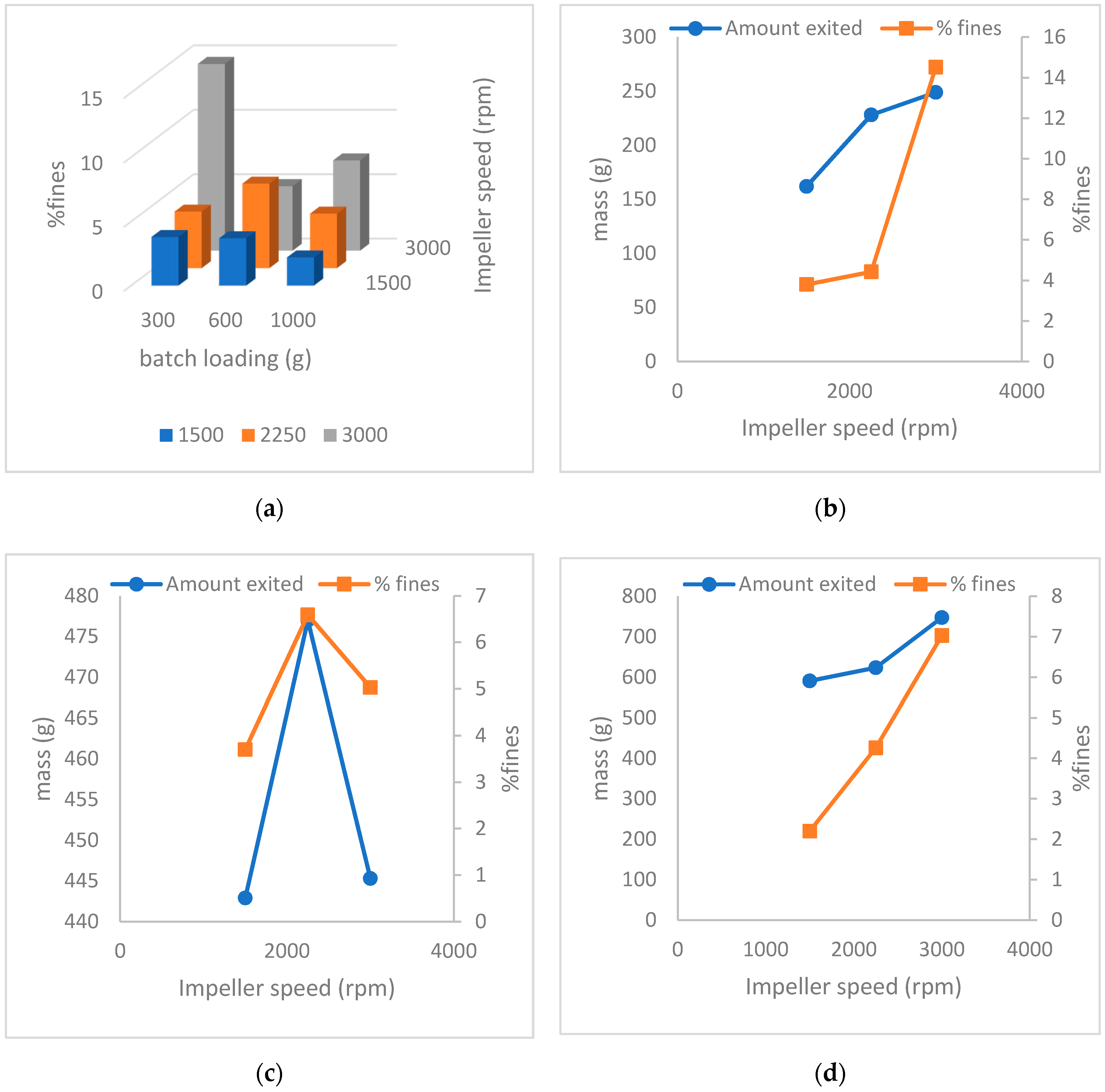
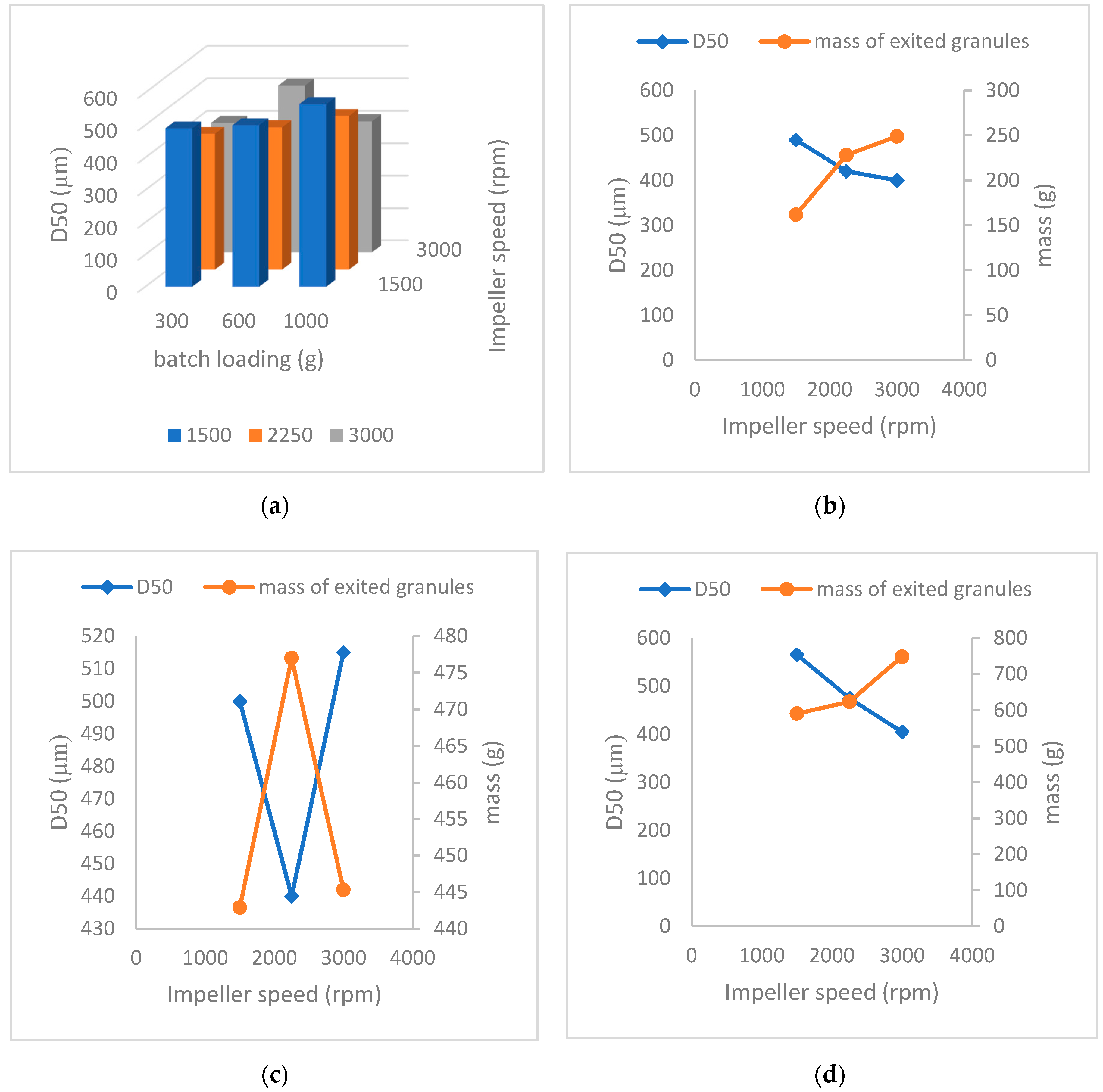
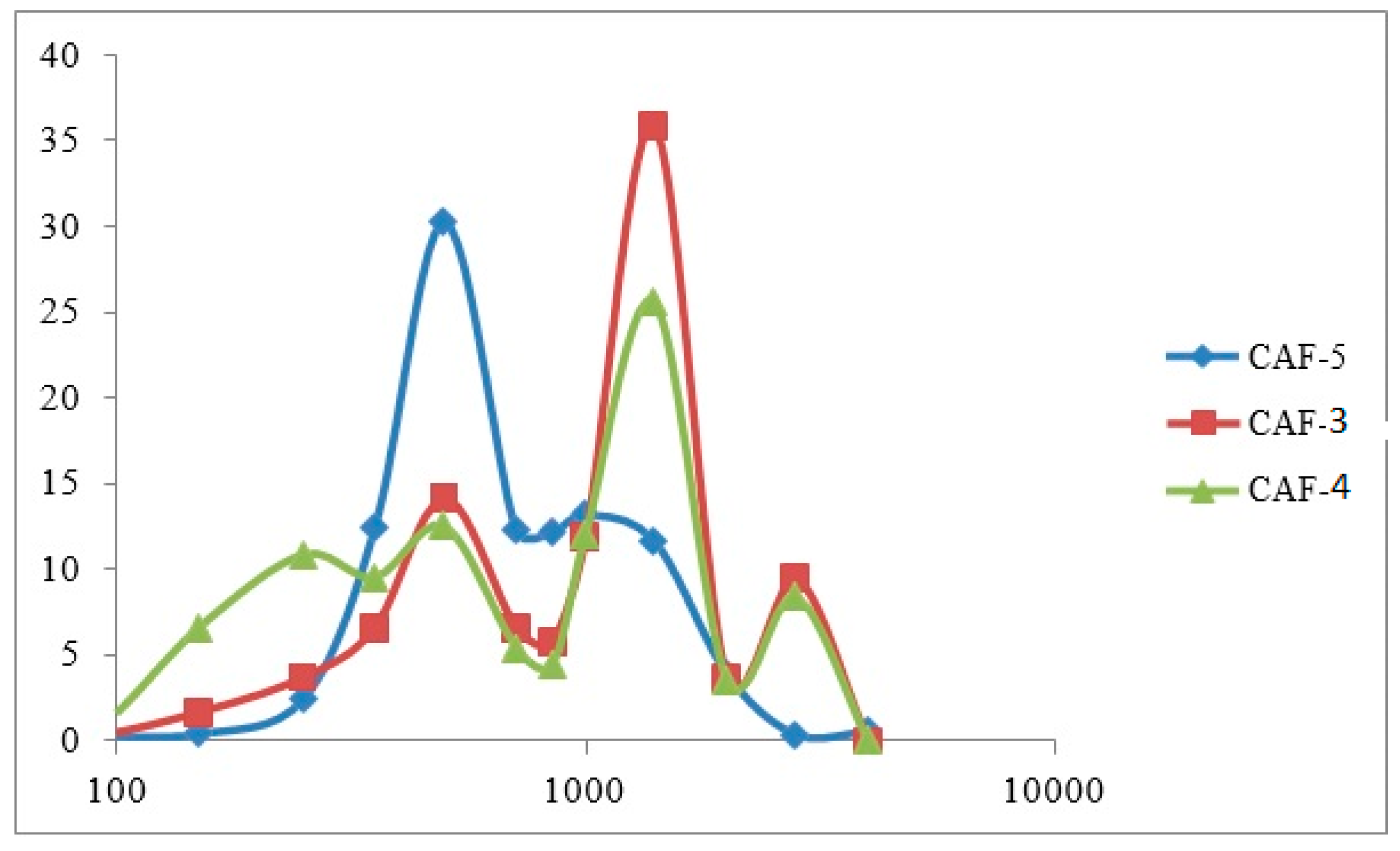
3.2. Effect of Impeller Speed and Batch Loading on PSD of the Milled Granule
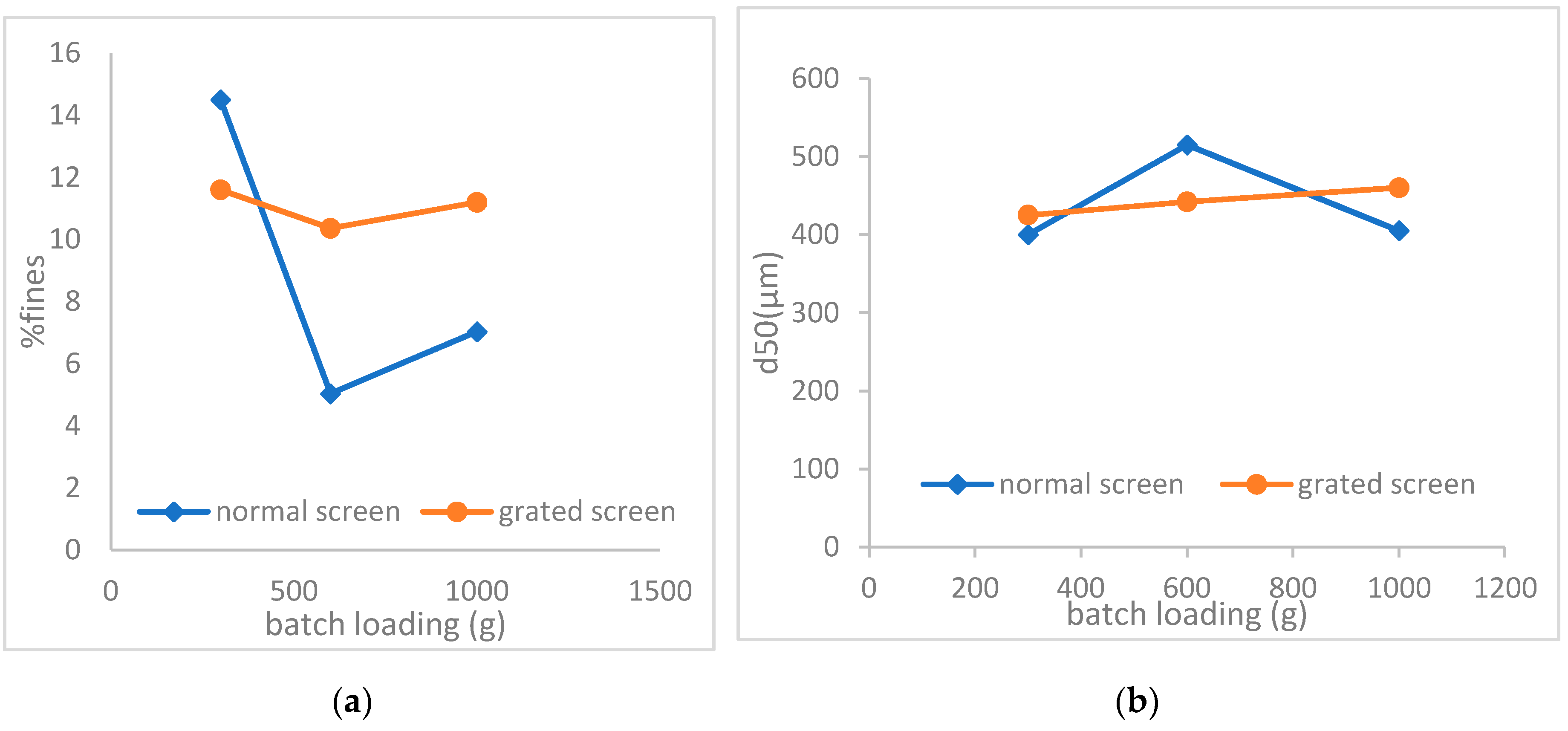
3.2.1. Fines
3.2.2. D50
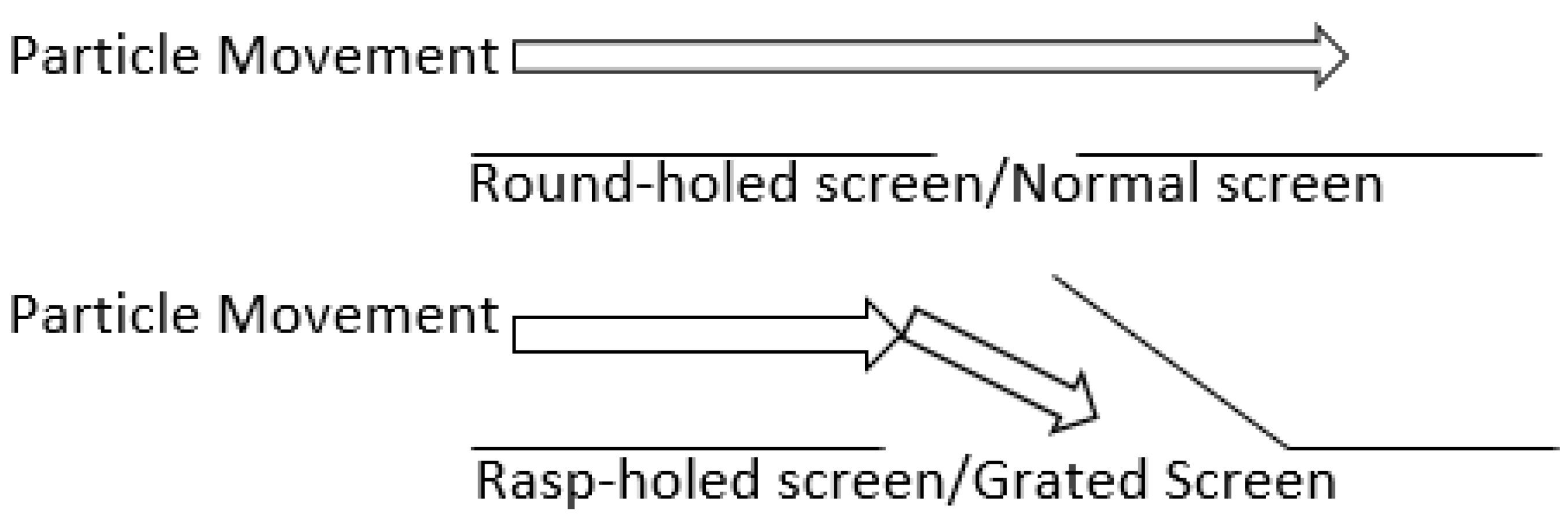
3.3. Effect of Mill Screen Type
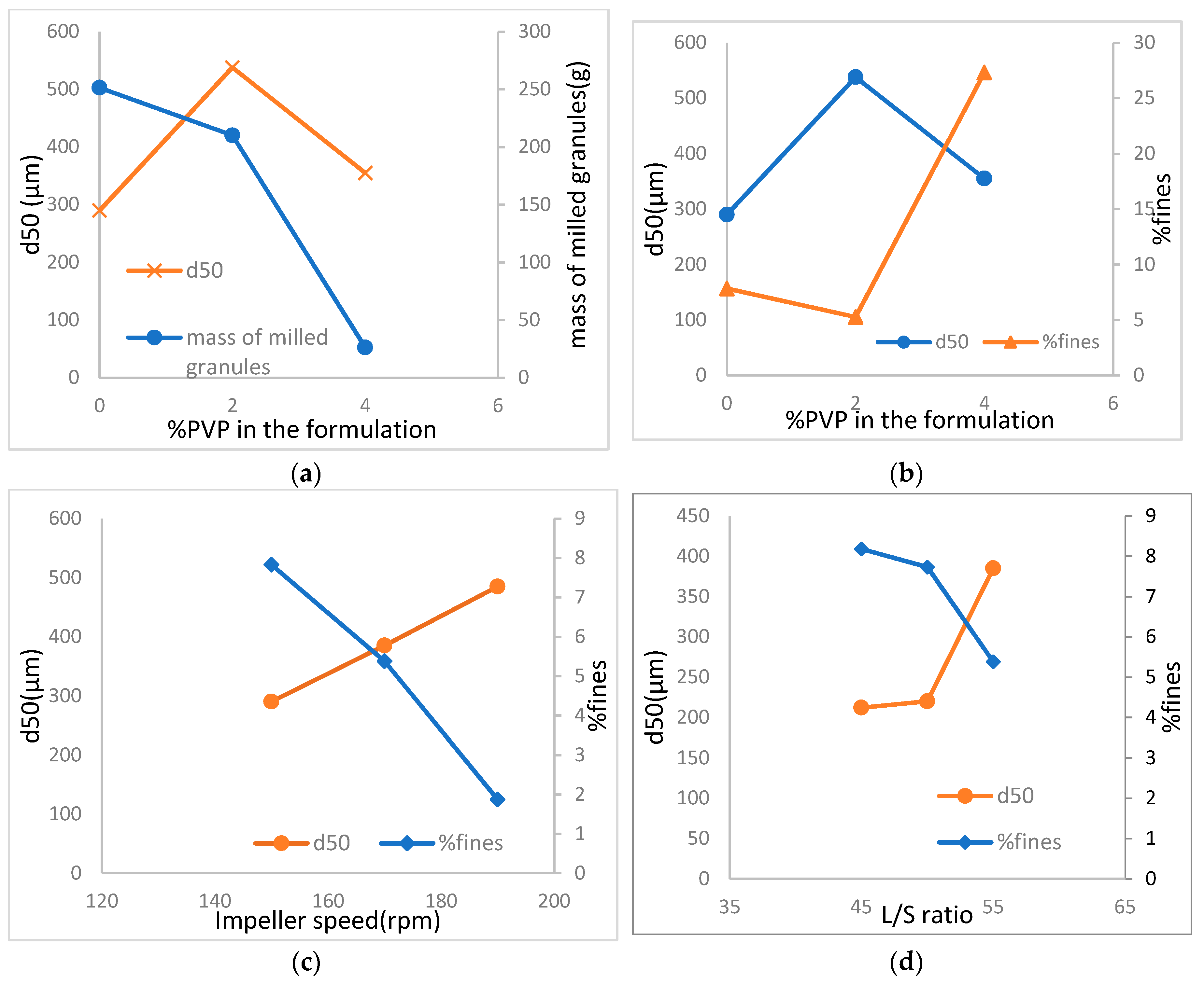
3.4. Effect of Granulation Parameters on Milling
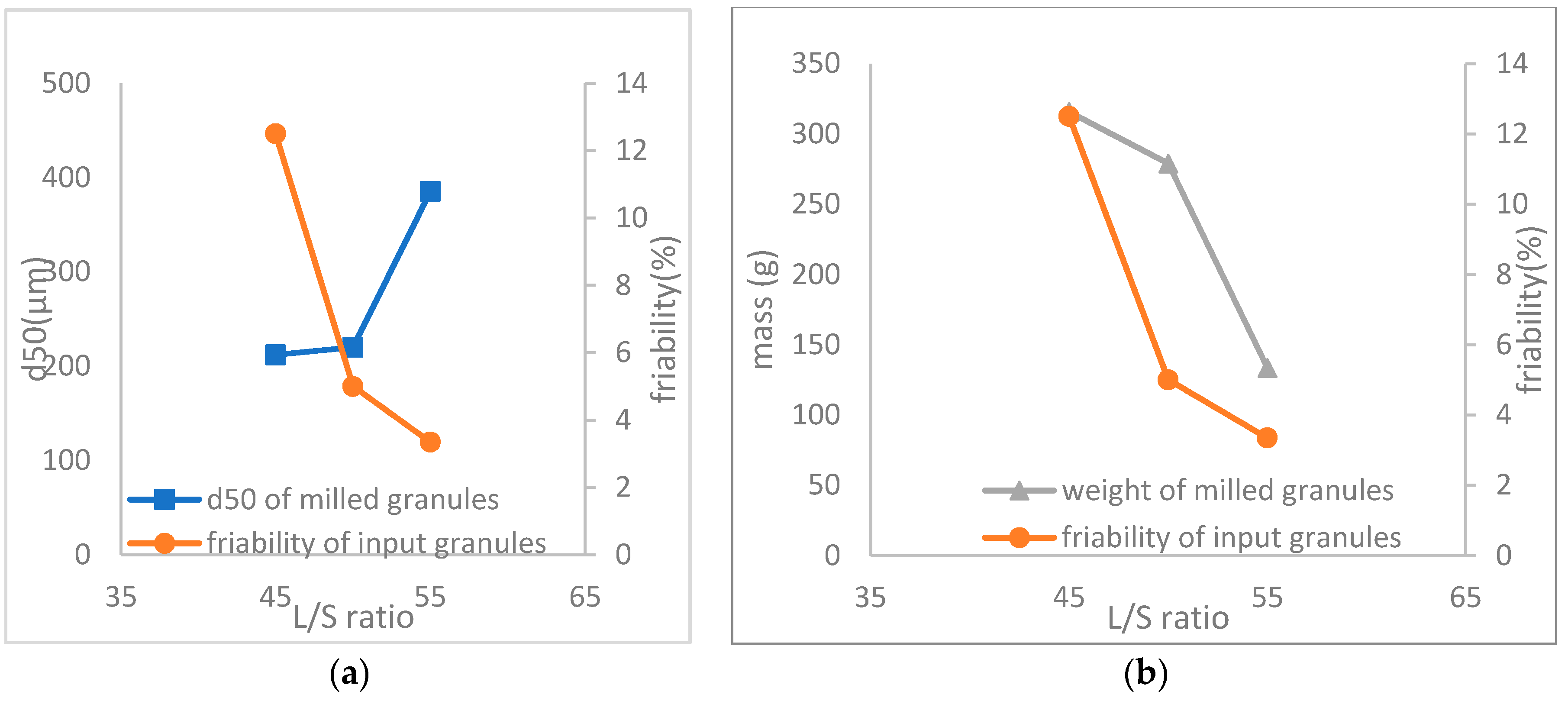
3.4.1. Liquid-to-Solid Ratio
3.4.2. Impeller Speed
3.4.3. Binder Addition
4. Conclusions
Supplementary Materials
Supplementary File 1Author Contributions
Funding
Conflicts of Interest
References
- Naik, S.; Chaudhuri, B. Quantifying Dry Milling in Pharmaceutical Processing: A Review on Experimental and Modeling Approaches. J. Pharm. Sci. 2015, 104, 2401–2413. [Google Scholar] [CrossRef] [PubMed]
- Samanta, A.K.; Ng, K.Y.; Heng, P.W.S. Cone milling of compacted flakes: Process. parameter selection by adopting the minimal fines approach. Int. J. Pharm. 2012, 422, 17–23. [Google Scholar] [CrossRef] [PubMed]
- Yin, S.X.; Franchini, M.; Chen, J.; Hsieh, A.; Jen, S.; Lee, T.; Hussain, M.; Smith, R. Bioavailability enhancement of a COX-2 inhibitor, BMS-347070, from a nanocrystalline dispersion prepared by spray-drying. J. Pharm. Sci. 2005, 94, 1598–1607. [Google Scholar] [CrossRef] [PubMed]
- Oka, S.; Kašpar, O.; Tokárová, V.; Sowrirajan, K.; Wu, H.; Khan, M.; Muzzio, F.; Štěpánek, F.; Ramachandran, R. A quantitative study of the effect of process parameters on key granule characteristics in a high shear wet granulation process involving a two component pharmaceutical blend. Adv. Powder Technol. 2015, 26, 315–322. [Google Scholar] [CrossRef]
- Woyna-Orlewicz, K.; Jachowicz, R. Analysis of wet granulation process with Plackett-Burman design-case study. Acta Pol Pharm. 2011, 68, 725–733. [Google Scholar] [PubMed]
- Barrasso, D.; Oka, S.; Muliadi, A.; Litster, J.D.; Wassgren, C.; Ramachandran, R. Population Balance Model. Validation and Predictionof CQAs for Continuous Milling Processes: Toward QbDin Pharmaceutical Drug Product Manufacturing. J. Pharm. Innov. 2013, 8, 147–162. [Google Scholar] [CrossRef]
- Byers, J.E.; Peck, G.E. The effect of Mill Variables on a Granulation Milling Process. Drug Dev. Ind. Pharm. 1990, 16, 1761–1779. [Google Scholar] [CrossRef]
- Motzi, J.J.; Anderson, N.R. The quantitative evaluation of a granulation milling process II. Effect of output screen size, mill speed and impeller shape. Drug Dev. Ind. Pharm. 1984, 10, 713–728. [Google Scholar] [CrossRef]
- Schenck, L.R.; Plank, R.V. Impact milling of pharmaceutical agglomerates in the wet and dry states. Int. J. Pharm. 2008, 348, 18–26. [Google Scholar] [CrossRef] [PubMed]
- Verheezen, J.J.A.M.; Maarschalk, K.v.d.V.; Faassen, F.; Vromans, H. Milling of agglomerates in an impact mill. Int. J. Pharm. 2004, 278, 165–172. [Google Scholar] [CrossRef] [PubMed]
- Subero, J.; Ghadiri, M. Breakage patterns of agglomerates. Powder Technol. 2001, 120, 232–243. [Google Scholar] [CrossRef]
- Pandey, P.; Tao, J.; Chaudhury, A.; Ramachandran, R.; Gao, J.Z.; Bindra, D.S. A combined experimental and modeling approach to study the effects of high-shear wet granulation process parameters on granule characteristics. Pharm. Dev. Technol. 2013, 18, 210–224. [Google Scholar] [CrossRef] [PubMed]
- The United States Pharmacopeial Convention. Bulk Density and Tapped Density of Powders; U.S. Pharmacopeia, Ed.; The United States Pharmacopeial Convention: North Bethesda, MD, USA, 2015. [Google Scholar]
- Vercruysse, J.; Díaz, D.C.; Peeters, E.; Fonteyne, M.; Delaet, U.; van Assche, I.; de Beer, T.; Remon, J.P.; Vervaet, C. Continuous twin screw granulation: Influence of process variables on granule and tablet quality. Eur. J. Pharm. Biopharm. 2012, 82, 205–211. [Google Scholar] [CrossRef] [PubMed]
- Meng, W.; Kotamarthy, L.; Panikar, S.; Sen, M.; Pradhan, S.; Marc, M.; Litster, J.D.; Muzzio, F.J.; Ramachandran, R. Statistical analysis and comparison of a continuous high shear granulator with a twin screw granulator: Effect of process parameters on critical granule attributes and granulation mechanisms. Int. J. Pharm. 2016, 513, 357–375. [Google Scholar] [CrossRef] [PubMed]
- El Hagrasy, A.S.; Cruise, P.; Jones, I.; Litster, J.D. In-line Size Monitoring of a Twin Screw Granulation Process. Using High-Speed Imaging. J. Pharm. Innov. 2013, 8, 90–98. [Google Scholar] [CrossRef]
- Metta, N.; Ghijs, M.; Schäfer, E.; Kumar, A.; Cappuyns, P.; Van Assche, I.; Singh, R.; Ramachandran, R.; De Beer, T.; Ierapetritou, M.; et al. Dynamic Flowsheet Model. Development and Sensitivity Analysis of a Continuous Pharmaceutical Tablet Manufacturing Process. Using the Wet Granulation Route. Processes 2019, 7, 234. [Google Scholar] [CrossRef]
- Yu, S.; Gururajan, B.; Reynolds, G.; Roberts, R.; Adams, M.J.; Wu, C.-Y. Experimental Investigation of Milling of Roll Compacted Ribbons. In Particulate Materials: Synthesis, Characterisation, Processing and Modelling; The Royal Society of Chemistry: Cambridge, UK, 2012; pp. 158–166. [Google Scholar]
- Vanarase, A.U.; Muzzio, F.J. Effect of operating conditions and design parameters in a continuous powder mixer. Powder Technol. 2011, 208, 26–36. [Google Scholar] [CrossRef]
- Gao, Y.; Muzzio, F.J.; Ierapetritou, M.G. Optimizing continuous powder mixing processes using periodic section modeling. Chem. Eng. Sci. 2012, 80, 70–80. [Google Scholar] [CrossRef]
- El Hagrasy, A.S.; Hennenkampb, J.R.; Burkec, M.D.; Cartwrightc, J.J.; Litsterad, J.D. Twin screw wet granulation: Influence of formulation parameters on granule properties and growth behavior. Powder Technol. 2013, 238, 108–115. [Google Scholar] [CrossRef]
- Sayin, R.; El Hagrasy, A.S.; Litster, J.D. Distributive mixing elements: Towards improved granule attributes from a twin screw granulation process. Chem. Eng. Sci. 2015, 125, 165–175. [Google Scholar] [CrossRef]


| Granulation Parameters | Mill Parameters | |||
|---|---|---|---|---|
| Impeller Speed (rpm) | L/S Ratio (%) | %PVP in Formulation | Impeller Speed (rpm) | Batch Loading (g) |
| 150 | 55 | 0 | 2250 | 600 |
| 150 | 55 | 0 | 1500 | 1000 |
| 150 | 55 | 0 | 2250 | 300 |
| 150 | 55 | 0 | 3000 | 600 |
| 150 | 55 | 0 | 1500 | 300 |
| 150 | 55 | 0 | 3000 | 1000 |
| 150 | 55 | 0 | 1500 | 600 |
| 150 | 55 | 0 | 2250 | 1000 |
| 150 | 55 | 0 | 3000 | 300 |
| Impeller Speed (rpm) | L/S Ratio (%) | %PVP | d10 (μm) | d50 (μm) | d90 (μm) |
|---|---|---|---|---|---|
| 170 | 45 | 0 | 190 | 600 | 1900 |
| 170 | 50 | 0 | 280 | 1060 | 2070 |
| 170 | 55 | 0 | 470 | 1400 | 2150 |
| 150 | 55 | 0 | 215 | 840 | 1930 |
| 190 | 55 | 0 | 450 | 750 | 1700 |
| 150 | 55 | 2 | 480 | 1020 | 2010 |
| 150 | 55 | 4 | 1075 | 1900 | 3200 |
| m (kg) | v (m/s) | RPM | mfinal | τ | t50 |
|---|---|---|---|---|---|
| 0.6 | 12,246 | 2250 | 0.780 | 56.85 | 58,195 |
| 1 | 8164 | 1500 | 0.553 | 20.67 | 48,660 |
| 0.3 | 12,246 | 2250 | 0.758 | 70.12 | 75,664 |
| 0.6 | 16,328 | 3000 | 0.675 | 46.26 | 62,486 |
| 0.3 | 8164 | 1500 | 0.522 | 53.93 | 170,761 |
| 1 | 16,328 | 3000 | 0.745 | 70.72 | 78,633 |
| 0.6 | 8164 | 1500 | 0.708 | 49.46 | 60,602 |
| 1 | 12,246 | 2250 | 0.584 | 28.45 | 55,197 |
| 0.3 | 16,328 | 3000 | 0.841 | 78.26 | 70,620 |
| d50 | d90 | d10 | |
|---|---|---|---|
| Input batch | 840 | 1930 | 215 |
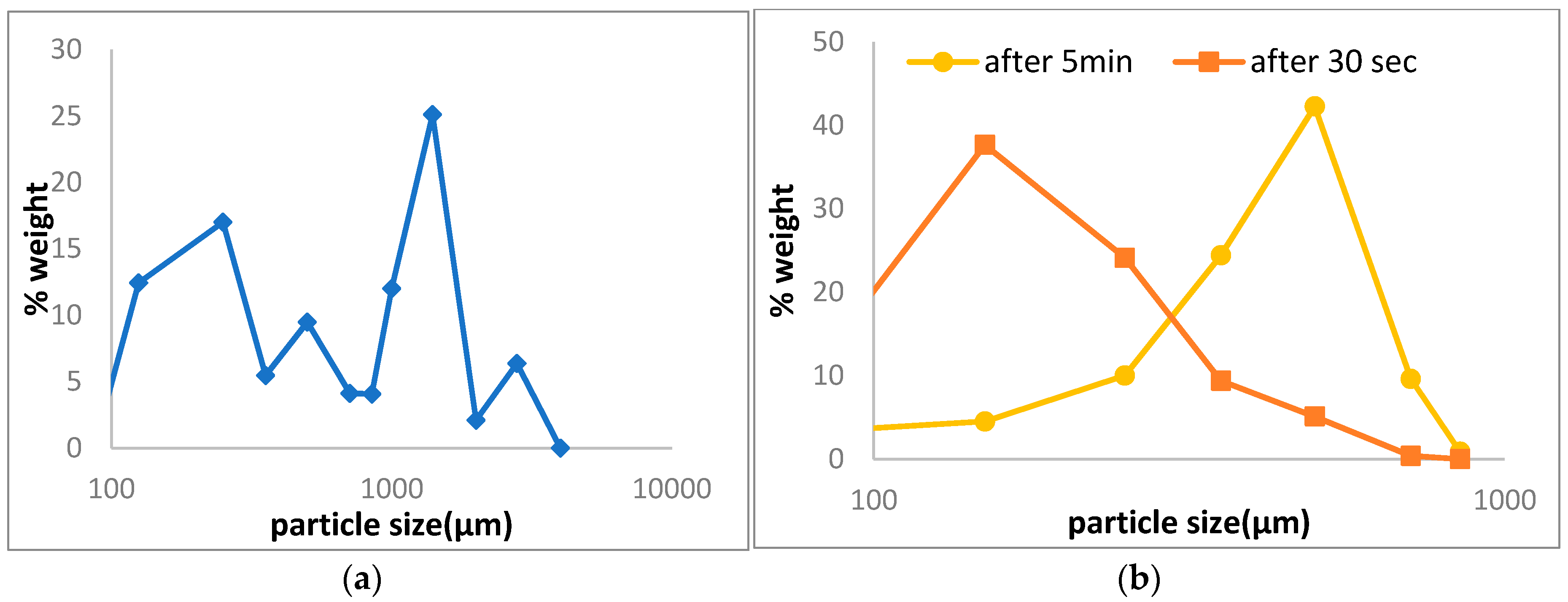
| Output batch, after 30 s | 290 | 500 | 110 |
| Output batch, after 5 min | 515 | 710 | 190 |
| CQA | p-Value |
|---|---|
| span | 9.11 × 10−9 |
| friability | 0.044 |
| porosity | 0.006 |
| bulk density | 0.00049 |
| tap density | 2.91 × 10−7 |
| Granulation Batch | Mass Below 1000 μm (g) |
|---|---|
| CAF-3 (170 rpm) | 201.18 |
| CAF-4 (150 rpm) | 311.13 |
| CAF-5 (190 rpm) | 422.14 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kotamarthy, L.; Metta, N.; Ramachandran, R. Understanding the Effect of Granulation and Milling Process Parameters on the Quality Attributes of Milled Granules. Processes 2020, 8, 683. https://doi.org/10.3390/pr8060683
Kotamarthy L, Metta N, Ramachandran R. Understanding the Effect of Granulation and Milling Process Parameters on the Quality Attributes of Milled Granules. Processes. 2020; 8(6):683. https://doi.org/10.3390/pr8060683
Chicago/Turabian StyleKotamarthy, Lalith, Nirupaplava Metta, and Rohit Ramachandran. 2020. "Understanding the Effect of Granulation and Milling Process Parameters on the Quality Attributes of Milled Granules" Processes 8, no. 6: 683. https://doi.org/10.3390/pr8060683
APA StyleKotamarthy, L., Metta, N., & Ramachandran, R. (2020). Understanding the Effect of Granulation and Milling Process Parameters on the Quality Attributes of Milled Granules. Processes, 8(6), 683. https://doi.org/10.3390/pr8060683





