1. Introduction
Cavitation is a phenomenon in which vapor forms over a solid surface when the local pressure over the surface drops below the saturated vapor pressure of the liquid. The cavitation phenomenon is inherently un-steady and comprises three processes. The first one is known as nucleation; in this, the onset of the cavitation occurs. This process is attributed to, the presence of impurities in the liquid, or/and presence of tiny bubbles, which in turn act as triggering nuclei for the cavitation [
1]. In the second stage, this nuclei grow and become unstable and thus lead to the shedding of the cavities. In the final stage, these cavities break and contribute to the regrowth of the cavity [
2]. These different stages from nucleation to regrowth of cavitation is quantified by a non-dimensional number called the cavitation number. The cavitation number is represented by
, and mathematically given by Equation (
1)
where,
,
are the free stream flow pressure and velocity, respectively,
Pa is the saturation pressure (at 30
C), and
is the water density. The phenomena of cavitation particularly happen in hydraulic applications such as underwater bodies, turbines, and pumps. Cavitation causes flow instabilities which hampers the functioning of flow devices, primarily by increasing the noise level, vibration, and in extreme cases the erosion of the devices.
Timoshevskiy et al. [
3] used 2 D PIV set up to understand the cavitation flow over a NACA0015 and a scaled-down model of high pressure guided vanes. They have studied and compared these 2 D models with different angles of attack in varying cavitating zones. Timoshevskiy et al. [
3] demonstrated that with the change in the configuration of the test piece, the cavitation and flow characteristics might change drastically depending on the angle of attack. This can be attributed to the intense turbulent wakes in the case of guided vanes because of the flow separation. However, with the change of cavitation number, the value of the coefficient of pressure maintains the same trend for the guided vanes in contrast with the NACA0015 hydrofoils in which the change in the coefficient of pressure is appreciable.
Timoshevskiy et al. [
4] experimentally reports the manipulation of cavitation by the wall jet on the 2D model of guide vanes of the Francis turbine. The slot for the jet is created at
times the chord length of the guided vane from the leading edge. Using LIF visualization and PIV technique, they have studied the effects of angle of attack and the injection velocity of the wall jet on the cavitation. For a small angle of attack, the low wall injection velocity at the guided vanes causes the local increase in the pressure value and also leads to the increase of the turbulent intensity in the wakes. Consequently, the local increase in pressure helps to decrease the cavitation effect while the increase in the turbulent intensity leads to the increase of the drag. Thus, the low injection velocity of the wall jet diminishes the cavitation effect, but on the other hand, the hydrodynamic performance of the guided vane is being adversely affected.
Liu et al. [
5] uses a 3D hybrid LES-RANS (DES) numerical model to study the passive cavitation control on the Clark-Y hydrofoil. In this work, they have created a slot over the hydrofoil at different locations with a varying width of the slot. Their numerical results indicate that the presence of a slot in the hydrofoil decreases the cavitation instabilities. However, the slot geometry plays an important role in determining the extent of cavitation control. For example: if the slot exit is near the trailing edge of the hydrofoil there is small or no effect on the cavitation, but if the slot exit is closer to the leading edge, it suppresses the cavitation. This trend of cavitation control is because of the momentum jet created due to the slot geometry which acts as a suction at one end and acts as a jet on the other end. This momentum jet adds energy to the low pressure (cavitating) zone, which in turn creates the higher pressure area, which ultimately results in lowering the cavitation. This phenomenon of increasing the local pressure (or decreasing the cavitation effect) depends on the intensity of the momentum jet, which ultimately depends on the location and geometry of the slot.
Using OpenFoam, Capurso et al. [
6] numerically investigated the cavitation on a NACA0015 hydrofoil.
k-
SST and k-kl-
approaches are used to model the turbulence effects. The cavitation effect is modeled using three different cavitation mass transfer models: [
7,
8,
9]. In this work, they had compared different cavitation models and turbulence models against the experimental work of [
10]. They found that the combination of [
7] for the cavitation model along with the k-kl-
for the turbulence model gives the best results when comparing the
value against the experimental work of [
10].
Recently, Hidalgo et al. [
11] implemented the Zwart–Gerber–Belamri cavitation model in OpenFOAM for studying the cavitation flow over the NACA66 hydrofoil. The turbulence is modeled using two different approaches, viz:
k-
SST SAS (scale adaptive simulation) and ILES (implicit large eddy simulation). They concluded that for the same cavitation model (Zwart–Gerber–Belamri), the
k-
SST SAS predicts the unsteady cavitation more accurately as compared to the ILES.
The present manuscript is organized as follows. In
Section 2, we briefly outline the governing equations for the present work. This is followed by
Section 3, where the description of the geometry, computational domain, and boundary conditions is done. Results are explained in
Section 4. Finally, summary and future work are explained in
Section 5.
3. Computational Set-Up and Boundary Conditions
The hydrofoil used in the present work is a scaled-down model of guide vanes, taken from Timoshevskiy et al. [
4]. Using the coordinates described in Timoshevskiy et al. [
4], we further use the
polyfit and
polyval functions of the Octave (open source software) to make the profile of the hydrofoil smoother. In this hydrofoil, the slot is created at a distance of
C from the leading edge. Here C is the chord length, and its value is
m. From this slot, the injection of the water is done, and the injection velocity is defined by
. The 2D numerical simulations are carried out in the computational domain, shown in
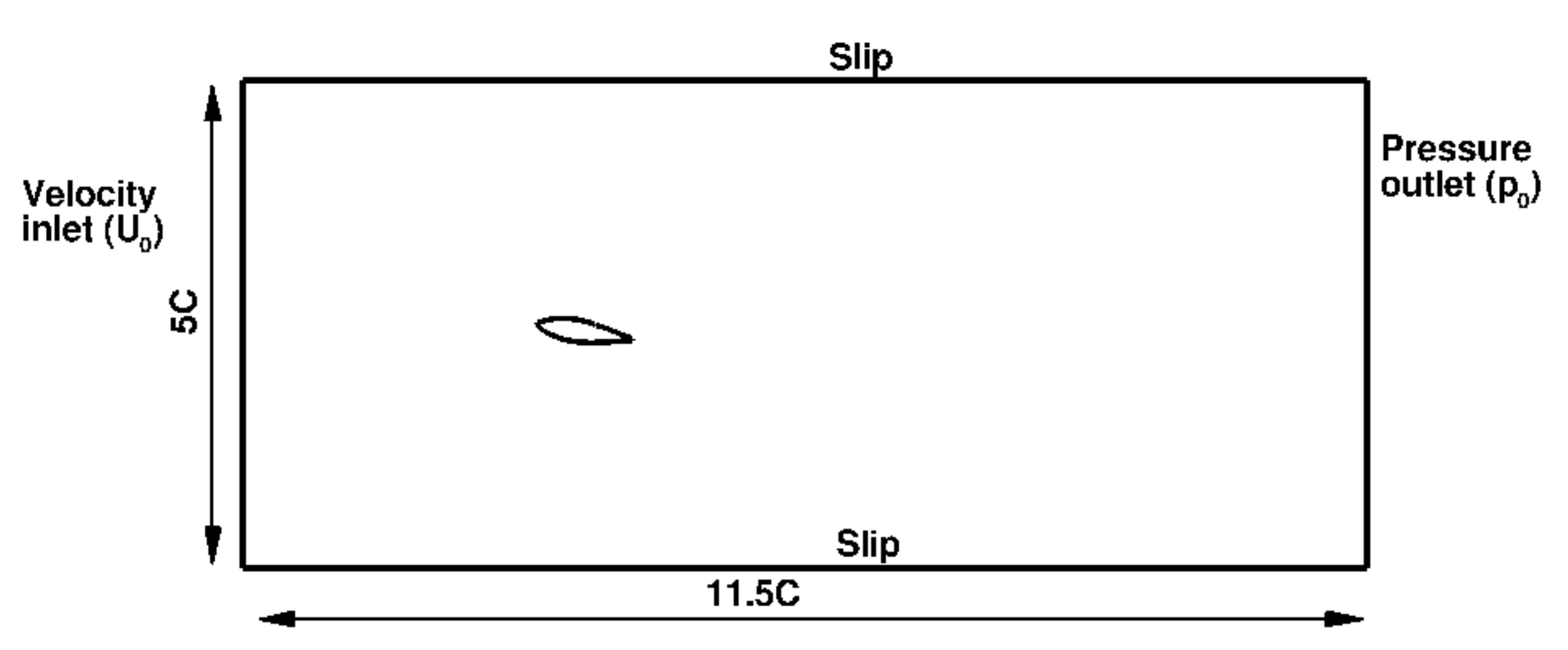
Figure 1. The streamwise and cross streamwise length of the computational domain are
C and 5C respectively, which is in agreement with the previous work of Capurso et al. [
6]. Velocity inlet and pressure outlet boundary conditions are imposed, and these values are changed as per the cavitation number, described in
Table 1 and
Table 2 corresponding to AOA
and
respectively. The top and bottom boundary conditions are set as slip boundary conditions. Turbulent intensity (
I) at the inlet is fixed to
. Inlet conditions for
k and
are set according to
and
. These values of turbulent intensity (
I) and
are selected following the previous work of Capurso et al. [
6].
The computational mesh is created using open-source software called GMSH, shown in
Figure 2. The mesh from GMSH is imported into the OpenFOAM using the
gmshToFoam. To convert the resulting mesh in the scale of
,
tranformPoints -scale “(0.1 0.1 0.1)” is used. The correctness of the final mesh is examined used
checkMesh utility. OpenFOAM is known to converge well if the cells are hexahedron in shape; thus, the majority of the cells used in the computations are hexahedron. The average
obtained after the converged solutions (from
SIMPLE simulations) are
and
for an angle of attack
and
respectively. However a sensitivity test is also carried out for an average
up to
∼ 150, and it was observed that there is no effect on the results (not shown in the manuscript). To further ensure that the results are independent of the wall resolution, standard wall functions are used for the flow variables. The CFL value is fixed at 2 (time-stepping ∼
s). For the cavitation study, the averaging of the fields is done for about 17 flow-through times. For extracting the non-dimensional velocity profiles and comparing against the experimental work of Timoshevskiy et al. [
4], the open-source software paraFoam and licensed version of Tecplot360 is used. The
axis is always normal to the surface of the hydrofoil. Also, to be noted here is that the
axis is shifted to fix the surface of the hydrofoil at the origin of the
axis.
4. Results
The grid independence study is carried out for no cavitation cases and for two angles of attack, AOA
(case AOA3a) and
(case AOA9a). These cases are validated against the experimental work of [
4] (referred here as Measured). To save the computational time, these cases are run using the steady-state solver in OpenFOAM, namely
SIMPLE algorithm.
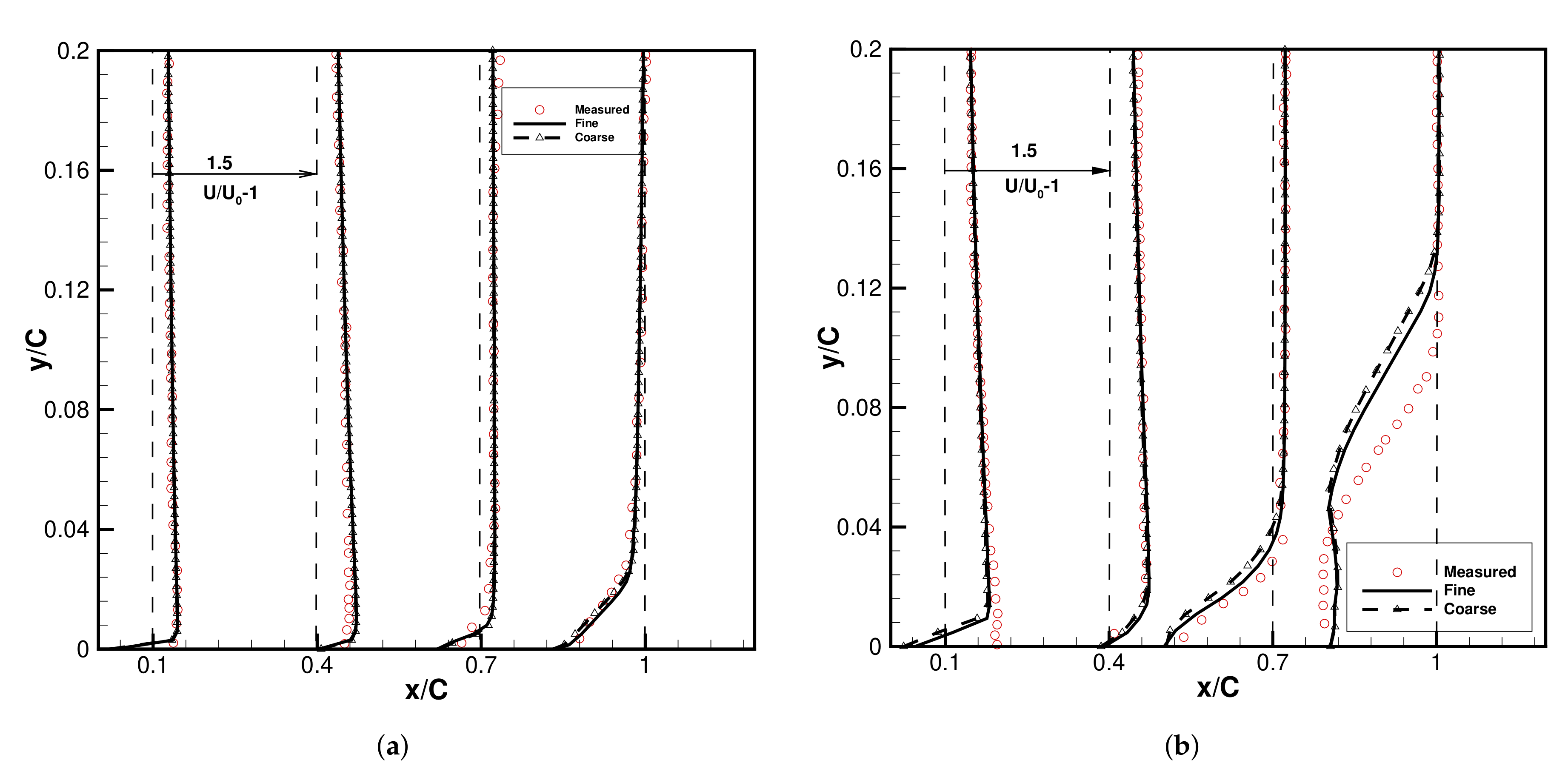
Figure 3a shows the grid independence corresponding to AOA
(case AOA3a), here the coarse refers to 155,660 cells and fine refers to 244,660 cells. The figure shows the velocity deficit at a different location. Similarly,
Figure 3b shows the grid independence corresponding to AOA
(case AOA9a), here the coarse refers to 209,133 cells, and fine refers to 248,634 cells. Thus, the rest of the simulations for the lower and higher angle of attack are done with the 155,660 cells and 209,133 cells respectively. The simulations for a smaller angle of attack comes to a well-converged state (residual <
) after t ∼ 170 s. But for the larger angle of attack, the simulations are run for t ∼ 2000 s. The grid convergence and the validation against the experimental work of [
4] for the lower angle of attack are in good agreement as compared to the higher angle of attack. This disagreement could be because of flow separation for a higher angle of attack.
4.1. Lower Angle of Attack AOA
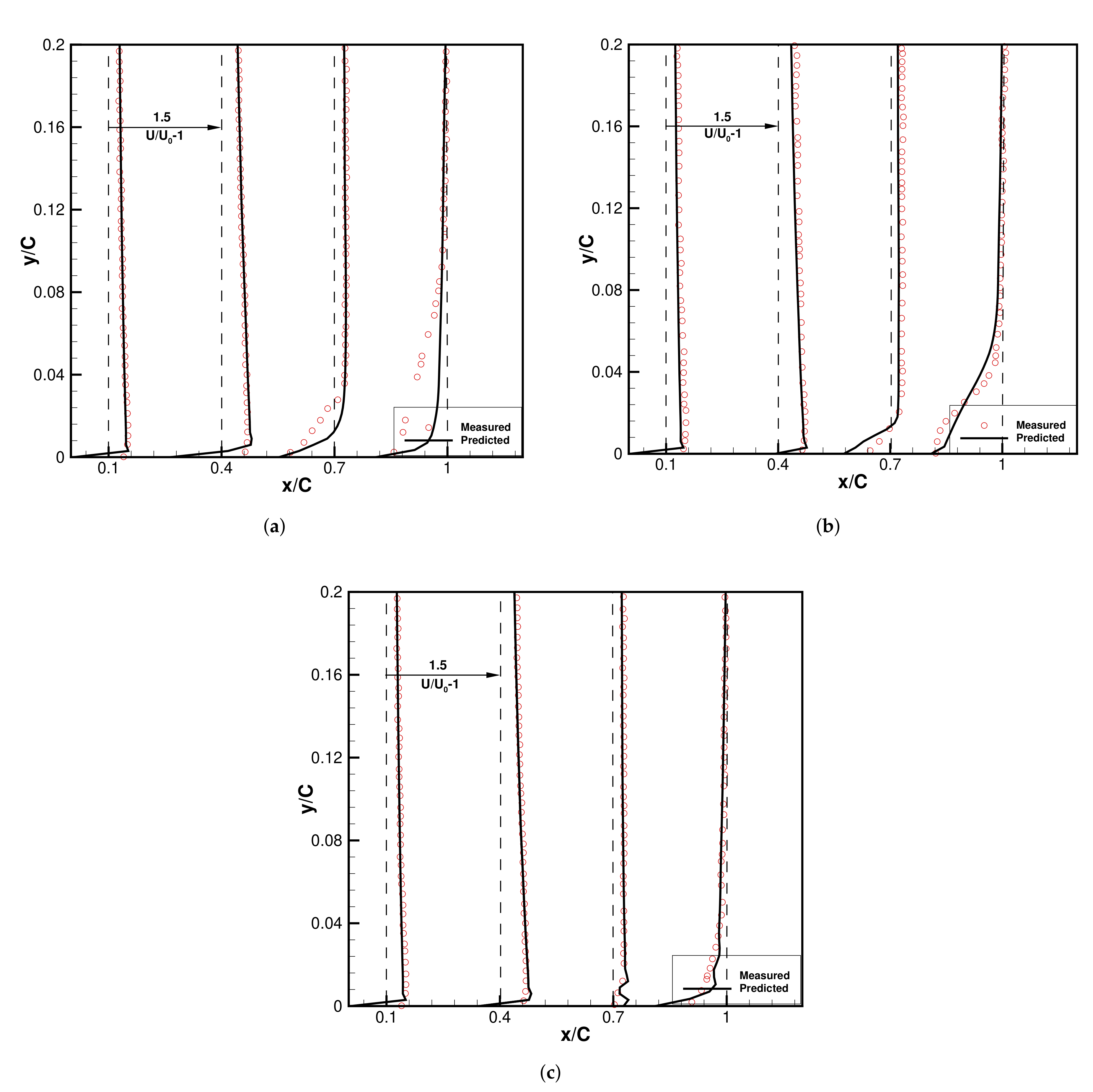
Figure 4a shows the velocity deficit at a different location without any injection and compared against the experimental work of [
4]. The present numerical work compares well at the
, but the agreement does not follow at the
correctly. However for the mild wall injection (case AOA3c) and high wall injection (case AOA3c), shown in
Figure 4b,c, there is a good agreement between the present simulations and the experimental work. This discrepancy may be because the injection is forcing the flow to remain 2D and more-over because of the wall injection the cavitation effect is truncated. This effect of the wall injection is explained in the next paragraph.
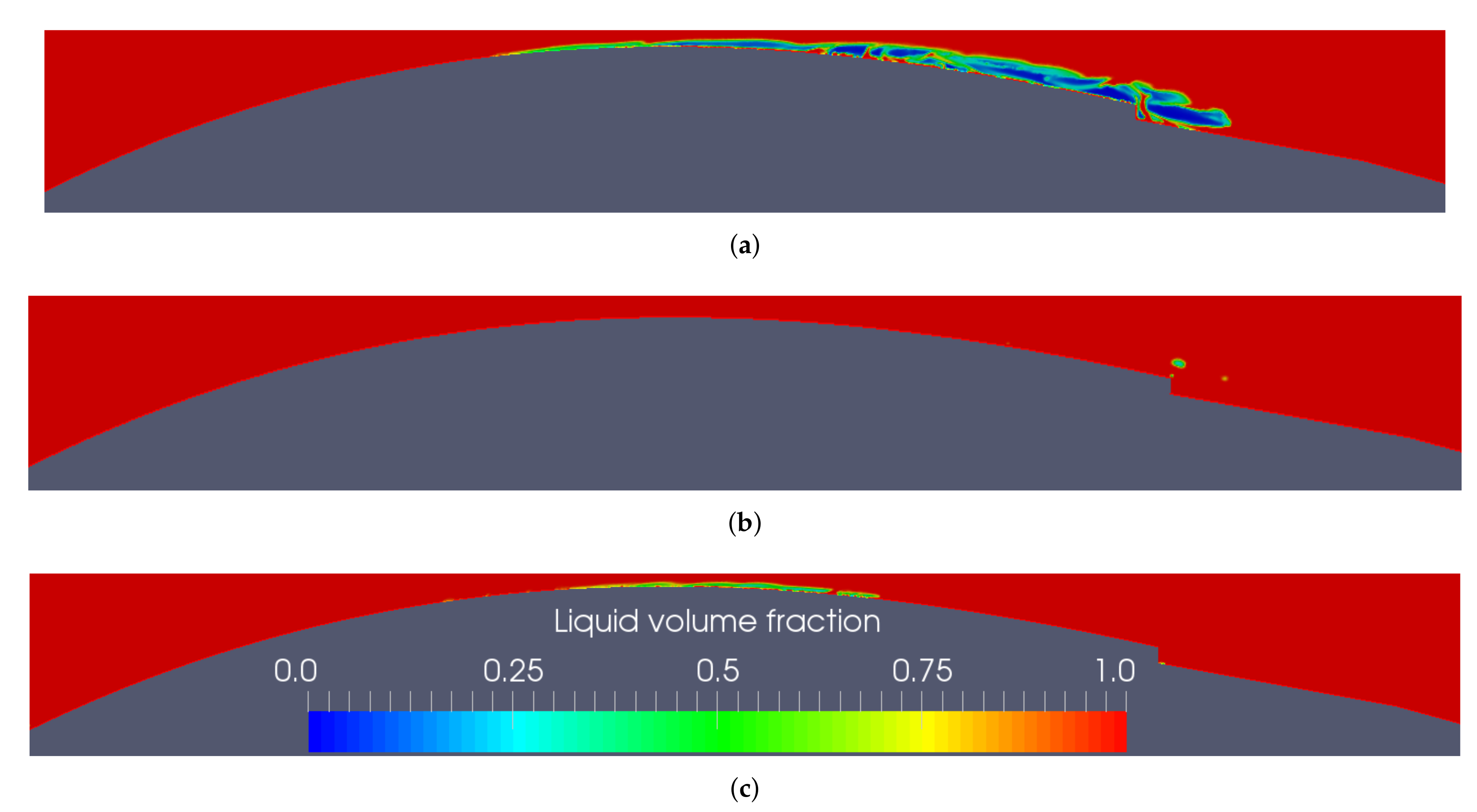
Figure 5a–c shows the contour of liquid volume fraction over the hydrofoil for no injection (case AOA3b), mild injection (case AOA3c)and high injection (case AOA3c) respectively. For the no injection case the bubbles or the phenomena of cavitation is seen extending from the
of chord length to the
of chord length. However, with the mild wall injection rate, this length of the cavity is drastically reduced. But if the injection rate is increased further (case AOA3d), the cavitation again appears. Thus the mild injection jet from the wall of the hydrofoil helps to mitigate the cavitation. These facts are already being highlighted by the experimental study of [
4].
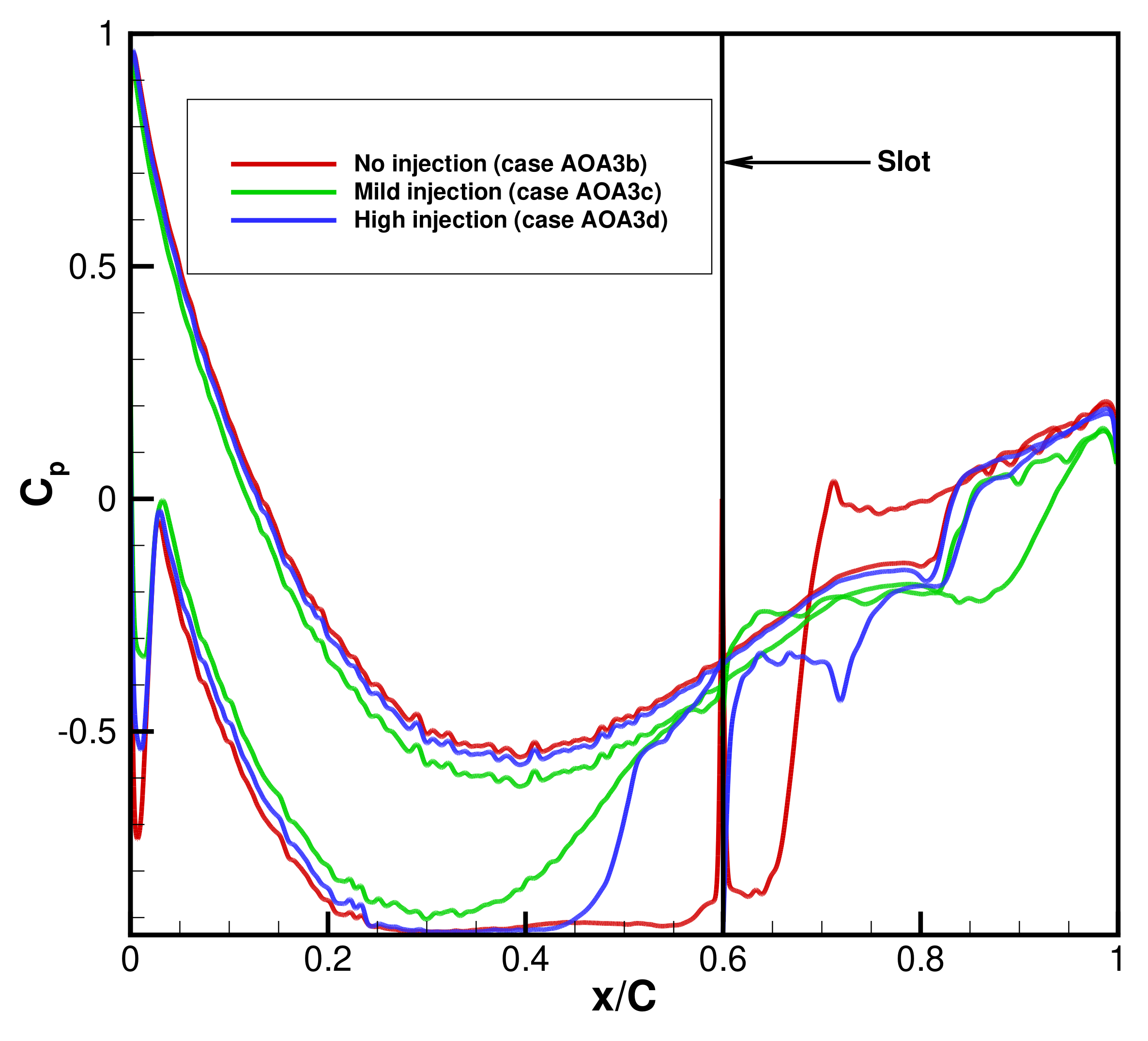
But on the other hand, if we compare the coefficient of pressure (
), to evaluate the effect on the hydrodynamic performance of the hydrofoil, then it can be clearly seen from the
Figure 6 that with the increase of the wall injection rate (case AOA3d) the difference in the (
) values for the suction side and the pressure side increases as compared with the mild injection rate (case AOA3c). This diminishing difference of
value in the pressure and suction side ultimately results in the decrease of the lift value, according to the relation:
here,
is the coefficient of pressure,
is leading edge location,
is the trailing edge location,
is coefficient of pressure on pressure side and
is coefficient of pressure on suction side. Thus, it can be seen that the mild wall injection is preferred for the cavitation control while the high wall injection is preferred for the hydrodynamic performance of the hydrofoil. This can be easily understood since for the mild injection, the local pressure increase, which inhibits the cavitation but adversely affects the hydrodynamic performance (in terms of Lift and/or coefficient of pressure).
4.2. Higher Angle of Attack AOA
Figure 7a–c shows the velocity deficit profiles for the higher angle of attack, for no injection (case AOA9b), mild injection (case AOA9c) and high injection (case AOA9d) respectively. There is a large discrepancy in the present set of simulations and the previous experimental work. This discrepancy can be attributed to the large flow separation. Thus for simulating large flow separation, the high fidelity simulations like the 3D LES could be useful.