Considering the Diffusive Effects of Cavitation in a Homogeneous Mixture Model
Abstract
1. Introduction
2. Mathematical Model
2.1. Homogeneous Mixture Cavitation Model
2.2. Constant-Transfer Coefficient Model
3. Validation
3.1. Gas Bubbles
3.2. Gas–Vapor Bubbles
4. Conclusions and Prospects
Author Contributions
Funding
Conflicts of Interest
References
- Lauer, E.; Hu, X.Y.; Hickel, S.; Adams, N.A. Numerical modelling and investigation of symmetric and asymmetric cavitation bubble dynamics. Comput. Fluids 2012, 69, 1–19. [Google Scholar] [CrossRef]
- Tiwari, A.; Freund, J.B.; Pantano, C. A diffuse interface model with immiscibility preservation. J. Comput. Phys. 2013, 252, 290–309. [Google Scholar] [CrossRef] [PubMed]
- Ding, S.T.; Luo, B.; Guo, L. A volume of fluid based method for vapor-liquid phase change simulation with numerical oscillation suppression. Int. J. Heat Mass Transf. 2017, 110, 348–359. [Google Scholar] [CrossRef]
- Singh, N.K.; Premachandran, B. A coupled level set and volume of fluid method on unstructured grids for the direct numerical simulations of two-phase flows including phase change. Int. J. Heat Mass Transf. 2018, 122, 182–203. [Google Scholar] [CrossRef]
- Plesset, M.S.; Prosperetti, A. Bubble dynamics and cavitation. Annu. Rev. Fluid Mech. 1977, 9, 145–185. [Google Scholar] [CrossRef]
- Wu, Q.; Huang, B.; Wang, G.; Gao, Y. Experimental and numerical investigation of hydroelastic response of a flexible hydrofoil in cavitating flow. Int. J. Multiphase Flow 2015, 74, 19–33. [Google Scholar] [CrossRef]
- Ye, Y.; Li, G. Modeling of hydrodynamic cavitating flows considering the bubble-bubble interaction. Int. J. Multiphase Flow 2016, 84, 155–164. [Google Scholar] [CrossRef]
- Chen, Y.; Li, J.; Gong, Z.; Chen, X.; Lu, C. Large eddy simulation and investigation on the laminar-turbulent transition and turbulence-cavitation interaction in the cavitating flow around hydrofoil. Int. J. Multiphase Flow 2019, 112, 300–322. [Google Scholar] [CrossRef]
- Liu, Y.; Lu, L.; Zhu, K. Numerical Analysis of the Diaphragm Valve Throttling Characteristics. Processes 2019, 7, 671. [Google Scholar] [CrossRef]
- Jiao, W.; Cheng, L.; Xu, J.; Wang, C. Numerical Analysis of Two-Phase Flow in the Cavitation Process of a Waterjet Propulsion Pump System. Processes 2019, 7, 690. [Google Scholar] [CrossRef]
- Li, H.; Li, H.; Huang, X.; Han, Q.; Yuan, Y.; Qi, B. Numerical and Experimental Study on the Internal Flow of the Venturi Injector. Processes 2020, 8, 64. [Google Scholar] [CrossRef]
- Jing, T.; Cheng, Y.; Wang, F.; Bao, W.; Zhou, L. Numerical Investigation of Centrifugal Blood Pump Cavitation Characteristics with Variable Speed. Processes 2020, 8, 293. [Google Scholar] [CrossRef]
- Li, W.; Li, E.; Shi, W.; Li, W.; Xu, X. Numerical Simulation of Cavitation Performance in Engine Cooling Water Pump Based on a Corrected Cavitation Model. Processes 2020, 8, 278. [Google Scholar] [CrossRef]
- Ye, Y.; Dong, C.; Zhang, Z.; Liang, Y. Modeling acoustic cavitation in homogeneous mixture framework. Int. J. Multiphase Flow 2020, 122, 103142. [Google Scholar] [CrossRef]
- Wang, Q.X. Oscillation of a bubble in a liquid confined in an elastic solid. Phys. Fluids 2017, 29, 072101. [Google Scholar] [CrossRef]
- Delale, C.F.; Schnerr, G.H.; Sauer, J. Quasi-one-dimensional steady-state cavitating nozzle flows. J. Fluid Mech. 2001, 427, 167–204. [Google Scholar] [CrossRef]
- Alehossein, H.; Qin, Z. Numerical analysis of Rayleigh-Plesset equation for cavitating water jets. Int. J. Numer. Meth. Eng. 2007, 72, 780–807. [Google Scholar] [CrossRef]
- Shams, E.; Finn, J.; Apte, S.V. A numerical scheme for Euler-Lagrange simulation of bubbly flows in complex systems. Int. J. Numer. Methods Fluids 2011, 67, 1865–1898. [Google Scholar] [CrossRef]
- Preston, A.T.; Colonius, T.; Brennen, C.E. A reduced-order model of diffusive effects on the dynamics of bubbles. Phys. Fluids 2007, 19, 502. [Google Scholar] [CrossRef]
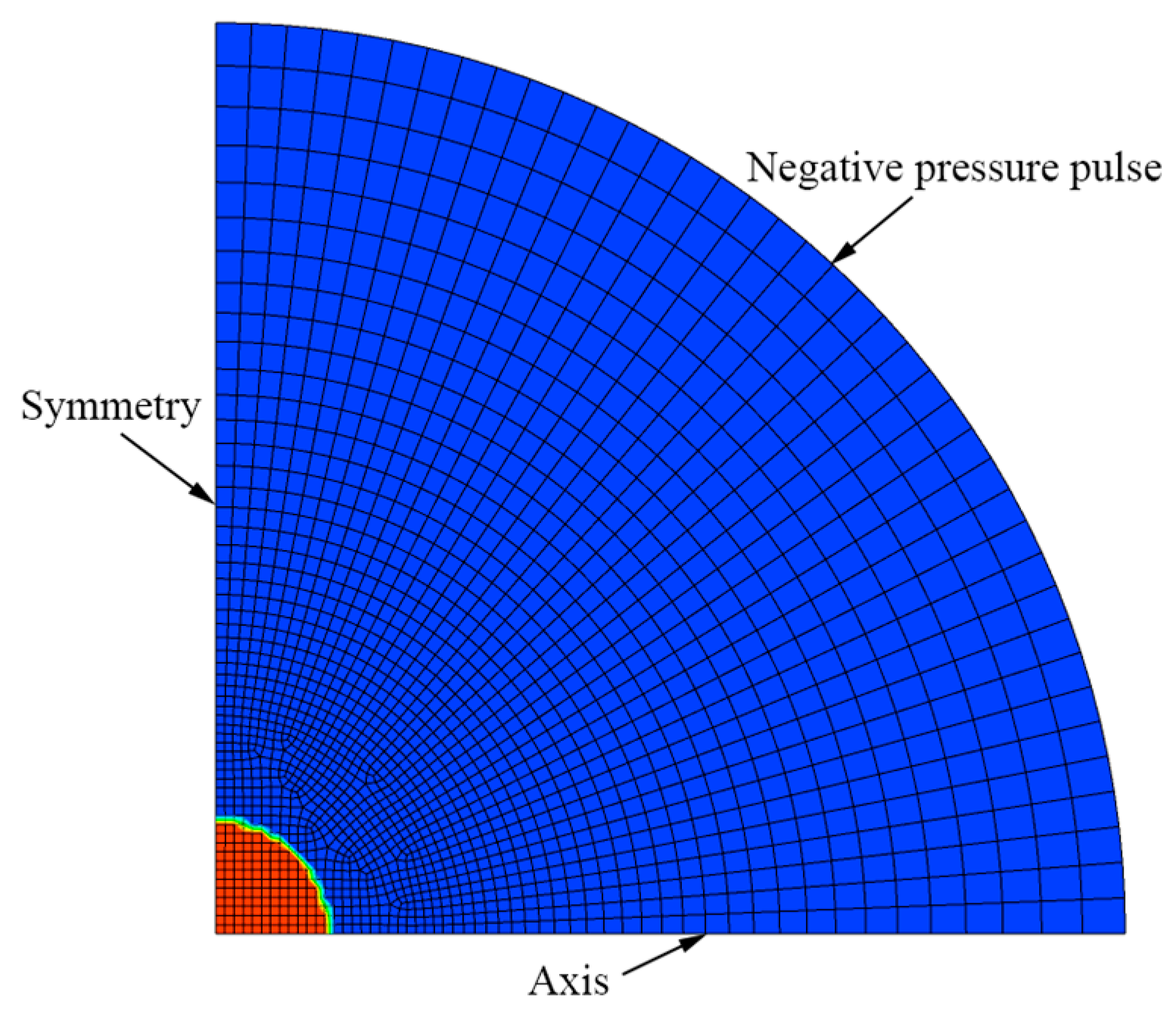


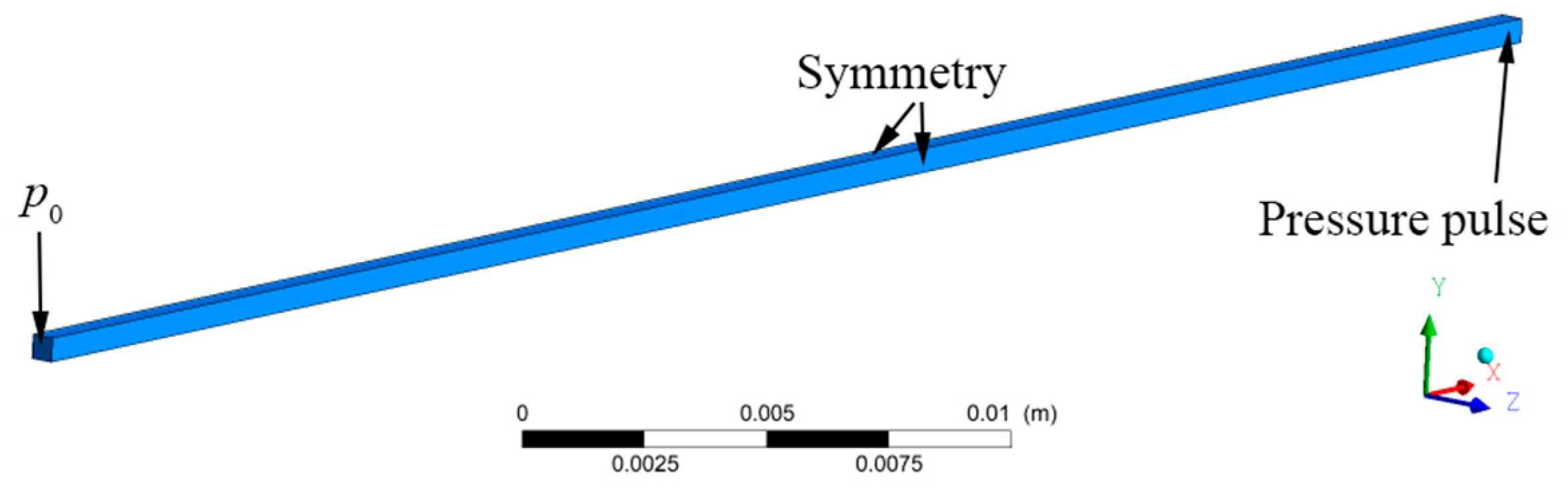



| Case | R0 (μm) | Re (mm) | p0 (kPa) | ps0 (Pa) | S (N/m) | Ω0 (kHz) | βT | βC | Ap | tw (s) |
|---|---|---|---|---|---|---|---|---|---|---|
| A | 10 | 5 | 101.325 | 0 | 0 | 1746 | 5.15 | - | 1 | 10−4 |
| B | 40 | 5 | 20 | 0 | 0 | 193.9 | 5.02 | - | 1 | 10−4 |
| C | 40 | 5 | 50 | 0 | 0 | 306.6 | 5.28 | - | 1 | 10−4 |
| D | 40 | 5 | 101.325 | 0 | 0 | 436.5 | 6.46 | - | 1 | 10−4 |
| E | 40 | 5 | 200 | 0 | 0 | 613.3 | 9.03 | - | 1 | 10−4 |
| F | 40 | 5 | 500 | 0 | 0 | 969.7 | 15.7 | - | 1 | 10−4 |
| G | 40 | 5 | 800 | 0 | 0 | 1227 | 21.4 | - | 1 | 10−4 |
| H | 100 | 5 | 101.325 | 0 | 0 | 174.6 | 8.69 | - | 1 | 10−4 |
| I | 40 | 1000 | 101.325 | 3142 | 0.072 | 434.9 | 6.56 | 6.21 | 0.985 | 10−4 |
| J | 40 | 1000 | 101.325 | 3142 | 0.072 | 434.9 | 6.56 | 6.21 | 0.97 | 10−3 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ye, Y.; Dong, C.; Zhang, Z.; Liang, Y. Considering the Diffusive Effects of Cavitation in a Homogeneous Mixture Model. Processes 2020, 8, 662. https://doi.org/10.3390/pr8060662
Ye Y, Dong C, Zhang Z, Liang Y. Considering the Diffusive Effects of Cavitation in a Homogeneous Mixture Model. Processes. 2020; 8(6):662. https://doi.org/10.3390/pr8060662
Chicago/Turabian StyleYe, Yanghui, Cong Dong, Zhiguo Zhang, and Yangyang Liang. 2020. "Considering the Diffusive Effects of Cavitation in a Homogeneous Mixture Model" Processes 8, no. 6: 662. https://doi.org/10.3390/pr8060662
APA StyleYe, Y., Dong, C., Zhang, Z., & Liang, Y. (2020). Considering the Diffusive Effects of Cavitation in a Homogeneous Mixture Model. Processes, 8(6), 662. https://doi.org/10.3390/pr8060662




