Abstract
Because of the promising results obtained by machine learning (ML) approaches in several fields, every day is more common, the utilization of ML to solve problems in bioinformatics. In genomics, a current issue is to detect and classify transposable elements (TEs) because of the tedious tasks involved in bioinformatics methods. Thus, ML was recently evaluated for TE datasets, demonstrating better results than bioinformatics applications. A crucial step for ML approaches is the selection of metrics that measure the realistic performance of algorithms. Each metric has specific characteristics and measures properties that may be different from the predicted results. Although the most commonly used way to compare measures is by using empirical analysis, a non-result-based methodology has been proposed, called measure invariance properties. These properties are calculated on the basis of whether a given measure changes its value under certain modifications in the confusion matrix, giving comparative parameters independent of the datasets. Measure invariance properties make metrics more or less informative, particularly on unbalanced, monomodal, or multimodal negative class datasets and for real or simulated datasets. Although several studies applied ML to detect and classify TEs, there are no works evaluating performance metrics in TE tasks. Here, we analyzed 26 different metrics utilized in binary, multiclass, and hierarchical classifications, through bibliographic sources, and their invariance properties. Then, we corroborated our findings utilizing freely available TE datasets and commonly used ML algorithms. Based on our analysis, the most suitable metrics for TE tasks must be stable, even using highly unbalanced datasets, multimodal negative class, and training datasets with errors or outliers. Based on these parameters, we conclude that the F1-score and the area under the precision-recall curve are the most informative metrics since they are calculated based on other metrics, providing insight into the development of an ML application.
Keywords:
transposable elements; metrics; machine learning; deep learning; detection; classification 1. Introduction
Transposable elements (TEs) are genomic units able to move within and among the genomes of virtually all organisms [1]. They are the main contributors to genomic diversity and genome size variations [2], except for of polyploidy events. Also, TEs perform key genomic functions involved in chromosome structuring, gene expression regulation and alteration, adaptation and evolution [3], and centromere composition in plants [4]. Currently, an important issue in genome sequence analyses is to rapidly identify and reliably annotate TEs. However, there are major obstacles and challenges in the analysis of these mobile elements [5], including their repetitive nature, structural polymorphism, species specificity, as well as high divergence rate, even across close relative species [6].
TEs are traditionally classified according to their replication mode [7]. Elements using an RNA molecule as an intermediate are called Class I or retrotransposons, while elements using a DNA intermediate are called Class 2 or transposons [8]. Each class of TEs is further sub-classified by a hierarchical system into orders, superfamilies, lineages, and families [9].
Several bioinformatic methods were developed to detect TEs in genome sequences, including homology-based, de novo, structure-based, and comparative genomic, but no combination of them can provide a reliable detection in a relatively short time [10]. Most of the algorithms currently available use a homology-based approach [11], displaying performance issues when analyzing elements in large plant genomes. In the current scenario of large-scale sequencing initiatives, such as the Earth BioGenome Project [12], disruptive technologies and innovative algorithms will be necessary for genome analysis in general and, particularly, for the detection and classification of TEs that represent the main portion of these genomes [13].
In recent years, several databases consisting of thousands of TE at all classification levels of several species and taxa have been created and published [3]. Furthermore, these databases have different characteristics, such as containing consensus [14,15,16] or genomic [17,18] TE sequences, coding domains [9,19], and also TE-related RNA [20,21]. These databases have been constructed with the TEs detected in species sequenced using bioinformatics approaches (commonly based on homology or structure), which can produce false positive if there is no a curation process [11]. As other biological sets (such as datasets of splice sites [22], or protein function predictions [23]), databases have distinct numbers of different types of TEs producing unbalanced classes [23]. For example in PGSB, the largest proportion of the elements corresponds to retrotransposons (at least 86%) [24]. The above is caused by the replication mode of each TE class. As in other detection tasks, the negative instances for identifying TEs are all other genomic elements than TEs (that constitute the positive instances) [25,26,27], such as introns, exons, CDS (coding sequences), and simple repeats, among others, making the negative class multimodal. These databases constitute valuable resources to improve tasks like TE detection and classification using bioinformatics or also novel techniques such as machine learning (ML).
ML is defined as a set of algorithms that can be calibrated based on previously processed data or past experience [28] and a loss function through an optimization process [29] to build a model. ML is applied to different bioinformatics problems, including genomics [30], systems biology, evolution [28], and metagenomics [31], demonstrating substantial benefits in terms of precision and speed. Several recent studies using ML to detect TEs report drastic improvements in the results [32,33,34] compared to conventional bioinformatics algorithms [13].
In ML, the selection of adequate metrics that measure the algorithms’ performance is one of the most crucial and challenging steps. Commonly used metric for classification tasks are accuracy, precision, recall, and ROC curves [35,36], but they are not appropriate for all datasets [37], especially when the positive and negative datasets are unbalanced [13]. Accuracy and ROC curves can be meaningless performance measurements in unbalanced datasets [22], because it does not reveal the true classification performance of the rare classes [38]. For example, ROC curves are not commonly used in TE classification, because only a small portion of the genome contains certain TE superfamilies [34]. On the other hand, precision and recall can be more informative since precision is the percentage of predictions that are correct [34] and recall is the percentage of true samples that are correctly detected [26], nevertheless it is recommended to use them in combination with other metrics since the use of only one of these metrics cannot provide a full picture of the algorithm performance [36].
Most of the classification and detection tasks addressed by ML define two classes, positive and negative [13]. Thus, expected results can be classified as true positive (tp) if they were classified as positive and are contained in the positive class, while as false negatives (fn) if they were rejected but did not belong to the negative class. On the other hand, samples that are contained in negative class and predicted to be positive constitute false positives (fp), or true negative (tn) if they are not [13,28,39]. These markers are related in the confusion matrix, and most of the metrics used in ML are calculated based on this matrix.
Depending on the goal of the application and the characteristics of the elements to be classified, other metrics addressing classification (binary, multiclass, hierarchical), class balance (i.e., if training dataset is imbalanced or not), and the importance of positive or negative instances [36] must be considered. Another point is the ability of a metric to preserve the value under a change in the confusion matrix, called measure invariance [40]. This properties give comparative parameters between metrics that are not based on datasets, but in the way they are calculated. Each of the properties of the invariance can be beneficial or unfavorable depending on the main objectives, the balance of the classes, the size of the data sets, the quality, and the composition of the negative class, among others [40]. Thus, invariance properties are useful tools in order to select the most informative metrics in each ML problem.
Recently, different ML-based software have been developed to tentatively detect repetitive sequences [34,41,42], classify them (at the order or superfamily levels) [27,43,44,45], or both [10,46]. Additionally, deep neural networks-based software were also developed to classify TEs [11,47]. Nevertheless, there are no studies about which metrics can be more suitable taking into account the unique characteristics of transposable element datasets and their dynamic structure. Here, we evaluated 26 metrics found in the literature for TE detection and classification, considering the main features of this type of data, the invariance properties and characteristics of each metric in order to select the more appropriate ones for each type of classification.
2. Materials and Methods
2.1. Bibliography Analysis
As a literature information source, we used the results obtained by [13], who applied the systematic literature review (SLR) process proposed by [48]. The authors applied the search Equation (1) to perform a systematic review of research articles, book chapters and other review papers presented in well-known bibliographic databases such as Scopus, Science Direct, Web of Science, Springer Link, PubMed, and Nature.
(“transposable element” OR retrotransposon OR transposon) AND (“machine learning” OR “deep learning”)
Applying the Equation (1), a total of 403 publications were identified of which authors removed those which do not satisfy certain conditions such as repeated (the same study was found in different databases); of different types (books, posters, short articles, letters and abstracts); and written in other languages (languages other than English). Then, authors used inclusion and exclusion criteria in order to select interested articles. Finally, 35 publications were selected as relevant in the fields of ML and TE [13]. Using these relevant publications, we identified the metrics used for the detection and classification of TEs, preserving information such as representation and observations (i.e., the properties measured). Next, we evaluated each metric that was reported as a decisive source in relevant publications. The characteristics and properties of each metric were analyzed regarding their application to TEs, considering that these elements have some characteristics, such as highly variant dynamics for each class, negative datasets with a large number of genomic elements for detection, a great divergence between elements of the same class, and species specificity.
2.2. Measure Invariance Analysis
Comparing the performance measures in ML approaches is not straightforward, and although the most common way to select most informative measures is by using empirical analysis [49,50], an alternative methodology was proposed [40], which consists of assessing whether a given metric changes its value under certain modifications in the confusion matrix. This property is named measure invariance, and can be used to compare performance metrics without focusing on their experimental results but using their measuring characteristics such as detecting variations in the number of true positives (tp), false positives (fp), false negative (fn), or true negatives (tn) presented in the confusion matrix [40]. Thus, a measure is invariant when its calculation function f which receives a confusion matrix produces the same value even if the confusion matrix has modifications. For example, consider the following confusion matrix , where tp = 10, fn = 4, fp = 3, and tn = 16 and the function for calculating accuracy , thus the accuracy for the confusion matrix presented above is . Now consider exchanging the positive (tp by tn) and negative (fp by fn) values in the confusion matrix obtaining the following . If we apply the function f over the new confusion matrix, so we obtain . In this case, we can conclude that accuracy cannot detect exchanges of positive and negative values and thus it is invariant due to .
In this work, we used eight invariance properties to compare measures which were selected in the bibliographic analysis. All these invariances were derived from basic matrix operations, such as addition, scalar multiplication, and transposition of rows or columns, as following [40]:
- Exchange of positives and negatives (I1): A measure presents invariance in this property if showing invariance corresponding to the distribution of classification results due to its inability to differentiate tp from tn and fn from fp. An invariant metric in this property may not be utilized in datasets highly unbalanced [40], such as the number of TEs belonging to each lineage in the Repbase or PGSB databases.
- Change of true negative counts (I2): A measure presents invariance in this property if , demonstrating the inability to recognize specificity of the classifiers. This property can be useful in problems with multi-modal negative class (the class with all elements other than the positive), i.e., in the detection of TEs, where negative class may be composed by all other genomic features such as genes, CDS (coding sequences), and simple repeats, among others.
- Change of true positive counts (I3): A measure presents invariance in this property if , losing the sensitivity of the classifiers, so their evaluation should be complementary to other metrics.
- Change of false negative counts (I4): A measure presents invariance in this property if , indicating stability even when the classifier has errors assigning negative labels. It is helpful in detecting or classifying TEs when non-curated databases are used in training (such as RepetDB), which may contain mistakes.
- Change of false positive counts (I5): A measure presents invariance in this property if , proving reliable results even though some classes contain outliers, which is common in elements classified at lineage level due to TE diversity in their nucleotide sequences [26].
- Uniform change of positives and negatives (I6): A measure presents invariance in this property if , with It indicates if a measure’s value changes when the size of the dataset increases. The non-invariance indicates that the application of the metric depends on size of the data.
- Change of positive and negative columns (I7): A measure presents invariance in this property if , with If a metric is unchanged in this way, it will not show changes when additional datasets differs from training datasets in quality (i.e., having more noise), and indicating the needed of other measures as complement. On the contrary, if a metric presents a non-invariant behavior then, it may be suitable if different performances are expected across classes.
- Change of positive and negative rows (I8): A measure presents invariance in this property if , with In this case, if a metric is non-invariant, its applicability depends on the quality of the classes. It may be useful, for example, when curated datasets are available such as Repbase.
Properties described above were calculated by [40] for commonly used performance measures and we used them to analyze selected metrics (Table 1), except for area under the precision-recall curve (auPRC) which was calculated by us, following the methodology proposed by authors.

Table 1.
Invariance properties of selected metrics. 0 for invariance and 1 for non-invariance. Adapted from [40].
2.3. Experimental Analysis
To test the behavior of the most commonly used metrics, such as accuracy, precision, and recall, and the best scoring metric found in this study, we performed several experiments addressing the specific problem of multi-class classification of LTR retrotransposons at the lineage level in plants. We selected this problem since LTR retrotransposons are the most common repeat sequences in almost all angiosperms and they represent an important fraction of their host genome; for instance, 75% in maize [51], 67% in wheat [52], 55% in Sorghum bicolor [53], and 42% in Robusta coffee [54]. As input, we used two well-known TE databases: Repbase (free version, 2017) [14] and PGSB [17]. For Repbase, we joined the LTR domains with the internal section (concatenating before and after) of each LTR retrotransposon found in the database. The first step was to generate a well-curated dataset of LTR retrotransposons; thus, we classified LTR retrotransposons from both databases at the lineage level using the homology-based Inpactor software [55] with RexDB nomenclature [9]. Inpactor has two filters for deleting nested elements: (1) Removing elements with domains belonging to two different superfamilies (i.e., Copia and Gypsy) and (2) removing elements with domains belonging to two or more different lineages. Additionally, we applied three extra filters: (1) Removing elements with lengths different from those reported by the Gypsy Database [19] with a tolerance of 20% (this value was chosen to filter elements with nested insertion of others TEs but keeping elements with natural divergence), (2) removing elements with less than two domains (incomplete elements derived from deletion processes), and (3) removing elements with insertions of partial or complete TEs from class II (present in Repbase). Finally, we removed elements from the following lineages: Alesia, Bryco, Lyco, Gymco, Osser, Tar, CHLAMYVIR, Retand, Phygy, and Selgy due to their very low frequency or absence in angiosperms.
Since the datasets used in this study are categorical (nucleotide sequences), we transformed them using the coding schemes shown in Table 2. Also, we used two additional techniques to automatically extract features from the sequences; (1) for each element, we obtained k-mer frequencies using k values between one and six (this range of values of k was selected due to k-mers with k > 6 are rare in sequences and probably do not provide informational features and they are computationally expensive to calculate) and (2) we extracted three physical-chemical (PC) properties, such as average hydrogen bonding energy per base pair (bp), stacking energy (per bp), and solvation energy (per bp), which are calculated by taking the first di-nucleotide and then moving in a sliding window of one base at a time [56]. Since the ML algorithms used here require sequences of the same lengths, we found the largest TE in each dataset and completed the smaller sequences by replicating their nucleotides.

Table 2.
Coding schemes for translating DNA characters in numerical representations. Adapted from [13].
We applied the workflow described in [62] to compare commonly used ML algorithms using supervised techniques. As the authors suggested, we applied four types of pre-processing strategies: none (raw data), scaling, data dimensionality reduction using principal component analysis (PCA), and both scaling and PCA. On the other hand, we used some of the most common ML algorithms [62], including linear support vector classifier (SVC), logistic regression (LR), linear discriminant analysis (LDA), K-nearest neighbors (KNN), naive Bayesian classifier (NB), multi-layer perceptron (MLP), decision trees (DT), and random forest (RF). All algorithms were tested by varying or tuning parameter values to find the best performance (Table 3).

Table 3.
Tested algorithm parameters.
The experiments consisted in executing all possible combinations between databases, coding schemes, pre-processing strategies, and ML algorithms (Figure 1 and Table 4). First, we used the accuracy and, the F1-score using the macro-averaging strategy as main metric in tuning process (Table 3). Finally, we calculated other common metrics using the best value of the tuned parameter in each algorithm for comparison. All the experiments were performed using Python 3.6 and Scikit-Learn library 0.22 [63], installed in a Anaconda environment in Linux over a CPU architecture. We ran our tests using the HPC cluster of IFB (https://www.france-bioinformatique.fr), IRD itrop (https://bioinfo.ird.fr/) and Genotoul Bioinformatics platform (http://bioinfo.genotoul.fr/), all of them are managed by Slurm.
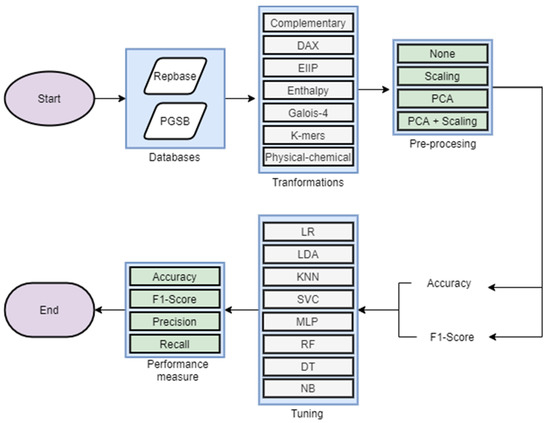
Figure 1.
Overall flow of the experimental analysis done in this work.

Table 4.
Description of experiments performed.
3. Results
3.1. Bibliography and Invariance Analysis
Based on relevant literature sources (articles) detected in [13], by searching in several databases, we collected 26 metrics that are commonly used in different types of classification tasks, such as binary, multi-class, and hierarchical (Table 5). We were interested in classification metrics because the detection task can be considered as a binary classification (using TEs as positive class and non-TEs as negative class). Additionally, we assigned an importance level for each metric (Table 5) based on the following aspects: (i) How appropriate is its application to analyzing TE datasets (detection and classification)? (ii) Which features are measured and how important are these features for TE analysis? For each metric, each aspect is assigned a level of importance (low, medium, high). Furthermore, the properties reported in relevant publications were used to evaluate each metric. In this way, we extracted and summarized information about each metric and we evaluated if its use for TE datasets is plausible. General observations of metrics can be found in the observations column in Table S4.

Table 5.
Metrics used in classification problems. Adopted from [22,34,35,40,64,65,66,67,68].
We performed invariance analyses on the metrics with the best evaluation for each classification type (Table 1). Precision-Recall curves were excluded for further analysis at this step since it is impossible to calculate graphics from a confusion matrix. We obtained the invariance properties for almost all metrics from [40], except for area under the precision recall curve (ID = 11). For this metric, we generated a random confusion matrix and applied all the transformations presented in [40] in order to calculate its value and determine if it changed or not. The invariance analyses were performed based on the one described by [40].
3.2. Experimental Analysis
To evaluate the relevance of the literature reports about metrics, we applied them to experiments on the multi-class classification of LTR retrotransposons in angiosperm plants at the lineage level. Using nucleotide sequences from Repbase [14] (free version, 2017) and PGSB [17] as input, we performed a classification process using Inpactor [55]. We generated high-quality datasets by removing sequences that did not satisfy certain filters (See Materials and Methods). After filtering and homology-based classification, we obtained 2,842 TEs from Repbase and 26,371 elements from PGSB (Table 6).

Table 6.
Number of nucleotide sequences of each plant lineage used in Repbase and PGSB databases.
We executed four experiments using the generated datasets (Table 4) to evaluate the behavior of each metric in different configurations. In the first two experiments, we were interested in analyzing the performance of accuracy and F1-score metrics using a well-curated dataset (Repbase) but with a few different sequences in some lineages (Figure 2, Figures S1 and S2). In the last two experiments, we evaluated a larger dataset (PGSB) and tested the same two metrics (Figure 3, Figure S3 and S4). The complete results of all the experiments can be consulted in Tables S5–S8.
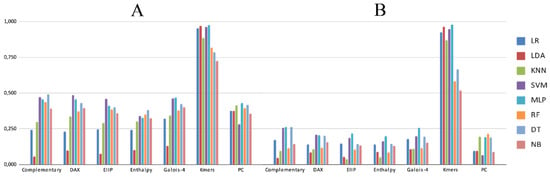
Figure 2.
Performance of machine learning (ML) algorithms and Repbase pre-processed data by principal component analysis (PCA) and scaling processes using as main metric: (A) accuracy and (B) F1-score.
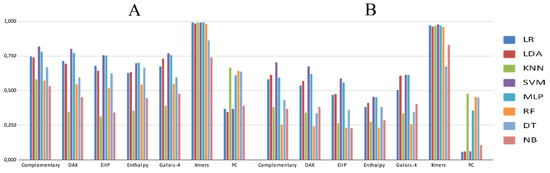
Figure 3.
Performance of ML algorithms and PGSB pre-processed data by PCA and scaling processes using as main metric: (A) Accuracy and (B) F1-score.
Figure 2 and Figure 3 show the best performance achieved by each algorithm after tuning one parameter (Table 3), using as main metric accuracy or F1-score. Since each coding scheme displayed a different behavior, we were interested in further analyzing how each metric behaves in different algorithms and coding schemes. K-mers (Figure 4) showed the best performance, PC (Figure 5) displayed the worst performances, and complementary (Figure 6) showed an intermediate performance, which were selected for further analyses.
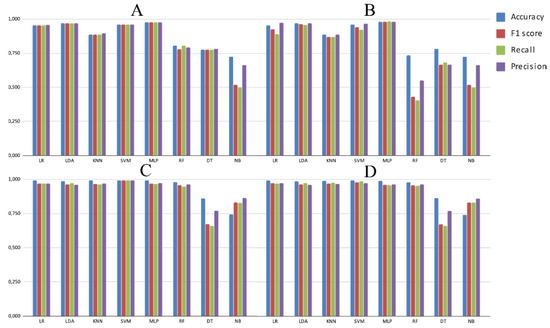
Figure 4.
Results of ML algorithms using nucleotide sequences transformed by k-mers, PCA and scaling, and applying accuracy, F1-score, recall and precision metrics. Experiments: (A) Exp1, (B) Exp2, (C) Exp3, and (D) Exp4.
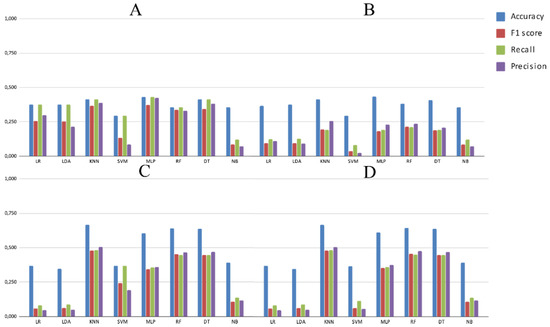
Figure 5.
Results of ML algorithms using sequences transformed by PC and PCA and scaling, and applying accuracy, F1-score, recall, and precision metrics. Experiments: (A) Exp1, (B) Exp2, (C) Exp3, and (D) Exp4.
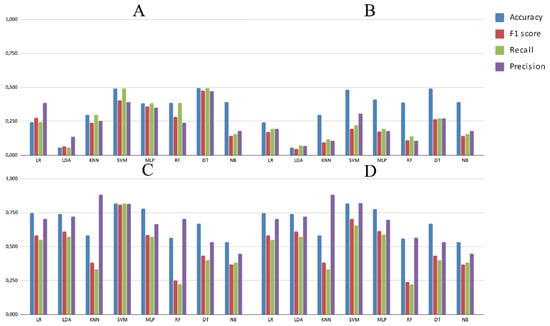
Figure 6.
Results of ML algorithms using sequences transformed by PC and PCA and scaling, and applying accuracy, F1-score, recall and precision metrics. Experiments: (A) Exp1, (B) Exp2, (C) Exp3, and (D) Exp4.
4. Discussion
The detection and classification of transposable elements is a crucial step in the annotation of sequenced genomes, because of their relation with genome evolution, gene function, regulation, and alteration of expression, among others [74,75]. This step remains challenging given their abundance and diverse classes and orders. In addition, other characteristics of TEs, such as a relatively low selection pressure and a more rapid evolution than coding genes [26], their dynamic evolution due to insertions of other TEs (nested insertion), illegitimate and unequal recombination, cellular gene capture, and inter-chromosomal and tandem duplications [76], make them difficult targets for accurate and rapid detection and classification procedures. Indeed, TEs showing uniform structures and well-established mechanisms of transposition can be easily clustered and classified into major groups such as orders or superfamilies (e.g., LTR retrotransposons) [77]. However, this task is relatively complex and time-consuming when classifying TEs into lower levels, such as lineages or families [78]. For these reasons, TE classification and annotation are complex bioinformatics tasks [79], in which, in some cases, manual curation of sequences is required by specialists. The ability of biologists to sequence any organism or a group of organisms in a relatively short time and at relatively low costs redefines the barrier of the genomic information. The current limitation is not the generation of genome sequences but the amount of information to be processed in a limited time. Complex bioinformatics tasks may be accomplished by machine learning algorithms, such as in drug discovery and other medical applications [80], genomic research [38,81], metagenomics [31,82], and multiple applications in proteomics [83].
Previous works apply ML and DL for TE analysis, such as Arango-López et al. (2017) [43] for the classification of LTR-retrotransposons, Loureiro et al. (2012) [84] for the detection and classification of TEs using developed bioinformatics tools, and Ashlock and Datta (2012) [69] distinguishing between retroviral LTRs and SINEs (short interspersed nuclear elements). Deep neural networks (DNN) are also used to hierarchically classify TEs by applying fully connected DNN [11] and through convolutional neural networks (CNN) and multi-class approaches [47].
In TE detection and classification, the dataset could be highly imbalanced [23]; therefore, commonly used metrics such as accuracy and ROC curves may not be fully adequate [36]. For the detection task, the positive class will be much lower than the negative, because the latter will have all other genomic elements. In classification, each type of TE (classes, orders, superfamilies, lineages, or families) has different dynamics that produce a distinct number of copies. For example, in the coffee genus, LTR-retrotransposons show large copy number differences depending on the lineage [85]. In Oryza australiensis [86] and pineapple genomes [87], only one family of LTR-retrotransposons contributes to 26% and 15% (Pusofa) of the total genome size, respectively.
For binary classification (for example, to detect TEs or classify them into class 1 and class 2), the most appropriate metric is F1-score (id = 7), which considers precision and recall values. Precision is a useful parameter when the number of false-positive must be limited and recall measures how many positive samples are captured by the positive predicted [36]. However, the use of only one of these metrics cannot provide a full picture of the algorithm performance. Altogether, our results suggest that F1-score is appropriate for TE analyses.
In multi-class approaches (such as TE classification into orders, superfamilies, or lineages), F1-score (id = 20) also seems to be the most suitable metric, combined with the macro-averaging strategy, probably due to the high diversity of intra-class samples. For TE detection and classification, it appears more important to weigh all classes equally than to weigh each sample equally (micro-averaging strategy). Finally, for hierarchical classification approaches (i.e., considering the hierarchical classification of TEs proposed by Wicker and coworkers [8]), F1-score↓ (id = 26) and F1-score↑ (id = 23) seem most suitable. These results demonstrate the importance of calculating the performance of each hierarchical level. Additionally, precision-recall curves and area under the precision-recall curve provided the best results for binary classification, demonstrating that, for TE datasets, they are more appropriate than the commonly used ROC curves.
Area under the precision-recall curve, auPRC (id = 11), is a unique metric, which showed invariance in I1 and non-invariance in I2. Its invariance properties make auPRC a robust measure of the overall performance of an algorithm and it is insensitive to the performance for a specific class (I1). However, it less appropriate for data with a multi-modal negative class (~I2).
All metrics presented invariance in I3, indicating that they could not measure true positive change. This suggests that they can be used when the positive class is not very strong. PrecisionM (id = 18) and Precision↓(id = 21) showed non-invariance in I4, which demonstrates that these metrics may be less reliable when manual labeling follows rigorous rules for a negative class. On the other hand, RecallM (id = 19) and Recall↓ (id = 22) exhibited non-invariance in I5, indicating that these metrics may not provide a conservative estimate when the positive class has outliers, as commonly found in TE datasets. Thus, these metrics might not be informative in TE detection and classification. The non-invariance properties of all metrics in I6, shown in Table 1, demonstrated that these metrics can vary in data with large size differences. Consequently, these metrics must be used carefully for comparison with other and different datasets.
Non-invariance in I7 shown by precision (id = 18 and 21) supported the combined use of this metric with other metrics (such as in F1-score) common in ML algorithms. Finally, auPRC (id = 11), RecallM (id = 19), and Recall↓ (id = 22) may be better choices for the evaluation of classifiers if different data sizes exhibit the same quality of positive (negative) characteristics, as in the case of generated (simulated) data due to their non-invariance properties in I8.
Our tests for the multi-class classification task of LTR retrotransposons at the lineage level show an overestimation of the performance of all ML algorithms used here (Figure 2 and Figure 3) for both datasets (Repbase and PGSB). Furthermore, our experiments support the information found in the literature, indicating that accuracy is not the most informative metric for highly unbalanced datasets, such as those used in this study. Additionally, Figure 2 and Figure 3 indicate that this tendency of overestimation is generalized for nearly all the algorithms, pre-processing techniques, and coding schemes used here.
A clear exception, however, is shown by k-mers (in both training and validation datasets, Tables S4–S7), for which accuracy and F1-scores did not show any differences. Nevertheless, if the F1-score is used in the tuning process (Figure 4B,D, Figure 5B,D, and Figure 6B,D), accuracy also overestimates the performance of almost all the algorithms in comparison to F1-score, sensitivity (recall), and precision. Interestingly, RF performs in a similar manner to that of the other algorithms when PGSB (with more than 26,000 elements) is used, but DT presents the same behavior in both datasets.
When the performance of a given scheme is low, the overestimation shown by accuracy is more evident (Figure 5 and Figure 6). This is due to the extremely low performance on some lineages and, thus, accuracy is not very informative if it is not used combined with another metric. As suggested by the literature and invariance analyses, F1-score appears to be the most adequate and informative metric in the experiments performed here, since it is a harmonic estimate of precision and sensitivity by measuring the combined amount of false-positive and positive samples captured by the algorithm.
Overall, the results shown here can also be applied to data similar to TEs, such as retrovirus and endogenous retrovirus or data with highly imbalanced classes, high intra-class diversity, and negative multi-modal classes (in detection tasks).
5. Conclusions
Altogether, our analyses suggest that F1-score may be the best metric for each of the ML classification types, except for simulated data, for which auPRC and Recall should be more appropriate because of their invariance properties. Conversely, precision should be used in combination with other metrics to avoid non-realistic estimates of algorithm performance. In binary classification, precision-recall curves must be used instead of ROC curves. In multi-class classification approaches, the macro-averaging strategy seems to be more appropriate for TE detection and classification. As future work, we propose to develop a ML model based on the databases, algorithms, and coding schemes used here and using F1-score in the tuning process, to improve classification of LTR retrotransposons at the lineage level in angiosperms.
Supplementary Materials
The following are available online at https://www.mdpi.com/2227-9717/8/6/638/s1: Figure S1. Performance of ML algorithms and Repbase using accuracy as the main metric (experiment 1) and the following pre-processing techniques: (a) None, (b) scaling, (c) PCA, (d) PCA + scaling. Figure S2. Performance of ML algorithms and Repbase using F1-score as the main metric (experiment 2) and the following pre-processing techniques: (a) None, (b) scaling, (c) PCA, (d) PCA + scaling. Figure S3. Performance of ML algorithms and PGSB using accuracy as the main metric (experiment 3) and the following pre-processing techniques: (a) None, (b) scaling, (c) PCA, (d) PCA + scaling. Figure S4. Performance of ML algorithms and PGSB using F1-score as the main metric (experiment 4) and the following pre-processing techniques: (a) None, (b) scaling, (c) PCA, (d) PCA + scaling. Table S1. Metrics used in binary classification. Adopted from [22,34,35,40,64,65,66,67,68]. Table S2. Metrics used in multi-class classification. Adopted from [22,34,35,40,64,65,66,67,68]. Table S3. Metrics used in hierarchical classification. Adopted from [22,34,35,40,64,65,66,67,68]. Table S4. Evaluation for metric collection. Table S5. Results of experiment 1. Table S6. Results of experiment 2. Table S7. Results of experiment 3. Table S8. Results of experiment 4.
Author Contributions
Conceptualization, S.O.-A., G.I., and R.G.; methodology, S.O.-A., J.S.P., and R.T.-S.; writing—original draft preparation, S.O.-A., R.T.-S., J.S.P., L.F.C.-O., G.I., and R.G.; writing—review and editing, S.O.-A., R.T.-S., J.S.P., L.F.C.-O., G.I., and R.G.; supervision, G.I. and R.G. All authors have read and agreed to the published version of the manuscript.
Funding
Simon Orozco-Arias is supported by a Ph.D. grant from the Ministry of Science, Technology and Innovation (Minciencias) of Colombia, Grant Call 785/2017. The authors and publication fees were supported by Universidad Autónoma de Manizales, Manizales, Colombia under project 589-089, and Romain Guyot was supported by the LMI BIO-INCA. The funders had no role in the study design, data collection and analysis, the decision to publish, or preparation of the manuscript.
Acknowledgments
The authors acknowledge the IFB Core Cluster that is part of the National Network of Compute Resources (NNCR) of the Institut Français de Bioinformatique (https://www.france-bioinformatique.fr), the Genotoul Bioinformatics platform (http://bioinfo.genotoul.fr/), and the IRD itrop (https://bioinfo.ird.fr/) at IRD Montpellier for providing HPC resources that have contributed to the research results reported in this paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Mita, P.; Boeke, J.D. How retrotransposons shape genome regulation. Curr. Opin. Genet. Dev. 2016, 37, 90–100. [Google Scholar] [CrossRef] [PubMed]
- Keidar, D.; Doron, C.; Kashkush, K. Genome-wide analysis of a recently active retrotransposon, Au SINE, in wheat: Content, distribution within subgenomes and chromosomes, and gene associations. Plant Cell Rep. 2018, 37, 193–208. [Google Scholar] [CrossRef] [PubMed]
- Orozco-Arias, S.; Isaza, G.; Guyot, R. Retrotransposons in Plant Genomes: Structure, Identification, and Classification through Bioinformatics and Machine Learning. Int. J. Mol. Sci. 2019, 20, 781. [Google Scholar] [CrossRef] [PubMed]
- De Castro Nunes, R.; Orozco-Arias, S.; Crouzillat, D.; Mueller, L.A.; Strickler, S.R.; Descombes, P.; Fournier, C.; Moine, D.; de Kochko, A.; Yuyama, P.M.; et al. Structure and Distribution of Centromeric Retrotransposons at Diploid and Allotetraploid Coffea Centromeric and Pericentromeric Regions. Front. Plant Sci. 2018, 9, 175. [Google Scholar] [CrossRef] [PubMed]
- Ou, S.; Chen, J.; Jiang, N. Assessing genome assembly quality using the LTR Assembly Index (LAI). Nucleic Acids Res. 2018, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Mustafin, R.N.; Khusnutdinova, E.K. The Role of Transposons in Epigenetic Regulation of Ontogenesis. Russ. J. Dev. Biol. 2018, 49, 61–78. [Google Scholar] [CrossRef]
- Chaparro, C.; Gayraud, T.; De Souza, R.F.; Domingues, D.S.; Akaffou, S.S.; Vanzela, A.L.L.; De Kochko, A.; Rigoreau, M.; Crouzillat, D.; Hamon, S.; et al. Terminal-repeat retrotransposons with GAG domain in plant genomes: A new testimony on the complex world of transposable elements. Genome Biol. Evol. 2015, 7, 493–504. [Google Scholar] [CrossRef]
- Wicker, T.; Sabot, F.; Hua-Van, A.; Bennetzen, J.L.; Capy, P.; Chalhoub, B.; Flavell, A.; Leroy, P.; Morgante, M.; Panaud, O.; et al. A unified classification system for eukaryotic transposable elements. Nat. Rev. Genet. 2007, 8, 973–982. [Google Scholar] [CrossRef]
- Neumann, P.; Novák, P.; Hoštáková, N.; MacAs, J. Systematic survey of plant LTR-retrotransposons elucidates phylogenetic relationships of their polyprotein domains and provides a reference for element classification. Mob. DNA 2019, 10, 1–17. [Google Scholar] [CrossRef]
- Loureiro, T.; Camacho, R.; Vieira, J.; Fonseca, N.A. Improving the performance of Transposable Elements detection tools. J. Integr. Bioinform. 2013, 10, 231. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Nakano, F.K.; Mastelini, S.M.; Barbon, S.; Cerri, R. Improving Hierarchical Classification of Transposable Elements using Deep Neural Networks. In Proceedings of the Proceedings of the International Joint Conference on Neural Networks, Rio de Janeiro, Brazil, 8–13 July 2018; Volume 8–13 July. [Google Scholar]
- Lewin, H.A.; Robinson, G.E.; Kress, W.J.; Baker, W.J.; Coddington, J.; Crandall, K.A.; Durbin, R.; Edwards, S.V.; Forest, F.; Gilbert, M.T.P.; et al. Earth BioGenome Project: Sequencing life for the future of life. Proc. Natl. Acad. Sci. USA 2018, 115, 4325–4333. [Google Scholar] [CrossRef]
- Orozco-arias, S.; Isaza, G.; Guyot, R.; Tabares-soto, R. A systematic review of the application of machine learning in the detection and classi fi cation of transposable elements. PeerJ 2019, 7, 18311. [Google Scholar] [CrossRef] [PubMed]
- Jurka, J.; Kapitonov, V.V.; Pavlicek, A.; Klonowski, P.; Kohany, O.; Walichiewicz, J. Repbase Update, a database of eukaryotic repetitive elements. Cytogenet. Genome Res. 2005, 110, 462–467. [Google Scholar] [CrossRef] [PubMed]
- Cornut, G.; Choisne, N.; Alaux, M.; Alfama-Depauw, F.; Jamilloux, V.; Maumus, F.; Letellier, T.; Luyten, I.; Pommier, C.; Adam-Blondon, A.-F.; et al. RepetDB: A unified resource for transposable element references. Mob. DNA 2019, 10, 6. [Google Scholar]
- Wicker, T.; Matthews, D.E.; Keller, B. TREP: A database for Triticeae repetitive elements 2002. Available online: http://botserv2.uzh.ch/kelldata/trep-db/pdfs/2002_TIPS.pdf (accessed on 24 May 2020).
- Spannagl, M.; Nussbaumer, T.; Bader, K.C.; Martis, M.M.; Seidel, M.; Kugler, K.G.; Gundlach, H.; Mayer, K.F.X. PGSB PlantsDB: Updates to the database framework for comparative plant genome research. Nucleic Acids Res. 2015, 44, D1141–D1147. [Google Scholar] [CrossRef] [PubMed]
- Du, J.; Grant, D.; Tian, Z.; Nelson, R.T.; Zhu, L.; Shoemaker, R.C.; Ma, J. SoyTEdb: A comprehensive database of transposable elements in the soybean genome. BMC Genom. 2010, 11, 113. [Google Scholar] [CrossRef]
- Llorens, C.; Futami, R.; Covelli, L.; Domínguez-Escribá, L.; Viu, J.M.; Tamarit, D.; Aguilar-Rodríguez, J.; Vicente-Ripolles, M.; Fuster, G.; Bernet, G.P.; et al. The Gypsy Database (GyDB) of Mobile Genetic Elements: Release 2.0. Nucleic Acids Res. 2011, 39, 70–74. [Google Scholar] [CrossRef]
- Pedro, D.L.F.; Lorenzetti, A.P.R.; Domingues, D.S.; Paschoal, A.R. PlaNC-TE: A comprehensive knowledgebase of non-coding RNAs and transposable elements in plants. Database 2018, 2018, bay078. [Google Scholar] [CrossRef]
- Lorenzetti, A.P.R.; De Antonio, G.Y.A.; Paschoal, A.R.; Domingues, D.S. PlanTE-MIR DB: A database for transposable element-related microRNAs in plant genomes. Funct. Integr. Genom. 2016, 16, 235–242. [Google Scholar] [CrossRef]
- Kamath, U.; De Jong, K.; Shehu, A. Effective automated feature construction and selection for classification of biological sequences. PLoS ONE 2014, 9, e99982. [Google Scholar] [CrossRef]
- Nakano, F.K.; Martiello Mastelini, S.; Barbon, S.; Cerri, R. Stacking methods for hierarchical classification. In Proceedings of the 16th IEEE International Conference on Machine Learning and Applications, Cancun, Mexico, 18–21 December 2017; Volume 2018–Janua, pp. 289–296. [Google Scholar]
- Nakano, F.K.; Pinto, W.J.; Pappa, G.L.; Cerri, R. Top-down strategies for hierarchical classification of transposable elements with neural networks. In Proceedings of the Proceedings of the International Joint Conference on Neural Networks, Anchorage, AK, USA, 14–19 May 2017; Volume 2017-May, pp. 2539–2546. [Google Scholar]
- Ventola, G.M.M.; Noviello, T.M.R.; D’Aniello, S.; Spagnuolo, A.; Ceccarelli, M.; Cerulo, L. Identification of long non-coding transcripts with feature selection: A comparative study. BMC Bioinform. 2017, 18, 187. [Google Scholar] [CrossRef] [PubMed]
- Rawal, K.; Ramaswamy, R. Genome-wide analysis of mobile genetic element insertion sites. Nucleic Acids Res. 2011, 39, 6864–6878. [Google Scholar] [CrossRef] [PubMed]
- Zamith Santos, B.; Trindade Pereira, G.; Kenji Nakano, F.; Cerri, R. Strategies for selection of positive and negative instances in the hierarchical classification of transposable elements. In Proceedings of the Proceedings - 2018 Brazilian Conference on Intelligent Systems, Sao Paulo, Brazil, 22–25 October 2018; pp. 420–425. [Google Scholar]
- Larrañaga, P.; Calvo, B.; Santana, R.; Bielza, C.; Galdiano, J.; Inza, I.; Lozano, J.A.; Armañanzas, R.; Santafé, G.; Pérez, A.; et al. Machine learning in bioinformatics. Brief. Bioinform. 2006, 7, 86–112. [Google Scholar] [CrossRef]
- Mjolsness, E.; DeCoste, D. Machine learning for science: State of the art and future prospects. Science (80-.) 2001, 293, 2051–2055. [Google Scholar] [CrossRef] [PubMed]
- Libbrecht, M.W.; Noble, W.S. Machine learning applications in genetics and genomics. Nat. Rev. Genet. 2015, 16, 321–332. [Google Scholar] [CrossRef] [PubMed]
- Ceballos, D.; López-álvarez, D.; Isaza, G.; Tabares-Soto, R.; Orozco-Arias, S.; Ferrin, C.D. A Machine Learning-based Pipeline for the Classification of CTX-M in Metagenomics Samples. Processes 2019, 7, 235. [Google Scholar] [CrossRef]
- Loureiro, T.; Camacho, R.; Vieira, J.; Fonseca, N.A. Boosting the Detection of Transposable Elements Using Machine Learning. In 7th International Conference on Practical Applications of Computational Biology & Bioinformatics; Springer: Heidelberg, Germany, 2013; pp. 85–91. [Google Scholar]
- Santos, B.Z.; Cerri, R.; Lu, R.W. A New Machine Learning Dataset for Hierarchical Classification of Transposable Elements. In Proceedings of the XIII Encontro Nacional de Inteligência Artificial-ENIAC, Sao Paulo, Brazil, 9–12 October 2016. [Google Scholar]
- Schietgat, L.; Vens, C.; Cerri, R.; Fischer, C.N.; Costa, E.; Ramon, J.; Carareto, C.M.A.; Blockeel, H. A machine learning based framework to identify and classify long terminal repeat retrotransposons. PLoS Comput. Biol. 2018, 14, e1006097. [Google Scholar] [CrossRef] [PubMed]
- Ma, C.; Zhang, H.H.; Wang, X. Machine learning for Big Data analytics in plants. Trends Plant Sci. 2014, 19, 798–808. [Google Scholar] [CrossRef] [PubMed]
- Müller, A.C.; Guido, S. Introduction to Machine Learning with Python: A Guide for Data Scientists; O’Reilly Media, Inc.: Sebastopol, CA, USA, 2016. [Google Scholar]
- Liu, Y.; Zhou, Y.; Wen, S.; Tang, C. A Strategy on Selecting Performance Metrics for Classifier Evaluation. Int. J. Mob. Comput. Multimed. Commun. 2014, 6, 20–35. [Google Scholar] [CrossRef]
- Eraslan, G.; Avsec, Ž.; Gagneur, J.; Theis, F.J. Deep learning: New computational modelling techniques for genomics. Nat. Rev. Genet. 2019, 20, 389–403. [Google Scholar] [CrossRef]
- Tsafnat, G.; Setzermann, P.; Partridge, S.R.; Grimm, D. Computational inference of difficult word boundaries in DNA languages. In Proceedings of the ACM International Conference Proceeding Series; Barcelona; Kyranova Ltd, Center for TeleInFrastruktur: Barcelona, Spain, 2011. [Google Scholar]
- Sokolova, M.; Lapalme, G. A systematic analysis of performance measures for classification tasks. Inf. Process. Manag. 2009, 45, 427–437. [Google Scholar] [CrossRef]
- Girgis, H.Z. Red: An intelligent, rapid, accurate tool for detecting repeats de-novo on the genomic scale. BMC Bioinform. 2015, 16, 1–19. [Google Scholar] [CrossRef] [PubMed]
- Su, W.; Gu, X.; Peterson, T. TIR-Learner, a New Ensemble Method for TIR Transposable Element Annotation, Provides Evidence for Abundant New Transposable Elements in the Maize Genome. Mol. Plant 2019, 12, 447–460. [Google Scholar] [CrossRef] [PubMed]
- Arango-López, J.; Orozco-Arias, S.; Salazar, J.A.; Guyot, R. Application of Data Mining Algorithms to Classify Biological Data: The Coffea canephora Genome Case. In Colombian Conference on Computing; Springer: Cartagena, Colombia, 2017; Volume 735, pp. 156–170. ISBN 9781457720819. [Google Scholar]
- Hesam, T.D.; Ali, M.-N. Mining biological repetitive sequences using support vector machines and fuzzy SVM. Iran. J. Chem. Chem. Eng. 2010, 29, 1–17. [Google Scholar]
- Abrusán, G.; Grundmann, N.; Demester, L.; Makalowski, W. TEclass - A tool for automated classification of unknown eukaryotic transposable elements. Bioinformatics 2009, 25, 1329–1330. [Google Scholar] [CrossRef]
- Castellanos-Garzón, J.A.; Díaz, F. Boosting the Detection of Transposable Elements UsingMachine Learning. Adv. Intell. Syst. Comput. 2013, 222, 15–22. [Google Scholar]
- Da Cruz, M.H.P.; Saito, P.T.M.; Paschoal, A.R.; Bugatti, P.H. Classification of Transposable Elements by Convolutional Neural Networks. In Lecture Notes in Computer Science; Springer International Publishing: New York, NY, USA, 2019; Volume 11509, pp. 157–168. ISBN 9783030209155. [Google Scholar]
- Kitchenham, B.; Charters, S. Guidelines for Performing Systematic Literature Reviews in Software Engineering; Version 2.3 EBSE Technical Report EBSE-2007-01; Department of Computer Science University of Durham: Durham, UK, 2007. [Google Scholar]
- Marchand, M.; Shawe-Taylor, J. The set covering machine. J. Mach. Learn. Res. 2002, 3, 723–746. [Google Scholar]
- Caruana, R.; Niculescu-Mizil, A. An empirical comparison of supervised learning algorithms. In Proceedings of the Proceedings of the 23rd International Conference on Machine Learning, New York, NY, USA, 25–29 June 2006; pp. 161–168. [Google Scholar]
- Schnable, P.S.; Ware, D.; Fulton, R.S.; Stein, J.C.; Wei, F.; Pasternak, S.; Liang, C.; Zhang, J.; Fulton, L.; Graves, T.A.; et al. The B73 Maize Genome: Complexity, Diversity, and Dynamics. Science (80-.) 2009, 326, 1112–1115. [Google Scholar] [CrossRef]
- Choulet, F.; Alberti, A.; Theil, S.; Glover, N.; Barbe, V.; Daron, J.; Pingault, L.; Sourdille, P.; Couloux, A.; Paux, E.; et al. Structural and functional partitioning of bread wheat chromosome 3B. Science (80-.) 2014, 345, 1249721. [Google Scholar] [CrossRef]
- Paterson, A.H.; Bowers, J.E.; Bruggmann, R.; Dubchak, I.; Grimwood, J.; Gundlach, H.; Haberer, G.; Hellsten, U.; Mitros, T.; Poliakov, A.; et al. The Sorghum bicolor genome and the diversification of grasses. Nature 2009, 457, 551–556. [Google Scholar] [CrossRef]
- Denoeud, F.; Carretero-Paulet, L.; Dereeper, A.; Droc, G.; Guyot, R.; Pietrella, M.; Zheng, C.; Alberti, A.; Anthony, F.; Aprea, G.; et al. The coffee genome provides insight into the convergent evolution of caffeine biosynthesis. Science (80-.) 2014, 345, 1181–1184. [Google Scholar] [CrossRef] [PubMed]
- Orozco-arias, S.; Liu, J.; Id, R.T.; Ceballos, D.; Silva, D.; Id, D.; Ming, R.; Guyot, R. Inpactor, Integrated and Parallel Analyzer and Classifier of LTR Retrotransposons and Its Application for Pineapple LTR Retrotransposons Diversity and Dynamics. Biology (Basel) 2018, 7, 32. [Google Scholar] [CrossRef] [PubMed]
- Jaiswal, A.K.; Krishnamachari, A. Physicochemical property based computational scheme for classifying DNA sequence elements of Saccharomyces cerevisiae. Comput. Biol. Chem. 2019, 79, 193–201. [Google Scholar] [CrossRef] [PubMed]
- Yu, N.; Guo, X.; Gu, F.; Pan, Y. DNA AS X: An information-coding-based model to improve the sensitivity in comparative gene analysis. In Proceedings of the International Symposium on Bioinformatics Research and Applications, Norfolk, VA, USA, 6–9 June 2015; pp. 366–377. [Google Scholar]
- Nair, A.S.; Sreenadhan, S.P. A coding measure scheme employing electron-ion interaction pseudopotential (EIIP). Bioinformation 2006, 1, 197. [Google Scholar] [PubMed]
- Akhtar, M.; Epps, J.; Ambikairajah, E. Signal processing in sequence analysis: Advances in eukaryotic gene prediction. IEEE J. Sel. Top. Signal Process. 2008, 2, 310–321. [Google Scholar] [CrossRef]
- Kauer, G.; Blöcker, H. Applying signal theory to the analysis of biomolecules. Bioinformatics 2003, 19, 2016–2021. [Google Scholar] [CrossRef]
- Rosen, G.L. Signal Processing for Biologically-Inspired Gradient Source Localization and DNA Sequence Analysis. Ph.D. Thesis, Georgia Institute of Technology, Atlanta, GA, USA, 12 July 2006. [Google Scholar]
- Tabares-soto, R.; Orozco-Arias, S.; Romero-Cano, V.; Segovia Bucheli, V.; Rodríguez-Sotelo, J.L.; Jiménez-Varón, C.F. A comparative study of machine learning and deep learning algorithms to classify cancer types based on microarray gene expression. Peerj Comput. Sci. 2020, 6, 1–22. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Chen, L.; Zhang, Y.-H.; Huang, G.; Pan, X.; Wang, S.; Huang, T.; Cai, Y.-D. Discriminating cirRNAs from other lncRNAs using a hierarchical extreme learning machine (H-ELM) algorithm with feature selection. Mol. Genet. Genom. 2018, 293, 137–149. [Google Scholar] [CrossRef] [PubMed]
- Yu, N.; Yu, Z.; Pan, Y. A deep learning method for lincRNA detection using auto-encoder algorithm. BMC Bioinform. 2017, 18, 511. [Google Scholar] [CrossRef] [PubMed]
- Smith, M.A.; Seemann, S.E.; Quek, X.C.; Mattick, J.S. DotAligner: Identification and clustering of RNA structure motifs. Genome Biol. 2017, 18, 244. [Google Scholar] [CrossRef] [PubMed]
- Segal, E.S.; Gritsenko, V.; Levitan, A.; Yadav, B.; Dror, N.; Steenwyk, J.L.; Silberberg, Y.; Mielich, K.; Rokas, A.; Gow, N.A.R.; et al. Gene Essentiality Analyzed by In Vivo Transposon Mutagenesis and Machine Learning in a Stable Haploid Isolate of Candida albicans. MBio 2018, 9, e02048-18. [Google Scholar] [CrossRef] [PubMed]
- Brayet, J.; Zehraoui, F.; Jeanson-Leh, L.; Israeli, D.; Tahi, F. Towards a piRNA prediction using multiple kernel fusion and support vector machine. Bioinformatics 2014, 30, i364–i370. [Google Scholar] [CrossRef] [PubMed]
- Ashlock, W.; Datta, S. Distinguishing endogenous retroviral LTRs from SINE elements using features extracted from evolved side effect machines. IEEE/ACM Trans. Comput. Biol. Bioinforma. 2012, 9, 1676–1689. [Google Scholar] [CrossRef]
- Zhang, Y.; Babaian, A.; Gagnier, L.; Mager, D.L. Visualized Computational Predictions of Transcriptional Effects by Intronic Endogenous Retroviruses. PLoS ONE 2013, 8, e71971. [Google Scholar] [CrossRef] [PubMed]
- Douville, C.; Springer, S.; Kinde, I.; Cohen, J.D.; Hruban, R.H.; Lennon, A.M.; Papadopoulos, N.; Kinzler, K.W.; Vogelstein, B.; Karchin, R. Detection of aneuploidy in patients with cancer through amplification of long interspersed nucleotide elements (LINEs). Proc. Natl. Acad. Sci. USA 2018, 115, 1871–1876. [Google Scholar] [CrossRef]
- Rishishwar, L.; Mariño-Ramírez, L.; Jordan, I.K. Benchmarking computational tools for polymorphic transposable element detection. Brief. Bioinform. 2017, 18, 908–918. [Google Scholar] [CrossRef]
- Youden, W.J. Index for rating diagnostic tests. Cancer 1950, 3, 32–35. [Google Scholar] [CrossRef]
- Gao, D.; Abernathy, B.; Rohksar, D.; Schmutz, J.; Jackson, S.A. Annotation and sequence diversity of transposable elements in common bean (Phaseolus vulgaris). Front. Plant Sci. 2014, 5, 339. [Google Scholar] [CrossRef]
- Jiang, N. Overview of Repeat Annotation and De Novo Repeat Identification. In Plant Transposable Elements; Humana Press: Totowa, NJ, USA, 2013; pp. 275–287. [Google Scholar]
- Garbus, I.; Romero, J.R.; Valarik, M.; Vanžurová, H.; Karafiátová, M.; Cáccamo, M.; Doležel, J.; Tranquilli, G.; Helguera, M.; Echenique, V. Characterization of repetitive DNA landscape in wheat homeologous group 4 chromosomes. BMC Genom. 2015, 16, 375. [Google Scholar] [CrossRef]
- Eickbush, T.H.; Jamburuthugoda, V.K. The diversity of retrotransposons and the properties of their reverse transcriptases. VIRUS Res. 2008, 134, 221–234. [Google Scholar] [CrossRef] [PubMed]
- Negi, P.; Rai, A.N.; Suprasanna, P. Moving through the Stressed Genome: Emerging Regulatory Roles for Transposons in Plant Stress Response. Front. Plant Sci. 2016, 7, 1448. [Google Scholar] [CrossRef] [PubMed]
- Bousios, A.; Minga, E.; Kalitsou, N.; Pantermali, M.; Tsaballa, A.; Darzentas, N. MASiVEdb: The Sirevirus Plant Retrotransposon Database. BMC Genom. 2012, 13, 158. [Google Scholar] [CrossRef] [PubMed]
- Naresh, E.; Kumar, B.P.V.; Shankar, S.P. Others Impact of Machine Learning in Bioinformatics Research. In Statistical Modelling and Machine Learning Principles for Bioinformatics Techniques, Tools, and Applications; Springer: Singapore, 2020; pp. 41–62. [Google Scholar]
- Yue, T.; Wang, H. Deep Learning for Genomics: A Concise Overview. arXiv 2018, arXiv:1802.008101–40. [Google Scholar]
- Soueidan, H.; Nikolski, M. Machine learning for metagenomics: Methods and tools. arXiv 2015, arXiv:1510.06621. 2015. [Google Scholar] [CrossRef]
- Captur, G.; Heywood, W.E.; Coats, C.; Rosmini, S.; Patel, V.; Lopes, L.R.; Collis, R.; Patel, N.; Syrris, P.; Bassett, P.; et al. Identification of a multiplex biomarker panel for Hypertrophic Cardiomyopathy using quantitative proteomics and machine learning. Mol. Cell. Proteom. 2020, 19, 114–127. [Google Scholar] [CrossRef]
- Loureiro, T.; Fonseca, N.; Camacho, R. Application of Machine Learning Techniques on the Discovery and Annotation of Transposons in Genomes. Master’s Thesis, Faculdade De Engenharia, Universidade Do Porto, Porto, Portugal, 2012. [Google Scholar]
- Guyot, R.; Darré, T.; Dupeyron, M.; de Kochko, A.; Hamon, S.; Couturon, E.; Crouzillat, D.; Rigoreau, M.; Rakotomalala, J.-J.; Raharimalala, N.E.; et al. Partial sequencing reveals the transposable element composition of Coffea genomes and provides evidence for distinct evolutionary stories. Mol. Genet. Genom. 2016, 291, 1979–1990. [Google Scholar] [CrossRef]
- Piegu, B.; Guyot, R.; Picault, N.; Roulin, A.; Saniyal, A.; Kim, H.; Collura, K.; Brar, D.S.; Jackson, S.; Wing, R.A.; et al. Doubling genome size without polyploidization: Dynamics of retrotransposition-driven genomic expansions in Oryza australiensis, a wild relative of rice. Genome Res. 2006, 16, 1262–1269. [Google Scholar] [CrossRef]
- Ming, R.; VanBuren, R.; Wai, C.M.; Tang, H.; Schatz, M.C.; Bowers, J.E.; Lyons, E.; Wang, M.-L.; Chen, J.; Biggers, E.; et al. The pineapple genome and the evolution of CAM photosynthesis. Nat. Genet. 2015, 47, 1435–1442. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).