Enhanced Specific Heat Capacity of Liquid Entrapped between Two Solid Walls Separated by a Nanogap
Abstract
1. Introduction
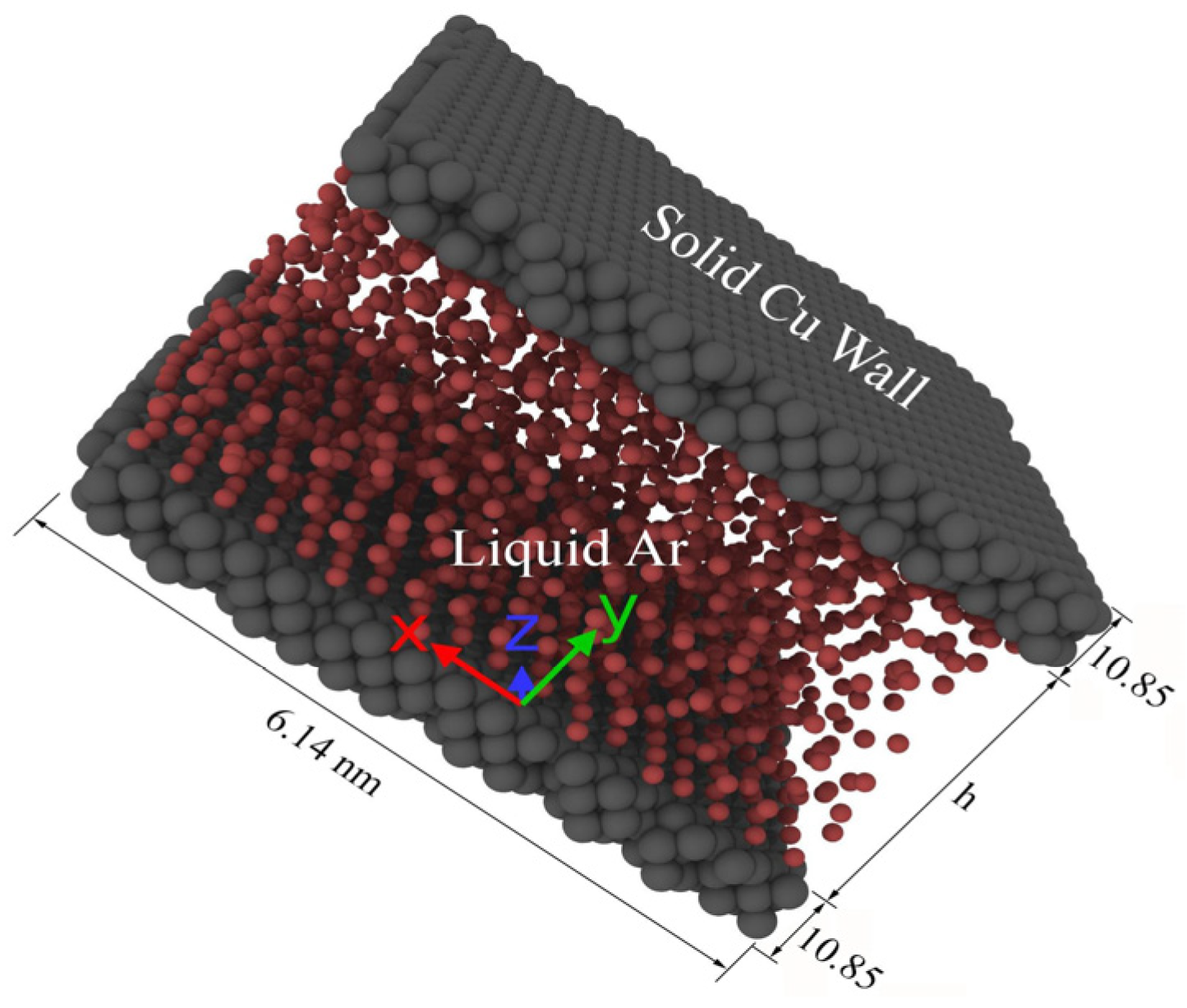
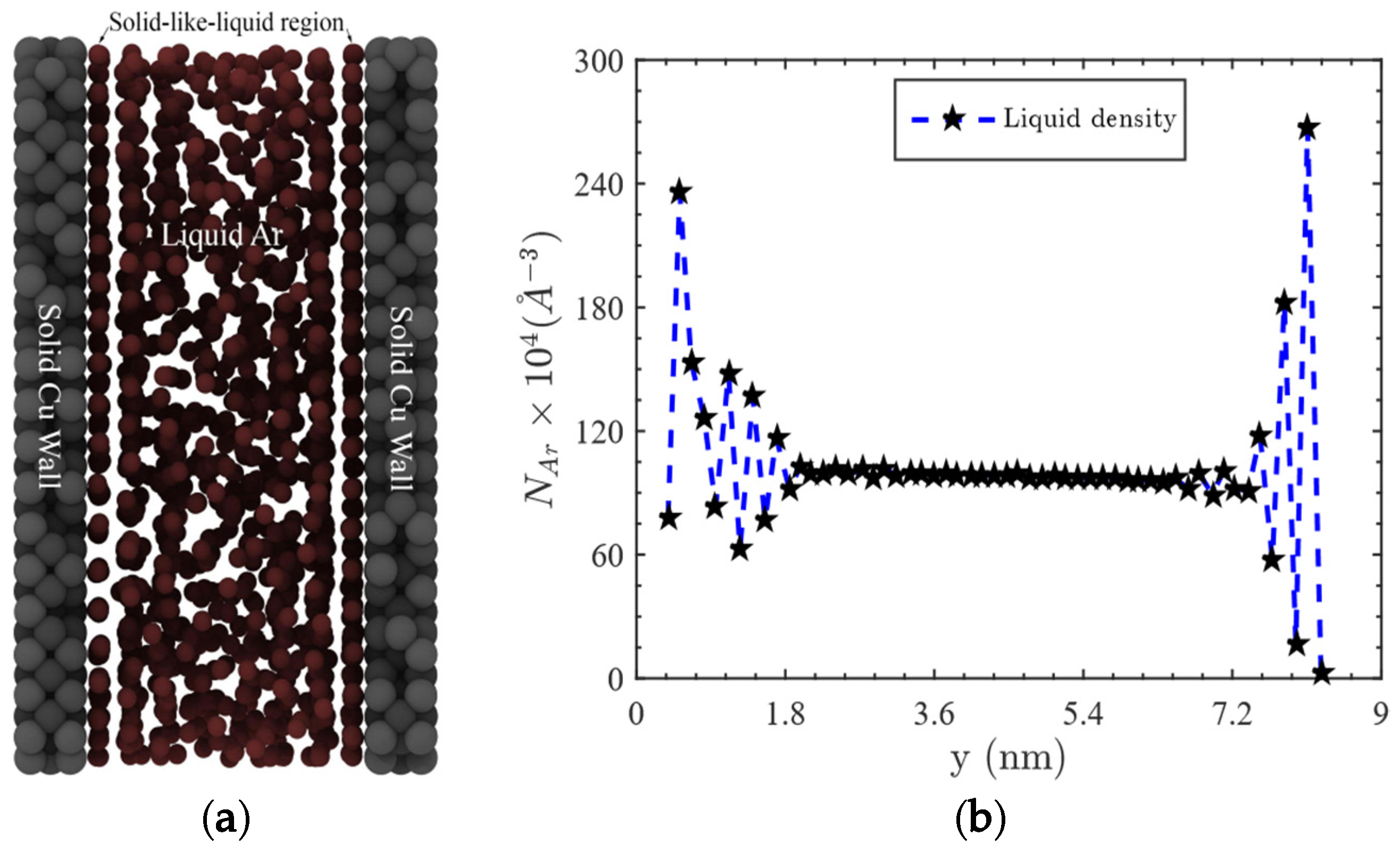
2. Modeling and Simulation Procedures
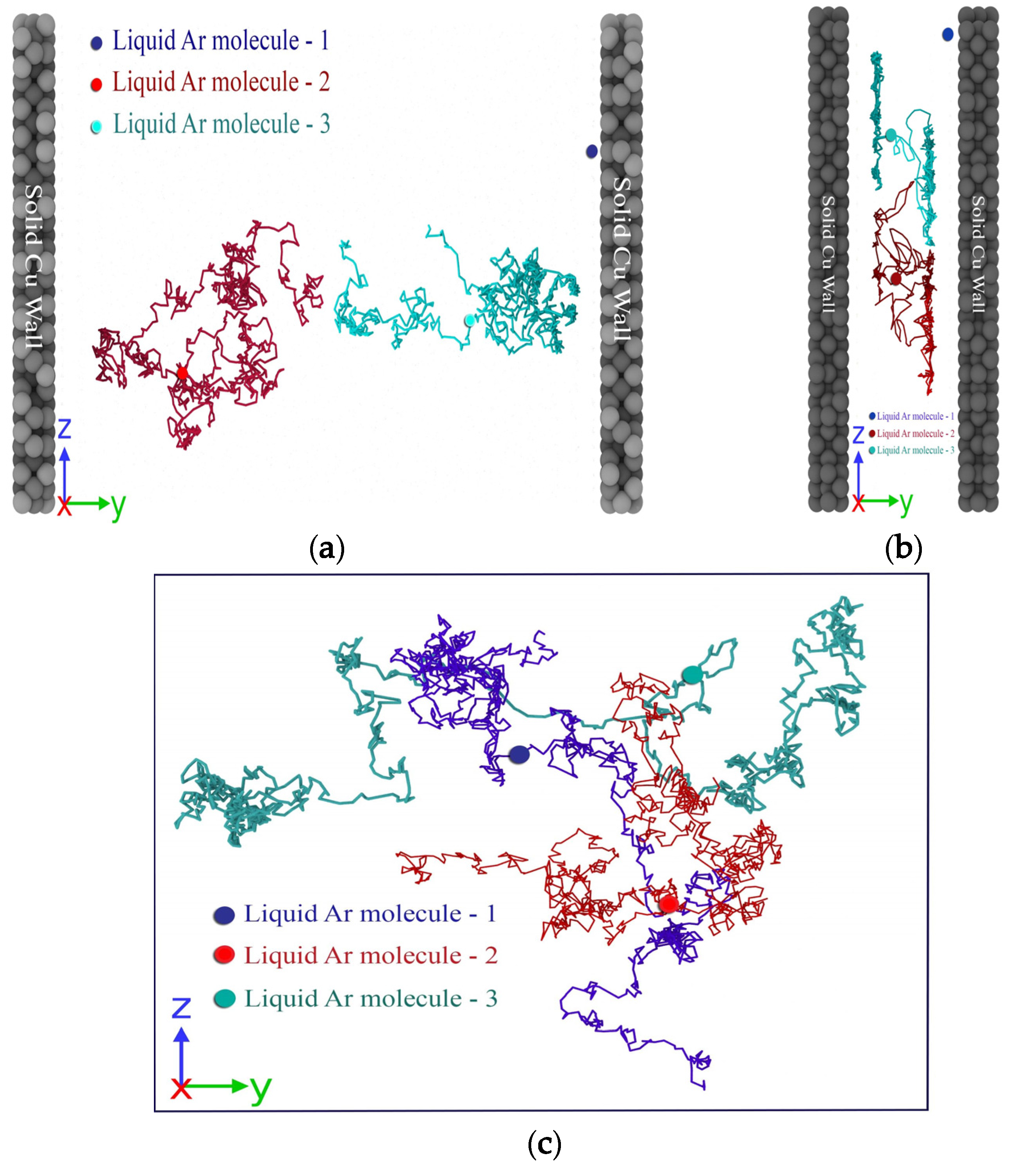
3. Results and Discussions
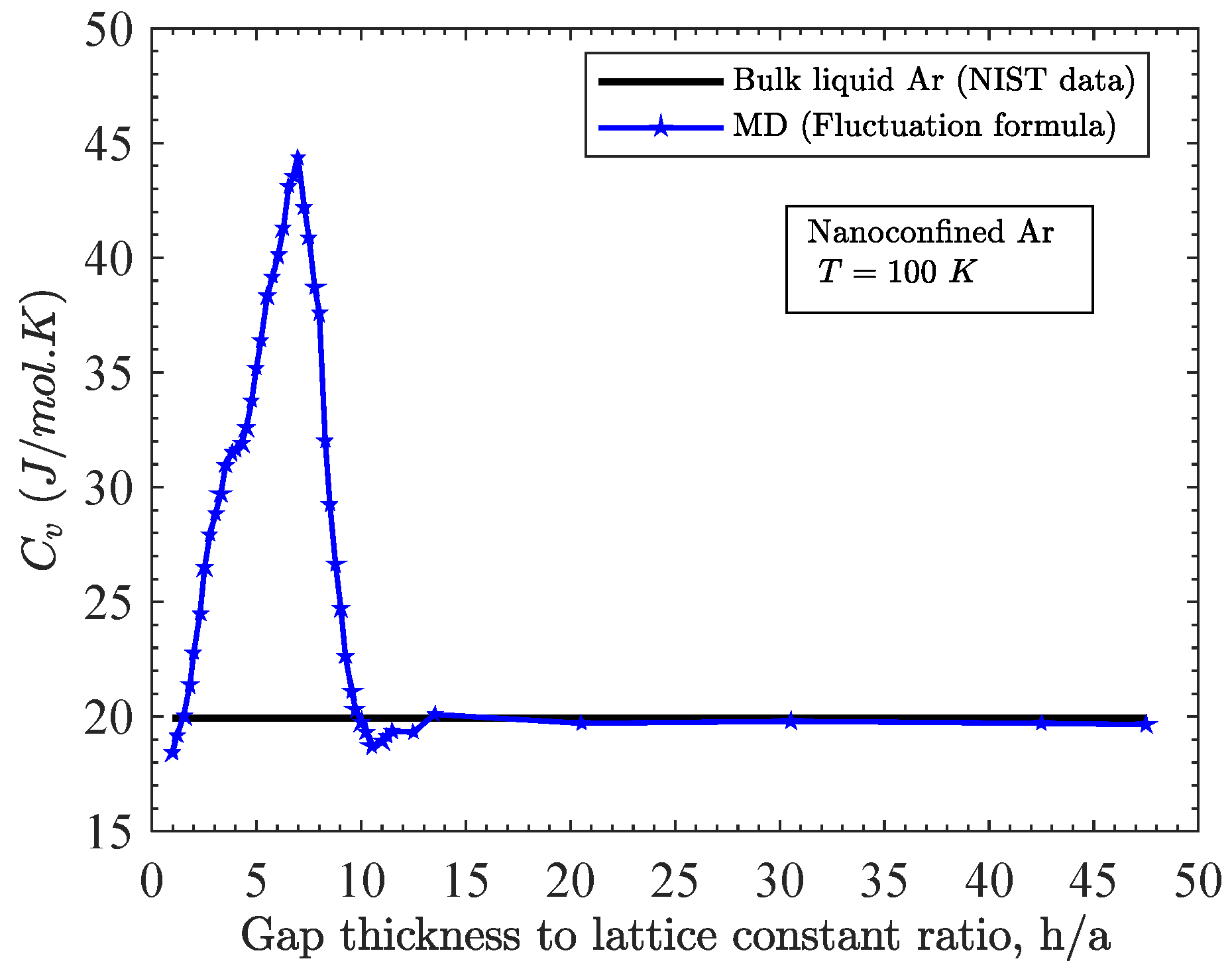
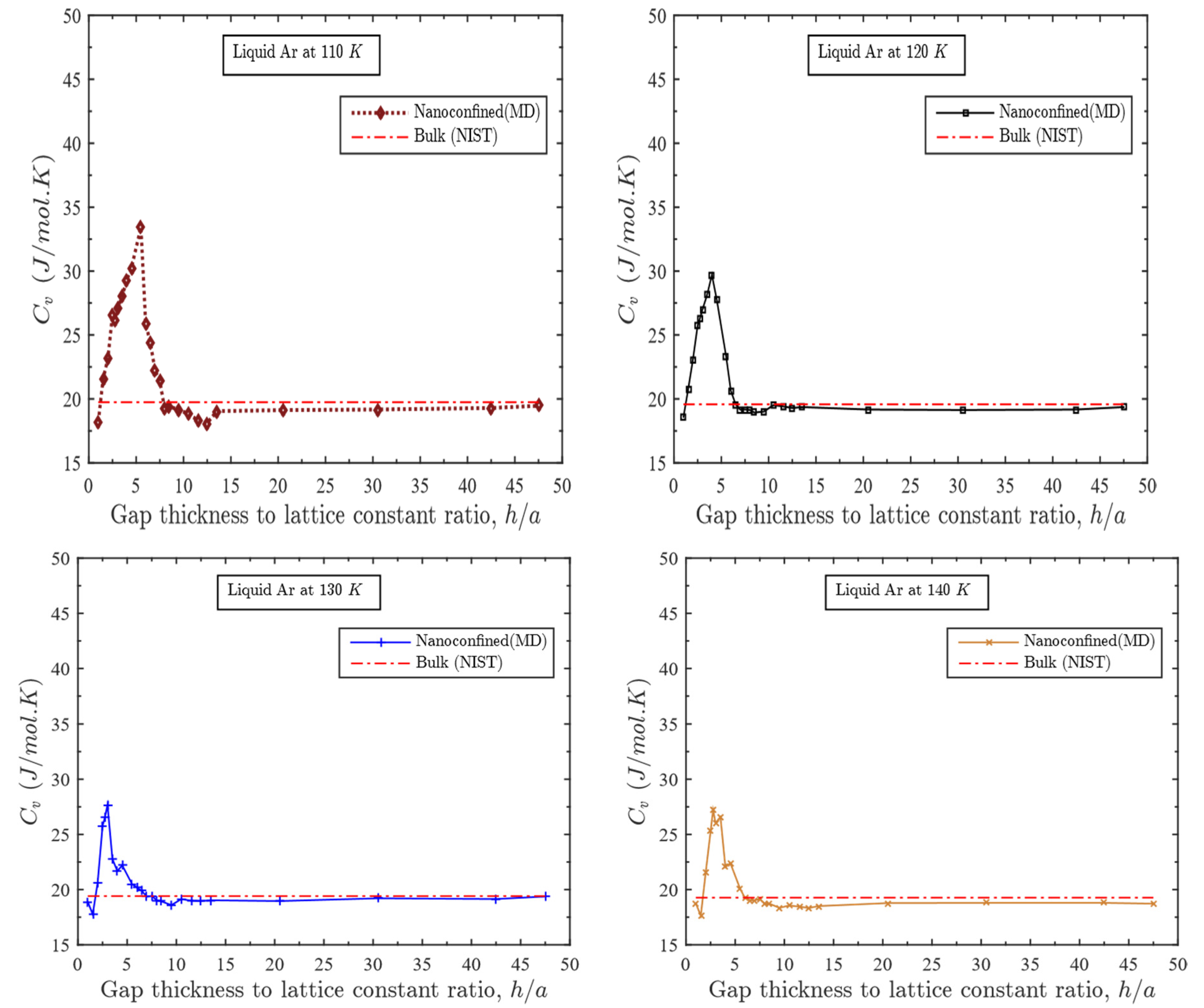
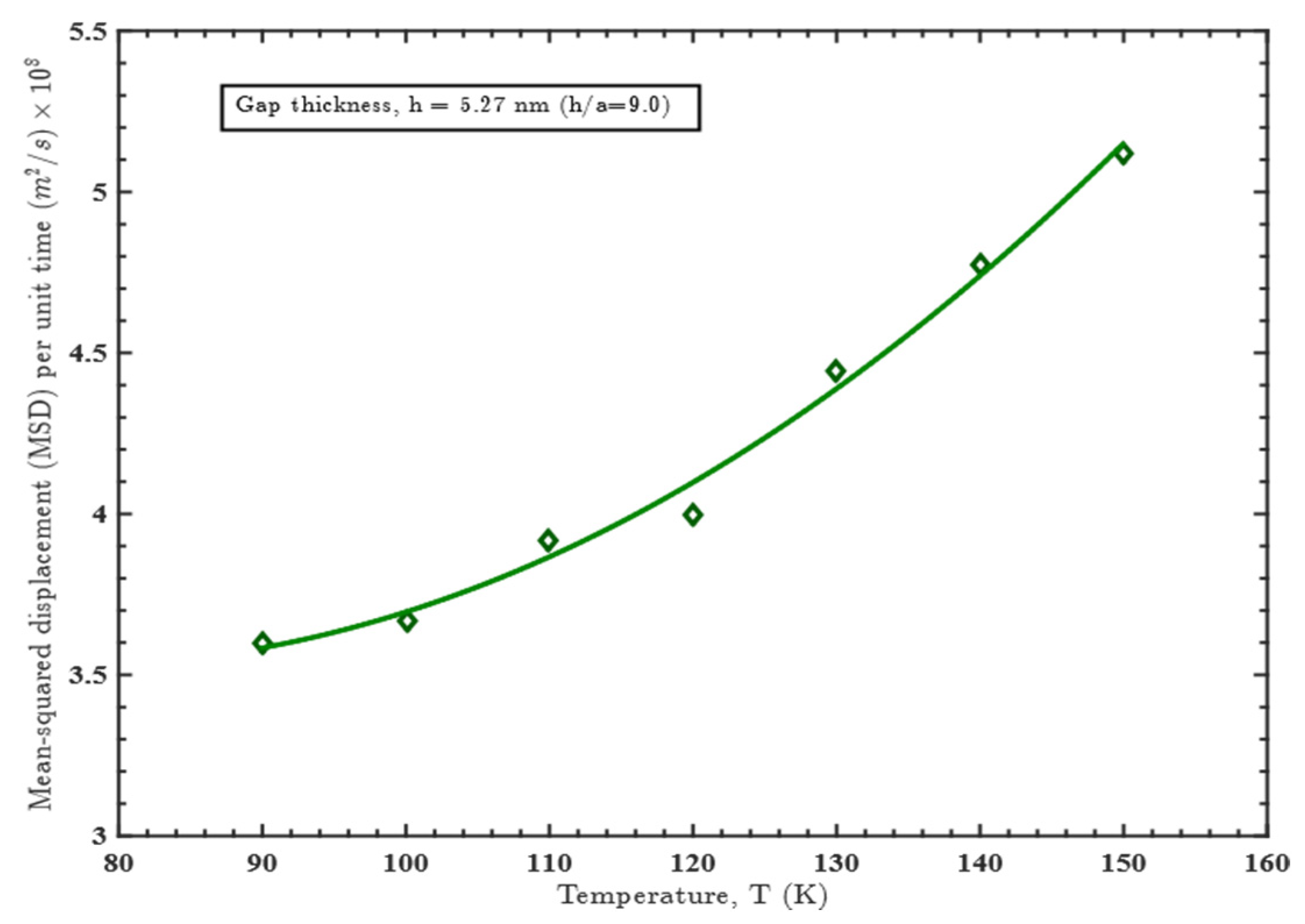
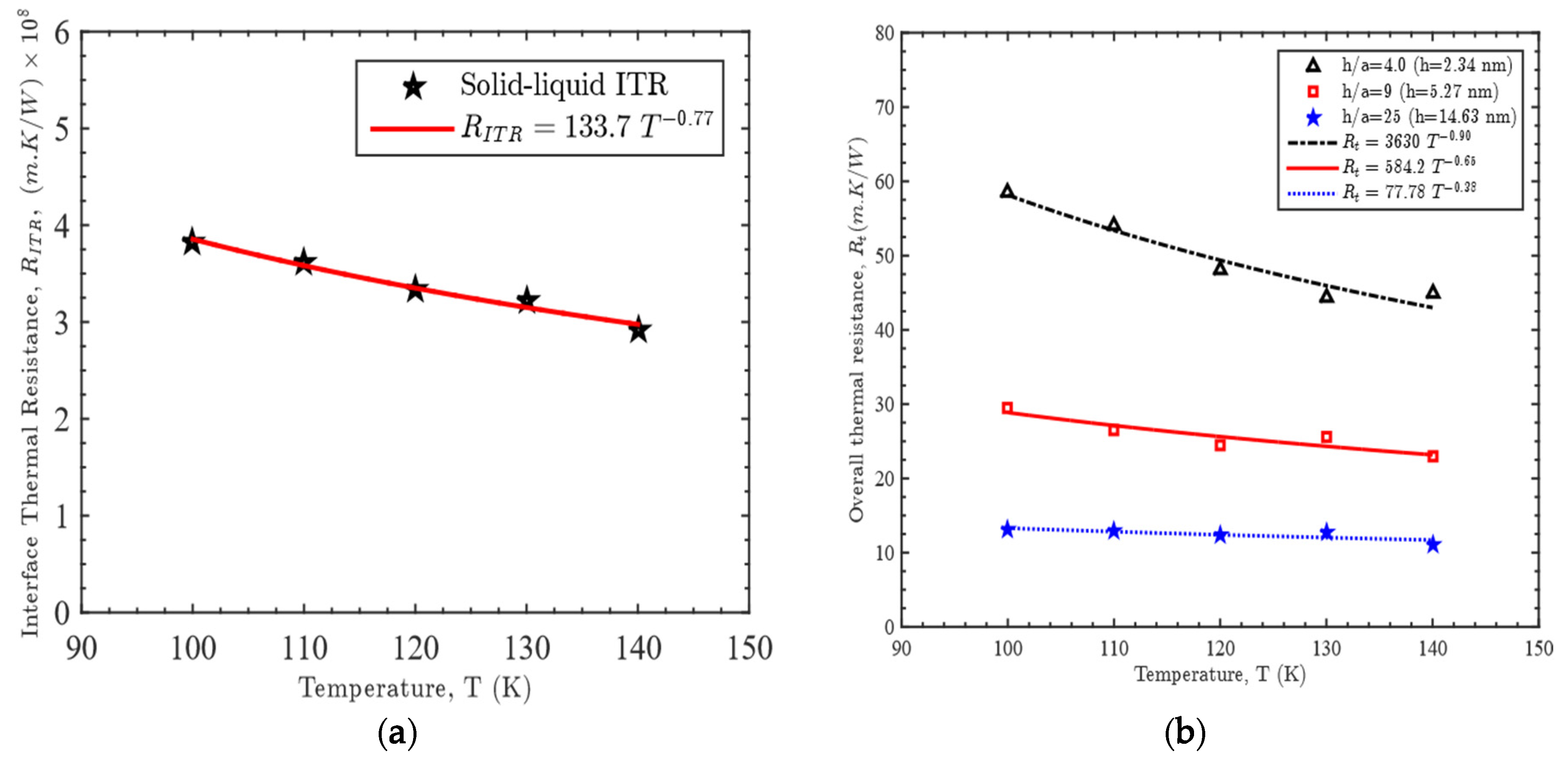
3.1. Effect of Gap Thickness on Heat Capacity
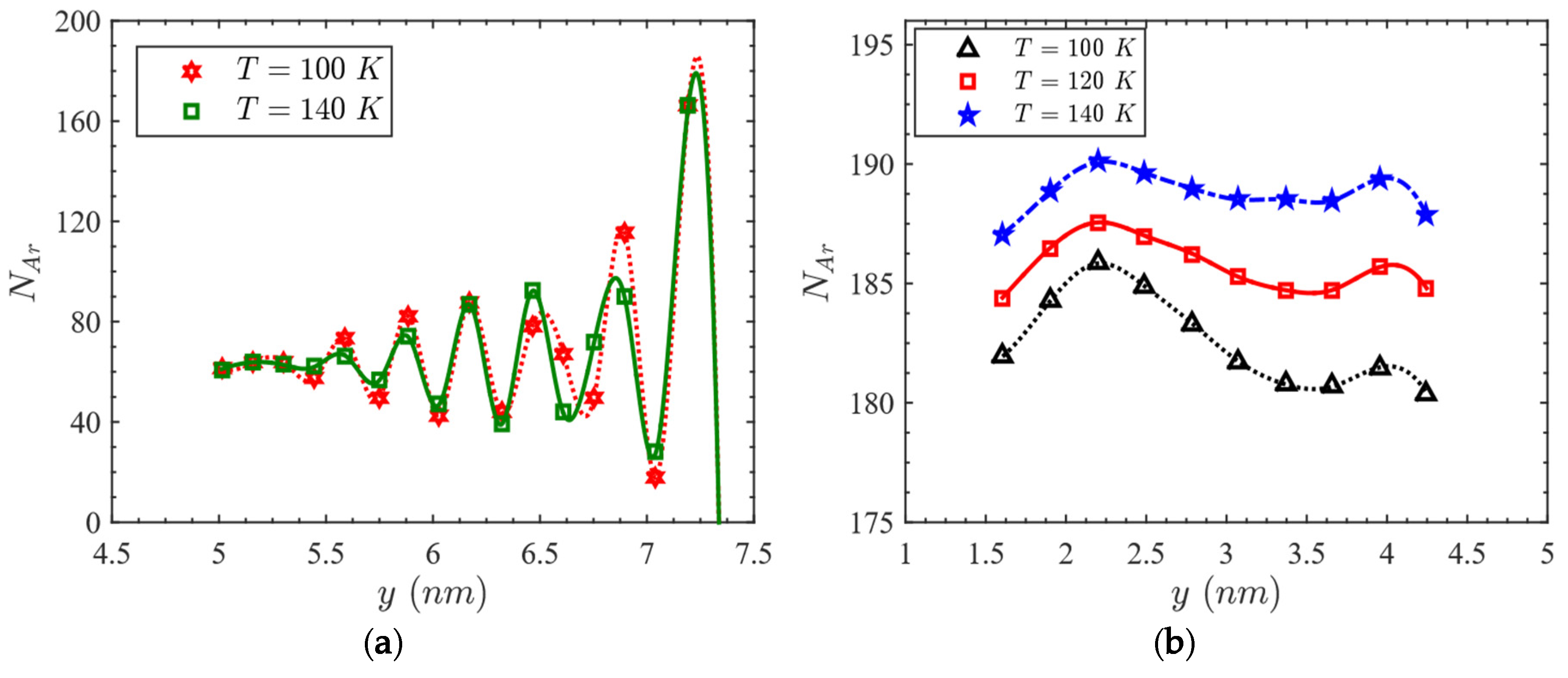
3.2. Effect of Temperature on Heat Capacity
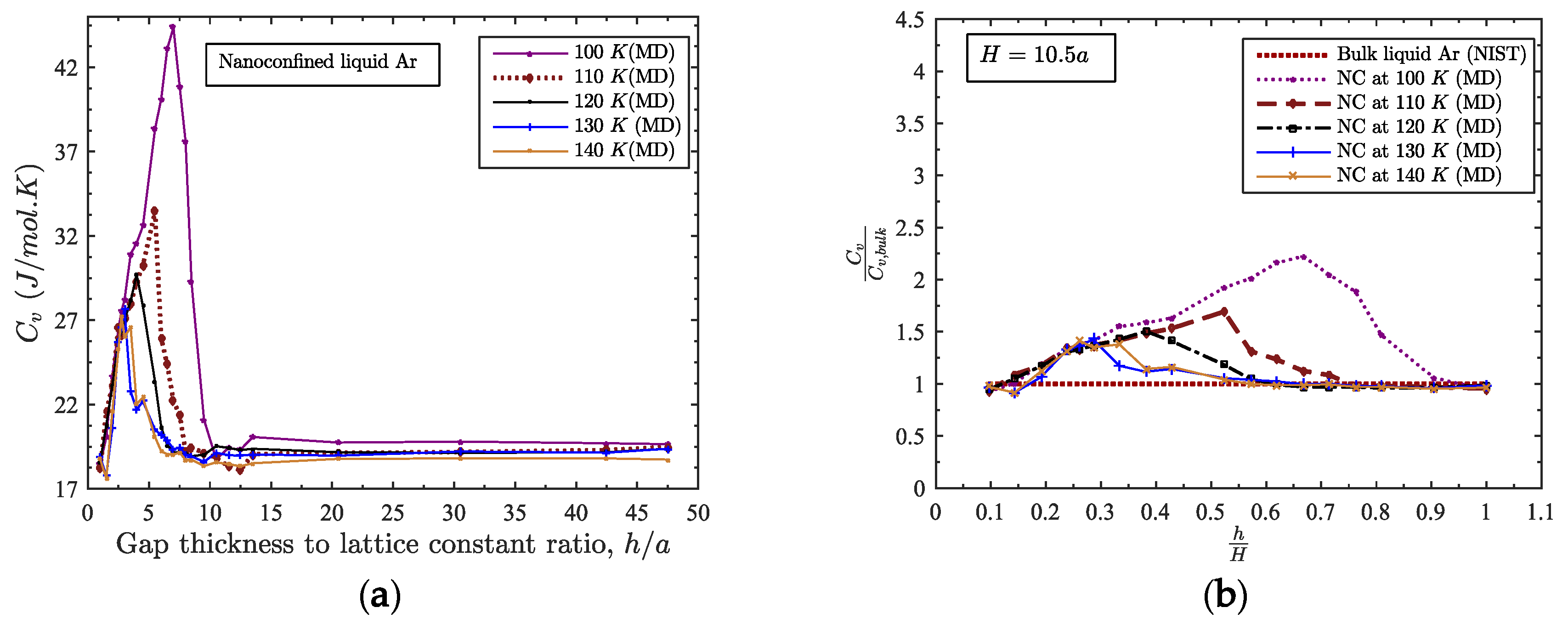
3.3. Relation among Gap Thickness, Temperature and Heat Capacity
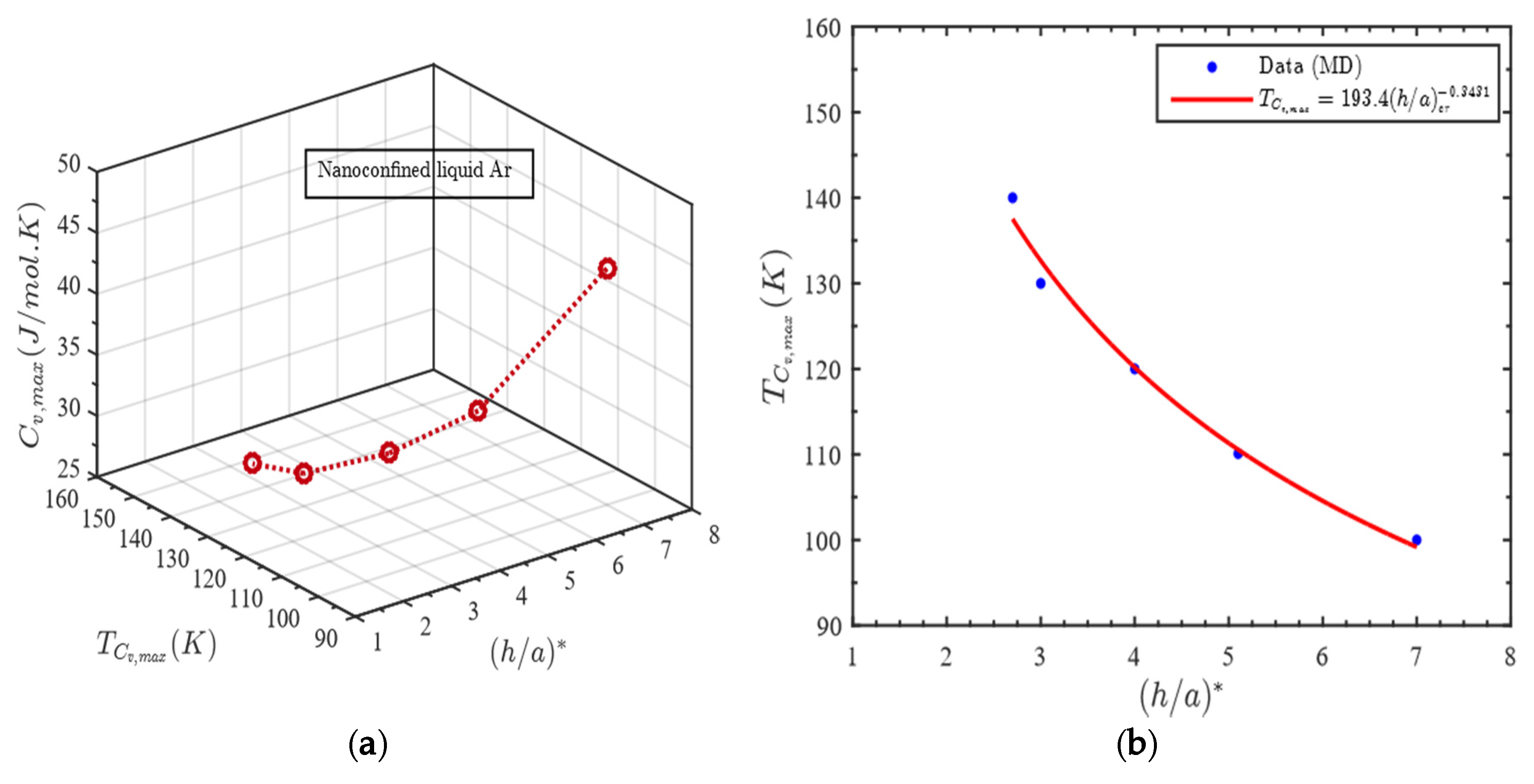
3.4. Maximum Heat Capacity of the Confined Liquid
Relation between Gap Thickness and Temperature for Maximum Heat Capacity
4. Conclusions
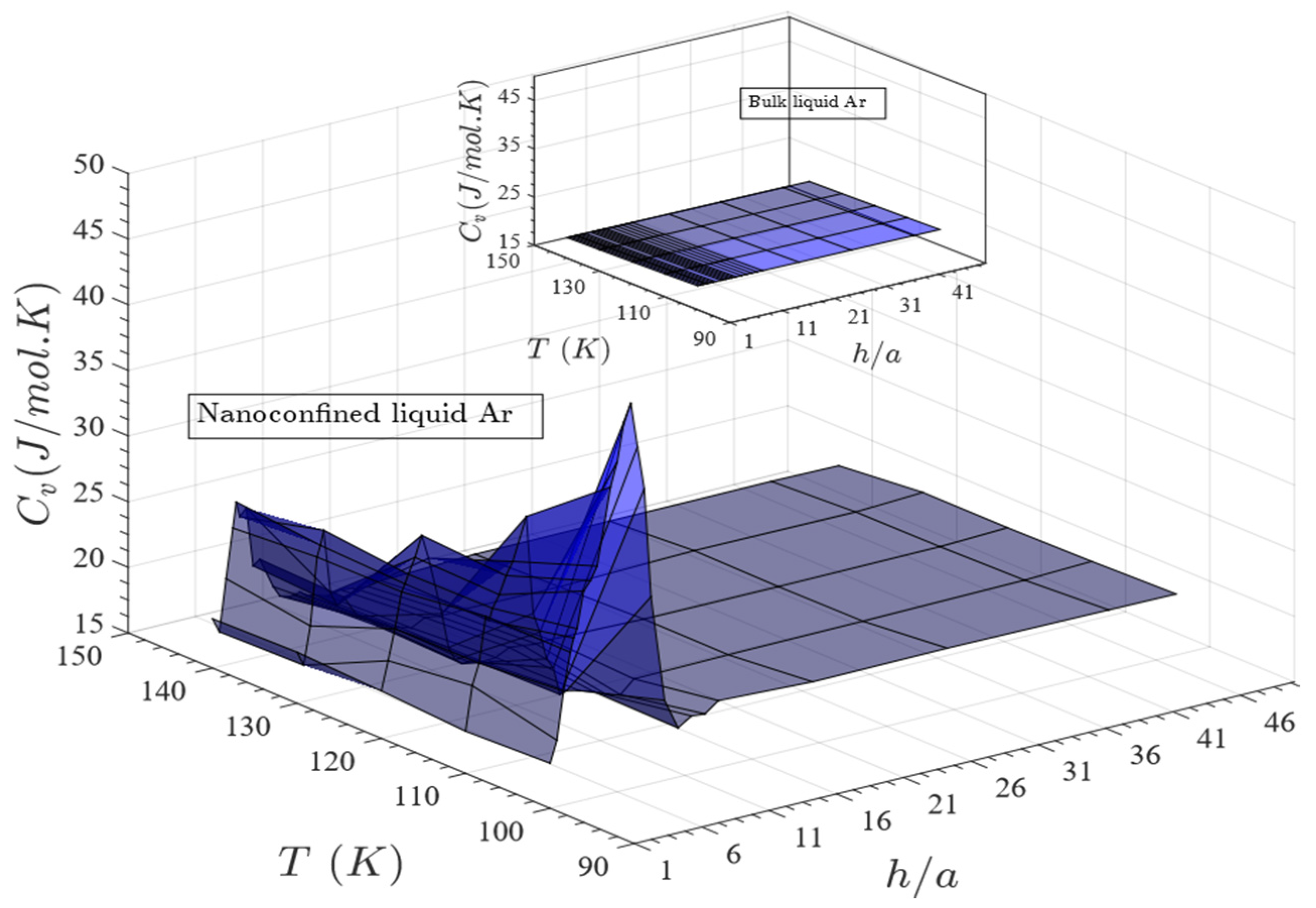
- Nanoconfinement increases the heat capacity of the liquid within a specific range of gap thickness and temperature beyond which heat capacity of the confined liquid approaches to that of its bulk counterpart. Dependence of heat capacity on pore size and temperature was reported earlier for different fluids including water, hydrogen, deuterium, etc. confined in cylindrical nanopores [12,16,20,38].
- For a fixed temperature, as the gap thickness increases beyond one atomic layer, the heat capacity increases dramatically at first; reaches a maximum value at some specified gap thickness and eventually decreases to align to that of the bulk liquid;
- This specific range of gap thickness depends directly on temperature. This range gets narrower with the increase in temperature;
- Maximum heat capacity, gap thickness and temperature all are correlated. The temperature at which maximum heat capacity occurs for a nanoconfined liquid is observed to vary with gap thickness following the power law, ;
- The broad maximum in Cv against h/a plot for nanoconfined liquid shifts to a lower value at higher temperature i.e., the more the temperature of the confined liquid, the lower the value of its maximum heat capacity;
- A heat capacity, almost two times larger than its bulk counterpart, is achievable for a predefined gap thickness and temperature (Cv,nc ≈ 2.3 × Cv,bulk for h = 4.1 nm and T = 100 K);
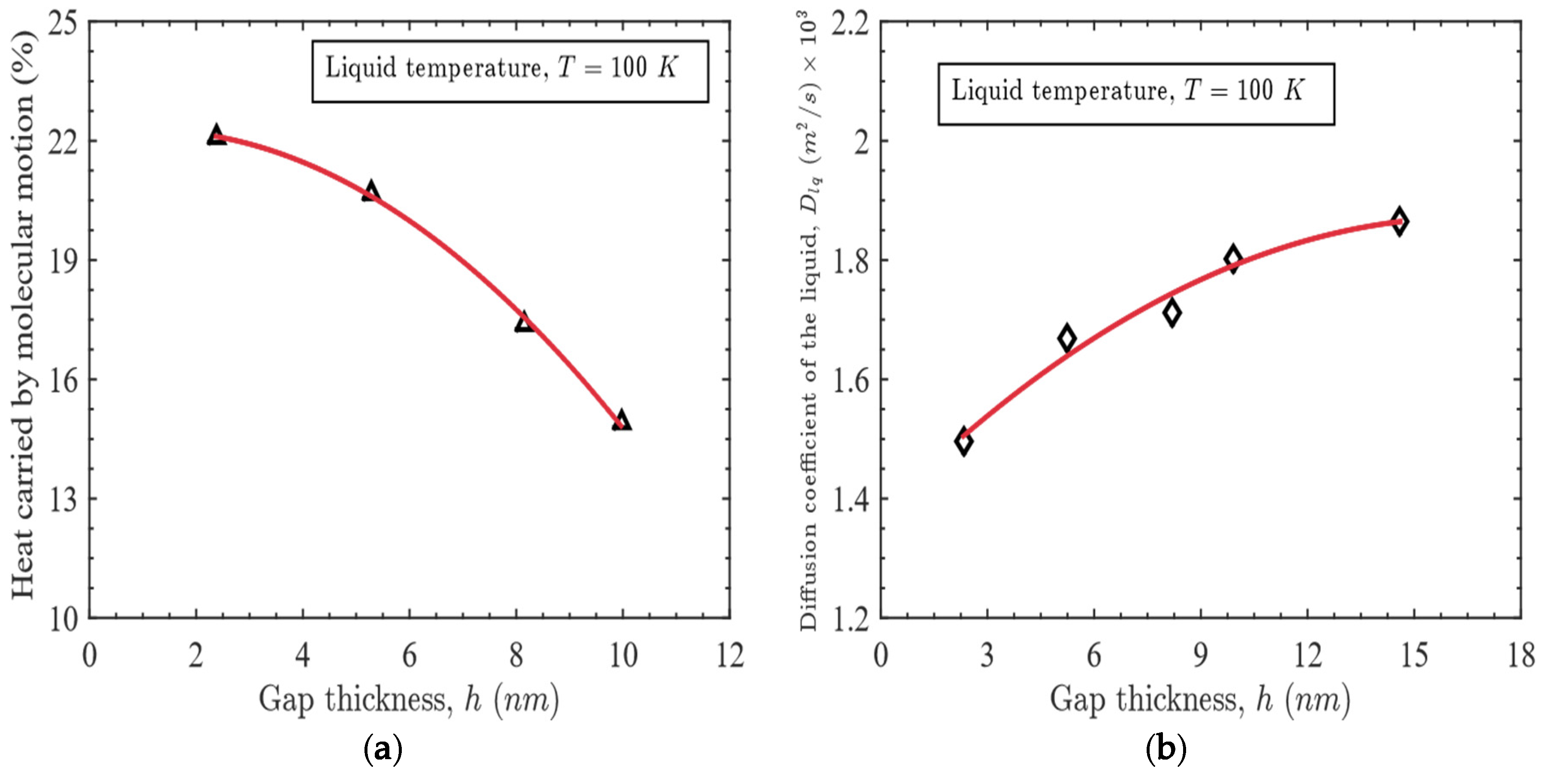
- The enhanced heat capacity is attributed to the simultaneous effects of configurational and non-configurational contributions of the confined liquid.
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Shi, L.; Dames, C.; Lukes, J.R.; Reddy, P.; Duda, J.; Cahill, D.G.; Lee, J.; Marconnet, A.; Goodson, K.E.; Bahk, J.-H.; et al. Evaluating Broader Impacts of Nanoscale Thermal Transport Research. Nanoscale Microscale Thermophys. Eng. 2015, 19, 127–165. [Google Scholar] [CrossRef]
- Mosaddeghi, H.; Alavi, S.; Kowsari, M.H.; Najafi, B. Simulations of structural and dynamic anisotropy in nano-confined water between parallel graphite plates. J. Chem. Phys. 2012, 137, 184703. [Google Scholar] [CrossRef]
- Solveyra, E.G.; De La Llave, E.; Molinero, V.; Illia, G.J.S.; Scherlis, D.A. Structure, Dynamics, and Phase Behavior of Water in TiO2 Nanopores. J. Phys. Chem. C 2013, 117, 3330–3342. [Google Scholar] [CrossRef]
- Köhler, M.; Bordin, J.R.; Da Silva, L.B.; Barbosa, M.C. Structure and dynamics of water inside hydrophobic and hydrophilic nanotubes. Phys. A Stat. Mech. Its Appl. 2018, 490, 331–337. [Google Scholar] [CrossRef]
- Nomura, K.; Kaneko, T.; Bai, J.; Francisco, J.S.; Yasuoka, K.; Zeng, X.C. Evidence of low-density and high-density liquid phases and isochore end point for water confined to carbon nanotube. Proc. Natl. Acad. Sci. USA 2017, 114, 4066–4071. [Google Scholar] [CrossRef]
- Han, S.; Choi, M.; Kumar, P.; Stanley, H.E. Phase transitions in confined water nanofilms. Nat. Phys. 2010, 6, 685–689. [Google Scholar] [CrossRef]
- Gautam, S.; Liu, T.; Patankar, S.; Tomasko, D.; Cole, D. Location dependent orientational structure and dynamics of ethane in ZSM5. Chem. Phys. Lett. 2016, 648, 130–136. [Google Scholar] [CrossRef]
- Dhiman, I.; Bhowmik, D.; Shrestha, U.R.; Cole, D.; Gautam, S. Effect of molecular shape on rotation under severe confinement. Chem. Eng. Sci. 2018, 180, 33–41. [Google Scholar] [CrossRef]
- Calvo-Schwarzwälder, M.; Hennessy, M.G.; Torres, P.; Myers, T.; Alvarez, F. A slip-based model for the size-dependent effective thermal conductivity of nanowires. Int. Commun. Heat Mass Transf. 2018, 91, 57–63. [Google Scholar] [CrossRef]
- Avramov, I.; Michailov, M. Specific heat of nanocrystals. J. Phys. Condens. Matter 2008, 20, 295224. [Google Scholar] [CrossRef]
- Bolmatov, D.; Brazhkin, V.V.; Trachenko, K. The phonon theory of liquid thermodynamics. Sci. Rep. 2012, 2, 421. [Google Scholar] [CrossRef] [PubMed]
- Tombari, E.; Salvetti, G.; Ferrari, C.; Johari, G.P. Heat capacity of water in nanopores. J. Chem. Phys. 2005, 123, 214706. [Google Scholar] [CrossRef]
- Nagoe, A.; Kanke, Y.; Oguni, M.; Namba, S. Findings of C p Maximum at 233 K for the Water within Silica Nanopores and Very Weak Dependence of the T max on the Pore Size. J. Phys. Chem. B 2010, 114, 13940–13943. [Google Scholar] [CrossRef] [PubMed]
- Leng, Y. Hydration force and dynamic squeeze-out of hydration water under subnanometer confinement. J. Phys. Condens. Matter 2008, 20, 354017. [Google Scholar] [CrossRef]
- Sengers, J.V.; Klein, M. The technological importance of accurate thermophysical property information. In The Technological Importance of Accurate Thermophysical Property Information; Nat. Bur. Stand. (U.S.), Special Publication 590; U.S. Government Print: Washington, DC, USA, 1980. [Google Scholar]
- Bianco, V.; Franzese, G. Critical behavior of a water monolayer under hydrophobic confinement. Sci. Rep. 2014, 4, 4440. [Google Scholar] [CrossRef] [PubMed]
- Tombari, E.; Salvetti, G.; Ferrari, C.; Johari, G.P. Thermodynamic functions of water and ice confined to 2 nm radius pores. J. Chem. Phys. 2005, 122, 104712. [Google Scholar] [CrossRef] [PubMed]
- Mochizuki, K.; Koga, K. Solid-liquid critical behavior of water in nanopores. Proc. Natl. Acad. Sci. USA 2015, 112, 8221–8226. [Google Scholar] [CrossRef] [PubMed]
- Abbaspour, M.; Akbarzadeh, H.; Salemi, S.; Jalalitalab, E. Density-dependent phase transition in nano-confinement water using molecular dynamics simulation. J. Mol. Liq. 2018, 250, 26–34. [Google Scholar] [CrossRef]
- Kucheyev, S.O.; Lenhardt, J.M. Freezing Hydrogen in Nanoconfinement. Fusion Sci. Technol. 2018, 73, 293–297. [Google Scholar] [CrossRef]
- Van Cleve, E.; Worsley, M.A.; Kucheyev, S.O. Liquid–solid phase transition of hydrogen and deuterium in silica aerogel. J. Appl. Phys. 2014, 116, 163517. [Google Scholar] [CrossRef]
- Liang, Z.; Tsai, H.-L. Effect of molecular film thickness on thermal conduction across solid-film interfaces. Phys. Rev. E 2011, 83, 061603. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Cheng, P.; Quan, X. Molecular dynamics simulations of thermal boundary resistances in a liquid between two solid walls separated by a nano gap. Int. Commun. Heat Mass Transf. 2016, 77, 183–189. [Google Scholar] [CrossRef]
- Morshed, A.M.; Paul, T.C.; Khan, J.A. Atomistic simulation of temperature dependent thermal transport across nanoconfined liquid. Phys. E Low-Dimens. Syst. Nanostruct. 2013, 47, 246–251. [Google Scholar] [CrossRef]
- Allen, M.P.; Tildesley, D.J. Computer Simulation of Liquids; Clarendon Press: New York, NY, USA; Oxford University Press: Oxford, UK, 1987. [Google Scholar]
- Plimpton, S. Computational limits of classical molecular dynamics simulations. Comput. Mater. Sci. 1995, 4, 361–364. [Google Scholar] [CrossRef]
- Stukowski, A. Visualization and analysis of atomistic simulation data with OVITO–the Open Visualization Tool. Model. Simul. Mater. Sci. Eng. 2009, 18, 15012. [Google Scholar] [CrossRef]
- Ladd, M. Introduction to Physical Chemistry; Cambridge University Press (CUP): Cambridge, UK, 1998. [Google Scholar]
- Iacobazzi, F.; Milanese, M.; Colangelo, G.; Lomascolo, M.; De Risi, A. An explanation of the Al2O3 nanofluid thermal conductivity based on the phonon theory of liquid. Energy 2016, 116, 786–794. [Google Scholar] [CrossRef]
- Li, X. Phonon Transport across Dissimilar Material Interfaces and in Nanostructured Materials. Ph.D. Thesis, University of Colorado Boulder, Boulder, CO, USA, April 2012. [Google Scholar]
- Shchepetov, A.; Prunnila, M.; Alzina, F.; Schneider, L.; Cuffe, J.; Jiang, H.; Kauppinen, E.I.; Torres, C.M.S.; Ahopelto, J. Ultra-thin free-standing single crystalline silicon membranes with strain control. Appl. Phys. Lett. 2013, 102, 192108. [Google Scholar] [CrossRef]
- Marconnet, A.; Asheghi, M.; Goodson, K.E. From the Casimir Limit to Phononic Crystals: 20 Years of Phonon Transport Studies Using Silicon-on-Insulator Technology. J. Heat Transf. 2013, 135, 061601. [Google Scholar] [CrossRef]
- Li, D.; Wu, Y.; Kim, P.; Shi, L.; Yang, P.; Majumdar, A. Thermal conductivity of individual silicon nanowires. Appl. Phys. Lett. 2003, 83, 2934–2936. [Google Scholar] [CrossRef]
- Joshi, A.A.; Majumdar, A. Transient ballistic and diffusive phonon heat transport in thin films. J. Appl. Phys. 1993, 74, 31–39. [Google Scholar] [CrossRef]
- Cui, W.; Shen, Z.; Yang, J.; Wu, S. Molecular dynamics simulation on the microstructure of absorption layer at the liquid–solid interface in nanofluids. Int. Commun. Heat Mass Transf. 2016, 71, 75–85. [Google Scholar] [CrossRef]
- Israelachvili, J. LIQUIDS: Putting Liquids under Molecular-Scale Confinement. Science 2001, 292, 867–868. [Google Scholar] [CrossRef]
- Thermophysical Properties. Available online: http://webbook.nist.gov/cgi/fluid.cgi?ID=C7440371&Action=Page (accessed on 11 April 2017).
- Xu, L.; Molinero, V. Is There a Liquid–Liquid Transition in Confined Water? J. Phys. Chem. B 2011, 115, 14210–14216. [Google Scholar] [CrossRef] [PubMed]
- McNutt, N.W.; Wang, Q.; Rios, O.; Keffer, D.J. Entropy-driven structure and dynamics in carbon nanocrystallites. J. Nanopart. Res. 2014, 16. [Google Scholar] [CrossRef]
- Shao, C.; Bao, H. A molecular dynamics investigation of heat transfer across a disordered thin film. Int. J. Heat Mass Transf. 2015, 85, 33–40. [Google Scholar] [CrossRef]
- Song, G.; Min, C. Temperature dependence of thermal resistance at a solid/liquid interface. Mol. Phys. 2013, 111, 903–908. [Google Scholar] [CrossRef]
- Gorelli, F.A.; Bryk, T.; Krisch, M.; Ruocco, G.; Santoro, M.; Scopigno, T. Dynamics and Thermodynamics beyond the critical point. Sci. Rep. 2013, 3, 1203. [Google Scholar] [CrossRef]
| Pair Interaction | ||
|---|---|---|
| Liquid-Liquid | 1.67 × 10−21 | 0.3405 |
| Solid-Solid | 6.59 × 10−20 | 0.2340 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mahmud, R.; Morshed, A.K.M.M.; Paul, T.C. Enhanced Specific Heat Capacity of Liquid Entrapped between Two Solid Walls Separated by a Nanogap. Processes 2020, 8, 459. https://doi.org/10.3390/pr8040459
Mahmud R, Morshed AKMM, Paul TC. Enhanced Specific Heat Capacity of Liquid Entrapped between Two Solid Walls Separated by a Nanogap. Processes. 2020; 8(4):459. https://doi.org/10.3390/pr8040459
Chicago/Turabian StyleMahmud, Rifat, A.K.M. Monjur Morshed, and Titan C. Paul. 2020. "Enhanced Specific Heat Capacity of Liquid Entrapped between Two Solid Walls Separated by a Nanogap" Processes 8, no. 4: 459. https://doi.org/10.3390/pr8040459
APA StyleMahmud, R., Morshed, A. K. M. M., & Paul, T. C. (2020). Enhanced Specific Heat Capacity of Liquid Entrapped between Two Solid Walls Separated by a Nanogap. Processes, 8(4), 459. https://doi.org/10.3390/pr8040459






