A Wavelet Transform-Assisted Convolutional Neural Network Multi-Model Framework for Monitoring Large-Scale Fluorochemical Engineering Processes
Abstract
1. Introduction
2. Background and Methods
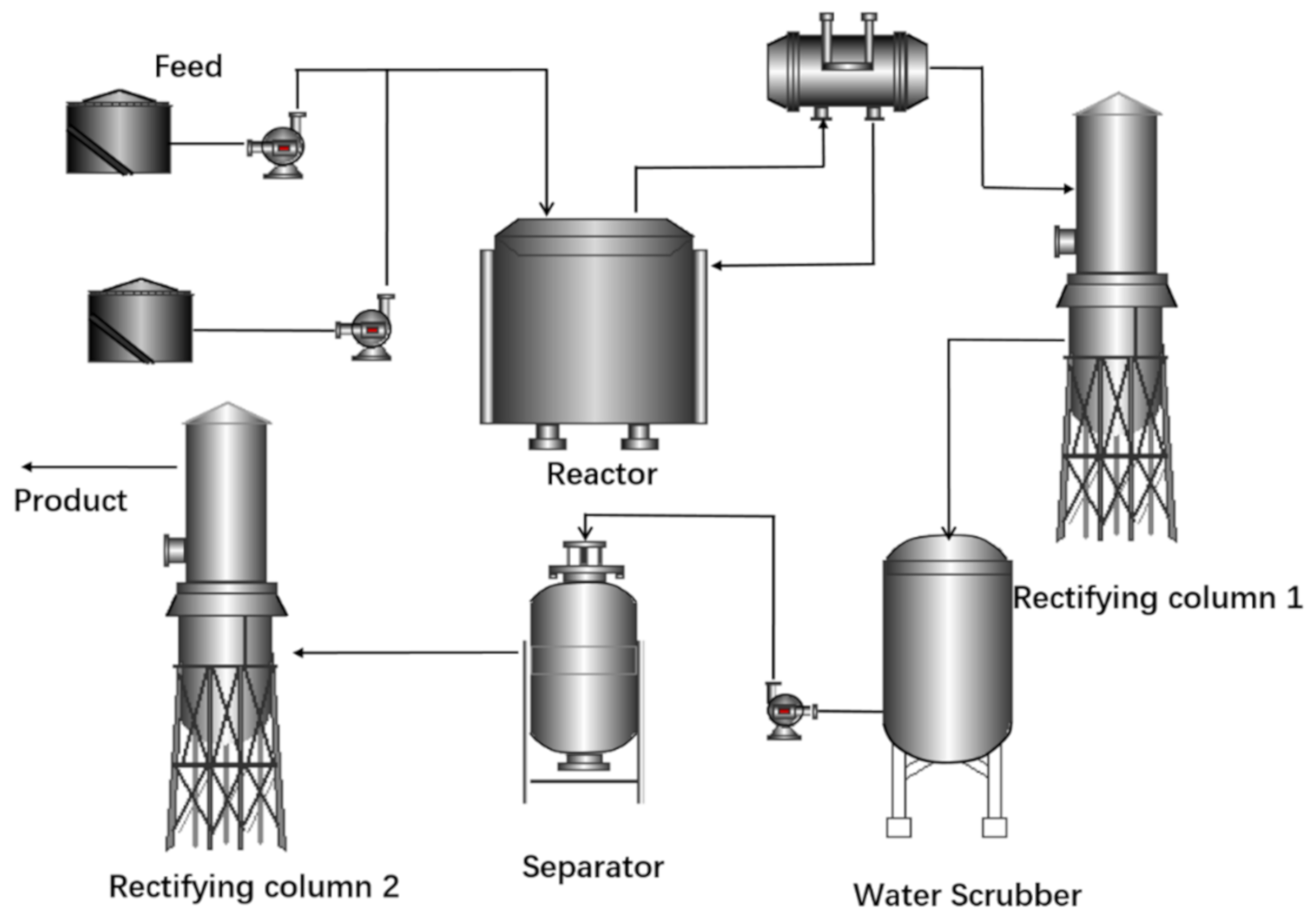
2.1. Brief Introduction to R-22 Refrigerant Producing Process
2.2. Brief Introduction of Wavelet Transform Algorithm
2.3. Brief Introduction to Convolutional Neural Network (CNN)
3. The Proposed Wavelet Transform-Assisted Convolutional Neural Network (WCNN)-Based Multi-Model Framework for Dynamic Process Monitoring
- A preliminary diagnosis model is trained with CNN algorithm to detect all faults with the minimized time-delay. Additionally, for ETD faults, the corresponding diagnosis information is also provided by this preliminary model at the same time for a further response.
- For HTD faults, a wavelet transform algorithm is introduced to preprocess sampled data by filtering out the inherent noise and transforming it into a compacter space, then a secondary CNN model is trained to diagnose them.
- For online monitoring, a queue assembly updating method is proposed to reduce the time delay in FDD, whose details will be described in Section 3.3.
- The priceless background knowledge can be utilized by labelling faults into ETD and HTD classes.
- Different kinds of conventional function and structure of CNNs can be used in the preliminary and secondary models, which remarkably reduces the training burden for both models.
- The conventional functions and structures of CNN in the secondary model can be more specifically designed to further improve the diagnosis accuracies for all HTD faults without causing any time-delay in fault detection.
- The performance of the secondary CNN model can be improved by introducing a wavelet transform function for data preprocessing.
3.1. The Preliminary CNN Fault Detecting and Diagnosing Model
3.2. The Secondary CNN Fault Diagnosing Model
3.3. Online Queue Assembly Updating Method
- Initiating the updating matrix with a training matrix including only normal samples;
- Every time, a new sample is available, adding it to the end of the queue and removing one old sample;
- Input this matrix to the WCNN model to obtain the FDD prediction information;
- Repeat steps 2–4.
4. Application Results and Discussion
4.1. The Monitroing Performance of Fluorochemical Engineering Processes
4.2. The Monitoring Performance for the Tennessee Eastman Process
- To cover the normal data distribution as comprehensive as possible, the simulator ran in a normal state 10 times with 10 different set points, respectively. For each normal state run, the simulator continued to run for 50 h to collect the normal data for each normal state. Therefore, 25,000 (50 h × 50 samples × 10 times) normal samples were collected in total.
- For each IDV state, except for IDV6, the disturbance was introduced after 10 h of normal operation. Then the simulator kept running for another 40 h to collect the IDV data. This simulation process was repeated for 10 times with different production set points. Therefore, 20,000 (40 h × 50 samples × 10times) samples for each IDV were collected.
- Because the simulator automatically shut down about 6h after IDV6 was introduced. Only 3000 (6 h × 50 samples × 10 times) samples were collected for it.
- For IDV5, IDV12 and IDV 18, only DBN obtained FDRs for IDV5 and IDV12 testing samples lower than 90%. All other deep-learning methods can diagnose them correctly;
- Even IDV3 was considered as one of HTD IDVs, but the performance of all deep-learning methods were all higher than 90%;
- For IDV9, a HTD IDV, the test performance for neither DBN nor the regular CNN were good enough. But for WCNN, it was improved to 70%;
- For IDV15, another HTD IDV, neither DBN nor the regular CNN could diagnose it. The train performance of WCNN was as high as 98%, but the test performance was only 63%.
- For IDV16, the forth HTD IDV, neither DBN nor the regular CNN could diagnose it. However, both training and testing performance of WCNN were good enough (99% and 81%, respectively).
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Yin, L.; Parekh, A.; Selesnick, I.W. Stable principal component pursuit via convex analysis. IEEE Trans. Signal Process. 2019, 67, 2595–2607. [Google Scholar] [CrossRef]
- Camarrone, F.; Van Hulle, M.M. Fast Multiway Partial Least Squares Regression. IEEE Trans. Biomed. Eng. 2018, 66, 433–443. [Google Scholar] [CrossRef]
- Feng, L.; Zhao, C.; Huang, B. A slow independent component analysis algorithm for time series feature extraction with the concurrent consideration of high-order statistic and slowness. J. Process. Control. 2019, 84, 1–12. [Google Scholar] [CrossRef]
- Pisner, D.A.; Schnyer, D.M. Chapter 6-Support vector machine. In Machine Learning; Mechelli, A., Vieira, S., Eds.; Academic Press: Cambridge, MA, USA, 2020; pp. 101–121. [Google Scholar]
- Rocha, A.D.; Lima-Monteiro, P.; Parreira-Rocha, M.; Barata, J. Artificial immune systems based multi-agent architecture to perform distributed diagnosis. J. Intell. Manuf. 2017, 30, 2025–2037. [Google Scholar] [CrossRef]
- Shahnazari, H. Fault diagnosis of nonlinear systems using recurrent neural networks. Chem. Eng. Res. Des. 2020, 153, 233–245. [Google Scholar] [CrossRef]
- Hinton, G.E. Reducing the dimensionality of data with neural networks. Science 2006, 313, 504–507. [Google Scholar] [CrossRef] [PubMed]
- Hinton, G.E.; Osindero, S.; Teh, Y.-W. A Fast learning algorithm for deep belief nets. Neural Comput. 2006, 18, 1527–1554. [Google Scholar] [CrossRef] [PubMed]
- Le Cun, Y.; Jackel, L.D.; Boser, B.; Denker, J.S.; Graf, H.P.; Guyon, I.; Henderson, D.; Howard, R.E.; Hubbard, W. Handwritten digit recognition: Applications of neural network chips and automatic learning. IEEE Commun. Mag. 1989, 27, 41–46. [Google Scholar] [CrossRef]
- Schmidhuber, J. Deep learning in neural networks: An overview. Neural Netw. 2015, 61, 85–117. [Google Scholar] [CrossRef]
- Fukushima, K. Neocognitron: A self-organizing neural network model for a mechanism of pattern recognition unaffected by shift in position. Biol. Cybern. 1980, 36, 193–202. [Google Scholar] [CrossRef]
- LeCun, Y.; Kavukcuoglu, K.; Farabet, C. Convolutional networks and applications in vision. Proceedings of 2010 IEEE International Symposium on Circuits and Systems, Paris, France, 30 May –2 June 2010; pp. 253–256. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet classification with deep convolutional neural networks. In Advances in Neural Information Processing Systems 25; Pereira, F., Burges, C.J.C., Bottou, L., Weinberger, K.Q., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2012; pp. 1097–1105. [Google Scholar]
- Zeiler, M.D.; Fergus, R. Visualizing and Understanding Convolutional Networks. arXiv 2013, arXiv:1311.2901. Available online: https://arxiv.org/abs/1311.2901 (accessed on 17 November 2020).
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going deeper with convolutions. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 1–9. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 26 June–1 July 2016; pp. 770–778. [Google Scholar]
- Hoang, D.-T.; Kang, H.J. Rolling element bearing fault diagnosis using convolutional neural network and vibration image. Cogn. Syst. Res. 2019, 53, 42–50. [Google Scholar] [CrossRef]
- Zhang, W.; Li, C.; Peng, G.; Chen, Y.; Zhang, Z. A deep convolutional neural network with new training methods for bearing fault diagnosis under noisy environment and different working load. Mech. Syst. Signal Process. 2018, 100, 439–453. [Google Scholar] [CrossRef]
- Arneodo, A.; Grasseau, G.; Holschneider, M. Wavelet Transform of Multifractals. Phys. Rev. Lett. 1988, 61, 2281–2284. [Google Scholar] [CrossRef] [PubMed]
- Stein, E.M.; Weiss, G. Introduction to Fourier Analysis on Euclidean Spaces (PMS-32); Prinston University Press: Princeton, NJ, USA, 1972. [Google Scholar]
- Wu, J.; Li, J.; Guo, L.; Tang, X.; Wang, J.; Yang, L.; Bai, J. The differences analysis on filtering properties of wavelet decomposition and empirical mode decomposition. In Proceedings of the International Conference on Information Technology and Management Engineering (ITME 2011), Wuhan, China, 23–25 September 2011; pp. 23–26. [Google Scholar]
- Liu, P.; Zhang, H.; Lian, W.; Zuo, W. Multi-Level Wavelet Convolutional Neural Networks. IEEE Access 2019, 7, 74973–74985. [Google Scholar] [CrossRef]
- Li, B.; Chen, X. Wavelet-based numerical analysis: A review and classification. Finite Elem. Anal. Des. 2014, 81, 14–31. [Google Scholar] [CrossRef]
- Chen, J.; Li, Z.; Pan, J.; Chen, G.; Zi, Y.; Yuan, J.; Chen, B.; He, Z. Wavelet transform based on inner product in fault diagnosis of rotating machinery: A review. Mech. Syst. Signal Process. 2016, 1–35. [Google Scholar] [CrossRef]
- Graps, A. An introduction to wavelets. IEEE Comput. Sci. Eng. 1995, 2, 50–61. [Google Scholar] [CrossRef]
- Daubechies, I. Orthonormal bases of compactly supported wavelets. Commun. Pure Appl. Math. 1988, 41, 909–996. [Google Scholar] [CrossRef]
- Mallat, S.E.G. A theory of multiresolution signal decomposition: The wavelet representation. IEEE Trans. Pattern Anal. Mach. Intell. 1989, 11, 674–693. [Google Scholar] [CrossRef]
- Gu, J.; Wang, Z.; Kuen, J.; Ma, L.; Shahroudy, A.; Shuai, B.; Liu, T.; Wang, X.; Wang, G.; Cai, J.; et al. Recent advances in convolutional neural networks. Pattern Recognit. 2018, 77, 354–377. [Google Scholar] [CrossRef]
- Hao, W.; Zhao, J. Deep convolutional neural network model based chemical process fault diagnosis. Comput. Chem. Eng. 2018, 115, 185–197. [Google Scholar]
- Li, C.; Zhao, D.; Mu, S.; Zhang, W.; Shi, N.; Li, L. Fault diagnosis for distillation process based on CNN–DAE. Chin. J. Chem. Eng. 2019, 27, 598–604. [Google Scholar] [CrossRef]
- Wang, H.; Liu, Z.; Liu, Z.; Qin, Y. Understanding and learning discriminant features based on multiattention 1DCNN for wheelset bearing fault diagnosis. IEEE Trans. Ind. Inform. 2019, 16, 5735–5745. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2014, arXiv:1412.6980. Available online: https://arxiv.org/abs/1412.6980 (accessed on 17 November 2020).
- Dauphin, Y.N.; De Vries, H.; Bengio, Y. Equilibrated adaptive learning rates for non-convex optimization. arXiv 2015, arXiv:1502.04390. Available online: https://arxiv.org/abs/1502.04390 (accessed on 17 November 2020).
- Zeiler, M.D. ADADELTA: An Adaptive Learning Rate Method. arXiv 2012, arXiv:1212.5701. Available online: https://arxiv.org/abs/1212.5701 (accessed on 17 November 2020).
- Chakrabarty, S.; Habets, E.A.P. Multi-speaker DOA estimation using deep convolutional networks trained with noise signals. IEEE J. Sel. Top. Signal Process. 2019, 13, 8–21. [Google Scholar] [CrossRef]
- Szegedy, C.; Vanhoucke, V.; Ioffe, S.; Shlens, J.; Wojna, Z. Rethinking the Inception Architecture for Computer Vision. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 2818–2826. [Google Scholar]
- Motard, R.L. Wavelet Applications in Chemical Engineering; Springer: Boston, MA, USA, 1994. [Google Scholar]
- Bakshi, B.R.; Stephanopoulos, G. Compression of chemical process data by functional approximation and feature extraction. AIChE J. 1996, 42, 477–492. [Google Scholar] [CrossRef]
- Raghavan, V.K. Wavelet Representation of Sensor Signals for Monitoring and Control. Master’s Thesis, Oklahoma State University, Oklachoma City, OK, USA, May 1995. [Google Scholar]
- Thornhill, N.F.; Choudhury, M.S.; Shah, S.L. The impact of compression on data-driven process analyses. J. Process. Control. 2004, 14, 389–398. [Google Scholar] [CrossRef]
- Cohen, A.; Daubechies, I.; Feauveau, J.-C. Biorthogonal bases of compactly supported wavelets. Commun. Pure Appl. Math. 1992, 45, 485–560. [Google Scholar] [CrossRef]
- Daubechies, I.; Heil, C. Ten lectures on wavelets. J. Comput. Phys. 1998, 6, 1671. [Google Scholar]
- Shen, Y.; Ding, S.X.; Haghani, A.; Hao, H.; Ping, Z. A comparison study of basic data-driven fault diagnosis and process monitoring methods on the benchmark Tennessee Eastman process. J. Process. Control. 2012, 22, 1567–1581. [Google Scholar]
- Laurens, V.D.M.; Hinton, G. Visualizing data using t-SNE. J. Mach. Learn. Res. 2008, 9, 2579–2605. [Google Scholar]
- Zhang, Y. Enhanced statistical analysis of nonlinear processes using KPCA, KICA and SVM. Chem. Eng. Sci. 2009, 64, 801–811. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhao, J. A deep belief network based fault diagnosis model for complex chemical processes. Comput. Chem. Eng. 2017, 107, 395–407. [Google Scholar] [CrossRef]
- Bathelt, A.; Ricker, N.L.; Jelali, M. Revision of the Tennessee Eastman process model. IFAC-PapersOnLine 2015, 48, 309–314. [Google Scholar] [CrossRef]
- Tennessee Eastman Challenge Archive. Available online: http://depts.washington.edu/control/LARRY/TE/download.html (accessed on 17 November 2020).





| No. | Type | Tag Number |
|---|---|---|
| 1 | PV | FIQ-3002 |
| 2 | PV | TICA-3002 |
| 3 | PV | WIA-3001 |
| 4 | PV | LICA-3003 |
| 5 | CPV | FIQ-3017 |
| 6 | PV | TRCA-3001A |
| 7 | PV | TRCA-3001B |
| 8 | PV | TRCA-3001C |
| 9 | PV | TRCA-3001D |
| 10 | PV | TRCA-3001E |
| Model | Architecture | FDR (%) |
|---|---|---|
| 1 | Conv(64)-Pool-FC(1024)-FC(3) | 88.3 |
| 2 | Conv(32)-Conv(64)-Pool-FC(1024)-FC(3) | 90 |
| 3 | Conv(32)-Conv(64)-Conv(128)-Pool-FC(1024)-FC(3) | 90 |
| 4 | Conv(64)-Pool-Conv(128)-Pool-FC(1024)-FC(3) | 91.7 |
| 5 | Conv(32)-Conv(64)-Pool-Conv(128) -Conv(128)-Pool-FC(1024)-FC(3) | 93.3 |
| 6 | Conv(32)-Conv(64)-Conv(128)-Pool-Conv(128)-Conv(128)-Pool-FC(1024)-FC(3) | 91.7 |
| FDR-SVM (%) | FDR-DBN (%) | FDR-CNN (%) | FDR-WCNN (%) | |
|---|---|---|---|---|
| Normal case | 100 | 95 | 100 | 100 |
| Abnormal case 1 | 65 | 70 | 75 | 90 |
| Abnormal case 2 | 90 | 85 | 95 | 100 |
| Abnormal case 3 | 85 | 90 | 85 | 90 |
| Abnormal case 4 | 100 | 100 | 100 | 100 |
| Abnormal case 5 | 100 | 100 | 100 | 100 |
| Average | 90 | 90.83 | 92.5 | 96.7 |
| CNN | The Preliminary Model | The Secondary Model | |
|---|---|---|---|
| Training time for one epoch (s) | 2.36 | 1.77 | 0.88 |
| Epoch Times of convergence | 160 | 30 | 200 |
| Total training time (s) | 377 | 53 | 176 |
| Inference frames per second | 30.2 | 49.3 | 90.9 |
| Category | Process Variable | Type |
|---|---|---|
| IDV(1) | A/C feed ratio, B composition constant (stream 4) | Step |
| IDV(2) | B composition, A/C ratio constant (stream 4) | Step |
| IDV(3) | D feed temperature (stream 2) | Step |
| IDV(4) | Reactor cooling water inlet temperature | Step |
| IDV(5) | Condenser cooling water inlet temperature | Step |
| IDV(6) | A feed loss (stream 1) | Step |
| IDV(7) | C header pressure loss-reduced availability (stream 4) | Step |
| IDV(8) | A,B,C feed composition(stream 4) | Random |
| IDV(9) | D feed temperature (stream 2) | Random |
| IDV(10) | C feed temperature (stream 4) | Random |
| IDV(11) | Reactor cooling water inlet temperature | Random |
| IDV(12) | Condenser cooling water inlet temperature | Random |
| IDV(13) | Reaction kinetics | Slow drift |
| IDV(14) | Reactor cooling water valve | Sticking |
| IDV(15) | Condensor cooling water valve | Sticking |
| IDV(16) | Unknown | Unknown |
| IDV(17) | Unknown | Unknown |
| IDV(18) | Unknown | Unknown |
| IDV(19) | Unknown | Unknown |
| IDV(20) | Unknown | Unknown |
| Status Index | FDR (%) | |||||
|---|---|---|---|---|---|---|
| Train-DBN | Train-CNN | Train-WCNN | Test-DBN 1 | Test-CNN 2 | Test-WCNN | |
| Nomal | - | 91.6 | 97 | - | 97.8 | 91 |
| IDV 01 | 100 | 99.8 | 100 | 100 | 98.6 | 100 |
| IDV 02 | 100 | 99.6 | 99 | 99 | 98.5 | 97.5 |
| IDV 03 | 99 | 99.6 | 99 | 95 | 91.7 | 93 |
| IDV 04 | 98 | 99.9 | 100 | 98 | 97.6 | 100 |
| IDV 05 | 90 | 99.8 | 100 | 86 | 91.5 | 100 |
| IDV 06 | 100 | 99.8 | 100 | 100 | 97.5 | 100 |
| IDV 07 | 100 | 99.9 | 100 | 100 | 99.9 | 100 |
| IDV 08 | 96 | 98.5 | 96 | 78 | 92.2 | 91.3 |
| IDV 09 | 65.5 | 97.3 | 97 | 57 | 58.4 | 70 |
| IDV 10 | 97.5 | 97.7 | 98.6 | 98 | 96.4 | 95 |
| IDV 11 | 97.5 | 99.5 | 99 | 87 | 98.4 | 95 |
| IDV 12 | 85.5 | 99.2 | 98.7 | 85 | 95.6 | 91 |
| IDV 13 | 96.5 | 97.8 | 100 | 88 | 95.7 | 98.8 |
| IDV 14 | 96 | 99.8 | 99 | 87 | 98.7 | 95 |
| IDV 15 | 0 | 99.7 | 98 | 0 | 28 | 63 |
| IDV 16 | 0 | 91.2 | 99 | 0 | 44.2 | 81 |
| IDV 17 | 100 | 98.8 | 99 | 100 | 94.5 | 95 |
| IDV 18 | 100 | 97 | 99 | 98 | 93.9 | 94.3 |
| IDV 19 | 97 | 99.6 | 100 | 93 | 98.6 | 98 |
| IDV 20 | 98.7 | 97.1 | 97 | 93 | 93.3 | 95 |
| Average | 85.9 | 98.6 | 98.8 | 82.1 | 88.2 | 93 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Zhou, K.; Xue, F.; Chen, Z.; Ge, Z.; Chen, X.; Song, K. A Wavelet Transform-Assisted Convolutional Neural Network Multi-Model Framework for Monitoring Large-Scale Fluorochemical Engineering Processes. Processes 2020, 8, 1480. https://doi.org/10.3390/pr8111480
Li X, Zhou K, Xue F, Chen Z, Ge Z, Chen X, Song K. A Wavelet Transform-Assisted Convolutional Neural Network Multi-Model Framework for Monitoring Large-Scale Fluorochemical Engineering Processes. Processes. 2020; 8(11):1480. https://doi.org/10.3390/pr8111480
Chicago/Turabian StyleLi, Xintong, Kun Zhou, Feng Xue, Zhibing Chen, Zhiqiang Ge, Xu Chen, and Kai Song. 2020. "A Wavelet Transform-Assisted Convolutional Neural Network Multi-Model Framework for Monitoring Large-Scale Fluorochemical Engineering Processes" Processes 8, no. 11: 1480. https://doi.org/10.3390/pr8111480
APA StyleLi, X., Zhou, K., Xue, F., Chen, Z., Ge, Z., Chen, X., & Song, K. (2020). A Wavelet Transform-Assisted Convolutional Neural Network Multi-Model Framework for Monitoring Large-Scale Fluorochemical Engineering Processes. Processes, 8(11), 1480. https://doi.org/10.3390/pr8111480








