Quantitative Methods to Support Data Acquisition Modernization within Copper Smelters

Abstract

Sensors and process control systems are essential for process automation and optimization. Many sectors have adapted to the Industry 4.0 paradigm, but copper smelters remain hesitant to implement these technologies without appropriate justification, as many critical functions remain subject to ground operator experience. Recent experiments and industrial trials using radiometric optoelectronic data acquisition, coupled with advanced quantitative methods and expert systems, have successfully distinguished between mineral species in reactive vessels with high classification rates. These experiments demonstrate the increasing potential for the online monitoring of the state of a charge in pyrometallurgical furnaces, allowing data-driven adjustments to critical operational parameters. However, the justification to implement an innovative control system requires a quantitative framework that is conducive to multiphase engineering projects. This paper presents a unified quantitative framework for copper and nickel-copper smelters, which integrates thermochemical modeling into discrete event simulation and is, indeed, able to simulate smelters, with and without a proposed set of sensors, thus quantifying the benefit of these sensors. Sample computations are presented, which are based on the authors’ experiences in smelter reengineering projects.

1. Introduction

Modern metallurgical installations such as steel plants and copper smelters require a range of plant sensors and process control systems to attain their highest efficiency. It is often stated that the levels of so-called “smart automation” today represents the fourth-generation industrial revolution (sometimes also called “Industry 4.0”)—following the first, considered as the power generation and mechanical automation (early 1800s), the second as widespread industrialization (early 1900s), the third as electronic automation (starting 1950s), and, now, the fourth [1], benefitting from modern information and communication technology (ICT), as illustrated in Figure 1. Learning from history, it is well-known that if a plant does not remain up to date, taking advantage of modern but proven equipment and controls, then it lags its competitors. This paper discusses the application of techniques, sensors, and mathematical modeling that can support copper smelters in their endeavors to modernize their operations through data acquisition and, thus, remain competitive.

By way of background, copper smelters [2] are quite complex, with a number of individual high-performance operating units functioning together. Two of the key primary instrumentation and control needs in copper smelting today—and throughout history—are air (or oxygen) measurement and control and furnace temperature. In February 1956, a paper was presented at the AIME Annual Meeting in New York on the fine and well-recognized converter operation at the Noranda smelter (now Glencore Horne) located in Rouyn-Noranda, Quebec, Canada [3].

After describing how the production capacity at the fairly new plant increased over the previous two decades since the start-up (in 1927) by simply installing additional and/or larger units, the author discussed a major effort at further increasing production capacity that included the installation of reliable instruments for measuring both the instantaneous air flow and reporting the accumulated air blown over any given time interval. The significance and benefits of this new instrumentation (higher production rates) were subsequently described; of interest, the converters at this plant reached record or near-record air blowing rates in the industry at this time, reflecting the fact that it was one of the leading plants of the day. Of course, such equipment is mandatory today, coupled with the distributed control system (DCS) and advanced computer models to provide feedback for optimizing the operation.

Furnace temperature measurements at the time were made by an optical pyrometer mounted so that it pointed downward onto the molten bath. While generally reliable, it was often prone to dust and fume build-up affecting a clear sight line; unsmelted flux and other materials on the bath could also lead to low temperature readings. Some thirty years after the above noted paper [3], a new pyrometer instrument operated by sighting directly into the bath through one of the tuyères was described at the Copper 87 conference held in Viña del Mar, Chile [4]. During the discussion, the authors were asked about the cost of the new instrument. An indicative preproduction price range was given when the questioner loudly stated that he could buy “a Mercedes-Benz automobile” for the price mentioned, whereupon the authors responded that if the questioner installed one of these instruments at his plant, the profits he would make would allow him to purchase quite a few Mercedes! The point is that proper selection and use of reliable instruments for automated data acquisition and control are vital for a proper functioning plant to remain competitive, as the cost of sensors are comparatively modest.

In batch processes, such as steelmaking or copper converting, knowledge of the precise endpoint of the operation is extremely important for compositional control and optimization of the subsequent refining operations.

The Boliden’s Rönnskär smelter, located at Skelleftehamn, Sweden, operates one of the best converter aisles in the world today, in the authors’ opinion. They also pioneered the use of the ingenious Semtech Optical Process Control (OPC) sensor device for precise endpoint determination [5] to detect when the last of the iron was expelled into slag and, subsequently, when the last of the sulfur was expelled into the SO₂ offgas. This instrument spectrometrically measures trace amounts of lead and copper sulfides and oxides in the offgas and signals when the level of sulfides starts to decrease, signaling the end of the batch [6]. The precise endpoint control saves significantly in processing time at Rönnskär in the subsequent anode furnace, thus lowering operating costs and allowing higher throughput.

In spite of the successful implementations of modern sensors at certain smelters such as Rönnskär, there is a general hesitance for copper smelters to adopt sensor arrays, as it is often unclear what the operational implications will be. Indeed, it is unclear what will be the series of changes that will be necessary so that the perceived benefits of the sensors will be manifest, and it is therefore difficult to quantify what will be the true impact of these new sensors. This paper presents a unified quantitative framework for copper and nickel-copper smelters, which integrate thermochemical modeling into discrete event simulations and is intended to assist in smelter reengineering projects that feature innovative sensors in consideration the Industry 4.0 paradigm.

2. Radiometric Sensors for Extractive Pyrometallurgy of Copper

Within copper smelters, the reality is that even the 3.0 industrial revolution (information technology (IT) and automation) still has room for continued development. This current condition limits the ability to integrate Industry 4.0 developments for process optimization. Indeed, the degree of analytical instrumentation usage for the monitoring and control of the smelter processes is limited. As a result, the information available for operational decision-making at many plants is mainly based on static mass and energy balances. In such cases, the operational dynamics continues to depend largely on the experience of ground operators.

Only a handful of advanced measurement instruments have gained industry acceptance for operational monitoring and control in copper pyrometallurgical reactors. The aforementioned Semtech OPC system, which has been on the market for more than 25 years, monitors pyrometallurgical variables by analyzing the emission spectrum of flames emitted by gases during the conversion of copper sulfide mattes within Peirce-Smith (PS) converters. Additionally, the Noranda Pyrometer, configured solely for bath furnaces using blowing tuyères, has been on the market since the 1980s without any change to the original concept and with only some upgrades to the unit’s robustness (with regard to assembly, material selection, etc.). By measuring radiation through an analog array, it monitors the temperature of the molten bath by applying Planck’s law for two fixed wavelengths. Other instruments include level measurement in a feed bin and furnace melts and equipment vibration monitoring.

One option for the advancement of process monitoring and control systems in copper smelters is to modernize the use of radiometric measurements, since this approach was previously validated with both the OPC system and the Noranda Pyrometer. A series of proposed concepts and results from initial industrial trials are discussed here.

2.1. Reactive Systems

A recent work focused on radiometric optoelectronic sensors that consider a broad spectrum, which includes the visible range up the near infrared range [7,8,9]. This approach is different from available commercialized sensors, which only analyze a limited selection of wavelengths. The idea here is to analyze both the continuous and discontinuous parts of the spectrum, as well as its dynamics in different time scales. The purpose is to correlate the measured spectral radiation to the operational conditions of the reactors following the emission of radiation from the oxidation reactions. These sensors also measure temperature with better precision than the Noranda Pyrometer by using more sophisticated techniques to select the appropriate (two or more) wavelengths. The sensor thus solves the complex problem of simultaneously measuring emissivity and temperature.

Results from an experiment using a drop tube setup for the flash oxidation of copper concentrates (Figure 2) validate the formation of wustite (FeO), magnetite (Fe₃O₄), and copper oxides (CuO/Cu₂O) as indicators of the concentrate smelting/oxidation/combustion process [7,8,9]. This information is of special interest to track the physicochemical dynamics of the process in real-time and establish operating criteria for a smelting reactor. Examples of such criteria could include adjustments to concentration/oxygen ratios, oxygen enrichment for the incoming blast, and the quantity of cold charge that will be required to maintain the heat balance.

The spectral acquisition system consists of a multicore optical fiber with its own cooling process (Figure 2b), which measures the combustion flame radiation. Figure 2b shows a simple combustion scheme for sulfide particles covering the physical phase changes that a particle can experience inside the reaction zone. However, measuring the spectrum is a complex task. As shown in Figure 2a, there is an ensemble of physical and chemical processes that complicate this measurement. One example is drop tube radiation caused by increased electrical resistance due to the higher temperatures; processing these spectral signals can, however, mitigate the effect of the unwanted radiation [8,9].

Applying specialized algorithms in the treatment of the spectral signals obtained from the experiment, coupled with multivariate data analysis methodologies, allows for the identification and classification of copper and iron sulfide minerals present in the blend [10]. These results are particularly important as they demonstrate that spectral data obtained from the oxidation process can be used to identify the type of charge being treated within a molten bath. The controlled bench-scale laboratory study was carried out on several different types of concentrate. An exploratory analysis of the results using principal component analysis (PCA) applied to the spectral data depicted high correlation features among species with different mineral characteristics but similar elemental compositions. Classification algorithms were tested on the spectral data, and a classification accuracy of 95.3% was achieved using a support vector machine (SVM) classifier with a Gaussian kernel. Initial industrial-scale trials with a prototype have confirmed these results [10].

2.2. Nonreactive Systems

Despite tremendous advances in the development of passive and active photonic sensors, such as hyperspectral imaging (HI) and laser-induced breakdown spectroscopy (LIBS), real-time analytical sensors do not exist at present for the conditions of pyrometallurgical copper processing. To date, there is no commercial instrument capable of online quantification of copper content (% Cu) without contact during tapping operations. Nor can the available sensors discriminate between the phases that are of particular interest to smelter operations. The distinction between matte and slag during the tapping of a smelting furnace can significantly impact copper recovery, yet this function is heavily reliant on the experience of operators involved in tapping.

However, in the last decade, the spectral behavior of pig iron and slag in the ferrous industry has been studied to estimate different variables that allow for improved control of the tapping process [11,12]. These models describe the parameters contained in the iron–slag mixture during blast furnace tapping, such as iron emissivity, casting depth, slag layer thickness and absorption coefficients, and radiometric parameters (e.g., reflectance at the iron-slag interface). The methodology begins by determining a spectral range in which the radiation of the molten phases is comparatively high. This facilitates detection by a silicon charge coupled device (CCD) camera, which is sensitive in the visible spectral range and part of the near-infrared. An optical filter centered at 650 nm was used together with the optics, such that the radiation emitted by the wash was partially filtered in the indicated spectral range.

The results confirm that the difference in emissivity of iron and slag at 650 nm allows for the spatial distinction of these phases. Furthermore, it was identified that the radiation intensity of the molten iron remains practically constant during the process, while that of the slag fluctuates. This fluctuation is due to differences in the thickness of the slag layer, as it absorbs and transmits the radiation coming from the steel to varying degrees. Additionally, the optical system was calibrated with a high-temperature black-body radiator, allowing the temperatures to be estimated at 1500–1600 °C, which is considerably higher than the copper smelter temperatures (1200–1350 °C). The results confirm that, by using sensitive optoelectronic systems in the molten iron spectral emission band, coupled with appropriate spectral models and processing software, it is possible to develop reliable and robust systems at both the laboratory and industrial scales. The authors believe that this approach could be adapted for copper smelter processes and represents a natural pathway for future work.

3. Unifying Framework for Copper and Nickel–Copper Smelter Dynamics

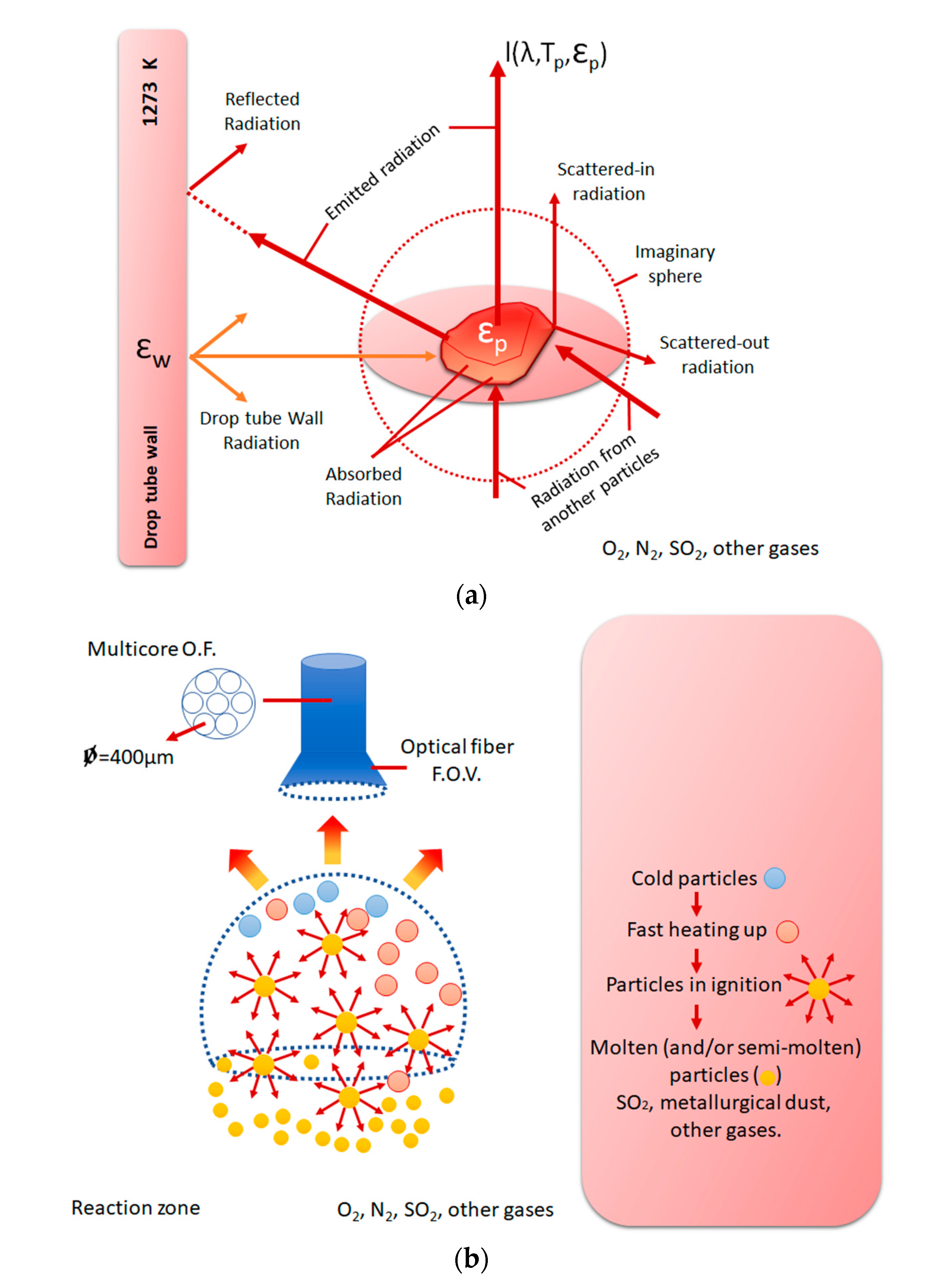
3.1. Overview of Copper and Nickel–Copper Smelter Operations

The copper pyrometallurgy process treats mineral concentrates to produce copper anodes that are, in turn, electrorefined to generate effectively pure (99.99% Cu) end-product cathodes. The concentrates are comprised of copper–iron sulfide minerals with particle sizes of generally less than 150 μm. Elemental compositions typically range from 25% to 30% Cu, 25% to 35% S, and 20% to 40% Fe, with the remainder made up of gangue material (oxides). The smelter targets the selective oxidation of Fe and S in order to retain Cu for the final product. Specifically, the iron is skimmed away as liquid slag and the sulfur is removed as SO₂ offgas, eventually resulting in molten copper [13,14]. 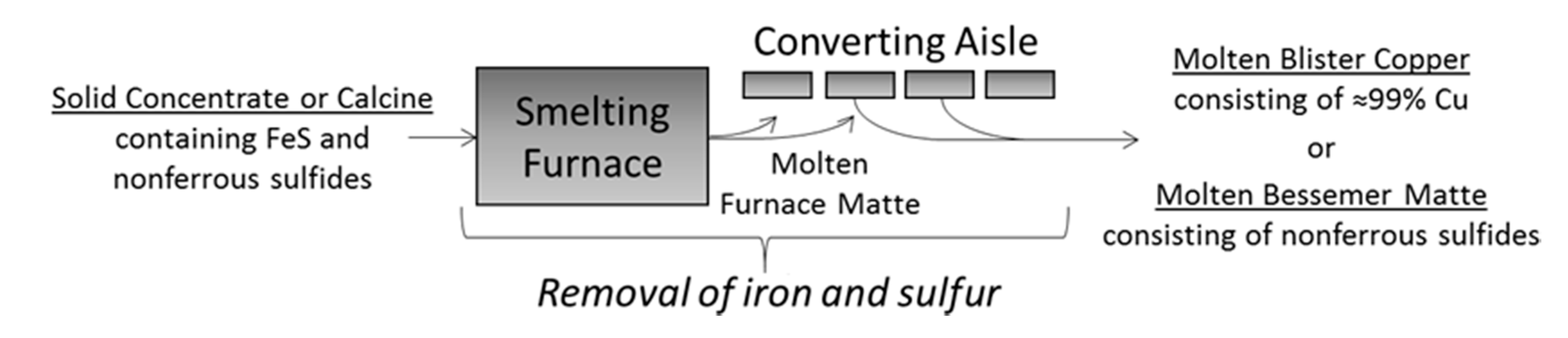This pyrometallurgical technique accounts for approximately 75% of the primary copper production worldwide [15,16], the majority of which is carried out using the conventional approach depicted in Figure 3. In some cases, the incoming concentrates are subject to roasting reactions prior to being fed into the smelting operation; these roasted concentrates are known as calcines.

Within a copper smelter, the concentrate or calcine is smelted by exothermic reactions while controlling the oxygen mass balance, which produces an intermediate matte phase composed of copper, iron, and sulfur. This molten matte is then subject to further oxidation, which converts the matte into a molten metal product called blister copper (>98% purity). The subsequent liquid–state refinement (fire-refining) precedes the casting of a Cu anode product (~99.5% purity). The anodes are then transferred to an electrorefinery for a final upgrade to end-product Cu cathodes that are 99.99% pure; the electrorefinery also recovers gold, silver, and other valuable byproducts that are contained in the anodes. Nonetheless, smelting and converting are the central processes in a copper smelter, since they transform the mineral input into an initial metallic output [14].

The smelting operation is a continuous process typically executed in one (or at certain large plants, two) large furnace(s). There are two main smelting technologies that induce similar chemical transformations but differ in the mechanism by which oxygen is delivered to the concentrate. Flash smelting, in which the oxidation of the concentrate takes place in a generally vertically mounted burner, currently accounts for roughly 45% of the world copper smelting capacity [2,15,17]. Within a flash smelting furnace, the refractory-lined reaction shaft is like an industrial scale “drop tube” (Figure 2). On the other hand, bath smelting technologies inject air or oxygen-enriched air into the molten bath either via a top-mounted lance (called top smelting lance or TSL technology) or via submerged tuyères; bath smelting technologies account for roughly 50% of smelting capacity, and this proportion has recently increasing due to new bath smelting technologies introduced in China [15,17].

Peirce-Smith (PS) converting is the most longstanding and widely used technology in conventional copper smelters [14] and is performed in discrete batches. PS converting is indeed a remnant of the second industrial revolution (Figure 1) and was influenced by the 19th century developments of Sir Henry Bessemer in steelmaking [16]. PS batch conversions are often carried out in parallel (Figure 3) and may share a limited set of resources (e.g., oxygen and offgas handling capacities). The continuous-discrete contrast of smelting converting is central to conventional smelter dynamics, in which PS converting can be a major bottleneck in conventional copper smelters [14]. Moreover, PS converting is also a feature of nickel–copper smelters (Figure 3), noting the difference in the final discharge product (Figure 3). Copper PS results in blister copper, whereas nickel–copper PS converting is simply to remove the iron and its associated sulfur; the resulting iron-free matte still contains considerable sulfur and is known as Bessemer matte, in honor of Sir Henry Bessemer.

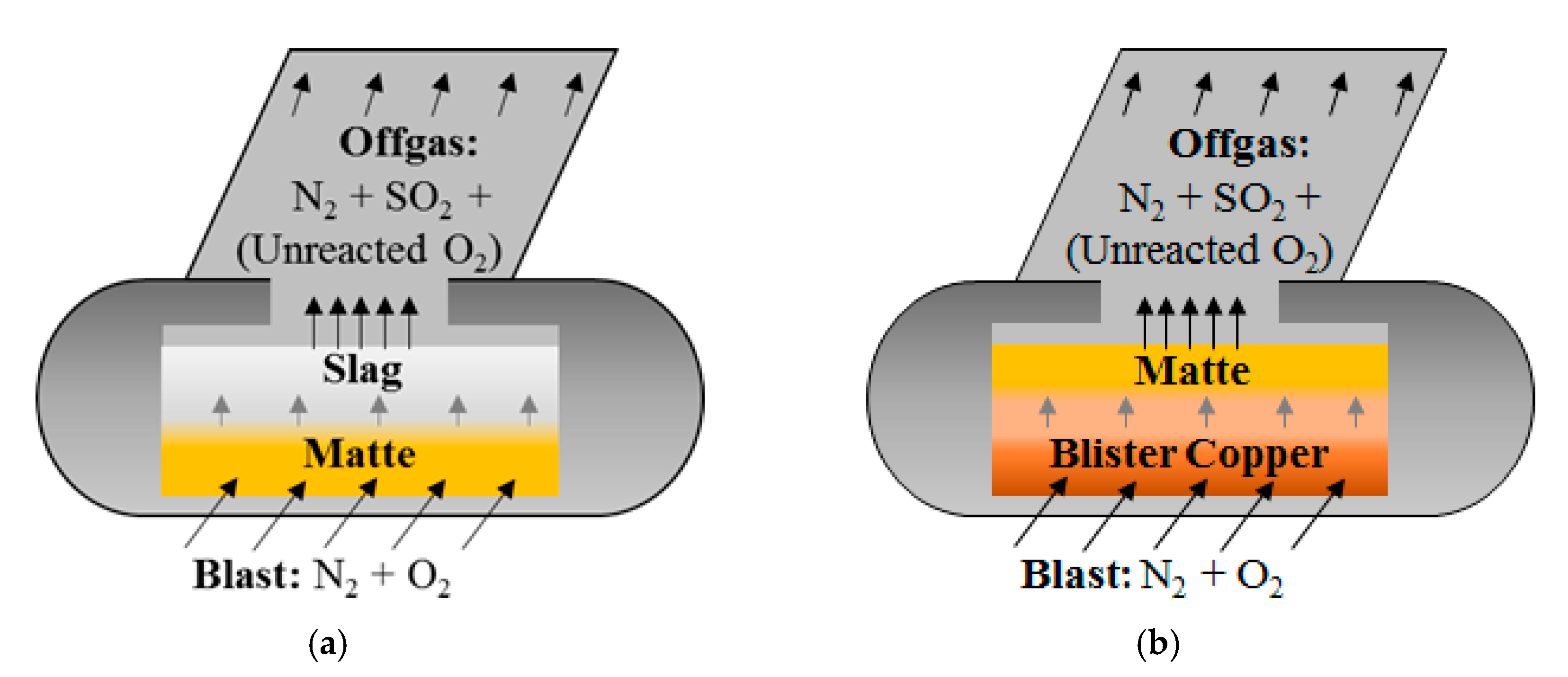
Smelting furnaces can generally produce, and hold, matte in excess of the converting capacity, which means that the smelting schedule can depend on the converting schedule. Given that smelting and converting are central to the overall smelter operation, all other critical functions at the smelter plant can also be restricted by the converting cycles. Each converting cycle begins when a fresh charge of matte (and possibly some amount of cold charge) is delivered to an empty converter and ends with the final discharge. The matte is subjected to pressurized blowing wherein oxygen-enriched air is blown into the melt, and N₂ and SO₂ are exhausted through a hood mounted on the vessel (Figure 4). The offgas is captured in order to convert SO₂ into sulfuric acid; meanwhile, N₂ acts as a coolant in the process [14]. Copper and nickel–copper smelters both apply the first stage of PS converting, which is called the slag-blow, producing an iron-rich slag that forms atop the denser matte (Figure 4a). This stage may require intermittent pauses in order to skim away slag accumulation and replenish the vessel with fresh matte and cold charge. Once all of the slag is removed (<1% Fe in matte), copper smelters continue blowing the remaining matte; this final stage of converting is known as the copper-blow, as it results in the formation of blister copper that sinks to the bottom of the vessel (Figure 4b). The copper-blow does not produce any more slag and, therefore, does not require intermittent skimming. Nickel–copper smelters, however, only apply the slag-blow (Figure 4a), not the copper-blow. In either context, the cycle is complete when all of the matte is converted to the correct endpoint and discharged (Figure 3).

In addition to scheduling constraints, various process parameters are also subject to statistical variations, including the chemical composition of incoming plant feed, matte grade, furnace performance, and converter cycle times, among other global factors. It is critical to measure, model, and simulate such uncertainties in order to streamline and support the decision-making processes in the design, development, and operation stages of industrial systems.

3.2. Detailing of Smelter Dynamics Within Discrete Event Simulation

In a previous work, Navarra et al. [18,19] incorporated thermochemical equilibria within a discrete event simulation (DES); it was suggested generally that the hybridization of time-adaptive finite differences (TAFD) and DES is a suitable paradigm for multiphase smelter reengineering projects [20]. Within copper and nickel–copper smelters, thermochemical equilibria determine the iron-speciation of smelting and converting slags, as described in the following section. However, the early phases of a smelter reengineering project can assume fixed molar ratios of iron and oxygen.

Assuming that the smelter feed is composed mainly of iron, sulfur, and copper, a smelter accomplishes the following unbalanced reaction:

$${\left(\mathrm{Cu},\mathrm{Fe},\mathrm{S}\right)}_{\left(\mathrm{Feed}\right)}+{\mathrm{O}}_{2\left(\mathrm{Blast}\right)}+\mathrm{Flux}\to {\left({\mathrm{FeO}}_x,\mathrm{Flux}\right)}_{\left(\mathrm{Slag}\right)}+{\mathrm{SO}}_{2\left(\mathrm{Offgas}\right)}+{\mathrm{Cu}}_{\left(\mathrm{Blister}\right)}$$

(1a)

In which FeO_x represents a mixture of wustite FeO and magnetite Fe₃O₄, such that x = 1 and x = 1.25 corresponds to pure wustite and magnetite, respectively. For simplicity, x can be fixed to 1, although typical values can range between 1.0 and 1.1, depending on the nature and quantity of the flux and the monitoring and control of the process itself; in particular, a low level of magnetite in slag is desirable, which is associated with low slag viscosity. In practice, the flux is predominantly silica SiO₂, but certain smelters include varying quantities of CaO and other stable oxides; CaO is especially common in continuous converting [21], which is an alternative to the conventional PS converting [16]. The SO₂ is captured for sulfuric acid production, and the blister copper is subject to fire refining prior to being cast into anodes that undergo electrolytic refining. A similar reaction can describe nickel–copper smelters:

$$\begin{array}{l}{\left(\mathrm{NI},\mathrm{CU},\mathrm{CO},\mathrm{FE},\mathrm{S}\right)}_{\left(\mathrm{FEED}\right)}+{\mathrm{O}}_{2\left(\mathrm{Blast}\right)}+\mathrm{Flux}\\ \to {\left({\mathrm{FeO}}_x,\mathrm{Flux}\right)}_{\left(\mathrm{Slag}\right)}+{\mathrm{SO}}_{2\left(\mathrm{Offgas}\right)}+{\left(\mathrm{Ni},\mathrm{Cu},\mathrm{Co},\mathrm{S}\right)}_{\left(\mathrm{Bessemer}\right)}\end{array}$$

(1b)

The subsequent processing of Bessemer matte depends on the given nickel–copper plant. Equation (1a,b) provide more detail to Figure 3 for copper and nickel–copper smelters, respectively.

Depending on the scope and phase of the project, x can be regarded as a single global value for the entire smelter or as distinct values for the smelting furnace(s) and converters. Equation (1a) can thus be rewritten

$$\begin{array}{l} {\left(\mathrm{Cu},\mathrm{Fe},\mathrm{S}\right)}_{\left(\mathrm{Feed}\right)}+{\mathrm{O}}_{2\left(\mathrm{Blast}\right)}+\mathrm{SFlux}+\mathrm{CFlux}\\ \to {\left({\mathrm{FeO}}_{x_{\mathrm{S}}},\mathrm{SFlux}\right)}_{\left(\mathrm{SSlag}\right)}+{\left({\mathrm{FeO}}_{x_{\mathrm{C}}},\mathrm{CFlux}\right)}_{\left(\mathrm{CSlag}\right)}+{\mathrm{SO}}_{2\left(\mathrm{Offgas}\right)}+{\mathrm{Cu}}_{\left(\mathrm{Blister}\right)}\end{array}$$

(2)

For copper smelters, which decompose the global x into x_S and x_C, characterize the slag of the smelting furnace. A similar decomposition of the global x could be applied to Equation (1b) in the case of nickel–copper smelters.

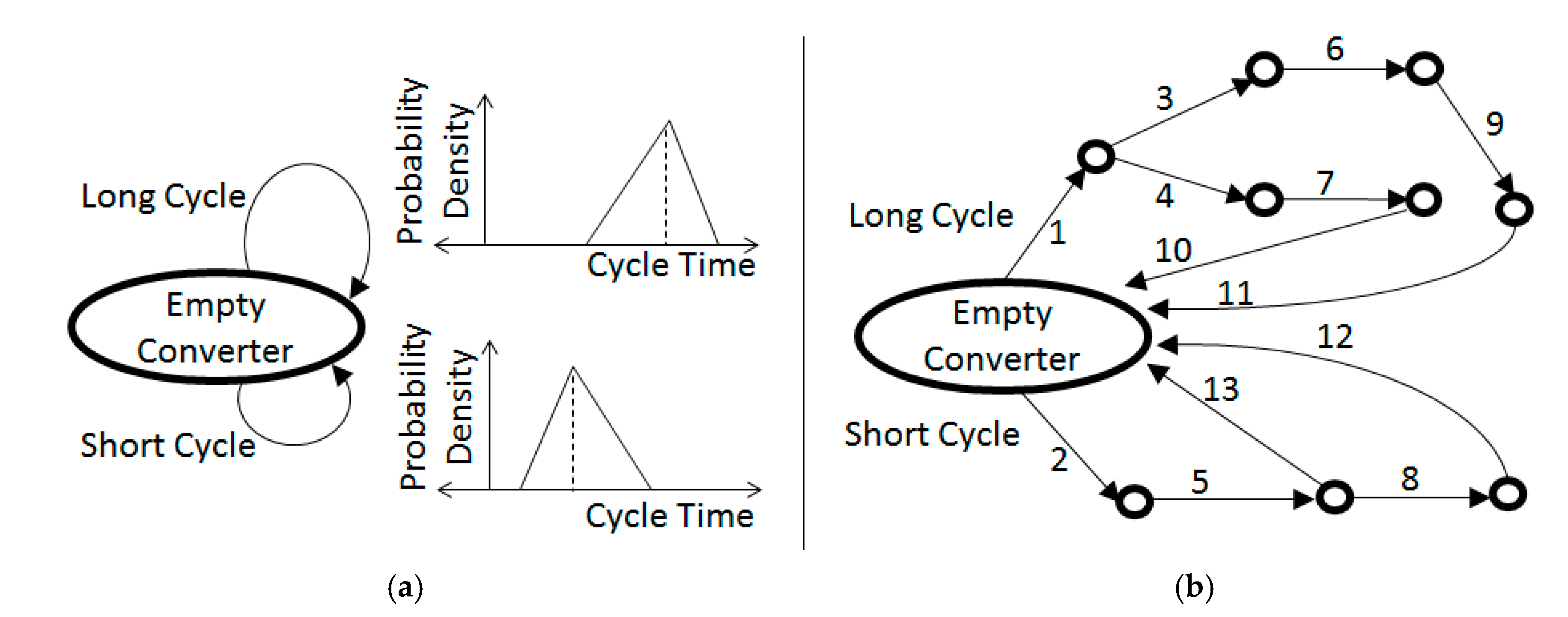
Moreover, the individual slag-blow segments of PS cycles can each be assigned appropriate x values. Therefore, Equation (2) could be further detailed as:

$$\begin{array}{c}{\left(\mathrm{Cu},\mathrm{Fe},\mathrm{S}\right)}_{\left(\mathrm{Feed}\right)}+{\mathrm{O}}_{2\left(\mathrm{Blast}\right)}+\mathrm{SFlux}+\mathrm{CFlux}1+\mathrm{CFlux}2+\cdots +\mathrm{CFlux}n\\ \to \\ {\left({\mathrm{FeO}}_{x_{\mathrm{S}}},\mathrm{SFlux}\right)}_{\left(\mathrm{SSlag}\right)}+{\left({\mathrm{FeO}}_{x_{\mathrm{C}1}},\mathrm{CFlux}1\right)}_{\left(\mathrm{CSlag}1\right)}+{\left({\mathrm{FeO}}_{x_{\mathrm{C}2}},\mathrm{CFlux}2\right)}_{\left(\mathrm{CSlag}2\right)}+\cdots \\ +{\left({\mathrm{FeO}}_{x_{\mathrm{C}n}},\mathrm{CFlux}n\right)}_{\left(\mathrm{CSlag}n\right)}+{\mathrm{SO}}_{2\left(\mathrm{Offgas}\right)}+{\mathrm{Cu}}_{\left(\mathrm{Blister}\right)}\end{array}$$

(3)

In which x_S characterizes the slag of the smelting furnace, and, depending on the level of detail, x_Ci can characterize the types of converter cycles or can characterize the individual types of slag-blow segments, for i = 1 to n. For example, Figure 5a shows an action graph that occurs within a smelter that practices two kinds of converter cycles, long and short; hence, n = 2. Figure 5b shows a more detailed representation, which considers 13 kinds of blow segments. (The slag-blow segments are punctuated with charging and skimming actions, although these are not explicitly shown in Figure 5b). For a conventional copper smelter, actions 1–9 describe slag-blow segments (Figure 4a); hence, n = 9, and the remaining actions 10–13 represent copper-blow segments (Figure 4b) that complete the cycle as a batch of blister copper is discharged. In the case of a nickel–copper smelter, all of the arcs represent slag-blow segments; hence, n = 13, noting that the discharge is the so-called Bessemer matte (Ni, Cu, Co and S) that is described in Figure 3 and Equation (1b).

The decision to apply one segment versus another (e.g., segment 3 versus 4) would depend on the state of the plant, to the extent that the state variables can monitored with the available sensors. Even if the resulting slag compositions for the different cycles (Figure 5a) or blow segments (Figure 5b) are relatively consistent, it may be unclear how frequently each cycle or segment will be applied, e.g., depending on how often certain plant conditions occur. A global mass balance based on Equation (3) requires an estimation of how often each of the different cycles (Figure 5a) or segments (Figure 5b) are applied; such estimations are the result of DES computations, as described below.

The broad distributions of Figure 5a approximate the combined effects of narrower distributions that would characterize the individual segments of Figure 5b. A proposed technological change within the smelter (e.g., installation of new sensors) may require a rethinking of the slag-blow and the definition of new action graphs. Depending on the project, it may be necessary to further decompose the actions of Figure 5b into sub-actions and sub-sub-actions, possibly including thermochemical modeling [22,23] or computational fluid dynamics [24]. This decomposition may be essential in order to properly simulate the system with and without the technological change, thereby evaluating the benefit of the proposed change. In the case of sensors, it is necessary to simulate how the additional information will be incorporated into the decisions and operational actions of the smelter, thereby computing the value of these better-informed decisions and actions.

In many reengineering projects, the phenomena that occur within the smelter may be less important than the phenomena that occur outside of the smelter. For instance, the DES model of the Hernán Videla Lira (HVL) Smelter developed by Navarra et al. [25] focuses on the smelter-wide response to changing meteorological conditions and has a comparatively simple representation of converter cycles, similar to Figure 5a. The HVL Smelter considers distinct categories of meteorological conditions—normal, unfavorable, and extreme—to describe the potential for the surrounding atmosphere to disperse the SO₂ effluent. If the smelter is running in its normal operational mode when the unfavorable meteorological conditions emerge, there is a so-called “environmental incident”. The model of Navarra et al. [25] computes the trade-off between production and environmental risk. Moreover, this model quantifies the improved trade-off that can result from a more accurate array of meteorological sensors.

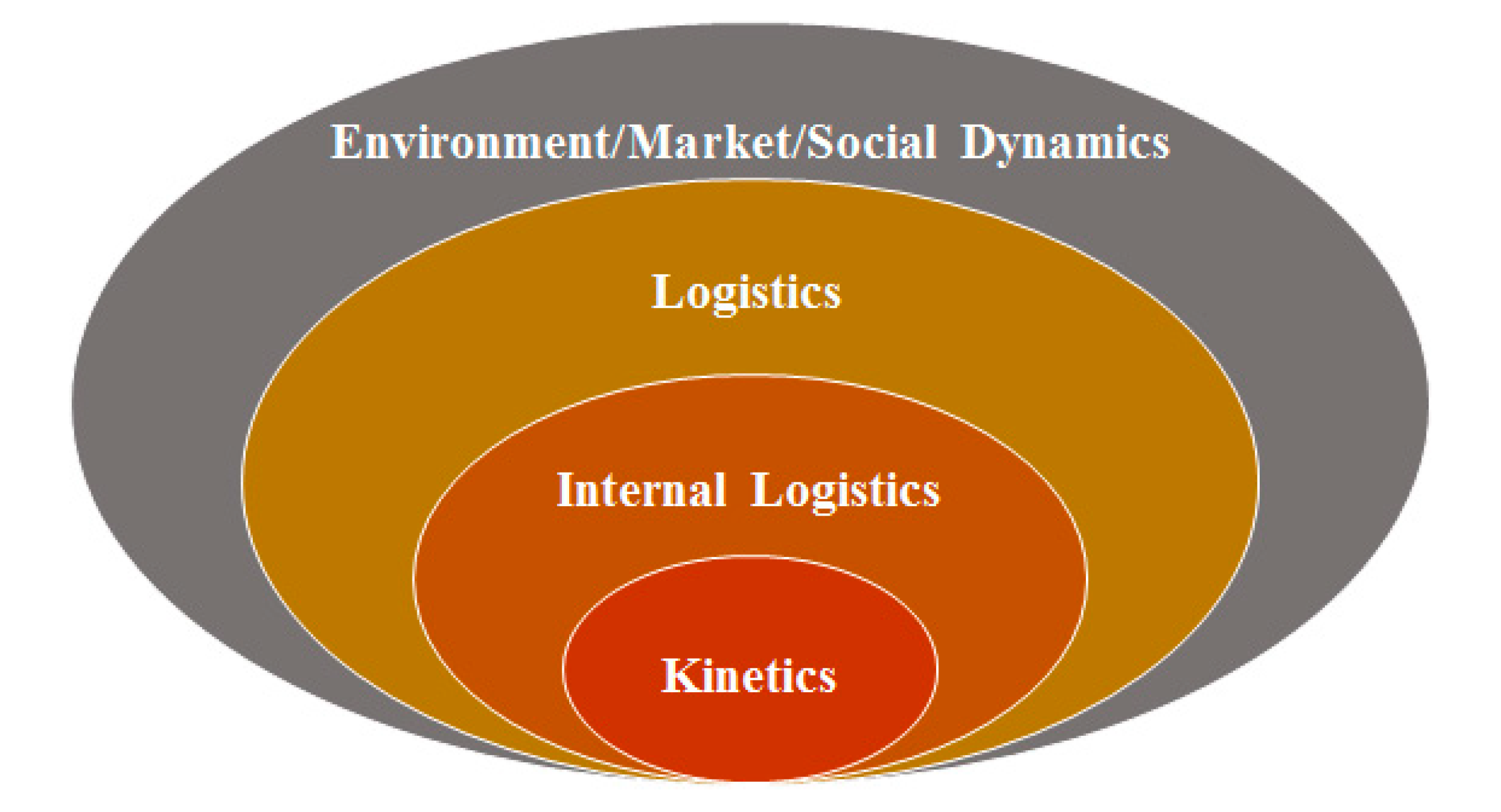
DES development is a means to extend the static mass balances, to detail the critical phenomena that are driving and/or constraining a particular phase of an engineering project. The simulated events can dynamically affect the mass balances that are detailed throughout the model. Figure 6 makes the distinction between the events that occur outside of the smelter and within the smelter, which constitute the external and internal logistics, respectively. There is a further distinction between the logistical coordination of smelter equipment (furnaces, ladles, cranes, etc.) and the kinetics that occur within the equipment. In general, the state variables that describe the system, and the events that would alter these variables, can be positioned within the concentric ellipses of Figure 6. The incorporation of variables and events within a DES model must be guided by the scope and the phase of the engineering project. For example, it is not recommended to detail individual crane movements, unless the particular project would benefit from a comprehension of this aspect [26]. Likewise, it is not recommended to detail particular equipment breakdown events, unless the project would benefit from a comprehension of this aspect [27].

The computational efficiency of DES is due to adaptive time stepping, as the virtual clock advances from one event to the next without explicitly representing the dynamics that occur between events (Figure 7a). The sequencing of events is governed by the future event list (Figure 7b). Within this scheme, a prolonged activity is represented by a sequence of events, including starting and ending the activity. For example, a basic representation of converter cycles described by Figure 5a may include only two events: the start and end of the cycle. A more detailed representation (e.g., Figure 5b) may include several intervening events to represent individual slag- and copper-blow segments, as well as the intervening skimming, charging, actions of the operators, etc. with the level of details that correspond to the given project. Incidentally, DES applies random number generation to determine the duration and outcome of the activities and is thus a form of Monte Carlo simulation [28]; the distributions and action paths illustrated in Figure 5 can be incorporated into the framework.

Moreover, the simultaneous operation of several converters in unison with other logistical phenomena is integrated into one single future event list (Figure 7b); hence, a system-wide representation. Periods of time with relatively few events are computed relatively quickly, thereby focusing the computational efforts on periods of time that are more heavily packed with activity. This time-adaptive aspect of DES allows the simulation of thousands of operating days within minutes.

A DES framework can include operational criteria that determine the action pathway of converter cycles, allowing the computation of frequency confidence intervals. Following the example of Figure 5a, the average frequency of short cycles may be between 2.8 and 3.2 cycles/day with 95% confidence and that of long cycles may be between 0.9 and 1.2 cycles/day with 95% confidence; this result will allow a mass balance based on Equation (3), given the data about the matte that are charged within each cycle and the corresponding flux and oxygen requirements. In a slightly more detailed representation, the DES framework may include the criteria that would determine the more detailed action paths of Figure 5b.

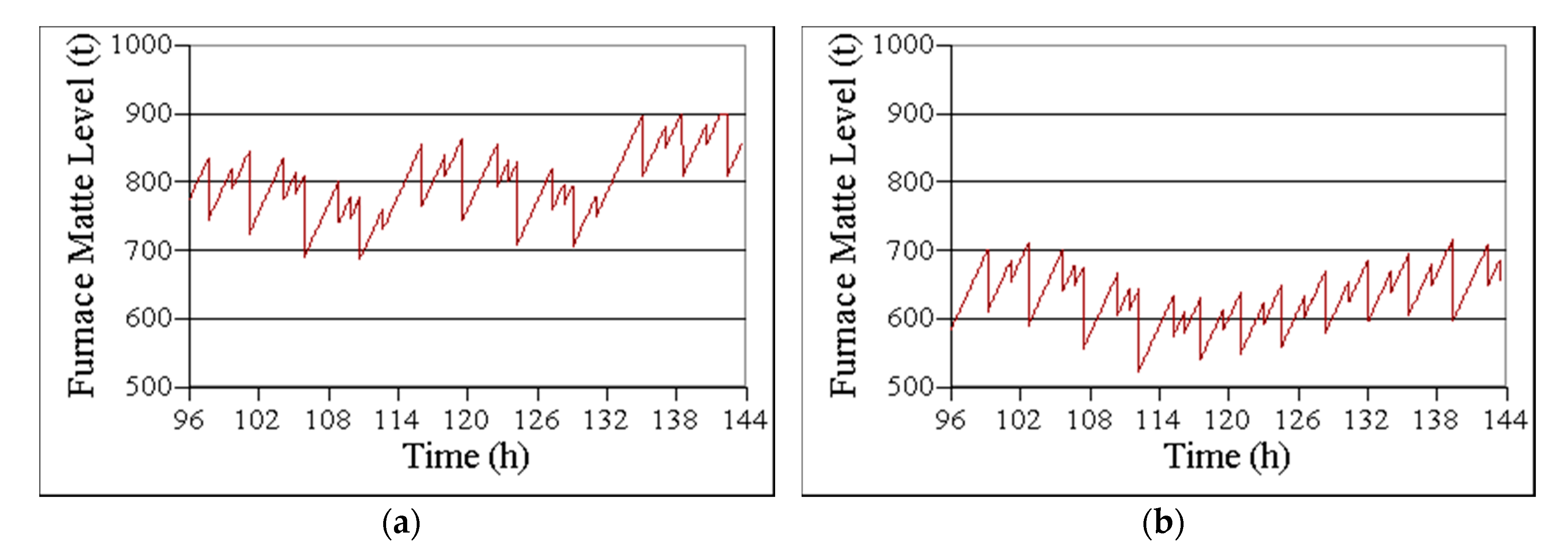
Standard DES frameworks do not explicitly represent the dynamics that occur between events. However, a linearly dynamic state variable can be represented as a combination of discretely dynamic state variables. For instance, the mass of feed stockpile k may be computed at a time t, as

$$m_k\left(t\right)=m_k^{\mathrm{Previous}}+{\dot{m}}_k^{\mathrm{Previous}}\cdot \left(t-t^{\mathrm{Previous}}\right)$$

(4)

in which $m_k^{\mathrm{Previous}}$ and ${\dot{m}}_k^{\mathrm{Previous}}$ are the mass and rate change of k that were computed at the previous event, which occurred at time t^Previous. Thus, each feed k would require two discretely dynamic variables ($m_k^{\mathrm{Previous}}$ and ${\dot{m}}_k^{\mathrm{Previous}}$), in addition to the t^Previous variable that remembers the time of the previous event. Equation (4) can used in simulations that consider alternating modes of operation that control feed blends in response to imbalances in incoming concentrates [29].

Other linearly continuous variables can be implemented in a manner similar to Equation (4), representing each of these continuous variables as two discrete variables: level and rate (e.g., $m_k^{\mathrm{Previous}}$ and ${\dot{m}}_k^{\mathrm{Previous}}$). Considering the DES representation of time (Figure 7), this constitutes a time-adaptive finite difference (TAFD) scheme. However, a full representation of the continuous dynamics requires the detection of threshold-crossing events, as described in Section 3.4. These threshold-crossing events are especially important in assessing the installation of sensors whose role may be to signal the need for corrective actions precisely when critical thresholds are crossed.

3.3. Slag Iron Speciation and Other Thermochemical Considerations

The iron oxide speciation, i.e., the balance between FeO and Fe₃O₄, can be quantified as the oxygen-to-iron ratio x presented in Equations (1)–(3). Indeed, x represents a degree of freedom that must be resolved in order to complete the mass balance. This degree of freedom can also be expressed as the ratio of ferric to ferrous ions within the slag, α = Fe³⁺/Fe²⁺, often called the degree of oxidation. The homeomorphic relationship between x and α is given by

$$x=\frac{2+3\alpha }{2+2\alpha }$$

(5)

Equation (1a) can thus be rewritten as

$${\left(\mathrm{Cu},\mathrm{Fe},\mathrm{S}\right)}_{\left(\mathrm{Feed}\right)}+{\mathrm{O}}_{2\left(\mathrm{Blast}\right)}+\mathrm{Flux}\to {({\mathrm{FeO}}_{\left(\frac{2+3\alpha }{2+2\alpha }\right)},\mathrm{Flux})}_{\left(\mathrm{Slag}\right)}+{\mathrm{SO}}_{2\left(\mathrm{Offgas}\right)}+{\mathrm{Cu}}_{\left(\mathrm{Blister}\right)}$$

(6)

similar to Equation (1b), in which the minimum α = 0 corresponds to pure wustite FeO and α = 2 corresponds to pure magnetite Fe₃O₄. Equation (6) can be further detailed in a similar manner as Equations (2) and (3) by assigning appropriate subscripts to α, as in [20].

In the modeling of slag chemistry, α is preferred over x to avoid ambiguity between the reactive oxygen of the blast and the inert oxygen that is strongly bonded within the flux (i.e., within the SiO₂, CaO, etc.). For instance, the role of SiO₂ flux is made more evident by expressing the wustite as a component within a fayalite matrix FeO·2SiO₂; hence, the balance of FeO versus Fe₃O₄ is considered as FeO·2SiO₂ and Fe₃O₄. In practice, SiO₂ is added into the slag in proportions that surpass the stoichiometry of fayalite and may be accompanied by other stable oxides. Under matte-processing conditions, the stable molecules SiO₂, CaO, etc. can be regarded as if they were indivisible atoms. Most notably, the strongly bonded oxygen is not explicitly represented in Equations (1)–(3) and is not taken into account in x; these equations only explicitly consider the blast oxygen. The degree of oxidation α considers only the iron species isolated from any mention of the blast and flux oxygen.

Within Equation (6) and its nickel–copper equivalent, the slag-blow reaction can be isolated and balanced as:

$${\mathrm{FeS}}_{\left(\mathrm{Matte}\right)}+\left(\frac{2+3\alpha }{4+4\alpha }\right){\mathrm{O}}_{2\left(\mathrm{Blast}\right)}\to {\mathrm{FeO}}_{\left(\frac{2+3\alpha }{2+2\alpha }\right)\left(\mathrm{Slag}\right)}+{\mathrm{SO}}_{2\left(\mathrm{Offgas}\right)}$$

(7)

which applies to both the smelting and converting furnaces for both copper and nickel–copper smelters. Indeed, the melting of the feed of Equation (6) results in molten matte that is a mixture of FeS and Cu₂S; in the case of nickel–copper smelters, the matte will also contain nickel and cobalt sulfides [18], but Equation (7) is still correct. The incoming blast includes N₂, as well as O₂ (see Figure 4). As the N₂ passes through the bath and is exhausted into the offgas, along with the SO₂, it carries away sensible heat and is a critical consideration in controlling the bath temperature.

To resolve the degree of freedom α (or equivalently x), the equilibrium between iron oxide species can be expressed as

$${\mathrm{FeS}}_{\left(\mathrm{Matte}\right)}+3{\mathrm{Fe}}_3{\mathrm{O}}_{4\left(\mathrm{Slag}\right)}\leftrightarrow 10{\mathrm{FeO}}_{\left(\mathrm{Slag}\right)}+{\mathrm{SO}}_{2\left(\mathrm{Offgas}\right)}$$

(8)

having enthalpy and entropy values ΔH₀ = 622,549 J/mol and ΔS₀ = 342.64 J/mol K, respectively, which can be obtained from HSC Chemistry^TM. The corresponding Gibbs free energy balance is

$$\mathsf{\Delta }G=\mathsf{\Delta }{H}_0-T\mathsf{\Delta }{S}_0+RT\ln \left[\frac{{\left(a_{\mathrm{FeO},\mathrm{Slag}}\right)}^{10}{p}_{\mathrm{SO}2,\mathrm{Offgas}}}{a_{\mathrm{FeS},\mathrm{Matte}}{\left(a_{\mathrm{Fe}3\mathrm{O}4,\mathrm{Slag}}\right)}^3}\right]$$

(9)

which is set to zero to assume equilibrium. R is the ideal gas constant, T is the bath temperature, and a_ij is the activity of species i within phase j. The activity of SO₂ in the offgas is taken to be the partial pressure p_SO2,Offgas.

Within Equation (9), the activities (a_FeS,Matte, a_FeO,Slag, and a_Fe3O4,Slag) can be re-expressed in terms of α, T, and the operational parameters. The usual parameters include the oxygen enrichment of the blast φ and the silica–iron mass ratio r = (m_SiO2,Slag/m_Fe,Slag), which are considered in Section 4. Empirical measurements relate the activities a_ij to their respective mole fractions X_ij. In particular, the classic model of Goto [30,31] is validated for smelting and converting, in both the copper and nickel–copper contexts [32], and is the subject of Appendix A.

Iron speciation computations are simpler for smelting furnaces than for converting, since the smelting bath temperature can usually be treated as if it were at a steady state and is approximately uniform and constant. Under this simplification, α can be resolved through an application of Newton’s Method [18,19]:

$${\alpha }^{\left(k\right)}={\alpha }^{\left(k-1\right)}-\raisebox{1ex}{$f_G$}\!\left/ \!\raisebox{-1ex}{$\frac{\partial f_G}{\partial \alpha }$}\right.$$

(10)

or, in case T is not constant,

$$\left(\begin{array}{c}{T}^{\left(k\right)}\\ {\alpha }^{\left(k\right)}\end{array}\right)=\left(\begin{array}{c}{T}^{\left(k-1\right)}\\ {\alpha }^{\left(k-1\right)}\end{array}\right)-\frac{1}{\frac{\partial f_H}{\partial T}\frac{\partial f_G}{\partial \alpha }-\frac{\partial f_H}{\partial \alpha }\frac{\partial f_G}{\partial T}}\left[\begin{array}{cc}\frac{\partial f_G}{\partial \alpha }& -\frac{\partial f_H}{\partial \alpha }\\ -\frac{\partial f_G}{\partial T}& \frac{\partial f_H}{\partial T}\end{array}\right]\left[\begin{array}{c}{f}_G\\ f_H\end{array}\right]$$

(11)

which is a two-variable form of Newton’s Method, in which (T^(k), α^(k)) denote the results of the kth Newton iteration. The righthand sides of Equations (10) and (11) include proxy functions, f_G and f_H, and their derivatives, which are all evaluated at the preceding values (T^(k−1), α^(k−1)), considering (T⁽⁰⁾, α⁽⁰⁾) = (1473 K, 0.15) as typical starting values. The proxy function f_G must be formulated so that f_G = 0 when the Gibbs free energy balance of Equation (9) is satisfied, i.e., when ΔG = 0. Appendix A presents a formulation of f_G that is based on the classic Goto model [30,31]. Likewise, f_H is formulated such that f_H = 0 when the heat balance is satisfied [19].

Following the results of Appendix A, it is relatively simple to program Equations (10) and (11) into a simulation platform, thereby relating slag chemistry to the wustite–magnetite balance and, indeed, to the overall mass balance. Depending on the project, Goto’s model may be an appropriate starting point, although it does not consider olivine slags [21], nor does it consider the transport of minor elements. In practice, it is preferable to have more wustite than magnetite, since the latter increases the slag viscosity and the entrainment of matte into the slag [21,33]. The modification of slag chemistry through flux additions affects the migration of minor elements [22,23], possibly at the expense of having higher slag viscosity [21].

There is an interest to develop DES platforms that draw upon state-of-the-art thermochemical databases [19] to assist in the retrieval of valuable elements such as gold, silver, and platinum and the handling of deleterious elements such as arsenic, bismuth, and antimony. The authors suspect that the partition of trace elements can be efficiently computed as a function of the main elements a posteriori when Equations (10) and (11) converge. This is an area of future research, and the resulting platforms would support smelter-wide strategies for the processing increasingly problematic feeds. Yet, in reality, for similar apparent conditions like matte grade, temperature, etc., the balance of FeO versus Fe₃O₄ can depend on various parameters, including flux quality, refractory wear, and amount of charge (hence, affecting mixing), and so, an empirical approach to speciation may be more effective.

3.4. Estimation of Threshold Crossing Times Using Time-Adaptive Finite Differences

Time-adaptive finite differences are an important feature of our smelter DES frameworks, allowing the correct placement of threshold-crossing events within the future event list (Figure 8). In the approach of Navarra et al. [18,19], the Newton iterations of Equations (10) and (11) are nested within the Runge-Kutta-Fehlberg (RKF) method, which is a well-known time-adaptive finite difference (TAFD) scheme [34,35]. This method is a combination of finite difference schemes based on fourth and fifth-order Taylor expansions [34]; an attempted timestep is only accepted if the fourth and fifth order estimates of T and α are within an acceptable error tolerance; otherwise, a smaller timestep is attempted. Moreover, each attempted timestep uses the previous results of T and α as a starting point for the Newton iterations, so that convergence is faster, thus making the computation more efficient.

The efficiency of DES depends on this time-adaptive aspect to limit the computational effort devoted to dynamics that occur between the discrete events (Figure 7). Alternatives to the approach of Navarra et al. [18,19] include the use of cubic Hermite spline interpolation [36,37] and Richardson extrapolation [38]. These techniques can be adapted to isolate the threshold crossing event of a state variable and improve the accuracy with which we can find the time at which it crosses. In fact, it is important to recognize that both the efficiency and accuracy of the method rely on an accurate time estimate for threshold crossing. In our case, the threshold is first contained in the interval bounded by the two timesteps bracketing an evaluation of the state variable below and above the threshold. This precisely guarantees we have access to values already computed at both of the upper and lower estimates (as a result of the RKF attempt), which includes state variable values, as well as their time derivatives (by direct evaluation if the right-hand side at the state variable values). With this data, we constructed a cubic Hermite spline, which is, therefore, a valid fourth-order interpolation of the solution over this interval. Since the Hermite spline is, in fact, a cubic polynomial, we can compute analytically the crossing time as a simple root-finding problem. We also note that this approach is robust, since the data at the end of the interval provided need not be exact. In fact, if the state variable data has a fourth-order accurate truncation error (e.g., by only using a third order Runge-Kutta integrator) and the derivatives are third-order accurate, the interpolant is guaranteed to be fourth-order accurate [37]. Further, while this approach is tailored to the RKF used here, it may be expanded by considering Hermite quintics if a further need for accuracy is required.

While conventional DES frameworks support basic representations of smelter logistics, a hybridization with time-adaptive finite differences supports a detailed representation of the kinetics that occur within the individual unit operations. In particular, the detailed representation of individual slag-blow segments may require a dynamic simulation of the evolving thermochemical states of matte and slag. Moreover, the DES-TAFD hybridization allows the simulation of several simultaneous converting cycles, in conjunction with the intervening actions involving cranes and ladles, the delivery of a cold charge, and other phenomena. Nonetheless, the explicit representation of slag-blow segments should only be implemented if it is beneficial to the particular engineering project. Beyond the internal dynamics of smelter, a project may require an explicit representation of market-related or environmental phenomena (Figure 6). The hybridization of DES and TAFD is indeed capable of linking detailed representations of diverse aspects throughout the smelter and beyond, whose coordination may be critical to the sustainability of the smelter. Furthermore, aging smelters will not be sustainable unless they can successfully modernize their operational practices, benefitting from sensors and other novel technology.

4. Sample Computations and Context

The sample calculations presented in this section are typical of an aging copper smelter that:

• has been successful for decades in processing reasonably clean feeds;
• is confronted with increasingly challenging feeds that carry excess quantities of arsenic, bismuth, and antimony; and
• is aware of an approach to draw a critical portion of the undesirable elements into the converting slag, which is only effective as the iron in matte approaches zero

Regarding the third point, there may be operator experiences in treating marginal feeds that had a manageable amount of the trace elements; such feeds were treated by driving the individual slag-blow segments to a relatively low iron content (e.g., ~3% Fe), in combination with particular flux compositions. Indeed, a more forceful elimination of the undesirable elements could be induced at an even lower iron content, but this would increase the level of entrained into the slag, under imperfect mixing, as blister copper would be precipitated heterogeneously in certain regions of the vessel. Better endpoint control on the individual segments would allow a more careful advance toward 0% Fe with a limited risk of copper entrainment and could be attained by adapting the endpoint approach at Boliden’s Rönnskär Smelter [5], mentioned earlier; this approach depended on customized sensor development [10,11,12].

From the authors’ experience in copper smelter projects, it is incumbent on outside experts to integrate their general understanding with the detailed understanding of in-house experts at the given smelter. There may be issues that were already confronted with some amount of success, but these issues may gradually become critical. For instance, the increasing presence of penalty elements is especially common in custom smelters that receive concentrates from a combination of regional mines, which are themselves confronted with ore blending challenges [29]. The experiences of the smelter should be cross-checked with thermochemical models and a literature review [22,23] in proposing new operational modes that may require a technological upgrade. In effect, this can be a standardization and optimization of approaches that the in-house experts were already considering.

The DES framework described in Section 3.1, Section 3.2, Section 3.3 and Section 3.4 was implemented using Rockwell Arena^TM software and replicated the general aspects of conventional smelters while incorporating smelter-specific data.

Table 1. Feed compositions entering the smelting furnace.

Element	Weight%
Copper	20
Iron	39
Sulfur	40
Arsenic	0.4–1.0
Bismuth	0.02–0.20
Antimony	0.02–0.10

,

Table 2. Examples of smelting furnace operational parameters.

Parameter	Value
Matte holding capacity	900 t
Bath temperature	1275 °C
Blast rate	1100 Nm3/min
Oxygen enrichment	50 vol%O2
SiO2/Fe in slag	0.7
Matte grade	60 wt% Cu

and

Table 3. Examples of Peirce–Smith (PS) converting data describing short and long cycles.

	Short Cycle		Long Cycle
	Duration (h)	* Ladles Added	Duration (h)	* Ladles Added
First slag-blow segment	2.0	3	3.0	4
Second slag-blow segment	0.5 ± 0.2	1	1.0	2
Third slag-blow segment	-	-	0.5 ± 0.2	1
Copper-blow	4.5 ± 0.7	-	5.0 ± 1.2	-

* Assume that ladles are added at the beginning of the segment, each carrying 30 t of matte.

contain sample data that are loosely based on published values from [2,5,6,13,39,40]. As stated in Section 3.1, conventional smelters have smelting capacities that normally exceed the downstream converting capacity; indeed, the smelting furnace should not usually produce matte at full capacity, nor should it function in fits and starts. The definition of so-called short and long converter cycles (Figure 6) provides the operational flexibility to set a fixed smelting rate. Moreover, some smelters may have several cycle types under consideration to respond to build-ups of cold charges or compositional imbalances in the feeds that are received from the supplying mines. For simplicity, the current computations consider only two types of cycles.

To maintain stable throughput, the blending strategy ensures comparatively stable portions of the main elements (Table 1) but with unavoidable fluctuations in the undesirable trace elements. Additionally, to maintain stable throughput, the smelting parameters are kept constant (Table 2), including the grade of the output furnace matte; given that the matte is a mixture of FeS and Cu₂S, an elemental mass balance determines that a 60% Cu grade corresponds to roughly 24% S and 16% Fe.

Effectively, the smelting furnace blasts 550 Nm³/min of oxygen into a bath in order to decrease the iron content from 39% to 16% as it burns the FeS. The smelting blast also includes 550 Nm³/min of nitrogen, which carries away a portion of the heat. The control of the temperature at 1275 °C depends on this nitrogen flow. Given the stable temperature T = 1275 °C = 1548 K, oxygen enrichment φ = 0.5, and silica-iron ratio r = 0.7, the Newton iterations of Equation (10) are used to obtain the degree of oxidation α = 0.166, with a corresponding throughput of 36.928 t/h of matte or equivalently 1.231 ladles/h. At a matte grade of 60% Cu, this corresponds to 22.157 t Cu/h.

Figure 9 shows graphs of the matte content using the data from Table 1, Table 2 and Table 3. The largest declines correspond to the initiation of long cycles (four ladles = 120 t) and short cycles (three ladles = 90 t), and the other declines correspond to the recharging actions that occur during the cycles at the second and third slag-blow segments. As is common in larger smelters, the offgas handling capacity allows for the execution of two simultaneous converter cycles.

Within Table 3, the times for the initial slag-blow segments are fixed as operational parameters. However, the durations of the final slag-blow segments depend on the exact nature of the charge (including the cold dope), as well as variable operator behavior and, potentially, other factors. By extension, the copper-blow durations are also variable. For the purposes of Figure 9, these fluctuating values are used to define uniform distributions, e.g., the copper-blow durations are uniformly distributed between 3.8 and 5.2 h for the short cycles and between 3.8 and 6.2 h for the long cycles. Uniform distributions, triangular distributions (Figure 5a), and other simple forms are typical of the early phases of a smelter project. More advanced phases can include more elaborate distributions that are supported by goodness-of-fit testing of the plant data [41].

An analysis of Table 3 reveals that the average conversion rates are 0.571 ladles/h and 0.737 ladles/h for the short and long cycles, respectively. Considering that the smelting furnace produces 1.231 ladles/h that is fed into two simultaneous converter cycles (i.e., 0.615 ladles/h per converter), the balancing of the smelting and converting throughput will require a combination of the long and short cycles. (Incidentally, the long cycle copper-blow is more productive than that of the short cycle; this may be because it is loaded with cold copper scrap, which makes the heat balance less dependent on the nitrogen convection, thus supporting a more intense higher-oxygen blast).

Figure 9 considers a threshold criterion that, whenever the matte level surpasses a critical value, the next several cycles are set to a long cycle. Poor adjustment of this threshold can diminish the overall throughput, as the smelting furnace is deactivated when it reaches the 900-t capacity given in Table 1; this is depicted in Figure 9a, in which the threshold is set to 800 t, which triggers two long cycles, which is insufficient to prevent the approach to 900 t observed at time 140 h. A balanced production is shown in Figure 9b, which applies a threshold of 700 t, which triggers three long cycles. In general, a DES-TAFD hybrid can be adapted to incorporate the operational decision-making of the smelter that is being studied; this flexibility is vital in the context of reengineering projects [20].

Table 4. Example of PS converting data, including short and long cycles that can be extended.

	Regular Short C.		Extended Short C.		Regular Long C.		Extended Long C.
	Duration (h)	* Ladles Added	Duration (h)	* Ladles Added	Duration (h)	* Ladles Added	Duration (h)	* Ladles Added
First SB segment	2.2 ± 0.2	3	2.2 ± 0.2	3	3.4 ± 0.2	4	3.4 ± 0.3	4
Second SB segment	0.3 ± 0.1	1	0.3 ± 0.1	1	0.7 ± 0.2	2	1.2 ± 0.2	3
Third SB segment	-	-	0.4 ± 0.1	1	0.4 ± 0.1	1	0.3 ± 0.1	1
Fourth SB segment	-	-	-	-	-	-	0.4 ± 0.1	1
Copper-blow	4.5 ± 0.7	-	5.6 ± 0.8	-	5.0 ± 1.2	-	7.0 ± 1.7	-

* Assume that ladles are added at the beginning of the segment, each carrying 30 t of matte.

and Figure 10 describe modified dynamics in which an array of sensors track the approach to 0% Fe and the presence of the undesirable trace elements. The data-driven approach to removing the iron is reflected by the (uniform) variation ascribed to all of the slag-blow segments, whereas the previous configuration (Table 3) fixed predetermined blow times for the initial segments. Moreover, Table 4 follows the action graph of Figure 5b, in which the commitment to an extended cycle is made only after the cycle begins. Indeed, the regular short cycles correspond to 2-5-13, the extended short cycles to 2-5-18-12, the regular long cycles to 1-4-7-10, and the extended long cycles to 1-3-6-9-11. For the sake of Figure 10, it is assumed that 30% of the short cycles are extended and 20% of the long cycles are extended, although different values could be tested and should be driven by actual forecasts of what the incoming feed might be.

A comparison between Figure 9 and Figure 10 shows the effect that responsive converter cycles (Table 4) can have on the matte levels; although the matte levels of Figure 10 remain mostly between 600 and 700 t, the pattern of peaks and dips is far less regular. These fluctuations may be acceptable, considering that it would allow the smelter to handle problematic feeds. Otherwise, the feed rate into the smelting furnace could be controlled in coordination with a variable blast rate, which may be the subject of a following stage of engineering.

To the authors’ knowledge, the computations of Figure 10 are the first published instance in which several converters are simultaneously drawing upon a smelting furnace and operational decisions are finalized after the cycles begin, i.e., in response to incoming sensor data. This level of detail is necessary to evaluate the utility of sensors in supporting smelter-wide responses to problematic feeds. The computations described by Table 4 and Figure 10 rely on the representation of individual slag-blow segments (Figure 5b), although other approaches might require the detailed representation of additional aspects within or surrounding the smelter (Figure 6).

5. Conclusions and Future Work

Not only warehouses and manufacturing facilities but metallurgical plants such as a steel plant or copper smelter—which are more difficult to automate—will be transformed in the future with use of new machine capabilities, automation, and improved sensors and controls. Steel is, by far, the major metal produced in the world, representing about 95% by tonnage of all metal production, with the world copper smelter output some 80 to 90 times less than world steel output. This, in part, helps understand that certainly more developments are attained in the iron and steel industry relative to copper. However, the computational framework described in this paper will help close the gap, regarding HI and LIBS and other radiometric sensors, as it enables the implementation of these technologies and justifies their further development within the copper industry. In particular, LIBS is expected to have an increasing importance in handling problematic feeds as existing copper smelters are confronted with increasing amounts of arsenic, bismuth, and antimony [42].

Modern sensors will be vital in supporting smelter-wide responses to increasingly challenging feeds that are being confronted throughout the world, as described in the previous section. It should be noted in particular that smelting and converting operations are central within copper and nickel–copper smelting and are linked to supporting operations throughout the smelter. High-quality and reliable process instrumentation and controls are therefore important in maximizing the global operating efficiency. Additionally, the monitoring of the furnace integrity, refractory wear, preventative maintenance, and plant safety are also key aspects that constantly need attention at the plant. Many high-performance smelting furnaces today include water-cooled copper blocks generally externally mounted on a furnace sidewall to protect the refractory lining at the hot face. The Peirce-Smith converter operates with a converter hood that includes water-cooled panels on the cold face in order to protect the steel wall at the hot face. Recent developments in the instrumentations for detecting and measuring the presence of small levels of water vapor in furnace offgas can signal a water leak and lead to improved furnace monitoring [43]. However, the implementation of such measures often requires quantitative justification.

This paper showed that combining thermochemical equilibrium data with a knowledge of smelting and converting dynamics provides a powerful tool for advancing smelting operations in the form of DES-TAFD hybrid simulations. The specialized use of Newton’s Method, Runge-Kutta-Fehlberg, and Hermite interpolation within a DES are, in fact, an advancement within the industrial system analysis, which can be adapted to other industrial contexts, supporting modernization projects that include novel sensors and other technology.