Prediction of the Solubility of CO2 in Imidazolium Ionic Liquids Based on Selective Ensemble Modeling Method
Abstract
1. Introduction
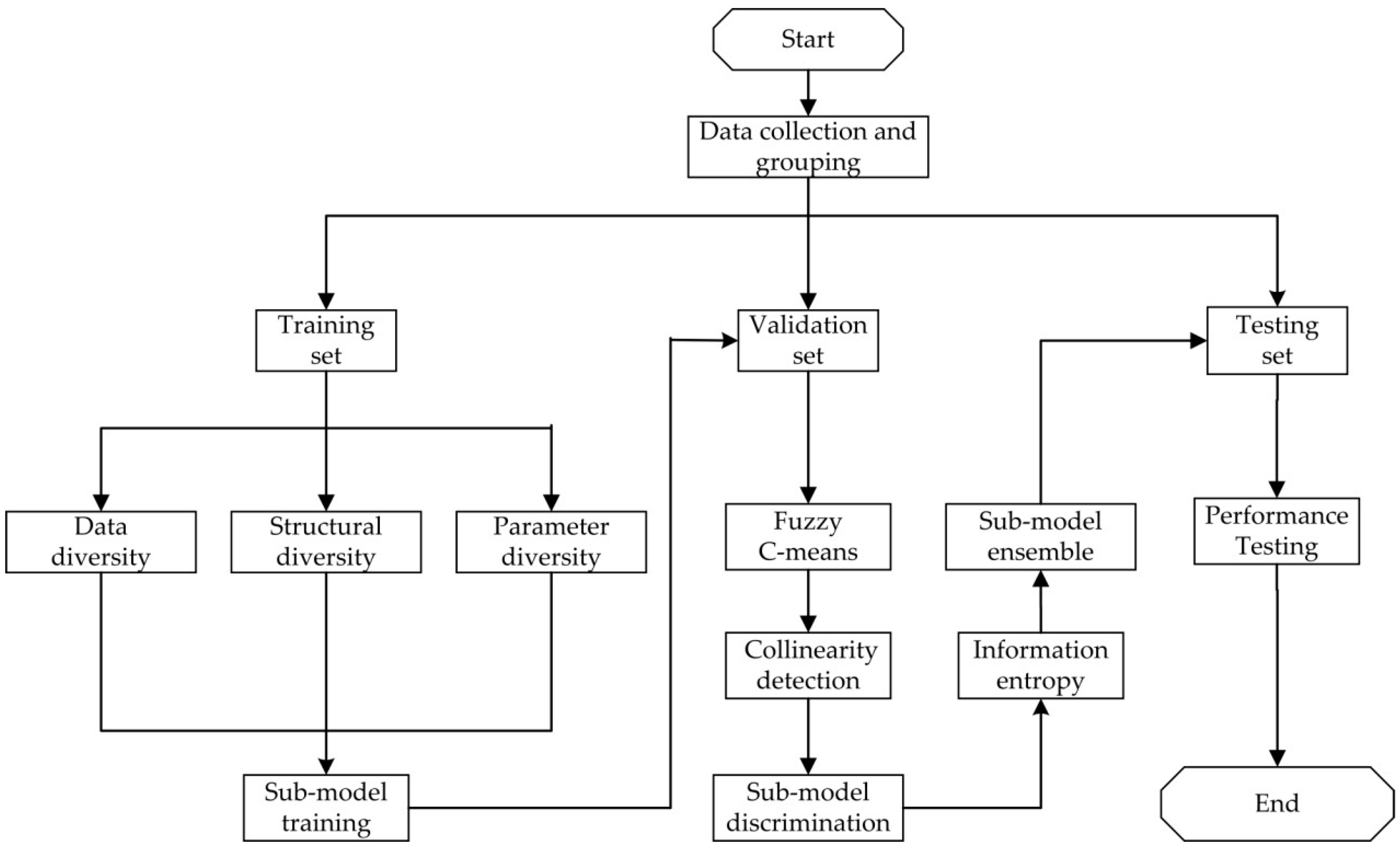
2. Methods
2.1. Sub–Model Training
2.1.1. Data Diversity
2.1.2. Structural Diversity
2.1.3. Parameter Diversity
2.2. Sub–Model Discrimination
2.3. Sub–Model Ensemble
2.4. Implementation Step
3. Results and Discussion
3.1. Data Collecting and Grouping
3.2. Selective Ensemble Model Developing
3.2.1. Sub–Model Training
3.2.2. Sub–Model Discrimination
3.2.3. Sub–Model Ensemble
3.3. Model Performance Testing
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Xu, M.M.; Wang, S.J. Research progress of liquid–liquid phase variable solvent trapping CO2 technology. Chinese J. Chem. Eng. 2018, 69, 1809–1818. [Google Scholar]
- Taimoor, A.A.; Al–Shahrani, S.; Muhammad, A. Ionic liquid (1–butyl–3–metylimidazolium methane sulphonate) corrosion and energy analysis for high pressure CO2 absorption process. Processes 2018, 6, 45. [Google Scholar] [CrossRef]
- Leonzio, G.; Zondervan, E. Surface–response analysis for the optimization of a carbon dioxide absorption process using [hmim][Tf2N]. Processes 2020, 8, 1063. [Google Scholar] [CrossRef]
- Rogers, R.D. Chemistry: Ionic liquids–solvents of the future? Science. 2003, 302, 792–793. [Google Scholar] [CrossRef]
- Ding, J.; Xiong, Y.; Yu, D.H. Solubility of CO2 in ionic liquids–measuring and modeling methods. Chem. Ind. Eng. Prog. 2012, 31, 732–741. [Google Scholar]
- Bahmani, A.R.; Sabzi, F.; Bahmani, M. Prediction of solubility of sulfur dioxide in ionic liquids using artificial neural network. J. Mol. Liq. 2015, 211, 395–400. [Google Scholar] [CrossRef]
- Bazargani, Z.; Sabzi, F. Thermodynamic modeling of CO2 absorption in 1–butyl–3–methylimidazolium–based ionic liquids. J. Mol. Liq. 2016, 223, 235–242. [Google Scholar] [CrossRef]
- Kamgar, A.; Rahimpour, M.R. Prediction of CO2 solubility in ionic liquids with QM and UNIQUAC models. J. Mol. Liq. 2016, 222, 195–200. [Google Scholar] [CrossRef]
- Venkatraman, V.; Alsberg, B.K. Krakenx: Software for the generation of alignment–independent 3D descriptors. J. Mol. Mode. 2016, 22, 92–100. [Google Scholar] [CrossRef]
- Bavoh, C.B.; Lal, B.; Nashed, O.; Khan, M.S.; Keong, L.K.; Bustam, M.A. COSMO–RS: An ionic liquid prescreening tool for gas hydrate mitigation. Chinese J. Chem. Eng. 2016, 24, 1619–1624. [Google Scholar] [CrossRef]
- Xia, L.Y.; Wang, J.C.; Liu, S.S.; Li, Z.; Pan, H.T. Prediction of CO2 solubility in ionic liquids based on multi–model fusion method. Processes 2019, 7, 258. [Google Scholar] [CrossRef]
- Kardani, M.N.; Baghban, A.; Sasanipour, J.; Mohammadi, A.H.; Habibzadeh, S. Group contribution methods for estimating CO2 absorption capacities of imidazolium and ammonium–based polyionic liquids. J. Clean. Prod. 2018, 203, 601–618. [Google Scholar] [CrossRef]
- Tatar, A.; Naseri, S.; Bahadori, M.; Hezave, A.Z.; Kashiwao, T.; Bahadori, A.; Darvish, H. Prediction of carbon dioxide solubility in ionic liquids using MLP and radial basis function (RBF) neural networks. J. Taiwan. Inst. Chem. E. 2015, 60, 151–164. [Google Scholar] [CrossRef]
- Alireza, B.; Amir, H.M.; Mohammad, S.T. Rigorous modeling of CO2 equilibrium absorption in ionic liquids. Int. J. Greenh. Gas. Con. 2017, 58, 19–41. [Google Scholar]
- Ghiasi, M.M.; Mohammadi, A.H. Application of decision tree learning in modelling CO2 equilibrium absorption in ionic liquids. J. Mol. Liq. 2017, 242, 594–605. [Google Scholar] [CrossRef]
- Mirarab, M.; Sharifi, M.; Ghayyem, M.A.; Mirarab, F. Prediction of solubility of CO2 in ethanol–[EMIM][Tf2N] ionic liquid mixtures using artificial neural networks based on genetic algorithm. Fluid. Phase. Equilibr. 2014, 371, 6–14. [Google Scholar] [CrossRef]
- Zhou, Z.H.; Wu, J.; Wei, T. Ensembling neural networks: Many could be better than all. Artif. Intell. 2002, 137, 239–263. [Google Scholar] [CrossRef]
- MendesMoreira, J.; Soares, C.; Jorge, A.M.; De Sousa, J.F. Ensemble approaches for regression: A survey. Acm. Comput. Surv. 2012, 45, 11–40. [Google Scholar]
- Zhu, P.F.; Xia, L.Y.; Pan, H.T. Multi–model fusion modeling method based on improved kalman filter algorithm. Chinese J. Chem. Eng. 2015, 66, 1388–1394. [Google Scholar]
- Ren, Y.; Zhang, L.; Suganthan, P.N. Ensemble classification and regression–recent developments, applications and future directions. IEEE. Comput. Intell. M. 2016, 11, 41–53. [Google Scholar] [CrossRef]
- Sagi, O.; Rokach, L. Ensemble learning: A survey. Wires. Data. Min. Knowl. 2018, 8, 1249–1266. [Google Scholar] [CrossRef]
- Martínez–Muoz, G.; HernándezLobato, D.; Suárez, A. An analysis of ensemble pruning techniques based on ordered aggregation. IEEE T. Pattern. Anal. 2009, 31, 245–259. [Google Scholar] [CrossRef] [PubMed]
- Mojarad, M.; Nejatian, S.; Parvin, H.; Mohammadpoor, M. A fuzzy clustering ensemble based on cluster clustering and iterative fusion of base clusters. Appl. Intell. 2019, 49, 2567–2581. [Google Scholar] [CrossRef]
- Bowen, F.; Yun, F.Q.; Wan, J.L. Fuzzy clustering ensemble model based on distance decision. Chin. J. Electron. 2018, 54, 823–831. [Google Scholar]
- Bagherinia, A.; MinaeiBidgoli, B.; Hossinzadeh, M.; Parvin, H. Elite fuzzy clustering ensemble based on clustering diversity and quality measures. Appl. Intell. 2019, 49, 1724–1747. [Google Scholar] [CrossRef]
- Li, K.; Huang, H.K. A selective neural network integration method based on clustering technology. Jcrd. 2005, 42, 594–598. [Google Scholar]
- Hashem, S. Optimal linear combinations of neural networks. Neural. Netw. 1997, 10, 599–614. [Google Scholar] [CrossRef]
- Fildes, R.B.R. Conditioning diagnostics: Collinearity and weak data in regression. J. Oper. Res. Soc. 1993, 44, 88–89. [Google Scholar]
- Rao, Y.Q.; Janet, E. Information entropy–based complexity measurement of manufacturing system and its application in scheduling. Chinese J. Chem. Eng. 2006, 42, 8–13. [Google Scholar]
- Zuan, P.; Huang, Y. Prediction of sliding slope displacement based on intelligent algorithm. Wireless. Pers. Commun. 2018, 102, 3141–3157. [Google Scholar] [CrossRef]
- Baghban, A.; Ahmadi, M.A.; Hashemi Shahraki, B. Prediction carbon dioxide solubility in presence of various ionic liquids using computational intelligence approaches. J. Supercrit. Fluids. 2015, 98, 50–64. [Google Scholar] [CrossRef]
- Yokozeki, A.; Shiflett, M.B.; Junk, C.P.; Grieco, L.M.; Foo, T. Physical and chemical absorptions of carbon dioxide in room–temperature ionic liquids. J. Phys. Chem. B. 2008, 112, 16654–16663. [Google Scholar] [CrossRef] [PubMed]
- Yim, J.H.; Lim, J.S. CO2 solubility measurement in 1–hexyl–3–methylimidazolium ([HMIM]) cation based ionic liquids. Fluid. Phase. Equilibr. 2013, 352, 67–74. [Google Scholar] [CrossRef]
- Tagiuri, A.; Sumon, K.Z.; Henni, A. Solubility of carbon dioxide in three [Tf2N] ionic liquids. Fluid. Phase. Equilibr. 2014, 380, 39–47. [Google Scholar] [CrossRef]
- Schilderman, A.M.; Raeissi, S.; Peters, C.J. Solubility of carbon dioxide in the ionic liquid 1–ethyl–3–methylimidazolium bis(trifluoromethylsulfonyl)imide. Fluid. Phase. Equilibr. 2007, 260, 19–22. [Google Scholar] [CrossRef]
- Kim, Y.S.; Jang, J.H.; Lim, B.D.; Kang, J.W.; Lee, C.S. Solubility of mixed gases containing carbon dioxide in ionic liquids: Measurements and predictions. Fluid. Phase. Equilibr. 2007, 256, 70–74. [Google Scholar] [CrossRef]
- Kim, Y.S.; Choi, W.Y.; Jang, J.H.; Yoo, K.P.; Lee, C.S. Solubility measurement and prediction of carbon dioxide in ionic liquids. Fluid. Phase. Equilibr. 2005, 228, 439–445. [Google Scholar] [CrossRef]
- Carvalho, P.J.; Álvarez, V.H.; Machado, J.J.B.; Pauly, J.; Daridon, J.L.; Marrucho, I.M.; Aznar, M.; Coutinho, J.A.P. High pressure phase behavior of carbon dioxide in 1–alkyl–3–methylimidazolium bis(trifluoromethylsulfonyl)imide ionic liquids. J. Supercrit. Fluids. 2009, 48, 99–107. [Google Scholar] [CrossRef]
- Blanchard, L.A.; Gu, Z.; Brennecke, J.F. High–pressure phase behaviour of ionic liquid/CO2 systems. J. Phys. Chem. B. 2001, 105, 2437–2444. [Google Scholar] [CrossRef]
- Bermejo, M.D.; Fieback, T.M.; Martín, Á. Solubility of gases in 1–alkyl–3methylimidazolium alkyl sulfate ionic liquids: Experimental determination and modeling. J. Chem. Thermodyn. 2013, 58, 237–244. [Google Scholar] [CrossRef]
- Afzal, W.; Liu, X.; Prausnitz, J.M. Solubilities of some gases in four immidazolium–based ionic liquids. J. Chem. Thermodyn. 2013, 63, 88–94. [Google Scholar] [CrossRef]




| NO. | Ionic Liquids | MW (g/mol) | Tc (K) | Pc (MPa) | w |
|---|---|---|---|---|---|
| 1 | [BMIM][BF4] | 226.03 | 623.30 | 2.040 | 0.8489 |
| 2 | [EMIM][TF2N] | 391.30 | 788.05 | 3.310 | 1.2250 |
| 3 | [EMIM][ETSO4] | 236.29 | 1061.10 | 4.040 | 0.3368 |
| 4 | [HMIM][TF2N] | 447.92 | 1292.78 | 2.389 | 0.3893 |
| 5 | [HMIM][TFO] | 316.34 | 1055.60 | 2.495 | 0.4890 |
| 6 | [HMIM][BF4] | 254.08 | 716.61 | 1.794 | 0.6589 |
| 7 | [HMIM][MESO4] | 278.37 | 1110.84 | 2.961 | 0.4899 |
| 8 | [BMMIM][TF2N] | 433.40 | 1255.80 | 2.031 | 0.3193 |
| 9 | [HMIM][PF6] | 312.24 | 759.16 | 1.550 | 0.9385 |
| NO. | Abbreviation | Name |
|---|---|---|
| 1 | [BMIM][BF4] | 1–butyl–3–methylimidazolium tetrafluoroborate |
| 2 | [EMIM][TF2N] | 1–ethyl–3–methylimidazolium bis(trifluoromethylsulfonyl)imide |
| 3 | [EMIM][ETSO4] | 1–ethyl–3–methylimidazolium ethylsulfate |
| 4 | [HMIM][TF2N] | 1–hexyl–3–methylimidazoliumbis(trifluoromethylsulfonyl)imide |
| 5 | [HMIM][TFO] | 1–hexyl–3–methylimidazolium trifluoromethanesulfonate |
| 6 | [HMIM][BF4] | 1–hexyl–3–methylimidazolium tetrafluoroborate |
| 7 | [HMIM][MESO4] | 1–hexyl–3–methylimidazolium methyl–sulfate |
| 8 | [BMMIM][TF2N] | 1–butyl–2,3–dimethylimidazoliumbis(trifluoromethanesulfonyl)imide |
| 9 | [HMIM][PF6] | 1–methyl–3–hexylimidazolium hexafluorophosphate |
| NO. | Ionic Liquids | Temperature Range (K) | Pressure Range (MPa) | CO2 Solubility Range (Mole Fraction) | NO. of Samples | Refs. |
|---|---|---|---|---|---|---|
| 1 | [BMIM][BF4] | 278.47–368.22 | 0.01–67.62 | 0.003–0.610 | 204 | [8,32,41] |
| 2 | [EMIM][TF2N] | 450.49–292.75 | 0.00–43.25 | 0.000–0.782 | 250 | [32,35,37,38,41] |
| 3 | [EMIM][ETSO4] | 398.04–353.15 | 0.10–9.46 | 0.000–0.457 | 82 | [39,40] |
| 4 | [HMIM][TF2N] | 278.12–450.49 | 0.01–45.28 | 0.001–0.824 | 394 | [8,33,38] |
| 5 | [HMIM][TFO] | 303.15–373.15 | 1.25–100.12 | 0.267–0.816 | 34 | [33] |
| 6 | [HMIM][BF4] | 293.18–373.15 | 0.31–86.60 | 0.071–0.703 | 160 | [8,33,37,39] |
| 7 | [HMIM][MESO4] | 303.15–373.15 | 0.87–50.14 | 0.158–0.602 | 48 | [33,39] |
| 8 | [BMMIM][TF2N] | 298.15–343.15 | 0.01–1.90 | 0.002–0.211 | 36 | [8,37] |
| 9 | [HMIM][PF6] | 298.15–373.15 | 0.30–94.60 | 0.058–0.727 | 160 | [8,34,36] |
| NO. | MAE | RMSE | R2 |
|---|---|---|---|
| 1 | 0.0069 | 0.0118 | 0.9971 |
| 2 | 0.0071 | 0.0126 | 0.9967 |
| 3 | 0.0085 | 0.0138 | 0.9961 |
| 4 | 0.0094 | 0.0147 | 0.9955 |
| 5 | 0.0054 | 0.0105 | 0.9977 |
| 6 | 0.0106 | 0.0159 | 0.9947 |
| 7 | 0.0116 | 0.0170 | 0.9939 |
| 8 | 0.0131 | 0.0186 | 0.9928 |
| 9 | 0.0091 | 0.0143 | 0.9957 |
| 10 | 0.0077 | 0.0133 | 0.9963 |
| NO. | MAE | RMSE | R2 |
|---|---|---|---|
| 1 | 0.0127 | 0.0180 | 0.9932 |
| 2 | 0.0123 | 0.0172 | 0.9938 |
| 3 | 0.0108 | 0.0161 | 0.9946 |
| 4 | 0.0097 | 0.0150 | 0.9953 |
| 5 | 0.0137 | 0.0189 | 0.9926 |
| 6 | 0.0159 | 0.0216 | 0.9902 |
| 7 | 0.0108 | 0.0158 | 0.9948 |
| 8 | 0.0127 | 0.0182 | 0.9930 |
| 9 | 0.0110 | 0.0158 | 0.9948 |
| 10 | 0.0076 | 0.0132 | 0.9964 |
| NO. | MAE | RMSE | R2 |
|---|---|---|---|
| 1 | 0.0037 | 0.0089 | 0.9983 |
| 2 | 0.0042 | 0.0094 | 0.9982 |
| 3 | 0.0062 | 0.0111 | 0.9974 |
| 4 | 0.0034 | 0.0081 | 0.9986 |
| 5 | 0.0035 | 0.0076 | 0.9988 |
| 6 | 0.0039 | 0.0083 | 0.9986 |
| 7 | 0.0048 | 0.0095 | 0.9981 |
| 8 | 0.0047 | 0.0096 | 0.9981 |
| 9 | 0.0040 | 0.0089 | 0.9984 |
| 10 | 0.0046 | 0.0101 | 0.9979 |
| NO. of Cluster | CH Value |
|---|---|
| 2 | 17.25 |
| 3 | 21.44 |
| 4 | 15.22 |
| 5 | 12.61 |
| Model | MAE | RMSE | R2 |
|---|---|---|---|
| Optimal BPNN | 0.0082 | 0.0137 | 0.9960 |
| Optimal ELM | 0.0094 | 0.0150 | 0.9952 |
| Optimal RBFNN | 0.0066 | 0.0118 | 0.9971 |
| Fully integrated model | 0.0055 | 0.0103 | 0.9978 |
| Selective ensemble model | 0.0049 | 0.0096 | 0.9981 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xia, L.; Liu, S.; Pan, H. Prediction of the Solubility of CO2 in Imidazolium Ionic Liquids Based on Selective Ensemble Modeling Method. Processes 2020, 8, 1369. https://doi.org/10.3390/pr8111369
Xia L, Liu S, Pan H. Prediction of the Solubility of CO2 in Imidazolium Ionic Liquids Based on Selective Ensemble Modeling Method. Processes. 2020; 8(11):1369. https://doi.org/10.3390/pr8111369
Chicago/Turabian StyleXia, Luyue, Shanshan Liu, and Haitian Pan. 2020. "Prediction of the Solubility of CO2 in Imidazolium Ionic Liquids Based on Selective Ensemble Modeling Method" Processes 8, no. 11: 1369. https://doi.org/10.3390/pr8111369
APA StyleXia, L., Liu, S., & Pan, H. (2020). Prediction of the Solubility of CO2 in Imidazolium Ionic Liquids Based on Selective Ensemble Modeling Method. Processes, 8(11), 1369. https://doi.org/10.3390/pr8111369





