Evolution and Physical Characteristics of a Raceway Based on a Transient Eulerian Multiphase Flow Model
Abstract
1. Introduction
2. Model Description
2.1. Conservation Equations
2.2. Constitutive Relations
2.3. Turbulence Equations
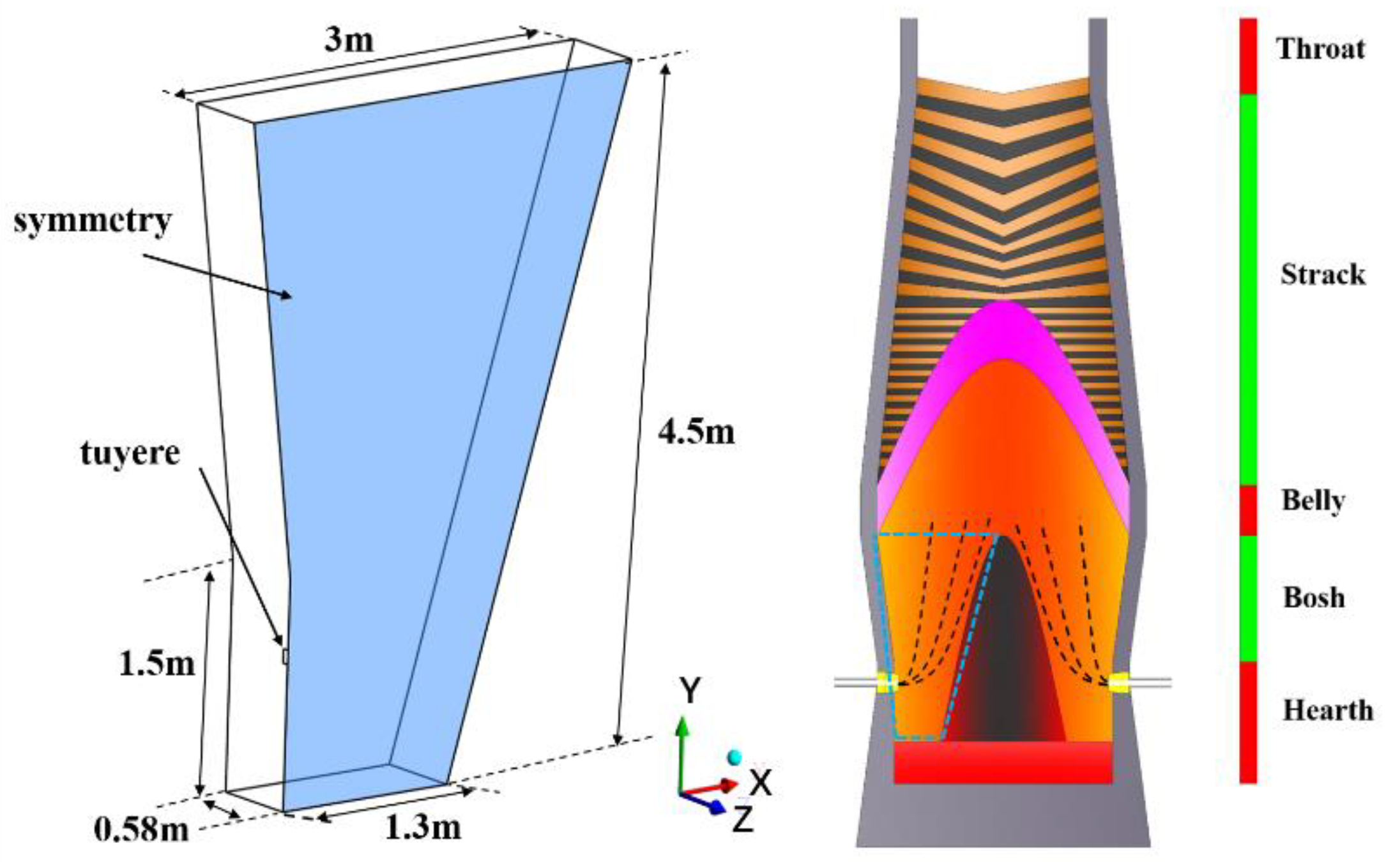
2.4. Geometry and Operating Conditions
2.5. Grid and Time Step Independence
3. Results and Discussion
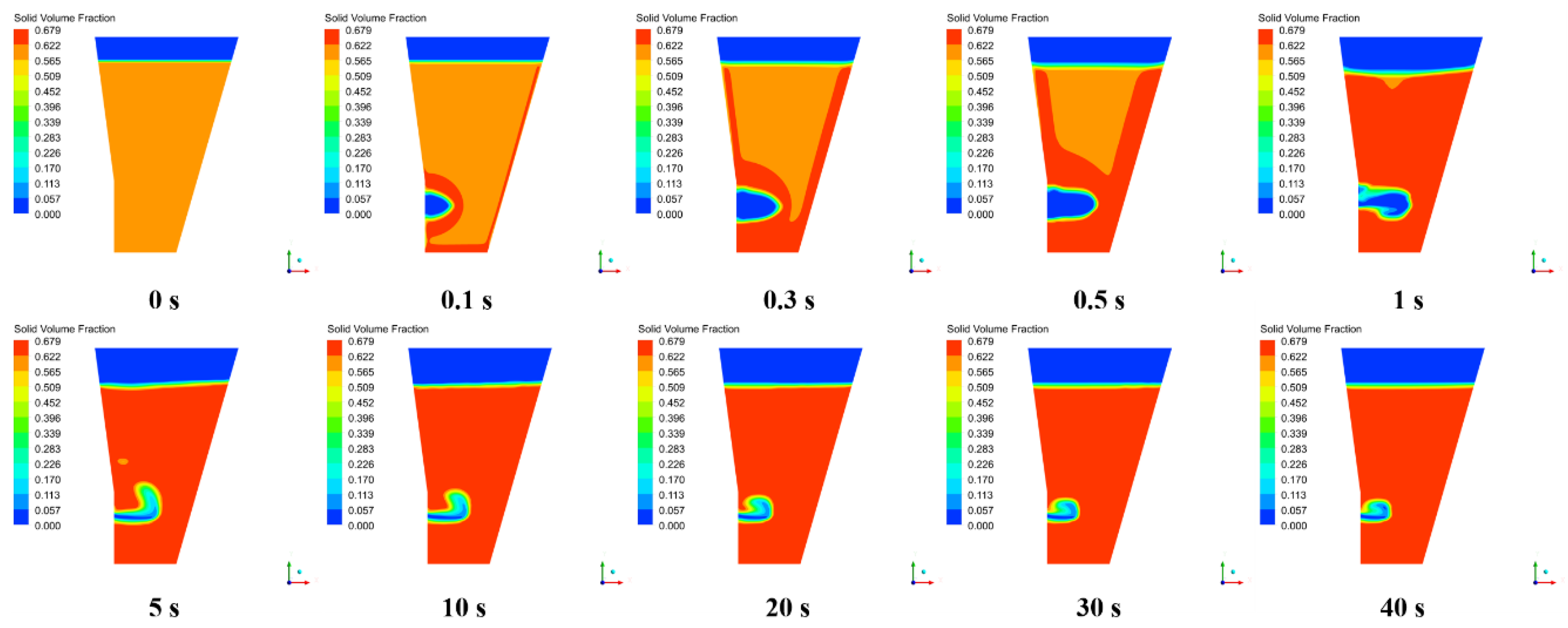
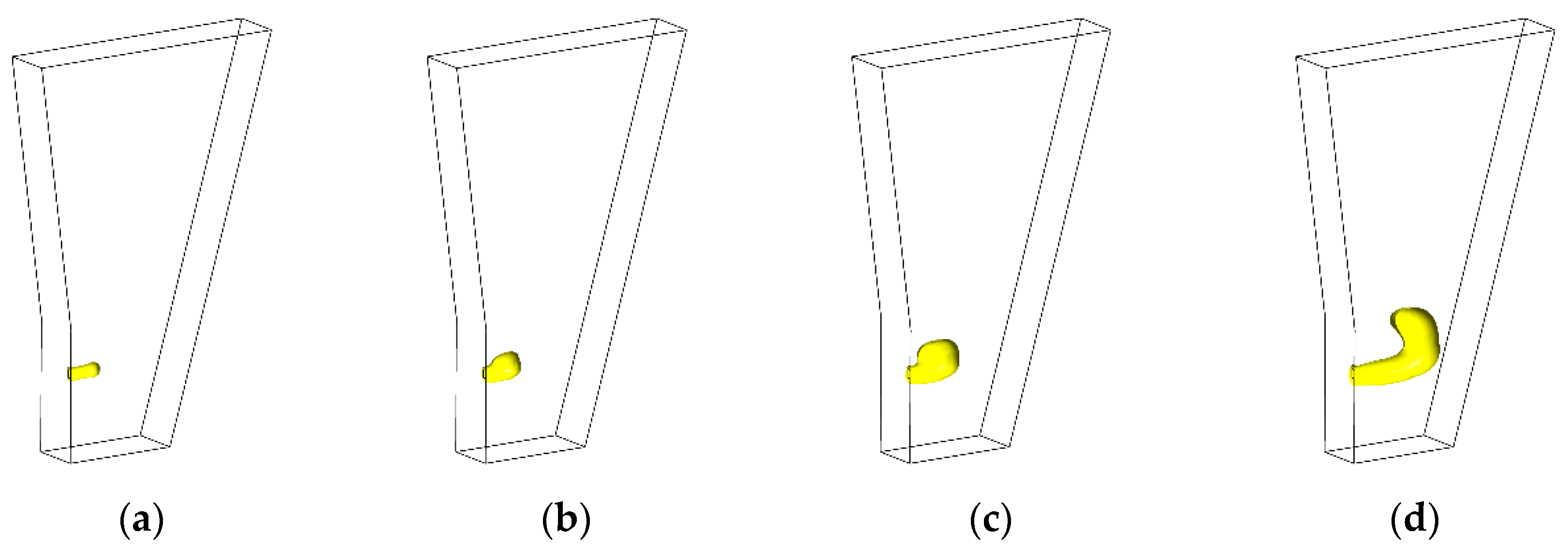
3.1. Raceway Evolution Characteristics
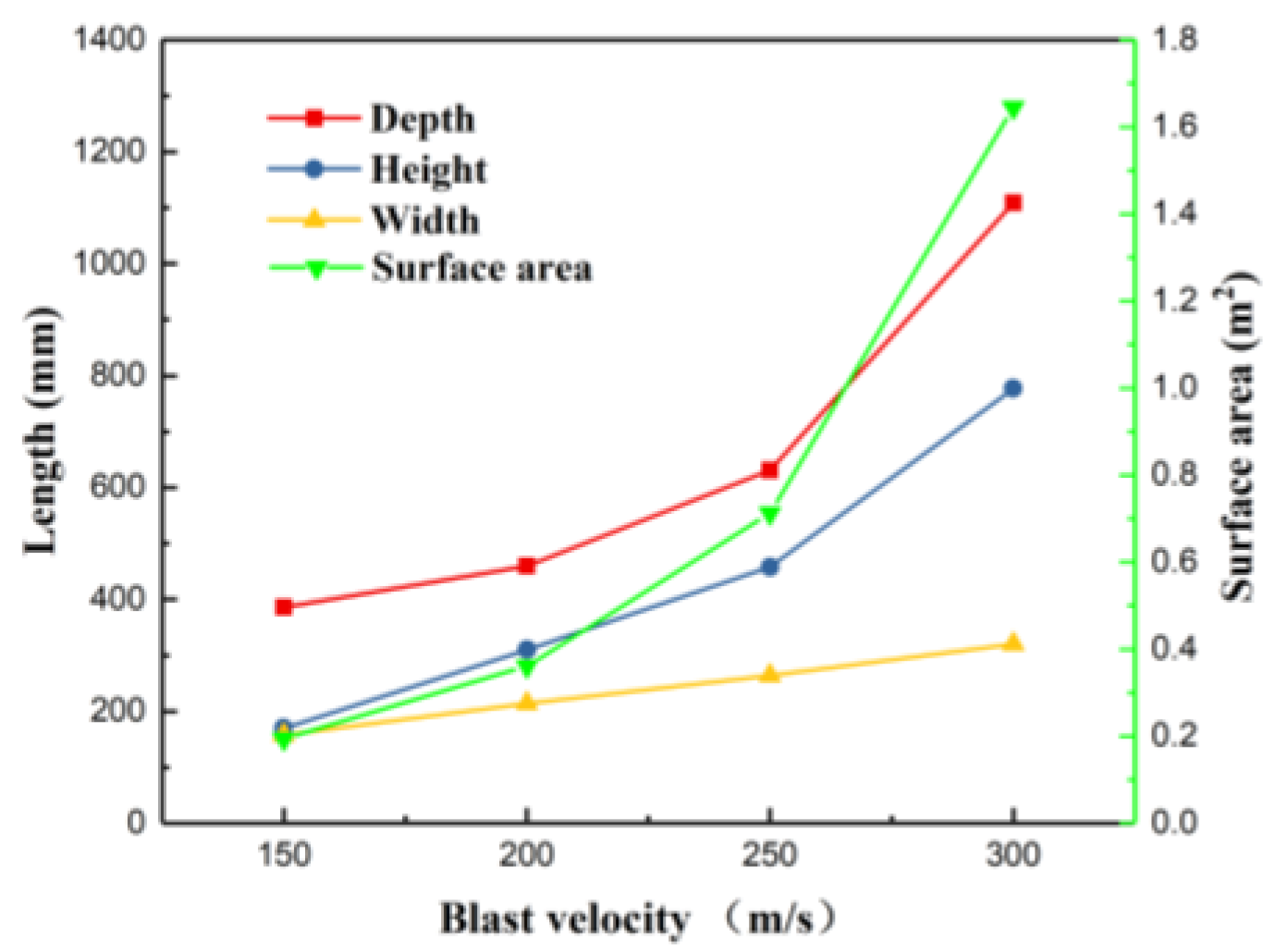
3.2. Raceway Size Characteristics
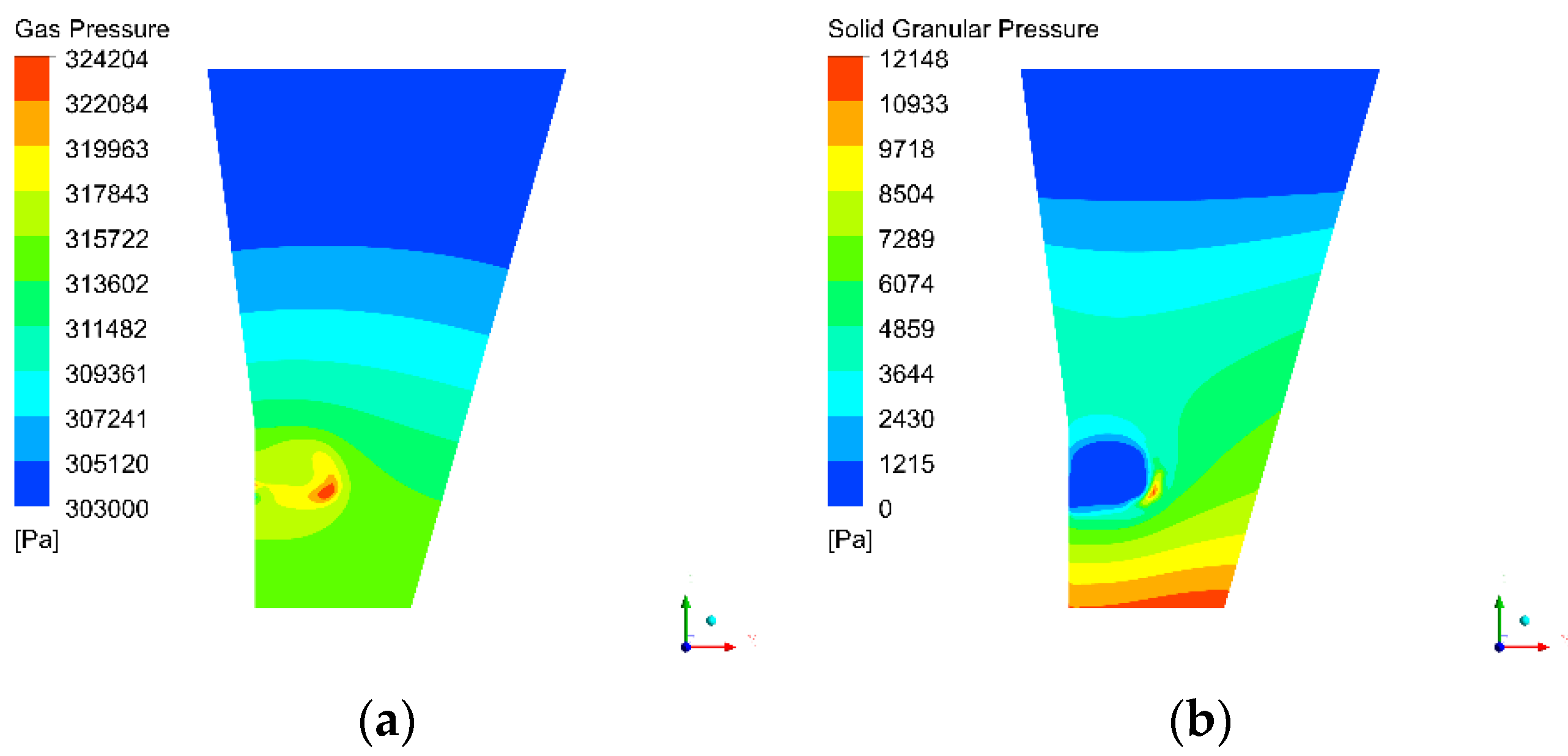
3.3. Pressure Distribution
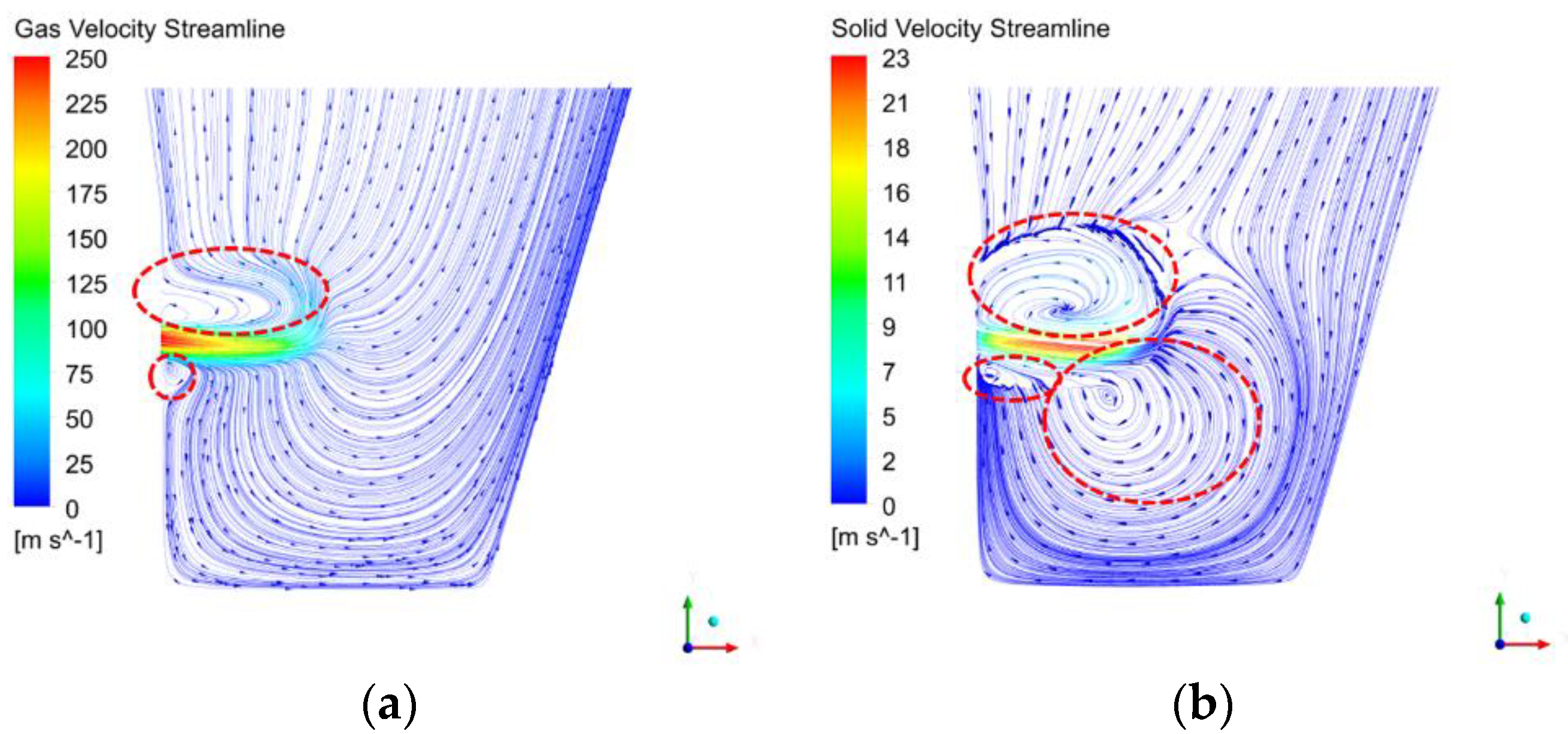
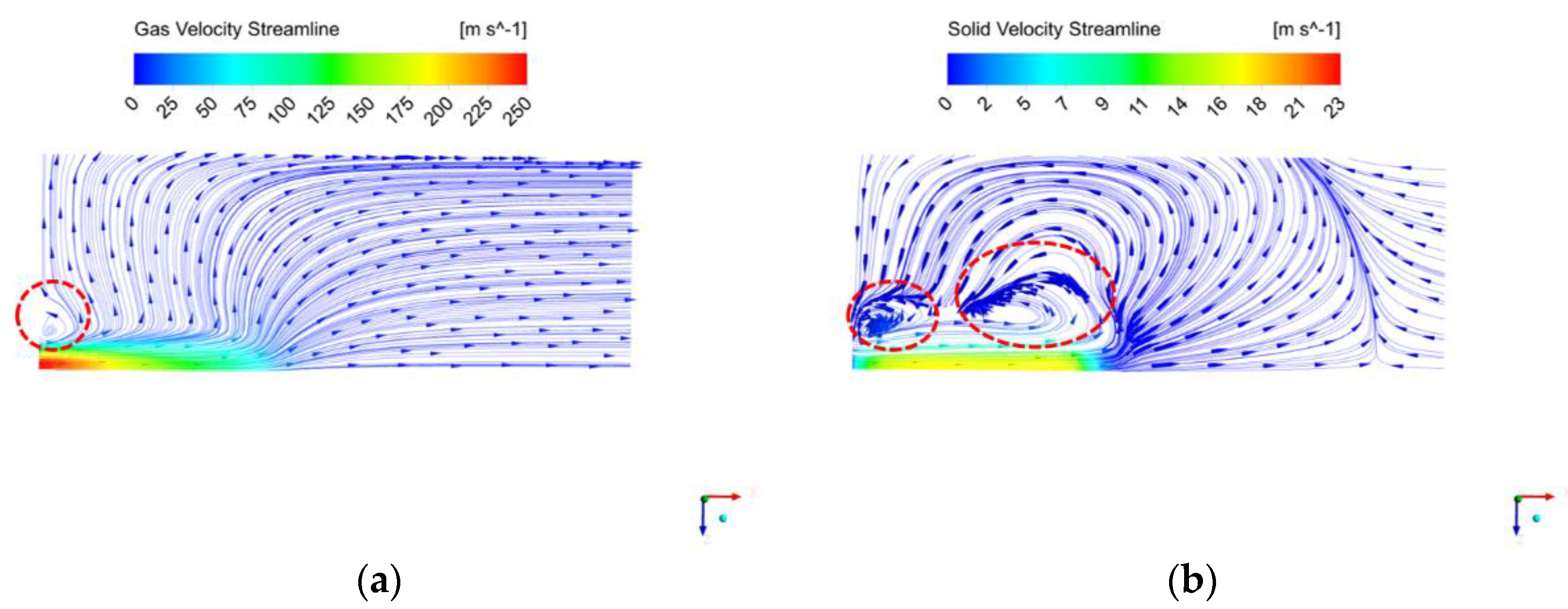
3.4. Flow Pattern
4. Conclusions
- (1)
- The evolution process of the raceway can be divided into three stages: rapid expansion, slow contraction, and gradual stabilization. The shape of the raceway was that of an upturned bag at high blast velocity.
- (2)
- The blast velocity had a significant effect on the size of the raceway. As the velocity increased, the depth, height, and surface area of the raceway considerably increased, while the width slightly increased.
- (3)
- The gas pressure in the raceway was higher than that of the particle bed, while the solid granular pressure was lower. The raceway did not exhibit a single-cycle flow pattern, but exhibited a complex multiphase and multi-cycle flow pattern.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Notation
| Symbol | Meaning |
| phase volume fraction | |
| phase density, kg/m3 | |
| phase velocity, m/s | |
| phase stress–strain tensor, Pa | |
| phase pressure, Pa | |
| Gravity acceleration, m/s2 | |
| Source term | |
| Momentum exchange coefficient | |
| Drag coefficient | |
| Solid-phase diameter, m | |
| Gas-phase viscosity, Pas | |
| Reynolds number | |
| Unit stress tensor | |
| Gas effective viscosity, Pas | |
| Gas turbulent kinetic energy, Pas | |
| Gas turbulent viscosity, Pas | |
| Gas turbulent dissipation rate | |
| Solid radial distribution function | |
| Coefficient of restitution for particle collisions | |
| Granular pseudo-temperature | |
| Diffusion coefficient | |
| Particle collisional dissipation of energy | |
| Friction packing limit | |
| Packing limit | |
| Solid bulk viscosity, Pas | |
| Solids shear viscosity, Pas | |
| Solid kinetic viscosity, Pas | |
| Solid collisional viscosity, Pas | |
| Solid frictional viscosity, Pas | |
| Frictional pressure, Pa | |
| Angle of internal friction | |
| Second invariant of the deviatoric stress tensor | |
| Froude number | |
| Gas-phase turbulent kinetic energy | |
| Turbulent kinetic energy source term | |
| Turbulent dissipation rate source term |
References
- Burgess, J.M. Fuel combustion in the blast furnace raceway zone. Prog. Energy Combust. Sci. 1985, 11, 61–82. [Google Scholar] [CrossRef]
- Zhou, Z.; Xue, Q.; Li, C.; Wang, G.; She, X.; Wang, J. Coal flow and combustion characteristics under oxygen enrichment way of oxygen-coal double lance. Appl. Therm. Eng. 2017, 123, 1096–1105. [Google Scholar] [CrossRef]
- Liu, Y.; Shen, Y. Three-dimensional modelling of charcoal combustion in an industrial scale blast furnace. Fuel 2019, 258, 116088. [Google Scholar] [CrossRef]
- Zhou, Z.; Yi, Q.; Wang, R.; Wang, G.; Ma, C. Numerical investigation on coal combustion in ultralow CO2 blast furnace: Effect of oxygen temperature. Processes 2020, 8, 877. [Google Scholar] [CrossRef]
- Gupta, G.S.; Rajneesh, S.; Rudolph, V.; Singh, V.; Sarkar, S.; Litster, J.D. Mechanics of raceway hysteresis in a packed bed. Metall. Mater. Trans. B Process Metall. Mater. Process. Sci. 2005, 36, 755–764. [Google Scholar] [CrossRef]
- Gupta, G.S.; Rudolph, V. Comparison of blast furnace raceway size with theory. ISIJ Int. 2006, 46, 195–201. [Google Scholar] [CrossRef]
- Guo, J.; Cheng, S.; Zhao, H.; Pan, H.; Du, P.; Teng, Z. A mechanism model for raceway formation and variation in a blast furnace. Metall. Mater. Trans. B Process Metall. Mater. Process. Sci. 2013, 44, 487–494. [Google Scholar] [CrossRef]
- Li, Y.L.; Cheng, S.S.; Zhang, P.; Guo, J. Development of 3-D mathematical model of raceway size in blast furnace. Ironmak. Steelmak. 2016, 43, 308–315. [Google Scholar] [CrossRef]
- Matsui, Y.; Yamaguchi, Y.; Sawayama, M.; Kitano, S.; Nagai, N.; Imai, T. Analyses on blast furnace raceway formation by micro wave reflection gunned through tuyere. ISIJ Int. 2005, 45, 1432–1438. [Google Scholar] [CrossRef][Green Version]
- Flint, P.J.; Burgess, J.M. A fundamental study of raceway size in two dimensions. Metall. Trans. B 1992, 23, 267–283. [Google Scholar] [CrossRef]
- Sarkar, S.; Gupta, G.S.; Litster, J.D.; Rudolph, V.; White, E.T.; Choudhary, S.K. A cold model study of raceway hysteresis. Metall. Mater. Trans. B Process Metall. Mater. Process. Sci. 2003, 34, 183–191. [Google Scholar] [CrossRef]
- Sastry, G.S.S.R.K.; Gupta, G.S.; Lahiri, A.K. Cold model study of raceway under mixed particle conditions. Ironmak. Steelmak. 2003, 30, 61–65. [Google Scholar] [CrossRef]
- Sastry, G.S.S.R.K.; Gupta, G.S.; Lahiri, A.K. Void formation and breaking in a packed bed. ISIJ Int. 2003, 43, 153–160. [Google Scholar] [CrossRef]
- Rajneesh, S.; Sarkar, S.; Gupta, G.S. Prediction of raceway size in blast furnace from two dimensional experimental correlations. ISIJ Int. 2004, 44, 1298–1307. [Google Scholar] [CrossRef]
- Mojamdar, V.; Gupta, G.S.; Puthukkudi, A. Raceway formation in a moving bed. ISIJ Int. 2018, 58, 1396–1401. [Google Scholar] [CrossRef]
- Lu, Y.; Jiang, Z.; Zhang, X.; Liu, S.; Wang, J.; Zhang, X. Determination of void boundary in a packed bed by laser attenuation measurement. Particuology 2020, 51, 72–79. [Google Scholar] [CrossRef]
- Xu, B.H.; Yu, A.B.; Chew, S.J.; Zulli, P. Numerical simulation of the gas-solid flow in a bed with lateral gas blasting. Powder Technol. 2000, 109, 13–26. [Google Scholar] [CrossRef]
- Feng, Y.-Q.; Pinson, D.; Yu, A.-B.; Chew, S.J.; Zulli, P. Numerical Study of Gas-Solid Flow in the Raceway of a Blast Furnace. Steel Res. Int. 2003, 74, 523–530. [Google Scholar] [CrossRef]
- Umekage, T.; Yuu, S.; Kadowaki, M. Numerical simulation of blast furnace raceway depth and height, and effect of wall cohesive matter on gas and coke particle flows. ISIJ Int. 2005, 45, 1416–1425. [Google Scholar] [CrossRef]
- Sarkar, S.; Gupta, G.S.; Kitamura, S.Y. Prediction of raceway shape and size. ISIJ Int. 2007, 47, 1738–1744. [Google Scholar] [CrossRef][Green Version]
- Miao, Z.; Zhou, Z.; Yu, A.B.; Shen, Y. CFD-DEM simulation of raceway formation in an ironmaking blast furnace. Powder Technol. 2017, 314, 542–549. [Google Scholar] [CrossRef]
- Cui, J.; Hou, Q.; Shen, Y. CFD-DEM study of coke combustion in the raceway cavity of an ironmaking blast furnace. Powder Technol. 2020, 362, 539–549. [Google Scholar] [CrossRef]
- Lu, Y.; Liu, S.; Zhang, X.; Jiang, Z.E.D. A Probabilistic Statistical Method for the Determination of Void Morphology with CFD-DEM Approach. Energies 2020, 13, 4041. [Google Scholar] [CrossRef]
- Hilton, J.E.; Cleary, P.W. Raceway formation in laterally gas-driven particle beds. Chem. Eng. Sci. 2012, 80, 306–316. [Google Scholar] [CrossRef]
- Lichtenegger, T.; Pirker, S. CFD-DEM modeling of strongly polydisperse particulate systems. Powder Technol. 2018, 325, 698–711. [Google Scholar] [CrossRef]
- Mondal, S.S.; Som, S.K.; Dash, S.K. Numerical predictions on the influences of the air blast velocity, initial bed porosity and bed height on the shape and size of raceway zone in a blast furnace. J. Phys. D Appl. Phys. 2005, 38, 1301–1307. [Google Scholar] [CrossRef]
- Singh, V.; Gupta, G.S.; Sarkar, S. Study of gas cavity size hysteresis in a packed bed using DEM. Chem. Eng. Sci. 2007, 62, 6102–6111. [Google Scholar] [CrossRef]
- Sun, Y.; Chen, R.; Zhang, Z.; Wu, G.; Zhang, H.; Li, L.; Liu, Y.; Li, X.; Huang, Y. Numerical simulation of the raceway zone in melter gasifier of COREX process. Processes 2019, 7, 867. [Google Scholar] [CrossRef]
- Rangarajan, D.; Shiozawa, T.; Shen, Y.; Curtis, J.S.; Yu, A. Influence of operating parameters on raceway properties in a model blast furnace using a two-fluid model. Ind. Eng. Chem. Res. 2014, 53, 4983–4990. [Google Scholar] [CrossRef]
- Gu, M.; Zhang, M.; Selvarasu, N.K.C.; Zhao, Y.C.Q.Z. Numerical Analysis of Pulverized Coal Combustion inside Tuyere and Raceway. Steel Res. Int. 2008, 79, 17–24. [Google Scholar] [CrossRef]
- Fu, D.; Zheng, D.; Zhou, C.Q.; D’Alessio, J.; Ferron, K.J.; Zhao, Y. Parametric studies on pci performances. ASME/JSME 2011 8th Therm. Eng. Jt. Conf. AJTEC 2011. [Google Scholar] [CrossRef]
- Okosun, T.; Street, S.J.; Zhao, J.; Wu, B.; Zhou, C.Q. Influence of conveyance methods for pulverised coal injection in a blast furnace. Ironmak. Steelmak. 2017, 44, 513–525. [Google Scholar] [CrossRef]
- Fu, D.; Tang, G.; Zhao, Y.; D’Alessio, J.; Zhou, C.Q. Integration of Tuyere, Raceway and Shaft Models for Predicting Blast Furnace Process. JOM 2018, 70, 951–957. [Google Scholar] [CrossRef]
- Wu, D.; Zhou, P.; Zhou, C.Q. Evaluation of pulverized coal utilization in a blast furnace by numerical simulation and grey relational analysis. Appl. Energy 2019, 250, 1686–1695. [Google Scholar] [CrossRef]
- Okosun, T.; Silaen, A.K.; Zhou, C.Q. Review on Computational Modeling and Visualization of the Ironmaking Blast Furnace at Purdue University Northwest. Steel Res. Int. 2019, 90, 1–16. [Google Scholar] [CrossRef]
- Zhuo, Y.; Shen, Y. Three-dimensional transient modelling of coal and coke co-combustion in the dynamic raceway of ironmaking blast furnaces. Appl. Energy 2020, 261, 114456. [Google Scholar] [CrossRef]
- Gidaspow, D. Multiphase Flow and Fluidization: Continuum and Kinetic Theory Descriptions; Academic Press: New York, NY, USA, 1994; 467p. [Google Scholar]
- Ding, J.; Gidaspow, D. A bubbling fluidization model using kinetic theory of granular flow. AIChE J. 1990, 36, 523–538. [Google Scholar] [CrossRef]
- Lun, C.K.K.; Savage, S.B.; Jeffrey, D.J.; Chepurniy, N. Kinetic theories for granular flow: Inelastic particles in Couette flow and slightly inelastic particles in a general flowfield. J. Fluid Mech. 1984, 140, 223–256. [Google Scholar] [CrossRef]
- Schaeffer, D.G. Instability in the evolution equations describing incompressible granular flow. J. Differ. Equ. 1987, 66, 19–50. [Google Scholar] [CrossRef]
- Ocone, R.; Sundaresan, S.; Jackson, R. Gas-Particle flow in a duct of arbitrary inclination with particle-particle interactions. AIChE J. 1993, 39, 1261–1271. [Google Scholar] [CrossRef]
- Johnson, P.C.; Jackson, R. Frictional–collisional constitutive relations for granular materials, with application to plane shearing. J. Fluid Mech. 1987, 176, 67–93. [Google Scholar] [CrossRef]



| Item | Formula |
|---|---|
| Gas stress | |
| Gas effective viscosity | |
| Gas turbulent viscosity | () |
| Item | Formula |
|---|---|
| Solid stress | |
| Solid pressure | |
| Diffusion coefficient | |
| Particle collisional dissipation of energy | |
| Solid radial distribution function | |
| Solid bulk viscosity | |
| Solids shear viscosity | |
| Solid kinetic viscosity | |
| Solid collisional viscosity | |
| Solid frictional viscosity | |
| Frictional pressure |
| Parameters | Value |
|---|---|
| Number of calculation units | 109,516 |
| Time Step | 0.0001 s |
| Particle density | 1000 kg/m3 |
| Angle of internal friction | 30° |
| Tuyere equivalent diameter | 0.113 m |
| Initial solid volume fraction | 0.6 |
| Solid packing limit | 0.7 |
| Friction packing limit | 0.61 |
| Initial bed particle height | 4 m |
| Outlet pressure | 303,000 Pa |
| Case | Blast Velocity (m/s) | Injection Angle | Particle Diameter (m) |
|---|---|---|---|
| 1 | 150 | 5° | 0.01 |
| 2 | 200 | 5° | 0.01 |
| 3 | 250 | 5° | 0.01 |
| 4 | 300 | 5° | 0.01 |
| Number of Grid Cells | Time Step (s) | Depth (mm) | Height (mm) | Width (mm) | Deviation |
|---|---|---|---|---|---|
| 109,516 | 0.0001 | 631 | 458 | 264 | - |
| 300,672 | 0.0001 | 640 | 461 | 267 | <2% |
| 109,516 | 0.00005 | 637 | 462 | 266 | <1% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peng, X.; Wang, J.; Zuo, H.; Xue, Q. Evolution and Physical Characteristics of a Raceway Based on a Transient Eulerian Multiphase Flow Model. Processes 2020, 8, 1315. https://doi.org/10.3390/pr8101315
Peng X, Wang J, Zuo H, Xue Q. Evolution and Physical Characteristics of a Raceway Based on a Transient Eulerian Multiphase Flow Model. Processes. 2020; 8(10):1315. https://doi.org/10.3390/pr8101315
Chicago/Turabian StylePeng, Xing, Jingsong Wang, Haibin Zuo, and Qingguo Xue. 2020. "Evolution and Physical Characteristics of a Raceway Based on a Transient Eulerian Multiphase Flow Model" Processes 8, no. 10: 1315. https://doi.org/10.3390/pr8101315
APA StylePeng, X., Wang, J., Zuo, H., & Xue, Q. (2020). Evolution and Physical Characteristics of a Raceway Based on a Transient Eulerian Multiphase Flow Model. Processes, 8(10), 1315. https://doi.org/10.3390/pr8101315






