A Hybrid Inverse Problem Approach to Model-Based Fault Diagnosis of a Distillation Column
Abstract
1. Introduction
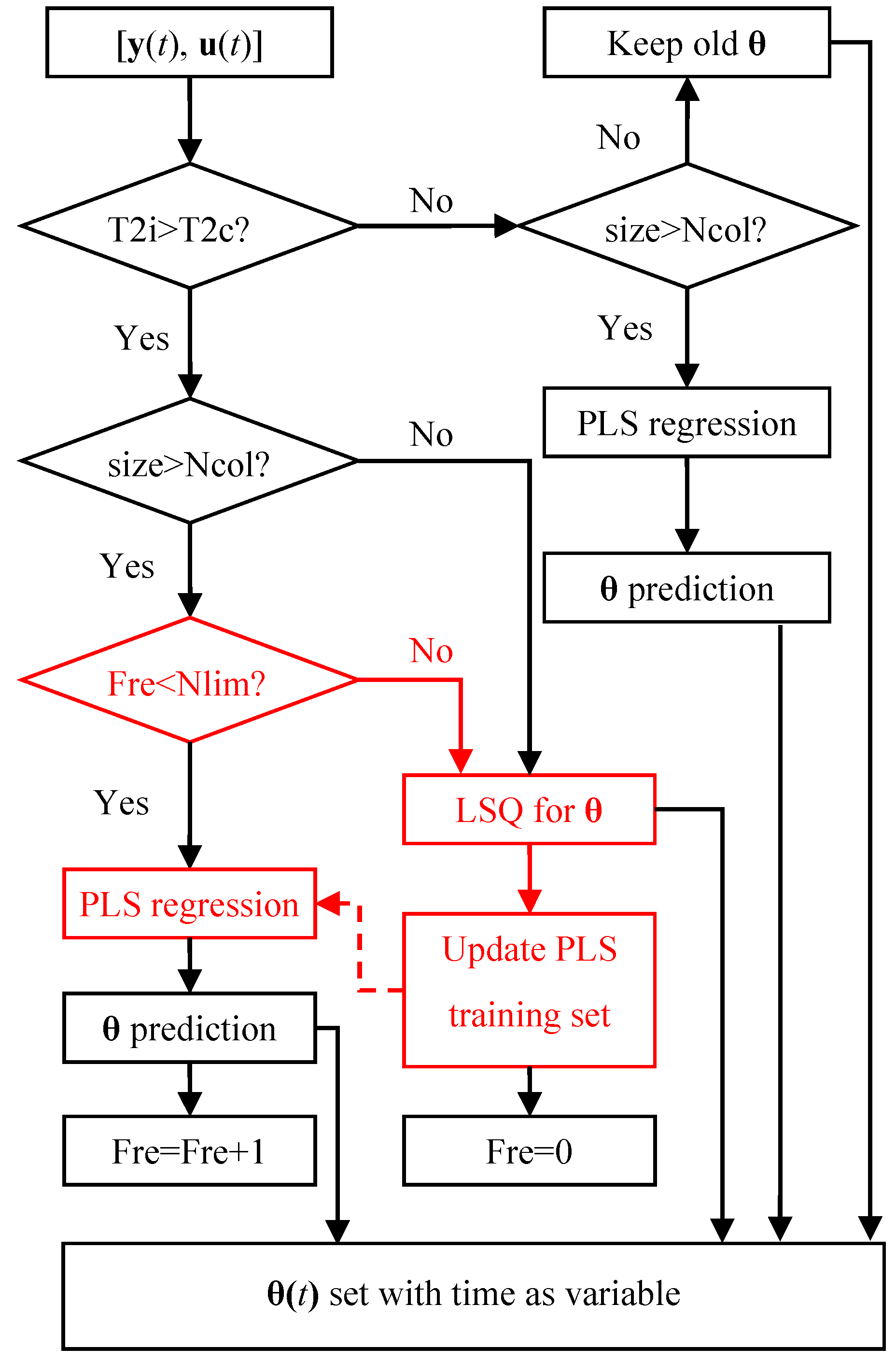
2. Hybrid Fault Diagnosis Structure
2.1. Obtaining Fault Parameters by the LSQ Algorithm
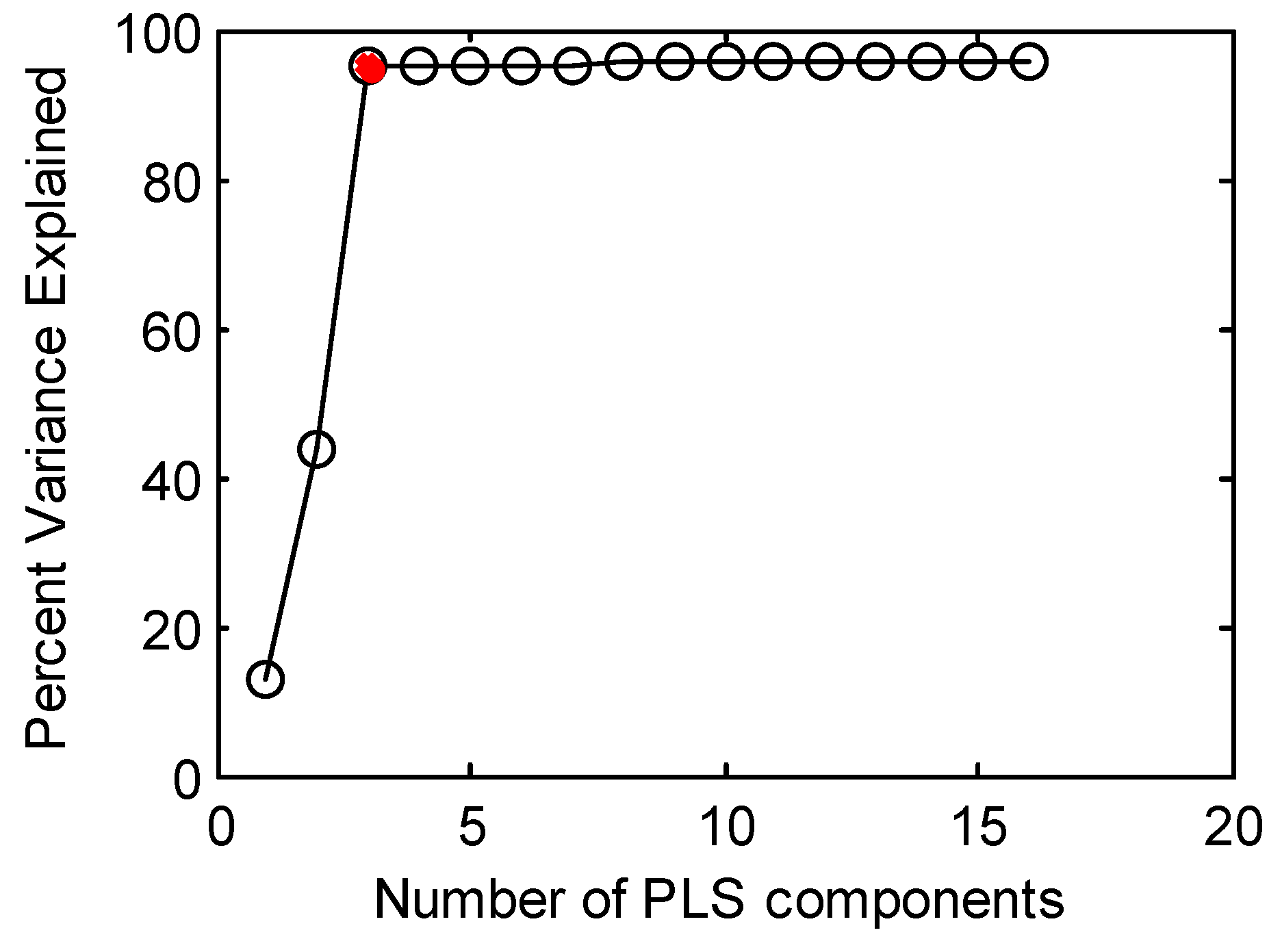
2.2. Obtaining Fault Parameters by the PLS Algorithm
2.3. Correcting PLS by LSQ
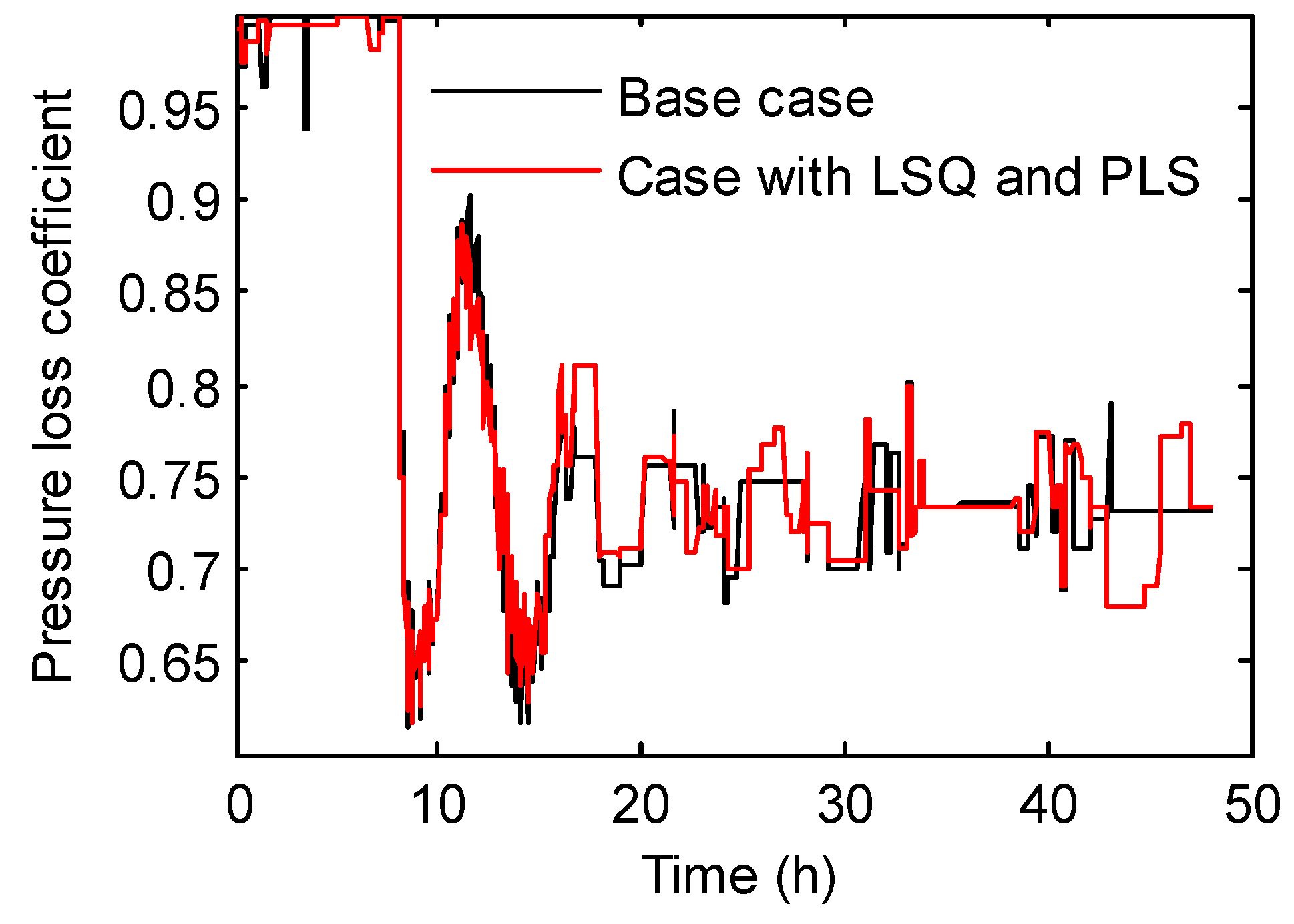
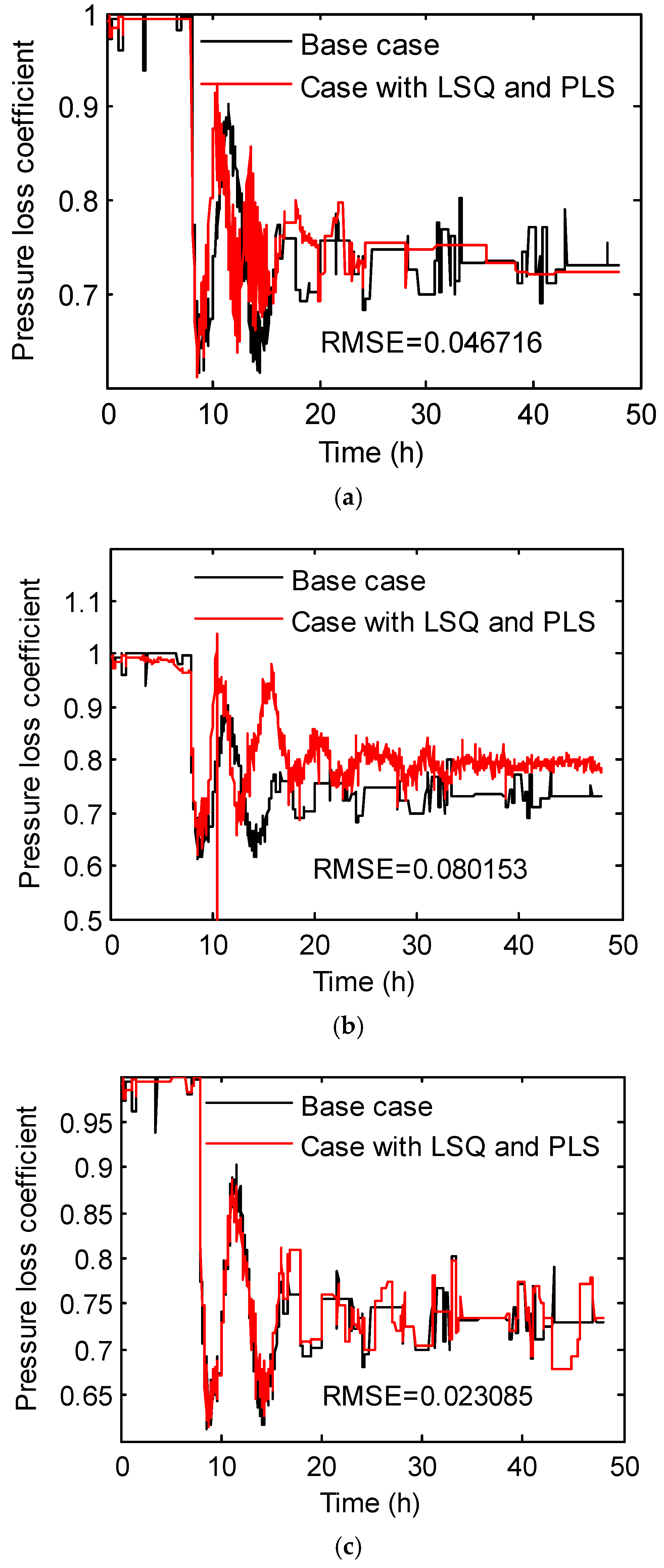
3. Case Study
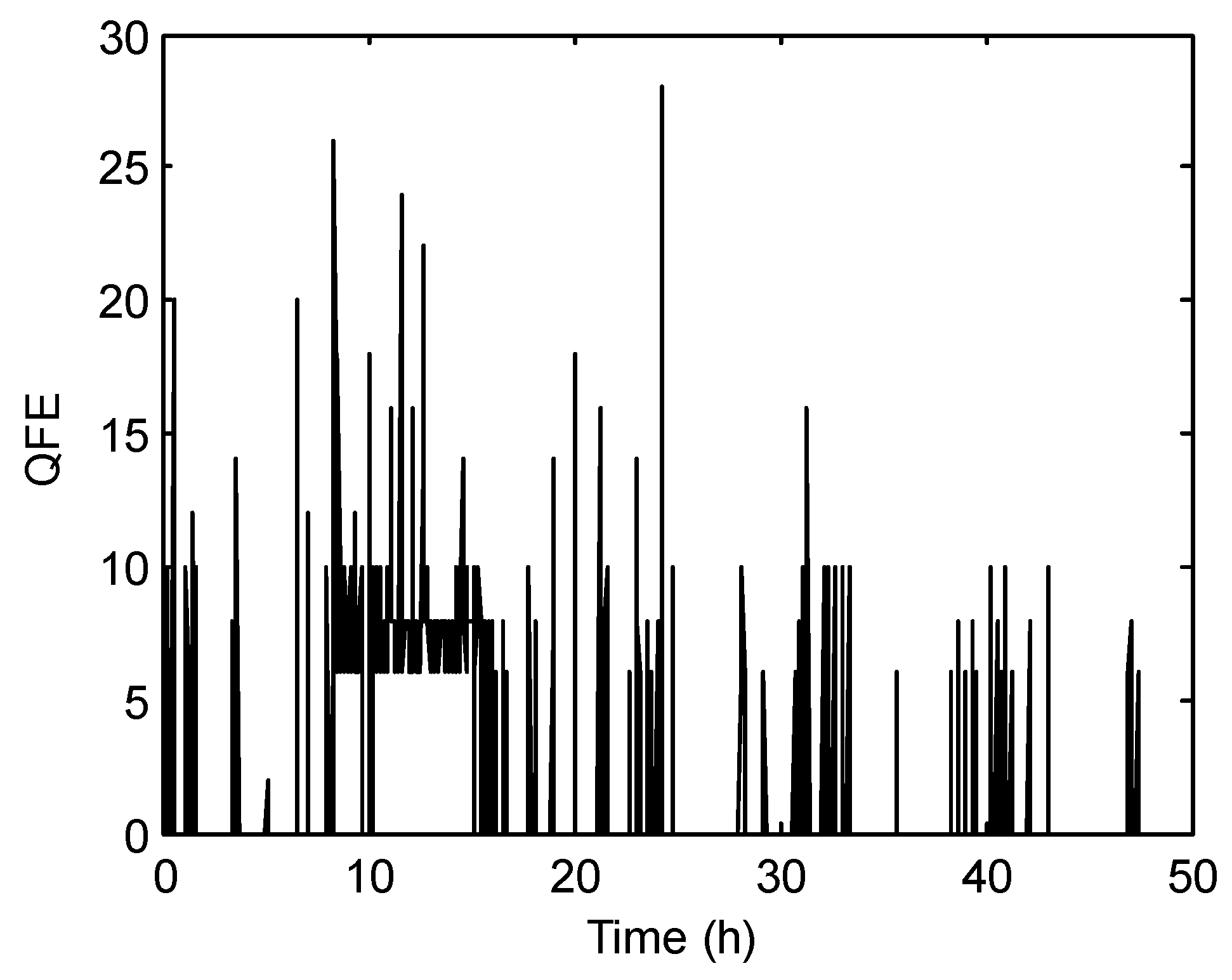
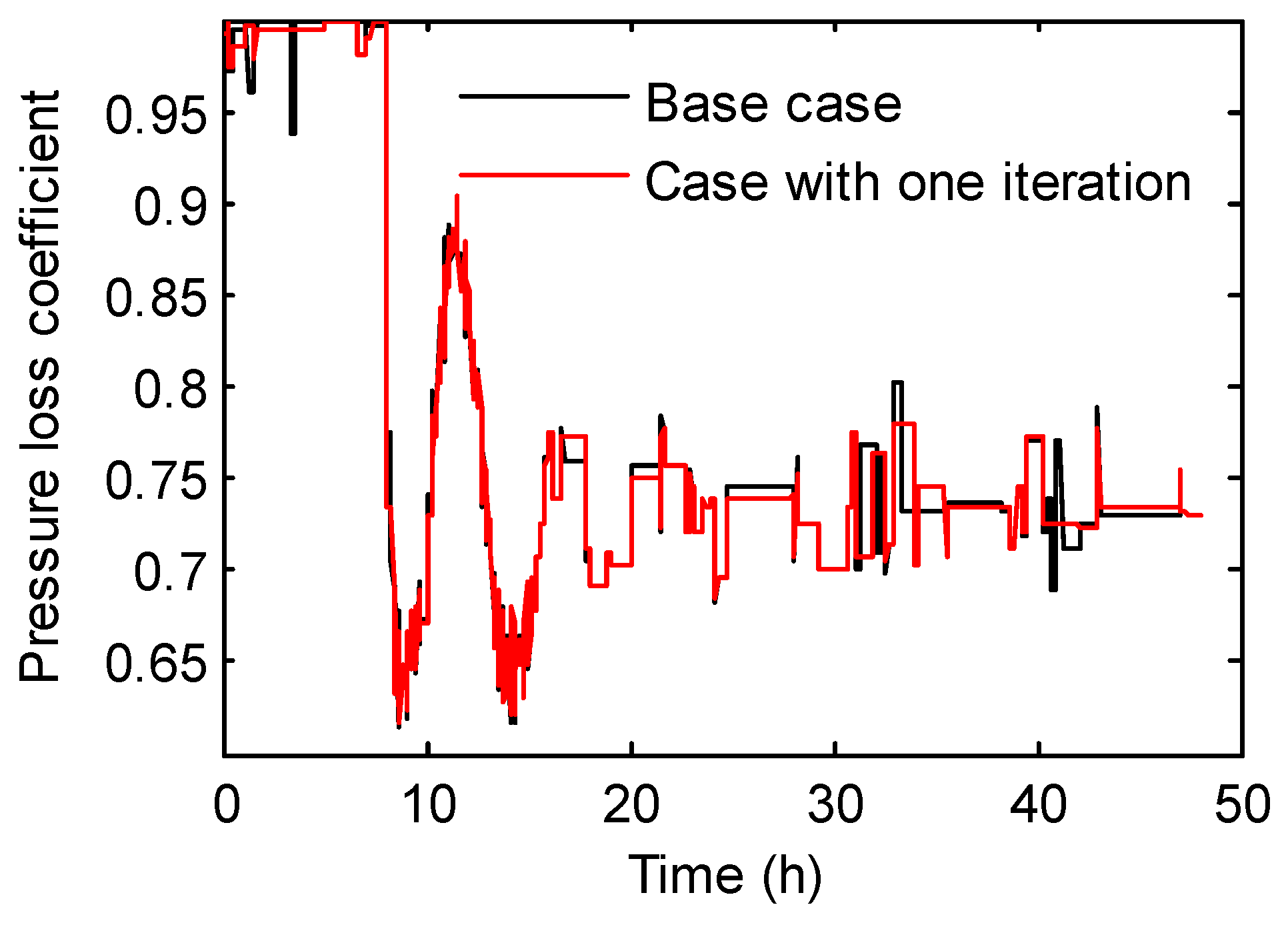
3.1. Solving the LSQ Inverse Problem with Different Initial Values
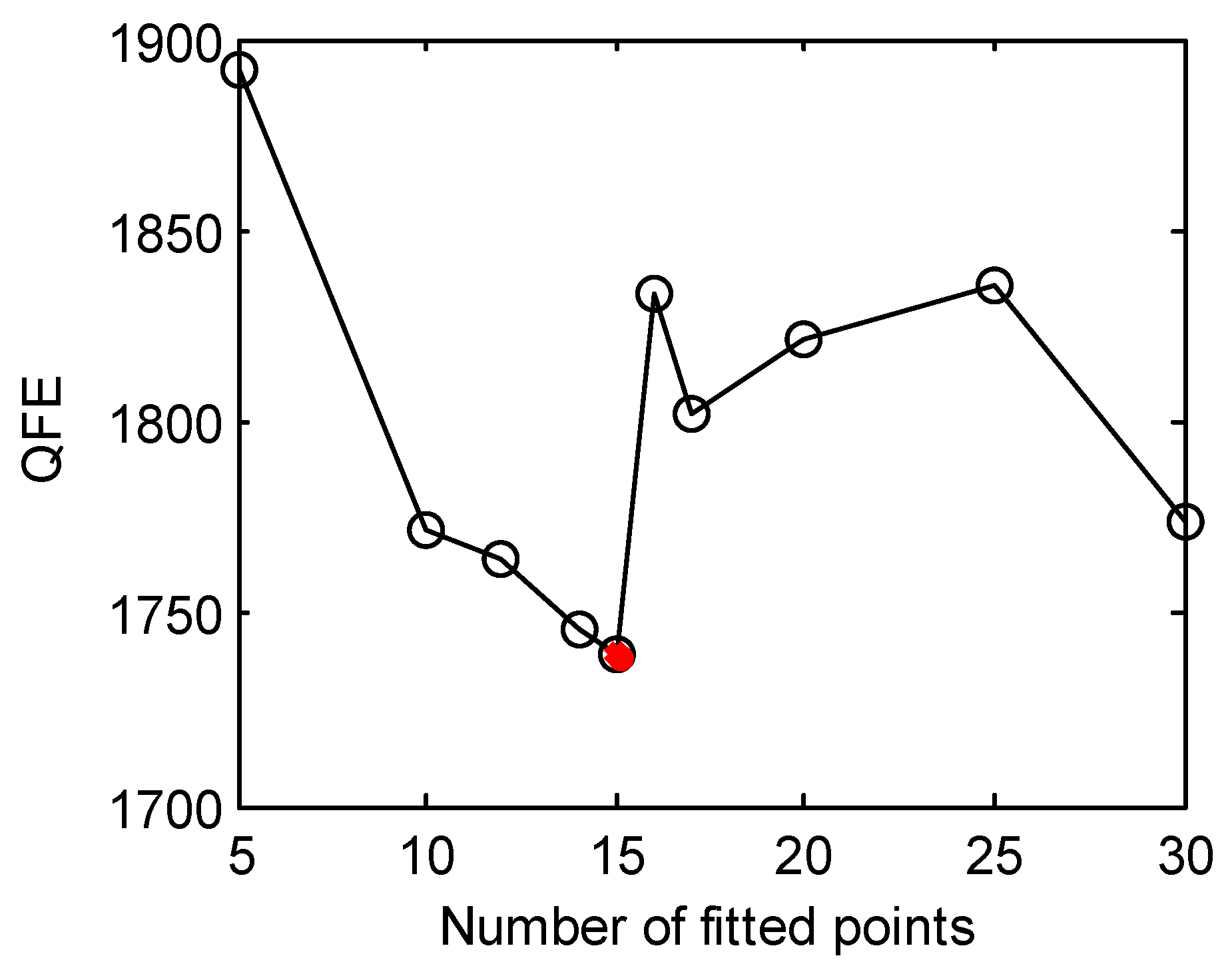
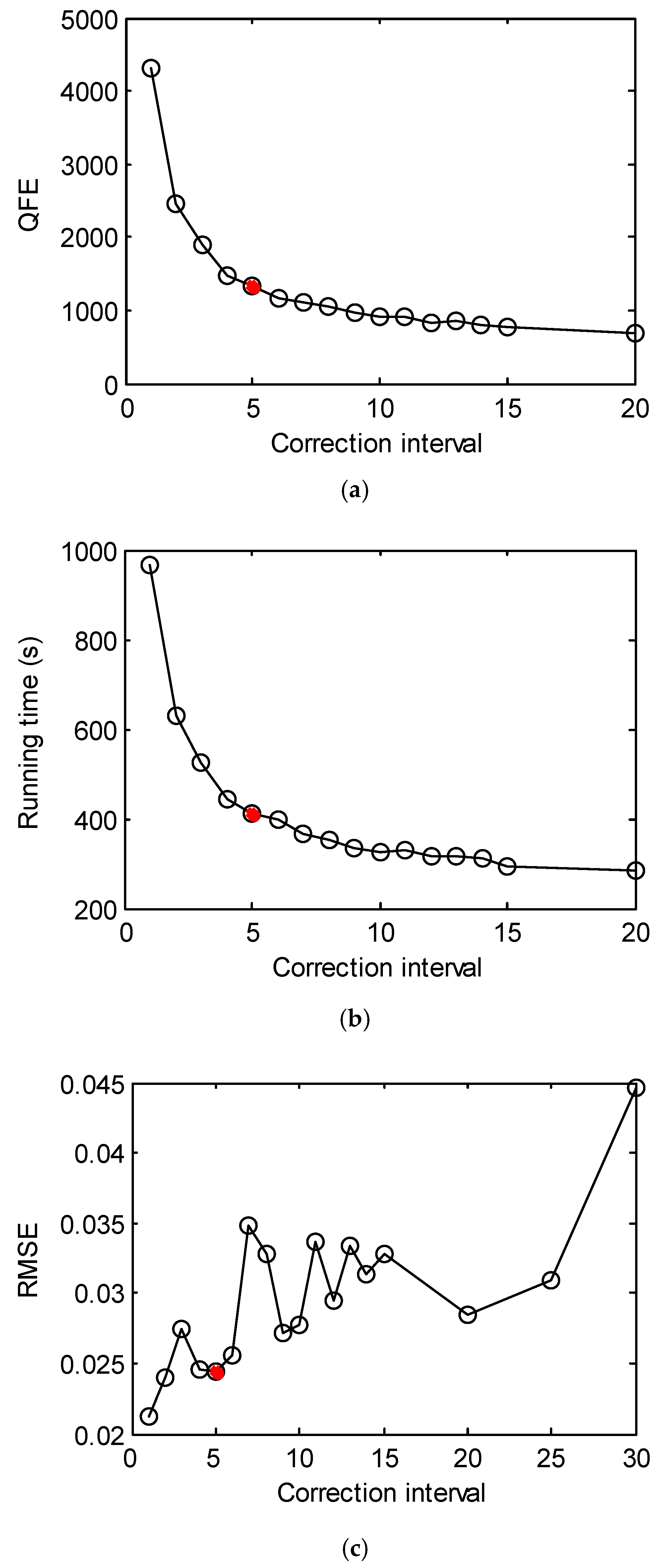
3.2. Solving the LSQ Inverse Problem with Different Numbers of Iterations
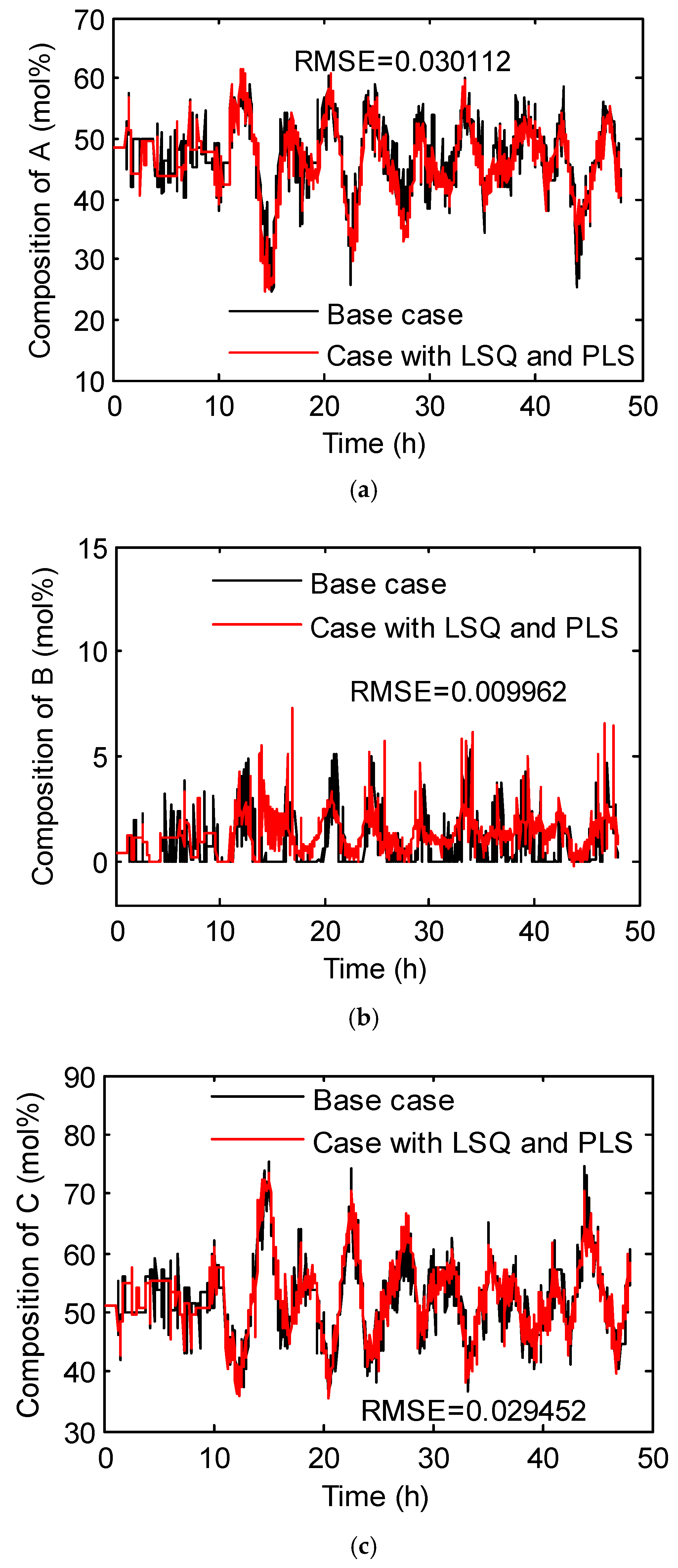
3.3. Hybrid Inverse Problem-Solving Strategy
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| a | Number of PLS components |
| B | Internal regression matrix of PLS |
| c | Output variable size of PLS |
| E, F | Residual matrix after input and output decomposition of PLS, respectively |
| h | Component index of PLS |
| l | Sample size |
| m | Number of measurable variables |
| n | Variable size of PLS |
| P, Q | Load vector of PLS input and output matrix, respectively |
| q | Element in load matrix of PLS output |
| Q | Fault detection statistic |
| r | Fault detection deviation |
| t, p | Element in score and load matrix of PLS input, respectively |
| T, U | Score matrix of PLS input and output matrix, respectively |
| u | Manipulated variable vector |
| v | Regression coefficient of component |
| w | Weight vector |
| x | State variable vector |
| X | Input matrix for PLS |
| y | Vector of measurable variables |
| Y | Output matrix for PLS |
| Greek Symbols | |
| θ | Fault parameter vector |
| α | Confidence |
| χ | Chi square distribution |
| ω | Disturbance vector |
| Superscripts | |
| * | Normalized |
| T | Transposition |
| ^ | Prediction value |
| Subscripts | |
| meas | Measured value |
| sim | Simulated value |
| Abbreviations | |
| ANN | Artificial neural networks |
| LSQ | Least squares |
| MIMO | Multiple input-multiple output |
| PLS | Partial least squares |
| QFE | Quantity of function evaluations |
| RMSE | Root mean square error |
References
- Jlassi, I.; Estima, J.O.; El Khil, S.K.; Bellaaj, N.M.; Cardoso, A.J.M. A Robust Observer-Based Method for IGBTs and Current Sensors Fault Diagnosis in Voltage-Source Inverters of PMSM Drives. IEEE Trans. Ind. Appl. 2017, 53, 2894–2905. [Google Scholar] [CrossRef]
- Sun, S.; Wei, X.; Zhang, H.; Karimi, H.R.; Han, J. Composite fault-tolerant control with disturbance observer for stochastic systems with multiple disturbances. J. Franklin Inst. 2018, 355, 4897–4915. [Google Scholar] [CrossRef]
- Ge, H.; Yue, D.; Xie, X. Observer-Based Fault Diagnosis of Nonlinear Systems via an Improved Homogeneous Polynomial Technique. Int. J. Fuzzy Syst. 2017, 20, 403–415. [Google Scholar] [CrossRef]
- Power, Y.; Bahri, P.A. A two-step supervisory fault diagnosis framework. Comput. Chem. Eng. 2004, 28, 2131–2140. [Google Scholar] [CrossRef]
- Mahmoud, H.; Abdallh, A.A.; Bianchi, N.; El-Hakim, S.M.; Shaltout, A.; Dupre, L. An Inverse Approach for Interturn Fault Detection in Asynchronous Machines Using Magnetic Pendulous Oscillation Technique. IEEE Trans. Ind. Appl. 2016, 52, 226–233. [Google Scholar] [CrossRef]
- Tian, W.; Sun, S.; Guo, Q. Fault detection and diagnosis for distillation column using two-tier model. Can. J. Chem. Eng. 2013, 91, 1671–1685. [Google Scholar] [CrossRef]
- Yu, H.; Khan, F.; Garaniya, V. Nonlinear Gaussian Belief Network based fault diagnosis for industrial processes. J. Process Control 2015, 35, 178–200. [Google Scholar] [CrossRef]
- Díaz, C.A.; Echevarría, L.C.; Prieto-Moreno, A.; Neto, A.J.S.; Llanes-Santiago, O. A model-based fault diagnosis in a nonlinear bioreactor using an inverse problem approach and evolutionary algorithms. Chem. Eng. Res. Des. 2016, 114, 18–29. [Google Scholar] [CrossRef]
- Lyu, T.; Xu, C.; Chen, G. Health state inversion of Jack-up structure based on feature learning of damage information. Eng. Struct. 2019, 186, 131–145. [Google Scholar] [CrossRef]
- Ramos, A.R.; de Lazaro, J.M.B.; Prieto-Moreno, A. An approach to robust fault diagnosis in mechanical systems using computational intelligence. J. Intell. Manuf. 2019, 30, 1601–1615. [Google Scholar] [CrossRef]
- Echevarría, L.C.; Velho, H.F.d.; Becceneri, J.C.; Neto, A.J.d.; Santiago, O.L. The fault diagnosis inverse problem with Ant Colony Optimization and Ant Colony Optimization with dispersion. Appl. Math. Comput. 2014, 227, 687–700. [Google Scholar] [CrossRef]
- Parolin, R.d.S.; Neto, A.J.d.S.; Rodrigues, P.P.G.W.; Santiago, O.L. Estimation of a contaminant source in an estuary with an inverse problem approach. Appl. Math. Comput. 2015, 260, 331–341. [Google Scholar] [CrossRef]
- Tarokh, M. Solving inverse problems by decomposition, classification and simple modeling. Inf. Sci. 2013, 218, 51–60. [Google Scholar] [CrossRef]
- Sever, A. A neural network algorithm to pattern recognition in inverse problems. Appl. Math. Comput. 2013, 221, 484–490. [Google Scholar] [CrossRef]
- Deshpande, A.P.; Patwardhan, S.C. Online Fault Diagnosis in Nonlinear Systems Using the Multiple Operating Regime Approach. Ind. Eng. Chem. Res. 2008, 47, 6711–6726. [Google Scholar] [CrossRef]
- Tian, W.; Guo, Q.; Sun, S. Dynamic simulation based fault detection and diagnosis for distillation column. Korean J. Chem. Eng. 2012, 29, 9–17. [Google Scholar] [CrossRef]
- Yin, S.; Zhu, X.; Kaynak, O. Improved PLS focused on key-performance-indicator-related fault diagnosis. IEEE Trans. Ind Electron. 2015, 62, 1651–1658. [Google Scholar] [CrossRef]
- Vitale, R.; Palaci-Lopez, D.; Kerkenaar, H.H.M. Kernel-Partial Least Squares regression coupled to pseudo-sample trajectories for the analysis of mixture designs of experiments. Chemom. Intell. Lab. Syst. 2018, 175, 37–46. [Google Scholar] [CrossRef]
- Choi, S.W.; Lee, I.-B. Multiblock PLS-based localized process diagnosis. J. Process Control 2005, 15, 295–306. [Google Scholar] [CrossRef]
- Zhang, Y.W.; Zhou, H.; Qin, S.J.; Chai, T.Y. Decentralized fault diagnosis of large-scale processes using multiblock kernel partial least squares. IEEE Trans. Ind. Inf. 2010, 60, 3–10. [Google Scholar] [CrossRef]
- Godoy, J.L.; Vega, J.R.; Marchetti, J.L. A fault detection and diagnosis technique for multivariate processes using a PLS-Decomposition of the measurement space. Chemom. Intell. Lab. Syst. 2013, 128, 25–36. [Google Scholar] [CrossRef]
- Downs, J.J.; Vogel, E.F. A plant-wide industrial process control problem. Comput. Chem. Eng. 1993, 17, 245–255. [Google Scholar] [CrossRef]
- Kayacan, E.; Ulutas, B.; Kaynak, O. Grey system theory-based models in time series prediction. Expert Syst. Appl. 2010, 37, 1784–1789. [Google Scholar] [CrossRef]
- Tserng, H.P.; Tserng, T.L.; Chen, P.C.; Tran, L.Q. A Grey System Theory-Based Default Prediction Model for Construction Firms. Comput.-Aided Civ. Infrastruct. Eng. 2015, 30, 120–134. [Google Scholar] [CrossRef]
- Yu, M.; Xiao, C.Y.; Jiang, W.H.; Yang, S.L.; Wang, H. Fault diagnosis for electromechanical system via extended analytical redundancy relations. IEEE Trans. Ind. Inf. 2018, 14, 5233–5244. [Google Scholar] [CrossRef]










| No. | Improvement Approach | Quantity of Function Evaluations | Cut Ratio (%) |
|---|---|---|---|
| 0 | base case | 1826 | - |
| 1 | linearly fitted initial values | 1790 | 1.97 |
| 2 | initial values provided with grey model | 1740 | 4.71 |
| 3 | one iteration only | 816 | 55.31 |
| 4 | partial least squares (PLS) mixed algorithm | 336 | 81.60 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, S.; Cui, Z.; Zhang, X.; Tian, W. A Hybrid Inverse Problem Approach to Model-Based Fault Diagnosis of a Distillation Column. Processes 2020, 8, 55. https://doi.org/10.3390/pr8010055
Sun S, Cui Z, Zhang X, Tian W. A Hybrid Inverse Problem Approach to Model-Based Fault Diagnosis of a Distillation Column. Processes. 2020; 8(1):55. https://doi.org/10.3390/pr8010055
Chicago/Turabian StyleSun, Suli, Zhe Cui, Xiang Zhang, and Wende Tian. 2020. "A Hybrid Inverse Problem Approach to Model-Based Fault Diagnosis of a Distillation Column" Processes 8, no. 1: 55. https://doi.org/10.3390/pr8010055
APA StyleSun, S., Cui, Z., Zhang, X., & Tian, W. (2020). A Hybrid Inverse Problem Approach to Model-Based Fault Diagnosis of a Distillation Column. Processes, 8(1), 55. https://doi.org/10.3390/pr8010055






