Abstract
Deadlock control approaches based on Petri nets are usually implemented by adding control places and related arcs to the Petri net model of a system. The main disadvantage of the existing policies is that many control places and associated arcs are added to the initially constructed Petri net model, which significantly increases the complexity of the supervisor of the Petri net model. The objective of this study is to develop a two-step robust deadlock control approach. In the first step, we use a method of deadlock prevention based on strict minimal siphons (SMSs) to create a controlled Petri net model. In the second step, all control places obtained in the first step are merged into a single control place based on the colored Petri net to mark all SMSs. Finally, we compare the proposed method with the existing methods from the literature.
1. Introduction
An automated manufacturing system (AMS) is a conglomeration of robots, machine tools, fixtures, and buffers. Several types of products enter the manufacturing system at separate points in time; the system can process these parts based on a specified sequence of operations and resource sharing. The sharing of resources leads to the occurrence of deadlock states, in which the local or global system is incapacitated [1,2,3,4]. Thus, an efficient deadlock-control algorithm is needed to prevent the deadlocks in an AMS. Petri nets are an excellent mathematical and graphical tool suitable for modeling, analyzing, and controlling deadlocks in AMSs [5,6]. The behavior and characteristics of an AMS (such as synchronization, conflict, and sequences) can be described by using Petri nets. Moreover, Petri nets may be used to provide the liveness and boundedness of a system [7]. To address the deadlock problem in AMSs, several approaches with Petri nets exist. These approaches are categorized into three strategies: (1) deadlock detection and recovery, (2) deadlock prevention, and (3) deadlock avoidance [7,8].
Traditionally, deadlock control approaches for AMS control are evaluated by using three criteria: structural complexity, computational complexity, and behavioral permissiveness [7]. Structural complexity means that a controller can be implemented with fewer monitors and arcs. When the computational complexity of a deadlock control approach is low, it can be applied to a large-scale system [7]. Behavioral permissiveness achieves high resource utilization in a controlled Petri net. Deadlock control may be implemented in AMS with reliable resources (resources without failures or breakdowns) or unreliable resources (resources with failures or breakdowns). For reliable resources, there are two main techniques to prevent deadlocks in AMSs using a Petri net: reachability graph analysis [9,10,11] and structural analysis [12,13]. The reachability graph analysis needs listing all or a part of the reachable markings of the Petri net model. There are two parts of the reachability graph: the deadlock zone (DZ) and the live zone (LZ). First-met bad markings (FBMs) are defined in and extracted from the DZ. In this case, the deadlock is eliminated by designing and adding a monitor to prohibit the first-met bad markings from being reached. In this process, all first-met bad markings can be prevented by using iterations [14]. Several policies have been developed to prevent deadlock states, including iterative methods, the theory of region, and siphon control [10,13,14,15,16,17,18,19]. The weakness of the reachability graph analysis is that the size of a reachability graph of a Petri net grows quickly and, in the worst case, grows exponentially with respect to the net size and its initial marking, and the net can easily reach an unmanageable level. Structural analysis is often applied to a typical structure of Petri nets, such as siphons. The control steps in this technique are simple: each minimal siphon is prohibited from being non-empty, and each unmarked minimal siphon needs an added monitor to ensure a system to be live. However, the weakness of this technique is that the number of control places will be increased when the size of a Petri net model is increased; hence, this results in high structural complexity [20].
In the literature, deadlock control approaches based on the structural analysis technique (siphons) for AMSs with the Petri nets framework can be implemented by inserting the control places and the associated arcs to the original net, so that its siphons are permanently non-empty. The main disadvantage of the current policies is that many control places and associated arcs are inserted into the original Petri net model, which leads to the increased complexity of the supervisor of the Petri net model, compared with the initial model for the Petri net supervisor. Hence, an efficient approach is needed to minimize the Petri net supervisors’ structural complexity for AMS. The objective of this study is to develop a two-step robust deadlock control policy. A technique based on SMSs developed in [21] is used in the first phase to develop a controlled Petri net model. In the second step, all control places obtained in the first step are merged into one control place based on colored Petri nets to make all SMSs marked.
The rest of the paper is organized as follows. Basic concepts of Petri nets are introduced in Section 2. Section 3 describes a deadlock prevention approach based on the SMS and the proposed robust control based on colored Petri nets. Section 4 shows an example from the literature. Finally, Section 5 presents conclusions and future research.
2. Preliminaries
This section introduces the basics of Petri nets and a general Petri net simulator (GPenSIM) tool.
2.1. Basics of Petri Nets
Let N = (P, T, F, W) be a Petri net, where P and T are finite non-empty sets of places and transitions, respectively. Elements in P ∪ T are named nodes. Here, P ∪ T ≠ ∅ and P ∩ T = ∅; P and T are depicted by circles and bars, respectively. Next, F ⊆ (P × T) ∪ (T × P) is the set of directed arcs that join the transitions with places (and vice versa), W: (P × T) ∪ (T × P) →IN is a mapping that assigns an arc’s weight, where IN = {0, 1, 2, …}.
N is known as an ordinary net if ∀ (p, t) ∈ F, W (p, t) = 1, where N = (P, T, F). N is named a weighted net if there is an arc between x and y such that W (x, y) > 1. Let N = (P, T, F, W) and node a ∈ P ∪ T. Then, ·a = {b ∈ P ∪ T | (b, a) ∈ F} is named the preset of node a, and a· = {b ∈ P ∪ T | (a, b) ∈ F} is named the postset of node a.
A marking M of N is a mapping M: P → IN. Next, (N, Mo) is a marked Petri net (PN), represented as PN = (P, T, F, W, Mo), where the initial marking of PN is Mo: P → IN. A transition t ∈ T is enabled at marking M if for all p ∈ ·t, M (p) ≥ W (p, t), which is denoted as M [. When a transition t fires, it takes W (p, t) token (s) from each place p ∈ ·t, and adds W (t, p) token (s) in each place p ∈ t·. Thus, it reaches a new marking M′, denoted as M [ M′, where M′(p) = M (p) − W (p, t) + W (t, p).
We call N self-loop free if for all a, b ∈ P ∪ T, W (a, b) > 0 implies W (b, a) = 0. Let [N] be an incidence matrix of net N, where [N] is an integer matrix that consists of |T| columns and |P| rows with [N] (p, t) = W (t, p) − W (p, t). The set of markings that are reachable from M in N is named the set of reachability of the Petri net model (N, M) denoted by R (N, M).
Let (N, Mo) be a marked Petri net. A transition t ∈ T is live if for all M ∈ R (N, M), there exists a reachable marking M′ ∈ R (N, M) such that M′[ holds. A transition is dead at Mo if there does not exist t ∈ T such that Mo [ holds. M′ is said to be reachable from M if there exists a finite transition sequence δ = t1 t2 t3 … tn that can be fired, and markings M1, M2, M3, …, and Mn−1 such that M [ M1 [ M2 [ M2 … Mn−1 [ M′, denoted as M [ M′, satisfies the state equation M′ = M + [N] , where : T → IN maps t in T to the number of appearances of t in δ and is called a Parikh vector or a firing count vector.
Let (N, Mo) be a marked Petri net. It is said to be k-bounded if for all M ∈ R (N, M0), for all p ∈ P, M(p) ≤ k (k ∈ {1, 2, 3, …}). A net is safe if all of its places are safe, i.e., in each place p, the number of tokens does not exceed one. In other words, a net is k-safe if it is k-bounded.
P-vectors (place vectors) and T-vectors (transition vectors) are column vectors. A P-vector I: P → Z cataloged by P is said to be a place invariant or P-invariant if I ≠ 0 and IT. [N] = 0T, and a T-vector J: T → Z cataloged by T is said to be a transition invariant or T-invariant if J ≠ 0 and [N]. J = 0, where Z is the set of integers.
When each element of I is nonnegative, place invariant I is called a place semiflow or P-semiflow. Assume that I is a P-invariant of a net with (N, Mo) and M is a marking reachable from the initial marking Mo. Then, ITM = ITMo. Let ||I|| = {p |I(p) ≠ 0} be the support of P-invariant I.
The supports of P-invariant I are classified into three types: (1) ||I||+ is the positive support of P-invariant I with ||I||+= {p|I (p) > 0}. (2) ||I||− is the negative support of P-invariant I with ||I||− = {p |I(p) < 0}. (3) I is a minimal P-invariant if ||I|| is not a superset of the support of any other one and its components are mutually prime. Let li be the coefficients of P-invariant I if for all pi ∈ P, li = I(pi).
A colored Petri net (CPN) is described as a nine-tuple CPN = (P, T, F, SC, Cf, Nf, Af, Gf, If), where
- P and T are finite nonempty sets of places and transitions, respectively, assuming P ∩ T = ∅. F is a set of flows (arcs), from pi ∈P to tj ∈T and from ti ∈ T to pj ∈ P.
- SC is a color set that contains colors ci and the operations on the colors.
- Cf is the color function that maps pi ∈P into colors ci ∈ SC.
- Nf is the node function that maps F into (P × T) ∪ (T × P).
- Af is the arc function that maps each flow (arc) f ∈ F into the term e.
- Gf is the guard function that maps each transition ti ∈ T to a guard expression g that has a Boolean value.
- If is the initialization function that maps each place pi ∈ P into an initialization expression.
2.2. GPenSIM Tool
GPenSIM was developed by R. Davidrajuh (the fourth author of our paper) and runs in MATLAB. GPenSIM has been designed to model, control, simulate, and analyze discrete event systems [22]. GPenSIM enables the integration of Petri net models with other toolboxes in MATLAB (e.g., “Control systems” and “Fuzzy logic”). Table 1 shows the advantages and disadvantages of GPenSIM compared to CPN Tools [23]. Compared to the CPN tools, it is simpler to create a colored Petri net in GPenSIM. For instance,

Table 1.
The advantages and disadvantages of GPenSIM compared to CPN Tools.
- Being versatile, CPN allows manipulation of the functions Cf, Nf, Af, Gf, and If independently. However, being simple and crude, these functions (Cf, Nf, Af, Gf, and If) are merged together in GPenSIM and are coded in the preprocessor files. Hence, GPenSIM allows fewer degrees of freedom when developing a model.
- In CPN tools, it is possible to impose logical constraints on places, transitions, and arcs. In GPenSIM, logical expressions can only be processed by transitions. Inevitably, this means GPenSIM poses restrictions in modeling compared to CPN. However, this is the price paid for achieving simplicity in GPenSIM (easiness in learning, using, and extending).
- The arc weights can dynamically alter in CPN tools because of the logic conditions connected to it. GPenSIM does not allow dynamic nets (e.g., dynamic arcs, run-time removal of places and transitions). Once a Petri net is defined in the Petri net definition file (PDF), it cannot be changed.
To model, simulate, analyze, and control the Petri net models in GPenSIM, three files should be coded: Petri net definition file (PDF), main simulation file (MSF), and pre- and postprocessor files.
- PDF defines the static elements of a Petri net (places, transitions, and arcs).
- Before the simulation starts, MSF loads a PDF into memory and the workbench, and then the simulation begins. During the simulation runs, MSF will be blocked; the control will be handed back to MSF together with the simulation results when the simulation is finished. Consequently, MSF has no control over what happens during the simulation.
- Pre-and postprocessors will be called during the simulation before and after firing of the transition. The preprocessor will inspect if the conditions of firing for a certain transition are met, and the postprocessor will execute post-firing activities if needed after a certain transition has been fired. These can be used to control the runtime of the system, as they are called during the simulation.
All tokens are homogeneous inside a place. It does not matter which token is first or last to arrive at the place. Similarly, it does not matter by which transition a token is deposited at the place. However, GPenSIM introduces the token colors. Each token can become identifiable and unique with a unique token identification number (tokID). Moreover, we can add some tags (“colors”) to each token. The following problems are crucial when using colors in GPenSIM:
- Only transitions can manipulate colors: the colors of the output tokens can be added, deleted, or changed in the preprocessor.
- By default, colors are inherited: the system gathers all colored tokens from the input places when a transition fires and then transfers the colored tokens to the output places. However, color inheritance can be avoided by overriding.
- An enabled transition may choose certain color-based input tokens.
- An enabled transition may choose certain time-based input tokens (e.g., when the creation time of the tokens is known).
- A token has the following structure: tokID, time of creation, and color setting.
- tokID: a single token identifier (integer value).
- creation_time: the transition time (real value) when the token was produced. Importantly, this time may differ when the transition actually deposited the token in an output place.
- t_color (text string set) is a color setting.
There are several GPenSIM functions used for color manipulation. One of the functions used in this study is tokenEXColor, which can be expressed as follows:
[set_of_tokID,nr_token_av] = tokenEXColor (place, nr_tokens_wanted, t_color), where the function requires three input arguments and returns two output values.
- Input arguments:
- (place, nr_tokens_wanted, t_color):
- Place: from which place the tokens are to be selected.
- nr_tokens_wanted: the number of required tokens with the specified color.
- t_color: a set of colors.
- Output values:
- [set_of_tokID,nr_token_av]
- set_of_tokID: a set of tokIDs that meet the color specifications. The set length of tokIDs is equal to the input argument of nr_tokens_wanted.
- nr_token_av: the number of valid tokIDs available in set_of_tokID; the set may have trailing zeros to match the length of nr_tokens_wanted.
3. Deadlock Prevention Policy Based on SMSs and Colored Petri Nets
In this section, we use a deadlock-prevention approach based on strict SMSs to design a controlled Petri net model. This approach is adopted from Ezpeleta et al. [1].
Definition 1
[23]. A PN N = (PA ∪ {p0}, T, F) is said to be a simple sequential process (S2P), if: (1) N is a strongly connected state machine and (2) each circuit N includes place p0, where p0 is named the idle process place and PA ≠ ∅ is an operation places set.
Definition 2
[23]. A PN N = ({p0} ∪ PA ∪ PR, T, F) is said to be a simple sequential process with resources (S2PR) such that:
- 1.
- The subnet generated by X = PA ∪ {p0} ∪ T is an S2P.
- 2.
- PR ≠ ∅ and (PA ∪ {p0}) ∩ PR = ∅, where PR is a resource places set.
- 3.
- ∀p ∈ PA, ∀t ∈.p, ∀t′ ∈ p.,rp ∈ PR, .t ∩ PR = t′. ∩ PR = {rp}.
- 4.
- ∀r ∈ PR, .r ∩ PA = r. ∩ PA ≠ ∅ and .r ∩ r. ≠ ∅.
- 5.
- (p0) ∩ PR = (p0). ∩ PR ≠ ∅.
Definition 3
[23]. Let N = ({p0} ∪ PA ∪ PR, T, F) be an S2PR, and Mo be an initial marking of N. An S2PR with such a marking is said to be acceptably marked if (1) Mo(p0) ≥ 1, Mo(r) ≥ 1, ∀r ∈ PR, and (3) Mo(p) = 0, ∀p ∈ PA.
Definition 4
[23]. A system of S2PR, named S3PR for abbreviation, is defined recursively as follows:
- 1.
- An S2PR is as well an S3PR
- 2.
- Let N1 and N2 be two S3PRs, where N1 = ({p01} ∪ PA1 ∪ PR1, T1, F1) and N2 = ({p02} ∪ PA2 ∪ PR2, T2, F2), such that ({p01} ∪ PA1) ∩ ({p02} ∪ PA2) = ∅, PA1 ∩ PA2 ≠ PC, PR1 ∩ PR2 = PC and T1 ∩ T2 ≠ ∅. Then, the net N = ({p0} ∪ PA ∪ PR, T, F) is also an S3PR resulting from the composition of N1 and N2 via the set of common PC and defined as follows: (1) p0 = {p01} ∪ {p02}, PR = PR1 ∪ PR2, PA = PA1 ∪ PA2, T = T1 ∪ T2, F = F1 ∪ F2.
The composition of n S2PR N1-Nn via PC, is denoted by . is used to denote the S2P from which the S2PR Ni is formed.
Definition 5
[23]. Let N = ({p0} ∪ PA ∪ PR, T, F) be an S3PR. Mo is an initial marking of N. (N, Mo) is said to be an acceptably marked S3PR if (1) (N, Mo) is an acceptably marked S2PR, (2) N = N1 N2, where (Ni, Moi) is said to be an acceptably marked S3PR and
- ∀p ∈ PAi ∪ {p0i}, Mo (p) = Moi (p), ∀i ∈ {1,2}.
- ∀r ∈ PRi PC, Mo(r) = Moi (r), ∀i ∈ {1,2}.
- ∀r ∈ PRi, Mo (p) = max {Mo1 (r), Mo2 (r)}, ∀i ∈ {1,2}.
Definition 6
[23]. Let N be an S3PR, A non-empty set S ⊆ P is said to be a siphon in N if · ⊆ ·. When a siphon does not include other siphons, it is said to be a minimal siphon.
Definition 7
[24]. Let S be a minimal siphon in an S3PR N. A minimal siphon S is said to be strict if · ·. Let = {S1, S2, S3, …, Sk} be a set of SMSs of N. We have = A R, R = PR, and A = \ R, where A denotes the places of operations and R denotes the places of resources.
Definition 8
[23]. Let r ∈ PR be a reliable resource place in an S3PR N. The operation places that use r are known as the set of holders of r, indicated by H(r) = {p\p ∈ PA, p ∈ .r ∩ PA ≠ ∅}. is said to be the complementary set of S if .
Definition 9
[24]. Let (Na, Ma) and (Nb, Mb) be marked Petri nets; Ni = (Pi, Ti, Fi, Wi), where i = a, b. We call (N, M) with N = (P, T, F, W) a synchronous net resulting from the integration of (Na, Ma) and (Nb, Mb) and denote it as (Na, Ma) ∥ (Nb, Mb) when the following conditions are satisfied: (1) P = Pa ∪ Pb, and Pa ∩ Pb = ∅. (2) T = Ta ∪ Tb. (3) F = Fa ∪ Fb. (4) W (e) = Wi (e), where e ∈ Fi, i= a, b. (5) M(p) = Mi (p), where p ∈ Pi, i = a, b.
Definition 10
[25]. Let (N, Mo) be an S3PR with N = (PA ∪ {p0} ∪ PR, T, F, Mo). The deadlock controller for (N, Mo) developed by Ezpeleta et al. [1] is denoted as (V, MVo) = (PV, TV, FV, MVo), where (1) PV = {VS \ S ∈ } is a set of control places. (2) TV = {t \ t ∈ ·VS ∪VS·}. (3) FV ⊆ (PV × TV) ∪ (TV × PV) is the set of directed arcs that join the control places with transitions (and vice versa). (4) For all VS ∈ PV, MVo (VS) = MVo (S) – 1, where MVo (VS) is called an initial marking of a control place VS.
We call (NV, MVo) a controlled Petri net model resulting from the integration of (V, MVo) and (N, Mo), denoted as (V, MVo) ∥ (N, Mo). A control place or monitor is inserted to each SMS to ensure the liveness of a Petri net, and all SMSs can never be unmarked. The proposed policy is simple and guarantees success. However, it leads to a more complex Petri-net-controlled system than the original Petri net model, because the number of added monitors is equal to that of the SMSs in the target Petri net model, and the number of associated arcs is larger than that of the added monitors. According to the strict minimal siphon concept, the developed deadlock prevention approach proposed by [1] is described by Algorithm 1.
| Algorithm 1: Strict minimal siphon-based algorithm |
| Input: Original S3PR Petri net model (N, Mo) |
| Output: Controlled net (NV, MVo). |
| Step 1: Compute the set of SMS for N. |
Step 2: for each S ∈ do
|
| end for |
| Step 3: Output a controlled net (NV, MVo). |
| Step 4: End |
Consider the S3PR Petri net model shown in Figure 1. The Petri net model involves eleven places and eight transitions. The places can be described as the following set partition: P0 = {p1, p8}, PR = {p9, p10, p11}, and PA = {p2, p3, …, p7}. The model has 20 reachable markings and eight minimal siphons, three of which are SMSs. The siphons are S1 = {p4, p7, p9, p10, p11}, S2 = {p4, p6, p10, p11}, and S3= {p3, p7, p9, p10}. According to Definitions 2, 3, and 5
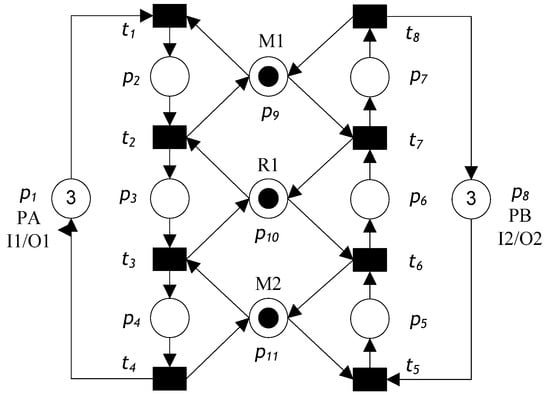
Figure 1.
S3PR Petri net model of an AMS.
- (1)
- For S1: SA = {p4, p7}, SR = {p9, p10, p11}, H (p9) = {p2, p7}, H (p10) = {p3, p6}, H (p11) = {p4, p5}, [S1] = {p2, p3, p5, p6}, ·VS1 = {t3, t7}, VS1· = {t1, t5}, and MVo (VS1) = 2.
- (2)
- For S2: SA = {p4, p6}, SR = {p10, p11}, H (p10) = {p3, p6}, H (p11) = {p4, p5}, [S2] = {p3, p5}, ·VS2 = {t3, t6}, VS2· = {t2, t5}, and MVo (VS2) = 1.
- (3)
- For S3: SA = {p3, p7}, SR = {p10, p11}, H (p10) = {p3, p6}, H (p11) = {p4, p5}, [S3] = {p2, p6}, ·VS3 = {t2, t7}, VS3· = {t1, t5}, and MVo (VS3) = 1.
After monitors have been added using Algorithm 1, we obtain the controlled Petri net model shown in Figure 2.
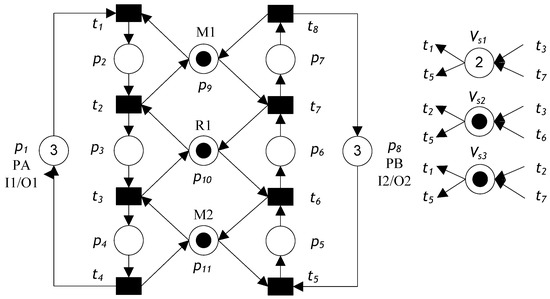
Figure 2.
Controlled S3PR Petri net model.
Definition 11.
Let (N, Mo) be an S3PR with N = (PA ∪ {p0} ∪ PR, T, F, Mo). The deadlock controller for (N, Mo) developed in Ezpeleta et al. [1] is denoted as (V, MVo) = (PV, TV, FV, MVo). Here, (V, MVo) can be reduced and replaced by a colored common deadlock control subnet, which is a PN NDC = ({pcombined}, {TDCi ∪ TDCo}, FDC, Cvsi), where pcombined is called the merged control place of all monitors PV = {VS \ S ∈ }. TDCi = {t \ t ∈ •VS}. TDCo = {t \ t ∈ VS•}. FDC ⊆ ({pcombined}× {TDCi ∪ TDCo}) ∪ ({TDCi ∪ TDCo}× {pcombined}) is the set of arrows that join the merged control place with transitions (and vice versa). Ccri is the color that maps pcombined into colors Cvsi ∈ SC, where SC = ∪i∈Vs {Cvsi}. (NDC, MDCo) is called a colored common deadlock control subnet. For all VS ∈ PV, MDCo (pcombined) = ∑MVo(VS), where MDCo (pcombined) is an initial token with the colors marking of the merged monitor.
Figure 3 shows pcombined, the merged control place of all monitors PV of the controlled Petri net model from Figure 2, according to Definition 6.
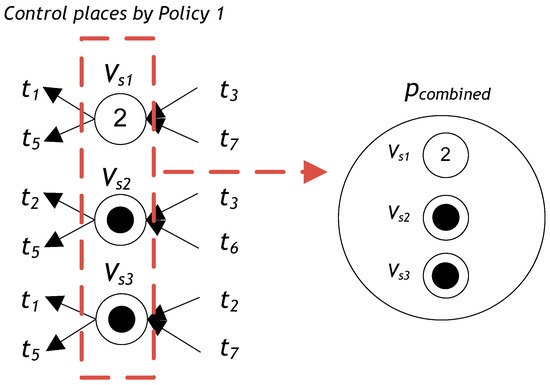
Figure 3.
Merged control place for all monitors PV.
The output arcs of pcombined are connected to the source transitions TDCo, which lead to the sink transitions of S. Transitions Vsi• for all monitors PV augmented from Algorithm 1 are defined as VS1· = {t1, t5}, VS2· = {t2, t5}, and VS3· = {t1, t5}. Thus, TDCo can be denoted as TDCo = ∪i∈Vs{VSi·}, so TDCo = {2t1, t2, 3t5}, as shown in Figure 4.
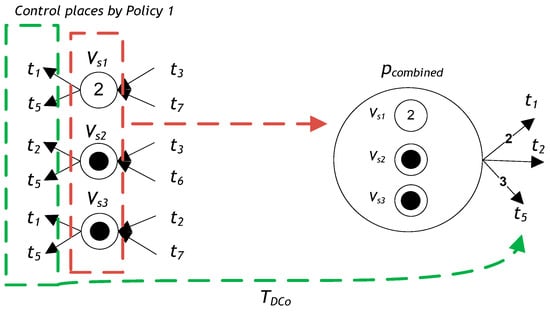
Figure 4.
Output arcs of pcombined for all monitors PV.
The input arcs of pcombined are connected with the output of , denoted as TDCi. Transitions ·Vsi for all monitors PV augmented from Algorithm 1 are defined as ·Vs1 = {t3, t7}, ·Vs2 = {t3, t6}, and ·Vs3 = {t2, t7}. Thus, TDCi can be represented by TDCi = ∪i∈Vs{·Vsi}, so TDCi = {t2, 2t3, t6, 2t7}, as shown in Figure 5.
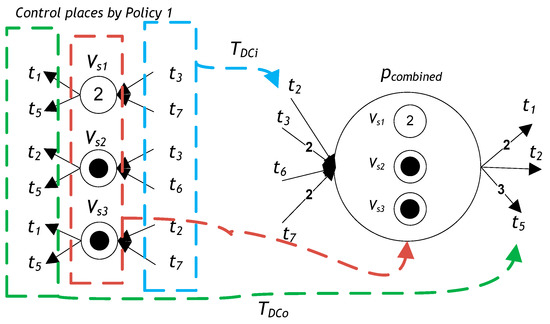
Figure 5.
Output arcs of pcombined for all monitors PV.
Moreover, MDCo (pcombined) = ∑MVo (VS) = MVo (VS1) + MVo (VS2) + MVo (VS3) = 2 + 1 + 1 = 4. Thus, in the model of the Petri net from Figure 2, we have three color types: SC = {Cvs1, Cvs2, Cvs3}. Therefore, the total number of colored tokens is 4: we have two tokens of Cvs1 color, one token of Cvs2 color, and one token of Cvs3 color, as shown in Figure 6.
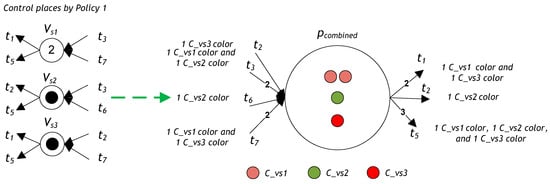
Figure 6.
Merged controller for all monitors PV.
Definition 12.
Let (N, Mo) be an S3PR with N = (PA ∪ {p0} ∪ PR, T, F, Mo) and (NDC, MDCo) a deadlock controller for (N, Mo) created by Definition 11 with NDC = {pcombined}, {TDCi ∪ TDCo}, FDC, Cvsi, MDCo). We call (NC, MCo) a controlled marked Petri net, denoted as (NC, MCo) = (N, Mo) ∥ (NDC, MDCo) and called the composition of (N, Mo) and (NDC, MDCo), where NC = (PA ∪ {p0} ∪ PR ∪ {pcombined}, T ∪ TDCi ∪ TDCo, F ∪ FDC, CR, MCo) be a colored controlled marked S3PR, and R(NC, MCo) be its reachable graph.
Theorem 1.
The colored controlled net (NC, MCo) is live.
Proof.
We must prove that all transitions T, TDCi, TDCo in (NC, MCo) are live. No strict minimal siphon is emptied. In addition, no new strict minimal siphon is created, since all t1 ∈ T are live. For all t2 ∈ TDCi; if ∀pi ∈ t2, MC(pi) > 0, then t2 can fire in any case because it is uncontrollable. Thus, MC (pcombined) > 0, for all t3 ∈ TDCo, if MC (pcombined) > 0, then t3 can fire. Therefore, controlled net (NC, MCo) is live. □
According to the concepts of SMSs and colored Petri nets, the developed policy is stated in Algorithm 2.
| Algorithm 2: Integrated Strict Minimal Siphon And Colored Petri Nets-Based Algorithm |
| Input: Petri net models (N, Mo) and (V, MVo). |
| Output: Colored controlled S3PR Petri net (NC, MCo). |
Step 1: Combine all monitors PV into one monitor (pcombined), considering the following steps:
|
| Step 2: Insert the combined monitor into the Petri net model (N, Mo). The obtained net is denoted as (NC, MCo). |
| Step 3: Output (NC, MCo). |
| Step 4: End |
Figure 7 shows the proposed single controller for the controlled Petri net model from Figure 2 by using Algorithm 2. In the net shown in Figure 7, when transition t1 fires, the system selects only one token from input place p1, one token from resource place p9, one token of color Cvs1 from pcombined, and one token of color Cvs3 from pcombined, and it transfers them into p2. Moreover, when transition t2 fires, the system selects only one token from operation place p2, one token from resource place p10, and one token of color Cvs2 from pcombined and transfers them into p3. When transition t5 fires, the system selects only one token from input place p8, one token from resource place p11, one token of color Cvs2 from pcombined, one token of color Cvs2 from pcombined, and one token of color Cvs3 from pcombined and transfers them into p5. When transition t2 fires, it creates a color Cvs3 on the tokens from p2 and p10 and transfers them into common place pcombined. In addition, when the transition t3 fires, it creates two colors Cvs1 and Cvs2 on the tokens from p3 and p11 and transfers them into place pcombined. Moreover, when transition t6 fires, the system creates a color Cvs2 on the tokens from p5 and p10 and transfers them into place pcombined. Finally, when transition t7 fires, the system creates two colors Cvs1 and Cvs3 on the tokens from p6 and p9 and transfers them into pcombined.
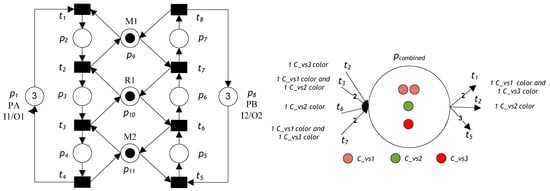
Figure 7.
Colored controlled S3PR Petri net model Algorithm 2.
By default, colors are inherited: when a transition TDCo fires, the system gathers all colored tokens from the input place pcombined and then transfers these colored tokens to the output place pi. However, color inheritance can be prohibited by overriding.
After implementing a Petri net model shown in Figure 7 by using the GPenSIM code, we usually obtain three files: the Petri net definition file (PDF), common processor file (COMMON_PRE file), and main simulation file (MSF). Figure 8 shows the resulting PDF file and defines the static Petri net model by declaring the sets of places, transitions, and arcs. Figure 9 shows the MSF file used to compute the simulation results. Figure 10 displays the resulting MSF COMMON_PRE file and defines the conditions for the enabled failure and recovery transitions to start firing based on the colored tokens, mean time to failure, and mean time to repair.
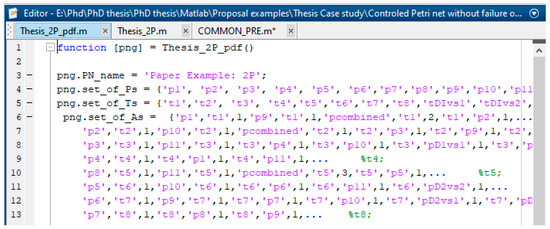
Figure 8.
PDF file of the colored controlled S3PR Petri net model from Figure 7.
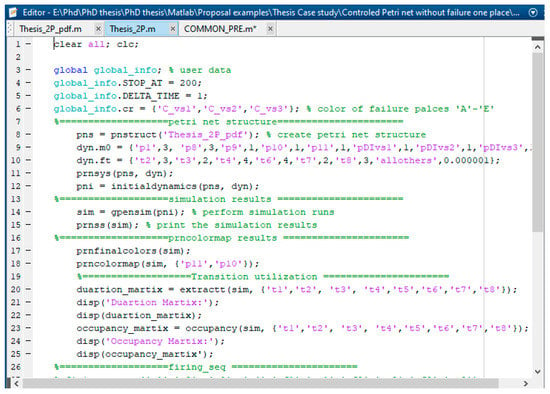
Figure 9.
Part of the MSF file of the colored controlled S3PR Petri net model from Figure 7.
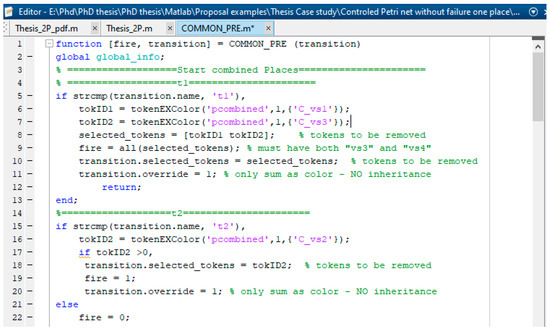
Figure 10.
Part of the COMMON_PRE file of the colored controlled S3PR Petri net model from Figure 7.
To make the work more solid and well-positioned, we have developed a Trust-based colored controlled Petri net (TCCPN) [26,27,28,29] and comparing the proposed work with relevant TCCPNs.
Definition 13.
Let (N TM, M TMo) be a Trust-based colored controlled Petri net (TCCPN) S3PR with NTM = (PA ∪ {p0} ∪ PR ∪ {pcombined}, T ∪ TDCi ∪ TDCo, F ∪ FDC, CR, η, τ, ψ, MTMo), and R (N TM, MTMo) be its reachable graph, where
- 1.
- η is the arcs weight, which denotes the importance or probability of input arcs into a transition. If there is an arc (p, t), η (p, t) = c indicates there is a probability of η (p, t) encouraging the token entering t from p. If the token has a capacity h, the new capacity will be h * c.
- 2.
- τ is a time guard for transition t ∈ (T ∪ TDCi ∪ TDCo), τ: t → [e, f], τ (t) indicates transition t can only fire during e and f. Particularly, if e = f, that indicates the transition can only occur through e.
- 3.
- ψ is the threshold of token in p ∈ (PA ∪ {p0} ∪ PR ∪ {pcombined}), ψ: p → R, and R is a real type data. Ψ (p) = r1, indicates when the number of tokens in p is less than or equal to r1, p can reach a new position.
To model a TCCPN, there are many types of factors that can have an influence on trust in colored controlled net S3PR, and a non-negative real number can represent the value of each factor type. An assessment process will consume factors for aggregating a new trust value. We use Ein to characterize the input factors consumed and use Eout to characterize the aggregation trust value. For an assessment process APk, Ein(APk) is related to the input place and Eou (APk) is related to the output place. There are rules for firing transitions in a TCCPN and are stated as below:
Definition 14.
Let (N TM, M TMo) be a Trust-based colored controlled Petri net (TCCPN) S3PR with NTM = (PA ∪ {p0} ∪ PR ∪ {pcombined}, T ∪ TDCi ∪ TDCo, F ∪ FDC, CR, η, τ, ψ, MTMo), a transition Tk under the marking M can be fired when the following conditions are satisfied:
- 1.
- t ∈ τ(Tk)
- 2.
- Ein(APk) > 0
- 3.
- Eout(APk) ≥ Ψ(pi)
- 4.
- for all p ∈ ·t, M(p) ≥ W (p, t)
where τ(t) is the valid firing time in TCCPN, and Ein (APk) is the current value of the token in the input place. Eout (APk) is the current value of the token in the output place, and Ψ (pi) is the threshold for entering pi. Note that an assessment process APk may have more than one input place and output place.
In addition, there are rules for new markings, when a transition t fires, a token value can be changed and it will be kept in a new place because of the threshold, Eout(APk) = ηi * Eini(APk), where nf is the number of input factors. Then, the new marking will be changed as M′(p) = M(p) − W(p, t) + W(t, p). In order to demonstrate the TCCPN, reconsider Figure 7, it describes a system as follows:
- τ(t): τ(t1) = 0, τ(t2) = 3, τ(t3) = 2, τ(t4) = 4, τ(t5) = 0, τ(t6) = 4, τ(t7) = 5, τ(t8) = 3;
- Mo = (p1 p2 p3 p4 p5 p6 p7 p8 p9 p10 p11 pcombined) = (3 0 0 0 0 0 0 3 1 1 1 4);
- Assessment process is a combined place Apcombined
- The input assessment process is Tk = {t2,2t3, t6, 2t7}
- The importance on arcs: η (p2, t2) = 0.5, η(p10, t2) = 0.5, η(p3, t3) = 0.5, η(p11, t3) = 0.5, η(p5, t6) = 0.5, η(p10, t5) = 0.5, η(p6, t7) = 0.5, η(p9, t7) = 0.5
- The factors’ values of Ein (Apcombined): if t2 enabled, Ein1(Apcombined) = (1, 1), if t3 enabled, Ein2(Apcombined) = (2, 2), if t6 enabled, Ein3(Apcombined) = (1, 1), if t7 enabled, Ein4(Apcombined) = (2, 2).
- Ψ(p): Ψ(p1) = 0, Ψ(p2) = 0, Ψ(p3) = 0, Ψ(p4) = 0, Ψ(p5) = 0, Ψ(p6) = 0, Ψ(p7) = 0, Ψ(p8) = 0, Ψ(p9) = 0, Ψ(p10) = 0, Ψ(p11) = 0, and Ψ (pcombined) ≤ 4
Places p1, p2, p3, p4, p5, p6, p7, p8, p9, p10 and p11 obtain tokens unconditionally, their thresholds are set as zero. t2, t3, t6, t7 represent the four transitions that can fire. If any of four transitions fires, new tokens with colors are built. For example, when transition t2 fires, it creates a color Cvs3 on the tokens from p2 and p10 and transfers them into common place pcombined. For transition t2, there are two factors: p2 and p10
Eout(Apcombined) = ηi * Eini (Apcombined) = η1* Ein1(Apcombined) + η2* Ein2(Apcombined) = 0.5*1 + 0.5*1= 1. Since if the current tokens in pcombined place + 1 ≤ 4, pcombined can be reached.
If transition t3 fires, it creates colors Cvs1 and Cvs2 on the tokens from p3 and p11 and transfers them into common place pcombined. For transition t3, there are two factors: p3 and p11
Eout(Apcombined) = ηi * Eini (Apcombined) = η1* Ein1(Apcombined) + η2* Ein2(Apcombined) = 0.5*2 + 0.5*2 = 2. Since if the current tokens in pcombined place + 2 ≤ 4 pcombined can be reached.
When transition t6 fires, it creates a color Cvs2 on the tokens from p5 and p10 and transfers them into common place pcombined. For transition t6, there are two factors: p5 and p10
Eout(Apcombined) = ηi * Eini(Apcombined) = η1* Ein1(Apcombined) + η2* Ein2(Apcombined) = 0.5*1 + 0.5*1 = 1. Since if the current tokens in pcombined place + 1 ≤ 4 pcombined can be reached.
If transition t7 fires, it creates colors Cvs1 and Cvs3 on the tokens from p6 and p9 and transfers them into common place pcombined. For transition t7, there are two factors: p6 and p9
Eout(Apcombined) = ηi * Eini(Apcombined) = η1* Ein1(Apcombined) + η2* Ein2(Apcombined) = 0.5*2 + 0.5*2 = 2. Since if the current tokens in pcombined place + 2 ≤ 4 pcombined can be reached.
Finally, comparing the proposed work with a relevant developed TCCPN is shown in Section 4.
4. Case Study
In this section, we show the results of the experiments with the proposed approach. Specifically, we use an AMS example available in the literature: the AMS Petri net model given in Piroddi et al. [30], Chen et al. [8], Chen and Li [31], Chen et al. [32], and TCCPN [26,27,28,29]. The Petri net model is displayed in Figure 11; it includes 14 transitions and 19 places. The places can be described as the following set partition: P0 = {p1, p19}, PR = {p13, …, p18}, and PA = {p2, …, p14}. The properties of the developed Petri net models are obtained using the free GPenSIM tool [22]. We find that it has 282 reachable markings, and the system is not live (it has a deadlock).
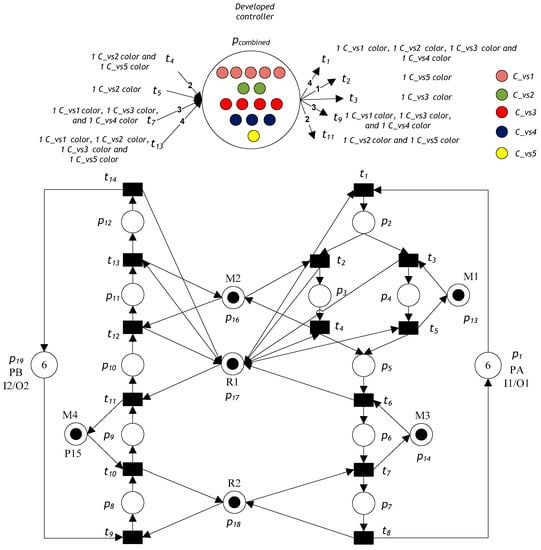
Figure 11.
Colored controlled Petri net model of the system.
We apply the proposed deadlock-prevention algorithm to this case study. Without considering recovery subnets, the system model has five SMSs that may be empty: S1 = {p7, p12, p13, p14, p15, p16, p17, p18}, S2 = {p5, p12, p13, p16, p17}, S3 = {p2, p7, p12, p14, p15, p16, p17, p18}, S4 = {p2, p7, p10, p12, p14, p15, p17, p18}, and S5 = {p2, p5, p12, p16, p17}. Based on the suggested deadlock-prevention algorithm (Algorithm 1), five monitors are inserted to protect the five SMSs from being emptied. The required control places using Algorithm 1 are designed as follows:
- (1)
- •VS1 = {t7, t13}, VS1• = {t1, t9}, and MVo(VS1) = 5.
- (2)
- •VS2 = {t4, t5, t13}, VS2• = {t1, t11}, and MVo(VS2) = 2.
- (3)
- •VS3 = {t7, t13}, VS3• = {t1, t9}, and MVo(VS3) = 4.
- (4)
- •VS4 = {t7, t11}, VS4• = {t1, t9}, and MVo(VS4) = 3.
- (5)
- •VS5 = {t4, t13}, VS5• = {t2, t11}, and MVo(VS5) = 3.
By Definition 11, a deadlock control subnet of the Petri net model illustrated in Figure 11 is NDC = (pcombined, {TDCi, TDCo}, FDC, Cvsi), where TDCo = {4t1, t2, t3, 3t9, 2t11}, and TDCi = {2t4, t5, 3t7, 4t13}. The initial token with a color marking of a combined monitor is MDCo(pcombined) = ∑MVo(VS) = MVo(VS1) + MVo(VS2) + MVo(VS3) + MVo(VS4) + MVo(VS5) = 5 + 2 + 4 + 3 + 1 = 15 tokens. Thus, in the Petri net model illustrated in Figure 11, there are five color types, which are SC = {Cvs1, Cvs2, Cvs3, Cvs4, Cvs5}. Therefore, the total number of colored tokens is 15: five tokens of color Cvs1, two tokens of color Cvs2, four tokens of color Cvs3, three tokens of color Cvs4, and one token of color Cvs5, as shown in Figure 11.
In the net displayed in Figure 11, when transition t1 fires, the system selects only one token from input place p1, one token from resource place p17. Additionally, the system selects tokens from pcombined: one token of color Cvs1, one token of color Cvs2, one token of color Cvs3, and one token of color Cvs4. If transition t2 is fired, the system selects only one token from place p2, one token from resource place p16, and one token of color Cvs5 from pcombined. Moreover, when transition t3 fires, the system selects only one token from input place p2, one token from resource place p13, and one token of color Cvs3 from pcombined.
If transition t9 fires, the system selects only one token from input place p19, one token from resource place p18, one token of color Cvs1 from pcombined, one token of color Cvs3 from pcombined, and one token of color Cvs4 from pcombined. In addition, when transition t11 fires, the system selects only one token from input place p9, one token from resource place p15, one token from resource place p17, one token of color Cvs2 from pcombined, and one token of color Cvs5 from pcombined.
When transition t4 fires, the system creates two colored tokens—one of color Cvs2 and one of color Cvs5—and transfers them into the common place pcombined. Moreover, when transition t5 fires, the system adds color Cvs2 to the tokens and transfers them into the common place pcombined. If transition t7 fires, the system creates three colored tokens—one of color Cvs1, one of color Cvs3, and one of color Cvs4—and transfers them into the common place pcombined. Finally, when transition t13 fires, the system creates four colored tokens—one of color Cvs1, one of color Cvs2, one of color Cvs3, and one of color Cvs5—and transfers them into the common place pcombined.
To test and validate the developed GPenSIM code, we compared it with the methods in Piroddi et al. [30], Chen et al. [8], Chen and Li [31], Chen et al. [32], and TCCPN [26,27,28,29]. The simulation was undertaken for 480 min. After running and simulating the Petri net model in MATLAB, we obtained the results summarized in Table 2 and Table 3. Table 2 shows the results in terms of the number of monitors, number of arcs, liveness, and reachable marking. We observe that the proposed approach provides a supervisor with only a single control place and 9 arcs, both of which are minimal compared with other techniques in Piroddi et al. [30], Chen et al. [8], Chen and Li [31], and Chen et al. [32]. Table 3 displays the results in terms of utilization of the robots and machines, throughput of Part A and Part B, work-in-process (WIP), and total time in system (throughput time). In terms of the resource utilization, all methods obtain approximately the same values, as shown in Figure 12. Moreover, from the viewpoint throughput, the proposed method can provide greater throughput than other techniques as shown in Figure 13. In term of WIP, the proposed method leads to better WIP than the other techniques as shown in Figure 14. With respect to throughput time of Part A and Part B, overall, the proposed method can obtain less throughput time than other techniques as shown in Figure 15 and Figure 16. Therefore, the proposed method is valid, it can give sufficiently accurate results, and it can potentially be applied to other cases.

Table 2.
Comparison with the existing policies: number of monitors, number of arcs, liveness, and reachable marking.

Table 3.
Comparison with the existing policies: utilization throughput, work-in-process, and throughput time.
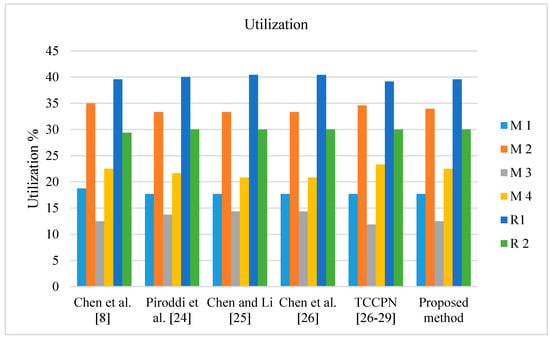
Figure 12.
Comparison of utilization for the Petri net model from Figure 11.
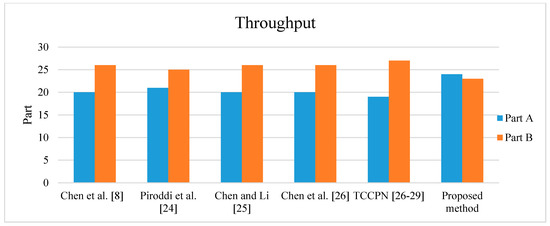
Figure 13.
Comparison of throughput for the Petri net model from Figure 11.
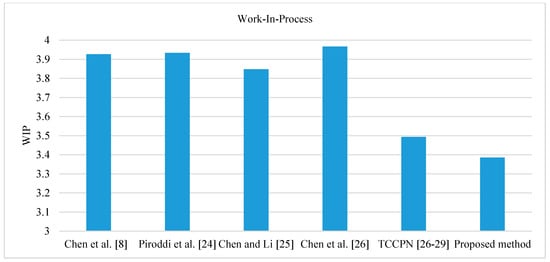
Figure 14.
Comparison of work-in-process for the Petri net model from Figure 11.
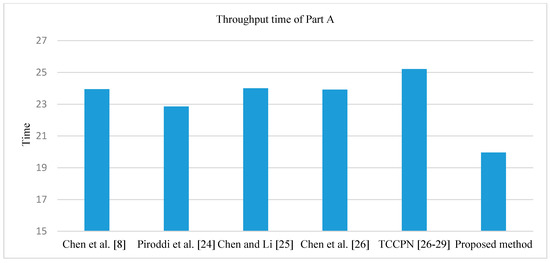
Figure 15.
Comparison of throughput time of Part A for the Petri net model from Figure 11.
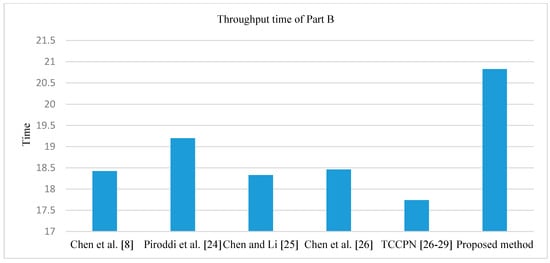
Figure 16.
Comparison of throughput time of Part B for the Petri net model from Figure 11.
5. Conclusions
In this paper, we introduce a two-step controlled deadlock policy. In the first step, we create a Petri net controlled model using the deadlock prevention method based on SMSs proposed by [1]. In the second step, all control places obtained after the first step are merged into a single control place based on the colored Petri nets to mark all SMSs. We compare the proposed method with the methods of Piroddi et al. [30], Chen et al. [8], Chen and Li [31], and Chen et al. [32], and TCCPN [26,27,28,29]. According to our results, the proposed controller is more powerful, has a simpler structure, and does not need to calculate reachability graphs; therefore, it has low-overhead computation. The most challenging research topic in the future is that the controlled system that developed by previous deadlock control approaches may undergo changes of control requirements and specifications such as:
- Adding or removing a machine
- New production ratio
- Adding new product
- Changing a resource capacity
- Resource faults and raw-material processing in a faulty resource
- The processing routes of the system are changed
- System contain uncontrollable transitions
When a system has these problems, a system needs to be reconfigurable. Then the deadlock-free system can have deadlocks. Therefore, the proposed robust deadlock control policy needs to be extended to improve efficiency for rapid and valid reconfiguration of Petri net-based supervisory controllers for reconfigurable manufacturing systems.
Author Contributions
Conceptualization, H.K. and A.A.-A.; software, H.K. and R.D.; resources, H.K., A.A.-A. and R.D.; formal analysis, H.K. and A.A.-A.; investigation, H.K., A.A.-A. and Z.L.; validation, H.K., A.A.-A., Z.L. and R.D.; writing—original draft preparation, H.K., A.A.-A. and Z.L.; writing—review and editing, H.K., A.A.-A., Z.L. and R.D.; visualization, H.K., A.A.-A. and Z.L.; supervision, A.A.-A., and Z.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by King Saud University, grant number (RSP-2019/62), and the APC was funded by King Saud University.
Acknowledgments
The authors would like to thank King Saud University for funding and supporting this research through Researchers Supporting Project Number (RSP-2019/62).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Li, Z.; Zhou, M.; Wu, N. A survey and comparison of petri net-based deadlock prevention policies for flexible manufacturing systems. IEEE Trans. Syst. Man Cybern. Part C Appl. Rev. 2008, 38, 173–188. [Google Scholar]
- Li, Z.; Wu, N.; Zhou, M. Deadlock control of automated manufacturing systems based on petri nets—A literature review. IEEE Trans. Syst. Man Cybern. Part C Appl. Rev. 2012, 42, 437–462. [Google Scholar]
- Abdulaziz, M.; Nasr, E.A.; Al-Ahmari, A.; Kaid, H.; Li, Z. Evaluation of deadlock control designs in automated manufacturing systems. In Proceedings of the 2015 International Conference on Industrial Engineering and Operations Management, Dubai, UAE, 3–5 March 2015; IEEE: Piscataway, NJ, UAE, 2015. [Google Scholar]
- Chen, Y.; Li, Z.; Barkaoui, K.; Giua, A. On the enforcement of a class of nonlinear constraints on petri nets. Automatica 2015, 55, 116–124. [Google Scholar] [CrossRef]
- Nasr, E.A.; El-Tamimi, A.M.; Al-Ahmari, A.; Kaid, H. Comparison and evaluation of deadlock prevention methods for different size automated manufacturing systems. Math. Probl. Eng. 2015, 501, 1–19. [Google Scholar] [CrossRef]
- Kaid, H.; Al-Ahmari, A.; El-Tamimi, A.M.; Abouel Nasr, E.; Li, Z. Design and implementation of deadlock control for automated manufacturing systems. S. Afr. J. Ind. Eng. 2019, 30, 1–23. [Google Scholar] [CrossRef]
- Chen, Y.; Li, Z.; Khalgui, M.; Mosbahi, O. Design of a maximally permissive liveness-enforcing petri net supervisor for flexible manufacturing systems. IEEE Trans. Autom. Sci. Eng. 2011, 8, 374–393. [Google Scholar] [CrossRef]
- Wysk, R.A.; Yang, N.-S.; Joshi, S. Detection of deadlocks in flexible manufacturing cells. IEEE Trans. Robot. Autom. 1991, 7, 853–859. [Google Scholar] [CrossRef]
- Ghaffari, A.; Rezg, N.; Xie, X. Design of a live and maximally permissive petri net controller using the theory of regions. IEEE Trans. Robot. Autom. 2003, 19, 137–141. [Google Scholar] [CrossRef]
- Uzam, M.; Zhou, M. Iterative synthesis of petri net based deadlock prevention policy for flexible manufacturing systems. In Proceedings of the 2004 IEEE International Conference on Systems, Man and Cybernetics, Hague, The Netherlands, 10–13 October 2004; IEEE: Piscataway, NJ, USA, 2004; pp. 4260–4265. [Google Scholar]
- Uzam, M. The use of the petri net reduction approach for an optimal deadlock prevention policy for flexible manufacturing systems. Int. J. Adv. Manuf. Technol. 2004, 23, 204–219. [Google Scholar] [CrossRef]
- Chao, D.Y. Direct minimal empty siphon computation using mip. Int. J. Adv. Manuf. Technol. 2009, 45, 397–405. [Google Scholar] [CrossRef]
- Chao, D.Y. Improvement of suboptimal siphon-and fbm-based control model of a well-known. IEEE Trans. Autom. Sci. Eng. 2011, 8, 404–411. [Google Scholar] [CrossRef]
- Uzam, M. An optimal deadlock prevention policy for flexible manufacturing systems using petri net models with resources and the theory of regions. Int. J. Adv. Manuf. Technol. 2002, 19, 192–208. [Google Scholar] [CrossRef]
- Chao, D.Y. Fewer monitors and more efficient controllability for deadlock control in s3pgr2 (systems of simple sequential processes with general resource requirements). Comput. J. 2010, 53, 1783–1798. [Google Scholar] [CrossRef]
- Li, Z.; Zhou, M. Elementary siphons of petri nets and their application to deadlock prevention in flexible manufacturing systems. IEEE Trans. Syst. Man Cybern. Part A Syst. Hum. 2004, 34, 38–51. [Google Scholar] [CrossRef]
- Pan, Y.-L.; Tseng, C.-Y.; Row, T.-C. Design of improved optimal and suboptimal deadlock prevention for flexible manufacturing systems based on place invariant and reachability graph analysis methods. J. Algorithms Comput. Technol. 2017, 11, 261–270. [Google Scholar] [CrossRef]
- Zhao, M.; Uzam, M. A suboptimal deadlock control policy for designing non-blocking supervisors in flexible manufacturing systems. Inf. Sci. 2017, 388, 135–153. [Google Scholar] [CrossRef]
- Cong, X.; Gu, C.; Uzam, M.; Chen, Y.; Al-Ahmari, A.M.; Wu, N.; Zhou, M.; Li, Z. Design of optimal petri net supervisors for flexible manufacturing systems via weighted inhibitor arcs. Asian J. Control 2018, 20, 511–530. [Google Scholar] [CrossRef]
- Lautenbach, K. Linear algebraic calculation of deadlocks and traps. In Concurrency and Nets, 1st ed.; Springer: Berlin/Heidelberg, Germany, 1987; pp. 315–336. [Google Scholar]
- Ezpeleta, J.; Colom, J.M.; Martinez, J. A petri net based deadlock prevention policy for flexible manufacturing systems. IEEE Trans. Robot. Autom. 1995, 11, 173–184. [Google Scholar] [CrossRef]
- Davidrajuh, R. Modeling discrete-event systems with gpensim: An introduction; Springer International Publishing: Gewerbestrasse, Cham, Switzerland, 2018. [Google Scholar]
- Ratzer, A.V.; Wells, L.; Lassen, H.M.; Laursen, M.; Qvortrup, J.F.; Stissing, M.S.; Westergaard, M.; Christensen, S.; Jensen, K. Cpn tools for editing, simulating, and analysing coloured petri nets. In Proceedings of the International Conference on Application and Theory of Petri Nets, Eindhoven, The Netherlands, 23–27 June 2003; Springer: Berlin, Heidelberg, Germany, 2003; pp. 450–462. [Google Scholar]
- Li, Z.; Zhou, M. Deadlock Resolution in Automated Manufacturing Systems: A Novel Petri Net Approach; Springer Science & Business Media: Holborn, London, UK, 2009. [Google Scholar]
- Wu, Y.; Xing, K.; Luo, J.; Feng, Y. Robust deadlock control for automated manufacturing systems with an unreliable resource. Inf. Sci. 2016, 346, 17–28. [Google Scholar] [CrossRef]
- Bidgoly, A.J.; Ladani, B.T. Trust modeling and verification using colored petri nets. In Proceedings of the 2011 8th International ISC Conference on Information Security and Cryptology, Mashhad, Iran, 14–15 September 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 1–8. [Google Scholar]
- Wahab, O.A.; Bentahar, J.; Otrok, H.; Mourad, A. A survey on trust and reputation models for web services: Single, composite, and communities. Decis. Support Syst. 2015, 74, 121–134. [Google Scholar] [CrossRef]
- Wahab, O.A.; Bentahar, J.; Otrok, H.; Mourad, A. Towards trustworthy multi-cloud services communities: A trust-based hedonic coalitional game. IEEE Trans. Serv. Comput. 2016, 11, 184–201. [Google Scholar] [CrossRef]
- Wang, N.; Wang, J.; Chen, X. A trust-based formal model for fault detection in wireless sensor networks. Sensors 2019, 19, 1916. [Google Scholar] [CrossRef] [PubMed]
- Piroddi, L.; Cordone, R.; Fumagalli, I. Selective siphon control for deadlock prevention in petri nets. IEEE Trans. Syst. Man Cybern. Part A Syst. Hum. 2008, 38, 1337–1348. [Google Scholar] [CrossRef]
- Chen, Y.; Li, Z. Design of a maximally permissive liveness-enforcing supervisor with a compressed supervisory structure for flexible manufacturing systems. Automatica 2011, 47, 1028–1034. [Google Scholar] [CrossRef]
- Chen, Y.; Li, Z.; Zhou, M. Behaviorally optimal and structurally simple liveness-enforcing supervisors of flexible manufacturing systems. IEEE Trans. Syst. Man Cybern. Part A Syst. Hum. 2012, 42, 615–629. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).