Multivariable System Identification Method Based on Continuous Action Reinforcement Learning Automata
Abstract
1. Introduction
2. Materials and Methods
2.1. Background
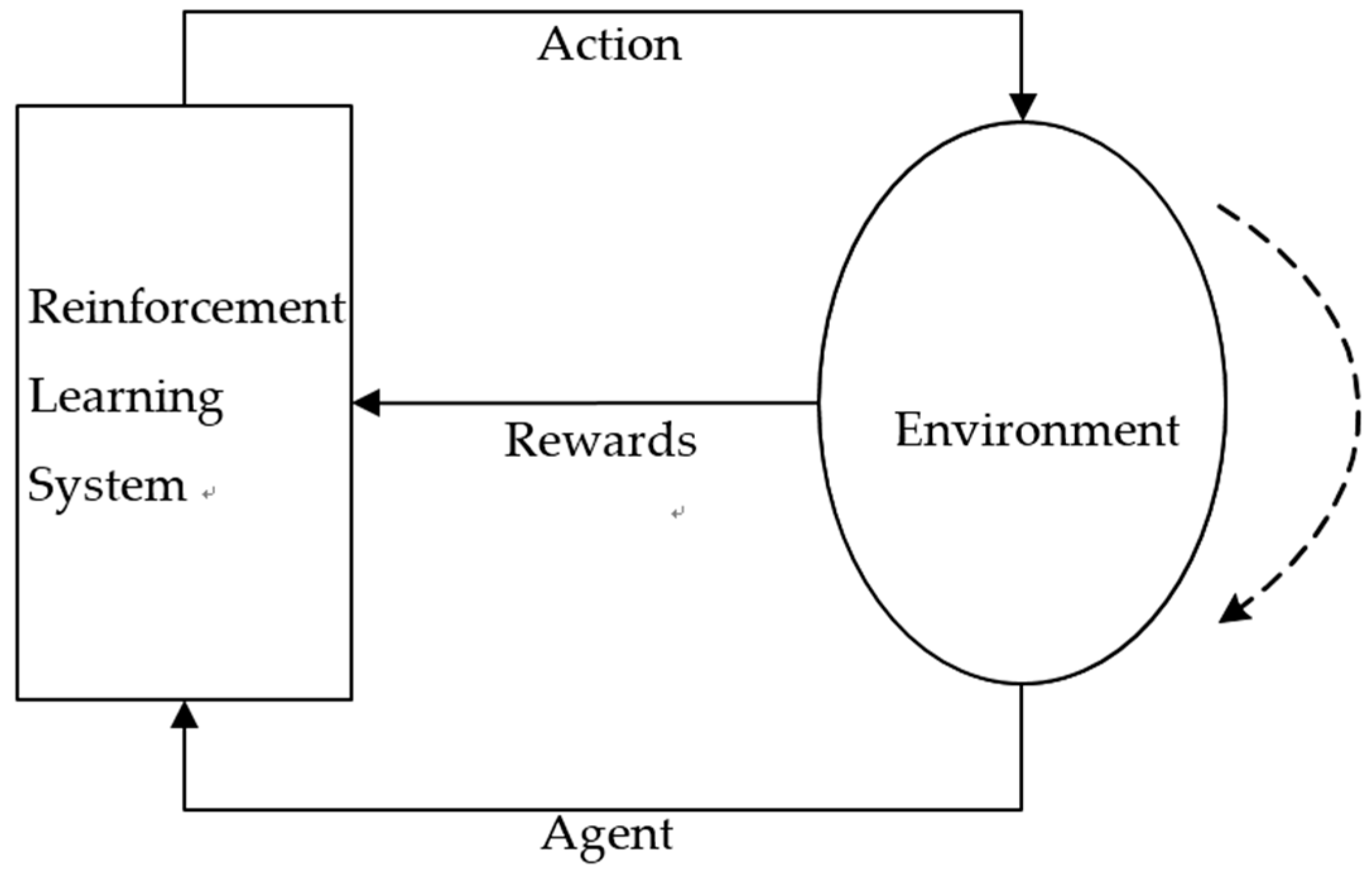
2.2. Basic Reinforcement Learning
2.3. Continuous Action Reinforcement Learning Automata (CARLA)
| CARLA algorithm |
| 1: Initialize the probability density function : establish the uniform distribution of CPDFs according to the range of the parameter; |
| 2: Actions selection: select actions (or parameters) randomly based on the CPDF value; |
| 3: System evaluation: take the action, substitute parameters into the system to obtain the responding curve, and calculate the fitness function ; |
| 4: Calculate the enhanced signal value according to the value of the fitness function; |
| 5: Update each CPDF value according to the enhanced signal value; |
| 6: Update behavior parameters: introduce the normal random number generator to update the action parameters at the next moment; |
| 7: If the stopping condition has not been reached, return to step 2 until the convergence condition is met. |
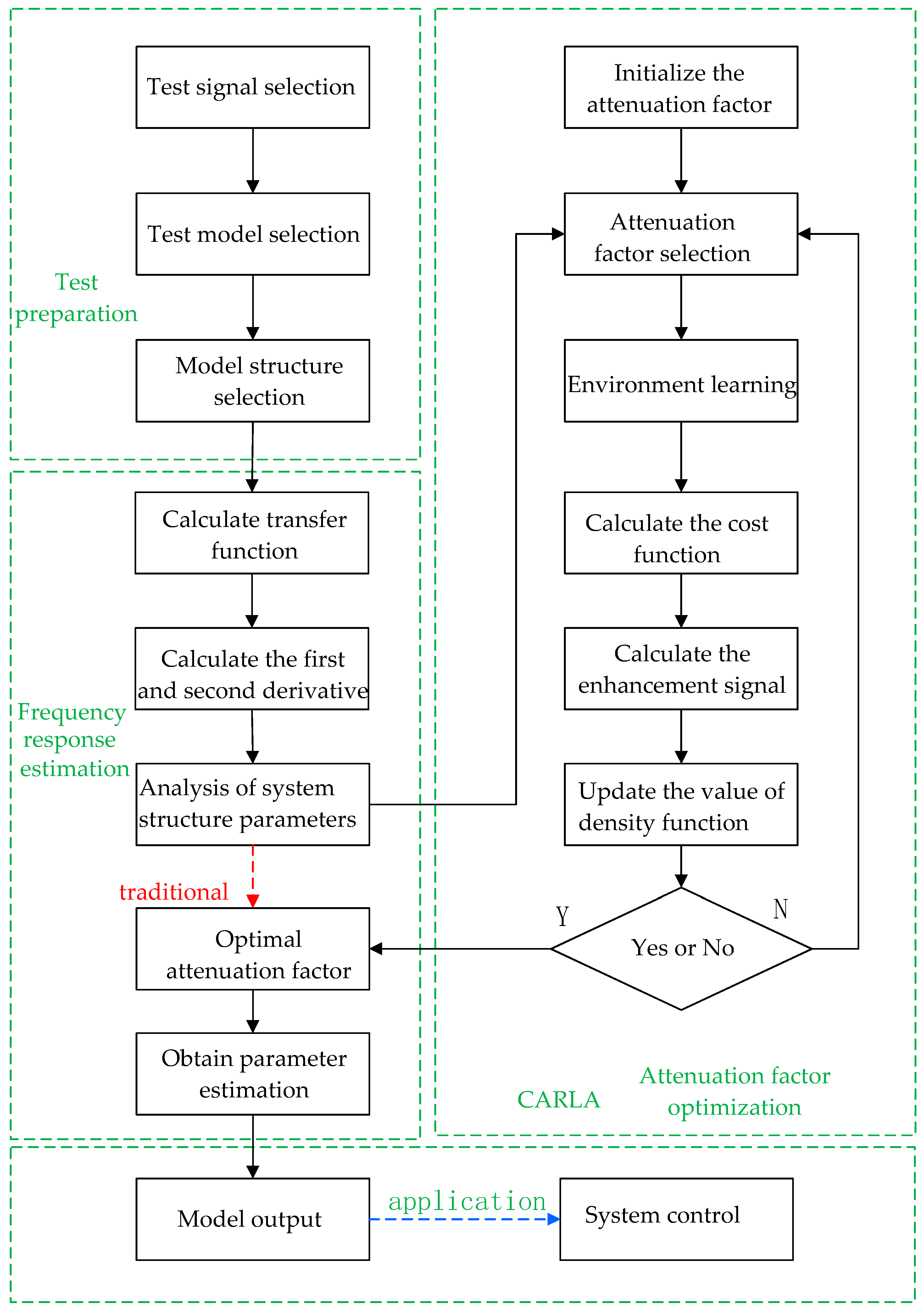
3. Frequency Response Estimation Based on CARLA (CARLA-FRE)
3.1. Frequency Response Estimation Based on CARLA (CARLA-FRE)
3.2. The Applications of CARLA-FRE in MIMO Systems
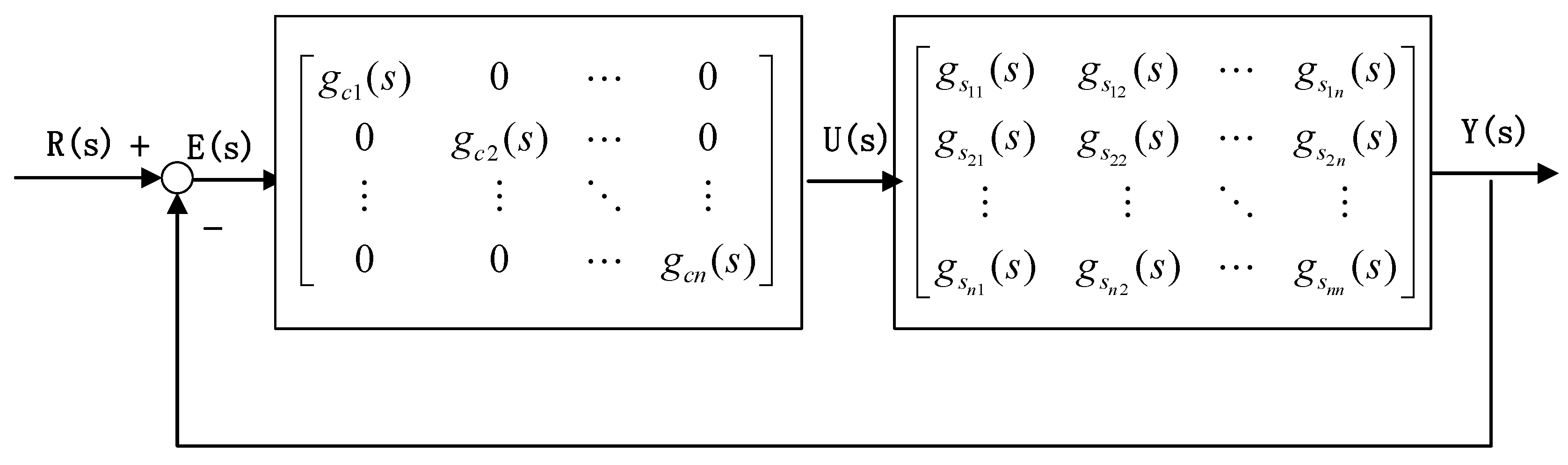
3.2.1. Closed-Loop Identification for Square Multivariate Systems
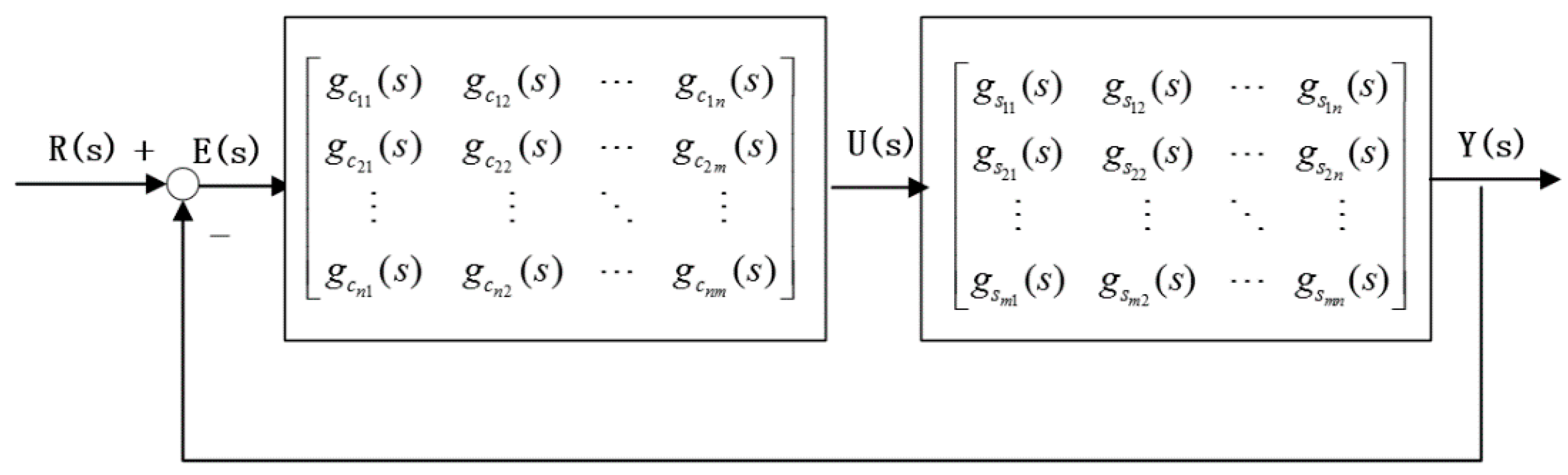
3.2.2. Closed-Loop Identification for Non-Square Multivariate Systems
4. CARLA Algorithm Performance Verification
5. Simulation
5.1. Square Multivariate System: Wood-Berry Model
5.2. Non-Square Multivariate System: Shell Model
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Gupta, R.D.; Fairman, F.W. Parameter estimation for multivariable systems. IEEE Trans. Autom. Control 1974, 19, 546–549. [Google Scholar] [CrossRef]
- Guidorzi, R. Canonical structures in the identification of multivariable systems. Automatica 1975, 11, 361–374. [Google Scholar] [CrossRef]
- Verhaegen, M. A novel non-iterative mimo state space model identification technique. IFAC Proc. Vol. 1991, 24, 749–754. [Google Scholar] [CrossRef]
- Nakayama, M.; Oku, H.; Ushida, S. Closed-loop identification for a continuous-time model of a multivariable dual-rate system with input fast sampling. IFAC PapersOnLine 2018, 51, 415–420. [Google Scholar] [CrossRef]
- Moor, B.D.; Overschee, P.V. Numerical algorithms for subspace state space system identification. In Trends in Control; Springer: London, UK, 1995. [Google Scholar]
- Gumussoy, S.; Ozdemir, A.A.; McKelvey, T.; Ljung, L.; Gibanica, M.; Singh, R. Improving linear state-space models with additional niterations. IFAC PapersOnLine 2018, 51, 341–346. [Google Scholar] [CrossRef]
- Larimore, W.E. Canonical variate analysis in identification, filtering, and adaptive control. In Proceedings of the 29th IEEE Conference on Decision and Control, Honolulu, HI, USA, 5–7 December 1990; pp. 596–604. [Google Scholar]
- Pilario, K.E.S.; Cao, Y.; Shafiee, M. Mixed kernel canonical variate dissimilarity analysis for incipient fault monitoring in nonlinear dynamic processes. Comput. Chem. Eng. 2019, 123, 143–154. [Google Scholar] [CrossRef]
- Zheng, W.X. Unbiased identification of multivariable systems subject to colored noise. In Proceedings of the 33rd IEEE Conference on Decision and Control, Lake Buena Vista, FL, USA, 14–16 December1994; Volume 2863, pp. 2864–2865. [Google Scholar]
- Feng, D.; Tongwen, C.; Li, Q. Bias compensation based recursive least-squares identification algorithm for miso systems. IEEE Trans. Circuits Syst. II Express Briefs 2006, 53, 349–353. [Google Scholar] [CrossRef]
- Elisei-Iliescu, C.; Stanciu, C.; Paleologu, C.; Benesty, J.; Anghel, C.; Ciochina, S. Efficient recursive least-squares algorithms for the identification of bilinear forms. Digit. Signal Process. 2018, 83, 280–296. [Google Scholar] [CrossRef]
- Ding, F.; Xie, X. Recursive estimation of parameters of transfer function matrix subsub-model: Instrumental model method. Control Decis. 1991, 6, 447–452. [Google Scholar]
- Du, J.; Dong, S.; Liu, T.; Zhao, J. Multi-innovation based identification of output error model with time delay under load disturbance. IFAC PapersOnLine 2018, 51, 224–228. [Google Scholar] [CrossRef]
- Ding, F.; Xie, X.; Fang, C. Multi-innovation identification method for time-varying systems. Acta Autom. Sin. 1996, 22, 85–91. [Google Scholar]
- Li, S.Y.; Qi, C.K. A Structured Closed-Loop Identification Method for Multivariable Systems based on Step Response Testing. Chinese Patent CN148268, 7 April 2004. [Google Scholar]
- Liu, T.; Gao, F. A frequency domain step response identification method for continuous-time processes with time delay. J. Process Control 2010, 20, 800–809. [Google Scholar] [CrossRef]
- Liu, T.; Zhang, W.; Gao, F. Analytical decoupling control strategy using a unity feedback control structure for mimo processes with time delays. J. Process Control 2007, 17, 173–188. [Google Scholar] [CrossRef]
- Romano, R.A.; Pait, F. Matchable-observable linear models and direct filter tuning: An approach to multivariable identification. IEEE Trans. Autom. Control 2017, 62, 2180–2193. [Google Scholar] [CrossRef]
- Morales Alvarado, C.S.; Garcia, C. Comparison of statistical metrics and a new fuzzy method for validating linear models used in model predictive control controllers. Ind. Eng. Chem. Res. 2018, 57, 3666–3677. [Google Scholar] [CrossRef]
- Jin, Q.B.; Cheng, Z.J.; Dou, J.; Cao, L.T.; Wang, K.W. A novel closed loop identification method and its application of multivariable system. J. Process Control 2012, 22, 132–144. [Google Scholar] [CrossRef]
- Li, M.; Miao, C.; Leung, C. A coral reef algorithm based on learning automata for the coverage control problem of heterogeneous directional sensor networks. Sensors 2015, 15, 30617–30635. [Google Scholar] [CrossRef]
- Mohammed, S.S.; Devaraj, D.; Ahamed, T.P.I. Learning automata based fuzzy mppt controller for solar photovoltaic system under fast changing environmental conditions. J. Intell. Fuzzy Syst. 2017, 32, 3031–3041. [Google Scholar] [CrossRef]
- Liting, C. Research of Identification and Internal Model Control for Non-Square Multivariable System with Time Delay; Beijing University of Chemical Technology: Beijing, China, 2015. [Google Scholar]
- Sutton, R.S.; Barto, A.G. Reinforcement learning: An introduction. IEEE Trans. Neural Netw. 1998, 9, 1054. [Google Scholar] [CrossRef]
- Najim, K.; Poznyak, A.S. Learning Automata: Theory and Applications; Pergamon: Oxford, UK, 1994. [Google Scholar]
- Narendra, K.S.; Thathachar, M.A. Learning Automata: An Introduction; Prentice-Hall: London, UK, 1989. [Google Scholar]
- Xuejing, G.; Mingru, Z.; Zhiliang, W.; Yucheng, G. Parameter learning optimization of intelligent controller based on carla-pso composite model. Appl. Res. Comput. 2019, 3, 678–680. [Google Scholar]
- Anari, B.; Torkestani, J.A.; Rahmani, A.M. Automatic data clustering using continuous action-set learning automata and its application in segmentation of images. Appl. Soft Comput. 2017, 51, 253–265. [Google Scholar] [CrossRef]
- Howell, M.N.; Best, M.C. On-line pid tuning for engine idle-speed control using continuous action reinforcement learning automata. Control Eng. Pract. 2000, 8, 147–154. [Google Scholar] [CrossRef]
- Irandoost, M.A.; Rahmani, A.M.; Setayeshi, S. A novel algorithm for handling reducer side data skew in mapreduce based on a learning automata game. Inf. Sci. 2018, 501, 662–679. [Google Scholar] [CrossRef]
- Jin, Q.; Jiang, B.; Cheng, Z. A novel identification method based on frequency response analysis. Trans. Inst. Meas. Control 2016, 38, 44–54. [Google Scholar] [CrossRef]
- Howell, M.N.; Frost, G.P.; Gordon, T.J.; Wu, Q.H. Continuous action reinforcement learning applied to vehicle suspension control. Mechatronics 1997, 7, 263–276. [Google Scholar] [CrossRef]
- Mei, H.; Li, S. Decentralized identification for multivariable integrating processes with time delays from closed-loop step tests. Isa Trans. 2007, 46, 189–198. [Google Scholar] [CrossRef]
- Mei, H.; Li, S.Y.; Cai, W.J.; Xiong, Q. Decentralized closed-loop parameter identification for multivariable processes from step responses. Math. Comput. Simul. 2005, 68, 171–192. [Google Scholar] [CrossRef]
- Jing, Q.; Yan, G.; Liu, Z.; Song, A. Decoupling internal model control for non-square process with time delays. In Proceedings of the IEEE 2010 International Conference on Measuring Technology and Mechatronics Automation (ICMTMA 2010), Changsha City, China, 13–14 March 2010. [Google Scholar]
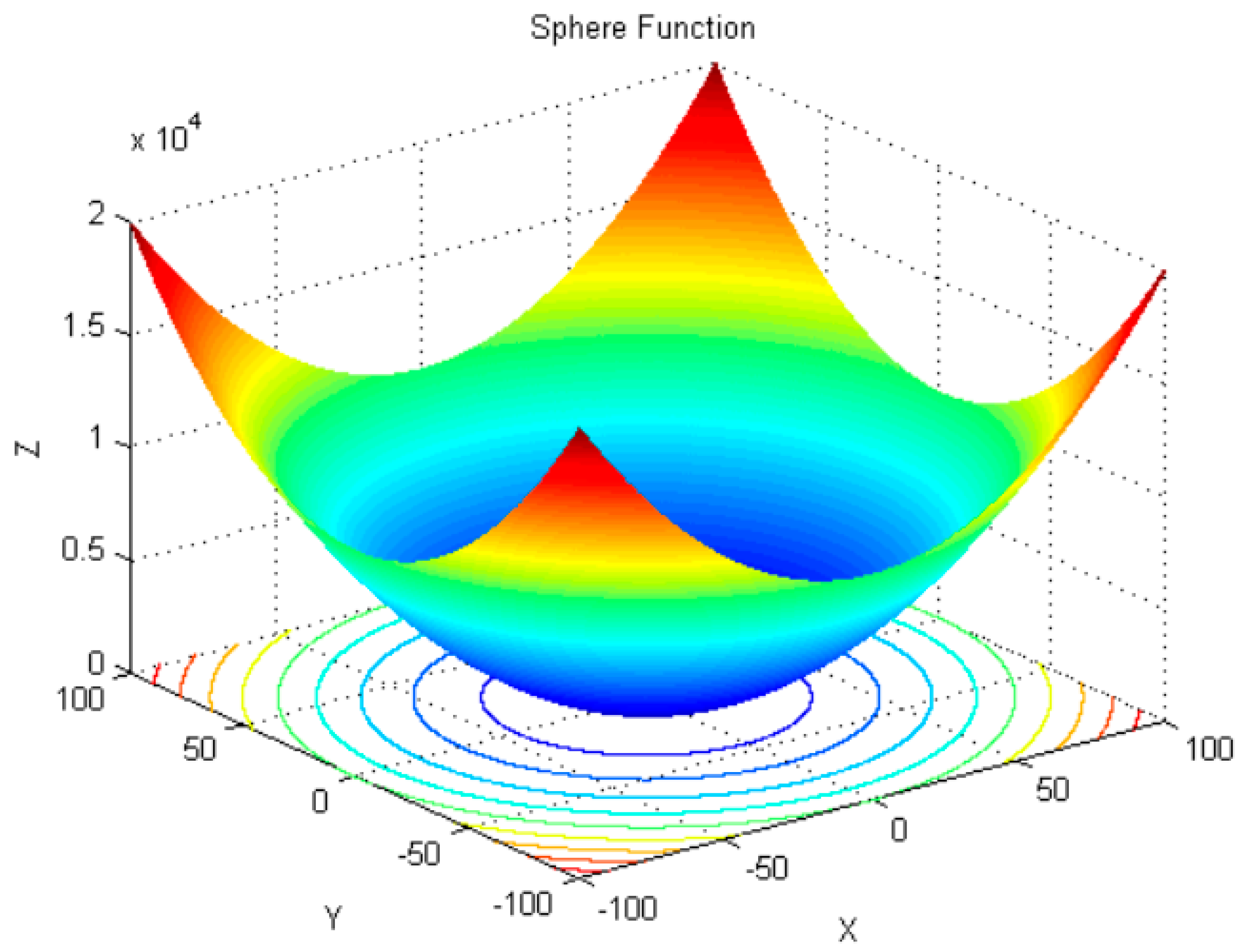
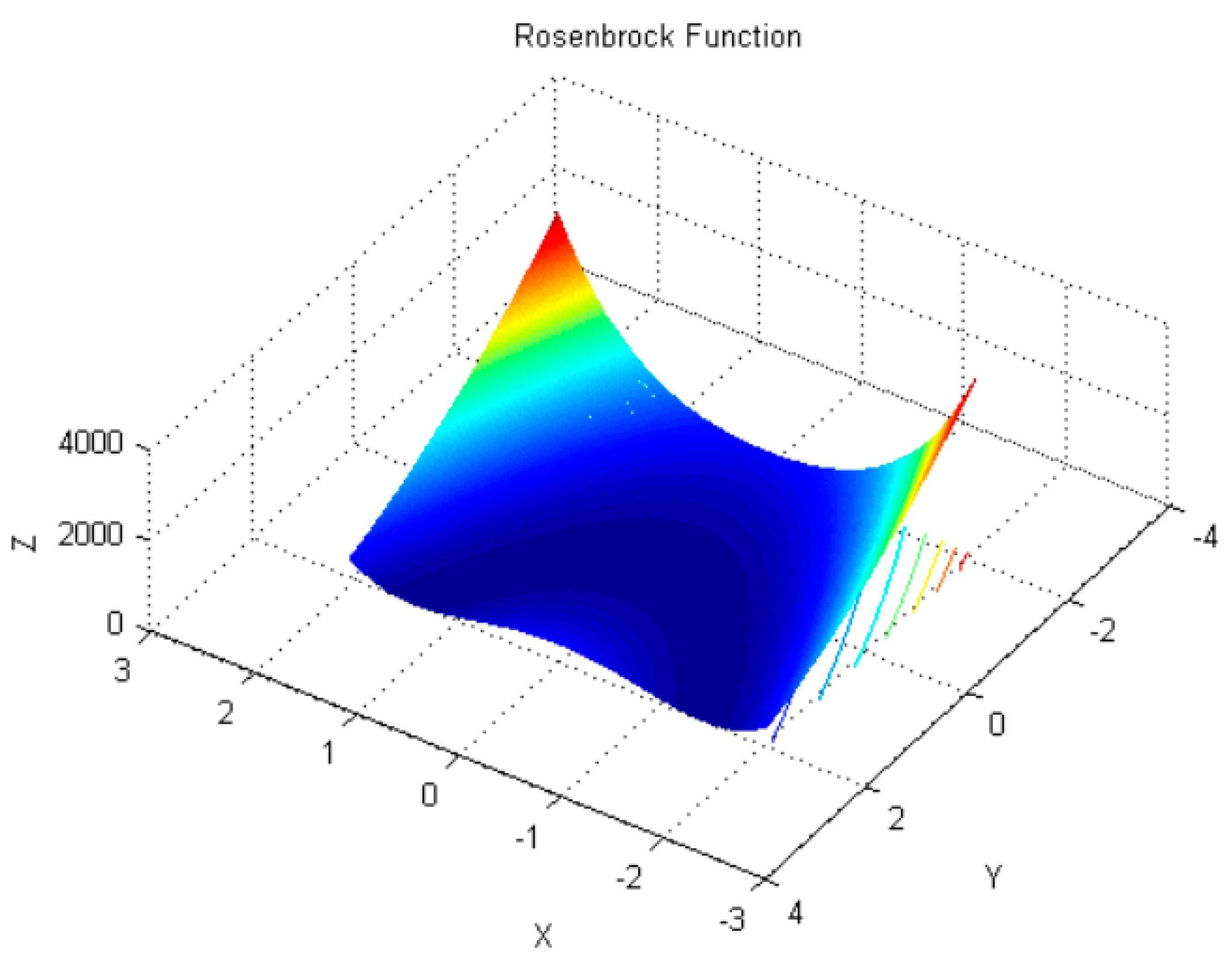
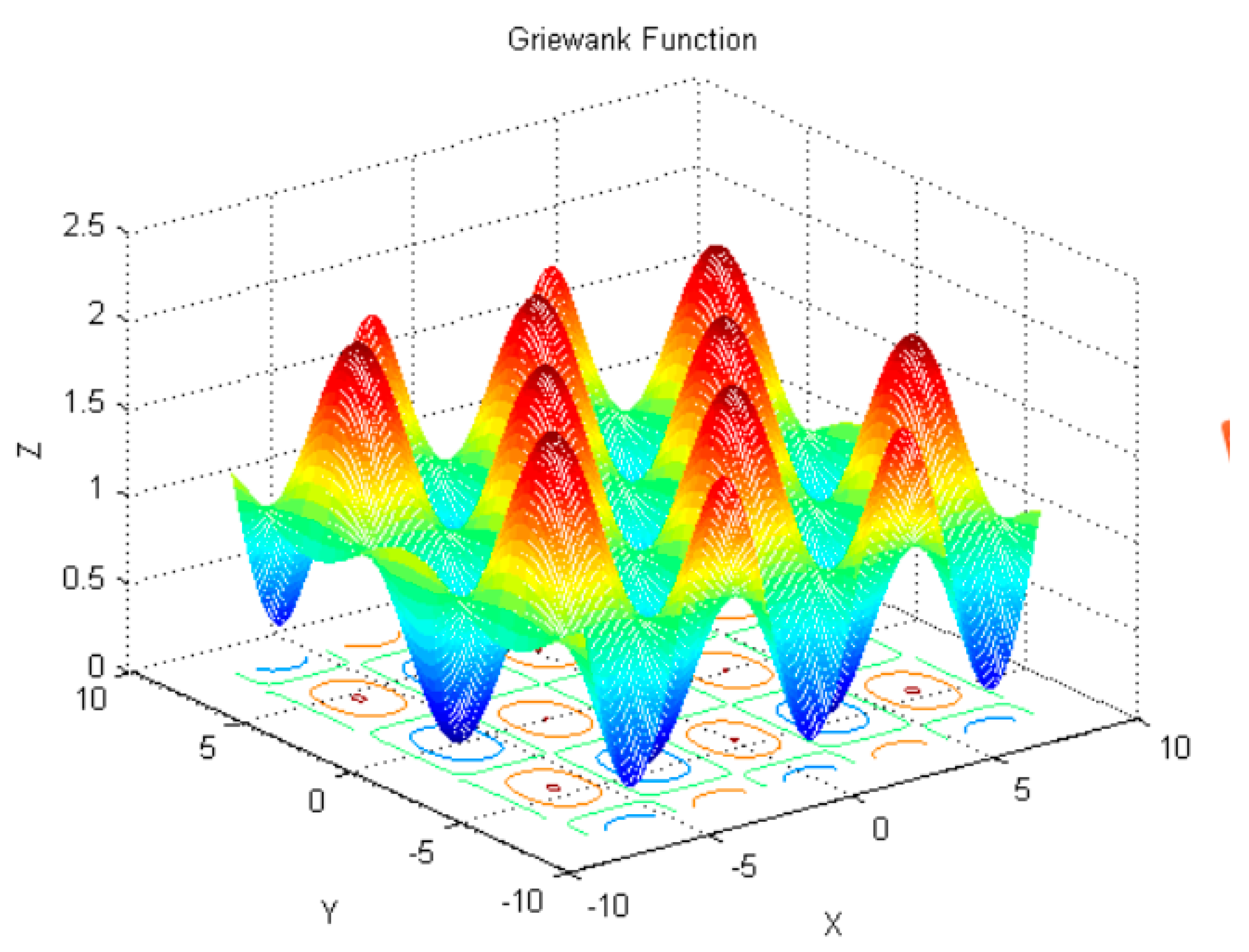
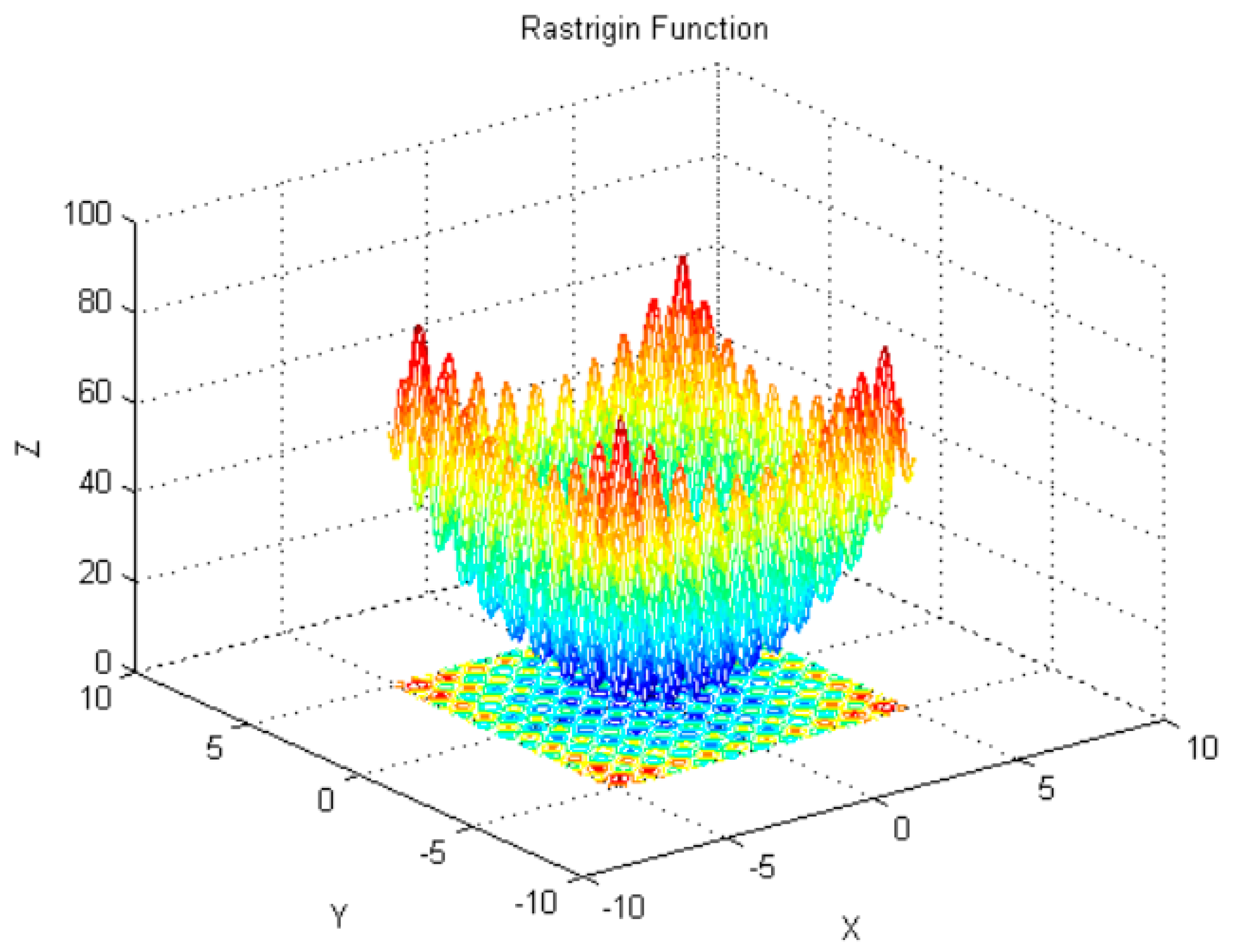


| Standard Function Type | Dimensionality | Sweet Spot | Optimal Fitness Value | Search Interval Settings |
|---|---|---|---|---|
| Sphere | 30 | [0,0,…,0] | 0 | (−100,100) |
| Rosenbrock | 30 | [1,1,…,1] | 0 | (−2.048,2.048) |
| Griewank | 30 | [0,0,…,0] | 0 | (−8,8) |
| Rastrigin | 30 | [0,0,…,0] | 0 | (−5.12,5.12) |
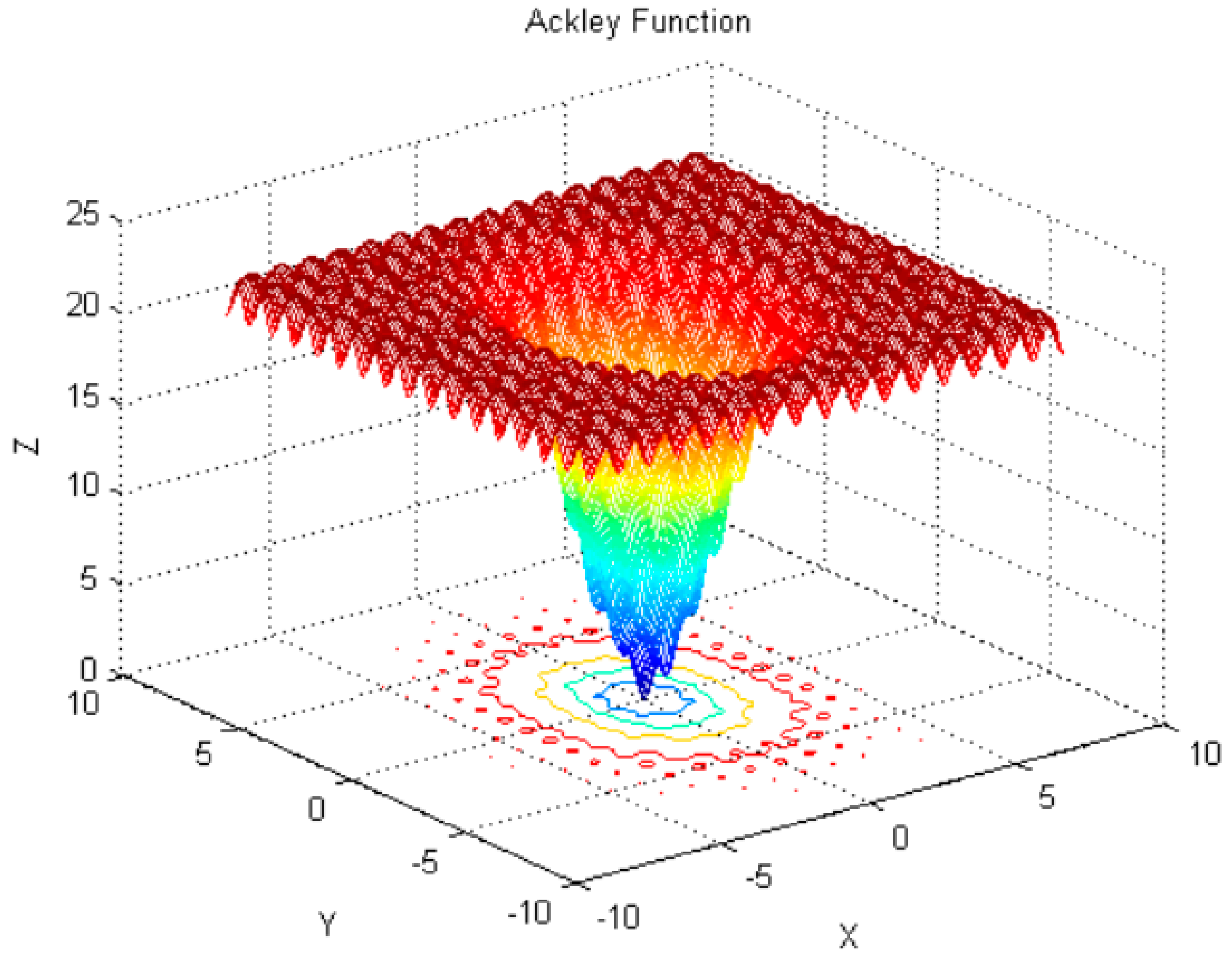
| Ackley | 30 | [0,0,…,0] | 0 | (−8,8) |
| Schwefel’s problem 22 | 30 | [0,0,…,0] | 0 | (−10,10) |
| Standard Function Type | PSO | FWA | CARLA | |||
|---|---|---|---|---|---|---|
| Mean Value | Standard Deviation | Mean Value | Standard Deviation | Mean Value | Standard Deviation | |
| Sphere | 0 | 0 | 0 | 0 | 0 | 0 |
| Rosenbrock | 66.59 | 204.29 | 12.16 | 12.82 | 8.91 | 10.22 |
| Griewank | 0 | 0.01 | 0 | 0 | 0 | 0 |
| Rastrigin | 6.77 | 7.70 | 0 | 0 | 0.01 | 0.21 |
| Ackley | 0.043 | 0.042 | 0 | 0 | 0 | 0 |
| Schwefel’s problem 22 | 23.93 | 13.61 | 0 | 0 | 0 | 0 |
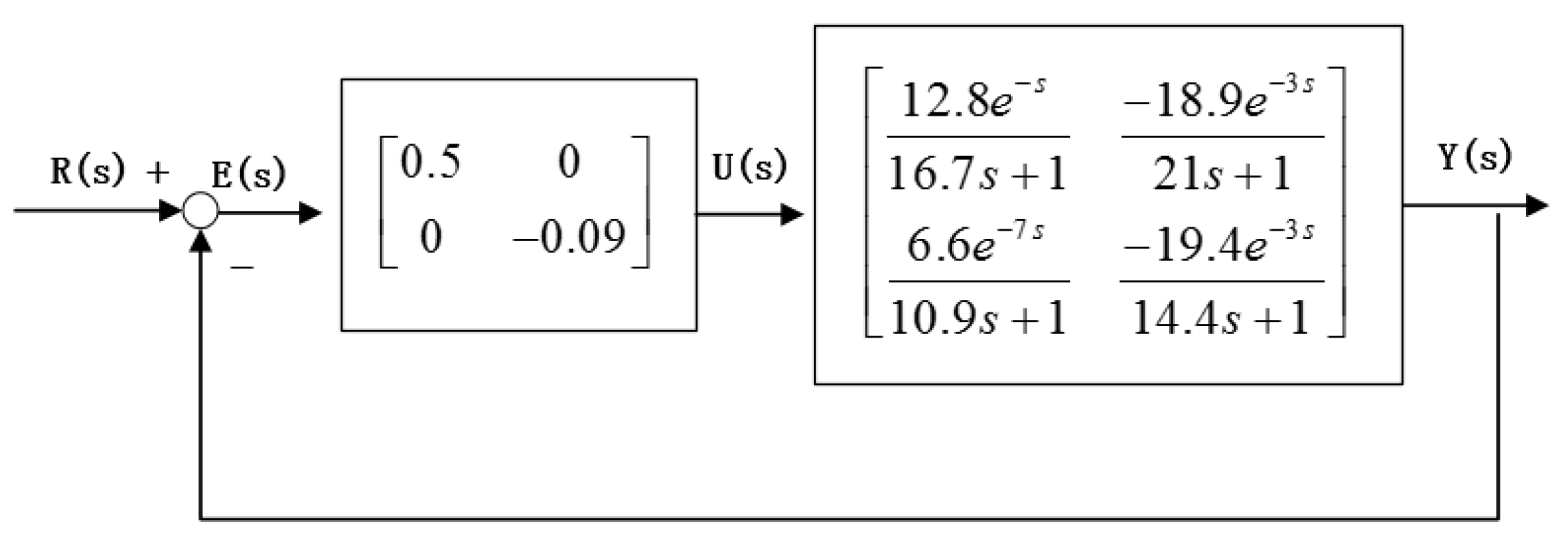
| Wood-Berry | ||||
|---|---|---|---|---|
| Actual model | ||||
| Method in [26] (FRE) | ||||
| error (%) | 0.98 | 0.34 | 0.40 | 0.47 |
| Method in [20] (NPSO-FRE) | ||||
| error (%) | 0.32 | 0.014 | 0.015 | 0.024 |
| Method in [23] (MFA-FRE) | ||||
| error (%) | 0.32 | 0.004 | 0.008 | 0.005 |
| Method in this paper (CARLA-FRE) | ||||
| error (%) | 0.21 | 0.013 | 0.012 | 0.021 |
| Actual Model | Noise 0% | Noise 20% | ||
|---|---|---|---|---|
| MFA-FRE | CARLA-FRE | MFA-FRE | CARLA-FRE | |
| error (%) | 0.47 | 0.29 | 1.16 | 0.32 |
| error (%) | 0.75 | 0.39 | 6.45 | 0.65 |
| error (%) | 1.41 | 0.61 | 7.71 | 1.05 |
| error (%) | 0.92 | 0.47 | 3.02 | 0.91 |
| error (%) | 0.52 | 0.31 | 2.31 | 0.81 |
| error (%) | 0.24 | 0.25 | 2.75 | 0.79 |
| error (%) | 0.91 | 0.74 | 4.39 | 1.27 |
| error (%) | 2.70 | 0.55 | 2.70 | 2.06 |
| error (%) | 0.31 | 0.62 | 0.29 | 1.67 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, M.; Jin, Q. Multivariable System Identification Method Based on Continuous Action Reinforcement Learning Automata. Processes 2019, 7, 546. https://doi.org/10.3390/pr7080546
Jiang M, Jin Q. Multivariable System Identification Method Based on Continuous Action Reinforcement Learning Automata. Processes. 2019; 7(8):546. https://doi.org/10.3390/pr7080546
Chicago/Turabian StyleJiang, Meiying, and Qibing Jin. 2019. "Multivariable System Identification Method Based on Continuous Action Reinforcement Learning Automata" Processes 7, no. 8: 546. https://doi.org/10.3390/pr7080546
APA StyleJiang, M., & Jin, Q. (2019). Multivariable System Identification Method Based on Continuous Action Reinforcement Learning Automata. Processes, 7(8), 546. https://doi.org/10.3390/pr7080546




