Application of Transformation Matrices to the Solution of Population Balance Equations
Abstract
1. Introduction
1.1. Flowsheet Simulation of Solid Phase Processes
- Aspen Plus [10], which is actively used in chemical industry as well as for simulation of polymers, minerals, metals etc.
- gPROMS FormulatedProducts [11], as a part of gPROMS platform, especially designed to investigate solid phase processes.
- JKSimMet [12], which is a flowsheeting software for simulation of comminution and classification circuits in the mineral processing industry.
- The HSC Sim [13] module of HSC Chemistry software intended for modelling various processes in chemistry, metallurgy, and mineralogy.
- CHEMCAD [14], which was developed to simulate chemical processes with limited consideration of the solid phase.
- Dyssol [7], a flowsheet simulation system designed to simulate complex dynamic processes in solids processing technology, developed within a research collaboration founded by the German Research Foundation.
1.2. Use of Population Balance Equations for Particulate Processes
2. Mathematical Formulations
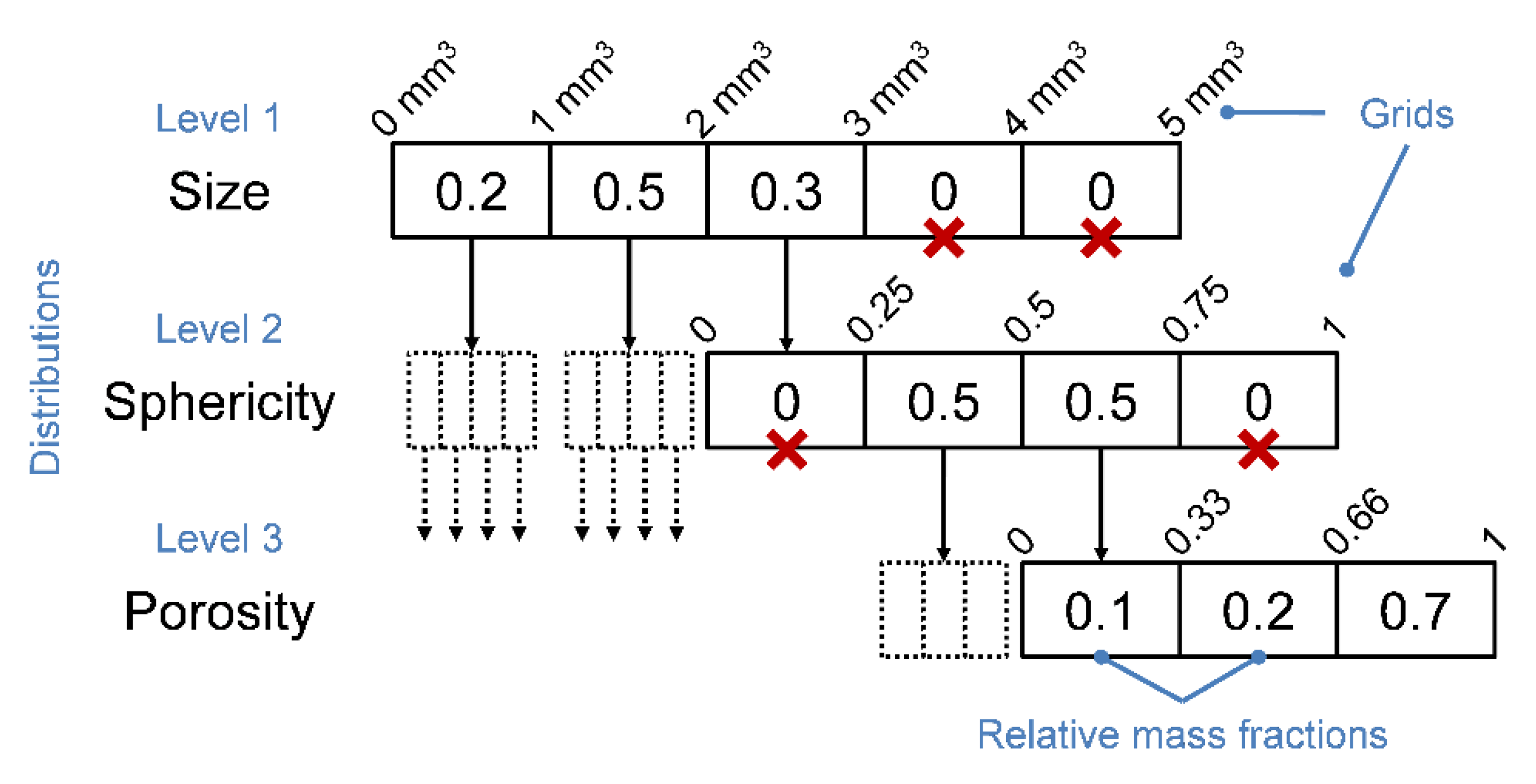
2.1. Transformation Matrices
- , —input and output stream variables;
- —control variables that describe the operating conditions of the process and are usually controlled in certain ranges;
- —model parameters, which are customizable settings of the model itself; they may or may not change over time;
- —design variables that represent structural features of apparatuses, such as physical dimensions and shapes, and usually do not change during the simulation.
- (1)
- Explicitly, by direct calculation of all state variables in holdups and outlet streams.
- (2)
- Implicitly, through the application of movement (transformation) matrices, which describe the transfer of material between discrete classes in multidimensional parameter space.
- (1)
- . The model considers in its equations all the distributed parameters given in the inlet streams. In this case, the explicit solution works well, since all distributed parameters can be calculated directly.
- (2)
- . The model will not work, since it requires more information about distributed parameters than is available in the flowsheet.
- (3)
- . The explicit scheme will provide proper results in the -dimensional parameter space, but will fail to deliver correct values for , since and cannot be properly applied for other dimensions, beyond those for which they were defined.
- The whole set of possible distributed parameters must be known during the development of the model and they all should be considered in its equations.
- If the number or composition of the distributed parameters alters in an individual simulation, the model itself should track these changes and react to them properly.
- The model must ensure setting all distributions defined at the input to its holdup and output, even those that are not explicitly considered in the model.
- Considering only those distributed parameters that are necessary for the model leads to the loss of information about the remaining ones, despite the fact that there may be enough information to calculate them.
2.2. Agglomeration
2.3. Breakage
3. Implementation Details
3.1. Dynamic Flowsheet Simulation in Dyssol
3.2. Application of Transformation Matrices
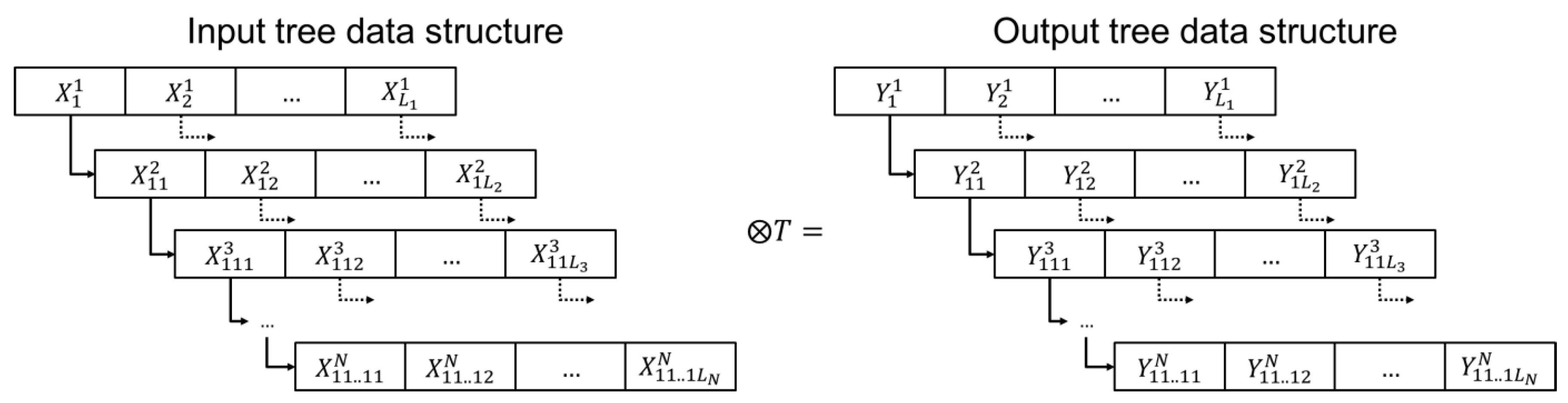
- Apply to the lowest –th hierarchy level of input distribution, using Equation (17) in the form ofFor example, for , the second level of the hierarchy should be calculated as
- Extract the transformation laws for the previous level () from and apply them using Equation (52). Repeat it up to the hierarchy level 1. For example, for , the first level will be calculated aswhich corresponds to Equation (14).
- Apply to calculate the remaining levels below asFor example, if and :
- For steady state units: copy the distribution from the input to the output, then apply the transformation matrix to the output.
- For dynamic units: use the input distribution to calculate the holdup, apply the transformation matrix to the holdup, and then calculate the output.
3.3. Implementation of Units
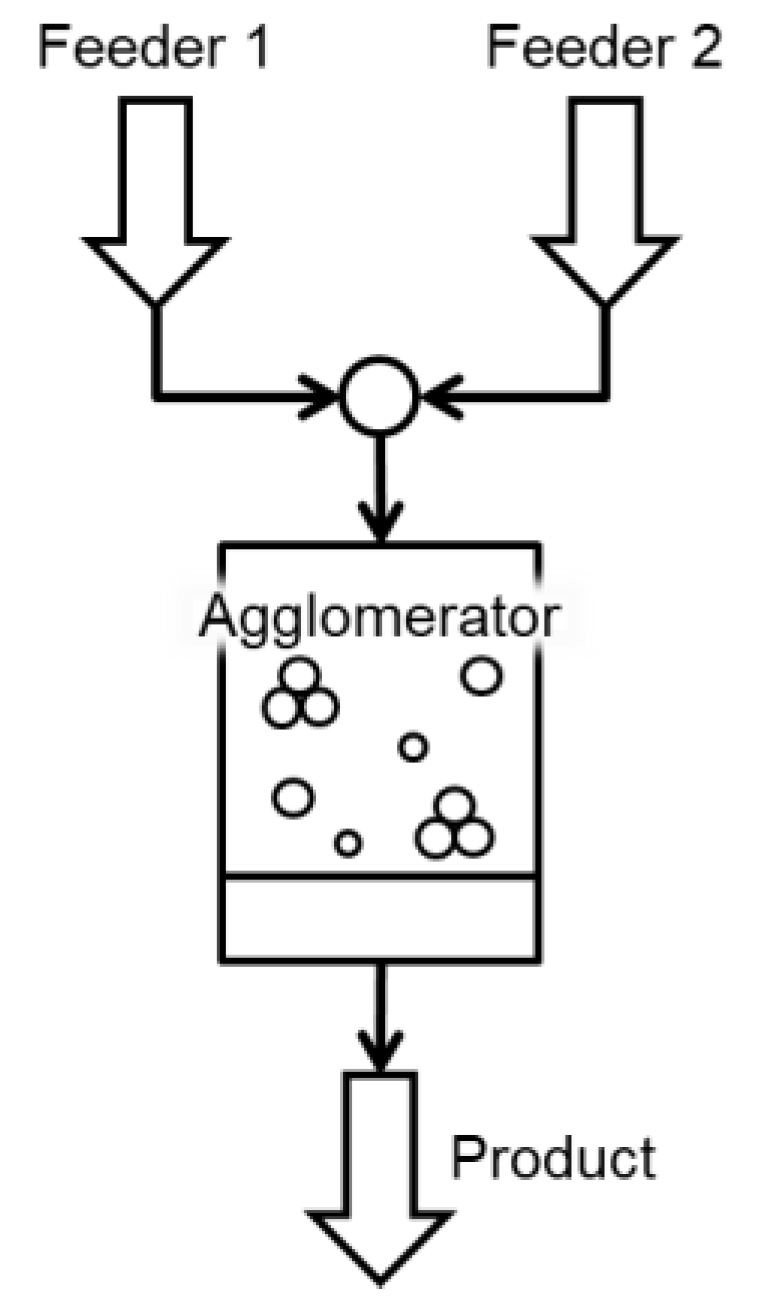
3.3.1. Agglomerator
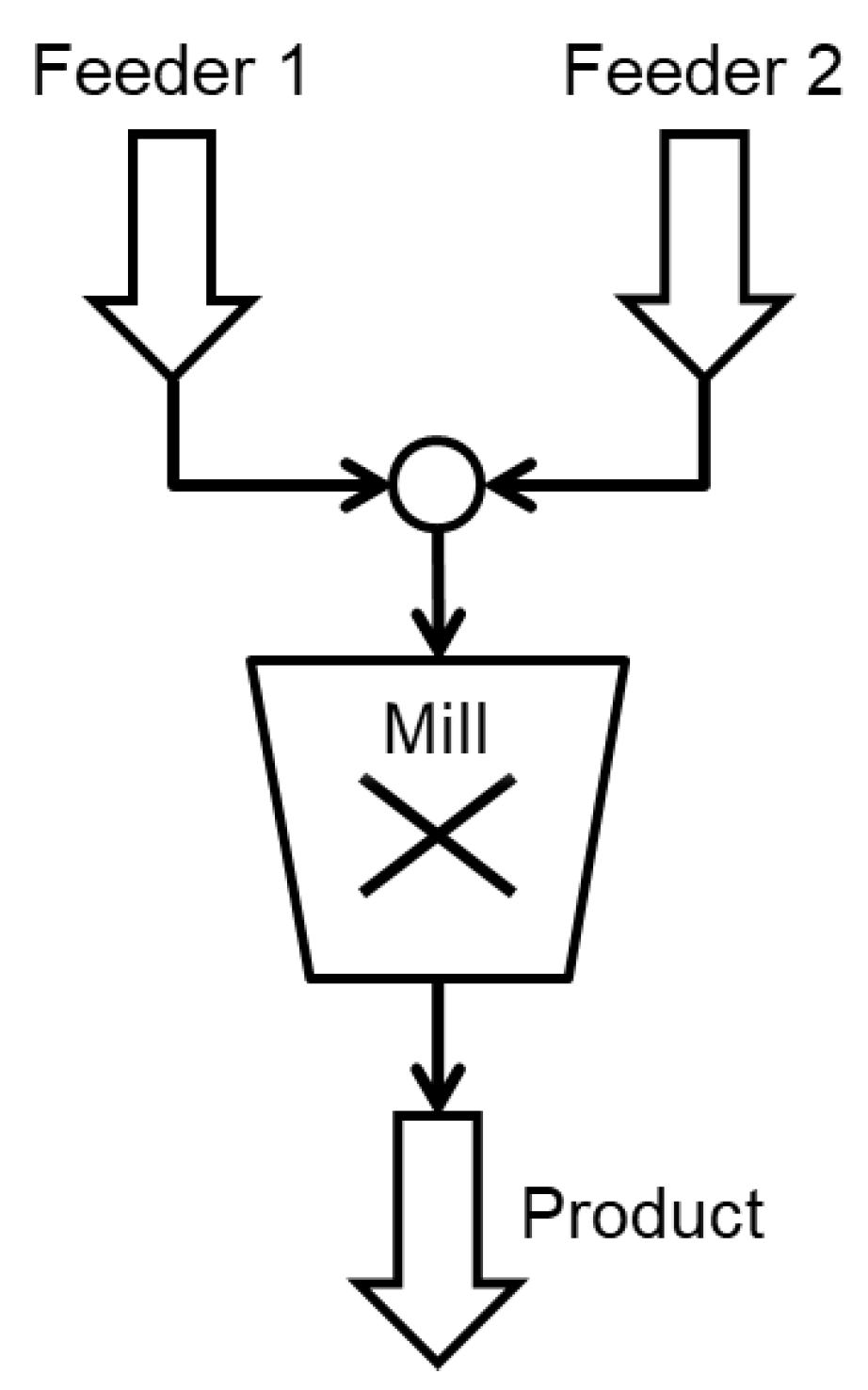
3.3.2. Mill
3.3.3. Screen
4. Simulation Examples
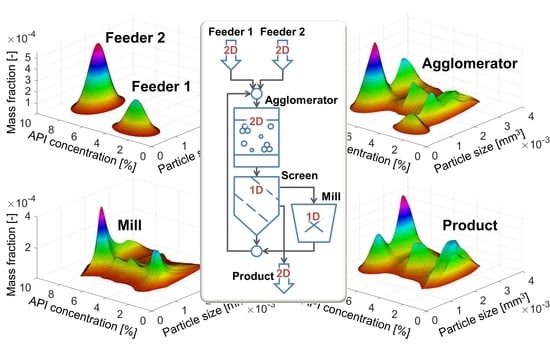
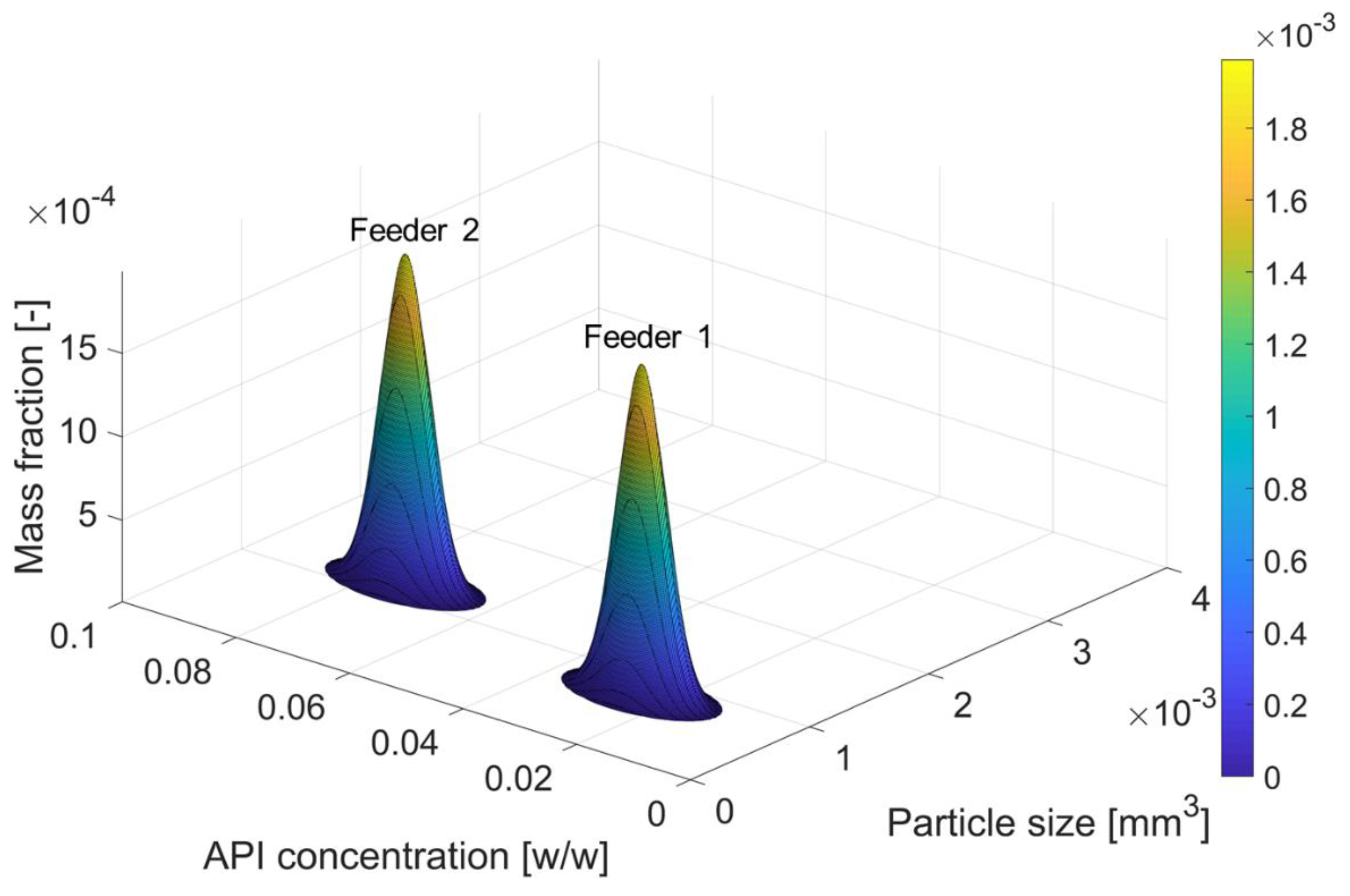
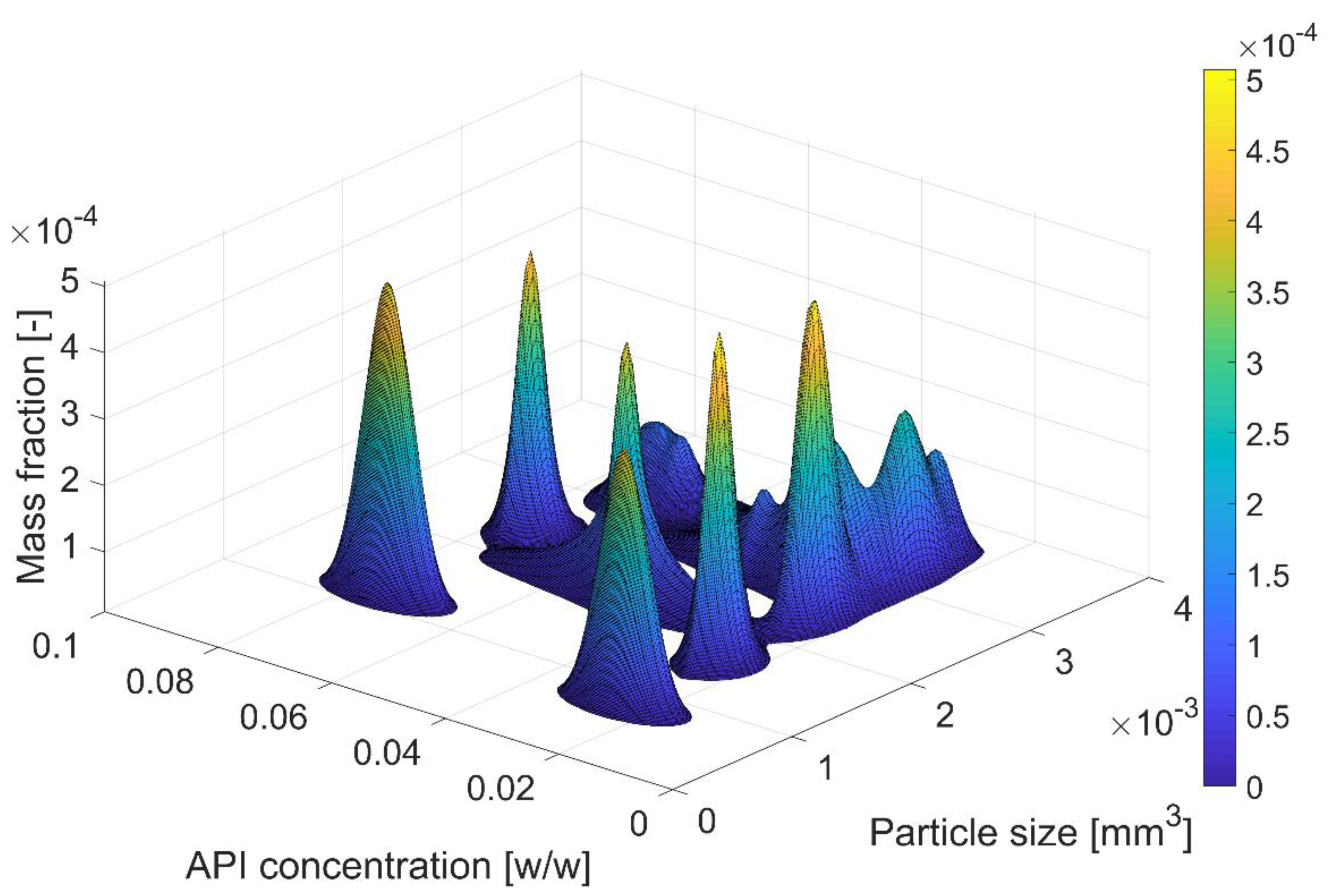
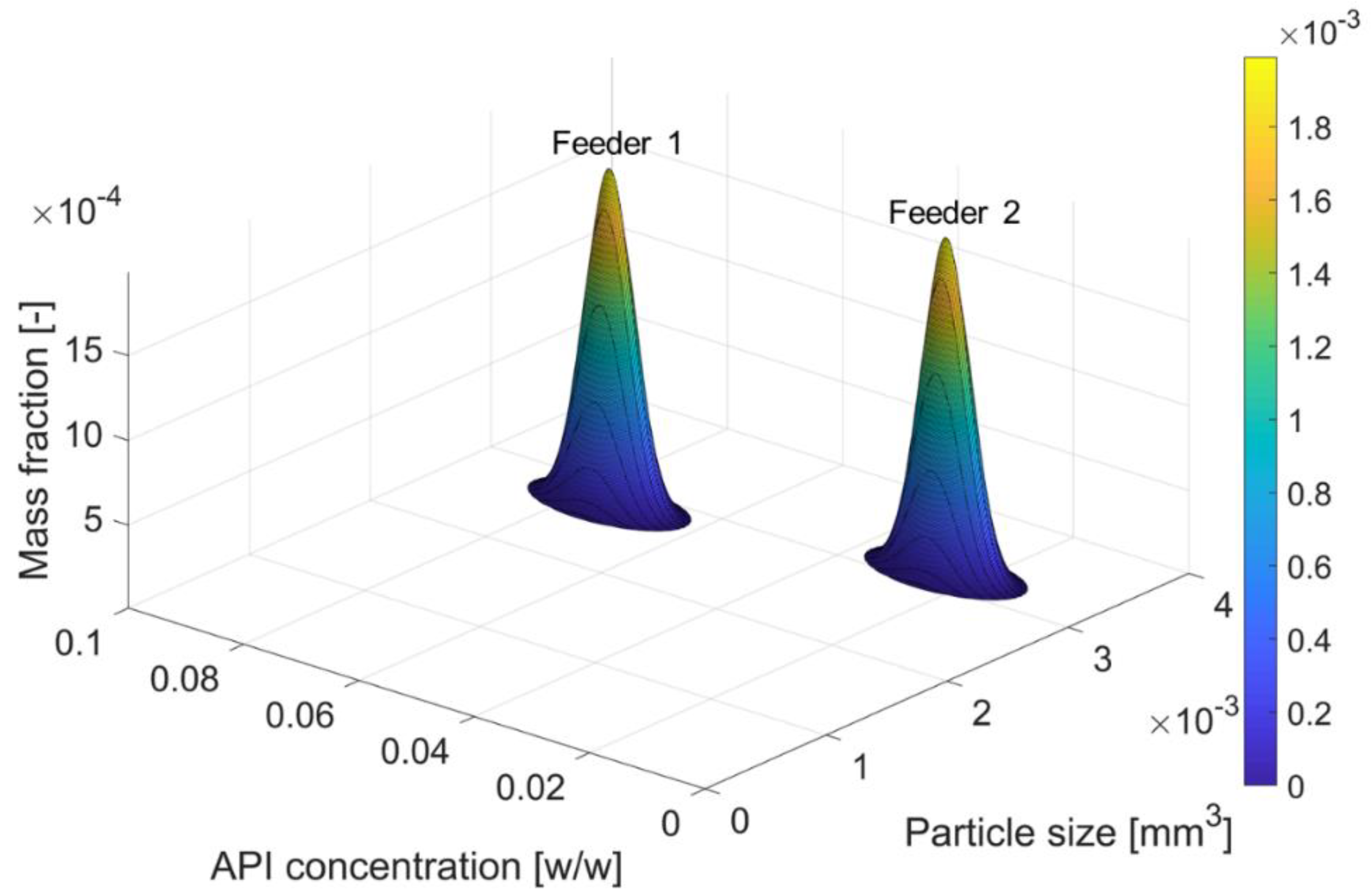
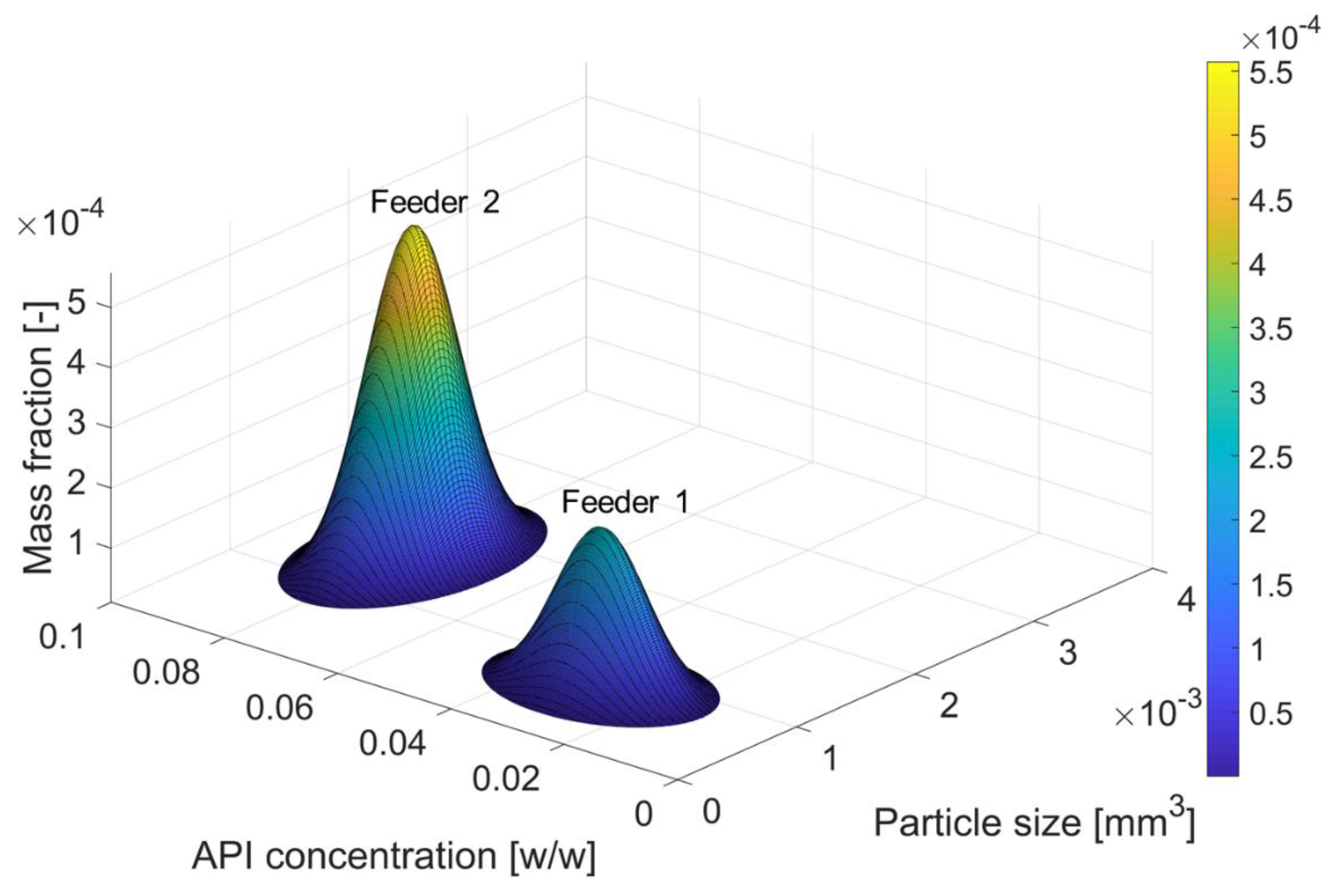
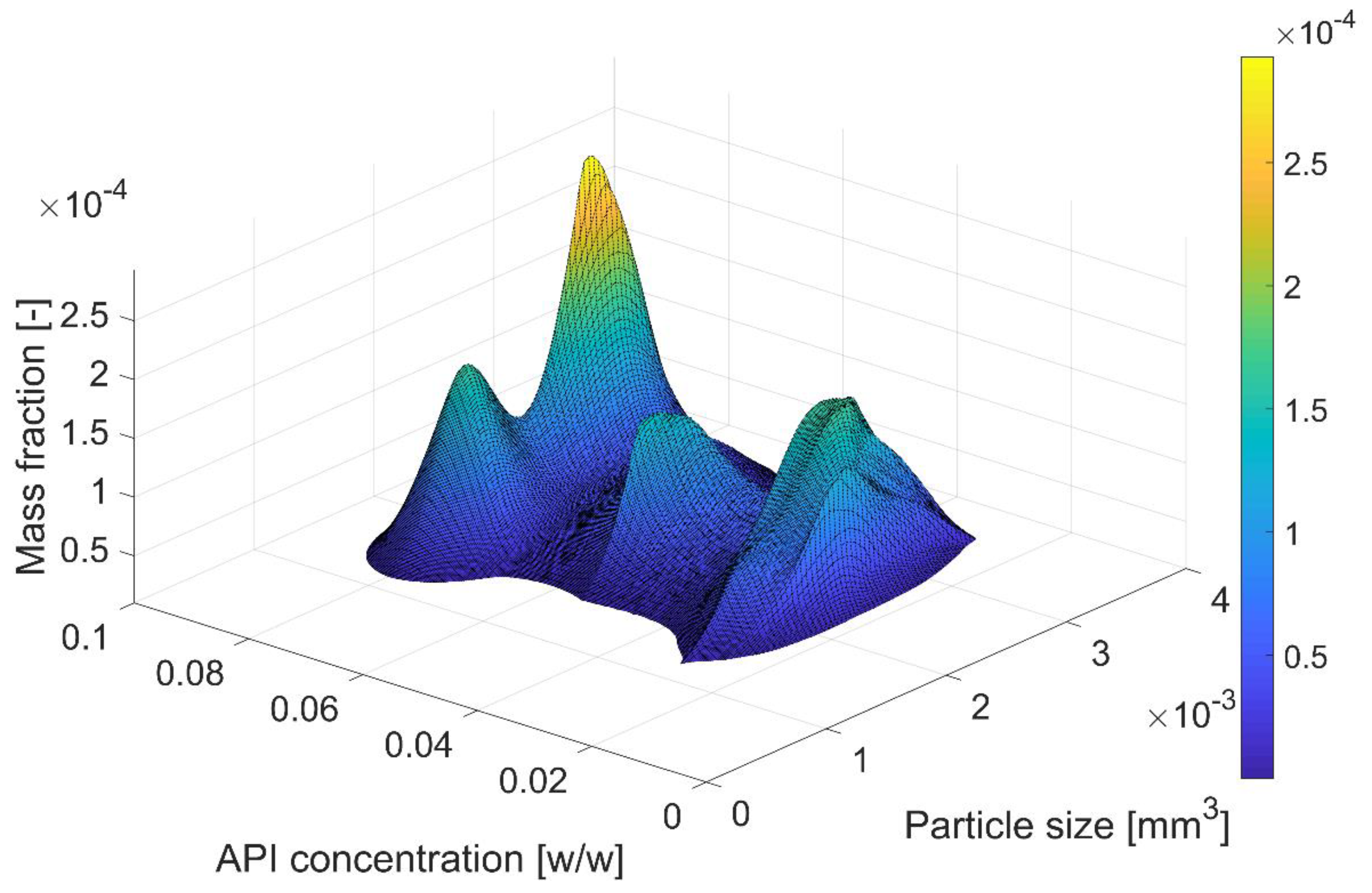
4.1. Agglomeration
- Particle size representing the volume of particles ranging from 0 to 4 × 10−3 mm3 and distributed over 100 equidistant classes; and
- the API concentration, which describes the mass content of an active ingredient from 0 to 10% divided into 500 equidistant classes.
- Feeder 1 supplies smaller particles with a lower API concentration;
- Feeder 2 supplies larger particles with a higher API concentration.
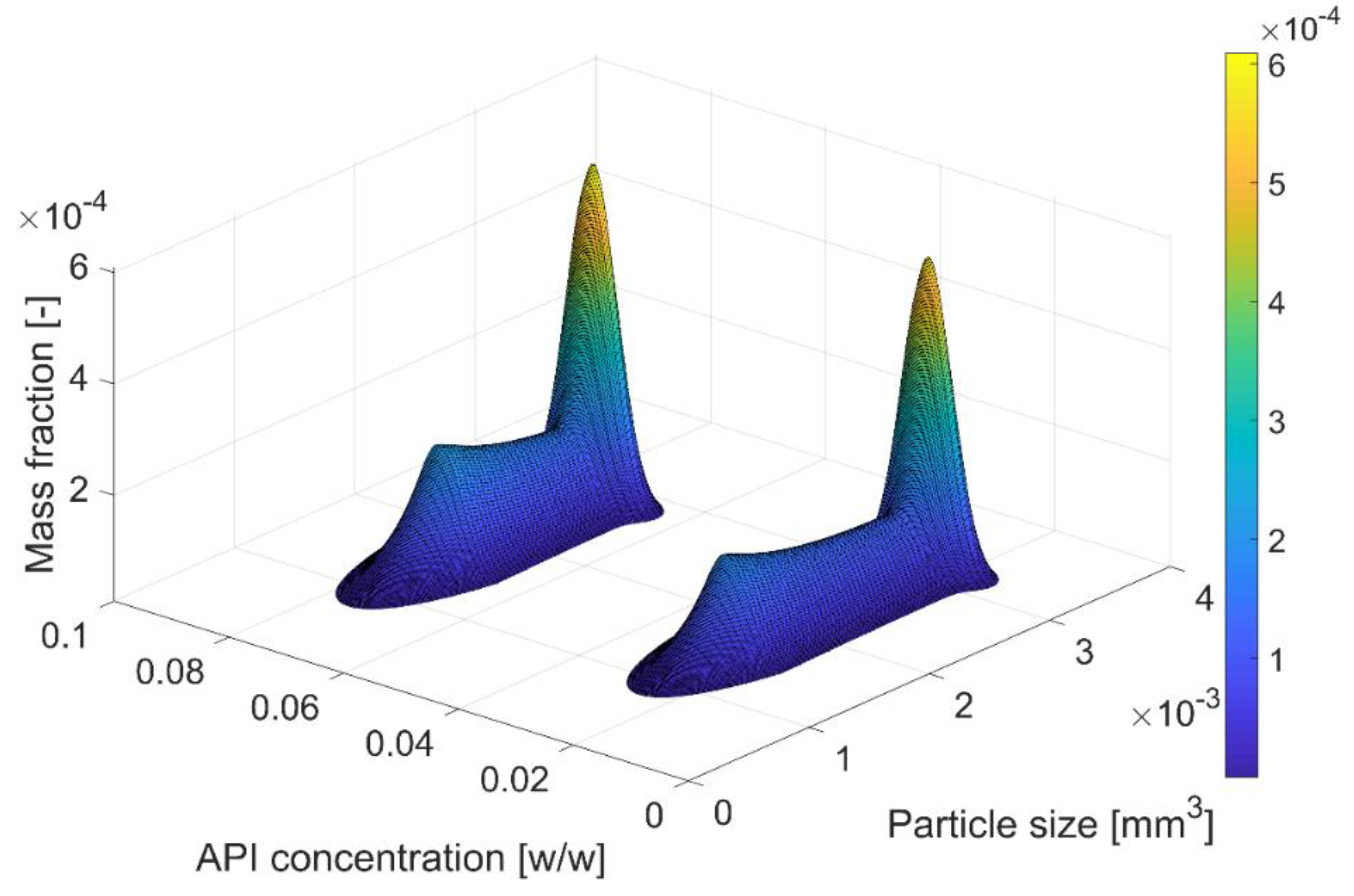
4.2. Breakage
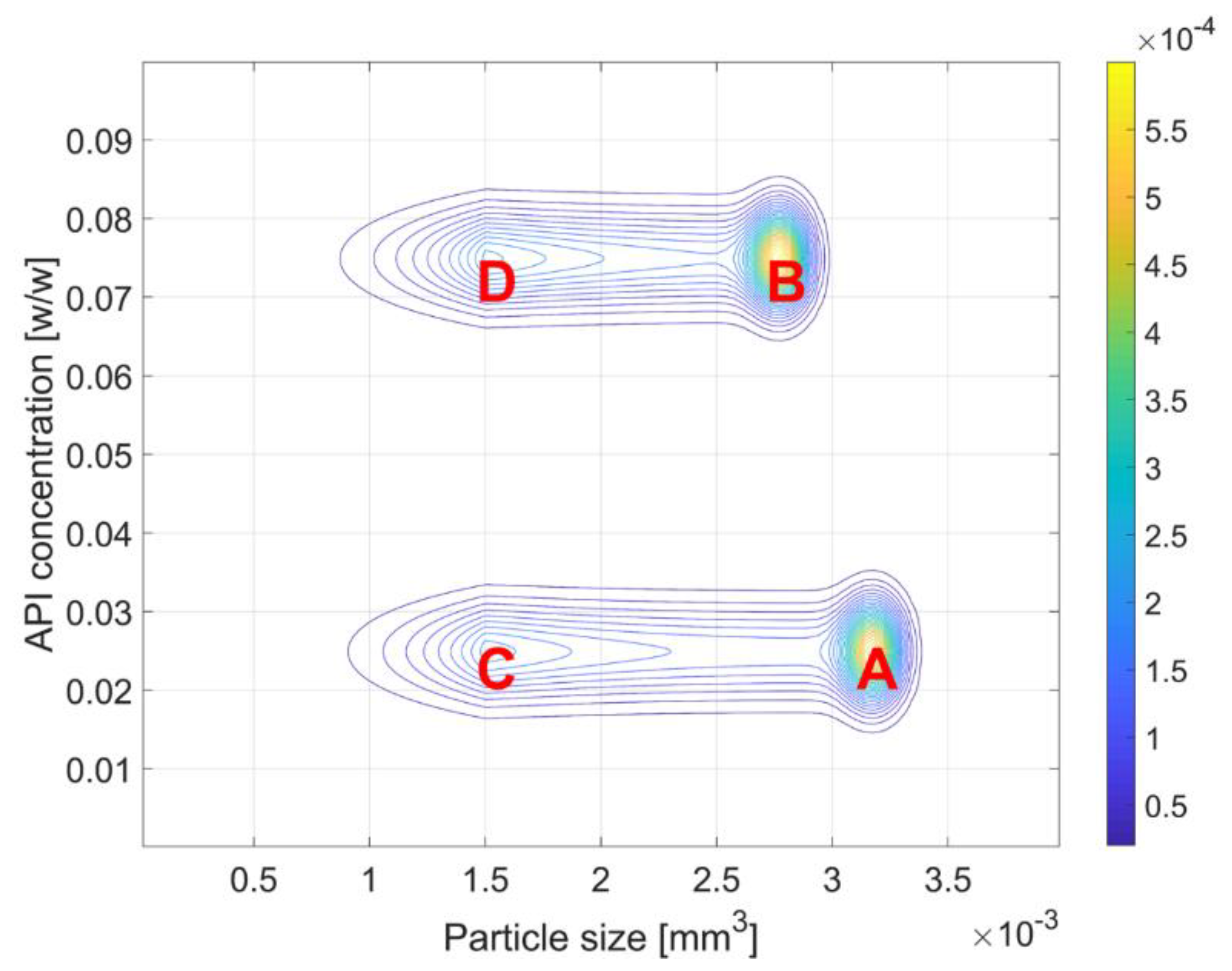
4.3. Coupled Agglomeration and Breakage
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Notation
| fraction of particles of size formed due to the breakage of a particle of size | |
| fraction of particles of size-class formed due to the breakage of a particle of size-class | |
| control variables of a unit | |
| mass fraction of granular material falling into class of two-dimensional distribution | |
| index of a distributed property | |
| , | model functions of a unit for calculating holdup and output, respectively |
| grade efficiency of the screen unit | |
| unit’s holdup variables | |
| identity matrix | |
| total number of discrete classes for all distributed properties | |
| number of discrete classes for distributed property | |
| , | mass flow at the inlet and at the outlet streams of a unit, respectively |
| number of distributed properties in a model | |
| power law exponent of the King’s selection function | |
| number of distributed properties in a flowsheet | |
| model parameters of a unit | |
| power law exponent of the Vogel breakage function | |
| , | distribution of particles by size at the input and at the output of a unit, respectively |
| design or structural parameters of a unit | |
| maximum size of particles in the considered interval | |
| parameter space formed by distributed parameters | |
| size-independent selection rate factor | |
| breakage rate of a particle of size | |
| breakage rate of a particle from size-class | |
| time | |
| transformation matrix, calculated at time to obtain the distribution after time step | |
| particular entry of a transformation matrix with specific indices | |
| , | transformation matrices to calculate holdups and output of a unit, respectively |
| mass fraction of particles of size | |
| mass fraction of particles of size at the initial moment of time | |
| mass fraction of particles from size-class | |
| , | weighting parameters for agglomeration, for birth and death of particles, respectively |
| , | particle sizes |
| critical sizes of particles for agglomeration | |
| critical sizes of particles for breakage | |
| cut size of the screen unit | |
| size of particles in a discrete class | |
| unit’s input variables | |
| relative mass fraction, stored in the –th class of the –th hierarchical level in the initial distribution | |
| particle size | |
| minimum fragment size of the Vogel breakage function | |
| unit’s output variables | |
| relative mass fraction, stored in the –th class of the –th hierarchical level in the transformed distribution | |
| separation sharpness of the screen unit | |
| agglomeration rate for particles of sizes and | |
| agglomeration rate for particles from size-classes and | |
| size-independent agglomeration rate constant | |
| size-dependent agglomeration rate constant | |
| length of size-class | |
| total number of particles of size appearing after breakage | |
| , | model functions of a unit in terms of the laws of material transition |
| mean value of the normal distribution function describing API concentration | |
| mean value of the normal distribution function describing particle sizes | |
| standard deviation of the normal distribution function describing API concentration | |
| standard deviation of the normal distribution function describing particle sizes | |
| , | weighting parameters for breakage, for birth and death of particles, respectively |
| operation of applying the transformation matrix | |
| set of indices to address any value in the –dimensional parameter space | |
| set of indices to address particles going from a lower to a higher cell |
References
- Kovačević, T.; Wiedmeyer, V.; Schock, J.; Voigt, A.; Pfeiffer, F.; Sundmacher, K.; Briesen, H. Disorientation angle distribution of primary particles in potash alum aggregates. J. Cryst. Growth 2017, 467, 93–106. [Google Scholar] [CrossRef][Green Version]
- Liu, L.X.; Litster, J.D.; Iveson, S.M.; Ennis, B.J. Coalescence of deformable granules in wet granulation processes. AIChE J. 2000, 46, 529–539. [Google Scholar] [CrossRef]
- Iveson, S.M.; Beathe, J.A.; Page, N.W. The dynamic strength of partially saturated powder compacts: The effect of liquid properties. Powder Technol. 2002, 127, 149–161. [Google Scholar] [CrossRef]
- Alaathar, I.; Hartge, E.-U.; Heinrich, S.; Werther, J. Modeling and flowsheet simulation of continuous fluidized bed dryers. Powder Technol. 2013, 238, 132–141. [Google Scholar] [CrossRef]
- Pogodda, M. Development of an Advanced System for the Modeling and Simulation of Solids Processes; Shaker Verlag: Aachen, Germany, 2007. [Google Scholar]
- Dosta, M. Dynamic Flowsheet Simulation of Solids Processes and Its Application to Fluidized Bed Spray Granulation; Cuvillier Verlag: Göttingen, Germany, 2013. [Google Scholar]
- Skorych, V.; Dosta, M.; Hartge, E.-U.; Heinrich, S. Novel system for dynamic flowsheet simulation of solids processes. Powder Technol. 2017, 314, 665–679. [Google Scholar] [CrossRef]
- Hartge, E.U.; Pogodda, M.; Reimers, C.; Schwier, D.; Gruhn, G.; Werther, J. Flowsheet simulation of solids processes. KONA Powder Part. J. 2006, 24, 146–158. [Google Scholar] [CrossRef]
- Werther, J.; Heinrich, S.; Dosta, M.; Hartge, E.-U. The ultimate goal of modelling—Simulation of system and plant performance. Particuology 2011, 9, 320–329. [Google Scholar] [CrossRef]
- Aspentech—Aspen Plus. Available online: https://www.aspentech.com/en/products/engineering/aspen-plus (accessed on 24 July 2019).
- PSE Products—gFORMULATE—gPROMS FormulatedProducts—Solids Processing. Available online: https://www.psenterprise.com/products/gproms/formulatedproducts (accessed on 24 July 2019).
- JKSimMet—JKTech Simulation of Comminution and Classification Circuits. Available online: https://jktech.com.au/jksimmet (accessed on 24 July 2019).
- HSC Sim—Process Simulation Module. Available online: https://www.outotec.com/products/digital-solutions/hsc-chemistry/hsc-sim-process-simulation-module (accessed on 24 July 2019).
- CHEMCAD—Chemical Engineering Simulation Software by Chemstations. Available online: https://www.chemstations.com/CHEMCAD (accessed on 24 July 2019).
- Dosta, M.; Heinrich, S.; Werther, J. Fluidized bed spray granulation: Analysis of the system behaviour by means of dynamic flowsheet simulation. Powder Technol. 2010, 204, 71–82. [Google Scholar] [CrossRef]
- Neugebauer, C.; Palis, S.; Bück, A.; Diez, E.; Heinrich, S.; Tsotsas, E.; Kienle, A. Influence of mill characteristics on stability of continuous layering granulation with external product classification. Comput. Aided Chem. Eng. 2016, 38, 1275–1280. [Google Scholar]
- Haus, J.; Hartge, E.-U.; Heinrich, S.; Werther, J. Dynamic flowsheet simulation for chemical looping combustion of methane. Int. J. Greenh. Gas Control 2018, 72, 26–37. [Google Scholar] [CrossRef]
- Koeninger, B.; Hensler, T.; Romeis, S.; Peukert, W.; Wirth, K.-E. Dynamics of fine grinding in a fluidized bed opposed jet mill. Powder Technol. 2018, 327, 346–357. [Google Scholar] [CrossRef]
- Sander, S.; Gawor, S.; Fritsching, U. Separating polydisperse particles using electrostatic precipitators with wire and spiked-wire discharge electrode design. Particuology 2018, 38, 10–17. [Google Scholar] [CrossRef]
- Boukouvala, F.; Niotis, V.; Ramachandran, R.; Muzzio, F.J.; Ierapetritou, M.G. An integrated approach for dynamic flowsheet modeling and sensitivity analysis of a continuous tablet manufacturing process. Comput. Chem. Eng. 2012, 42, 30–47. [Google Scholar] [CrossRef]
- Rogers, A.J.; Inamdar, C.; Ierapetritou, M.G. An integrated approach to simulation of pharmaceutical processes for solid drug manufacture. Ind. Eng. Chem. Res. 2014, 53, 5128–5147. [Google Scholar] [CrossRef]
- Skorych, V.; Dosta, M.; Hartge, E.-U.; Heinrich, S.; Ahrens, R.; Le Borne, S. Investigation of an FFT-based solver applied to dynamic flowsheet simulation of agglomeration processes. Adv. Powder Technol. 2019, 30, 555–564. [Google Scholar] [CrossRef]
- Sastry, K.V.S. Similarity size distribution of agglomerates during their growth by coalescence in granulation or green pelletization. Int. J. Miner. Process. 1975, 2, 187–203. [Google Scholar] [CrossRef]
- Hill, P.J.; Ng, K.M. Statistics of multiple particle breakage. AIChE J. 1996, 42, 1600–1611. [Google Scholar] [CrossRef]
- Hulburt, H.M.; Katz, S. Some problems in particle technology: A statistical mechanical formulation. Chem. Eng. Sci. 1964, 19, 555–574. [Google Scholar] [CrossRef]
- Barrett, J.; Jheeta, J. Improving the accuracy of the moments method for solving the aerosol general dynamic equation. J. Aerosol Sci. 1996, 27, 1135–1142. [Google Scholar] [CrossRef]
- Madras, G.; McCoy, B.J. Reversible crystal growth-dissolution and aggregation-breakage: Numerical and moment solutions for population balance equations. Powder Technol. 2004, 143, 297–307. [Google Scholar] [CrossRef]
- Marchisio, D.L.; Fox, R.O. Solution of population balance equations using the direct quadrature method of moments. J. Aerosol Sci. 2005, 36, 43–73. [Google Scholar] [CrossRef]
- Kumar, S.; Ramkrishna, D. On the solution of population balance equations by discretization—I. A fixed pivot technique. Chem. Eng. Sci. 1996, 51, 1311–1332. [Google Scholar] [CrossRef]
- Vale, H.M.; McKenna, T.F. Solution of the population balance equation for two-component aggregation by an extended fixed pivot technique. Ind. Eng. Chem. Res. 2005, 44, 7885–7891. [Google Scholar] [CrossRef][Green Version]
- Kruis, F.E.; Maisels, A.; Fissan, H. Direct simulation Monte Carlo method for particle coagulation and aggregation. AIChE J. 2000, 46, 1735–1742. [Google Scholar] [CrossRef]
- Lee, K.; Matsoukas, T. Simultaneous coagulation and break-up using constant-N Monte Carlo. Powder Technol. 2000, 110, 82–89. [Google Scholar] [CrossRef]
- Lin, Y.; Lee, K.; Matsoukas, T. Solution of the population balance equation using constant-number Monte Carlo. Chem. Eng. Sci. 2002, 57, 2241–2252. [Google Scholar] [CrossRef]
- Smith, M.; Matsoukas, T. Constant-number Monte Carlo simulation of population balances. Chem. Eng. Sci. 1998, 53, 1777–1786. [Google Scholar] [CrossRef]
- Mahoney, A.W.; Ramkrishna, D. Efficient solution of population balance equations with discontinuities by finite elements. Chem. Eng. Sci. 2002, 57, 1107–1119. [Google Scholar] [CrossRef]
- Nicmanis, M.; Hounslow, M. A finite element analysis of the steady state population balance equation for particulate systems: Aggregation and growth. Comput. Chem. Eng. 1996, 20, S261–S266. [Google Scholar] [CrossRef]
- Rigopoulos, S.; Jones, A.G. Finite-element scheme for solution of the dynamic population balance equation. AIChE J. 2003, 49, 1127–1139. [Google Scholar] [CrossRef]
- Hackbusch, W. On the efficient evaluation of coalescence integrals in population balance models. Computing 2006, 78, 145–159. [Google Scholar] [CrossRef]
- Le Borne, S.; Shahmuradyan, L.; Sundmacher, K. Fast evaluation of univariate aggregation integrals on equidistant grids. Comput. Chem. Eng. 2015, 74, 115–127. [Google Scholar] [CrossRef]
- Matveev, S.A.; Smirnov, A.P.; Tyrtyshnikov, E.E. A fast numerical method for the Cauchy problem for the Smoluchowski equation. J. Comput. Phys. 2015, 282, 23–32. [Google Scholar] [CrossRef]
- Kumar, J.; Peglow, M.; Warnecke, G.; Heinrich, S. An efficient numerical technique for solving population balance equation involving aggregation, breakage, growth and nucleation. Powder Technol. 2008, 182, 81–104. [Google Scholar] [CrossRef]
- Mostafaei, P.; Rajabi-Hamane, M. Numerical solution of the population balance equation using an efficiently modified cell average technique. Comput. Chem. Eng. 2017, 96, 33–41. [Google Scholar] [CrossRef]
- Kumar, J.; Saha, J.; Tsotsas, E. Development and convergence analysis of a finite volume scheme for solving breakage equation. SIAM J. Numer. Anal. 2015, 53, 1672–1689. [Google Scholar] [CrossRef]
- Kumar, J.; Kaur, G.; Tsotsas, E. An accurate and efficient discrete formulation of aggregation population balance equation. Kinet. Relat. Models 2016, 9, 373–391. [Google Scholar]
- Schwier, D.; Hartge, E.-U.; Werther, J.; Gruhn, G. Global sensitivity analysis in the flowsheet simulation of solids processes. Chem. Eng. Process. 2010, 49, 9–21. [Google Scholar] [CrossRef]
- Courant, R.; Friedrichs, K.; Lewy, H. Über die partiellen Differenzengleichungen der mathematischen physik. Math. Ann. 1928, 100, 32–74. [Google Scholar] [CrossRef]
- DFG-Priority Programme SPP 1679. Available online: https://www.dynsim-fp.de/en/home (accessed on 24 July 2019).
- Stroustrup, B. The C++ Programming Language, 4th ed.; Addison-Wesley: Boston, MA, USA, 2013. [Google Scholar]
- Stroustrup, B. Tour of C++, 4th ed.; Addison-Wesley: Boston, MA, USA, 2014; pp. 23–57. [Google Scholar]
- Hillestad, M.; Hertzberg, T. Dynamic simulation of chemical engineering systems by the sequential modular approach. Comput. Chem. Eng. 1986, 10, 377–388. [Google Scholar] [CrossRef]
- Dosta, M. Modular-based simulation of single process units. Chem. Eng. Technol. 2019, 42, 699–707. [Google Scholar] [CrossRef]
- Towler, G.; Sinnott, R. Chemical Engineering Design: Principles, Practice and Economics of Plant and Process Design, 2nd ed.; Butterworth-Heinemann: Kidlington, Oxford, UK, 2013; pp. 223–236. [Google Scholar]
- Dimian, A.C.; Bildea, C.S.; Kiss, A.A. Dynamic Simulation. Comput. Aided Chem. Eng. 2014, 35, 127–156. [Google Scholar]
- Lelarasmee, E.; Ruehli, A.E.; Sangiovanni-Vincintelli, A.L. The Waveform Relaxation Method for Time-Domain Analysis of Large Scale Integrated Circuits: Theory and Applications. Ph.D. Thesis, University of California, Berkeley, Berkeley, CA, USA, 1982. [Google Scholar]
- Smoluchowski, M. Versuch einer mathematischen Theorie der Koagulationskinetik kolloider Losungen. Z. Phys. Chem. 1916, 17, 129–168. [Google Scholar] [CrossRef]
- Aldous, D.J. Deterministic and stochastic models for coalescence (aggregation and coagulation): A review of the mean-field theory for probabilists. Bernoulli 1999, 5, 3–48. [Google Scholar] [CrossRef]
- Kuncir, G.F. Algorithm 103: Simpson’s rule integrator. Commun. ACM 1962, 5, 347. [Google Scholar] [CrossRef]
- Lyness, J.N. Notes on the adaptive Simpson quadrature routine. J. ACM 1969, 16, 483–495. [Google Scholar] [CrossRef]
- King, R.P. Modeling and Simulation of Mineral Processing Systems; Butterworth & Heinemann: Oxford, UK, 2001; p. 158. [Google Scholar]
- Vogel, L.; Peukert, W. Modelling of grinding in an air classifier mill based on a fundamental material function. KONA Powder Part. J. 2003, 21, 109–120. [Google Scholar] [CrossRef][Green Version]
- Plitt, L.R. The analysis of solid-solid separations in classifiers. CIM Bull. 1971, 64, 42–47. [Google Scholar]


| Feeder 1 | ||
| Mass Flow | 0.25 kg/s | |
| Mean value of the particle size distribution | 0.78 × 10−3 mm3 | |
| Standard deviation of the particle size distribution | 0.8 × 10−4 mm3 | |
| Mean value of the API concentration distribution | 0.025 | |
| Standard deviation of the API concentration distribution | 0.004 | |
| Feeder 2 | ||
| Mass Flow | 0.25 kg/s | |
| Mean value of the particle size distribution | 1.18 × 10−3 mm3 | |
| Standard deviation of the particle size distribution | 0.8 × 10−4 mm3 | |
| Mean value of the API concentration distribution | 0.075 | |
| Standard deviation of the API concentration distribution | 0.004 | |
| Agglomerator | ||
| Holdup mass | 200 kg | |
| Size-independent rate constant | 2 × 10−16 | |
| Minimum agglomeration size | 0.4 × 10-3 mm3 | |
| Maximum agglomeration size | 3.75 × 10−3 mm3 | |
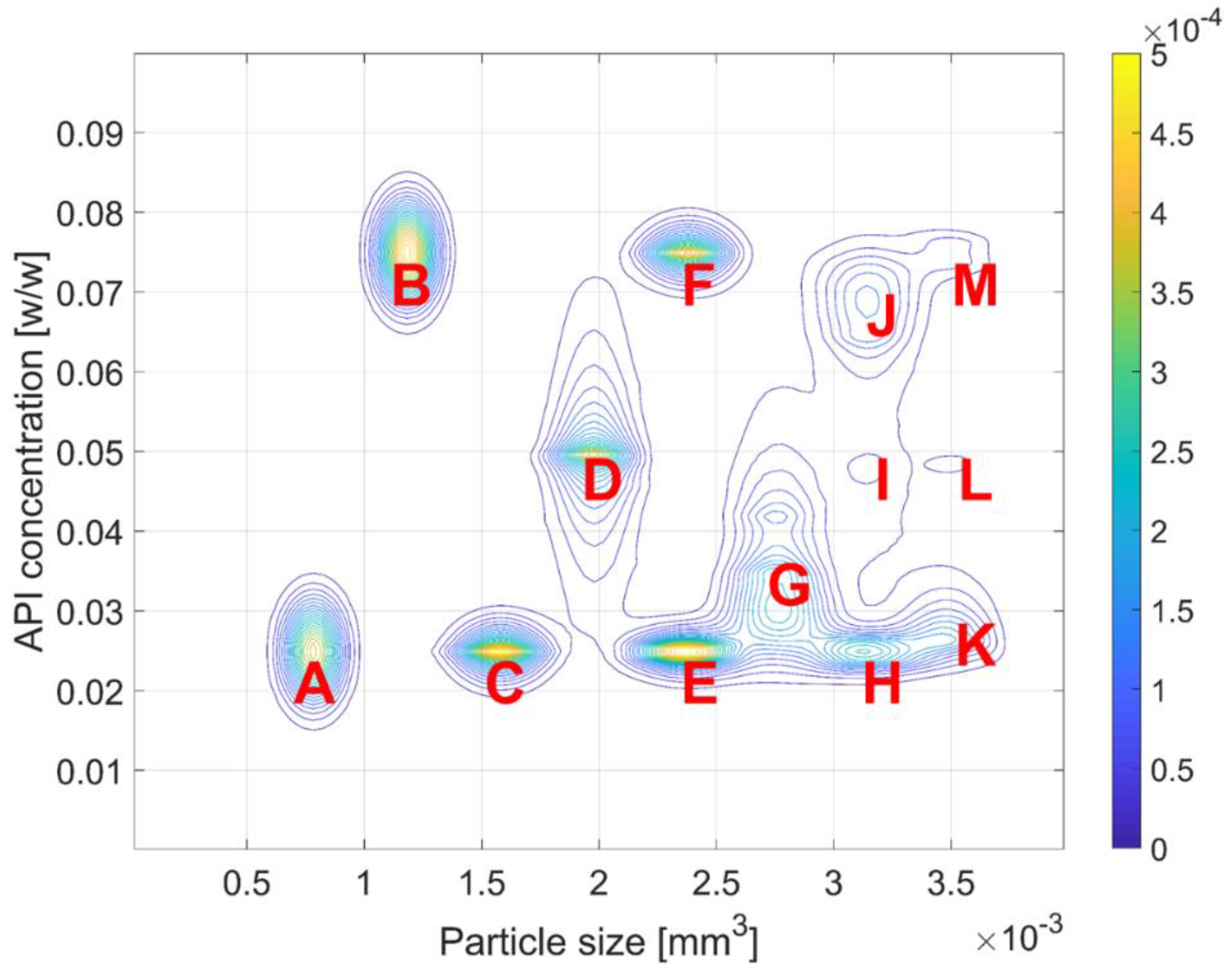
| + | A | B | C | D | E | F | G |
|---|---|---|---|---|---|---|---|
| A | C | D | E | G | H | I | K |
| B | F | G | J | L | M | - | |
| C | H | K | - | - | - |
| Feeder 1 | ||
| Mass Flow | 0.25 kg/s | |
| Mean value of the particle size distribution | 3.18 × 10−3 mm3 | |
| Standard deviation of the particle size distribution | 0.8 × 10−4 mm3 | |
| Mean value of the API concentration distribution | 0.025 | |
| Standard deviation of the API concentration distribution | 0.004 | |
| Feeder 2 | ||
| Mass Flow | 0.25 kg/s | |
| Mean value of the particle size distribution | 2.78 × 10−3 mm3 | |
| Standard deviation of the particle size distribution | 0.8 × 10−4 mm3 | |
| Mean value of the API concentration distribution | 0.075 | |
| Standard deviation of the API concentration distribution | 0.004 | |
| Mill | ||
| Holdup mass | 50 kg | |
| Selection rate factor | 3 × 10−2 | |
| Minimum breakage size | 1.5 × 10−3 mm3 | |
| Maximum breakage size | 4 × 10−3 mm3 | |
| Selection power law exponent | 3.1 | |
| Minimum fragment size | 0.5 × 10−3 mm3 | |
| Breakage power law exponent | 5.5 | |
| Feeder 1 | ||
| Mass Flow | 0.15 kg/s | |
| Mean value of the particle size distribution | 0.78 × 10−3 mm3 | |
| Standard deviation of the particle size distribution | 2.0 × 10−4 mm3 | |
| Mean value of the API concentration distribution | 0.03 | |
| Standard deviation of the API concentration distribution | 0.007 | |
| Feeder 2 | ||
| Mass flow | 0.35 kg/s | |
| Mean value of the particle size distribution | 1.58 × 10−3 mm3 | |
| Standard deviation of the particle size distribution | 3.2 × 10−4 mm3 | |
| Mean value of the API concentration distribution | 0.08 | |
| Standard deviation of the API concentration distribution | 0.005 | |
| Agglomerator | ||
| Holdup mass | 200 kg | |
| Size-independent rate constant | 2 × 10-16 | |
| Minimum agglomeration size | 0.4 × 10−3 mm3 | |
| Maximum agglomeration size | 3.75 × 10−3 mm3 | |
| Mill | ||
| Holdup mass | 50 kg | |
| Selection rate factor | 3 × 10-2 | |
| Minimum breakage size | 1.5 × 10−3 mm3 | |
| Maximum breakage size | 3.2 × 10−3 mm3 | |
| Selection power law exponent | 3.1 | |
| Minimum fragment size | 10−3 mm3 | |
| Breakage power law exponent | 5.5 | |
| Screen deck 1 | ||
| Cut size | 3.2 × 10−3 mm3 | |
| Separation sharpness | 13 | |
| Screen deck 2 | ||
| Cut size | 2.3 × 10−3 mm3 | |
| Separation sharpness | 13 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Skorych, V.; Das, N.; Dosta, M.; Kumar, J.; Heinrich, S. Application of Transformation Matrices to the Solution of Population Balance Equations. Processes 2019, 7, 535. https://doi.org/10.3390/pr7080535
Skorych V, Das N, Dosta M, Kumar J, Heinrich S. Application of Transformation Matrices to the Solution of Population Balance Equations. Processes. 2019; 7(8):535. https://doi.org/10.3390/pr7080535
Chicago/Turabian StyleSkorych, Vasyl, Nilima Das, Maksym Dosta, Jitendra Kumar, and Stefan Heinrich. 2019. "Application of Transformation Matrices to the Solution of Population Balance Equations" Processes 7, no. 8: 535. https://doi.org/10.3390/pr7080535
APA StyleSkorych, V., Das, N., Dosta, M., Kumar, J., & Heinrich, S. (2019). Application of Transformation Matrices to the Solution of Population Balance Equations. Processes, 7(8), 535. https://doi.org/10.3390/pr7080535