1. Introduction
In recent years, having benefited from the rapid progress in industrial process and its control system, thermal processing systems, especially those with temperature control, are attracting more attention for achieving high-quality and high-performance processing. In thermal processing, the temperature uniformity is one of the most basic and important requirements. For example, most of the applications of thermal processes are centered on the food industry, where requirements of temperature uniformity and faster transient response are strongly in demand.
Due to these requirements, various control methods have been proposed and introduced into temperature control systems. Among the various thermal processing techniques, the conventional proportional–integral–derivative (PID) controller has become the most commonly used control method benefiting from its simplicity and wide applicability [
1,
2,
3,
4,
5,
6]. However, due to the nonlinearity and the coupling influence of multi-point systems, it is difficult to realize precise temperature control based only on the conventional PID control method. Thus, the series the series connected fuzzy-proportional integral (SF-PI) control method is proposed to improve the control performance [
7].
For the coupling difficulties as stated above, a novel decoupling compensation or quasi- decoupling method has been investigated in multi-input, multi-output (MIMO) temperature control systems by building an equivalent model of multiple SISO (single-input, single-output) systems [
8,
9,
10,
11,
12,
13]. However, if we cannot obtain a precise plant model, that decoupling compensation method would not work as efficiently as expected. Thus, the system identification methods have been applied to the temperature control system, and the most popular method is the step response method [
14,
15,
16]. With the mathematical model of the system, the Model Predictive Control (MPC) method has been proposed on the heating system to provide precise control [
17].
Moreover, although a precise plant model has been obtained and the decoupling compensation method has been applied, there remain some difficulties, such as: dead-time difference between the multiple points and the large time delay in the plant. These difficulties have a significant impact on the transient response and temperature difference. Thus, some advanced compensation methods have been proposed: feed forward compensation, data-driven tuning, and gradient temperature control [
18,
19,
20,
21].
Furthermore, for the excessively complex thermal process system, the mathematic model could not be obtained precisely. Thus, the data-driven approaches have been proposed as a potential method for controlling that system [
22], and some optimization methods have also been proposed for these excessively complex processes [
23].
Although after all the above methods have been introduced into the temperature control system in the thermal process, there are still some problems with the transient response and the closely controlled temperature of the multi-point temperature control system with dead-time difference and strong coupling effects. For example, in MIMO heating systems the temperature difference between each point should be under 5% of the reference temperature, no matter whether the transient response is fast or slow. Until now, the abovementioned method still cannot achieve the effect we expected in multi-point temperature control systems that have a large time constant and big dead-time difference. For example, if the system is composed of only a Smith predictive control method, the temperature difference may not be prevented. Also, if the system is composed of only a gradient control method, the transient response may not be drastically improved. Our previous work has proposed a pole-zero cancellation with reference model method for such a class of temperature control system [
24]. This paper focuses on the multi-point temperature heating system, improving the transient response of each channel and reducing the temperature difference between each point, while also providing a systematic design method for the controller design, and a novel slow-mode-based control method is proposed for multi-point temperature control systems [
25]. In the proposed method, the temperature differences and transient characteristics of all points can be controlled by making the output of the fast modes follow the output of the slow mode. In this paper, the SMBC method combined with decoupling and dead-time compensation is applied to the MIMO temperature control system, in addition to the theoretical analysis of the system being introduced, and simulations and experiments to verify the control efficiency of the proposed SMBC control method are described. The results are then compared to the conventional PI control and gradient temperature control methods.
2. Difficulties in Multi-Point Temperature Control
From the viewpoint of practical application of multi-point temperature control, well-tuned PID controllers with decoupling and dead-time compensations are used. The Ziegler–Nichols ultimate gain method and the constant heating rate method are representative heuristic methods based on experimental data [
1,
2]. These methods attempt to make the actual temperatures follow the reference values while minimizing the temperature differences between multiple points. However, in many cases, the following difficulties still exist: (1) The PID controller must be designed considering the effect of the dead-time difference of the controlled objects. (2) Although the temperature difference is somewhat decreased due to this consideration, a significant improvement in the transient response cannot be expected. (3) The transient response needs to be improved. (4) When the reference values of multiple points are different, it is difficult to control the individual setting times with the same temperature ratio.
3. Configuration of SMBC System
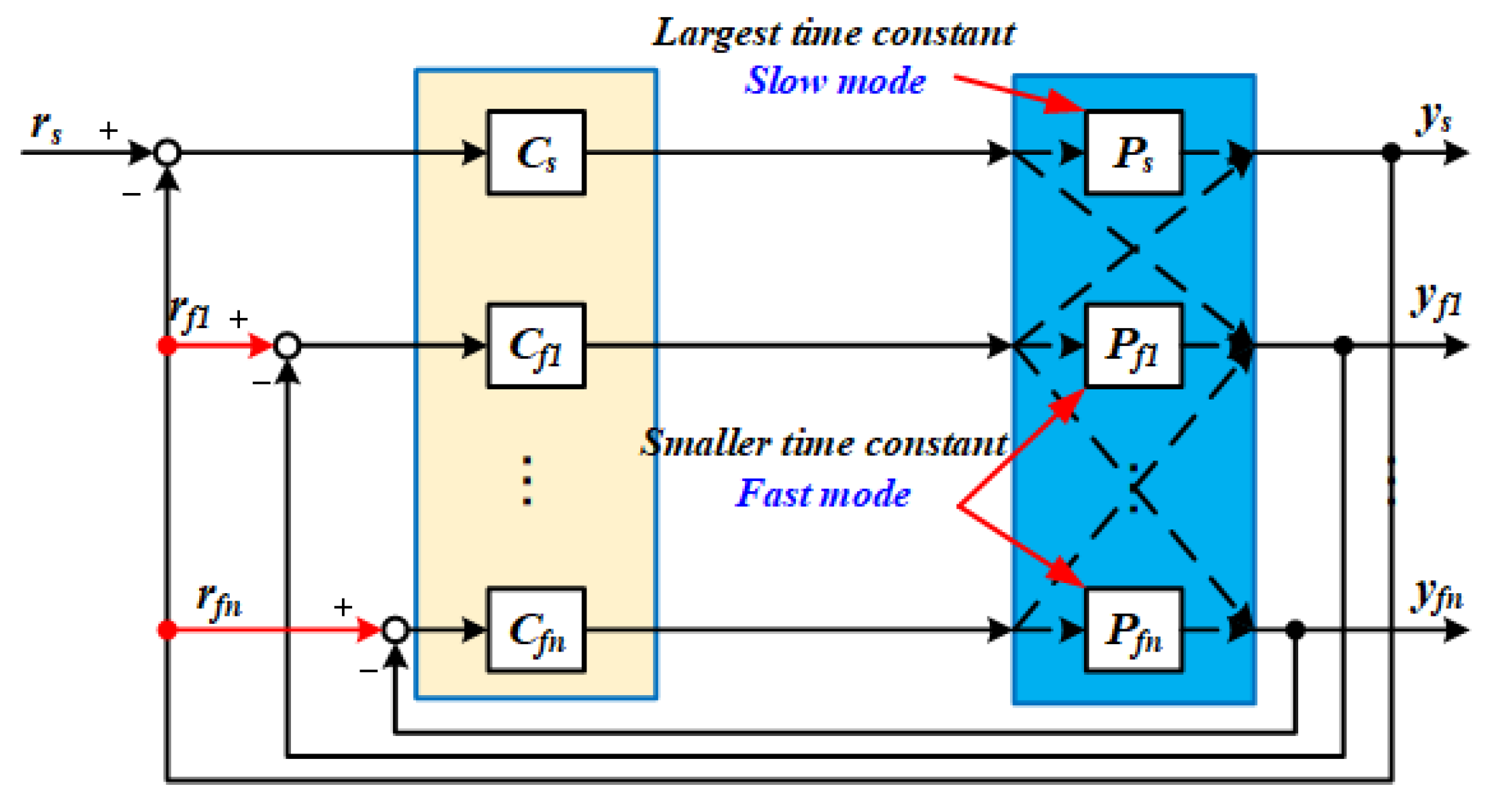
This section describes the proposed SMBC system. For convenience, the slow mode is defined as the plant system with the largest time constant, while the fast mode is defined as systems with smaller time constants. The block diagram of the proposed SMBC control system is shown in
Figure 1. In the figure,
is the reference value;
is the output temperature of the slow mode;
r and
r, which are equal to
y, are the reference values of the fast modes. In this proposal, the reference value of the fast modes is set to be the output value of the slow mode, and
y and
y are the outputs of the fast modes.
C is defined as the controller of the slow mode,
C and
C are indicate as the controllers of the fast modes.
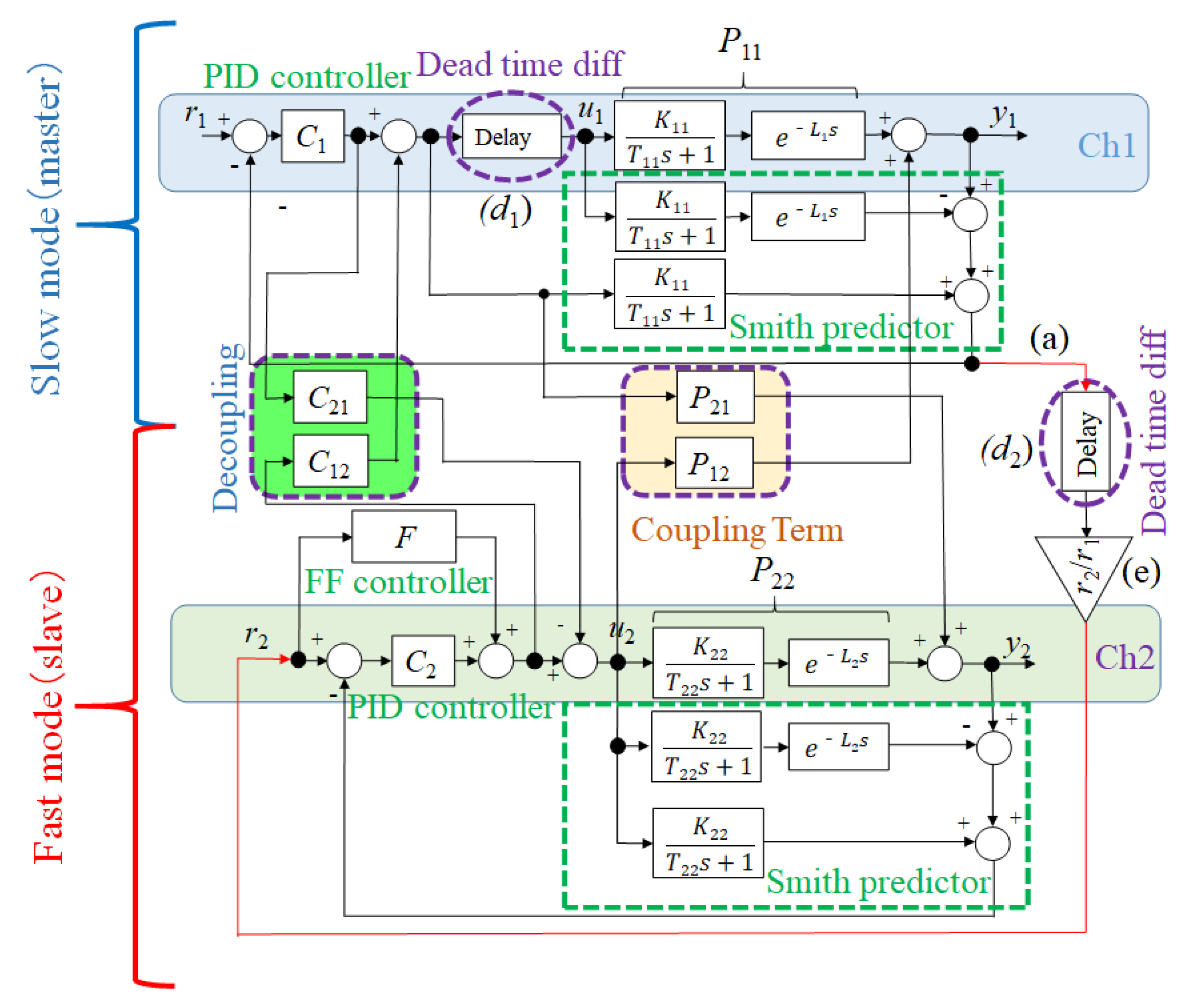
For simplicity, the proposed SMBC control method was applied to a simplified multi-point temperature control system with two inputs and two outputs. The block diagram is shown in
Figure 2, where
r and
y indicate the reference and the output temperatures respectively. The subscripts 1 (Ch1: channel 1) and 2 (Ch2: channel 2) refer to the slow mode and the fast mode, respectively. The steady-state gain, time constant, and dead time of the plant are expressed by
K,
T, and
L respectively. The proposed SMBC structure can be divided into seven blocks.
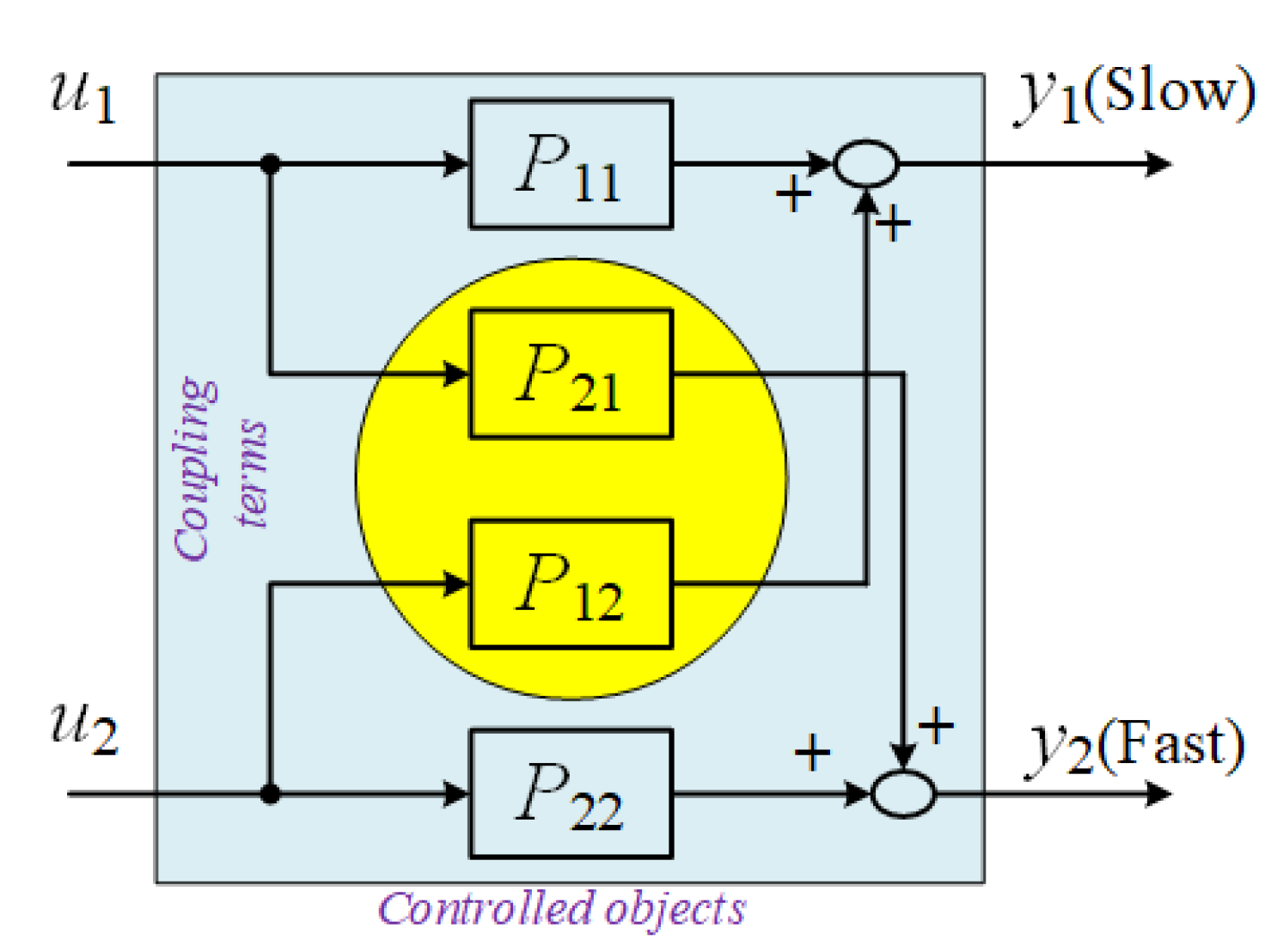
3.1. Structure in Which the Controlled Objects Are under Strong Coupling Effectiveness
Since the controlled plant has been simplified to a two inputs, two outputs system, the two channels are strongly under coupled effectiveness. The diagram of the two channels is shown in
Figure 3, where
P and
P indicate the controlled objects of Ch1 and Ch2, respectively, and
P and
P indicate the respective coupling terms between these two channels.
The transfer function of both the controlled objects and the coupling terms are expressed as a first-order plus time delay system as (1), where the plant parameters
K,
T, and
L have already been defined.
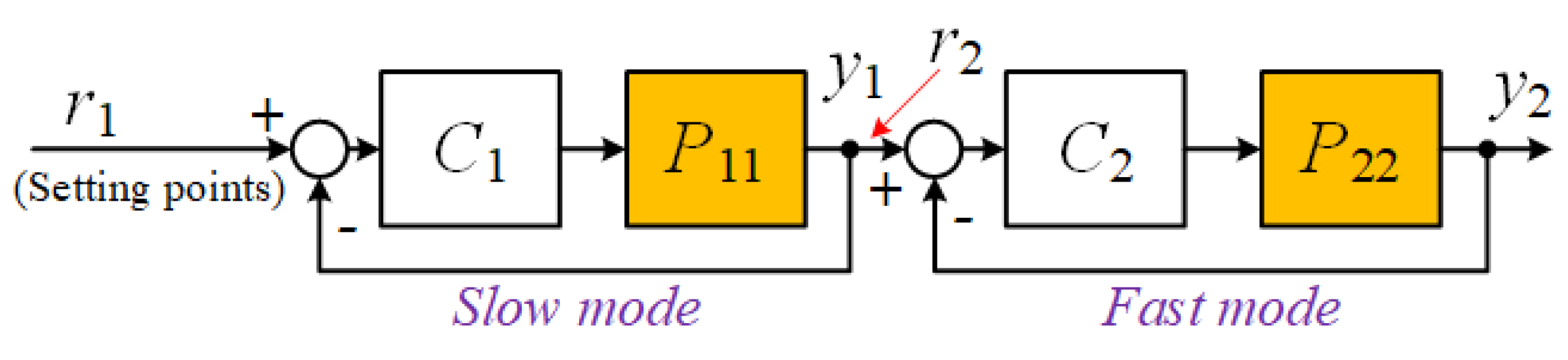
3.2. Structure in Which Fast-Mode Outputs Follow the Slow-Mode Output
To make the temperature difference between two points close to zero, the output of the slow response mode is used as the reference value for the fast response modes, so that the fast mode outputs follow the slow mode, as is shown in
Figure 4.
3.3. Structure for Obtaining a Fast-Mode Reference Value
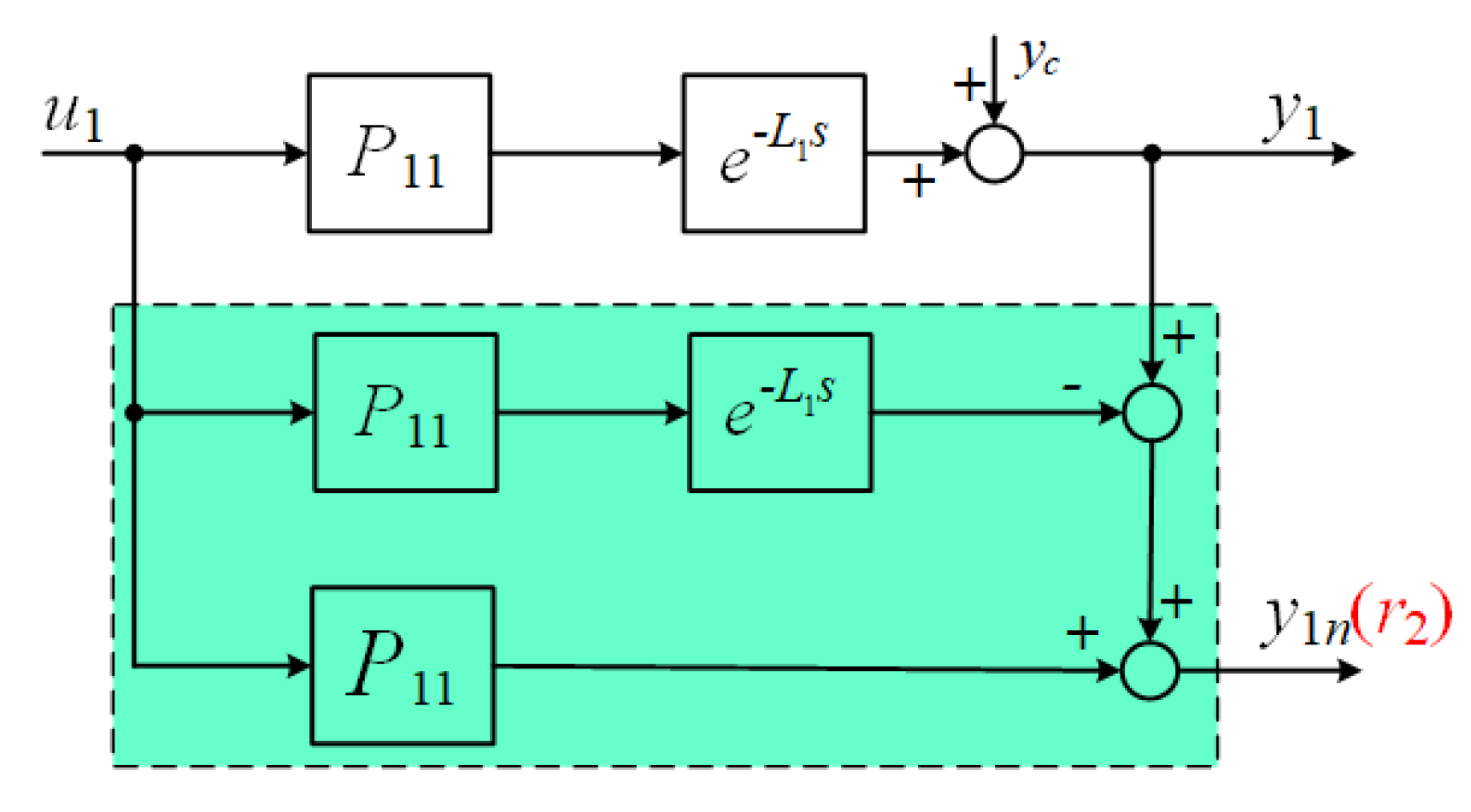
In the proposed control structure, the Smith predictor method is introduced for not only dead time compensation but for reference generation, as shown in
Figure 5. The model output without dead time, which is indicated by
y, is used as the reference value
r for the fast mode. This structure allows avoidance of a further delay of the fast mode response due to the delay of the slow-mode output. In this proposal, the model based method has been introduced for both Smith predictor and feed-forward compensation, and the model is approximated by coupled SISO systems with time delay.
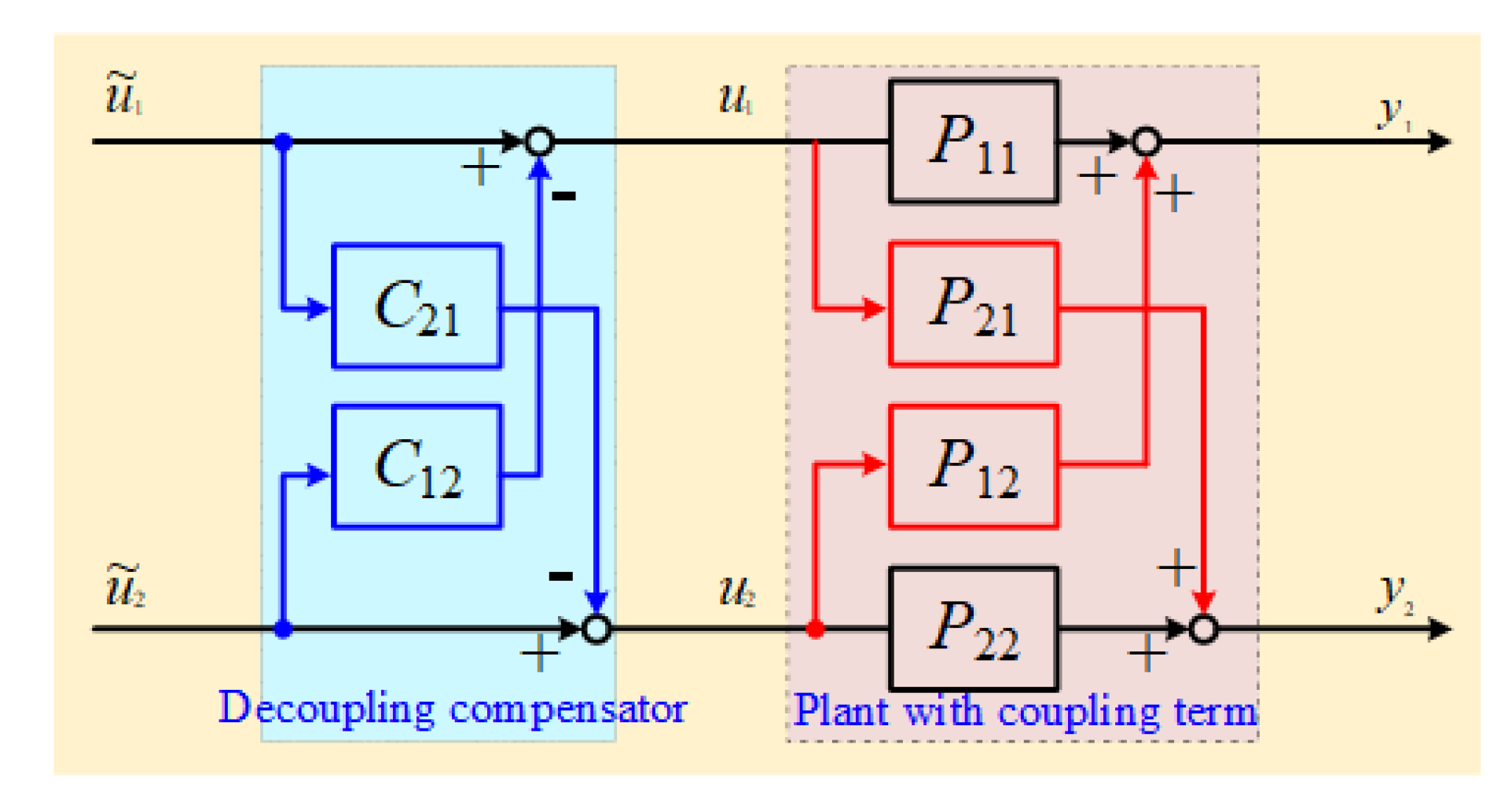
3.4. Structure in Which Decoupling Compensation Is Introduced to Compensate the Coupling Effect
The coupling influence affects the temperature of two points; thus, decoupling compensation was introduced into the system to reduce the influence of the coupling term between the two points. The structure of the decoupling compensation is shown in
Figure 6, where the
C and
C are the decoupling compensators. The decoupling compensators were designed as (2) and (3), respectively. In this proposal, the decoupling compensators consider the transient response between the two points using only the high-frequency gains.
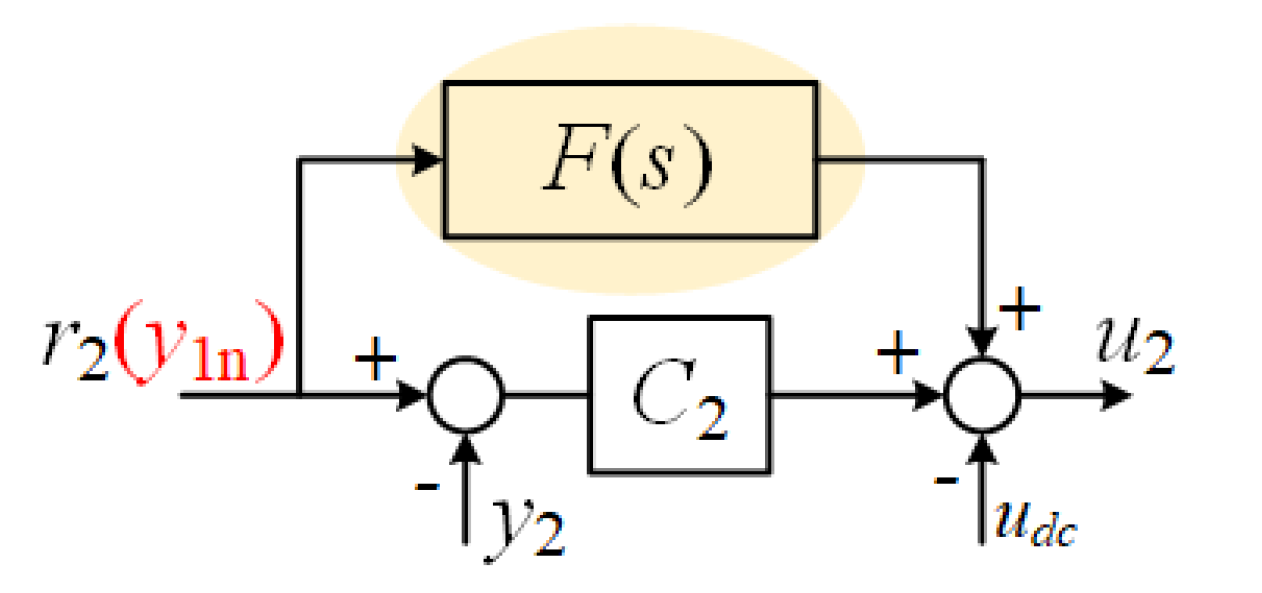
3.5. Structure of Feed-Forward Compensation to Follow Fast-Mode Reference Value
A feed-forward path was added to compensate for the dynamic delay of the fast-mode system, so that the fast-mode output can follow the slow-mode output without delay. This compensation makes the temperature differences between slow mode and fast modes extremely small. Its structure is shown in
Figure 7.
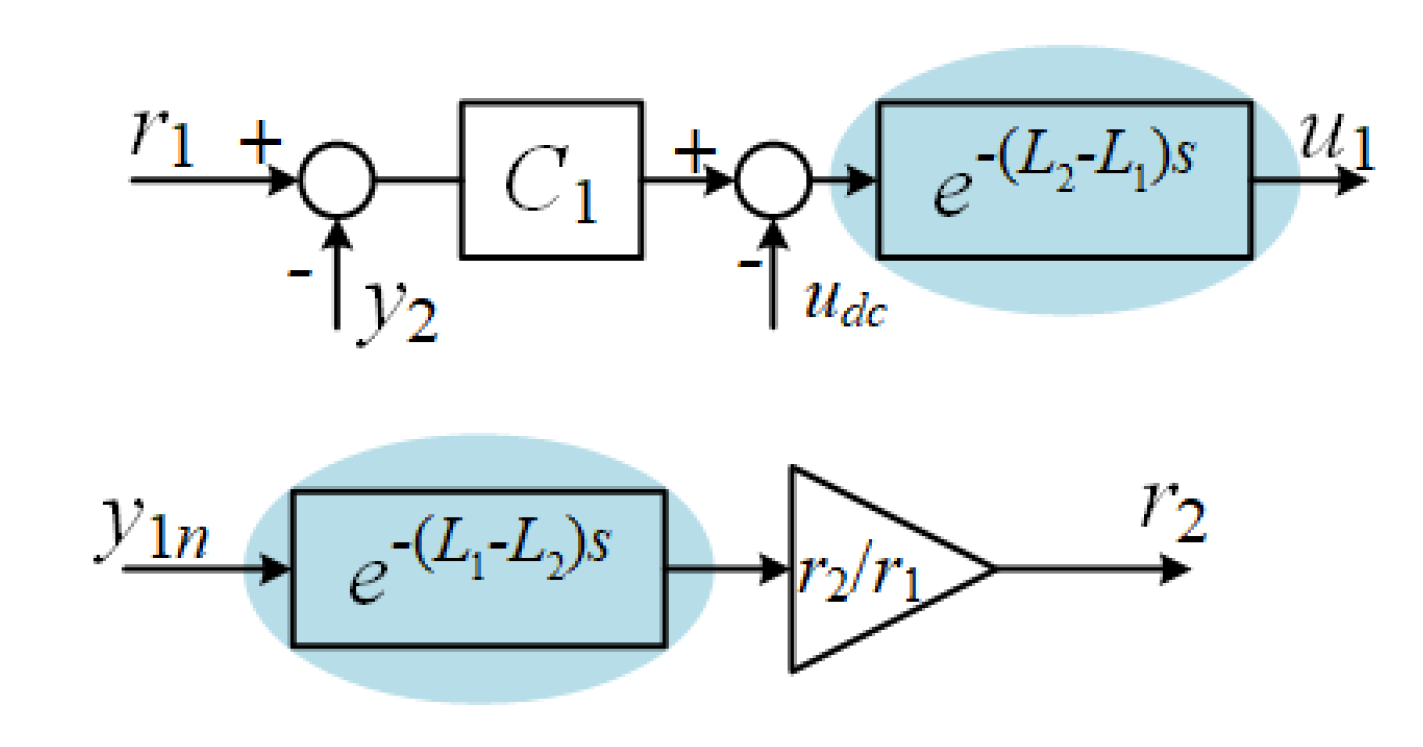
3.6. Structure of Compensation for Dead-Time Difference between Fast and Slow Modes
After the compensations described above are made, a temperature difference still remains in the outputs of both modes due to the dead-time difference between the fast and slow modes. To avoid this problem, when the dead time of the slow mode (
L) is larger than that of the fast mode (
L), the reference value of the fast mode is delayed by the difference (
L−
L), as indicated by (
d) in
Figure 2. This compensation causes both outputs to have the same dead time, that is,
L. Conversely, when
L is smaller than
L, the delay of the slow mode is included as (
L −
L), as indicated by (
d) in
Figure 2, so that both outputs have the same dead time, that is,
L. This effectively reduces the temperature difference between the two modes. The dead-time difference compensation of both the fast and slow modes is shown in
Figure 8.
3.7. Structure Enabling Control of the Output Ratio of Two Modes
In the proposed SMBC method, the output ratio can be controlled even when the reference temperatures at multiple points are different. The gain block (
r/
r), as indicated by (
e) in
Figure 2, which is located after the reference (
r), corresponds to this part. The fast-mode output follows different references from the slow-mode reference while maintaining a constant ratio. As a result, the setting time and ratio of each output’s trajectory can be precisely matched in each mode.
4. Controlled Objects Identification
In this proposal, to precisely verify the control efficiency of the SMBC method, the controlled object was based on a real plant system; thus, a step response experiment needed to be performed to obtain the transfer function of the controlled objects.
Figure 9 shows the experimental setup for the multi-point temperature control system with strong coupling effect, which use a DSP as the temperature controller. The system has four coupling channels, and each channel has two independent heaters and one temperature sensor. The temperature can be controlled through controlling the duty ratio of the PWM signal.
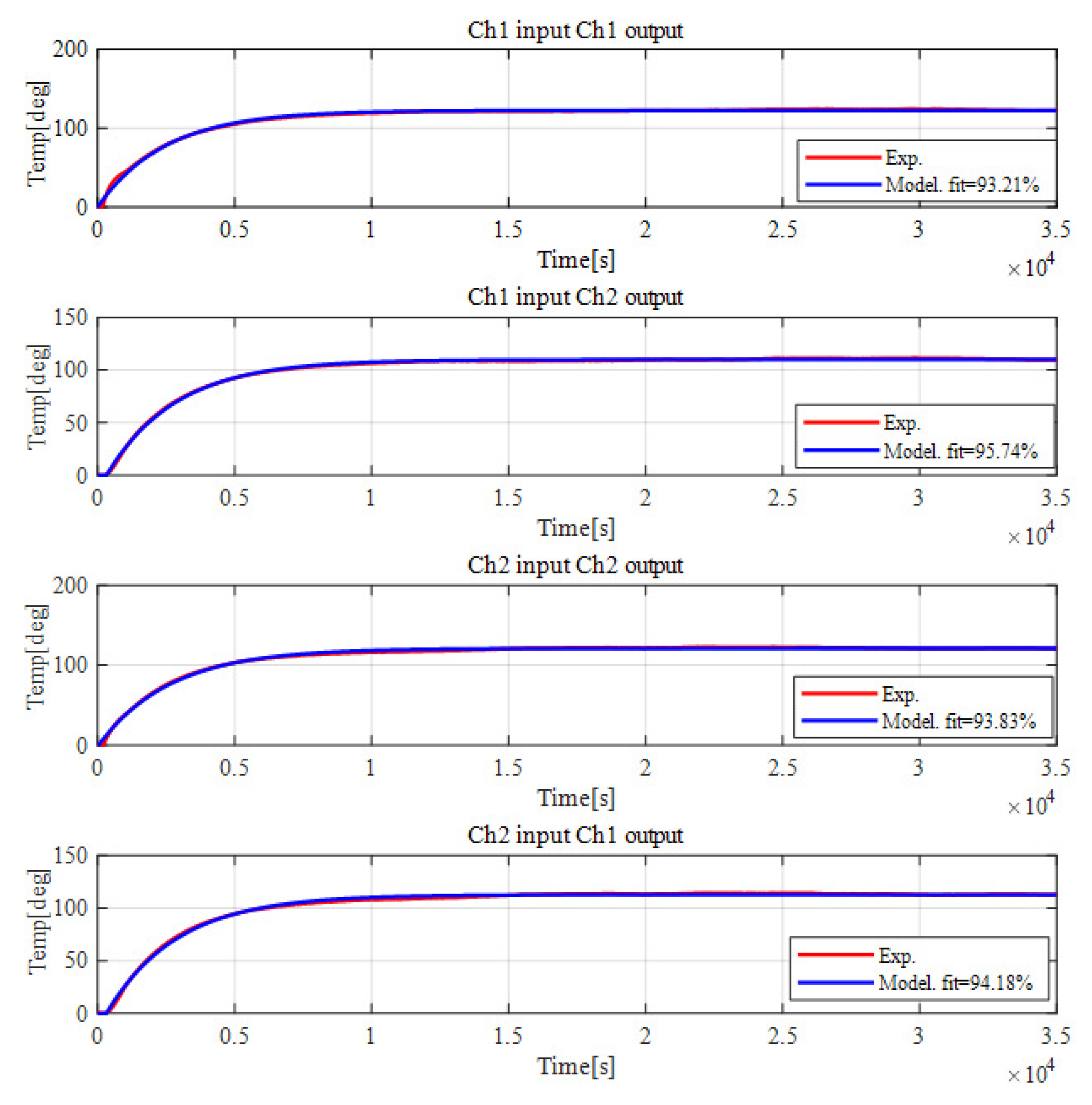
In this study, the two channels Ch1 and Ch2 were used as the controlled objects to apply the SMBC control method. A step response method was introduced to these two channels for controlled object identification, and the identification results for the paired coupling terms are shown in
Figure 10.
Thus, the identification results can be finalized as (4). The system controller parameters design, system simulation, and experiments are all based on the identified plant transfer functions.
5. System Simulation Results
To verify the control efficiency of the proposed control SMBC method, a simulation was carried out in the MATLAB/SIMULINK environment with the controlled objects described above. The results of the simulation focused on the transient response and the temperature difference between the two channels. Control efficiency was verified by comparison with the conventional PI and gradient control methods. In simulation, the controllers
C and
C were calculated as (5) and (6), respectively. Hence, one of the most important factors is the stability of the controller, and there have already existed several methods for controller stability analysis [
26,
27], however, as the PID controller in this proposed system is designed based on the Ziegler–Nichols method (step response tuning method), the stability has been ensured [
28]. The parameters
K,
T, and
T are decided by the plant parameters
K,
T, and
L which have already been defined.
Also, as already mentioned before, a decoupling compensation was added by considering only the high-frequency gain between the two channels, where the decoupling controllers
C and
C are as (7) and (8), respectively.
The feed-forward compensation of the fast mode reference delay time was designed as (9) and the dead time difference compensation between the slow mode and the fast mode were designed as (10). Hence, in this simulation the reference temperature of the two channels stays the same, so that the temperature difference ratio is set as 1, as shown in (11).
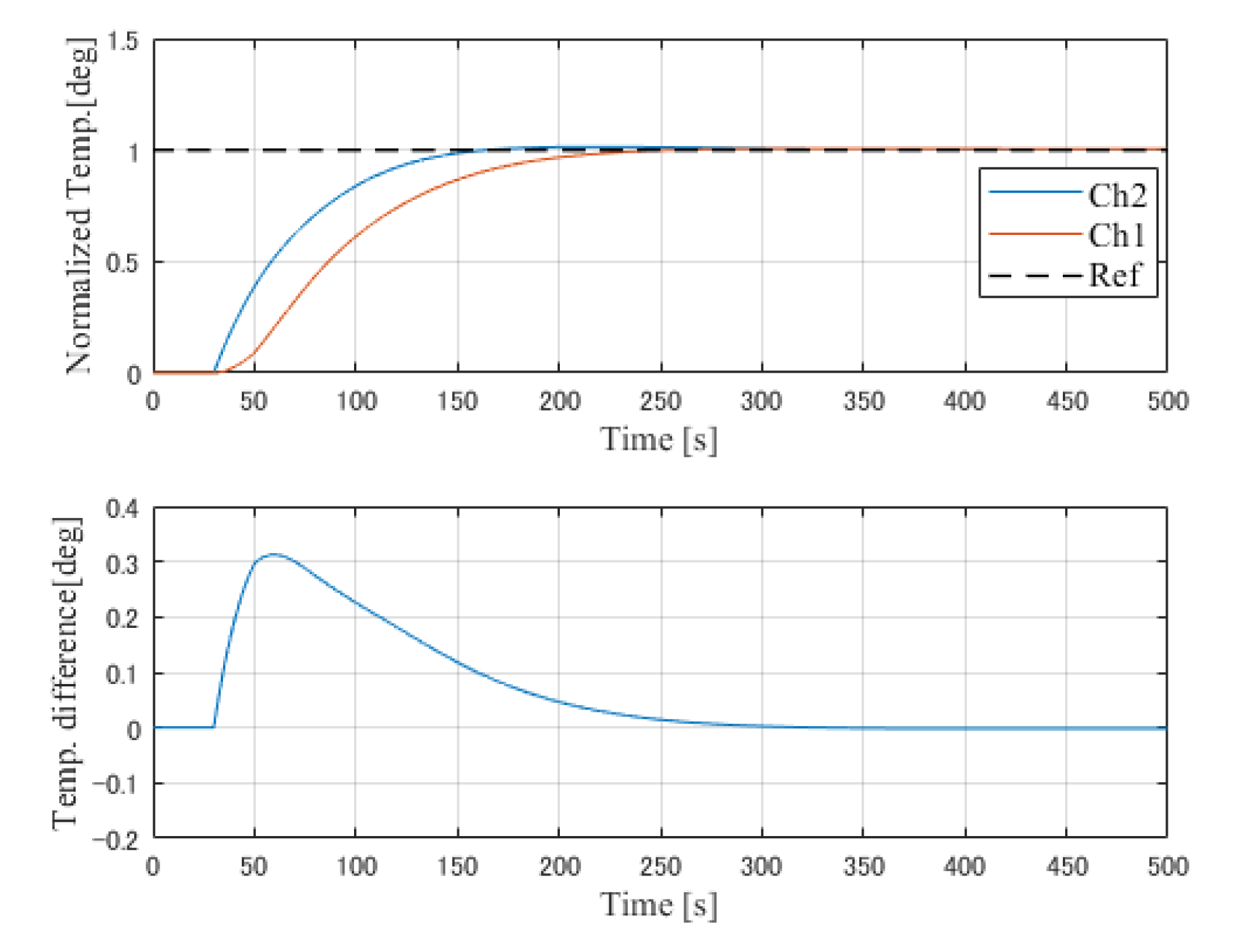
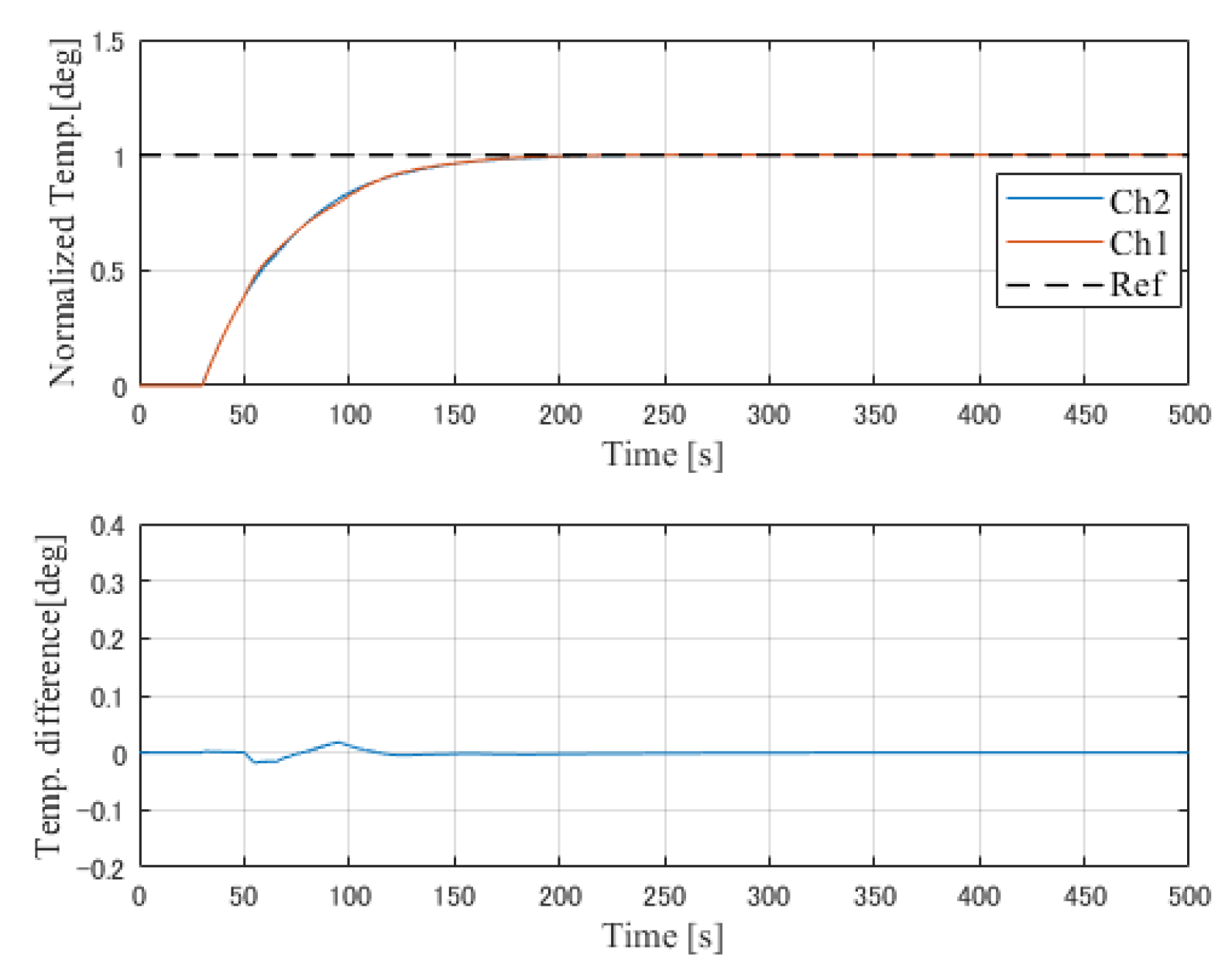
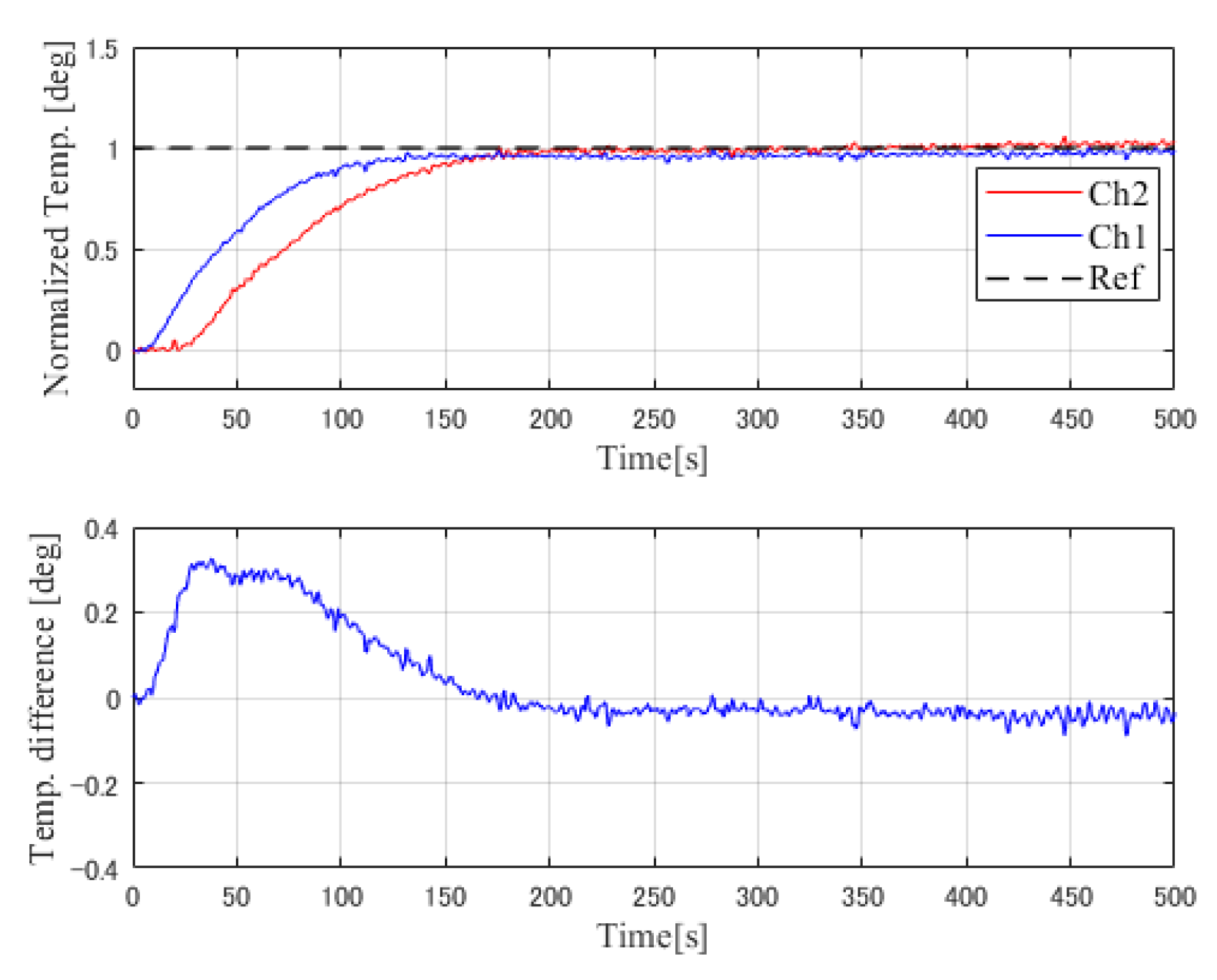
To realize the SMBC control structure, the simulation was divided into two phase. Phase 1 was the SMBC control system with Smith predictor compensation. Phase 2 was the SMBC control system with Smith, feed-forward, and decoupling compensation. A step signal was applied to the slow-mode reference (Ch1). Simulation results for the two phases are shown in
Figure 11 and
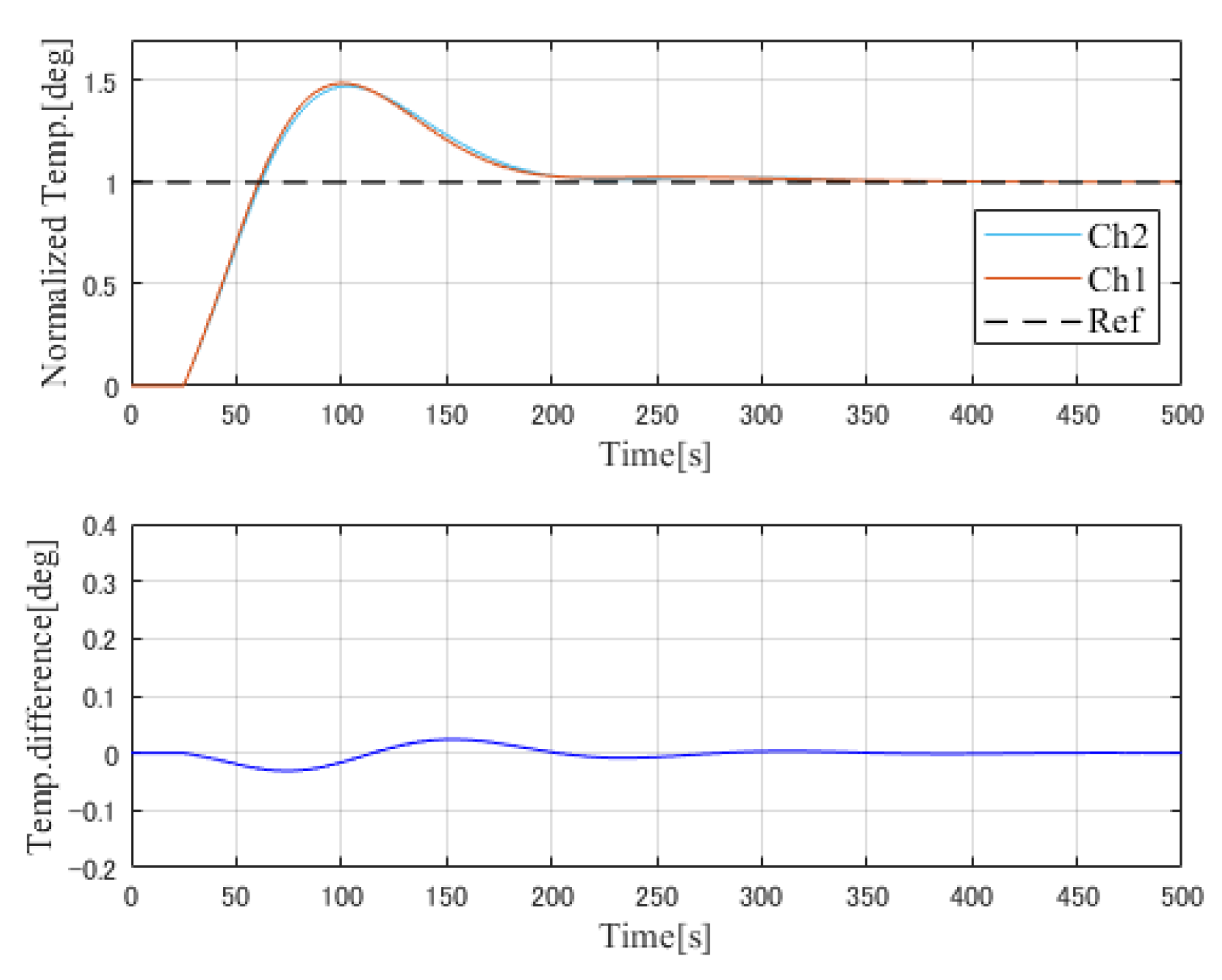
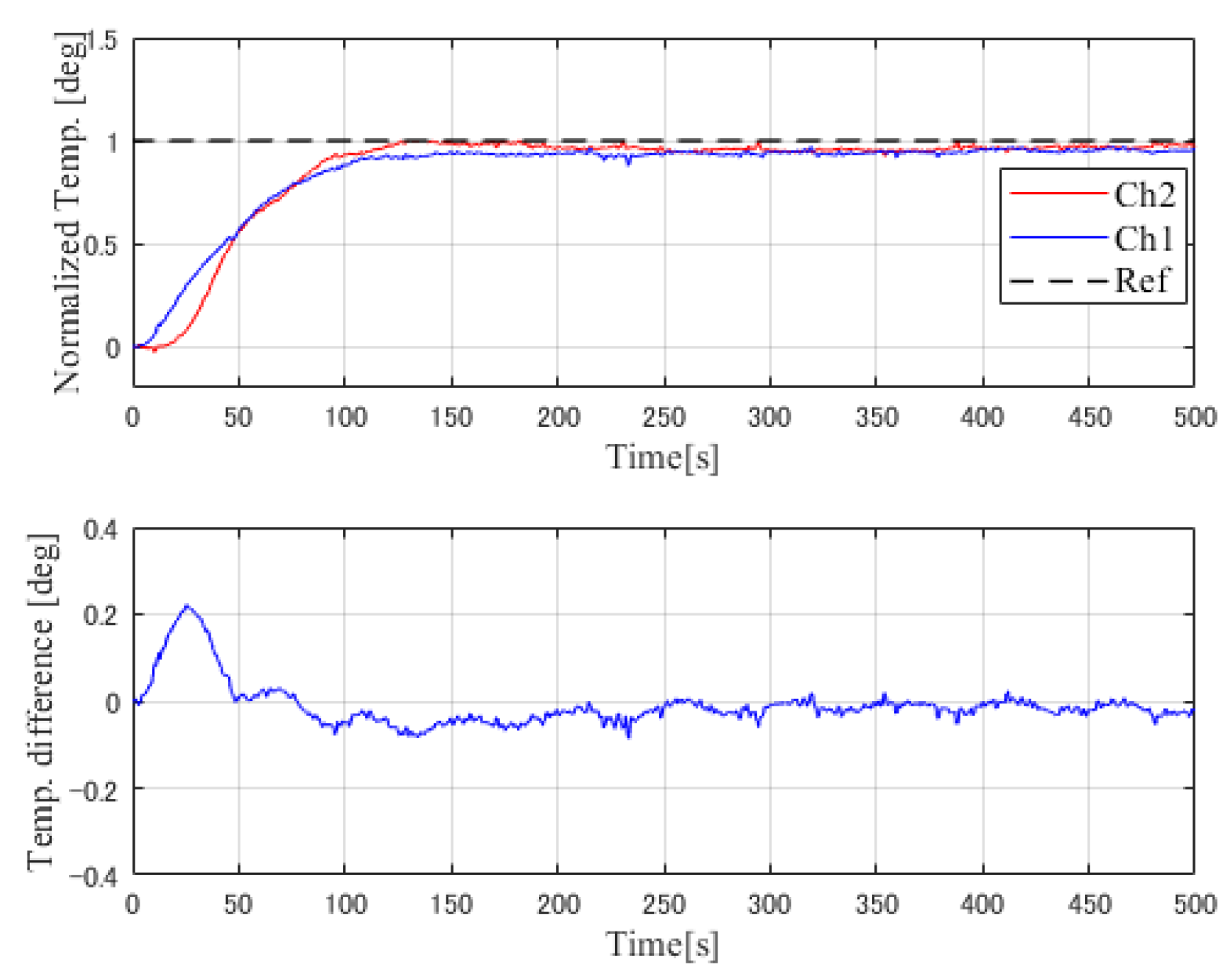
Figure 12, respectively. To evaluate the proposed SMBC control method, a simulation of the conventional PI control method and gradient control method with decoupling compensation were also carried out. Simulation results for the two methods are shown in
Figure 13 and
Figure 14 respectively.
The analysis of the simulation results can be devided into two phases. Phase 1: The transient response, the response time of both PI control method and gradient control system is about 60 s, similar to the proposed SMBC method, however, the conventional PI control system has an overshoot as 0.3 deg C (30% of the reference value) and the gradient control system has an overshoot as 0.5 deg C (50% of the reference value). For the SMBC with Smith preditive control system, there is no overshoot but with an asynchronous response between two channels, and it can be compensated by introducing feed-forward and decoupling compensation. Thus, the transient response has been improved. Phase 2: The temperature difference between the controlled two channels, as shown in the simulation results, yielded the maximum temperature difference of the conventional PI control system as 0.18 deg C (18% of the reference value) and that of gradient control system is about 0.05 deg C (5% of the reference value). However, the temperature difference of SMBC control system is only 0.01 deg C (1% of the reference value) and quickly dropped to 0 deg C, where we can observe that the temperature difference has been reduced. Thus, the control efficience of the proposed SMBC method has been evaluated.
6. Experimental Results
Experiments with the proposed SMBC control method were carried out using parameter values identical to those used in the simulation, and the experimental setup was the same as that shown in
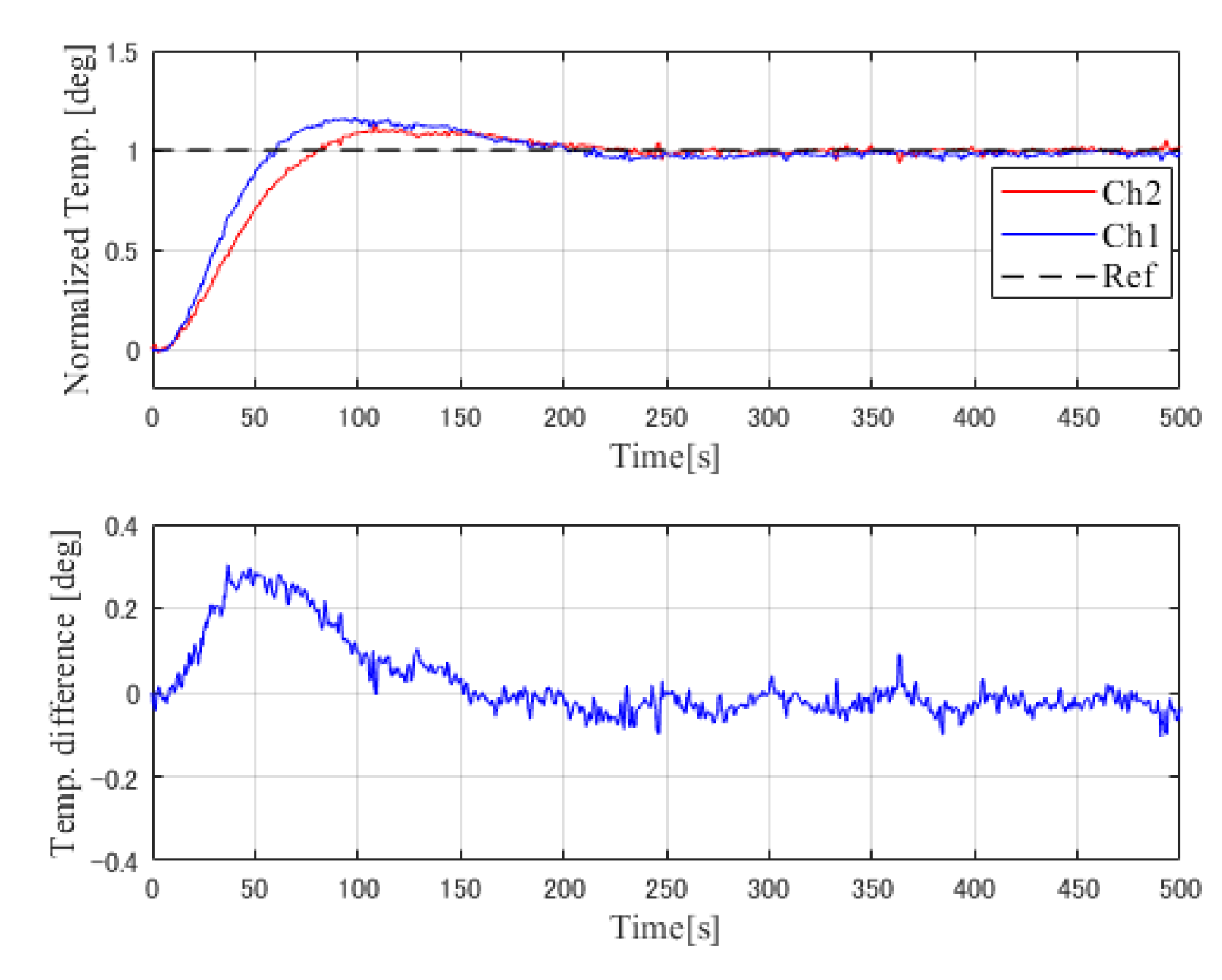
Figure 9. According to the identified plant transfer function, Ch1 was the slow response mode due to its larger time constant and Ch2 was the fast response mode with a smaller time constant. The experiments were carried out by using Ch1 output as the fast mode (Ch2) reference and making the Ch2 output follow the output of Ch1. The experiments were divided into the same two phases used in the simulation. Also, the step signal was applied to the slow-mode reference (Ch1). The experimental results for both phases are shown in
Figure 15 and
Figure 16, respectively. To evaluate the proposed SMBC control method, experiments with a conventional PI control system were also carried out. The results are shown in
Figure 17.
The analysis of the experimental results also can be divided into two phases. Phase 1: Transient response, from the results, the transient response of all control systems is simular as about 60 s rising time of each channel. However, the conventional PI control system has an overshoot of 0.3 deg C (30% of the reference value), while the proposed SMBC control system had no overshoot. Although the SMBC with Smith predictor compensation has an asynchronous response between the two channels, it can be improved by introducing feed-forward and decoupling compensation by which we could state that the transient response of both channel has been improved. Phase 2: The temperature difference. The conventional PI control system has a maximum temperature difference of 0.3 deg C (30% of the reference value), while that of proposed SMBC with Smith, feed-forward and decoupling compensation system is about 0.21 deg C (21% of the reference value) and quickly drops to 0 deg C, where the temperature difference has been reduced. As a result, the simulation and experimental results are shown to be similar, indicating a positive evaluation for the proposed SMBC control method.
7. Conclusions
In this paper, a novel SMBC method was proposed for the multi-point temperature control system. The controlled object was defined as a two inputs, two outputs temperature control system. A step-by-step introduction of the proposed control system was investigated. The system identification was carried out to obtain the transfer functions of the controlled objects, and the Ziegler–Nichols (step response) method was applied to the controller design. Simulation of the proposed SMBC control system was carried out in the MATLAB/SIMULINK environment, and the experiments were carried out with a DSP control platform. The effectiveness of the proposed SMBC method was verified by comparing the results to those for a conventional PI control system and gradient temperature system.
8. Patents
This section is not mandatory, but may be added if there are patents resulting from the work reported in this manuscript.
Author Contributions
Conceptualization, S.H. and S.X.; methodology, S.H.; software, S.X. and Y.J.; validation, S.X., S.H., Y.J. and W.J.; formal analysis, S.H. and S.X.; investigation, S.H.; resources, W.J.; data curation, S.X. and Y.J.; writing—original draft preparation, S.X.; writing—review and editing, S.H.; visualization, W.J.; supervision, W.J.; project administration, S.H., K.I., T.K. and R.I.; funding acquisition, S.H., K.I., T.K., R.I. and W.J.
Funding
This research received no external funding.
Acknowledgments
In this section you can acknowledge any support given which is not covered by the author contribution or funding sections. This may include administrative and technical support, or donations in kind (e.g., materials used for experiments).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Suda, N. PID Control; Asakura Publishing: Tokyo, Japan, 1992. [Google Scholar]
- Oshima, M. Process Control Systems; Corona Publishing: New York, NY, USA, 2003. [Google Scholar]
- Goodwin, G.C.; Fraebe, S.F.; Salgado, M.E. Control System Design; Prentice Hall: Upper Saddle River, NJ, USA, 2001. [Google Scholar]
- Morari, M.; Zafiriou, E. Robust Process Control; Prentice Hall: Upper Saddle River, NJ, USA, 1992. [Google Scholar]
- Maciejowski, J.M. Multivariable Feedback Design; Addison Wesley: Boston, MA, USA, 1989. [Google Scholar]
- Park, C.J. Dynamic Temperature Control with Variable Heat Flux for High Strength Steel. Int. J. Control Autom. Syst. 2012, 10, 659–665. [Google Scholar] [CrossRef]
- Ko, J.S.; Huh, J.H.; Kim, J.C. Improvement of Temperature Control Performance of Thermoelectric Dehumidifier Used Industry 4.0 by the SF-PI Controller. Processes 2019, 7, 98. [Google Scholar] [CrossRef]
- Liu, L.; Tian, S.; Xue, D.Y.; Zhang, T.; Chen, Y.Q.; Zhang, S. A Review of Industrial MIMO Decoupling Control. Int. J. Control Autom. Syst. 2019, 17, 1246–1254. [Google Scholar] [CrossRef]
- Song, B.Q.; Mills, J.K.; Liu, Y.H.; Fan, C.Z. Nonlinear Dynamic Modeling and Control of a Small-Scale Helicopter. Int. J. Control Autom. Syst. 2010, 8, 534–543. [Google Scholar] [CrossRef]
- Deng, M.; Bi, S. Operator-based robust nonlinear control system design for MIMO nonlinear plants with unknown coupling effects. Int. J. Control 2010, 83, 1939–1946. [Google Scholar] [CrossRef]
- Li, G.M.; Tsang, K.M. Concurrent Relay-PID Control for Motor Position Servo Systems. Int. J. Control Autom. Syst. 2007, 5, 234–242. [Google Scholar]
- Wang, Q.G.; Zhang, Y.; Chiu, M.S. Decoupling internal model control for multi-variable systems with multiple time delays. Chem. Eng. Sci. 2002, 57, 115–124. [Google Scholar] [CrossRef]
- Pop, C.I.; Ionescu, C.M.; Keyser, R.D. Time delay compensation for the secondary processes in a multi-variable carbon isotope separation unit. Chem. Eng. Sci. 2012, 80, 205–218. [Google Scholar] [CrossRef]
- Fujimori, A.; Ohara, S. Order Reduction of Plant and Controller in Closed Loop Identification based on Joint Input-Output Approach. Int. J. Control Autom. Syst. 2017, 15, 1217–1226. [Google Scholar] [CrossRef]
- Yao, Y.; Yang, K.; Huang, M.; Wang, L. A state-space model for dynamic response of indoor air temperature and humidity. Build. Environ. 2013, 64, 26–37. [Google Scholar] [CrossRef]
- Seong, Y.B.; Cho, Y.H. Development and evaluation of applicable optimal terminal box control algorithms for energy management control systems. Sustainability 2016, 8, 1151. [Google Scholar] [CrossRef]
- Ganesh, H.S.; Edgar, T.F.; Baldea, M. Model Predictive Control of the Exit Part Temperature for an Austenitization Furnace’. Processes 2016, 4, 53. [Google Scholar] [CrossRef]
- Jeng, J.C.; Chang, Y.J.; Lee, M.W. Novel design of dynamic matrix control with enhanced decoupling control performance. Comput. Aided Chem. Eng. 2014, 44, 541–546. [Google Scholar]
- Nanno, I.; Tanaka, M.; Matsunaga, N.; Kawaji, S. On Performance of the Gradient Temperature Control Method for Uniform Heating. IEEJ Trans. EIS 2004, 124, 1606–1612. [Google Scholar] [CrossRef]
- Matsunaga, N.; Kawaji, S.; Tanaka, M.; Nanno, I. A Novel Approach of Thermal Process Control for Uniform Temperature. In Proceedings of the 16th IFAC World Congress, Prague, Czech Republic, 3–8 July 2005; Volume 38, pp. 111–116. [Google Scholar]
- Xu, D.Z.; Song, X.Q.; Jiang, B.; Yang, W.L.; Yan, W.X. Data-driven Sliding Mode Control for MIMO systems and Its Application on Linear Induction Motors. Int. J. Control Autom. Syst. 2019, 17, 1717–1725. [Google Scholar] [CrossRef]
- Data-driven approaches for complex industrial systems. IEEE Trans. Ind. Inform. 2013, 9, 2210–2212. [CrossRef]
- Gao, Z.; Nguang, S.K.; Kong, D.X. Advances in Modelling, Monitoring, and Control for Complex Industrial Systems. Complexity 2019. [Google Scholar] [CrossRef]
- Xu, S.; Hashimoto, S.; Jiang, W. Pole-Zero Cancellation Method for Multi Input Multi Output (MIMO) Temperature Control in Heating Process System. Processes 2019, 7, 497. [Google Scholar] [CrossRef]
- Hashimoto, S.; Liu, Y.; Yoshida, K.; Izaki, K.; Kihara, T.; Ikeda, R.; Jiang, W. A Novel Multi-point Temperature Control Method Based on Slow Response Mode. In Proceedings of the IECON 2017—43rd Annual Conference of the IEEE Industrial Electronics Society, Beijing, China, 29 October–1 November 2017; pp. 5623–5627. [Google Scholar]
- Gao, R.; Gao, Z. Pitch control for wind turbine systems using optimization, estimation and compensation. Renew. Energy 2016, 91, 501–515. [Google Scholar] [CrossRef]
- Wang, J.; Tse, N.; Gao, Z. Synthesis on PI-based pitch controller of large wind turbines generator. Energy Convers. Manag. 2011, 52, 1288–1294. [Google Scholar] [CrossRef]
- Ziegler, J.G.; Nichols, N.B. Optimum settings for automatic controllers. Trans. ASME 1942, 64, 759–768. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).