Topological Characterization of Nanosheet Covered by C3 and C6
Abstract
:1. Introduction
2. Methods
3. Results
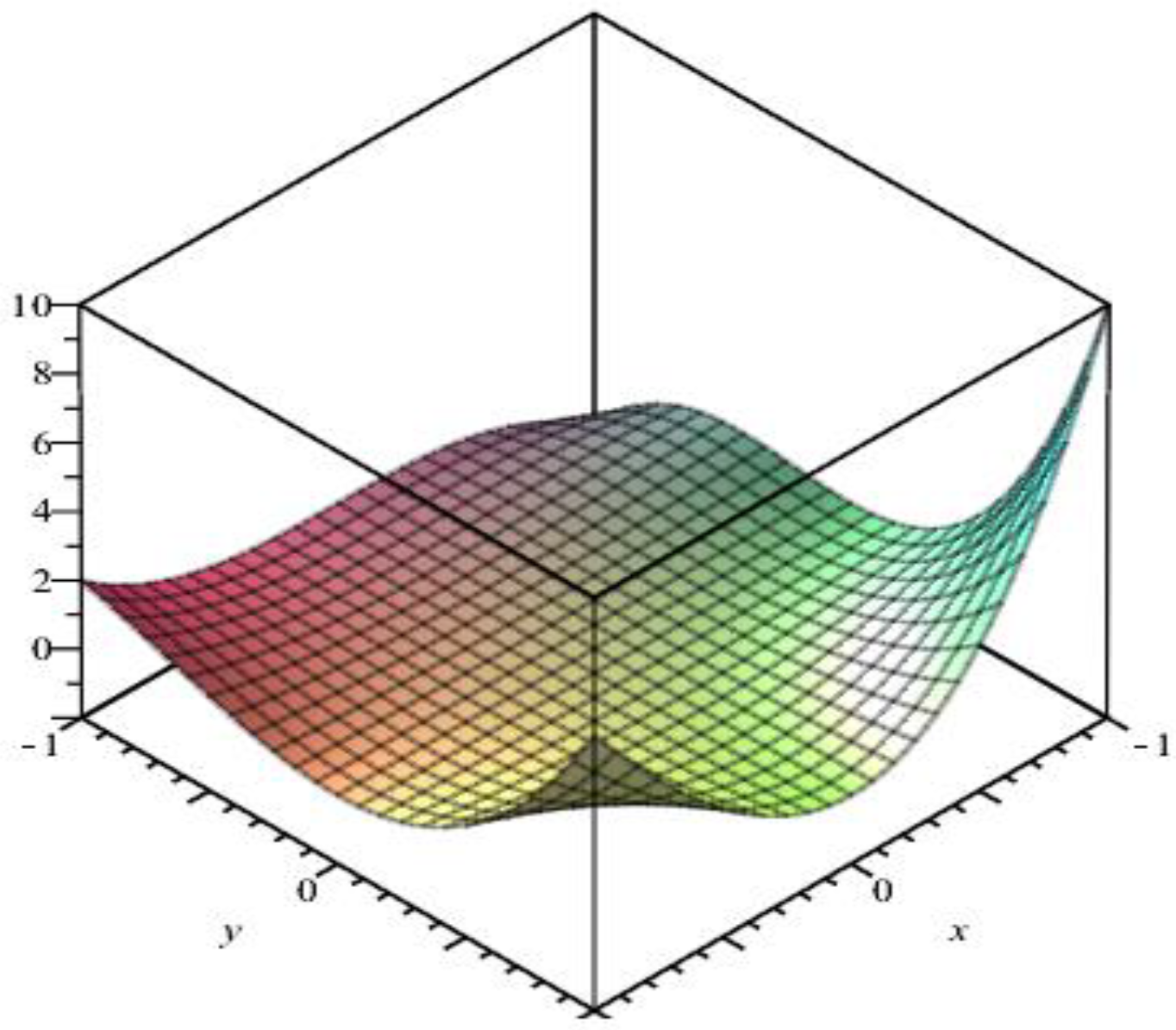
4. The M-Polynomial of Nanosheet
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Kim, S.; Wang, H.; Lee, Y.M. 2D Nanosheets and Their Composite Membranes for Water, Gas, and Ion Separation. Angew. Chem. Int. Ed. 2019. [Google Scholar] [CrossRef]
- Kim, K.S.; Lee, H.J.; Lee, C.; Lee, S.K.; Jang, H.; Ahn, J.H.; Kim, J.H.; Lee, H.J. Chemical vapor deposition-grown graphene: The thinnest solid lubricant. ACS Nano 2011, 5, 5107–5114. [Google Scholar] [CrossRef]
- Peng, Y.T.; Wang, Z.G.; Zout, K. Friction and Wear Properties of Different Types of Graphene Nanosheets as Effective Solid Lubricants. Langmuir 2015, 31, 7782–7791. [Google Scholar] [CrossRef]
- Berman, D.; Erdemir, A.; Sumant, A.V. Graphene: A new emerging lubricant. Mater. Today 2014, 17, 31–42. [Google Scholar] [CrossRef]
- He, X.; Cao, L.; He, G.; Zhao, A.; Mao, X.; Huang, T.; Li, Y.; Wu, H.; Sun, J.; Jiang, Z. A highly conductive and robust anion conductor obtained via synergistic manipulation in intra-and inter-laminate of layered double hydroxide nanosheets. J. Mater. Chem A 2018, 6, 10277–10285. [Google Scholar] [CrossRef]
- Răileanu, M.; Crişan, M.; Niţoi, I.; Ianculescu, A.; Oancea, P.; Crişan, D.; Todan, L. TiO2-based nanomaterials with photocatalytic properties for the advanced degradation of xenobiotic compounds from water. A literature survey. Water Air Soil Pollut. 2013, 224, 1548–1593. [Google Scholar] [CrossRef]
- Bawa, R. Nanoparticle-based therapeutics in humans: A survey. Nanotech. L. Bus. 2008, 5, 135–155. [Google Scholar]
- Staedler, D.; Magouroux, T.; Hadji, R.; Joulaud, C.; Extermann, J.; Schwung, S.; Passemard, S.; Kasparian, C.; Clarke, G.; Gerrmann, M.; et al. Harmonic nanocrystals for biolabeling: A survey of optical properties and biocompatibility. ACS Nano 2012, 6, 2542–2549. [Google Scholar] [CrossRef]
- Jakubinek, M.B.; Martinez-Rubi, Y.; Ashrafi, B.; Guan, J.; Kim, K.S.; O’Neill, K.; Kingston, C.T.; Simard, B. Polymer nanocomposites incorporating boron nitride nanotubes. In Proceedings of the Nanotech 2015 Conference, Washington, DC, USA, 14–17 June 2015. [Google Scholar]
- Katritzky, A.R.; Wang, Y.; Sild, S.; Tamm, T.; Karelson, M. QSPR studies on vapor pressure, aqueous solubility, and the prediction of water–air partition coefficients. J. Chem. Inf. Comput. Sci. 1998, 38, 720–725. [Google Scholar] [CrossRef]
- Burello, E. Review of QSAR models for regulatory assessment of nanomaterials risks. NanoImpact 2017, 8, 48–58. [Google Scholar] [CrossRef]
- Fourches, D.; Tropsha, A. Quantitative nanostructure-activity relationships: From unstructured dataaa to predictive models for designing nanomaterials with controlled properties. Nanotoxicol. Prog. Toward Nanomed. 2015, 1–39. [Google Scholar]
- Burello, E.; Worth, A.P. QSAR modeling of nanomaterials. Wiley Interdiscip. Rev. Nanomed. Nanobiotechnol. 2011, 3, 298–306. [Google Scholar] [CrossRef]
- Randic, M. On Characterization of molecular branching. J. Am. Chem. Soc. 1975, 97, 6609–6615. [Google Scholar] [CrossRef]
- Bollobás, B.; Erdös, P. Graphs of extermal weights. Ars Comb. 1998, 50, 225–233. [Google Scholar]
- Gutman, I.; Trinajstić, N. Graph theory and moleculer orbitals. Total φ-eletrone energy of alternant hydrocarbons. Chem. Phys. Lett. 1972, 17, 535–538. [Google Scholar] [CrossRef]
- Estrada, E.; Torres, L.; Rodríguez, L.; Gutman, I. An atom-bond connectivity index: Modelling the enthalpy of formation of alkanes. Indian J. Chem. Sect. A Inorg. Phys. Theor. Anal. Chem. 1998, 37, 849–855. [Google Scholar]
- Zhou, B.; Trinajstić, N. On general sum-connectivity index. J. Math. Chem. 2010, 47, 210–218. [Google Scholar] [CrossRef]
- Vukičević, D.; Furtula, B. Topological index based on the ratios of geometrical and arithmetical means of end vertex degrees of edges. J. Math. Chem. 2009, 46, 1369–1376. [Google Scholar] [CrossRef]
- Shirdel, G.H.; Rezapour, H.; Sayadi, A.M. The hyper Zagreb index of graph operations. Iran. J. Math. Chem. 2013, 4, 213–220. [Google Scholar]
- Ghorbani, M.; Hosseinzade, M.A. A new version of Zagreb indices. Filomat 2012, 26, 93–100. [Google Scholar] [CrossRef] [Green Version]
- Jagadeesh, R.; Kanna, M.R.; Indumathi, R.S. Some results on topological indices of graphene. Nanomater. Nanotechnol. 2016, 6. [Google Scholar] [CrossRef]
- Chen, S.; Jang, Q.; Hou, Y. The Wiener and Schultz index of nanotubes covered by C4. Match Commun. Math. Comput. Chem. 2008, 59, 429–435. [Google Scholar]
- Hayat, S.; Imran, M. Computation of certain topological indices of nanotubes covered by C5 and C7. J. Comput. Theor. Nanosci. 2015, 12, 533–541. [Google Scholar] [CrossRef]
- Aslam, A.; Ahmad, S.; Gao, W. On certain topological indices of boron triangular nanotubes. Z. Nat. A 2017, 72, 711–716. [Google Scholar] [CrossRef]
- Idrees, N.; Saif, M.J.; Sadiq, A.; Rauf, A.; Hussain, F. Topological indices of H-naphtalenic nanosheet. Open Chem. 2018, 16, 1184–1188. [Google Scholar] [CrossRef]
- Munir, M.; Nazeer, W.; Rafique, S.; Kang, S. M-polynomial and degree-based topological indices of polyhex nanotubes. Symmetry 2016, 8, 149. [Google Scholar] [CrossRef]
- Gao, W.; Wang, W.; Farahani, M.R. Topological indices study of molecular structure in anticancer drugs. J. Chem. 2016. [Google Scholar] [CrossRef]
- Hayat, S.; Imran, M. On degree based topological indices of certain nanotubes. J. Comput. Nanosci. 2015, 12, 1599–1605. [Google Scholar] [CrossRef]
- Yang, H.; Rashid, M.A.; Ahmad, S.; Khan, S.S.; Siddiqui, M.K. On molecular descriptors of face-centered cubic lattice. Processes 2019, 7, 280. [Google Scholar] [CrossRef]
- Tan, C.; Cao, X.; Wu, X.; He, Q.; Yang, J.; Zhang, X.; Chen, J.; Zhao, W.; Han, S.; Nam, G.; et al. Recent advances in ultrathin two-dimensional nanomaterials. Chem. Rev. 2017, 117, 6226–6227. [Google Scholar] [CrossRef]
- Deutsch, E.; Deutsch, S. M-polynomial and degree based topological indices. Iran. J. Math. Chem. 2015, 6, 93–102. [Google Scholar]
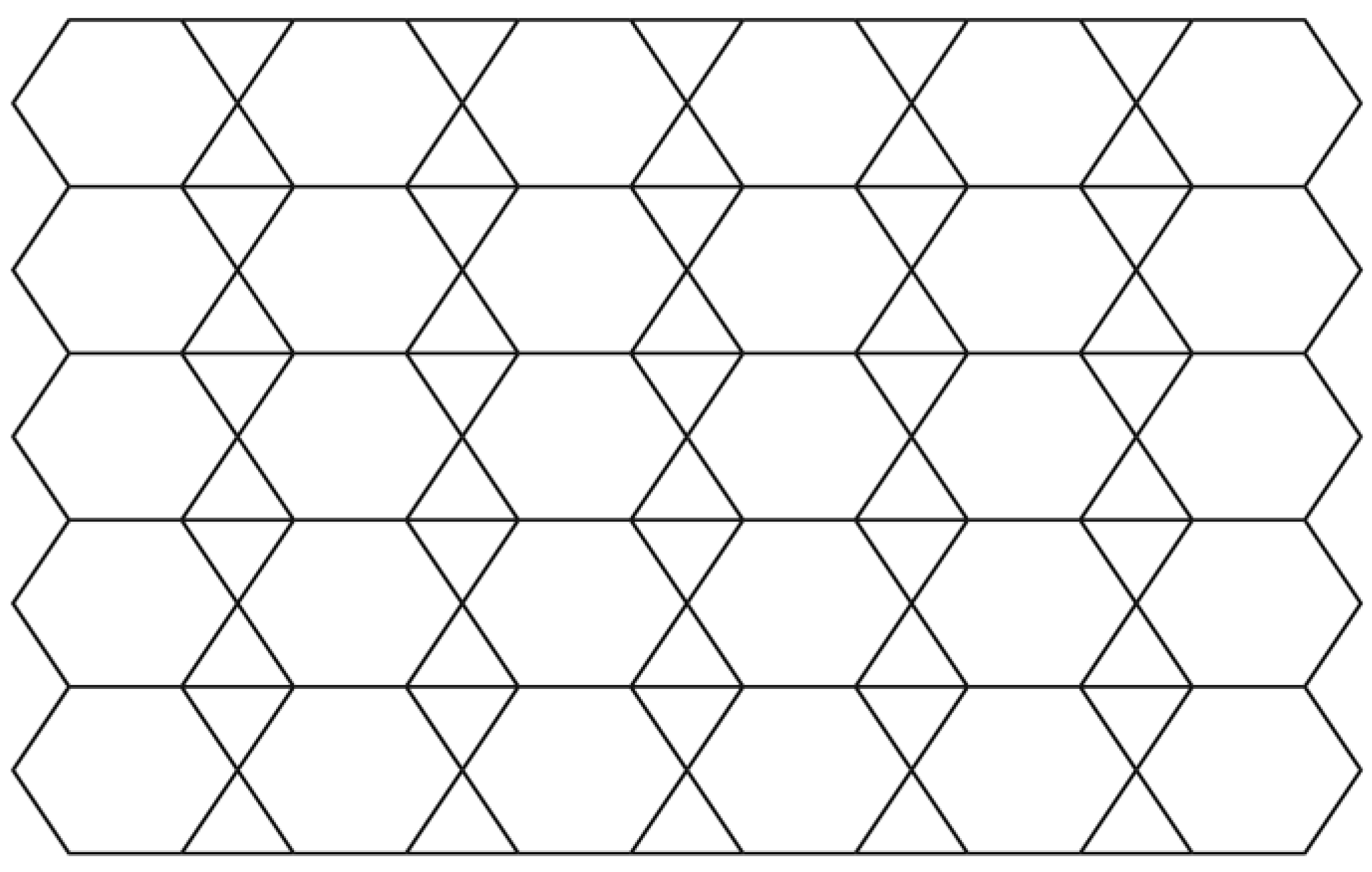
| Type of Edges | |||||
|---|---|---|---|---|---|
uv | (2,2) | (2,3) | (3,3) | (3,4) | (4,4) |
| Number of edges | 4 |
| Topological Index | ||
|---|---|---|
| 1st Zagreb index | ||
| 2nd Zagreb index | ||
| Randic index |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nasir, S.; Farooq, F.B.; Idrees, N.; Saif, M.J.; Saeed, F. Topological Characterization of Nanosheet Covered by C3 and C6. Processes 2019, 7, 462. https://doi.org/10.3390/pr7070462
Nasir S, Farooq FB, Idrees N, Saif MJ, Saeed F. Topological Characterization of Nanosheet Covered by C3 and C6. Processes. 2019; 7(7):462. https://doi.org/10.3390/pr7070462
Chicago/Turabian StyleNasir, Sumiya, Fozia Bashir Farooq, Nazeran Idrees, Muhammad Jawwad Saif, and Fatima Saeed. 2019. "Topological Characterization of Nanosheet Covered by C3 and C6" Processes 7, no. 7: 462. https://doi.org/10.3390/pr7070462





