Deep Learning-Based Pose Estimation of Apples for Inspection in Logistic Centers Using Single-Perspective Imaging
Abstract
:1. Introduction
2. Related Literature
3. Methods
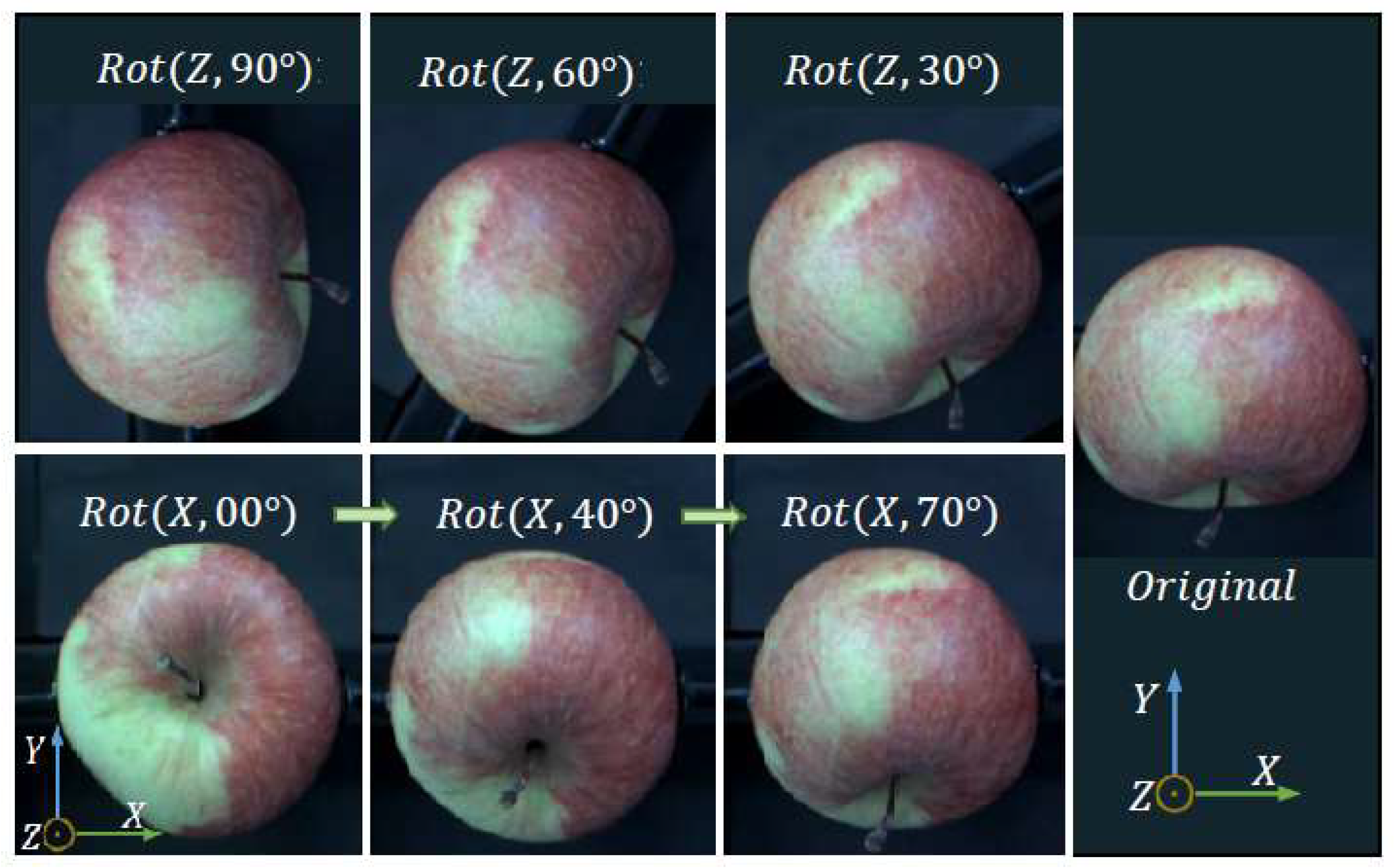
3.1. Representation of Orientation of a Rigid Body
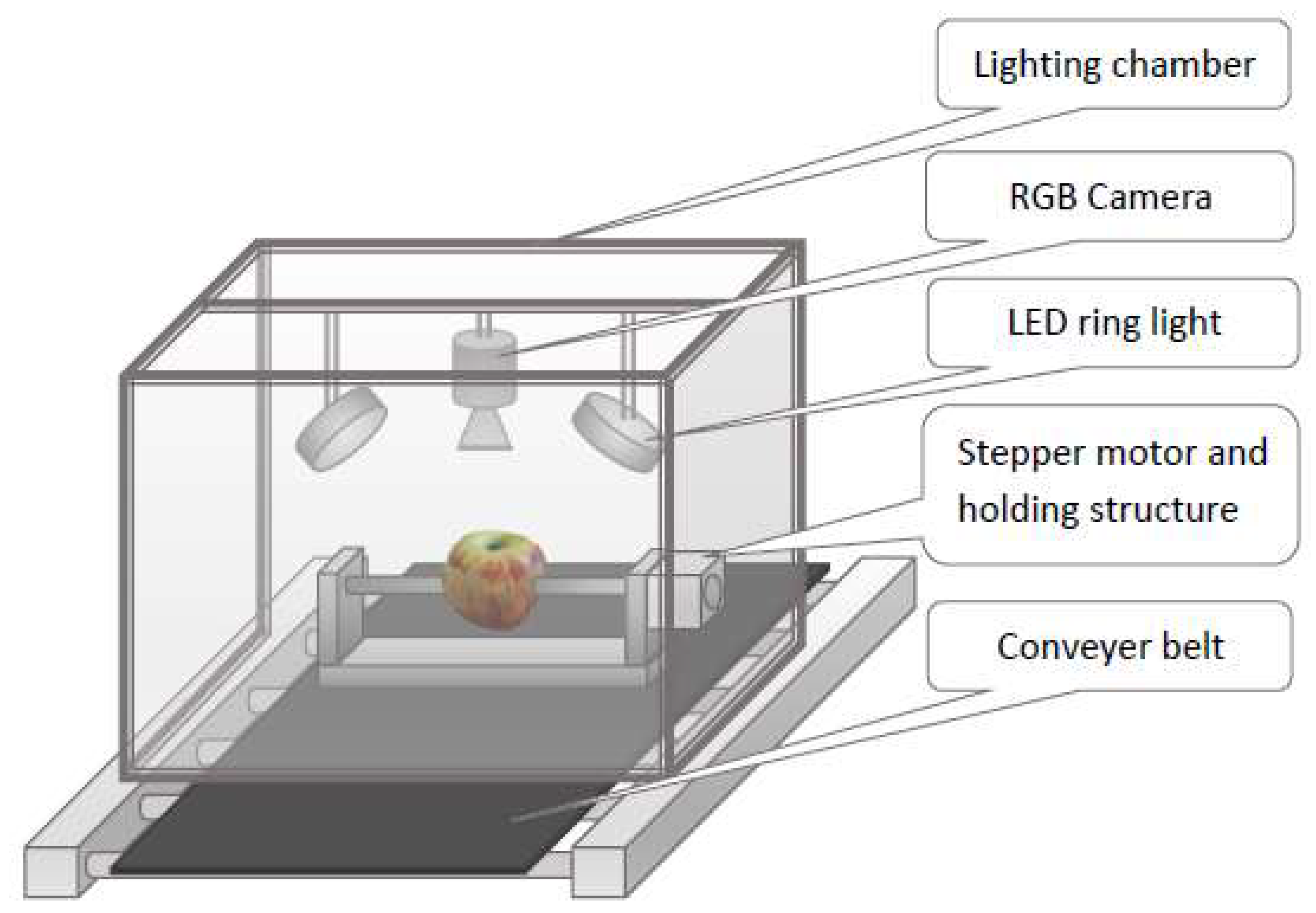
3.2. Image Capturing
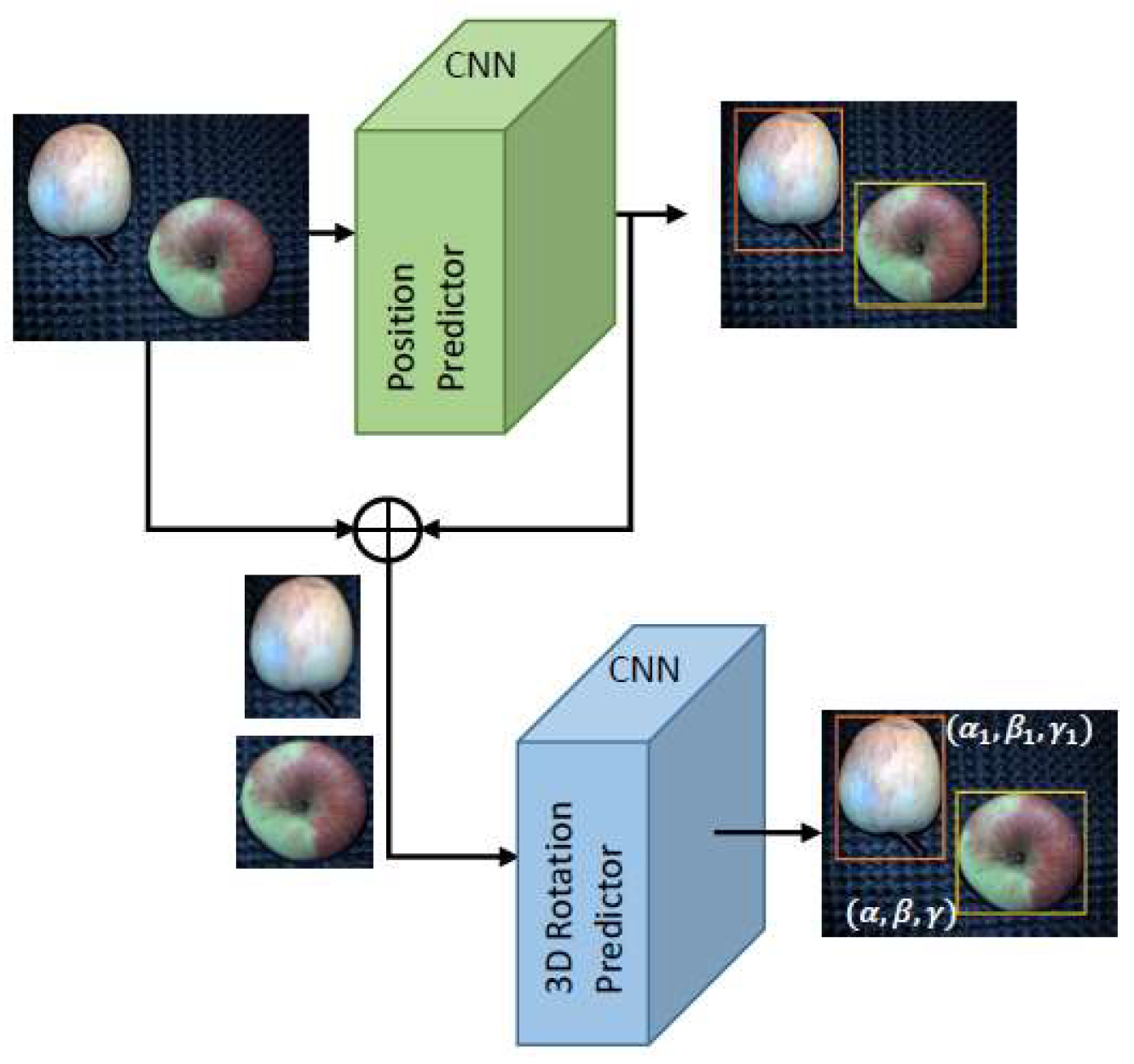
3.3. Convolutional Neural Network Architecture
3.4. Configuration
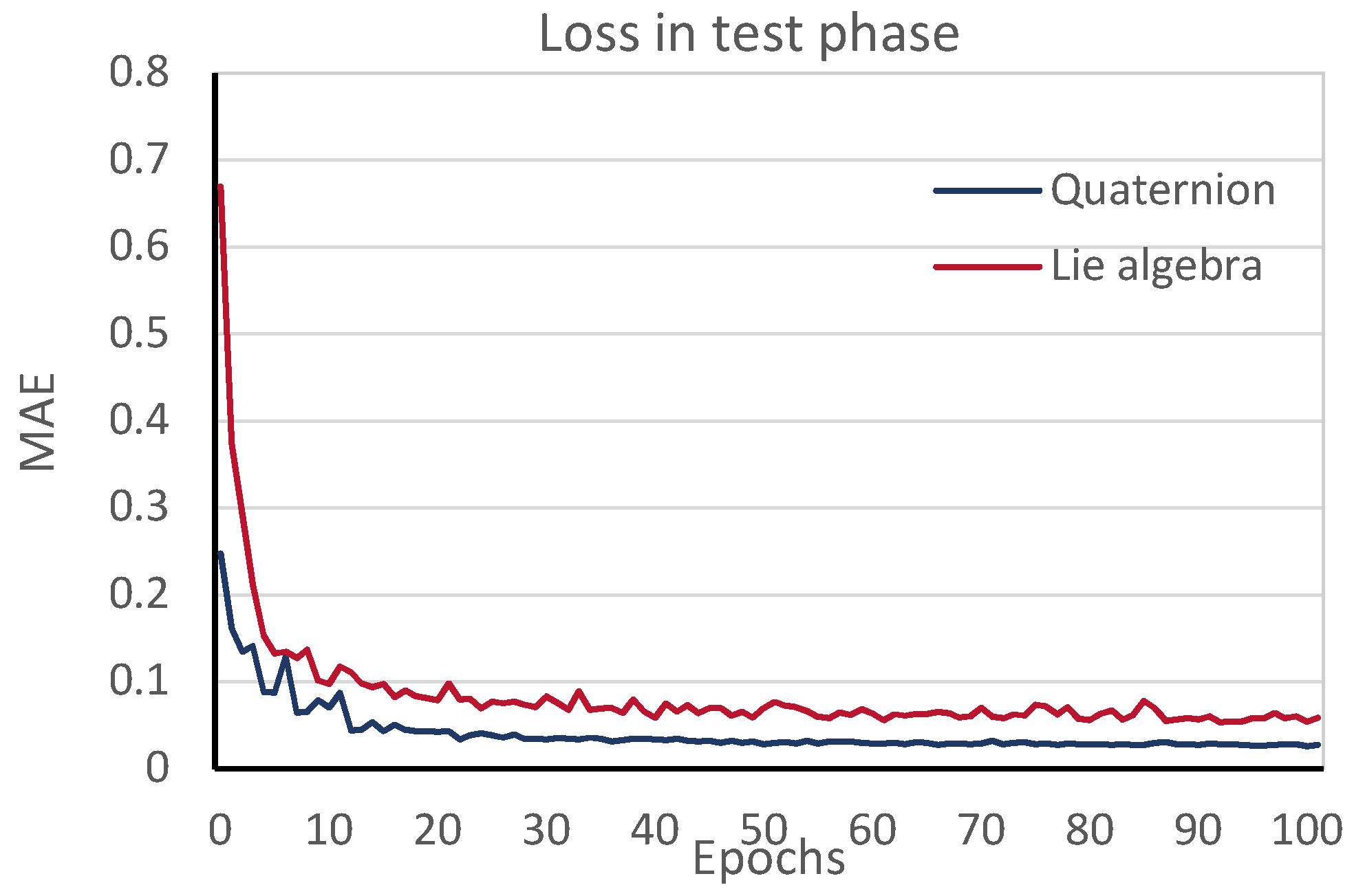
3.5. Training and Evaluation
4. Results
5. Discussion
Author Contributions
Funding
Conflicts of Interest
References
- Elakkiya, N.; Karthikeyan, S.; Ravi, T. (Eds.) Survey of grading process for agricultural foods by using artificial intelligence technique. In Proceedings of the 2018 Second international conference on electronics, communication and aerospace technology (ICECA), Coimbatore, India, 29–31 March 2018; IEEE: Piscataway, NJ, USA, 2018. [Google Scholar]
- Statista: Pro-Kopf-Konsum von Obst in Deutschland in den Wirtschaftsjahren 2004/2005 bis 2015/2016 (in Kilogramm). Available online: Https://de.statista.com/statistik/daten/studie/6300/umfrage/pro-kopf-verbrauch-von-obst-in-deutschland/ (accessed on 2 February 2019).
- Statista: Umsatz in der Obst- und Gemüseverarbeitung in Deutschland in den Jahren 1995 bis 2017 (in Millionen Euro). Available online: https://de.statista.com/statistik/daten/studie/37936/umfrage/umsatz-in-der-obst--und-gemueseverarbeitung-in-deutschland-seit-1995/ (accessed on 2 February 2019).
- Statista: Anzahl der Beschäftigten in der Obst- und Gemüseverarbeitung in Deutschland in den Jahren 2007 bis 2017. Available online: https://de.statista.com/statistik/daten/studie/37934/umfrage/beschaeftigte-in-der-obst--und-gemueseverarbeitung/ (accessed on 2 February 2019).
- Statista: Anzahl der Betriebe in der Obst- und Gemüseverarbeitung in Deutschland in den Jahren 2008 bis 2017. Available online: https://de.statista.com/statistik/daten/studie/37938/umfrage/betriebe-in-der-obst--und-gemueseverarbeitung/ (accessed on 2 February 2019).
- Zhong, R.Y.; Xu, X.; Klotz, E.; Newman, S.T. Intelligent manufacturing in the context of industry 4.0: A review. Engineering 2017, 3, 616–630. [Google Scholar] [CrossRef]
- Rawat, W.; Wang, Z. Deep convolutional neural networks for image classification: A comprehensive review. Neural Comput. 2017, 29, 2352–2449. [Google Scholar] [CrossRef] [PubMed]
- Do, T.T.; Cai, M.; Pham, T.; Reid, I. Deep-6DPose: Recovering 6D Object Pose from a Single RGB Image. Available online: https://arxiv.org/pdf/1802.10367 (accessed on 15 July 2018).
- Rad, M.; Lepetit, V. (Eds.) BB8: A scalable, accurate, robust to partial occlusion method for predicting the 3D poses of challenging objects without using depth. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017. [Google Scholar]
- Xiang, Y.; Schmidt, T.; Narayanan, V.; Fox, D. Posecnn: A convolutional neural network for 6d object pose estimation in cluttered scenes. arXiv 2017, arXiv:1711.00199. [Google Scholar]
- Periyasamy, A.S.; Schwarz, M. (Eds.) Robust 6D Object Pose Estimation in Cluttered Scenes using Semantic Segmentation and Pose Regression Networks. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; IEEE: Piscataway, NJ, USA, 2018. [Google Scholar]
- Kehl, W.; Manhardt, F.; Tombari, F. (Eds.) SSD-6D: Making RGB-based 3D detection and 6D pose estimation great again. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017. [Google Scholar]
- Giefer, L.A.; Arango, J.D.; Faghihabdolahi, M.; Freitag, M. (Eds.) Orientation Detection of Fruits by means of Convolutional Neural Networks and Laser Line Projection for the Automation of Fruit Packing Systems. In Proceedings of the 13th CIRP Conference on Intelligent Computation in Manufacturing Engineering, Gulf of Naples, Italy, 17–19 July 2019. [Google Scholar]
- Eizentals, P.; Oka, K. 3D pose estimation of green pepper fruit for automated harvesting. Comput. Electron. Agric. 2016, 128, 127–140. [Google Scholar] [CrossRef]
- Lin, G.; Tang, Y.; Zou, X.; Xiong, J.; Li, J. Guava detection and pose estimation using a low-cost RGB-D Sensor in the field. Sensors 2019, 19, 428. [Google Scholar] [CrossRef]
- Park, K.; Prankl, J.; Vincze, M. Mutual Hypothesis Verification for 6D Pose Estimation of Natural Objects. In Proceedings of the 2017 IEEE International Conference on Computer Vision Workshops (ICCVW), Venice, Italy, 22–29 October 2017; IEEE: Piscataway, NJ, USA, 2017. [Google Scholar]
- Lehnert, C.; Sa, I.; McCool, C.; Upcroft, B.; Perez, T. Sweet pepper pose detection and grasping for automated crop harvesting. In Proceedings of the 2016 IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 16–21 May 2016; IEEE: Piscataway, NJ, USA, 2016. [Google Scholar] [Green Version]
- Huang, L. A concise introduction to mechanics of rigid bodies. In Multidisciplinary Engineering; Springer: New York, NY, USA, 2012. [Google Scholar]
- Baker, A. Matrix Groups: An Introduction to Lie Group Theory; Springer Science & Business Media: Berlin, Germany, 2012. [Google Scholar]
- Perumal, L. Quaternion and its application in rotation using sets of regions. Int. J. Eng. Technol. Innov. 2011, 1, 35–52. [Google Scholar]
- Saxena, A.; Driemeyer, J.; Ng, A.Y. Learning 3-D object orientation from images. In Proceedings of the IEEE International Conference on Robotics and Automation, Kobe, Japan, 12–17 May 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 794–800. [Google Scholar] [CrossRef]
- Bourbaki, N. Lie Groups and Lie Algebras: Chapters 1–3; Springer: Berlin/Heidelberg, Germany, 1989. [Google Scholar]
- Selig, J.M. Geometrical Methods in Robotics; Springer Science & Business Media: Berlin, Germany, 2013. [Google Scholar]
- Liu, W.; Anguelov, D.; Erhan, D.; Szegedy, C. (Eds.) Ssd: Single Shot Multibox Detector. European Conference on Computer Vision; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Canziani, A.; Paszke, A.; Culurciello, E. An Analysis of Deep Neural Network Models for Practical Applications. arXiv 2016, arXiv:1605.07678. [Google Scholar]
- Szegedy, C.; Ioffe, S.; Vanhoucke, V.; Alemi, A. (Eds.) Inception-v4, inception-resnet and the impact of residual connections on learning. In Proceedings of the Thirty-First AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 4–9 February 2017. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. 2015. Available online: https://arxiv.org/pdf/1512.03385 (accessed on 15 March 2019).
- Simonyan, K.; Zisserman, A. Very Deep Convolutional Networks for Large-Scale Image Recognition. Available online: https://arxiv.org/pdf/1409.1556 2015 (accessed on 15 March 2019).
- Bishop, C.M. Pattern Recognition and Machine Learning; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Everingham, M.; Winn, J. The PASCAL visual object classes challenge 2012 (VOC2012) development kit. Pattern Analysis, Statistical Modelling and Computational Learning. Tech. Rep. Section 3.3, pg. 12, 2011. Available online: http://host.robots.ox.ac.uk/pascal/VOC/voc2012/devkit_doc.pdf (accessed on 15 March 2019).
- Ruder, S. An overview of gradient descent optimization algorithms. arXiv 2016, arXiv:1609.04747. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Zeiler, M.D. ADADELTA: An Adaptive Learning Rate Method. Available online: https://arxiv.org/pdf/1212.5701 2012 (accessed on 15 March 2019).


| Deep-6DPose [%] | InceptionV3 [%] | ResNet50 [%] | VGG19 [%] | |
|---|---|---|---|---|
| Lie algebra | 98.36 | 91.92 | 95.21 | 88.49 |
| Quaternion | 97.12 | 82.74 | 94.11 | 89.22 |
| Acc20deg [%] | Acc15deg [%] | Acc10deg [%] | Acc5deg [%] | |
|---|---|---|---|---|
| Lie algebra | 99.18 | 98.36 | 95.92 | 64.94 |
| Quaternion | 99.32 | 97.12 | 86.68 | 46.87 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Giefer, L.A.; Arango Castellanos, J.D.; Babr, M.M.; Freitag, M. Deep Learning-Based Pose Estimation of Apples for Inspection in Logistic Centers Using Single-Perspective Imaging. Processes 2019, 7, 424. https://doi.org/10.3390/pr7070424
Giefer LA, Arango Castellanos JD, Babr MM, Freitag M. Deep Learning-Based Pose Estimation of Apples for Inspection in Logistic Centers Using Single-Perspective Imaging. Processes. 2019; 7(7):424. https://doi.org/10.3390/pr7070424
Chicago/Turabian StyleGiefer, Lino Antoni, Juan Daniel Arango Castellanos, Mohammad Mohammadzadeh Babr, and Michael Freitag. 2019. "Deep Learning-Based Pose Estimation of Apples for Inspection in Logistic Centers Using Single-Perspective Imaging" Processes 7, no. 7: 424. https://doi.org/10.3390/pr7070424
APA StyleGiefer, L. A., Arango Castellanos, J. D., Babr, M. M., & Freitag, M. (2019). Deep Learning-Based Pose Estimation of Apples for Inspection in Logistic Centers Using Single-Perspective Imaging. Processes, 7(7), 424. https://doi.org/10.3390/pr7070424






