Process Simulation of the Separation of Aqueous Acetonitrile Solution by Pressure Swing Distillation
Abstract
:1. Introduction
2. Design of Separation Scheme for PSD
2.1. Feasibility Analysis
2.2. Pressure Selection of Two Columns
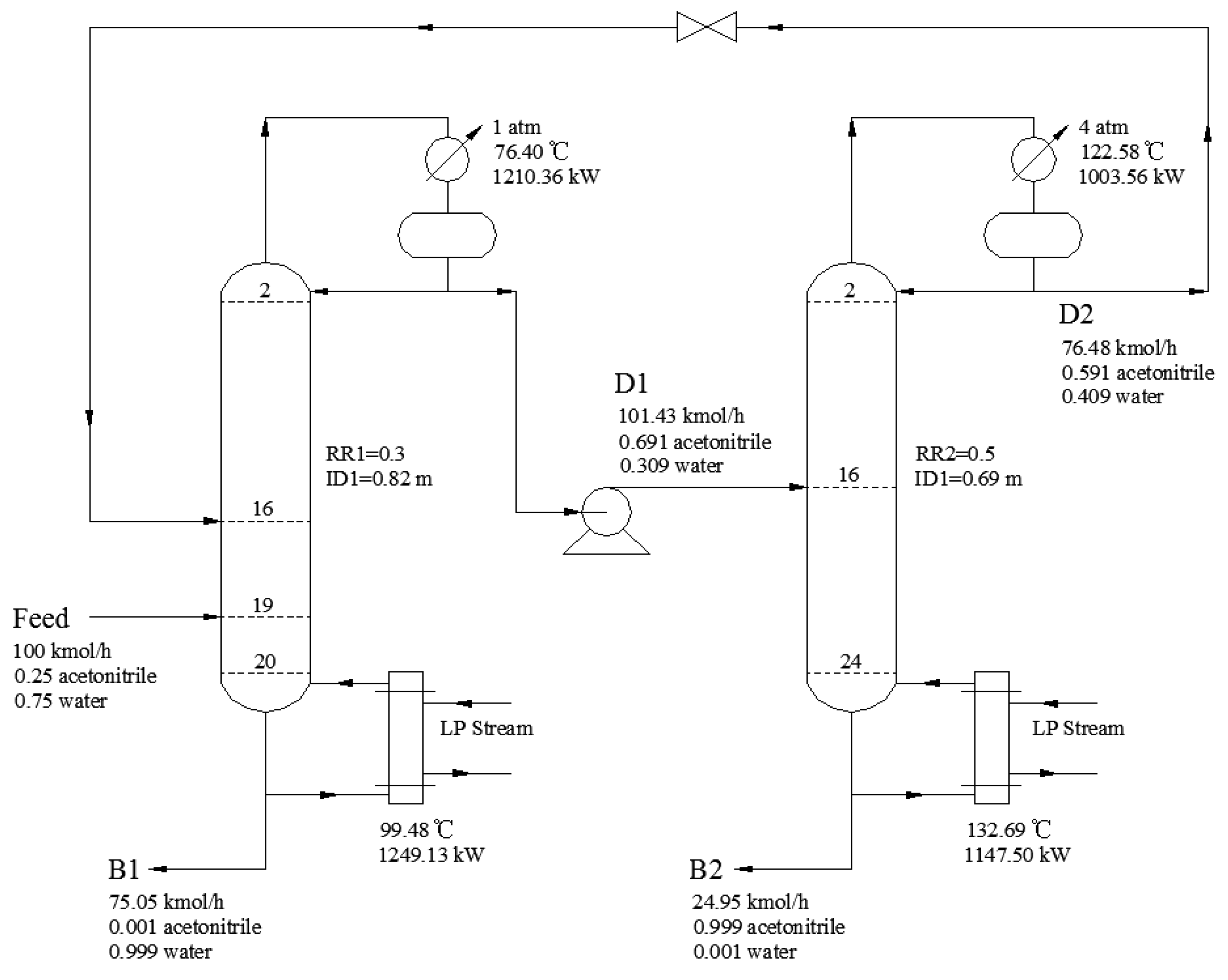
2.3. PSD Process Descripition
2.4. The Objective Function of the Process Optimization
3. Optimization of PSD
3.1. Optimization of PSD without Heat Integration
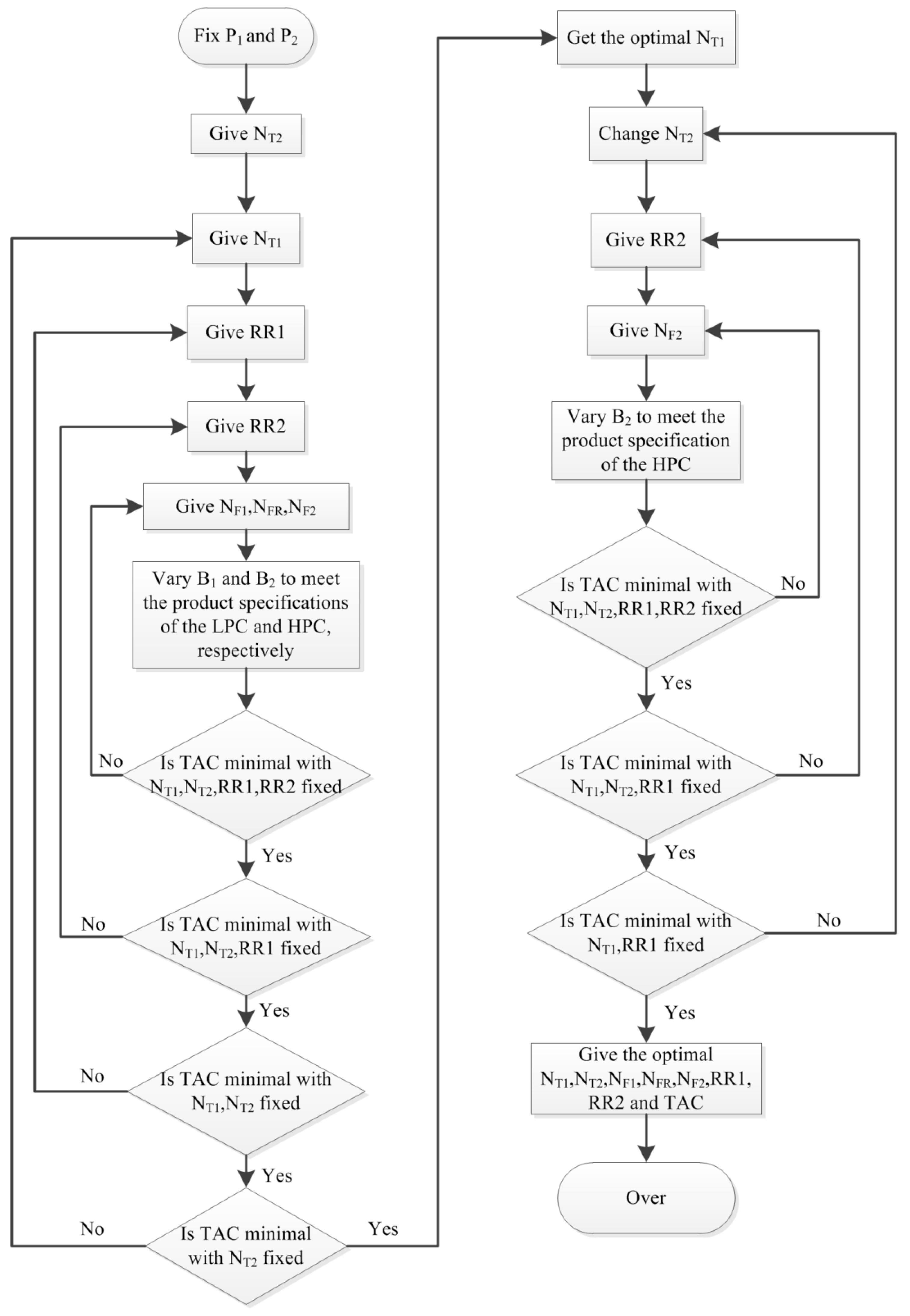
3.1.1. Process Optimization Sequence
3.1.2. The Optimization Results of PSD
3.2. Optimization of PSD with Full-Heat Integration
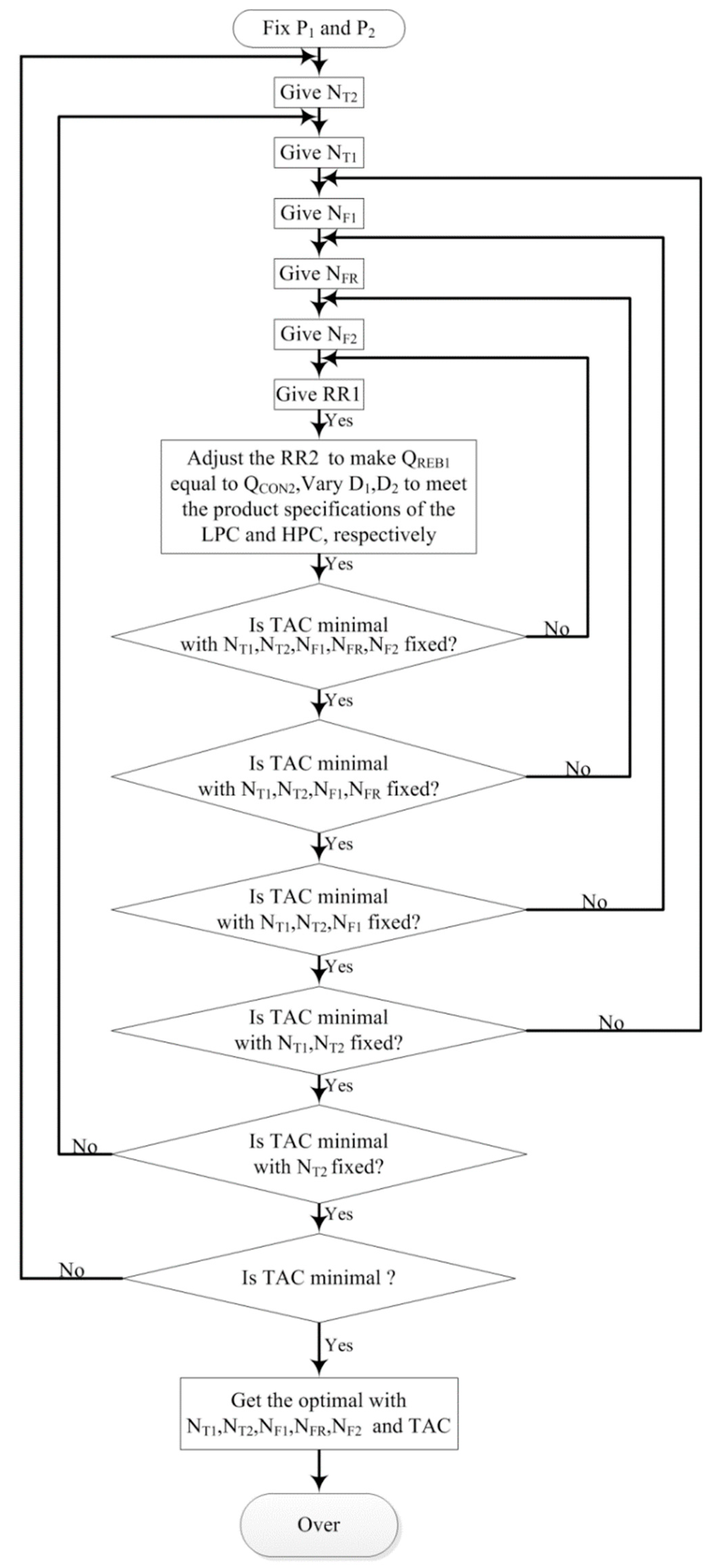
3.2.1. Process Optimization Sequence of PSD with Full-Heat Integration
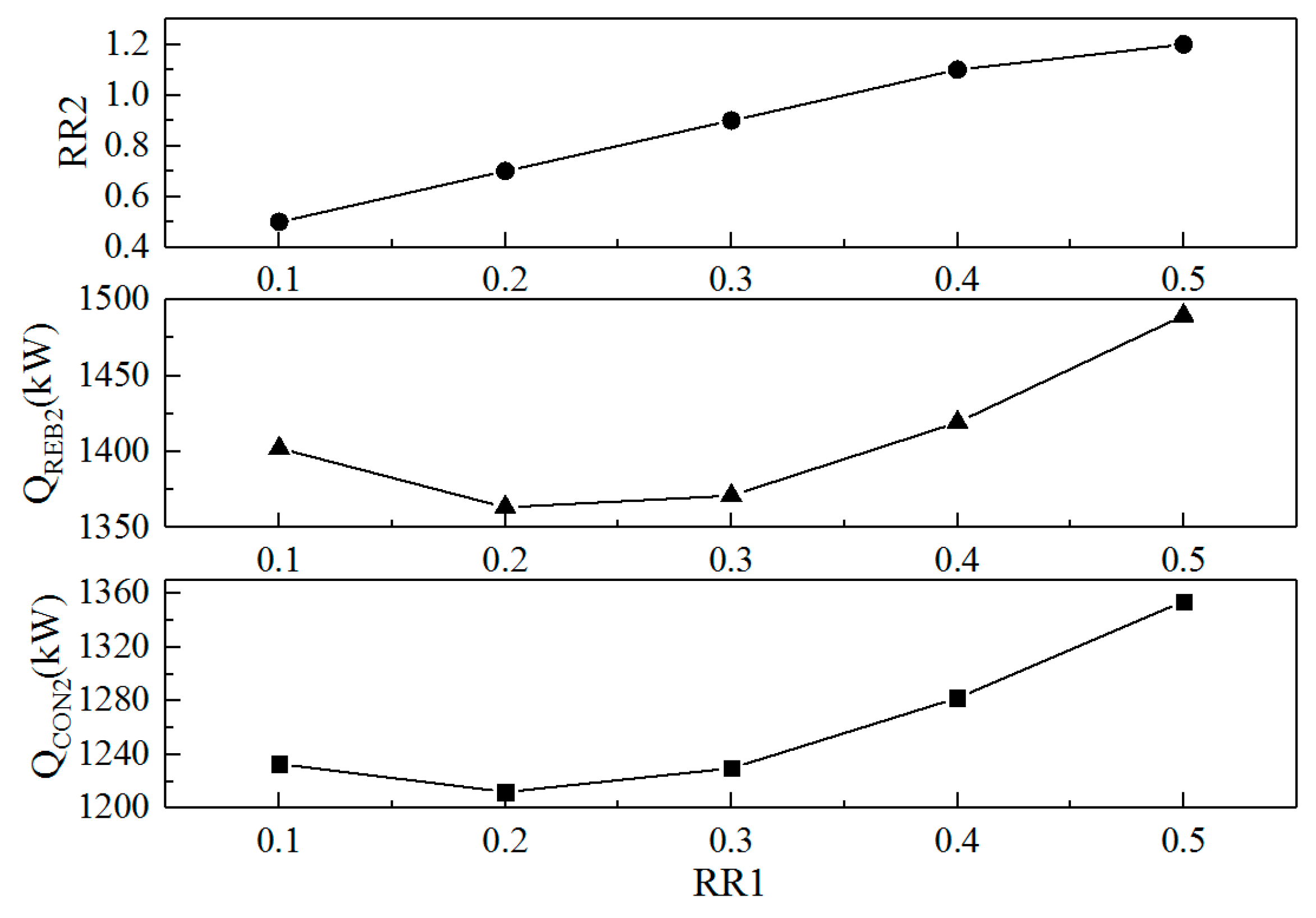
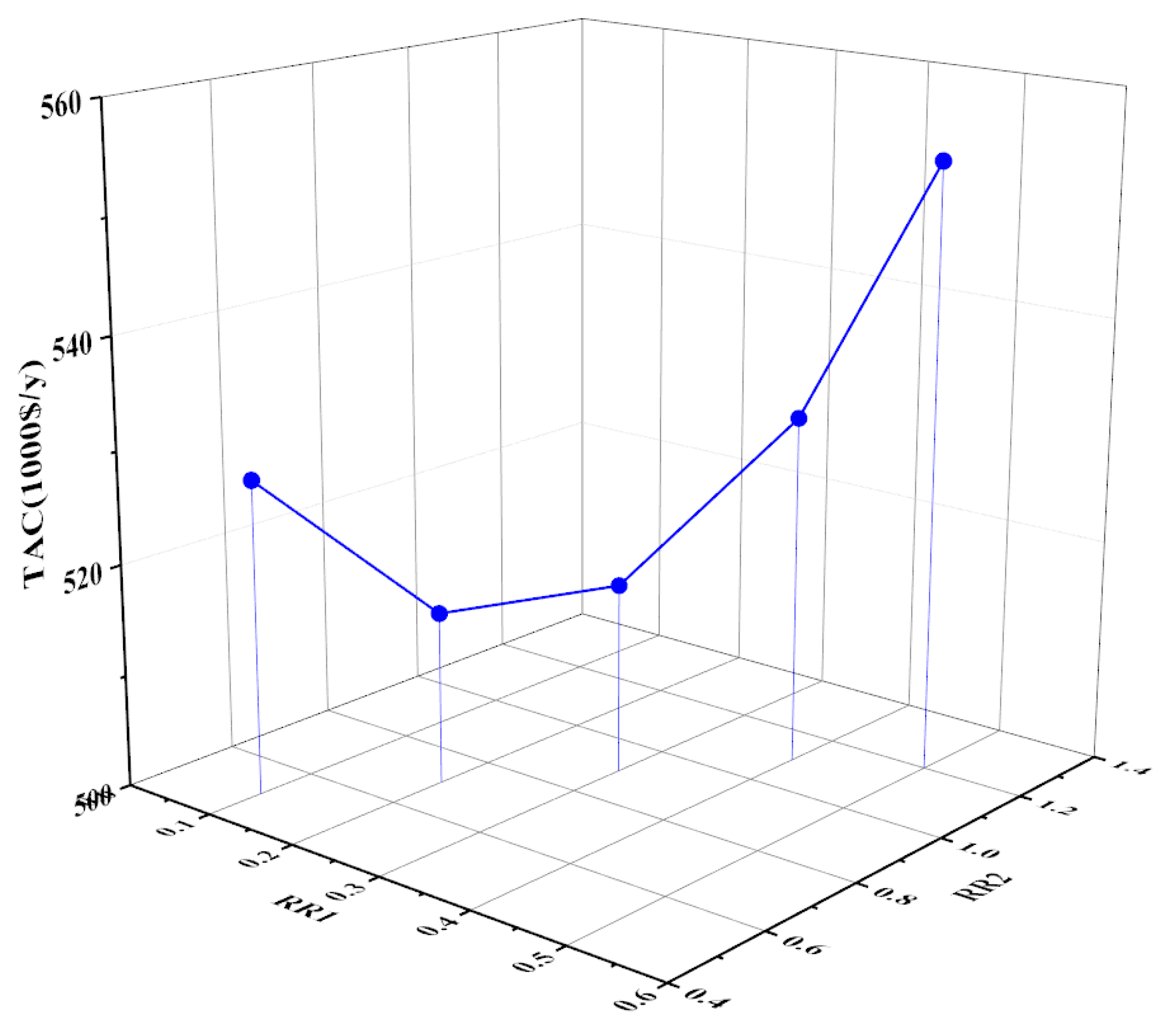
3.2.2. Optimization of the Reflux Ratios
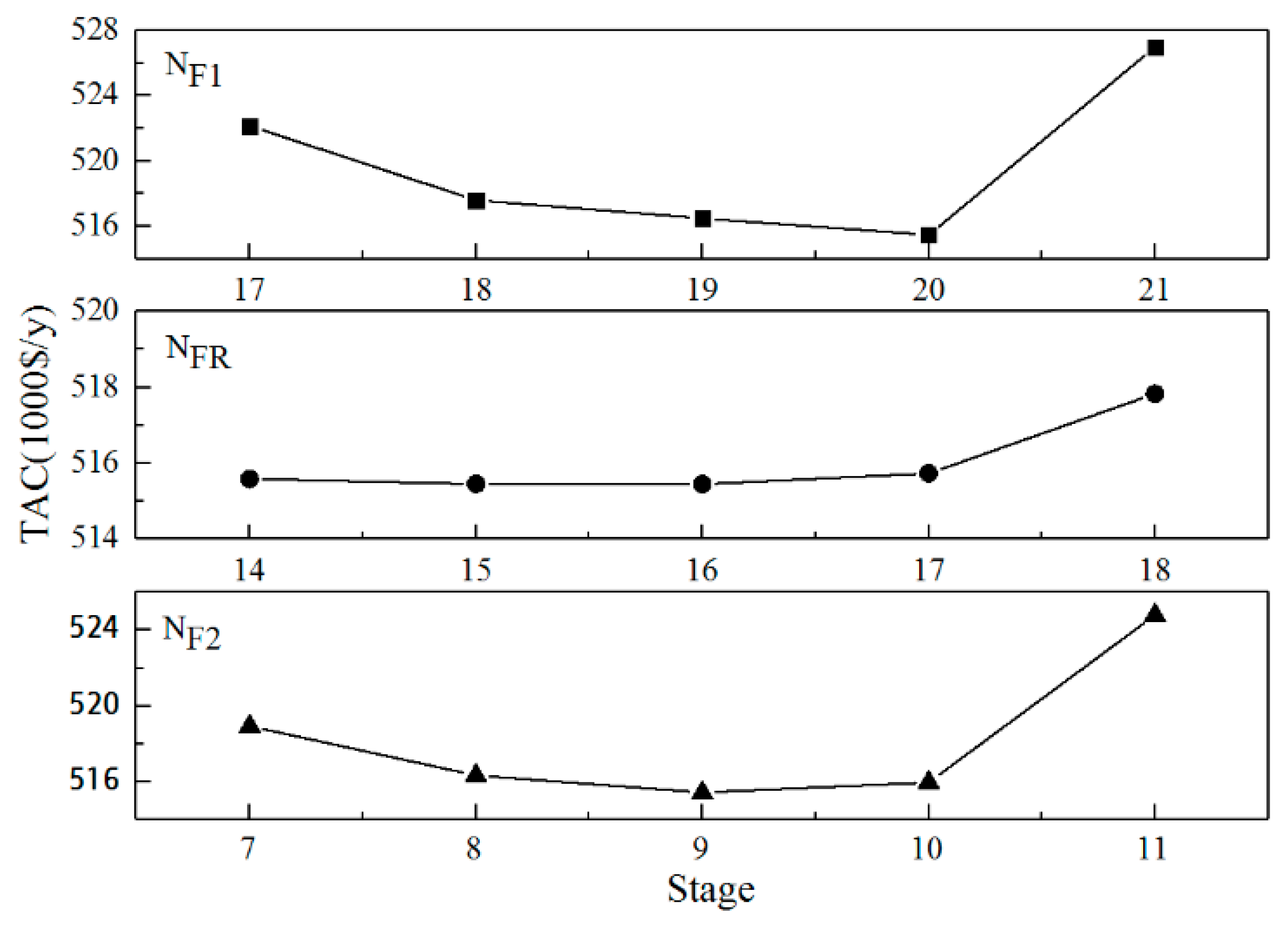
3.2.3. Optimization of the Feeding Positions
3.2.4. Optimization of the Tray Numbers
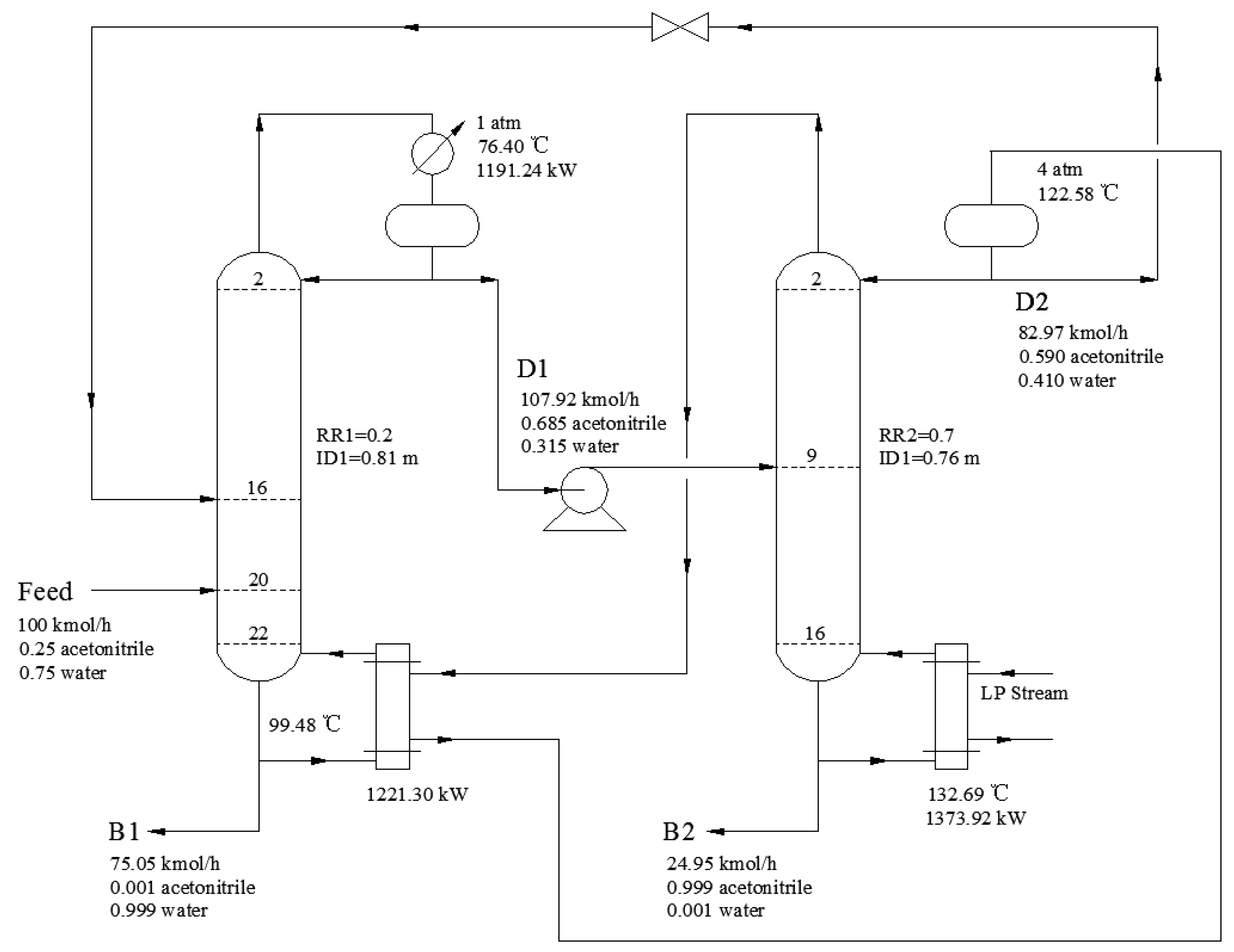
3.2.5. Process Optimization Results
3.3. Comparison of Two Technological Processes
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Wang, Y.L.; Bu, G.L.; Geng, X.L.; Zhu, Z.Y.; Cui, P.Z.; Liao, Z.W. Design optimization and operating pressure effects in the separation of acetonitrile/methanol/water mixture by ternary extractive distillation. J. Clean. Prod. 2019, 218, 212–224. [Google Scholar] [CrossRef]
- Jhoany, A.E.; Ivonne, R.D.; Ulises, J.H.; Lauro, N.P.; Eladio, P.F. Recovery of acetonitrile from aqueous waste by a combined process: Solvent extraction and batch distillation. Sep. Purif. Technol. 2006, 52, 95–101. [Google Scholar]
- Liang, K.; Li, W.S.; Luo, H.T.; Xia, M.; Xu, C.J. Energy-efficient extractive distillation process by combining preconcentration column and entrainer recovery column. Ind. Eng. Chem. Res. 2014, 53, 7121–7131. [Google Scholar] [CrossRef]
- Luyben, W.L. Comparison of extractive distillation and pressure-swing distillation for acetone/chloroform separation. Comp. Chem. Eng. 2013, 50, 1–7. [Google Scholar] [CrossRef]
- Liang, S.S.; Cao, Y.J.; Liu, X.Z.; Li, X.; Zhao, Y.T.; Wang, Y.K.; Wang, Y.L. Insight into pressure-swing distillation from azeotropic phenomenon to dynamic control. Chem. Eng. Res. Des. 2017, 117, 318–335. [Google Scholar] [CrossRef]
- Yang, A.; Shen, W.F.; Wei, S.A.; Dong, L.C.; Li, J.; Gerbaud, V. Design and control of pressure-swing distillation for separating ternary systems with three binary minimum azeotropes. AIChE J. 2019, 65, 1281–1293. [Google Scholar] [CrossRef] [Green Version]
- Shen, W.F.; Dong, L.C.; Wei, S.A.; Li, J.; Benyounes, H.; You, X.Q.; Gerbaud, V. Systematic design of extractive distillation for maximum-boiling azeotropes with heavy entrainers. AIChE J. 2015, 61, 3898–3910. [Google Scholar] [CrossRef]
- Zhao, Y.T.; Ma, K.; Bai, W.T.; Du, D.Q.; Zhu, Z.Y.; Wang, Y.L.; Gao, J. Energy-saving thermally coupled ternary extractive distillation process by combining with mixed entrainer for separating ternary mixture containing bioethanol. Energy 2018, 148, 296–308. [Google Scholar] [CrossRef]
- Rodriguez-Donis, I.; Acosta-Esquijarosa, J.; Gerbaud, V.; Joulia, X. Heterogeneous batch-extractive distillation of minimum boiling azeotropic mixtures. AIChE J. 2003, 49, 3074–3083. [Google Scholar] [CrossRef]
- Rodriguez-Donis, I.; Papp, K.; Rev, E.; Lelkes, Z.; Gerbaud, V.; Joulia, X. Column configurations of continuous heterogeneous extractive distillation. AIChE J. 2007, 53, 1982–1993. [Google Scholar] [CrossRef]
- Raeva, V.M.; Sazonova, A.Y. Separation of ternary mixtures by extractive distillation with 1, 2-ethandiol and glycerol. Chem. Eng. Res. Des. 2015, 99, 125–131. [Google Scholar] [CrossRef]
- Sazonova, A.Y.; Raeva, V.M. Recovery of acetonitrile from aqueous solutions by extractive distillation–effect of entrainer. Int. J. Chem. Mol. Nucl. Mater. Metall. Eng. 2015, 9, 288–291. [Google Scholar]
- You, X.; Gu, J.; Gerbaud, V.; Peng, C.; Liu, H. Optimization of pre-concentration, entrainer recycle and pressure selection for the extractive distillation of acetonitrile-water with ethylene glycol. Chem. Eng. Sci. 2018, 177, 354–368. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.; Du, Z.; Zhang, Y.; Wang, J.; Wang, J.; Sun, W. Optimization of distillation sequences with nonsharp separation columns. Processes 2019, 7, 323. [Google Scholar] [CrossRef]
- Salvador, T.A.; Arturo, J.G.; Juergen, H. Analysis of multi-loop control structures of dividing-wall distillation columns using a fundamental model. Processes 2014, 2, 180–199. [Google Scholar]
- Li, X.; Geng, X.L.; Cui, P.Z.; Yang, J.W.; Zhu, Z.Y.; Wang, Y.L.; Xu, D.M. Thermodynamic efficiency enhancement of pressure-swing distillation process via heat integration and heat pump technology. Appl. Therm. Eng. 2019, 154, 519–529. [Google Scholar] [CrossRef]
- Wang, Y.L.; Ma, K.; Yu, M.X.; Dai, Y.; Yuan, R.J.; Zhu, Z.Y.; Gao, J. An improvement scheme for pressure-swing distillation with and without heat integration through an intermediate connection to achieve energy savings. Comp. Chem. Eng. 2018, 119, 439–449. [Google Scholar] [CrossRef]
- Wang, K.L.; Li, J.; Liu, P.; Lian, M.L.; Du, T.Z. Pressure swing distillation for the separation of methyl acetate-methanol azeotrope. Asia-Pac J. Chem. Eng. 2019, 14, e2319. [Google Scholar] [CrossRef]
- Varbanov, P.; Klein, A.; Repke, J.U.; Wozny, G. Minimising the startup duration for mass- and heat-integrated two-column distillation systems: A conceptual approach. Chem. Eng. Process. 2008, 47, 1456–1469. [Google Scholar] [CrossRef]
- Rahman, I.; Sagar, S.A. Optimization of pressure-swing distillation by evolutionary techniques: Separation of ethanol-water and acetonitrile-water mixtures. Chem. Prod. Process. Model. 2018, 13, 20170007. [Google Scholar]
- Repke, J.U.; Forner, F.; Klein, A. Separation of homogeneous azeotropic mixtures by pressure swing distillation-analysis of the operation performance. Chem. Eng. Technol. 2005, 28, 1151–1157. [Google Scholar] [CrossRef]
- Kim, K.W.; Shin, J.S.; Kim, S.H.; Hong, S.K.; Cho, J.H.; Park, S.J. A computational study on the separation of acetonitrile and water azeotropic mixture using pressure swing distillation. J. Chem. Eng. Jpn. 2013, 46, 347–352. [Google Scholar] [CrossRef]
- Huang, F.; Zheng, S.; Chen, Y.; Zhou, M.; Sun, X. Simulation and optimization of pressure-swing distillation system for high purity acetonitrile. In ACSR-Advances in Computer Science Research, Proceedings of the 2016 International Conference on Modeling, Simulation and Optimization Technologies and Applications (MSOTA), Xiamen, China, 18–19 December 2016; Atlantis Press: Paris, France, 2016; Volume 58, pp. 96–100. [Google Scholar]
- Huang, K.; Shan, L.; Zhu, Q.; Qian, J. Adding rectifying/stripping section type heat integration to a pressure-swing distillation (PSD) process. Appl. Therm. Eng. 2008, 28, 923–932. [Google Scholar] [CrossRef]
- Matsuda, K.; Huang, K.; Iwakabe, K.; Nakaiwa, M. Separation of binary azeotrope mixture via pressure-swing distillation with heat integration. J. Chem. Eng. Jpn. 2011, 44, 969–975. [Google Scholar] [CrossRef]
- Gao, Z.; Saxen, H.; Gao, C. Guest editorial: Special section on data-driven approaches for complex industrial systems. IEEE Trans. Ind. Informat. 2013, 9, 2210–2212. [Google Scholar] [CrossRef]
- Gao, Z.; Nguang, S.K.; Kong, D.X. Advances in modelling, monitoring, and control for complex industrial systems. Complexity 2019, 2019, 2975083. [Google Scholar] [CrossRef]
- Dai, X.; Gao, Z. From model, signal to knowledge: A data-driven perspective of fault detection and diagnosis. IEEE Trans. Ind. Informat. 2013, 9, 2226–2238. [Google Scholar] [CrossRef]
- Zhai, C.; Liu, Q.; Romagnoli, J.A.; Sun, W. Modeling/simulation of the dividing wall column by using the rigorous model. Processes 2019, 7, 26. [Google Scholar] [CrossRef]
- Liang, T.; Guo, X.; Giwa, A.S.; Shi, J.; Li, Y.; Wei, Y.; Du, J. Design and optimization of a process for the production of methyl methacrylate via direct methylation. Processes 2019, 7, 377. [Google Scholar] [CrossRef]
- Petrovic, B.A.; Masoudi, S.M. Optimization of post combustion CO2 capture from a combined-cycle gas turbine power plant via taguchi design of experiment. Processes 2019, 7, 364. [Google Scholar] [CrossRef]
- Sarda, P.; Hedrick, E.; Reynolds, K.; Bhattacharyya, D.; Zitney, S.E.; Omell, B. Development of a dynamic model and control system for load-following studies of supercritical pulverized coal power plants. Processes 2018, 6, 226. [Google Scholar] [CrossRef]
- Gmehling, J.; Menke, J.; Fischer, K.; Krafczyk, J. Azeotropic Data; Wiley-VCH: Weinheim, Germany, 2004. [Google Scholar]
- Luyben, W.L.; Chien, I.L. Design and Control of Distillation Systems for Separating Azeotropes; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Luo, H.; Liang, K.; Li, W.; Li, Y.; Xia, M.; Xu, C. Comparison of pressure-swing distillation and extractive distillation methods for isopropyl alcohol/diisopropyl ether separation. Ind. Eng. Chem. Res. 2014, 53, 15167–15182. [Google Scholar] [CrossRef]
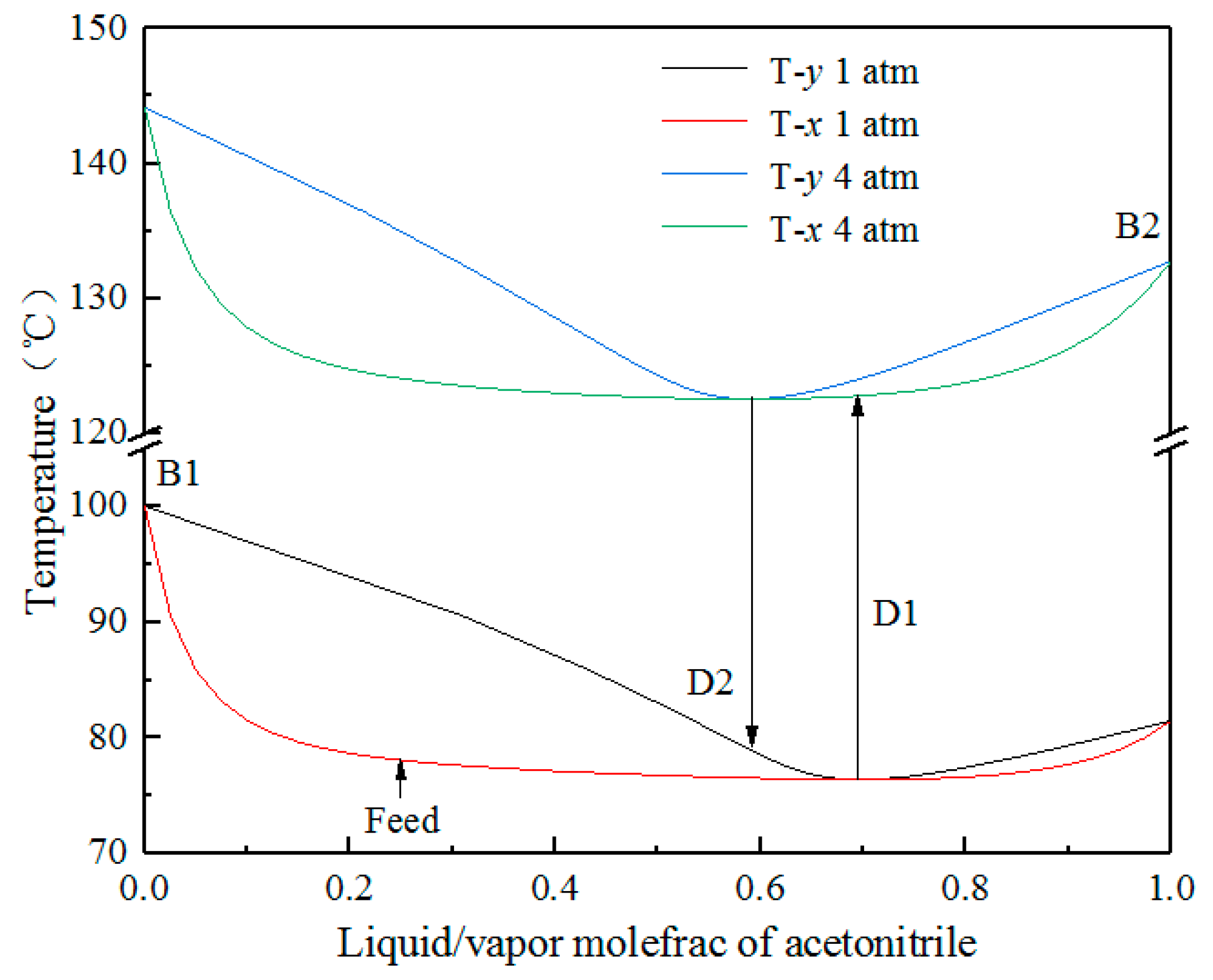
| Operating Pressure/Atm | Boiling Point of Acetonitrile/°C | Boiling Point of Water/°C | Boiling Point of Azeotrope/°C | Azeotropic Concentration (Mole) | |
|---|---|---|---|---|---|
| Acetonitrile | Water | ||||
| 1 | 81.48 | 100.02 | 76.40 | 0.6971 | 0.3029 |
| 2 | 105.33 | 120.69 | 98.06 | 0.6438 | 0.3562 |
| 3 | 120.91 | 134.05 | 112.01 | 0.6116 | 0.3884 |
| 4 | 132.79 | 144.16 | 122.58 | 0.5886 | 0.4114 |
| 5 | 142.52 | 152.41 | 131.18 | 0.5707 | 0.4293 |
| Design Variables | Case 1 | Case 2 | Case 3 | Case 4 | Case 5 |
|---|---|---|---|---|---|
| NT1 | 21 | 22 | 23 | 24 | 25 |
| NT2 | 17 | 17 | 17 | 17 | 17 |
| RR1 | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 |
| RR2 | 0.7 | 0.7 | 0.7 | 0.7 | 0.7 |
| ID1/m | 0.92 | 0.81 | 0.81 | 0.82 | 0.82 |
| ID2/m | 0.86 | 0.76 | 0.76 | 0.76 | 0.76 |
| RREC/kmol/h | 116.27 | 83.05 | 82.97 | 82.96 | 82.96 |
| Equipment investment cost/103 $ | 738.52 | 625.32 | 622.82 | 631.88 | 640.12 |
| Operation cost/103 $/y | 392.61 | 308.05 | 307.85 | 307.83 | 307.82 |
| TAC/103 $/y | 638.78 | 516.49 | 515.45 | 518.45 | 521.20 |
| Design Variables | Case 6 | Case 7 | Case 8 | Case 9 | Case 10 |
|---|---|---|---|---|---|
| NT1 | 23 | 23 | 23 | 23 | 23 |
| NT2 | 15 | 16 | 17 | 18 | 19 |
| RR1 | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 |
| RR2 | 0.7 | 0.7 | 0.7 | 0.7 | 0.7 |
| ID1/m | 0.83 | 0.82 | 0.81 | 0.81 | 0.81 |
| ID2/m | 0.77 | 0.76 | 0.76 | 0.76 | 0.76 |
| RREC/kmol/h | 88.13 | 83.76 | 82.97 | 82.75 | 82.69 |
| Equipment investment cost/103 $ | 621.25 | 618.81 | 622.82 | 630.15 | 637.76 |
| Operation cost/103 $/y | 320.56 | 309.79 | 307.85 | 307.31 | 307.14 |
| TAC/103 $/y | 527.65 | 516.06 | 515.45 | 517.36 | 519.73 |
| Design Variables | Without Heat Integration | Full-Heat Integration |
|---|---|---|
| NT1 | 21 | 23 |
| NT2 | 25 | 17 |
| NF1/NFR | 19/16 | 20/16 |
| NF2 | 16 | 9 |
| RR1/RR2 | 0.3/0.5 | 0.20/0.70 |
| QCON1/kW | 1210.36 | 1191.24 |
| QREB1/kW | 1249.13 | — |
| QCON2/kW | 1003.56 | — |
| QREB2/kW | 1147.50 | 1373.92 |
| Heat exchanger /kW | — | 1221.30 |
| ID1/m | 0.82 | 0.81 |
| ID2/m | 0.69 | 0.76 |
| RREC/kmol/h | 76.48 | 82.97 |
| Equipment investment cost/103 $ | 676.05 | 622.82 |
| Operation cost/103 $/y | 537.00 | 307.85 |
| TAC/103 $/y | 762.35 | 515.45 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Wang, K.; Lian, M.; Li, Z.; Du, T. Process Simulation of the Separation of Aqueous Acetonitrile Solution by Pressure Swing Distillation. Processes 2019, 7, 409. https://doi.org/10.3390/pr7070409
Li J, Wang K, Lian M, Li Z, Du T. Process Simulation of the Separation of Aqueous Acetonitrile Solution by Pressure Swing Distillation. Processes. 2019; 7(7):409. https://doi.org/10.3390/pr7070409
Chicago/Turabian StyleLi, Jing, Keliang Wang, Minglei Lian, Zhi Li, and Tingzhao Du. 2019. "Process Simulation of the Separation of Aqueous Acetonitrile Solution by Pressure Swing Distillation" Processes 7, no. 7: 409. https://doi.org/10.3390/pr7070409





