Comparison of Multi-Objective Evolutionary Algorithms to Solve the Modular Cell Design Problem for Novel Biocatalysis
Abstract
1. Introduction
2. Methods
2.1. Multi-Objective Modular Cell Design
2.2. Optimal Solutions for a Multi-Objective Optimization Problem
2.3. MOEA Selection
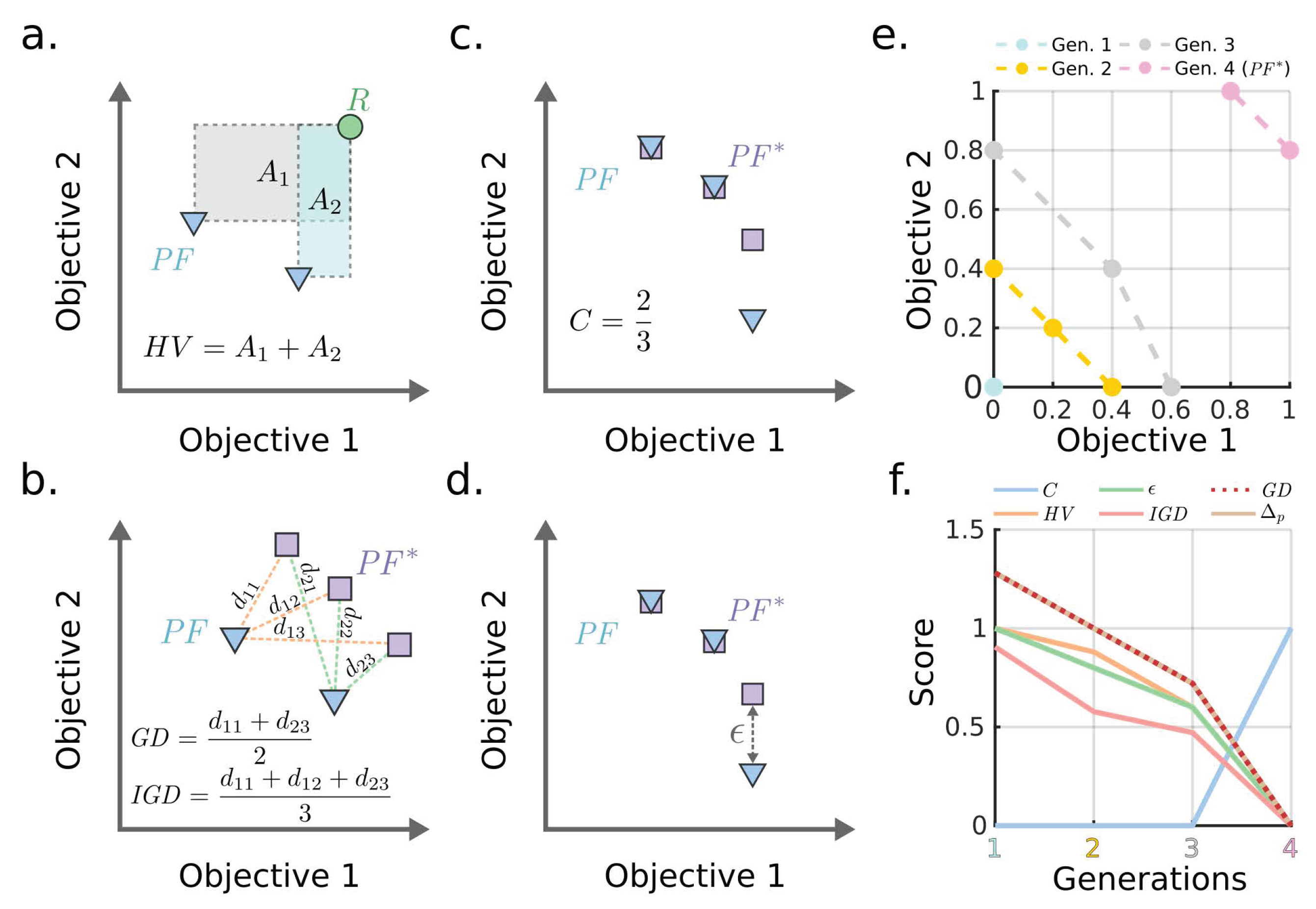
2.4. Performance Metrics
2.5. Algorithm Parameters
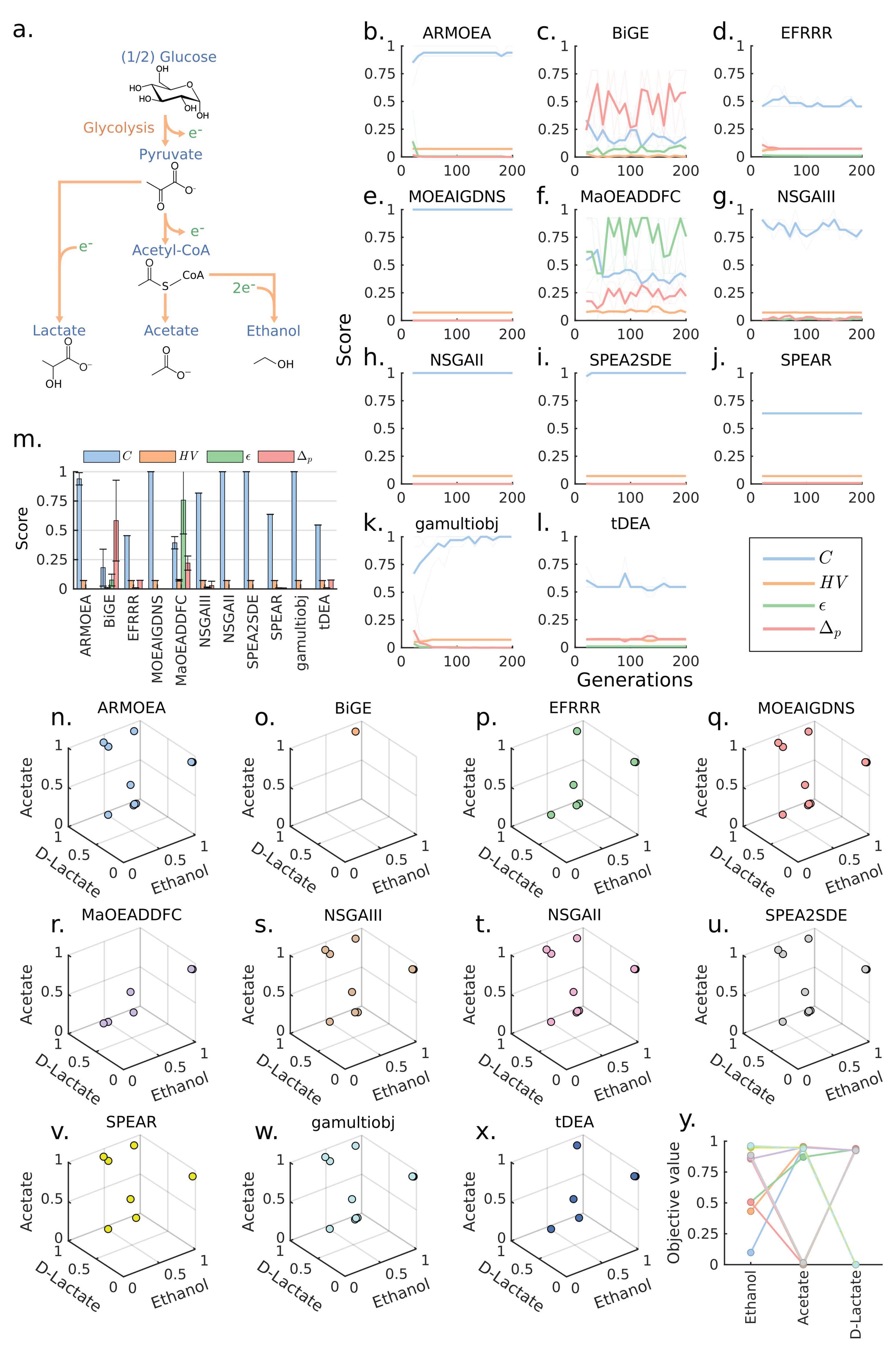
2.6. Metabolic Models
2.7. Implementation
3. Results and Discussion
3.1. Case 1: A 3-Objectives Design Problem
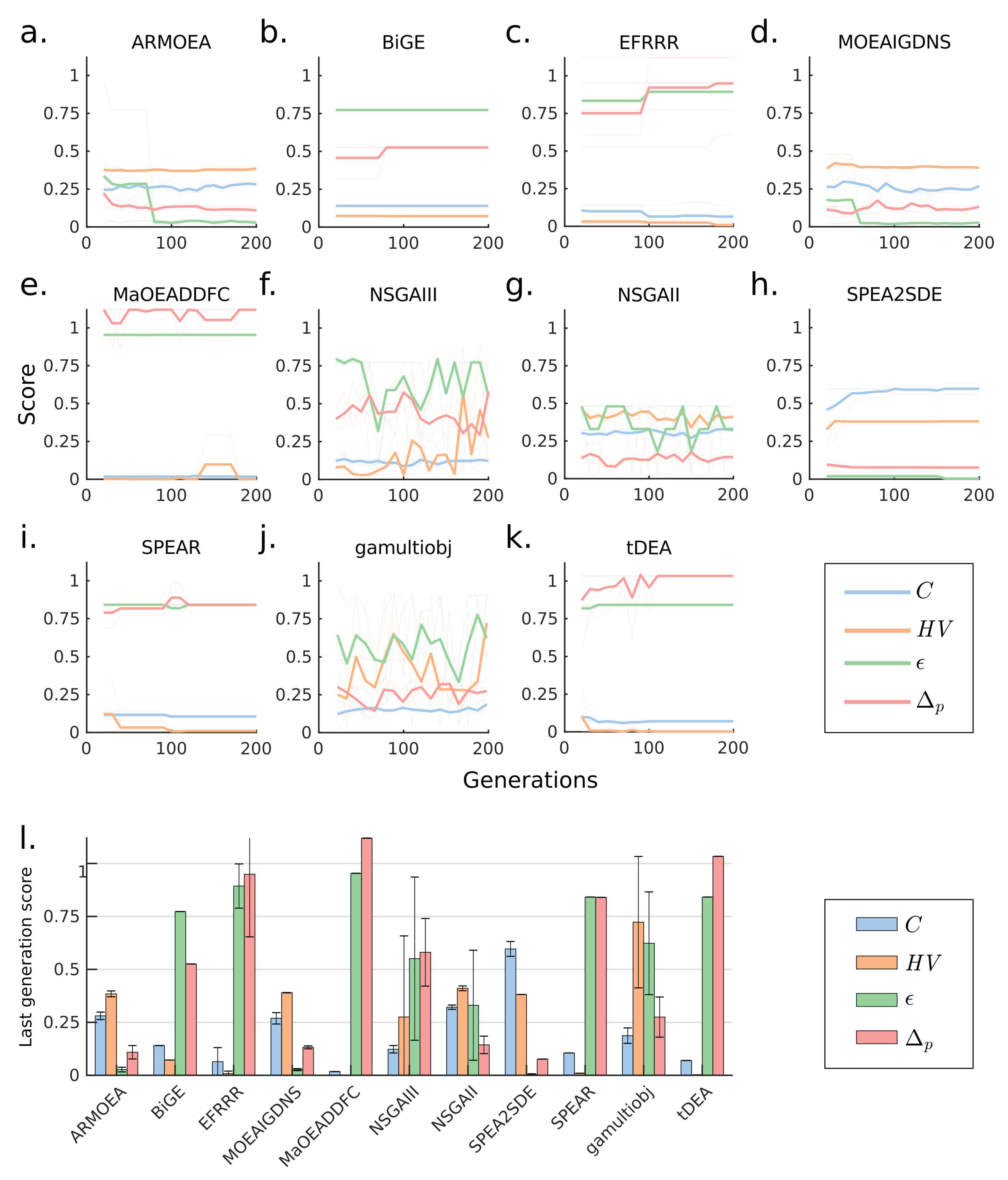
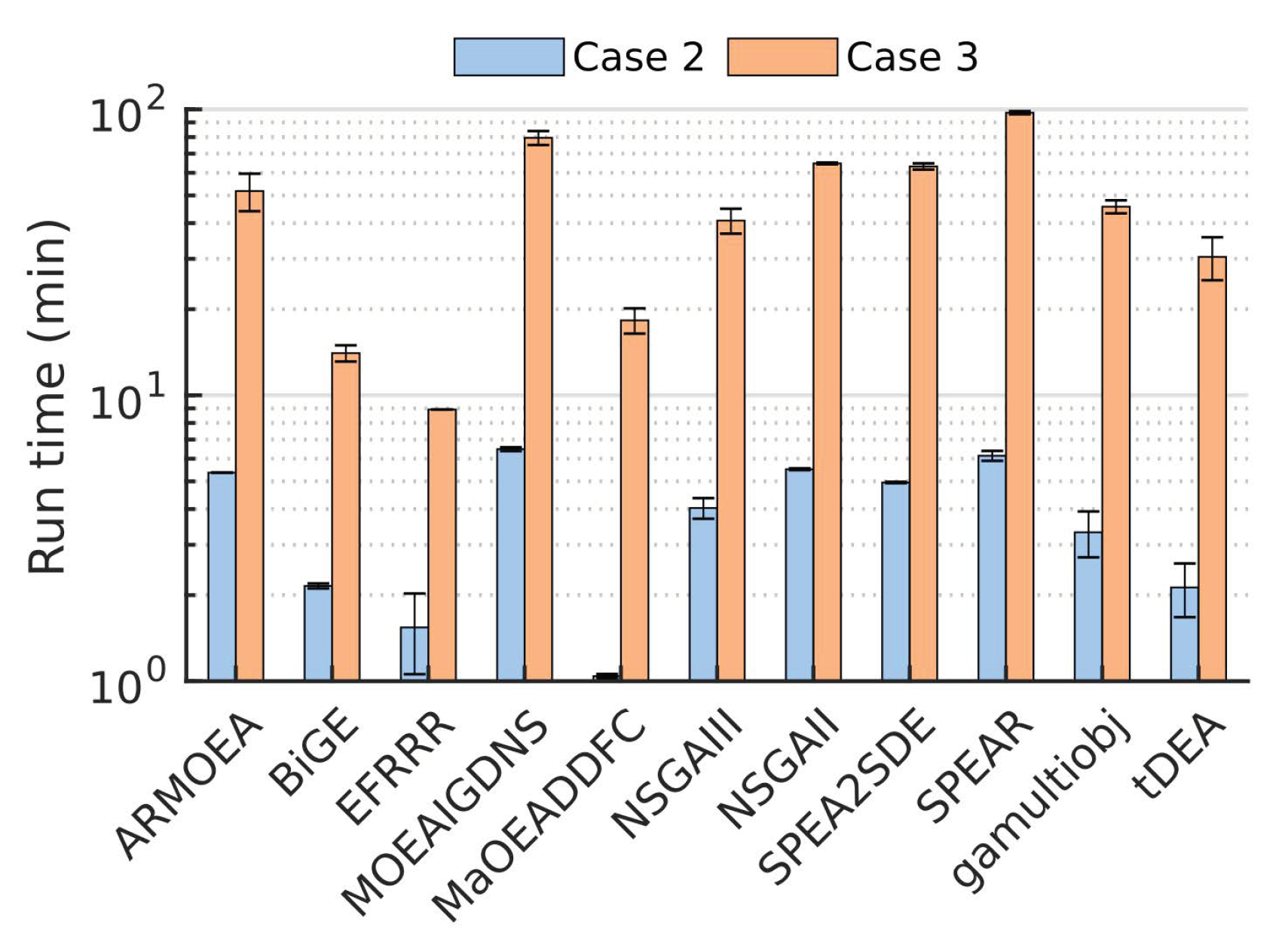
3.2. Case 2: A 10-Objectives Design Problem
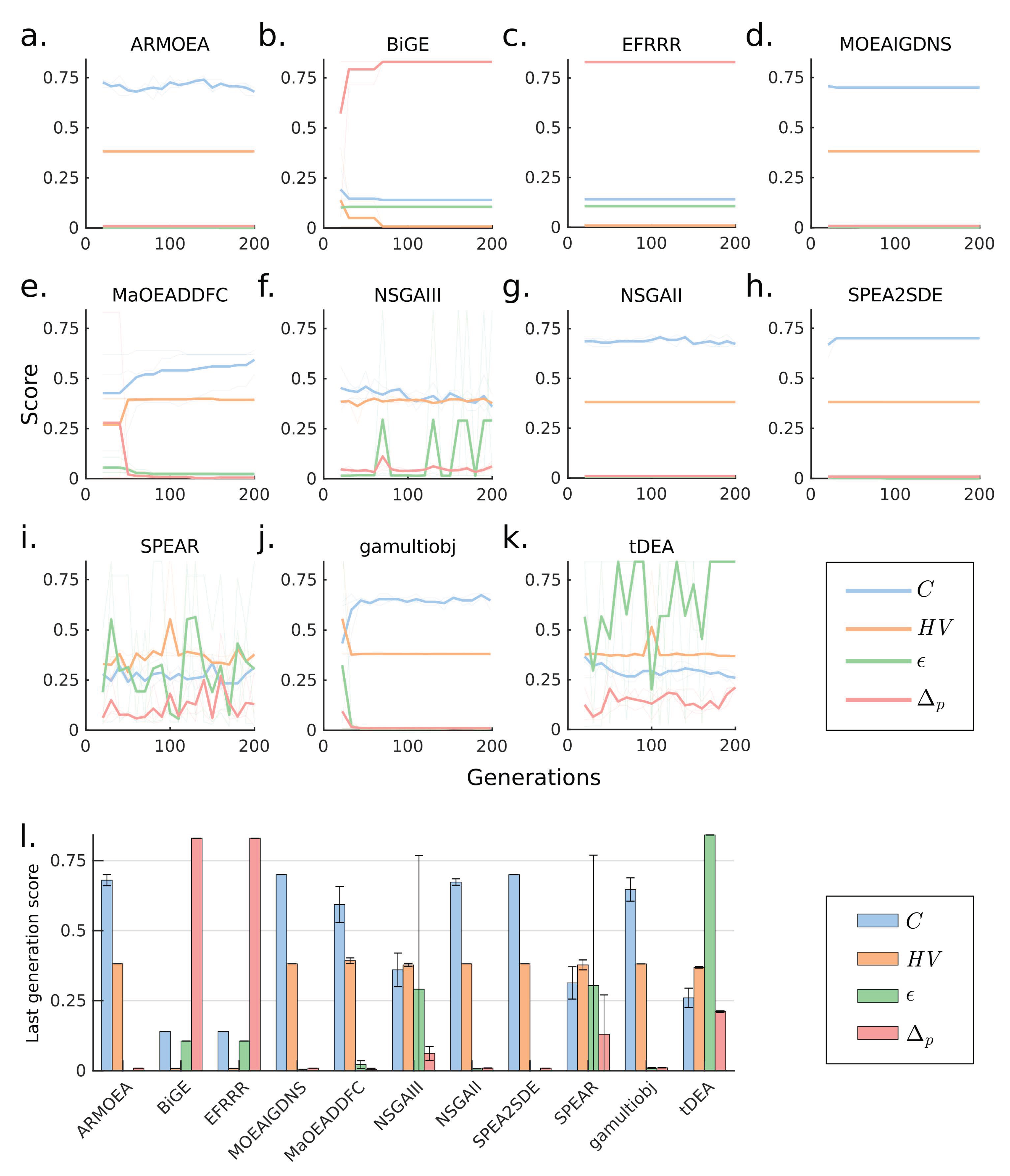
3.3. Case 3: Use of Large Population Size Overcomes Poor MOEA Performance
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Coello, C.A.C.; Lamont, G.B. Applications of Multi-Objective Evolutionary Algorithms; World Scientific: Singapore, 2004; Volume 1. [Google Scholar]
- Rangaiah, G.P. Multi-Objective Optimization: Techniques and Applications In Chemical Engineering; World Scientific: Singapore, 2009; Volume 1. [Google Scholar]
- Trinh, C.T.; Mendoza, B. Modular cell design for rapid, efficient strain engineering toward industrialization of biology. Curr. Opin. Chem. Eng. 2016, 14, 18–25. [Google Scholar] [CrossRef]
- Lee, S.Y.; Kim, H.U.; Chae, T.U.; Cho, J.S.; Kim, J.W.; Shin, J.H.; Kim, D.I.; Ko, Y.S.; Jang, W.D.; Jang, Y.S. A comprehensive metabolic map for production of bio-based chemicals. Nat. Catal. 2019, 2, 18. [Google Scholar] [CrossRef]
- Nielsen, J.; Keasling, J. Engineering Cellular Metabolism. Cell 2016, 164, 1185–1197. [Google Scholar] [CrossRef] [PubMed]
- Bonvoisin, J.; Halstenberg, F.; Buchert, T.; Stark, R. A systematic literature review on modular product design. J. Eng. Des. 2016, 27, 488–514. [Google Scholar] [CrossRef]
- Trinh, C.T. Elucidating and reprogramming Escherichia coli metabolisms for obligate anaerobic n-butanol and isobutanol production. Appl. Microbiol. Biotechnol. 2012, 95, 1083–1094. [Google Scholar] [CrossRef] [PubMed]
- Garcia, S.; Trinh, C. Multiobjective strain design: A framework for modular cell engineering. Metab. Eng. 2019, 51. [Google Scholar] [CrossRef] [PubMed]
- Trinh, C.T.; Liu, Y.; Conner, D.J. Rational design of efficient modular cells. Metab. Eng. 2015, 32, 220–231. [Google Scholar] [CrossRef]
- Garcia, S.; Trinh, C. Modular design: Applying proven engineering principles to biotechnology. 2019. under review. [Google Scholar]
- Trinh, C.T.; Li, J.; Blanch, H.W.; Clark, D.S. Redesigning Escherichia coli metabolism for anaerobic production of isobutanol. Appl. Environ. Microbiol. 2011, 77, 4894–4904. [Google Scholar] [CrossRef]
- Wilbanks, B.; Layton, D.; Garcia, S.; Trinh, C. A Prototype for Modular Cell Engineering. ACS Synthetic Biol. 2017. [Google Scholar] [CrossRef]
- Layton, D.S.; Trinh, C.T. Engineering modular ester fermentative pathways in Escherichia coli. Metab. Eng. 2014, 26, 77–88. [Google Scholar] [CrossRef] [PubMed]
- Layton, D.S.; Trinh, C.T. Expanding the modular ester fermentative pathways for combinatorial biosynthesis of esters from volatile organic acids. Biotechnol. Bioeng. 2016, 113, 1764–1776. [Google Scholar] [CrossRef] [PubMed]
- Layton, D.S.; Trinh, C.T. Microbial synthesis of a branched-chain ester platform from organic waste carboxylates. Metab. Eng. Commun. 2016, 3, 245–251. [Google Scholar] [CrossRef] [PubMed]
- Wierzbicki, M.; Niraula, N.; Yarrabothula, A.; Layton, D.S.; Trinh, C.T. Engineering an Escherichia coli platform to synthesize designer biodiesels. J. Biotechnol. 2016, 224, 27–34. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.; Trinh, C.T. De novo Microbial Biosynthesis of a Lactate Ester Platform. bioRxiv 2018. [Google Scholar] [CrossRef]
- Coello, C.A.C.; Lamont, G.B.; Van Veldhuizen, D.A. Evolutionary Algorithms for Solving Multi-Objective Problems; Springer: Berlin, Germany, 2007; Volume 5. [Google Scholar]
- Marler, R.T.; Arora, J.S. Survey of multi-objective optimization methods for engineering. Struct. Multidisc. Optim. 2004, 26, 369–395. [Google Scholar] [CrossRef]
- Li, B.; Li, J.; Tang, K.; Yao, X. Many-objective evolutionary algorithms: A survey. ACM Comput. Surv. (CSUR) 2015, 48, 13. [Google Scholar] [CrossRef]
- Matlab Documentation Gamultiobj Algorithm. Available online: https://www.mathworks.com/help/gads/gamultiobj-algorithm.html. (accessed on 4 February 2019).
- Kalyanmoy, D. Multi Objective Optimization Using Evolutionary Algorithms; John Wiley and Sons: Chichester, UK, 2001. [Google Scholar]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Zitzler, E.; Laumanns, M.; Thiele, L. SPEA2: Improving the Strength Pareto Evolutionary Algorithm; TIK-Report; ETH Zurich: Zurich, Switzerland, 2001; Volume 103. [Google Scholar]
- Zitzler, E.; Deb, K.; Thiele, L. Comparison of multiobjective evolutionary algorithms: Empirical results. Evol. Comput. 2000, 8, 173–195. [Google Scholar] [CrossRef]
- Deb, K.; Thiele, L.; Laumanns, M.; Zitzler, E. Scalable multi-objective optimization test problems. In Proceedings of the 2002 Congress on Evolutionary Computation. CEC’02 (Cat. No.02TH8600), Honolulu, HI, USA, 12–17 May 2002; Volume 1, pp. 825–830. [Google Scholar]
- Palsson, B.Ø. Systems Biology: Constraint-Based Reconstruction and Analysis; Cambridge University Press: Cambridge, UK, 2015. [Google Scholar]
- Tian, Y.; Cheng, R.; Zhang, X.; Jin, Y. PlatEMO: A MATLAB platform for evolutionary multi-objective optimization. IEEE Comput. Intell. Mag. 2017, 12, 73–87. [Google Scholar] [CrossRef]
- Tian, Y.; Zhang, X.; Cheng, R.; Jin, Y. A multi-objective evolutionary algorithm based on an enhanced inverted generational distance metric. In Proceedings of the 2016 IEEE Congress on Evolutionary Computation (CEC), Vancouver, BC, Canada, 24–29 July 2016; pp. 5222–5229. [Google Scholar]
- Tian, Y.; Cheng, R.; Zhang, X.; Cheng, F.; Jin, Y. An indicator-based multiobjective evolutionary algorithm with reference point adaptation for better versatility. IEEE Trans. Evol. Comput. 2018, 22, 609–622. [Google Scholar] [CrossRef]
- Yuan, Y.; Xu, H.; Wang, B.; Zhang, B.; Yao, X. Balancing convergence and diversity in decomposition-based many-objective optimizers. IEEE Trans. Evol. Comput. 2016, 20, 180–198. [Google Scholar] [CrossRef]
- Cheng, J.; Yen, G.G.; Zhang, G. A many-objective evolutionary algorithm with enhanced mating and environmental selections. IEEE Trans. Evol. Comput. 2015, 19, 592–605. [Google Scholar] [CrossRef]
- Jiang, S.; Yang, S. A strength Pareto evolutionary algorithm based on reference direction for multiobjective and many-objective optimization. IEEE Trans. Evol. Comput. 2017, 21, 329–346. [Google Scholar] [CrossRef]
- Yuan, Y.; Xu, H.; Wang, B.; Yao, X. A new dominance relation-based evolutionary algorithm for many-objective optimization. IEEE Trans. Evol. Comput. 2016, 20, 16–37. [Google Scholar] [CrossRef]
- Li, M.; Yang, S.; Liu, X. Bi-goal evolution for many-objective optimization problems. Artif. Intell. 2015, 228, 45–65. [Google Scholar] [CrossRef]
- Deb, K.; Jain, H. An evolutionary many-objective optimization algorithm using reference-point-based nondominated sorting approach, part I: Solving problems with box constraints. IEEE Trans. Evol. Comput. 2014, 18, 577–601. [Google Scholar] [CrossRef]
- Li, M.; Yang, S.; Liu, X. Shift-based density estimation for Pareto-based algorithms in many-objective optimization. IEEE Trans. Evol. Comput. 2014, 18, 348–365. [Google Scholar] [CrossRef]
- Riquelme, N.; Von Lücken, C.; Baran, B. Performance metrics in multi-objective optimization. In Proceedings of the 2015 Latin American Computing Conference (CLEI), Arequipa, Peru, 19–23 October 2015; pp. 1–11. [Google Scholar]
- Schutze, O.; Esquivel, X.; Lara, A.; Coello, C.A.C. Using the averaged Hausdorff distance as a performance measure in evolutionary multiobjective optimization. IEEE Trans. Evol. Comput. 2012, 16, 504–522. [Google Scholar] [CrossRef]
- Zitzler, E.; Thiele, L.; Laumanns, M.; Fonseca, C.M.; Da Fonseca Grunert, V. Performance Assessment of Multiobjective Optimizers: An Analysis And Review; TIK-Report; ETH Zurich: Zurich, Switzerland, 2002; Volume 139. [Google Scholar]
- King, Z.A.; Lu, J.; Dräger, A.; Miller, P.; Federowicz, S.; Lerman, J.A.; Ebrahim, A.; Palsson, B.O.; Lewis, N.E. BiGG Models: A platform for integrating, standardizing and sharing genome-scale models. Nucleic Acids Res. 2015, 44, D515–D522. [Google Scholar] [CrossRef]
- Tseng, H.C.; Prather, K.L. Controlled biosynthesis of odd-chain fuels and chemicals via engineered modular metabolic pathways. Proc. Natl. Acad. Sci. USA 2012, 109, 17925–17930. [Google Scholar] [CrossRef] [PubMed]
- Shen, C.R.; Lan, E.I.; Dekishima, Y.; Baez, A.; Cho, K.M.; Liao, J.C. High titer anaerobic 1-butanol synthesis in Escherichia coli enabled by driving forces. Appl. Environ. Microbiol. 2011. [Google Scholar] [CrossRef] [PubMed]
- Atsumi, S.; Hanai, T.; Liao, J.C. Non-fermentative pathways for synthesis of branched-chain higher alcohols as biofuels. Nature 2008, 451, 86. [Google Scholar] [CrossRef] [PubMed]
- Fonseca, C.M.; Paquete, L.; López-Ibánez, M. An improved dimension-sweep algorithm for the hypervolume indicator. In Proceedings of the 2006 IEEE International Conference on Evolutionary Computation, Vancouver, BC, Canada, 16–21 July 2006; pp. 1157–1163. [Google Scholar]
- Ishibuchi, H.; Sakane, Y.; Tsukamoto, N.; Nojima, Y. Evolutionary many-objective optimization by NSGA-II and MOEA/D with large populations. In Proceedings of the 2009 IEEE International Conference on Systems, Man and Cybernetics, San Antonio, TX, USA, 11–14 October 2009; pp. 1758–1763. [Google Scholar]
| Abbreviation | Name | Notes | Reference |
|---|---|---|---|
| NSGAII | Non-dominated sorting genetic algorithm 2 | Highly applied MOEA | [23] |
| gamultiobj | Matlab implementation of NSGAII | Used in the original ModCell2 study [8] | [21] |
| MOEAIGDNS | Multi-objective evolutionary algorihtm based on an enhanced inverted generational distance metric | General MOEA with an implementation that works well with discrete variables | [29] |
| ARMOEA | Adapation to reference points multi-objective evolutionary algorithm | Many-objective EA based on MOEAIGDNS | [30] |
| EFRRR | Ensemble fitness ranking with ranking restriction | Many-objective EA | [31] |
| MaOEADDFC | Many-objective evolutionary algorithm based on directional diversity and favorable convergence | Many-objective EA | [32] |
| SPEAR | Strength Pareto evolutionary algorithm based on reference direction | Many-objective EA | [33] |
| tDEA | -dominance evolutionary algorithm | Many-objective EA | [34] |
| BiGE | Bi-goal evolution | Many-objective EA | [35] |
| NSGAIII | Non-dominated sorting genetic algorithm 3 | Many-objective EA | [36] |
| SPEA2SDE | Strength Pareto evolutionary algorithm 2 with shift-based density estimation | Many-objective EA | [37] |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Garcia, S.; Trinh, C.T. Comparison of Multi-Objective Evolutionary Algorithms to Solve the Modular Cell Design Problem for Novel Biocatalysis. Processes 2019, 7, 361. https://doi.org/10.3390/pr7060361
Garcia S, Trinh CT. Comparison of Multi-Objective Evolutionary Algorithms to Solve the Modular Cell Design Problem for Novel Biocatalysis. Processes. 2019; 7(6):361. https://doi.org/10.3390/pr7060361
Chicago/Turabian StyleGarcia, Sergio, and Cong T. Trinh. 2019. "Comparison of Multi-Objective Evolutionary Algorithms to Solve the Modular Cell Design Problem for Novel Biocatalysis" Processes 7, no. 6: 361. https://doi.org/10.3390/pr7060361
APA StyleGarcia, S., & Trinh, C. T. (2019). Comparison of Multi-Objective Evolutionary Algorithms to Solve the Modular Cell Design Problem for Novel Biocatalysis. Processes, 7(6), 361. https://doi.org/10.3390/pr7060361






