Reactive Power Optimization of Large-Scale Power Systems: A Transfer Bees Optimizer Application
Abstract
1. Introduction
- (1)
- Compared with the traditional mathematic optimization methods, the TBO has a stronger global search ability by employing the scouts and workers for exploitation and exploration. Besides, it can approximate the global optimum more closely via global optimization instead of external equivalent-based local optimization.
- (2)
- Compared with the general AI algorithms, the TBO can effectively avoid a blind search in the initial optimization phase and implement a much faster optimization for a new task by utilizing prior knowledge from the source tasks.
- (3)
- The optimization performance of the TBO was thoroughly tested by RPO of large-scale power systems. Because of its high optimization flexibility and superior optimization efficiency, it can be extended to other complex optimization problems.
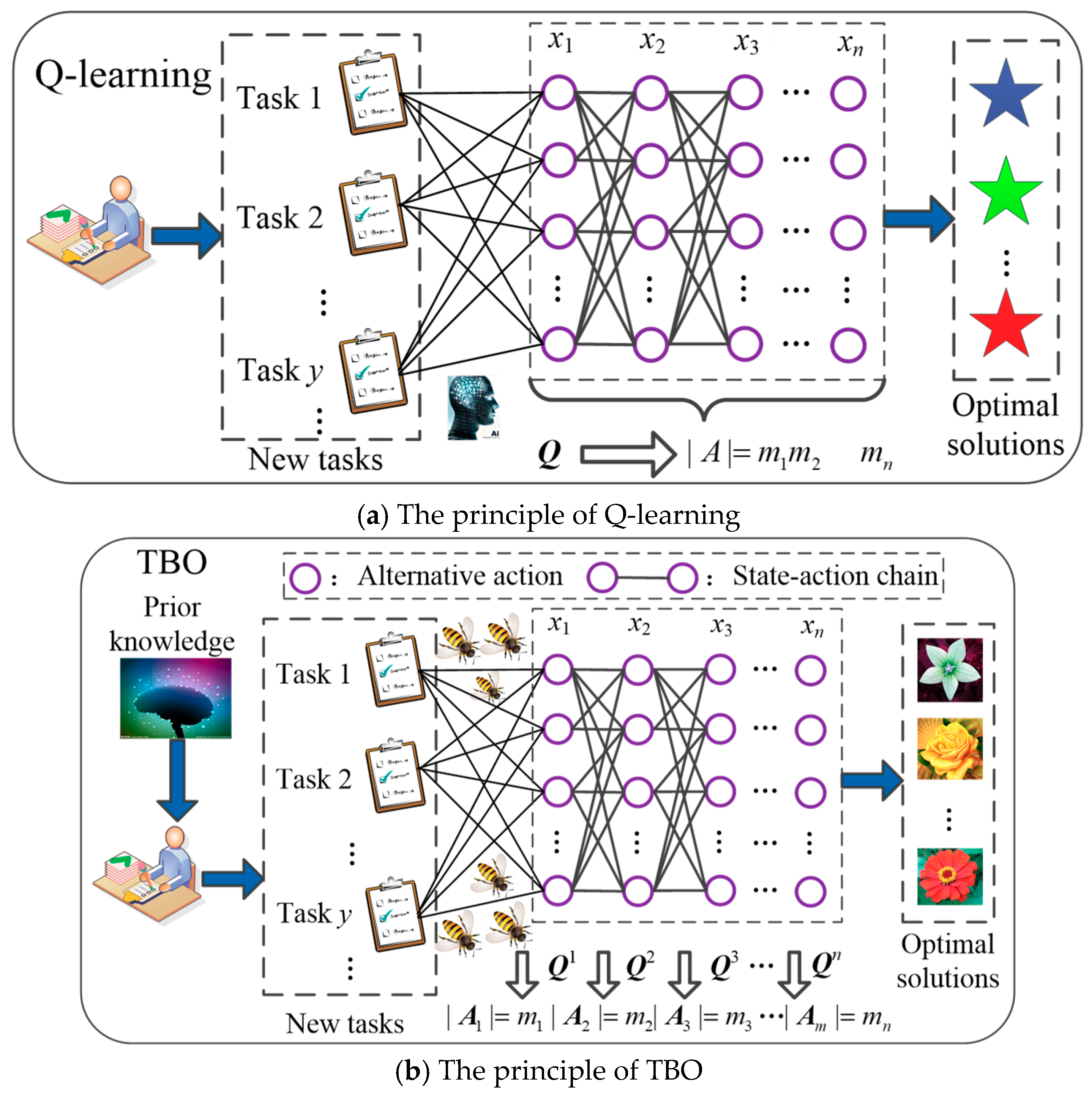
2. Transfer Bees Optimizer
2.1. State-Action Chain
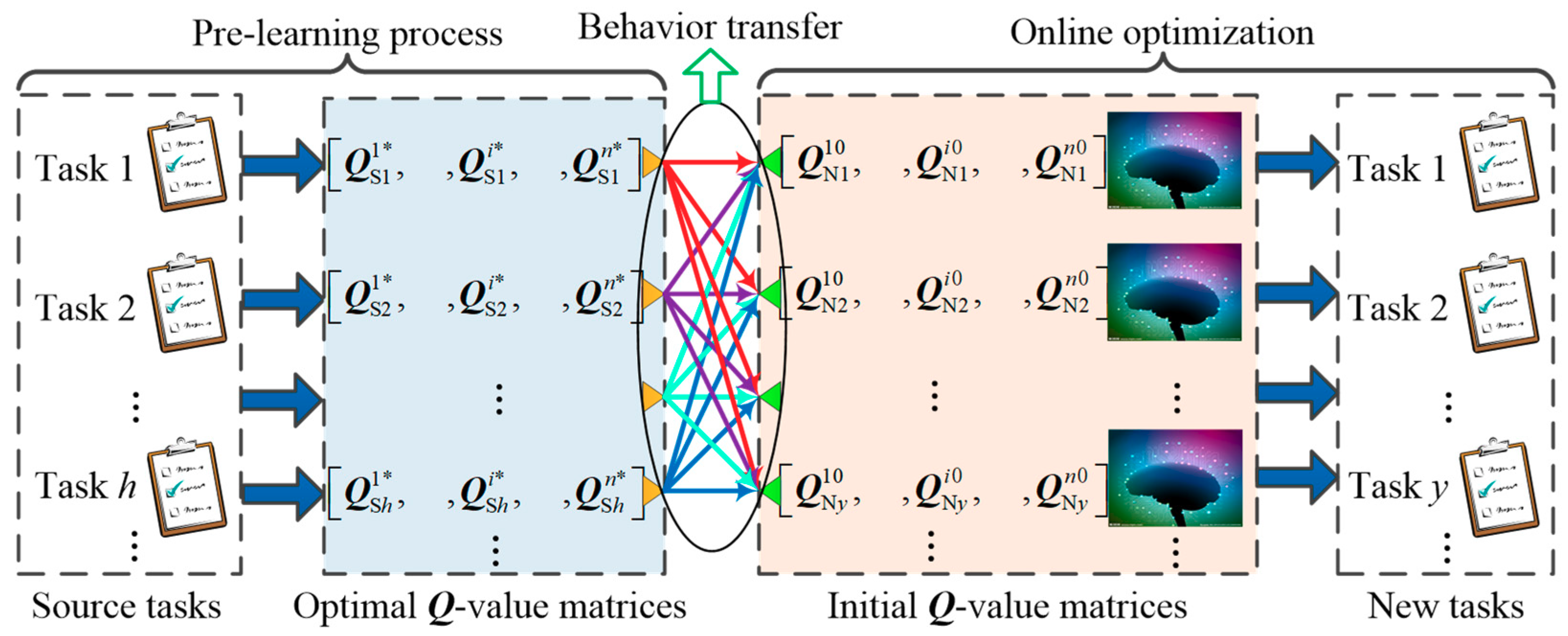
2.2. Knowledge Learning and Behavior Transfer
2.2.1. Knowledge learning
2.2.2. Behavior transfer
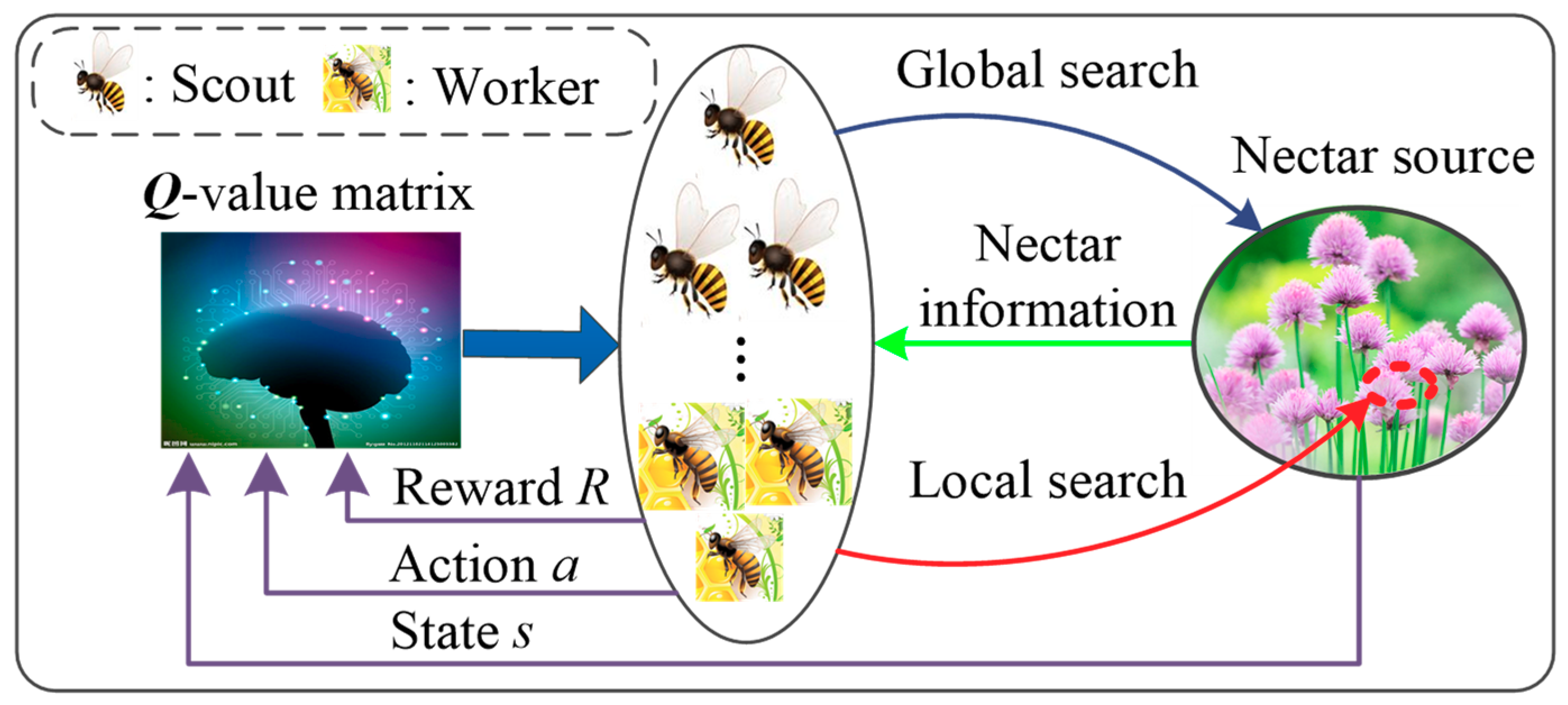
2.3. Exploration and Feedback
2.3.1. Action policy
2.3.2. Reward function
3. Design of the TBO for RPO
3.1. Mathematical Model of RPO
3.2. Design of the TBO
3.2.1. Design of state and action
3.2.2. Design of the reward function
3.2.3. Behavior transfer for RPO
- Step 1.
- Determine the source tasks according to a typical load curve in a day by Equation (12);
- Step 2.
- Complete the source tasks in the initial study process and store their optimal Q-value matrices;
- Step 3.
- Calculate the comparability between original tasks and new task according to the deviation of power demand according to Equations (13) and (14);
- Step 4.
- Obtain the original Q-value matrices in the new task by Equation (2).
3.2.4. Parameters setting
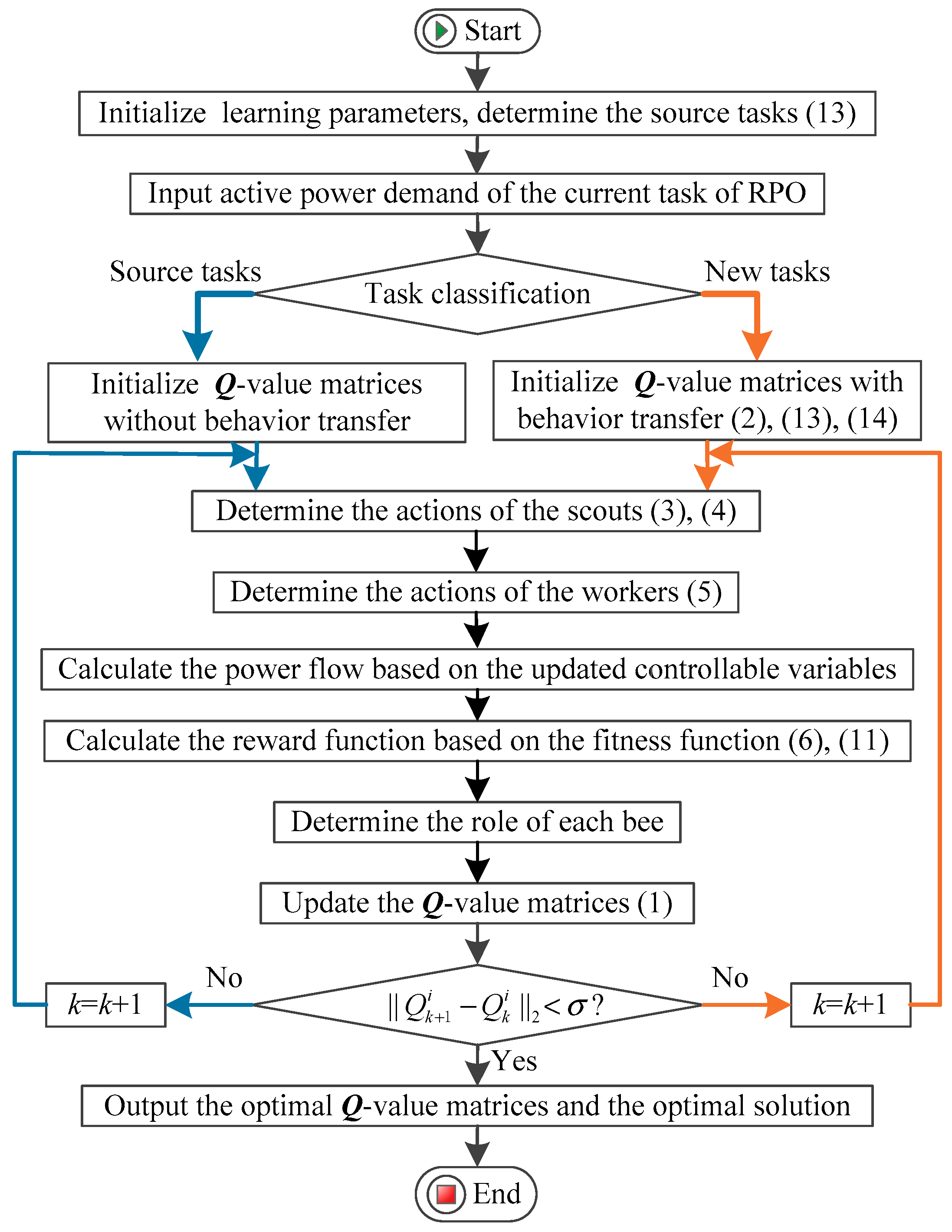
3.2.5. Execution Procedure of the TBO for RPO
4. Case Studies
4.1. Study of the Pre-Learning Process
4.2. Study of Online Optimization
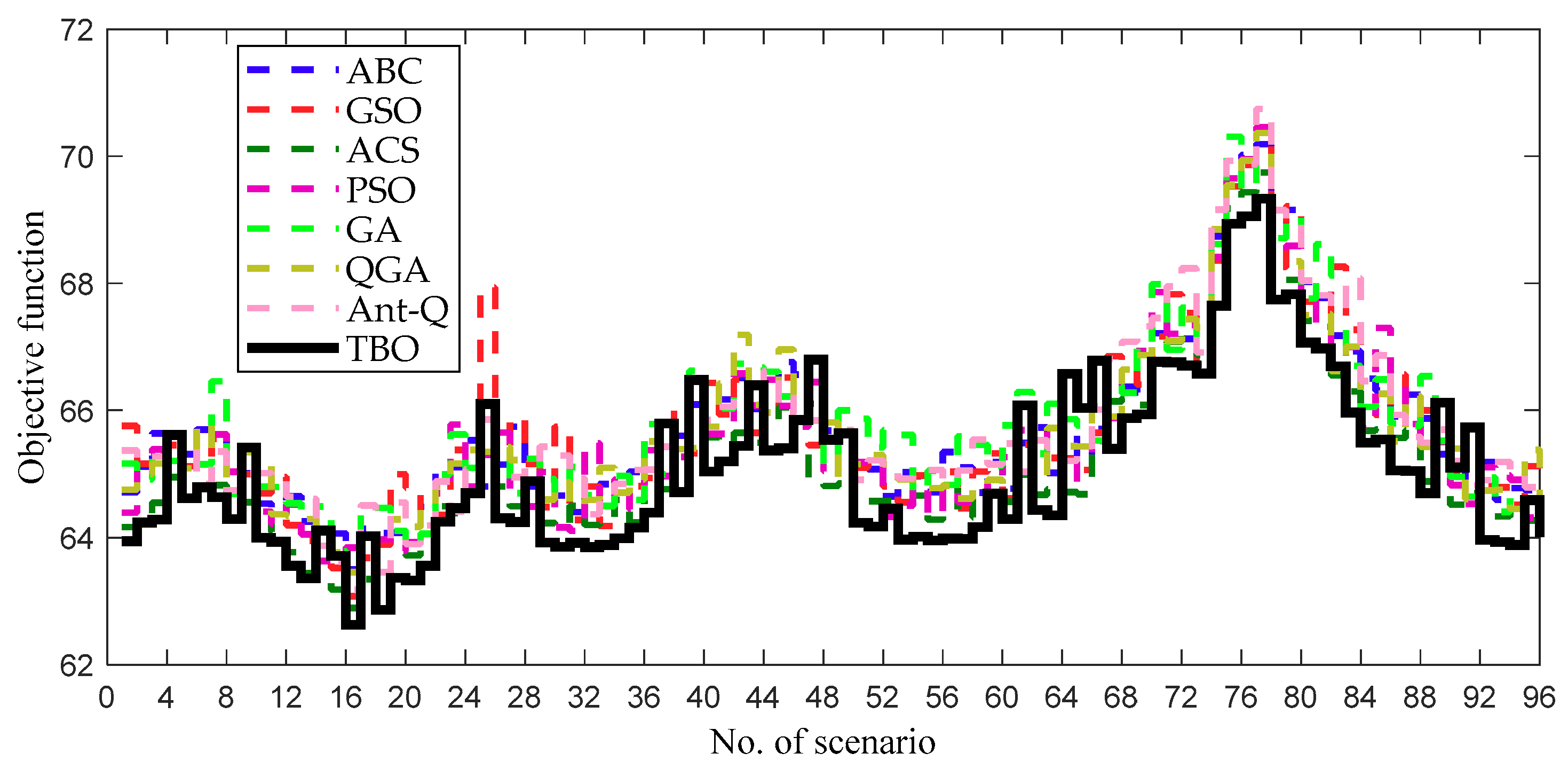
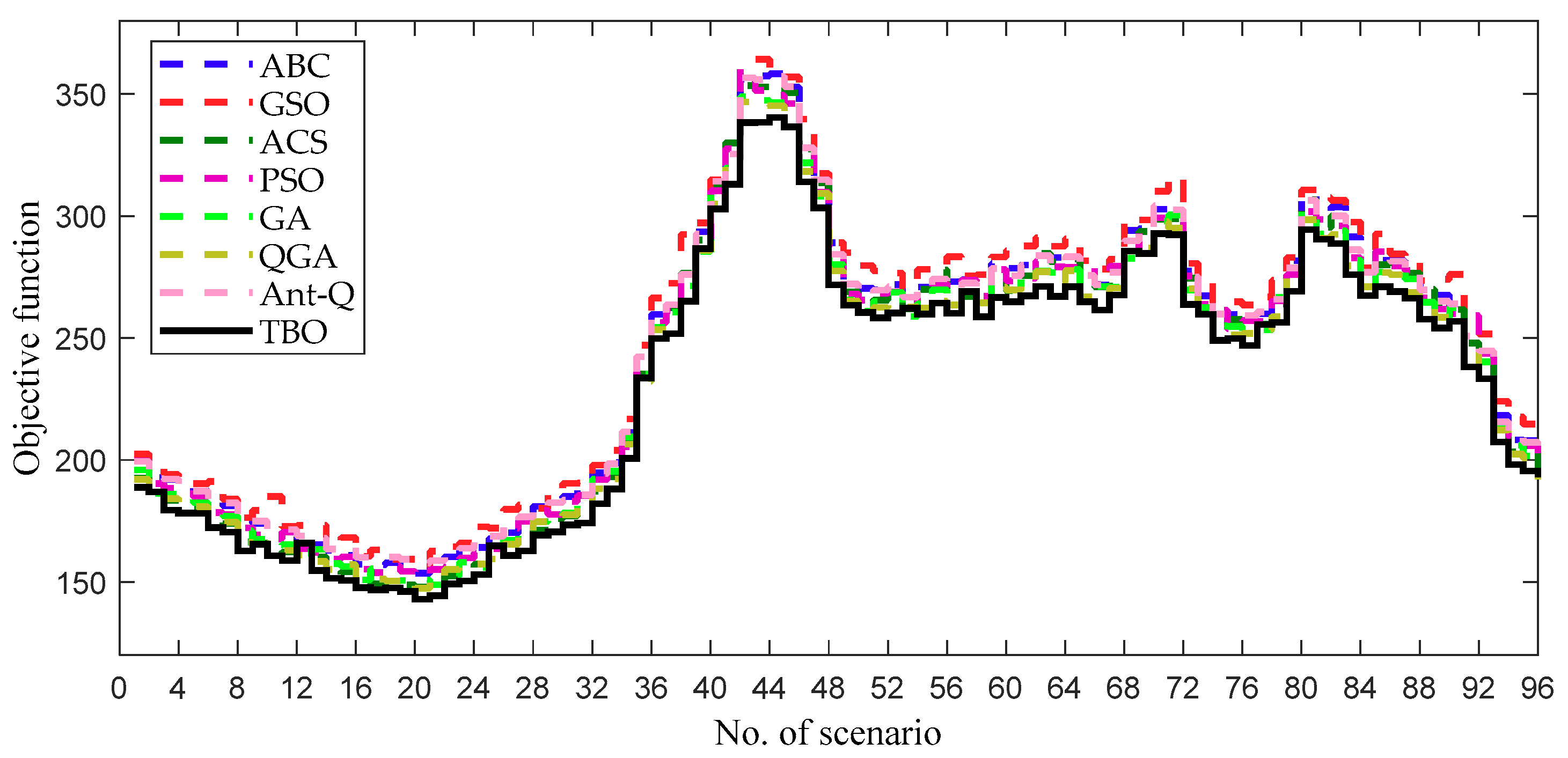
4.2.1. Study of behavior transfer
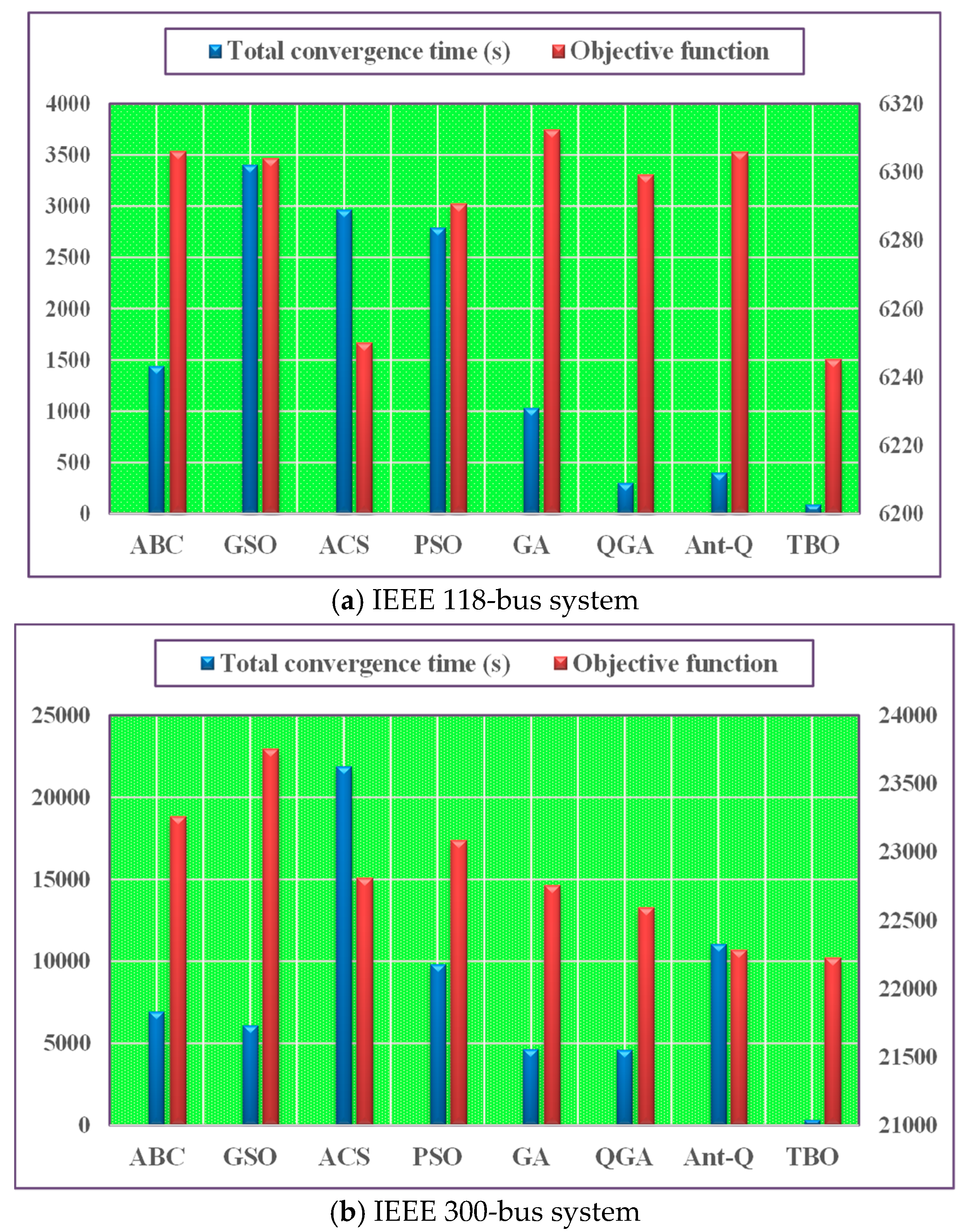
4.2.2. Comparative results and discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Grudinin, N. Reactive power optimization using successive quadratic programming method. IEEE Trans. Power Syst. 1998, 13, 1219–1225. [Google Scholar] [CrossRef]
- Li, C.; Johnson, R.B.; Svoboda, A.J. A new unit commitment method. IEEE Trans. Power Syst. 1997, 12, 113–119. [Google Scholar]
- Zhou, B.; Chan, K.W.; Yu, T.; Chung, C.Y. Equilibrium-inspired multiple group search optimization with synergistic learning for multiobjective electric power dispatch. IEEE Trans. Power Syst. 2013, 28, 3534–3545. [Google Scholar] [CrossRef]
- Sun, D.I.; Ashley, B.; Brewer, B. Optimal power flow by newton approach. IEEE Trans. Power Appar. Syst. 1984, 103, 2864–2880. [Google Scholar] [CrossRef]
- Fan, J.Y.; Zhang, L. Real-time economic dispatch with line flow and emission constraints using quadratic programming. IEEE Trans. Power Syst. 1998, 13, 320–325. [Google Scholar] [CrossRef]
- Wei, H.; Sasaki, H.; Kubokawa, J.; Yokoyama, R. An interior point nonlinear programming for optimal power flow problems with a novel data structure. IEEE Trans. Power Syst. 1998, 13, 870–877. [Google Scholar] [CrossRef]
- Dai, C.; Chen, W.; Zhu, Y.; Zhang, X. Seeker optimization algorithm for optimal reactive power dispatch. IEEE Trans. Power Syst. 2009, 24, 1218–1231. [Google Scholar]
- Abu-Mouti, F.S.; El-Hawary, M.E. Optimal distributed generation allocation and sizing in distribution systems via artificial bee colony algorithm. IEEE Trans. Power Del. 2011, 26, 2090–2101. [Google Scholar] [CrossRef]
- Han, Z.; Zhang, Q.; Shi, H.; Zhang, J. An improved compact genetic algorithm for scheduling problems in a flexible flow shop with a multi-queue buffer. Processes 2019, 7, 302. [Google Scholar] [CrossRef]
- Han, P.; Fan, G.; Sun, W.; Shi, B.; Zhang, X. Research on identification of LVRT characteristics of photovoltaic inverters based on data testing and PSO algorithm. Processes 2019, 7, 250. [Google Scholar] [CrossRef]
- He, S.; Wu, Q.H.; Saunders, J.R. Group search optimizer: An optimization algorithm inspired by animal searching behavior. IEEE Trans. Evol. Comput. 2009, 13, 973–990. [Google Scholar] [CrossRef]
- Gómez, J.F.; Khodr, H.M.; De Oliveira, P.M.; Ocque, L.; Yusta, J.M.; Urdaneta, A.J. Ant colony system algorithm for the planning of primary distribution circuits. IEEE Trans. Power Syst. 2004, 19, 996–1004. [Google Scholar] [CrossRef]
- Yang, B.; Yu, T.; Zhang, X.S.; Huang, L.N.; Shu, H.C.; Jiang, L. Interactive teaching–learning optimiser for parameter tuning of VSC-HVDC systems with offshore wind farm integration. IET Gener. Transm. Distrib. 2017, 12, 678–687. [Google Scholar] [CrossRef]
- Yang, B.; Zhang, X.S.; Yu, T.; Shu, H.C.; Fang, Z.H. Grouped grey wolf optimizer for maximum power point tracking of doubly-fed induction generator based wind turbine. Energy Convers. Manag. 2017, 133, 427–443. [Google Scholar] [CrossRef]
- Yang, B.; Zhong, L.E.; Zhang, X.S.; Shu, H.C.; Li, H.F.; Jiang, L.; Sun, L.M. Novel bio-inspired memetic salp swarm algorithm and application to MPPT for PV systems considering partial shading condition. J. Clean. Prod. 2019, 215, 1203–1222. [Google Scholar] [CrossRef]
- Yang, B.; Yu, T.; Zhang, X.S.; Li, H.F.; Shu, H.C.; Sang, Y.Y.; Jiang, L. Dynamic leader based collective intelligence for maximum power point tracking of PV systems affected by partial shading condition. Energy Convers. Manag. 2019, 179, 286–303. [Google Scholar] [CrossRef]
- Montoya, F.G.; Alcayde, A.; Arrabal-Campos, F.M.; Raul, B. Quadrature current compensation in non-sinusoidal circuits using geometric algebra and evolutionary algorithms. Energies 2019, 12, 692. [Google Scholar] [CrossRef]
- Yu, T.; Liu, J.; Chan, K.W.; Wang, J.J. Distributed multi-step Q (λ) learning for optimal power flow of large-scale power grids. Int. J. Electr. Power Energy Syst. 2012, 42, 614–620. [Google Scholar] [CrossRef]
- Mühürcü, A. FFANN optimization by ABC for controlling a 2nd order SISO system’s output with a desired settling time. Processes 2019, 7, 4. [Google Scholar] [CrossRef]
- Sundareswaran, K.; Sankar, P.; Nayak, P.S.R.; Simon, S.P.; Palani, S. Enhanced energy output from a PV system under partial shaded conditions through artificial bee colony. IEEE Trans. Sustain. Energy 2014, 6, 198–209. [Google Scholar] [CrossRef]
- Chandrasekaran, K.; Simon, S.P. Multi-objective unit commitment problem with reliability function using fuzzified binary real coded artificial bee colony algorithm. IET Gener. Transm. Distrib. 2012, 6, 1060–1073. [Google Scholar] [CrossRef]
- Gao, Z. Advances in Modelling, monitoring, and control for complex industrial systems. Complexity 2019, 2019, 2975083. [Google Scholar] [CrossRef]
- Tognete, A.L.; Nepomuceno, L.; Dos Santos, A. Framework for analysis and representation of external systems for online reactive-optimisation studies. IEE Gener. Transm. Distrib. 2005, 152, 755–762. [Google Scholar] [CrossRef]
- Tognete, A.L.; Nepomuceno, L.; Dos Santos, A. Evaluation of economic impact of external equivalent models used in reactive OPF studies for interconnected systems. IET Gener. Transm. Distrib. 2007, 1, 140–145. [Google Scholar] [CrossRef]
- Britannica Academic, S.V. The Life of Bee. Available online: http://academic.eb.com /EBchecked/topic/340282/The-Life-of-the-Bee (accessed on 24 April 2019).
- Pan, S.J.; Yang, Q. A survey on transfer learning. IEEE Trans. Knowl. Data Eng. 2009, 22, 1345–1359. [Google Scholar] [CrossRef]
- Ramon, J.; Driessens, K.; Croonenborghs, T. Transfer learning in reinforcement learning problems through partial policy recycling. In Learn ECML; Springer: Heidelberg/Berlin, Germany, 2007; pp. 699–707. [Google Scholar]
- Gao, Z.; Saxen, H.; Gao, C. Data-driven approaches for complex industrial systems. IEEE Trans. Ind. Inform. 2013, 9, 2210–2212. [Google Scholar] [CrossRef]
- Taylor, M.E.; Stone, P. Transfer learning for reinforcement learning domains: A survey. J. Mach. Learn. Res. 2009, 10, 1633–1685. [Google Scholar]
- Pan, J.; Wang, X.; Cheng, Y.; Cao, G. Multi-source transfer ELM-based Q learning. Neurocomputing 2014, 137, 57–64. [Google Scholar] [CrossRef]
- Bianchi, R.A.C.; Celiberto, L.A.; Santos, P.E.; Matsuura, J.P.; Mantaras, R.L.D. Transferring knowledge as heuristics in reinforcement learning: A case-based approach. Artif. Intell. 2015, 226, 102–121. [Google Scholar] [CrossRef]
- Watkins, J.C.H.; Dayan, P. Q-learning. Mach. Learn. 1992, 8, 279–292. [Google Scholar] [CrossRef]
- Ghavamzadeh, M.; Mahadevan, S. Hierarchical average reward reinforcement learning. J. Mach. Learn. Res. 2007, 8, 2629–2669. [Google Scholar]
- Dietterich, T.G. Hierarchical reinforcement learning with the MAXQ value function decomposition. J. Artif. Intel. 2000, 13, 227–303. [Google Scholar] [CrossRef]
- Yu, T.; Zhou, B.; Chan, K.W.; Chen, L.; Yang, B. Stochastic optimal relaxed automatic generation control in Non-Markov environment based on multi-step Q (λ) learning. IEEE Trans. Power Syst. 2011, 26, 1272–1282. [Google Scholar] [CrossRef]
- Maloosini, A.; Blanzieri, E.; Calarco, T. Quantum genetic optimization. IEEE Trans. Evol. Comput. 2008, 12, 231–241. [Google Scholar] [CrossRef]
- Dorigo, M.; Gambardella, L.M. A study of some properties of Ant-Q. In International Conference on Parallel Problem Solving from Nature; Springer-Verlag: Berlin, Germany, 1996; pp. 656–665. [Google Scholar]
- Zhang, X.S.; Yu, T.; Yang, B.; Cheng, L. Accelerating bio-inspired optimizer with transfer reinforcement learning for reactive power optimization. Knowl. Base. Syst. 2017, 116, 26–38. [Google Scholar] [CrossRef]
- Rajaraman, P.; Sundaravaradan, N.A.; Mallikarjuna, B.; Jaya, B.R.M.; Mohanta, D.K. Robust fault analysis in transmission lines using Synchrophasor measurements. Prot. Control. Mod. Power Syst. 2018, 3, 108–110. [Google Scholar]
- Hou, K.; Shao, G.; Wang, H.; Zheng, L.; Zhang, Q.; Wu, S.; Hu, W. Research on practical power system stability analysis algorithm based on modified SVM. Prot. Control Mod. Power Syst. 2018, 3, 119–125. [Google Scholar] [CrossRef]
- Ren, C.; Xu, Y.; Zhang, Y.C. Post-disturbance transient stability assessment of power systems towards optimal accuracy-speed tradeoff. Prot. Control Mod. Power Syst. 2018, 3, 194–203. [Google Scholar] [CrossRef]
- Dabra, V.; Paliwal, K.K.; Sharma, P.; Kumar, N. Optimization of photovoltaic power system: A comparative study. Prot. Control Mod. Power Syst. 2017, 2, 29–39. [Google Scholar] [CrossRef]
- Yang, B.; Yu, T.; Shu, H.C.; Dong, J.; Jiang, L. Robust sliding-mode control of wind energy conversion systems for optimal power extraction via nonlinear perturbation observers. Appl. Energy 2018, 210, 711–723. [Google Scholar] [CrossRef]
- Yang, B.; Jiang, L.; Wang, L.; Yao, W.; Wu, Q.H. Nonlinear maximum power point tracking control and modal analysis of DFIG based wind turbine. Int. J. Electr. Power Energy Syst. 2016, 74, 429–436. [Google Scholar] [CrossRef]
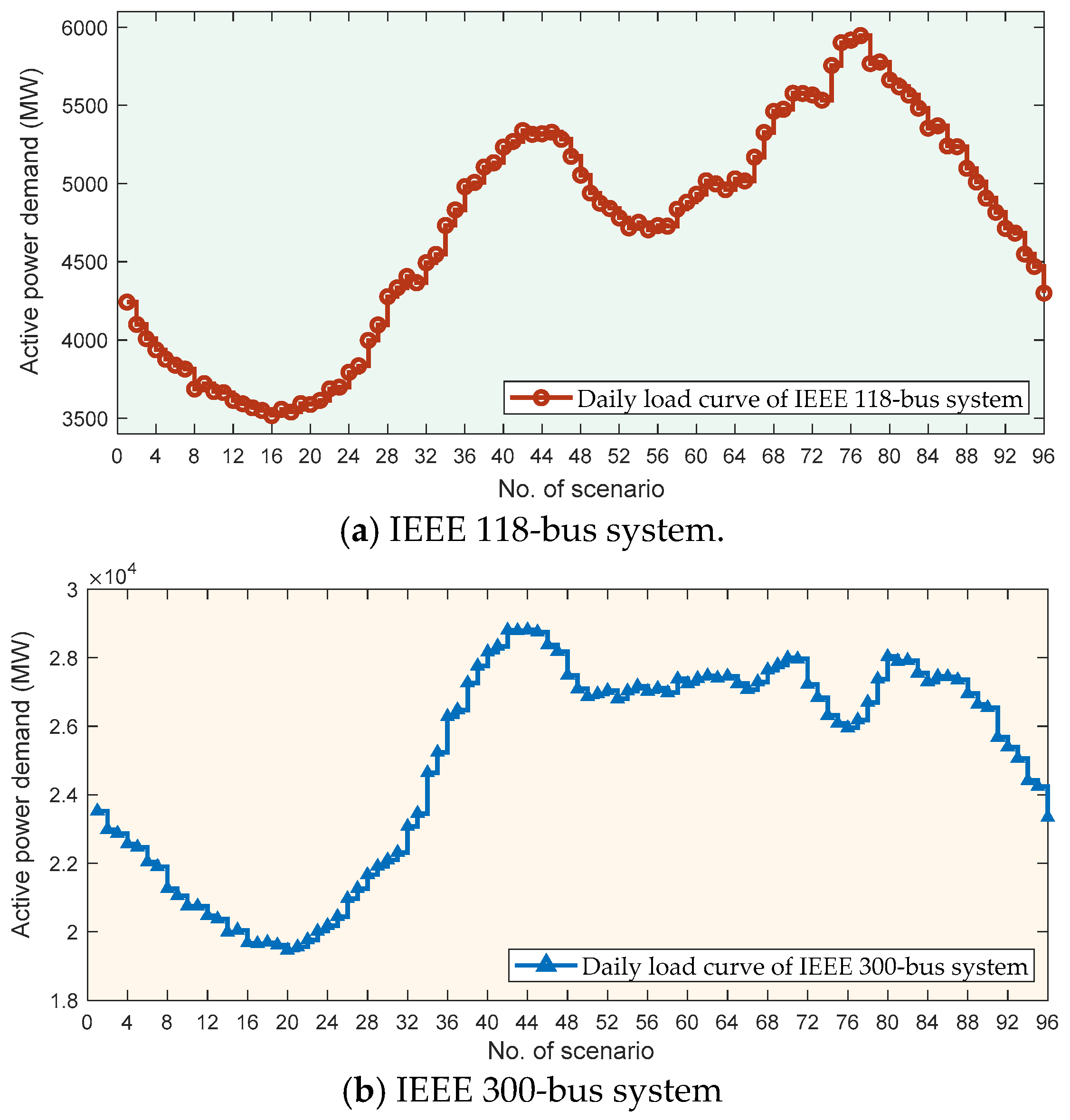
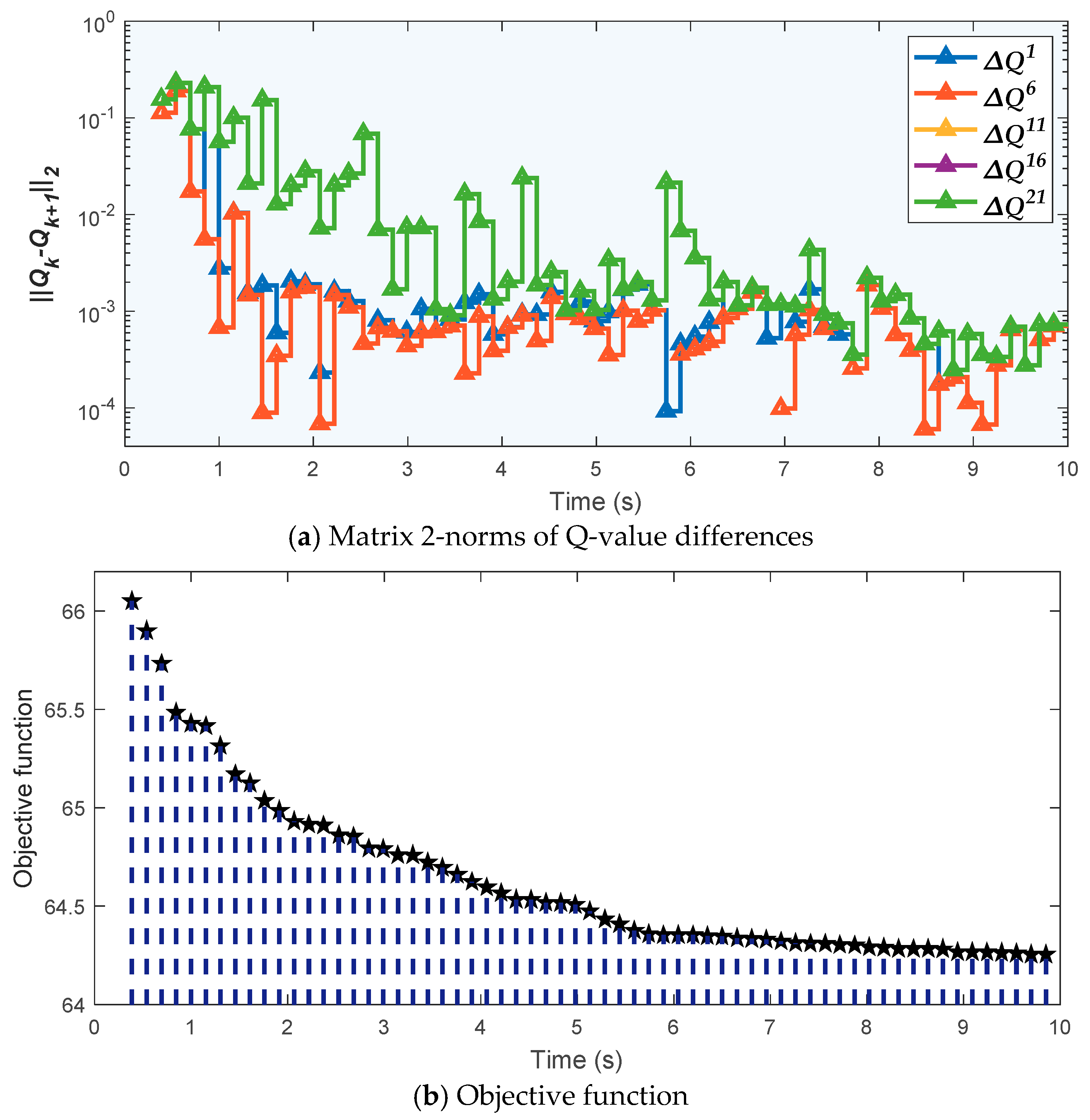

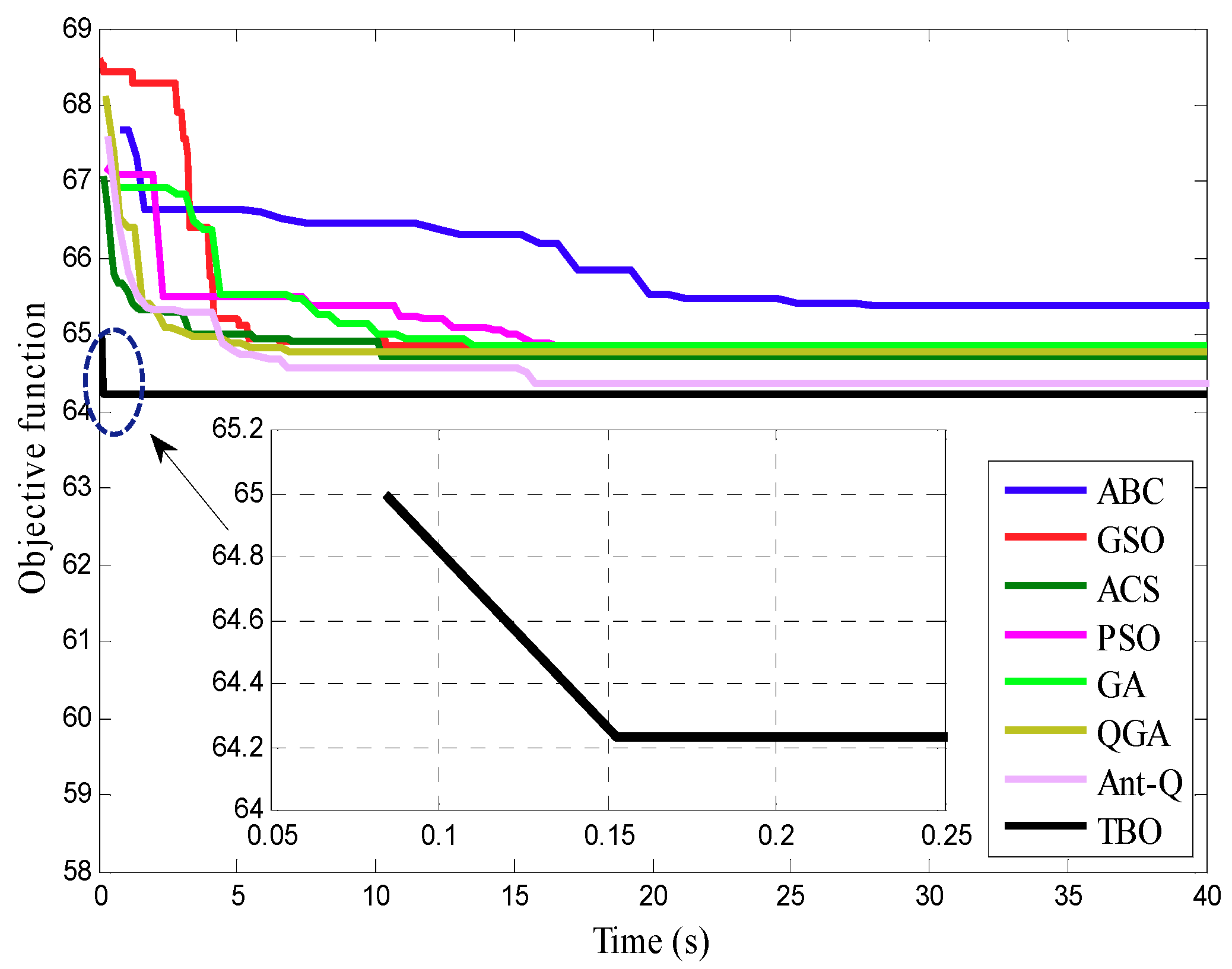
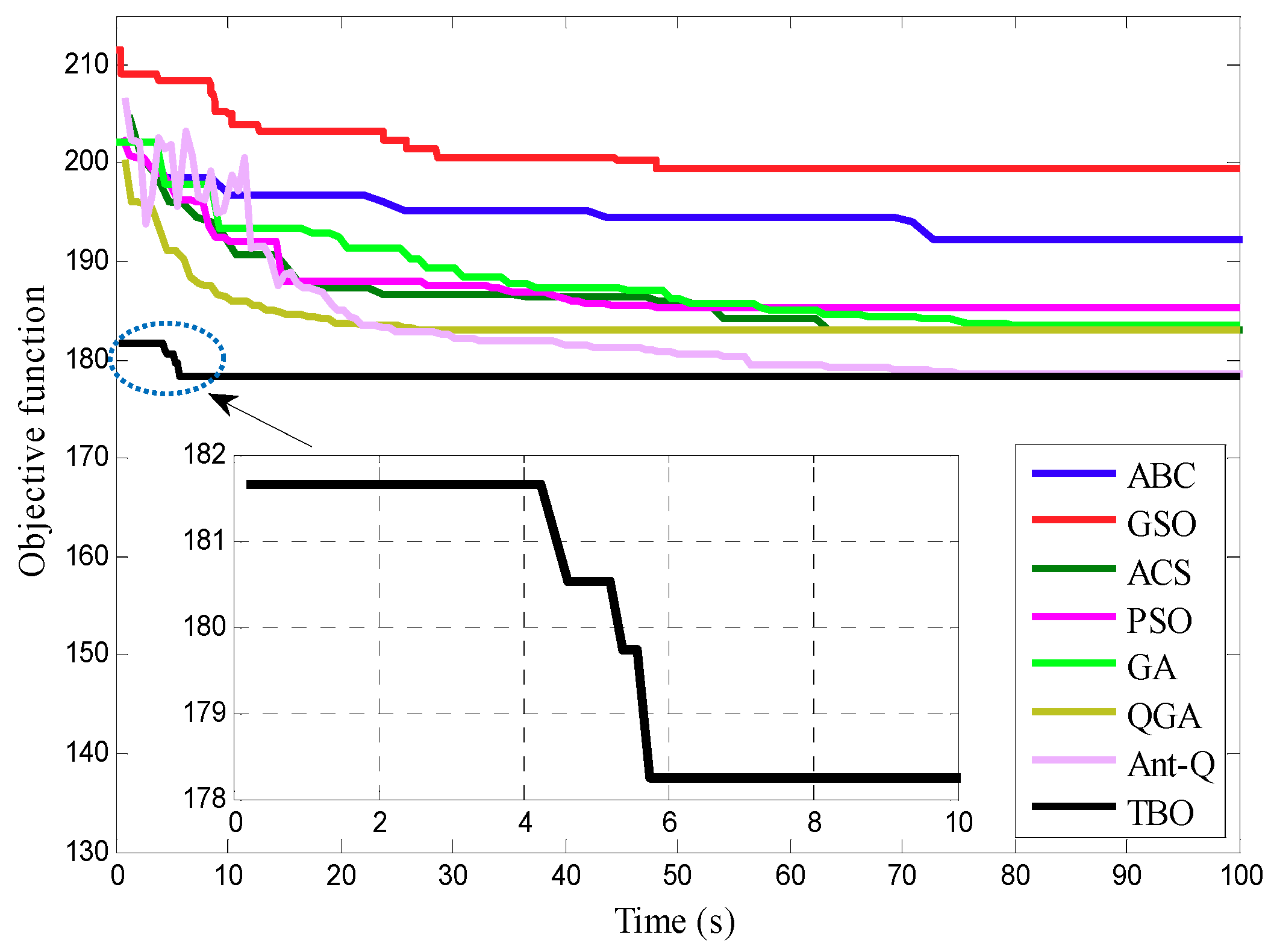
| Parameter | Range | IEEE 118-Bus System | IEEE 300-Bus System | ||
|---|---|---|---|---|---|
| Pre-Learning | Online Optimization | Pre-Learning | Online Optimization | ||
| α | 0 < α < 1 | 0.95 | 0.99 | 0.9 | 0.95 |
| γ | 0 < γ < 1 | 0.2 | 0.2 | 0.3 | 0.3 |
| J | J ≥ 1 | 15 | 5 | 30 | 10 |
| ε0 | 0 < ε0 <1 | 0.9 | 0.98 | 0.95 | 0.98 |
| β | 0 < β < 1 | 0.95 | 0.95 | 0.98 | 0.98 |
| C | C > 0 | 1 | 1 | 1 | 1 |
| η | η > 0 | 10 | 10 | 50 | 50 |
| W | W ≥ 0 | — | 50 | — | 100 |
| Algorithm Index | ABC | GSO | ACS | PSO | GA | QGA | Ant-Q | TBO |
|---|---|---|---|---|---|---|---|---|
| Convergence time (s) | 15 | 35.5 | 30.9 | 29.1 | 10.8 | 3.99 | 4.16 | 0.94 |
| Ploss (MW) | 1.11 × 104 | 1.11 × 104 | 1.11 × 104 | 1.11 × 104 | 1.11 × 104 | 1.11 × 104 | 1.11 × 104 | 1.10 × 104 |
| Vd (%) | 1.51 × 103 | 1.49 × 103 | 1.44 × 103 | 1.48 × 103 | 1.50 × 103 | 1.51 × 103 | 1.50 × 103 | 1.48 × 103 |
| f | 6.31 × 103 | 6.30 × 103 | 6.25 × 103 | 6.29 × 103 | 6.31 × 103 | 6.30 × 103 | 6.31 × 103 | 6.25 × 103 |
| Best | 6.30 × 103 | 6.30 × 103 | 6.24 × 103 | 6.28 × 103 | 6.31 × 103 | 6.30 × 103 | 6.30 × 103 | 6.24 × 103 |
| Worst | 6.31 × 103 | 6.31 × 103 | 6.25 × 103 | 6.30 × 103 | 6.32 × 103 | 6.30 × 103 | 6.31 × 103 | 6.25 × 103 |
| Variance | 4.02 | 19.3 | 6.43 | 16.3 | 12 | 6.37 | 8.57 | 2.27 |
| Std. Dev. | 2.01 | 4.39 | 2.54 | 4.03 | 3.46 | 2.52 | 2.93 | 1.51 |
| Rel. Std. Dev | 3.18 × 10−4 | 6.96 × 10−4 | 4.06 × 10−4 | 6.41 × 10−4 | 5.49 × 10−4 | 4.01 × 10−4 | 4.64 × 10−4 | 2.41 × 10−4 |
| Algorithm Index | ABC | GSO | ACS | PSO | GA | QGA | Ant-Q | TBO |
|---|---|---|---|---|---|---|---|---|
| Convergence time (s) | 72.3 | 63.4 | 228 | 102 | 48.3 | 47.8 | 115 | 3.37 |
| Ploss (MW) | 3.82 × 104 | 3.86 × 104 | 3.83 × 104 | 3.81 × 104 | 3.77 × 104 | 3.76 × 104 | 3.74 × 104 | 3.75 × 104 |
| Vd (%) | 8.34 × 103 | 8.87 × 103 | 7.36 × 103 | 8.07 × 103 | 7.78 × 103 | 7.56 × 103 | 7.14 × 103 | 6.94 × 103 |
| f | 2.33 × 104 | 2.38 × 104 | 2.28 × 104 | 2.31 × 104 | 2.28 × 104 | 2.26 × 104 | 2.23 × 104 | 2.22 × 104 |
| Best | 2.32 × 104 | 2.37 × 104 | 2.28 × 104 | 2.30 × 104 | 2.27 × 104 | 2.26 × 104 | 2.23 × 104 | 2.22 × 104 |
| Worst | 2.33 × 104 | 2.38 × 104 | 2.28 × 104 | 2.32 × 104 | 2.28 × 104 | 2.26 × 104 | 2.23 × 104 | 2.22 × 104 |
| Variance | 381 | 1.29 × 103 | 228 | 2.37× 103 | 178 | 194 | 221 | 66.4 |
| Std. Dev. | 19.5 | 36 | 15.1 | 48.7 | 13.4 | 13.9 | 14.9 | 8.15 |
| Rel. Std. Dev | 8.39 × 10−4 | 1.51 × 10−3 | 6.61 × 10−4 | 2.11 × 10−3 | 5.87 × 10−4 | 6.16× 10−4 | 6.67 × 10−4 | 3.67 × 10−4 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, H.; Yu, T.; Zhang, X.; Yang, B.; Wu, Y. Reactive Power Optimization of Large-Scale Power Systems: A Transfer Bees Optimizer Application. Processes 2019, 7, 321. https://doi.org/10.3390/pr7060321
Cao H, Yu T, Zhang X, Yang B, Wu Y. Reactive Power Optimization of Large-Scale Power Systems: A Transfer Bees Optimizer Application. Processes. 2019; 7(6):321. https://doi.org/10.3390/pr7060321
Chicago/Turabian StyleCao, Huazhen, Tao Yu, Xiaoshun Zhang, Bo Yang, and Yaxiong Wu. 2019. "Reactive Power Optimization of Large-Scale Power Systems: A Transfer Bees Optimizer Application" Processes 7, no. 6: 321. https://doi.org/10.3390/pr7060321
APA StyleCao, H., Yu, T., Zhang, X., Yang, B., & Wu, Y. (2019). Reactive Power Optimization of Large-Scale Power Systems: A Transfer Bees Optimizer Application. Processes, 7(6), 321. https://doi.org/10.3390/pr7060321






