Optimal Strategies for Dengue Prevention and Control during Daily Commuting between Two Residential Areas
Abstract
:1. Introduction
- Suppression of the mosquito population using chemical substances (e.g., insecticides or larvicides), biological control agents (natural predators of mosquito larvae and pupae), environmental management (e.g., lethal ovitraps or elimination of mosquito breeding sites in and around households), and the release of genetically modified mosquitoes (sterile males or insects carrying a dominant lethal gene).
- Reduction of effective contact between female mosquitoes and humans (or mosquito bites) through the use of repellents, mosquito nets, insecticide-treated clothing, and other measures targeting personal protection.
2. Two-Patch Dengue Transmission Model
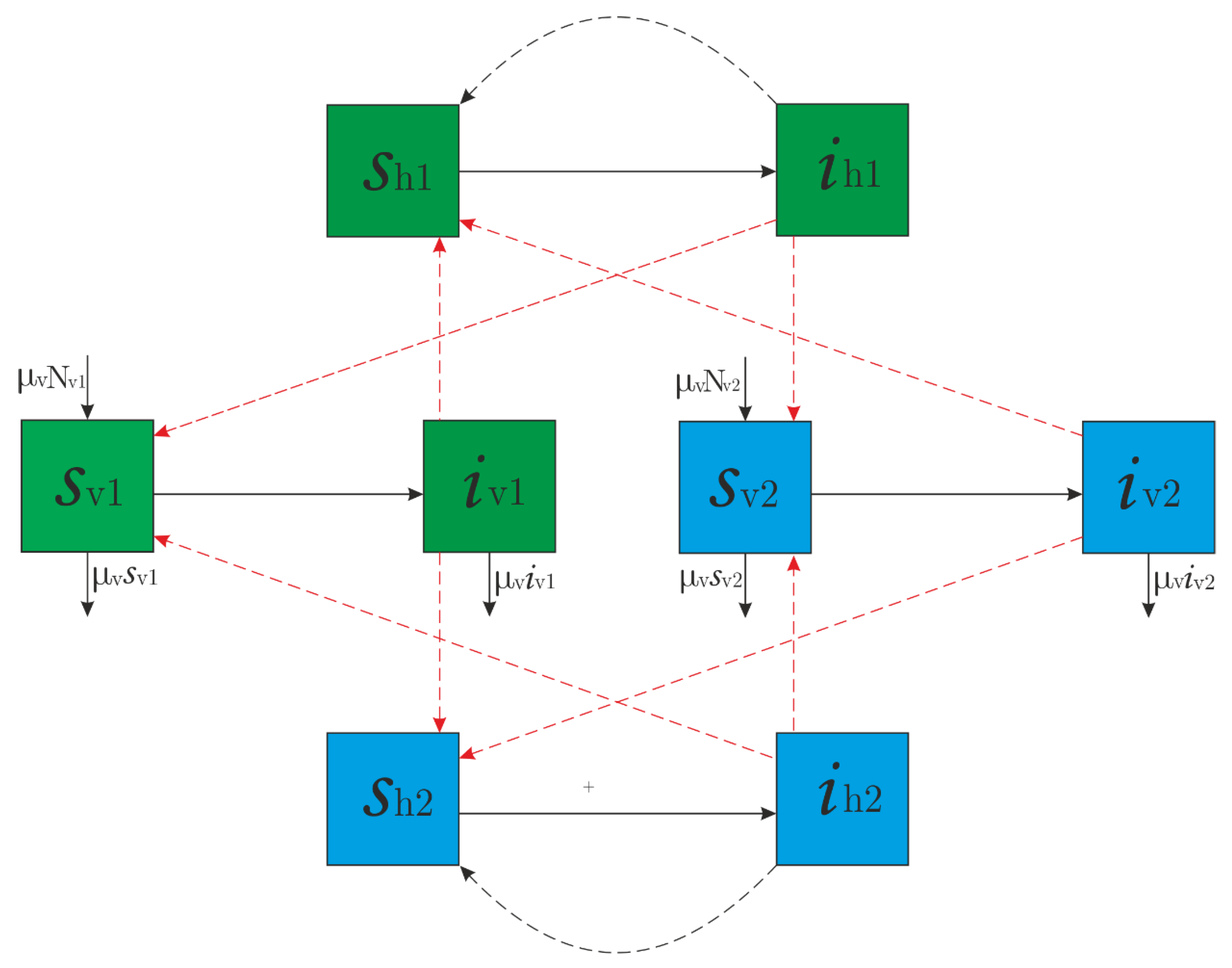
2.1. Formulation of the Model
- Human and vector populations remain essentially invariant in time.
- Populations of human hosts and vectors are homogeneous in terms of susceptibility, attraction, and exposure.
- Virus incubation periods within both humans and mosquitoes are ignored.
- Once infected, mosquitoes do not recover and die being infectious.
- Disease-induced death in humans or in vectors is not considered.
- Superinfection does not occur in either humans or mosquitoes; only susceptible or fully recovered individuals may get infected.
- Gradual acquisition of immunity in human hosts is ignored; they become susceptible immediately after recovery.
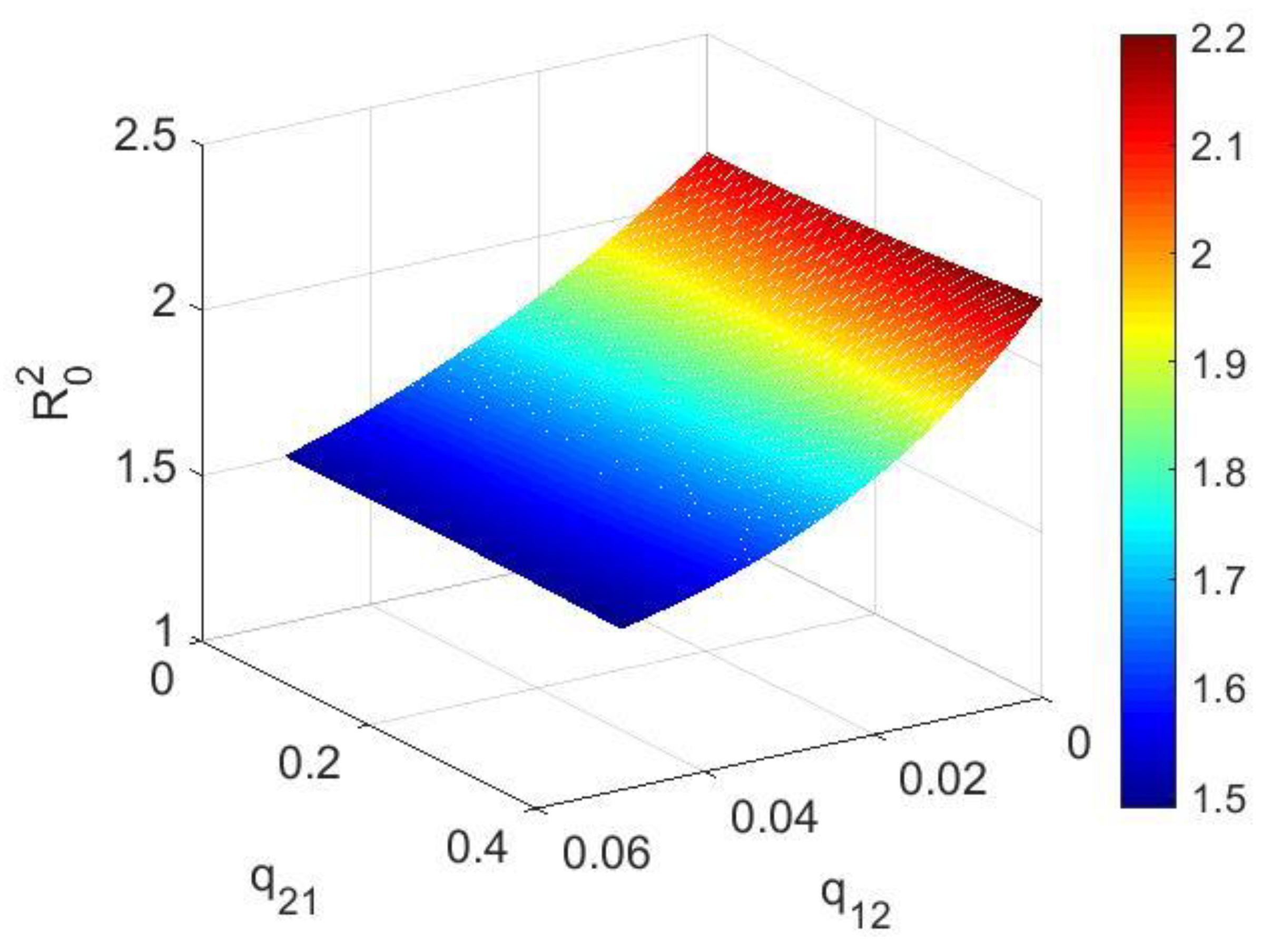
2.2. Calculation of Basic Reproductive Number
3. Optimal Control Framework for Two-Patch Model (9)
3.1. Formulation of the Optimal Control Problem
3.2. Existence of Optimal Controls
- State trajectories of the controlled dynamical system (12) remain bounded for all admissible controls and for all
- The integrand of the objective functional (13) is convex with respect to the state and control variables.
- The right-hand side of the dynamical system (12) is linear with respect to both controls and .
- By definition, the set of admissible controls is compact.
- The sets of all possible initial and terminal states of the system (12) are compact; that is, .
3.3. Characterization of Optimal Controls
- Four direct equations (12) plus four adjoint equations (17), where are replaced by their characterizations (18);
- Four initial conditions (14) specified at , plus four transversality conditions from (17) specified at
4. Results
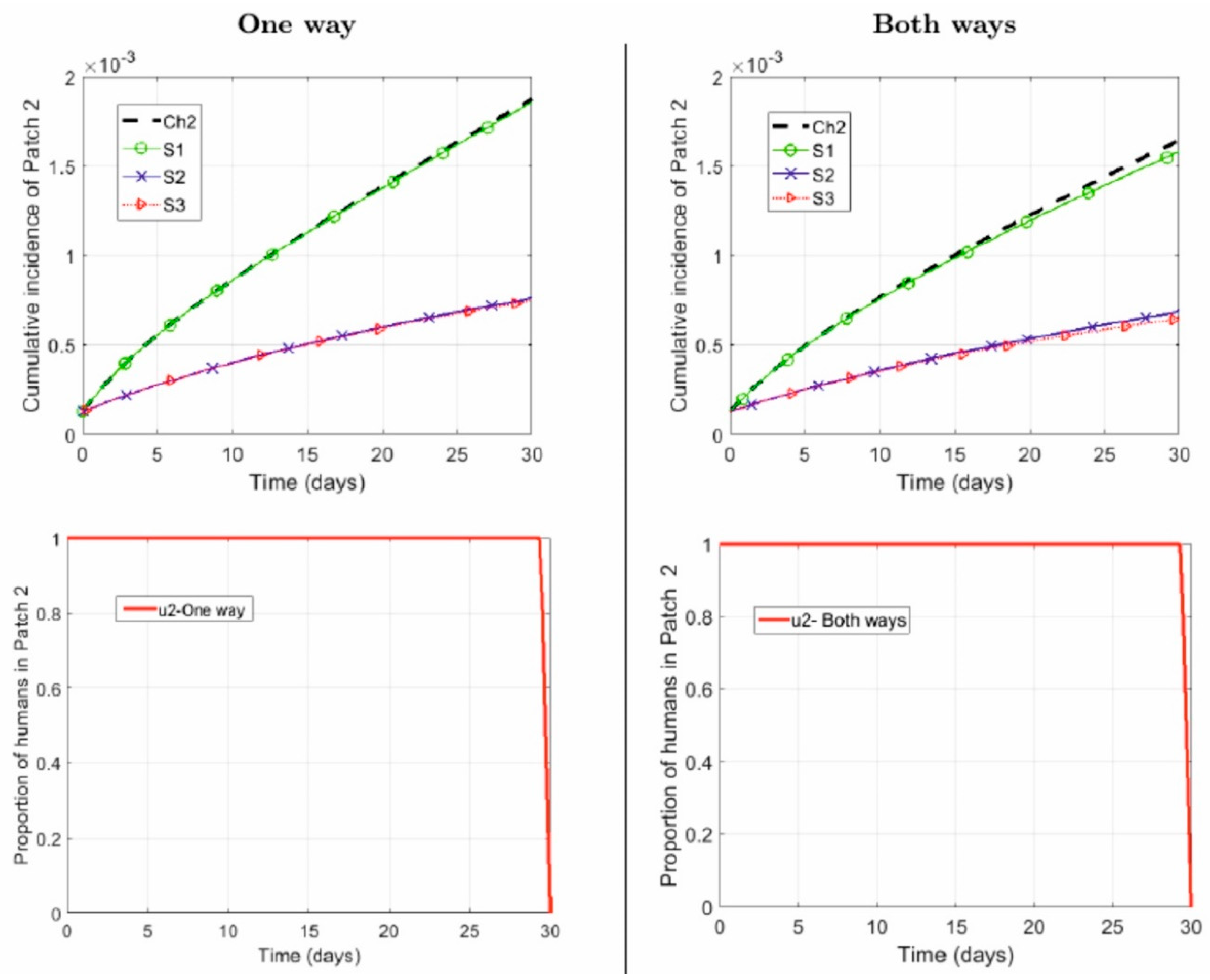
4.1. Numerical Simulations
- Smaller towns and settlements in Colombia are known to have problems with sanitation and intermittent water supply. Therefore, water storage tanks kept by suburban residents contribute to mosquito proliferation.
- In contrast to major Colombian cities located in dengue endemic areas (such as Cali–Patch 1), vector control measures in suburban areas are irregular or absent [20].
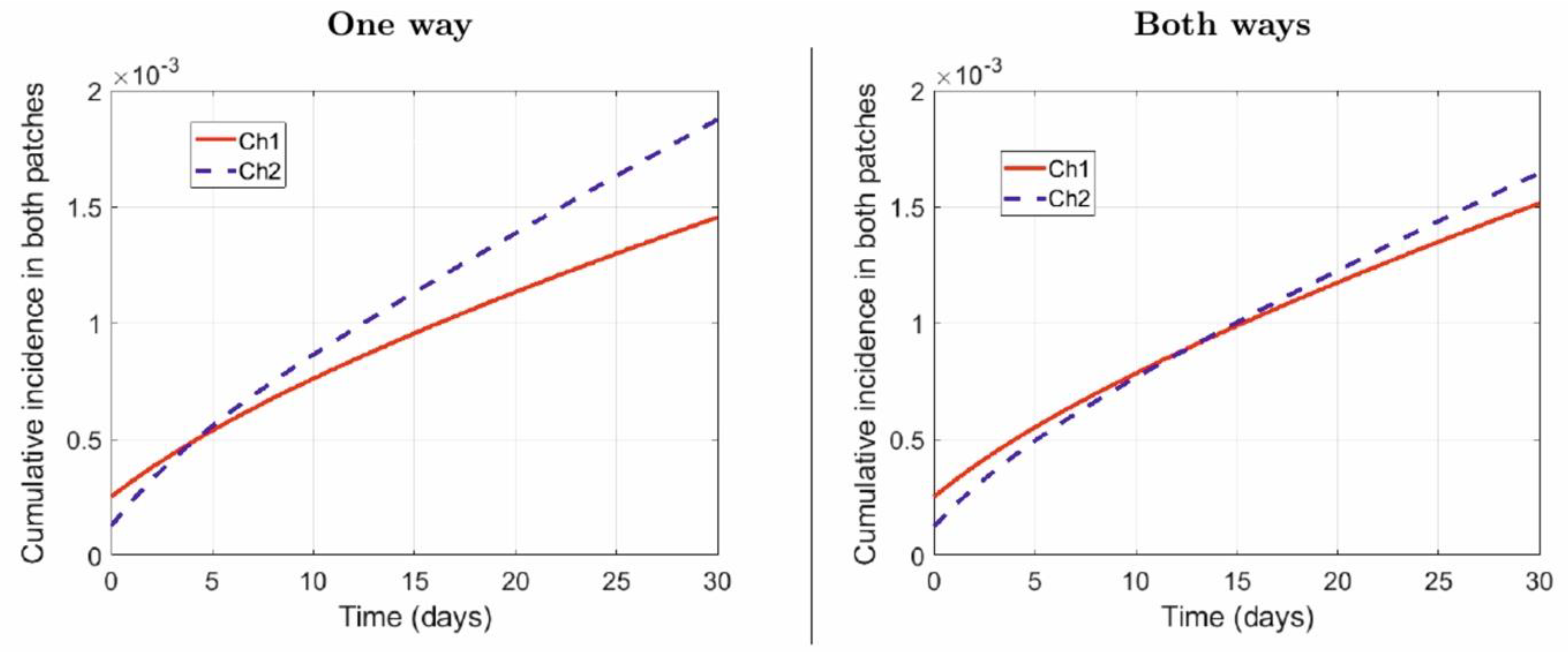
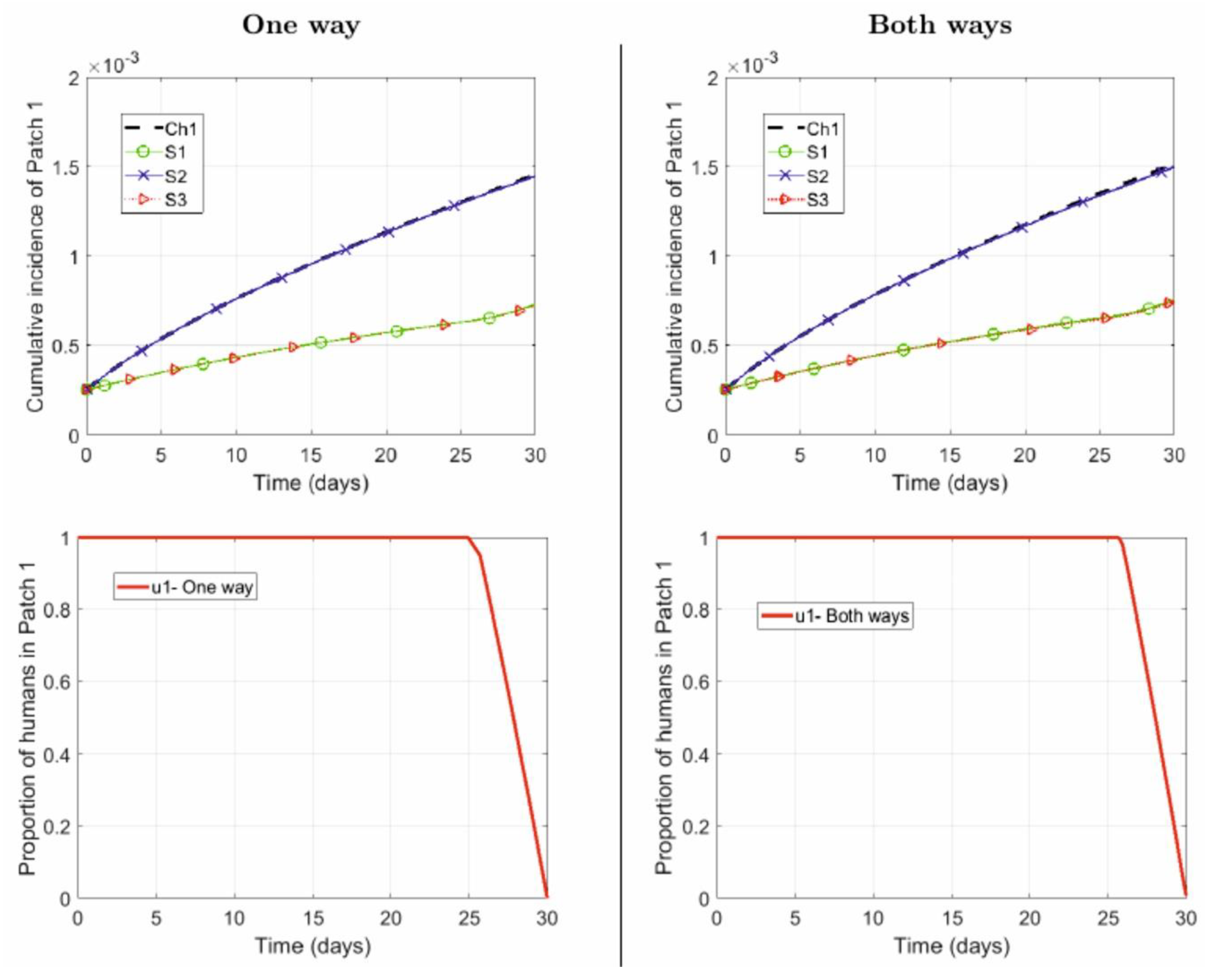
- One way: Suburban residents (Patch 2) spend, on average, 40% of their time in the city (Patch 1), while the city residents do not commute to the suburbs:
- Both ways: Suburban residents (Patch 2) spend, on average, 40% of their time in the city (Patch 1), while the city residents spend, on average, 5% of their time in the suburbs:
- Repellent is used only by the city residents .
- Repellent is used only by the suburban residents .
- Repellent used by human populations in both patches .
4.2. Cost-Effectiveness Analysis
- The human population size of Patch 2 is smaller than that of Patch 1. Therefore, the cost associated with educational campaigns promoting personal protection measures among residents of Patch 2 is lower than the cost of similar campaigns targeting residents of Patch 1.
- Both average and effective vectorial density is higher in Patch 2 than in Patch 1. Therefore, residents of Patch 2 are at greater risk of receiving mosquito bites, and reducing their contact with vectors (bites) by applying repellent should have a greater effect on residents of Patch 2 than on residents of Patch 1 (where both average and effective vectorial density is lower).
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Halstead, S.B. (Ed.) Dengue; World Scientific Publishing Co.: Singapore, 2008. [Google Scholar]
- Capeding, M.; Tran, N.; Hadinegoro, S.; Ismail, H.; Chotpitayasunondh, T.; Chua, M.; Luong, C.; Rusmil, K.; Wirawan, D.; Nallusamy, R.; et al. Clinical efficacy and safety of a novel tetravalent dengue vaccine in healthy children in Asia: A phase 3, randomised, observer-masked, placebo-controlled trial. Lancet 2014, 384, 1358–1365. [Google Scholar] [CrossRef]
- Mendez, F.; Barreto, M.; Arias, J.; Rengifo, G.; Munoz, J.; Burbano, M.; Parra, B. Human and mosquito infections by dengue viruses during and after epidemics in a dengue–endemic region of Colombia. Am. J. Trop. Med. Hyg. 2006, 74, 678–683. [Google Scholar] [CrossRef] [PubMed]
- Lenhart, S.; Workman, J. Optimal Control Applied to Biological Models; CRC Press: Boca Raton, FL, USA, 2007; p. 258. [Google Scholar]
- Sepulveda, L.; Vasilieva, O.; Martinez, H.; Arias, J. Ross-Macdonald: A model for the dengue dynamic in Cali, Colombia. Rev. Salud Publica 2015, 17, 749–761. [Google Scholar] [CrossRef] [PubMed]
- Sepulveda, L.; Vasilieva, O. Optimal control approach to dengue reduction and prevention in Cali, Colombia. Math. Methods Appl. Sci. 2016, 39, 5475–5496. [Google Scholar] [CrossRef]
- Lee, S.; Castillo-Chavez, C. The role of residence times in two-patch dengue transmission dynamics and optimal strategies. J. Theor. Biol. 2015, 374, 152–164. [Google Scholar] [CrossRef] [PubMed]
- Bichara, D.; Castillo-Chavez, C. Vector-borne diseases models with residence time: A Lagrangian perspective. Math. Biosci. 2016, 281, 128–138. [Google Scholar] [CrossRef] [PubMed]
- Barrios, E.; Lee, S.; Vasilieva, O. Assessing the effects of daily commuting in two-patch dengue dynamics: A case study of Cali, Colombia. J. Theor. Biol. 2018, 453, 14–39. [Google Scholar] [CrossRef] [PubMed]
- van den Driessche, P.; Watmough, J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 2002, 180, 29–48. [Google Scholar] [CrossRef]
- Martcheva, M. An Introduction to Mathematical Epidemiology; Springer: New York, NY, USA, 2015; p. 452. [Google Scholar]
- Debboun, M.; Strickman, D. Insect repellents and associated personal protection for a reduction in human disease. Med. Vet. Entomol. 2013, 27, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Fradin, M.S.; Day, J.F. Comparative efficacy of insect repellents against mosquito bites. N. Engl. J. Med. 2002, 347, 13–18. [Google Scholar] [CrossRef] [PubMed]
- Webb, C.E.; Russell, R.C. Advice to travelers on topical insect repellent use against dengue mosquitoes in Far North Queensland, Australia. J. Travel Med. 2011, 18, 282–283. [Google Scholar] [CrossRef] [PubMed]
- Goodyer, L.I.; Croft, A.M.; Frances, S.P.; Hill, N.; Moore, S.J.; Onyango, S.P.; Debboun, M. Expert review of the evidence base for arthropod bite avoidance. J. Travel Med. 2010, 17, 182–192. [Google Scholar] [CrossRef] [PubMed]
- Okosun, K.; Rachid, O.; Marcus, N. Optimal control strategies and cost-effectiveness analysis of a malaria model. BioSystems 2013, 111, 83–101. [Google Scholar] [CrossRef] [PubMed]
- Barrios, E.; Gajardo, P.; Vasilieva, O. Sustainable thresholds for cooperative epidemiological models. Math. Biosci. 2018, 302, 9–18. [Google Scholar] [CrossRef] [PubMed]
- Fleming, W.; Rishel, R. Deterministic and Stochastic Optimal Control; Springer: New York, NY, USA, 1986; p. 222. [Google Scholar]
- Rao, A.; Benson, D.; Darby, C.; Patterson, M.; Francolin, C.; Sanders, I.; Huntington, G. Algorithm 902: GPOPS, a MATLAB software for solving multiple-phase optimal control problems using the Gauss pseudospectral method. ACM Trans. Math. Softw. 2010, 37, 1–22. [Google Scholar] [CrossRef]
- Padilla, J.; Rojas, D.; Gómez, R. Dengue en Colombia: Epidemiología de la Reemergencia a la Hiperendemia [Dengue in Colombia: Epidemiology of Hyperendemic Re-Emergence]; Guías de Impresión Ltda.: Bogota, Colombia, 2012; p. 249. [Google Scholar]
- Menger, D.; van Loon, J.; Takken, W. Assessing the efficacy of candidate mosquito repellents against the background of an attractive source that mimics a human host. Med. Vet. Entomol. 2014, 28, 407–413. [Google Scholar] [CrossRef] [PubMed]
- Phillips, C.; Thompson, G. What Is Cost-Effectiveness? Available online: http://www.bandolier.org.uk/painres/download/whatis/Cost-effect.pdf (accessed on 21 March 2019).
| Variable | Description |
|---|---|
| Population of susceptible human hosts in Patch i, i = 1, 2 | |
| Population of infected human hosts in Patch i, i = 1, 2 | |
| Population of susceptible mosquitoes in Patch i, i = 1, 2 | |
| Population of infected mosquitoes in Patch i, i = 1, 2 |
| Parameter | Description | Unit |
|---|---|---|
| Mosquito biting rate | ||
| Probability of infection in humans | dimensionless | |
| pv | Probability of infection in mosquitoes | dimensionless |
| Nhi | Human population size in Patch i, i = 1,2 | No. of individuals |
| Mosquito population size in Patch i, i = 1,2 | No. of individuals | |
| γ | Human recovery rate | |
| Mosquito mortality rate | ||
| Residence times | dimensionless |
| Parameter | Description | Assumed Value | Reference |
|---|---|---|---|
| Mosquito biting rate | 0.36065 | [5] | |
| Probability of infection in humans | 0.22687 | [5] | |
| Probability of infection in mosquitos | 0.08058 | [5] | |
| Human recovery rate | 1/10 | [5,6] | |
| Mosquito mortality rate | 1/30 | [5,6] | |
| Human population in Patch 1 | [9] | ||
| Human population in Patch 2 | [9] | ||
| Average vectorial density in Patch 1 | [5,6] | ||
| Average vectorial density in Patch 2 | assumed | ||
| Maximal proportions of residents in Patches 1 and 2 to use the repellent | 1 | assumed | |
| Efficiency of repellent | 70% | [6,21] | |
| T | Observation period (in days) | 30 | assumed |
| Daily societal cost per one infected human host in Patches 1 and 2 ($) | 60 | [6] | |
| Cost associated with repellent application in Patch 1 | estimated | ||
| Cost associated with repellent application in Patch 2 | [6,16] |
| Scenario | No. of Human Infections in Patch 1 | No. of Human Infections in Patch 2 | No. of Averted Infections in Patch 1 | No. of Averted Infections in Patch 2 |
|---|---|---|---|---|
| Mobility option: One way | ||||
| 3408 | 989 | 0 | 0 | |
| 1 | 1709 | 978 | 1699 | 11 |
| 2 | 3392 | 405 | 16 | 584 |
| 3 | 1700 | 399 | 1708 | 590 |
| Mobility option: Both ways | ||||
| 3550 | 867 | 0 | 0 | |
| 4 | 1773 | 833 | 1777 | 34 |
| 5 | 3509 | 366 | 41 | 501 |
| 6 | 1752 | 346 | 1798 | 521 |
| Scenario | Total Cost | No. of Averted Human Infections in Both Patches | ACER |
|---|---|---|---|
| Mobility option: One way | |||
| 1 | 148.2675 | 1710 | 0.0867 |
| 2 | 35.6250 | 600 | 0.0594 |
| 3 | 183.4698 | 2298 | 0.0798 |
| Mobility option: Both ways | |||
| 4 | 149.3466 | 1811 | 0.0825 |
| 5 | 35.6066 | 542 | 0.0657 |
| 6 | 184.2195 | 2319 | 0.0794 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lasluisa, D.; Barrios, E.; Vasilieva, O. Optimal Strategies for Dengue Prevention and Control during Daily Commuting between Two Residential Areas. Processes 2019, 7, 197. https://doi.org/10.3390/pr7040197
Lasluisa D, Barrios E, Vasilieva O. Optimal Strategies for Dengue Prevention and Control during Daily Commuting between Two Residential Areas. Processes. 2019; 7(4):197. https://doi.org/10.3390/pr7040197
Chicago/Turabian StyleLasluisa, Daniel, Edwin Barrios, and Olga Vasilieva. 2019. "Optimal Strategies for Dengue Prevention and Control during Daily Commuting between Two Residential Areas" Processes 7, no. 4: 197. https://doi.org/10.3390/pr7040197
APA StyleLasluisa, D., Barrios, E., & Vasilieva, O. (2019). Optimal Strategies for Dengue Prevention and Control during Daily Commuting between Two Residential Areas. Processes, 7(4), 197. https://doi.org/10.3390/pr7040197





