1. Introduction
In mature oil fields on the Norwegian Continental Shelf, the amount of water extracted in 2016 accounted for more than twice the amount of produced oil [
1]. This produced water is transported topside for separation and cleaning. Eventually, the water treatment capacity of the topside facilities will be reached which causes a bottleneck in the production and leaves a substantial part of the hydrocarbon processing capacity left unused. Furthermore, a high amount of water in the well stream will cause a loss of pressure in the transportation pipelines, leading to a lower production. Removing the water on the seabed frees up capacity at the topside facility, which can be utilized for new tie-ins to existing fields.
In offshore oil and gas production, the processing of oil and gas on the seabed is also considered an enabler for more efficient liquid boosting, longer range gas compression from subsea to onshore, cost efficient hydrate management, more efficient riser slug depression, and access to challenging field developments [
2].
Large vessels, referred to as gravity separators, are commonly used offshore for separation of oil, water and gas. These separators are robust and have a high performance, but they are not suited for use at ultra deep waters (≥3000 m) due to the required size, which makes the installation and maintenance economically challenging [
2]. Detailed descriptions on modelling and control of gravity separators can be found in [
3,
4].
A novel separator concept not relying on vessels, but rather on separation in multiple pipes (
Figure 1), was recently developed [
5]. This separator has been dubbed the MPPS, the Multiple Parallel Pipe Separator. The reduced diameter of the pipes compared to that of vessels makes the pipe separator better suited for installation at deeper waters. A prototype of the separator has been built at the Department of Geoscience and Petroleum at the Norwegian University of Science and Technology and the steady-state performance has been evaluated [
6].
Currently, the separator laboratory does not have a control system and all valves are opened and closed manually via a LabView human–machine interface. Automatic control of key variables in the separator is important, as it helps counteract the effects of external disturbances, enables tracking of setpoints, enables optimal operation, and ensures that safety requirements are met.
The separator is equipped with several sensors providing measurements that may serve as controlled variables (CVs). Two valves are used as inputs, or manipulated variables (MVs). It is not straightforward to select a CV, as some variables may be more difficult to control and more sensitive to disturbances. This issue is addressed in
Section 2.5 of this paper. Furthermore, some variables may be difficult or impossible to control directly, and, hence, finding a secondary variable that is easier to control and has an effect on the primary control variable can be very helpful.
In [
7], a control design study was performed for a complete subsea separation system including a pipe separator. The liquid level in the pipe separator was chosen as the CV, and Proportional-Integral-Derivative (PID) controllers were used in all control loops. The authors state that controlling the system is challenging due to strong interactions between process components, constraints in valve openings and opening/closing speed of the valves. The study does not go into detail about the tuning of the controllers, nor is a control structure analysis presented.
The same is true for the work presented in [
8]. Here, PID controllers, tuned by trial and error, was used to achieve the desired performance. The level of the oil/water interface in the pipe separator was controlled. The authors also stated that a control system should be able to adapt to varying operating conditions.
Other previous control-related work on pipe separators [
9,
10,
11] do not go into detail on the selected control structure or control algorithm used. In this paper, the pairing of the MVs and CVs is analyzed. A detailed presentation of the Proportional-Integral (PI) controller tuning, and a comparison of the separator efficiency when using different candidate CVs is presented. Furthermore, model reference adaptive control is applied to a pipe separator. Adaptive control schemes have seen applications in process control [
12] and offshore oil and gas production [
13,
14,
15], but the authors have not been able to locate any prior published work on adaptive control of pipe separators.
Although the pipe separator used in this study is different from those used in [
7,
8,
9,
10,
11], it is the authors’ belief that the results are transferable and that the results presented here can serve as a basis for future control design of pipe separators.
This work contains an initial control structure analysis and an initial controller design for the MPPS. The purpose is to investigate, analyze and test several control structures, hence both a conventional PI controller and an adaptive controller is developed and tested in the laboratory. The PI controller tuning is based on the well-established simple internal model control (SIMC) tuning rules [
16]. The performance of the different control structures and controllers are qualitatively and quantitatively compared and a basis for future work is established.
2. Materials and Methods
2.1. Separator Concept
The separator being tested in this paper is the Multiple Parallel Pipe Separator (MPPS), a multi-pipe arrangement for oil–water bulk separation. The concept was previously presented in [
5,
6], where the reader can find detailed information on design considerations and performance evaluation. Experiments are carried out on a two-pipe 150.6 mm ID prototype, which is depicted in
Figure 1.
An oil–water mixture enters at the separator inlet (
), where the flow is divided into two parallel and identical separator branches. The fluids pass through the horizontal pipe segments, where they separate and are then extracted through their respective outlets. Water is extracted through the water extraction line (
), while oil is extracted through the oil extraction line (
). As seen in
Figure 1, an inclined extraction section is utilized in the design. This is to increase the water holdup in the horizontal pipe sections prior to extraction and to slow down and build up water close to the water extraction point.
The inlet has a tangential configuration and is fitted with novel phase-rearranging internals. Detailed information on the inlet configuration can be found in [
6]. The total horizontal length of the separator prototype is 6.1 m.
2.2. Test Facility
The test fluids used in the separator are distilled water with added wt% 3.2 NaCl, and Exxsol D60 model oil. To prevent bacterial growth, 750 ppm of the biocide IKM CC-80 was added to the water. Furthermore, 0.015 g/L of the colorant Oil Red O has been added to the Exssol D60 for phase distinction. The test fluid properties are given in
Table 1.
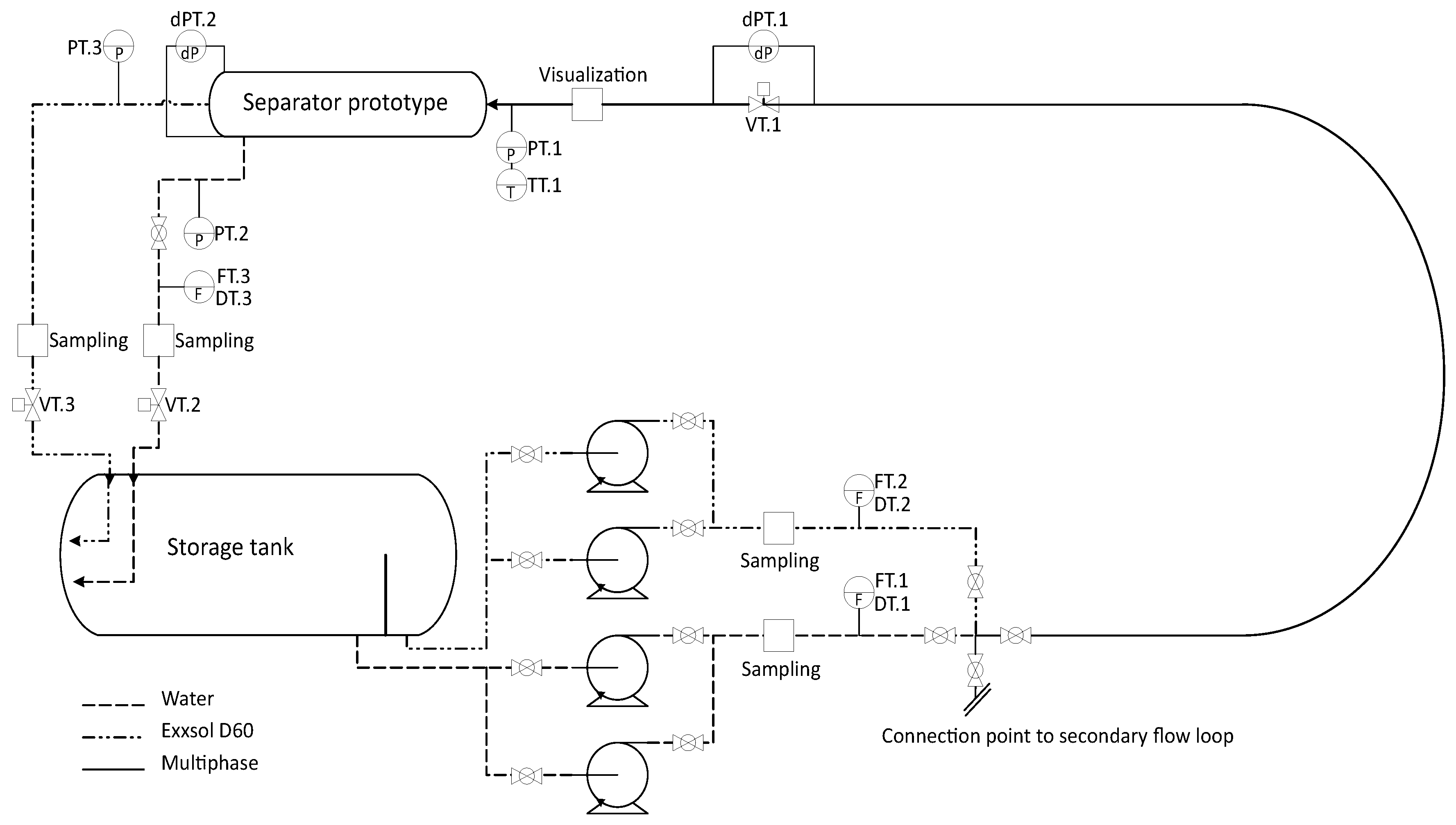
A piping and instrumentation diagram (P&ID) of the test facility is given in
Figure 2. The storage tank is a gravity separator with a diameter of 1.2 m and a length of 5.5 m. It has a capacity of 6 m
3 and serves as a baseline separator. The gravity separator provides two clean phase outlets (water and Exxsol D60), which are connected to a pump manifold.
The pump manifold consists of four centrifugal pumps, two of which are used at any given time. The pumps used for the presented experiments each have a flow capacity of 100–700 L/min and a maximum head specification of 55 m. The pumps are controlled by 0–50 Hz frequency converters, where 50 Hz constitutes a maximum rpm of 2900. Two flow lines are connected to the pump manifold, one for each phase.
Both flow lines are fitted with a Coriolis flow meter measuring flow rate (FT.1/2) and density (DT.1/2). The flow meters allow accurate adjustment of the desired inlet flow and water cut (WC), as well as monitoring of phase purities.
Downstream from the Coriolis flow meters, the flow lines merge in a Y-junction to a multiphase flow line. The multiphase flow line is a 67.8 mm ID transparent polyvinyl chloride (PVC) pipe, which consists of a 5.5 m long straight section, a 720 mm radius 180° turn, and a secondary 5 m long straight section down to the inlet of the MPPS prototype.
Static gauge pressure (PT.1) and temperature (TT.1) are measured at the MPPS inlet. A ball-type inlet choke valve (VT.1) is fitted two meters upstream from the MPPS inlet. The differential pressure (dPT.1) is measured across the valve. For all presented experiments, VT.1 has been 100% open with zero pressure loss over the inlet choke valve.
Two return lines, one for water and one for Exxsol D60, are connected to the MPPS prototype. The return lines are fitted to their respective separator outlets and . Static pressure transducers (PT.2/3) are fitted to each return line, and a third Coriolis flow meter (FT.3/DT.3) is mounted on the water return line. This allows tracking of the amount of water extracted from the separator, as well as calculation of the purity of the water extracted. Detailed information on logged and calculated parameters will follow in the next section.
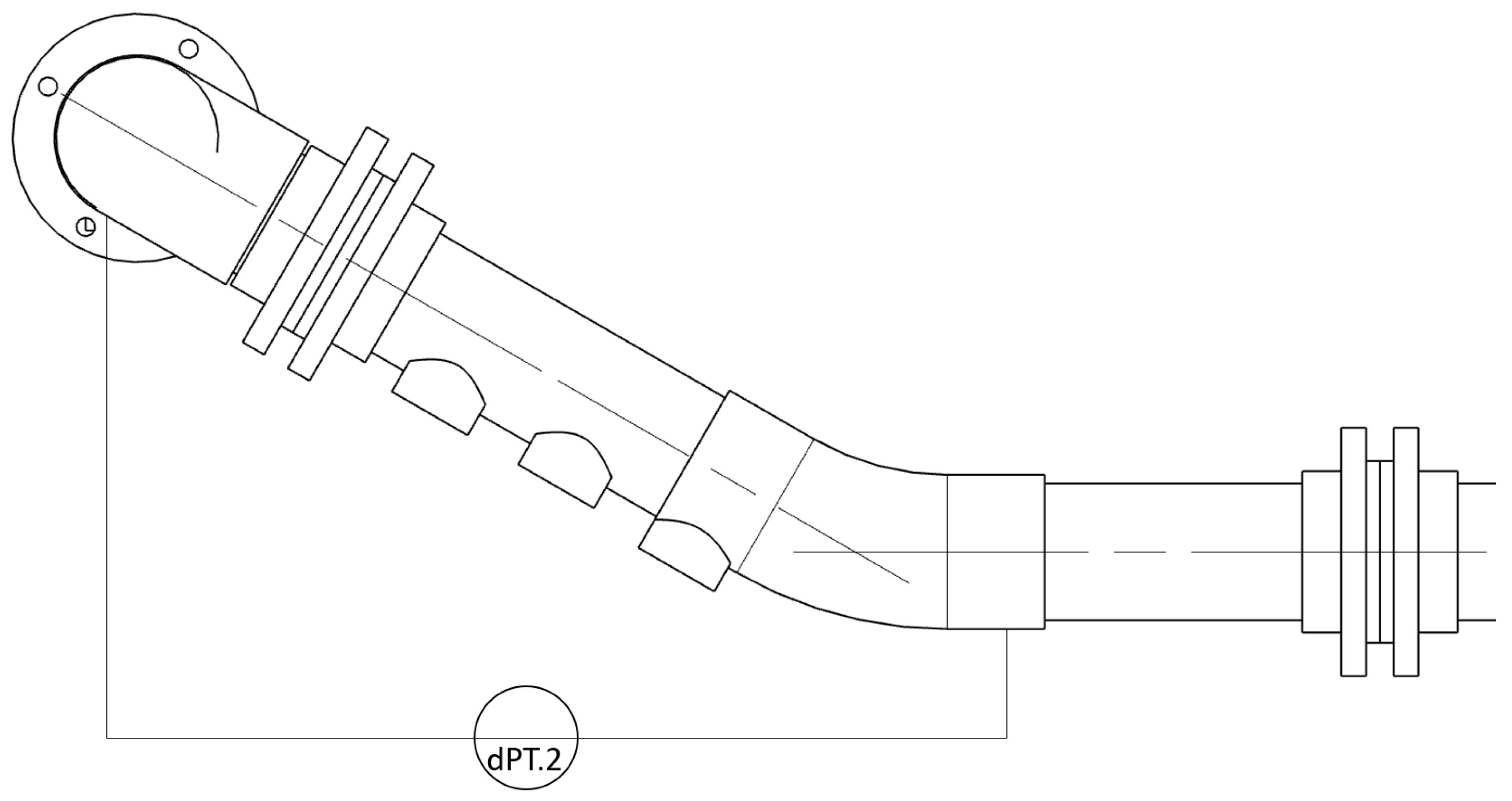
A second dP transducer (dPT.2) is installed at the water extraction point of the MPPS prototype. This measures the dP over the inclined extraction pipe, serving as a proxy level indicator for water in the section. An illustration of the sensor mounting is given in
Figure 3. The connector lines are filled with water, and the left side connection is the positive side, hence the dP measurement will be zero when the entire inclined section is filled with water and increase with the amount of oil present. The dP transducer is, unfortunately, working in the extreme end of its range and thus the measurements are quite noisy. Furthermore, low-frequency waves form in the pipeline leading up to the incline, causing a continuous disturbance on the dP measurement.
Lastly, both return lines are fitted with control valves for pressure and extraction rate control. The water return line is fitted with an electrically controlled ball valve (VT.2), while the oil return line is fitted with a pneumatic membrane valve (VT.3).
2.3. Test Parameters
All recorded test parameters are listed in
Table 2. The table includes tag names, parameter names, parameter units and specified sensor range. The values for VT.2 and VT.3 are specified values sent to the valves by the controllers, not the actual measured position of the valves.
As mentioned in
Section 2.2, three Coriolis flow meters are used to adjust inlet flow rate and water cut, monitor phase purities, determine the amount of water extracted from the MPPS prototype, and the purity of the extracted water. The WC in the respective flow lines is determined by
Here,
is the measured density at DT.1/2/3, while
and
are the pre-determined temperature-corrected densities of the water and Exxsol D60, respectively. For pure-phase feed streams, WC
1 should be equal to 100% while WC
2 should be equal to 0%. From calculated WC and measured flow rates, the actual WC in the multiphase transport line (
) is calculated as
where
and
are the water and oil flow, respectively, before mixing. When running experiments,
and
are adjusted such that the desired total flow and
are reached.
The amount of water extracted from the MPPS prototype is determined by the extraction rate (ER). The ER is the flow rate through the water extraction line divided by the flow rate in the water feed line:
where
is the flow at the water outlet of the MPPS.
As the test loop is a closed system, the water and Exxsol D60 phases will be contaminated over time. Microscopic droplets of water will be dispersed in the oil and vice versa. In order to give a performance measurement that is independent of occurring contamination, the WC ratio is calculated. The WC ratio is equal to the WC at the water extraction line (WC
3) divided by the WC at the water feed line (WC
1):
A equal to 100% means that the extracted water from the MPPS prototype is of equal quality to the water, leaving the baseline separator prior to being mixed with the oil. A of 100% is thus the upper limit on the purity that can realistically be achieved by the MPPS prototype.
2.4. System Identification
A dynamic model of the system is very helpful when designing controllers. A classical way to identify the dynamic relations between a manipulated variable and a control variable is to perform a step response experiment and calculate the transfer function. In this work, the procedure from [
16] was followed, and it was assumed that the dynamic model between each input and output could be described by a first-order plus time delay transfer function on the form
where
y is the output,
u is the input, and
s is the Laplace variable. The transfer function variables describing the dynamic response,
k,
and
are of special interest. These variables represent the plant gain, the time constant and the time delay, respectively. The plant gain provides the steady-state output of the plant, for a specific input, and is given by
The time constant, , is the time it takes the output to reach 63% of the steady-state value, and the time delay, , is the amount of time it takes the input to cause a reaction on the output.
The step response experiments were performed with one valve at a time, with the other valve in a fixed position, and at a fixed inlet flow rate and inlet WC. The valve openings, inlet flow rate and inlet WCs are listed in
Table 3.
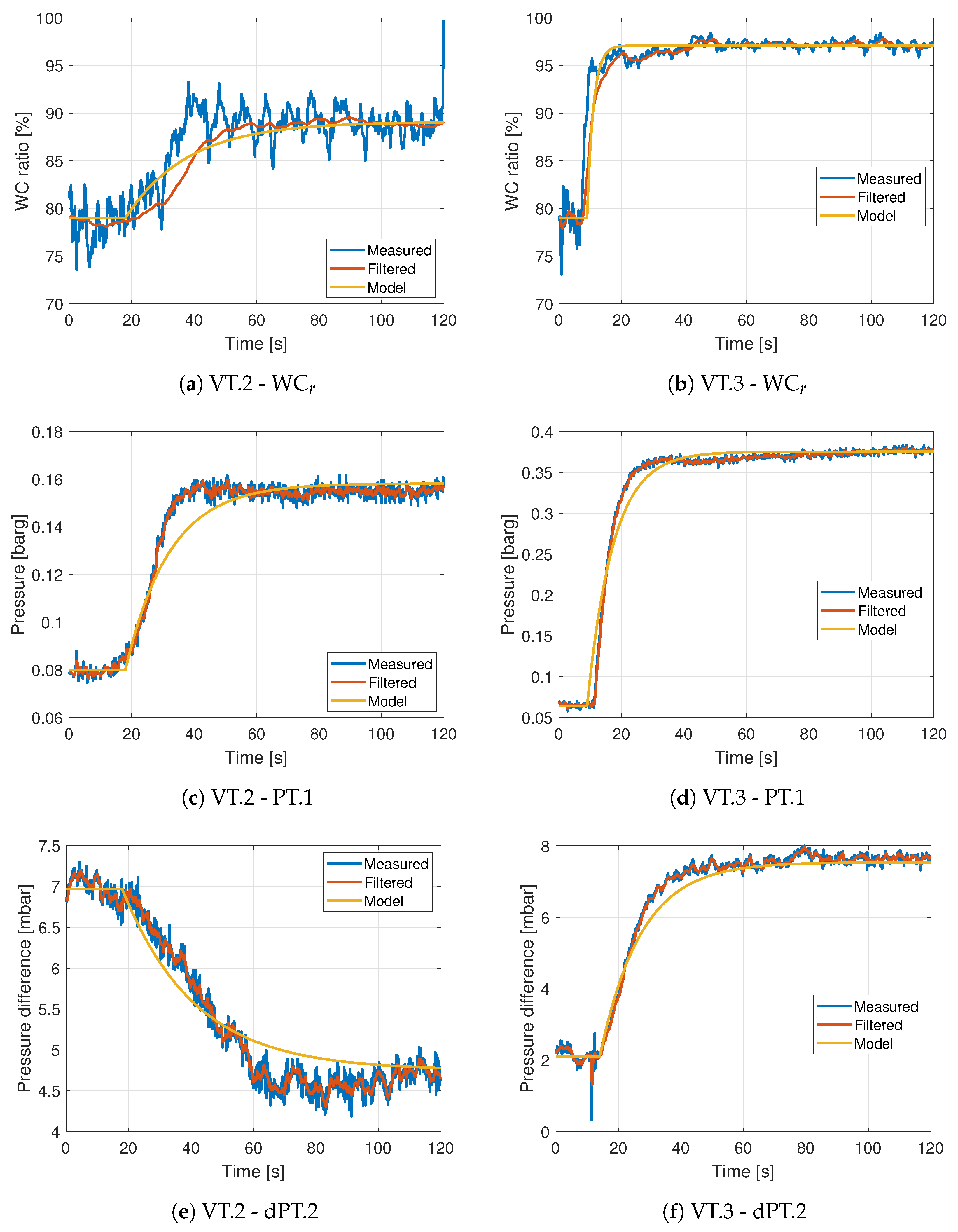
Some of the measurements contained significant measurement noise, hence the measured values where filtered using a 1st order Butterworth filter before the parameter analysis was performed. The transfer function between each input and output was then calculated and validated by comparing it to the original response. If any deviations were present, the transfer function variables were tuned manually to improve the fit.
The step response experiments were performed on the two inputs VT.2 and VT.3, and three measurements were chosen as candidate CVs. The pressure PT.1 is a necessary CV for safety reasons. A measurement that gives a direct indication of the separator efficiency is the the water cut ratio , and hence this is also a candidate CV. The laboratory is not equipped with a level measurement sensor, instead the pressure drop dPT.2 over the incline is used for this purpose. The level is often used as an CV in previous work, as mentioned in the Introduction, and will also be a candidate CV in this work.
From the step response experiments, the following transfer functions were identified:
A comparison between the measured response, the filtered response, and the transfer function response is shown in
Figure 4. Here, we see that some of the responses could be better described by a second-order transfer function. In particular, the transfer functions between VT.2 and the different outputs (note the second order dynamics in
in
Figure 4a not captured by
and the overshoot in dPT.2 in
Figure 4e not captured by
). However, for the control study in this work, it is assumed that a first order model is sufficient. The fluctuations present are purely caused by measurement and process noise.
2.5. Control Structure Analysis
The separator is a multiple input multiple output (MIMO) system with two inputs and several possible outputs. It is not straightforward to pair an input with an output, and hence a relative gain array (RGA) analysis ([
17], Section 3.4) was performed. The RGA provides a measure of interactions between the inputs and outputs and [
17,
18] recommends pairing inputs and outputs such that the rearranged system has an RGA matrix close to identity. Furthermore, negative steady-state RGA elements should be avoided. The RGA for a square system on the form
is found by calculating the element-wise matrix product
where
is the steady-state transfer function matrix of
in Equation (
13).
Another parameter to consider when investigating the pairing of CVs and MVs is the Niederlinski index (NI) ([
18], Section 2.2.1)
where
are the diagonal elements of
. If the open-loop system is stable (which is the case here), one should select pairings corresponding to positive NI values [
19]; otherwise, the closed-loop system will be unstable ([
18], Th. 1). The RGA matrices and the NI for the separator is shown in
Table 4. From the RGA analysis, it is clear that VT.2 should be paired with
or dPT.2, and VT.3 with PT.1, as this corresponds to the pairing closest to 1. The NI is positive for both possible pairings, hence no pairing will lead to an unstable system.
2.6. Controller Design
A multivariable system, such as the one investigated here, could benefit from a multivariable control scheme. However, since this is an initial control study, the developed controllers are decoupled, single-loop controllers.
2.6.1. PI Control
A PI controller has the form
where
is the proportional gain,
is the integral time in seconds,
r is the reference and
y is the measured output to be controlled. PI controllers are developed for the separator by applying the SIMC tuning rules [
16]. The SIMC tuning rules states that the proportional gain and integral time of the PI controller should be chosen as
where
is the proportional gain,
is the integral time, and
is the desired closed-loop time constant, which is the only tuning parameter. For tight and robust control, Ref. [
16] recommends choosing
. Although the RGA analysis recommended a specific pairing of inputs and outputs, PI controllers are developed and tested for all configurations. The parameters used in the PI controllers are found in
Section 3.2.1.
A derivative part could have been added to the controllers, but this would have required a measurement of the derivative of the CV. This is not available but could have been calculated numerically. However, as the control objective is to keep the CVs at steady-state, the derivative of the CV would be close to zero when operating at steady-state and the contribution would only be from the measurement noise. Derivative action is uncommon in process control applications where the plants are stable with overdamped responses and first-order dominant dynamics (which is the case here), since the performance improvement is usually too small compared to the added complexity [
17,
20].
2.6.2. Adaptive Control
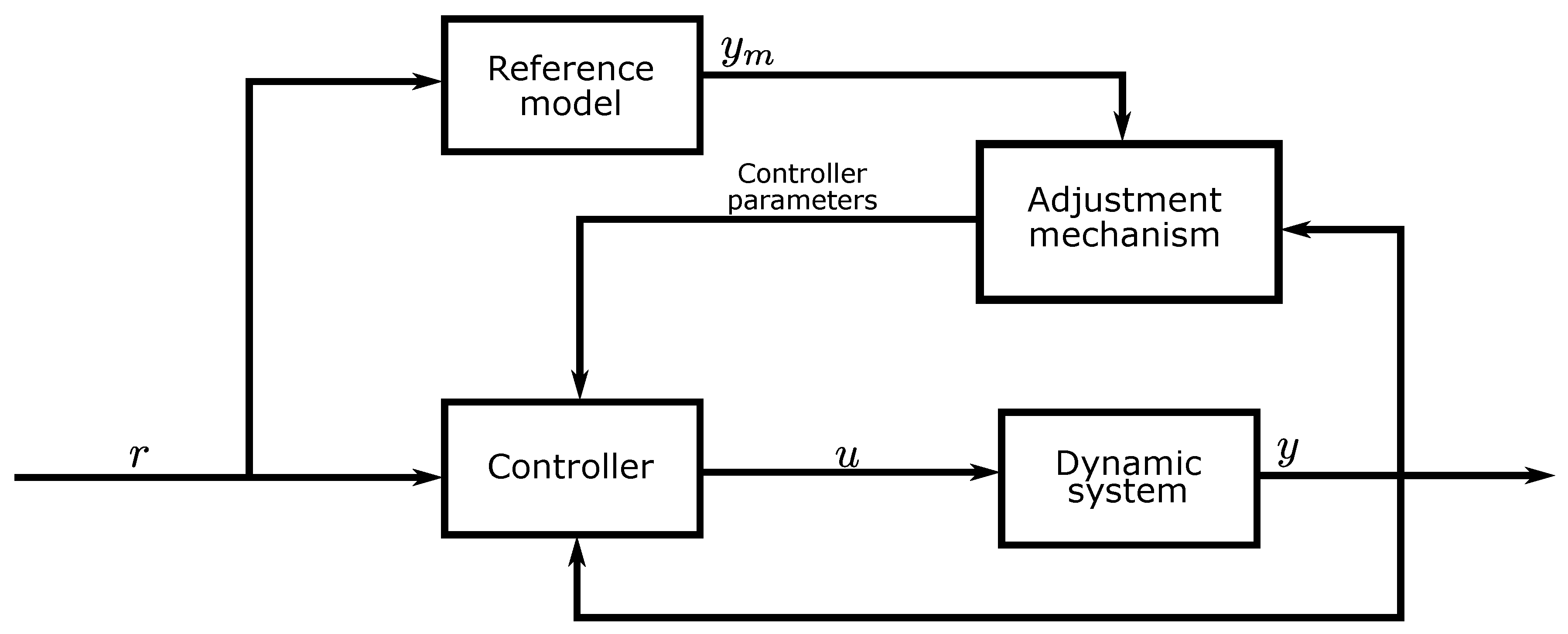
As an alternative to conventional PI control, a model reference adaptive controller (MRAC) ([
21], Section 6.2.2) was implemented and tested for the two control configurations recommended by the RGA analysis, i.e., VT.3 controls PT.1 and VT.2 controls either
or dPT.2.
When using MRAC, the controller parameters are automatically updated such that the error between the measured variable and the output of a reference model is reduced. This could be very beneficial if the process parameters change over time or at different operating points, which may lead to poor control when using a controller with fixed gains. The MRAC structure is different from a PI controller structure, i.e., there is no proportional and integral gain in the MRAC, but rather two parameters that try to approximate a value that causes the closed-loop system dynamics to be equal to the reference model dynamics. Hence, using the proportional and integral gain of a PI controller as initial values in an MRAC is not necessarily helpful. A schematic of the MRAC is shown in
Figure 5.
The MRAC has the form
where
and
are time-varying gains, updated by the adaptive laws
where
are adaptation gains,
y is the measured value to be controlled,
r is the reference and
is either 1 or
. The error signal
, where
is the output of the reference model
where
and
are chosen by the operator and specify the desired closed-loop dynamics of the system.
The only system knowledge required by the MRAC is the sign of
k. It can be shown ([
21], Section 6.2.2) that, if
is the state in a linear system, the controller given by Equations (
19)–(
23) causes
asymptotically for
. The parameters used in the MRAC are found in
Section 3.2.2.
3. Results
In total, six experiments were carried out in the laboratory: four experiments with PI controllers and two experiments with MRAC. When using PI control, all control pairings were tested, but with MRAC only the pairings recommended by the RGA analysis was carried out.
3.1. LabView Implementation
The laboratory is controlled through a computer running LabView 2015 (National Instruments, Austin, TX, USA) on Windows 7 (Microsoft, Redmond, WA, USA) with an Intel i7 4770S (Santa Clara, CA, USA), 3.1 GHz processor and 16 GB RAM. The PI controllers could be readily implemented in the LabView 2015 block diagram through existing PI controller blocks.
The MRAC, however, had to be implemented using an add-on for LabView called MathScript Module. This module allows the user to write code, and execute it at each iteration of the LabView program. To calculate the MRAC input in Equation (
19), the differential equations in Equations (
20)–(
22) must be solved. This was done using first-order Euler integration with a step length of 0.0001 s. A dead band was introduced to the adaptation algorithms, i.e., the adaptation was stopped if the error was less than 5% of the setpoint for dPT.2 and PT.1 and less than 0.5% for
.
3.2. Controller Tuning
3.2.1. PI Controllers
A transfer function model is only an approximation of the real system dynamics. It was assumed that the transfer functions were of first order. The controller parameters may require re-tuning if the transfer function models differ significantly from the real dynamics (they may change with operating point and inlet conditions) or if nonlinearities in the valve openings are not considered. Furthermore, there are interactions between the control loops; hence, a multivariable controller would probably be a better choice. This, however, has not been studied in this work.
It was found during initial testing that the choice of
was too aggressive for VT.2 and, hence,
s was chosen for this valve. For VT.3,
could only be used when controlling
. Otherwise,
s was used. The controller parameters for the different PI controllers are listed in
Table 5.
3.2.2. Model Reference Adaptive Controller
It was found during testing in the laboratory that the initial values
and
as well as the adaptation gains
had to be chosen with care. This is due to the fact that time delays and measurement noise was ignored when the controller was derived. The adaptive controller parameters used are listed in
Table 6.
3.3. Test Sequence and Control Objectives
All experiments presented here were performed on the same day. Prior to each experiment, the lab was operated at nominal inlet conditions for 5 min, i.e., a flow rate of 350 L/min and 60% WC. The valves were manually set to VT.2 = 30% closed and VT.3 = 70% closed. This led to an initial pressure PT.1 ~ 0.1 barg, an initial ~ 99% and an initial dPT.2 ~ 1.9 mbar when the controllers were activated. The static pressure is initialized at 0.1 barg in order to see how the controllers, and especially the adaptive controllers, perform during an initial transient. A setpoint of 0.4 barg for PT.1 was necessary as the valve controlling the pressure could then operate in the middle of its range, and not saturate, when the inlet flow rate was high.
The inlet conditions were varied in order to emulate situations that may occur in a subsea oil/water separator. The inlet variables available for manipulation are the total liquid flow and the inlet WC.
Table 7 shows the different inlet conditions and the scenarios they emulate.
The main control objectives in all experiments are to maintain the desired pressure PT.1 and to keep as high as possible. The latter is important in order to ensure that the water quality is high enough for the downstream water cleaning equipment. A setpoint of 99% is chosen for the . Looking only at may, however, be misleading, since it says nothing about how much water is extracted. For this, the ER is used. It is important to maintain a high ER while maintaining a high . If the ER is very low, almost no liquid is leaving the separator through the water outlet. In this case, the may be high, but a lot of water is leaving through the oil outlet.
In Experiments 1 and 2, the
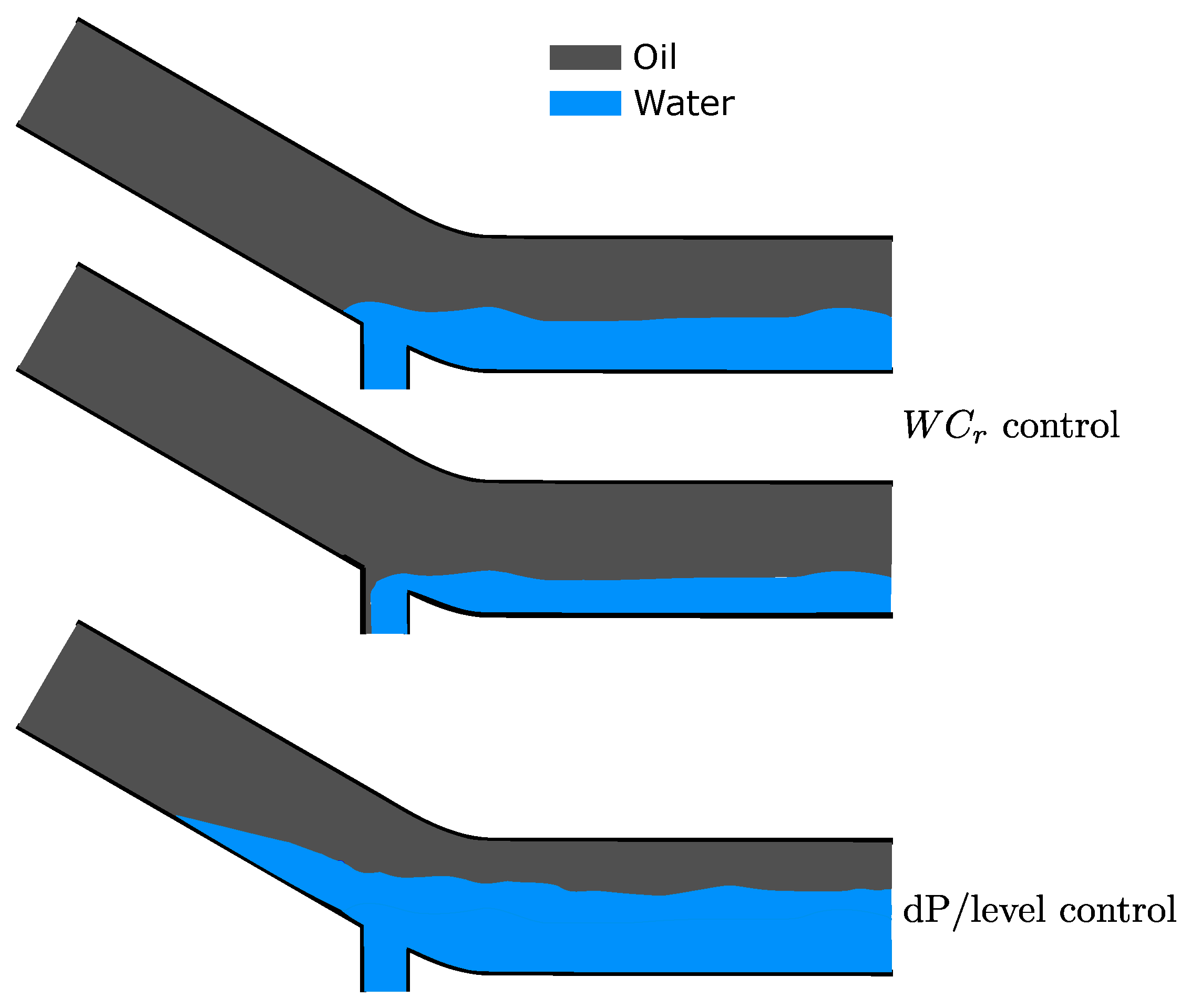
is controlled directly using either VT.2 or VT.3. In Experiments 3, 4 and 6, the dP between the bottom of the outlet incline and the top of the outlet incline is controlled. This serves as a proxy level measurement of the water level in the incline. When controlling the dP, and the level, by proxy, a buffer of water is built up in the incline, making the
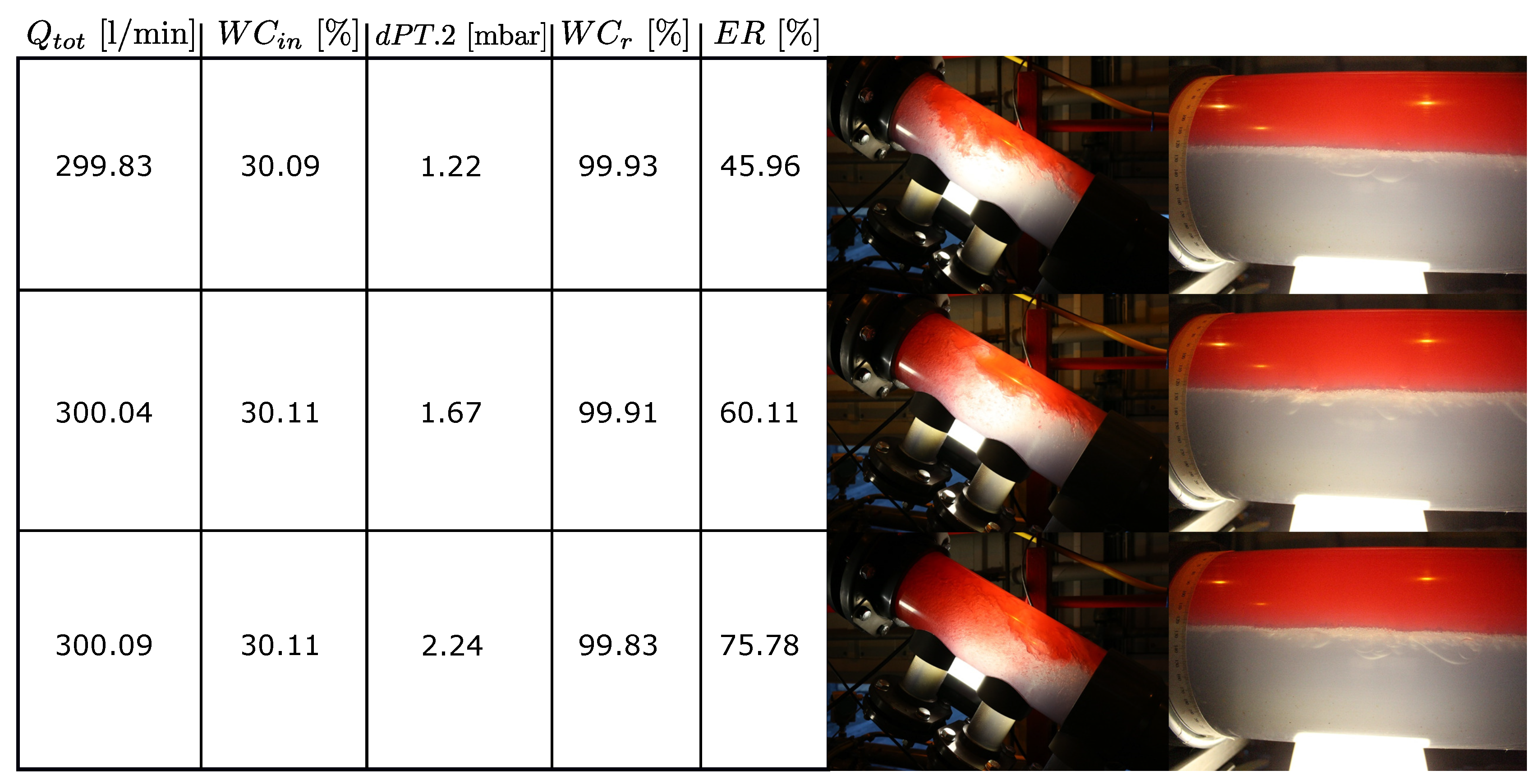
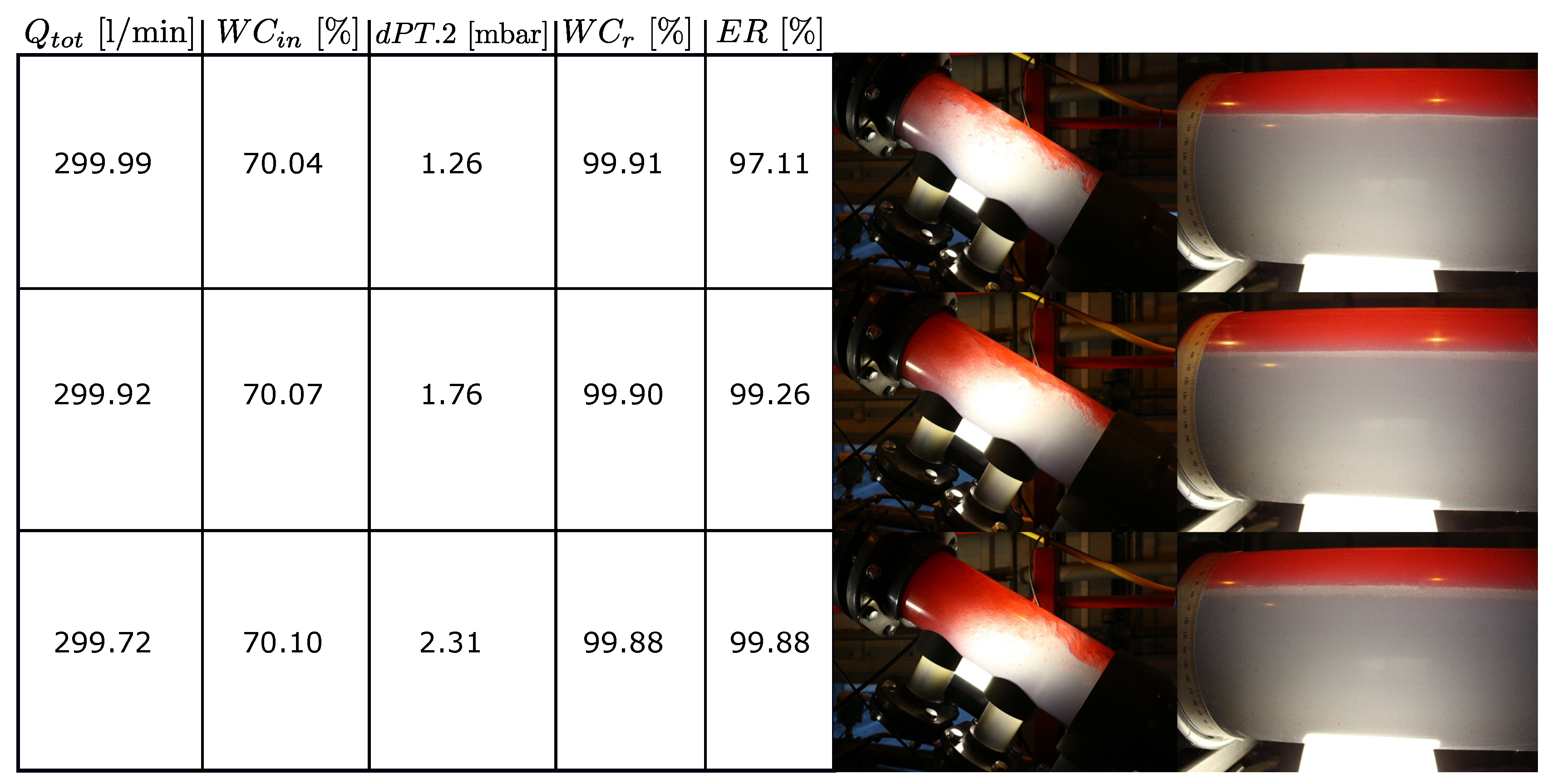
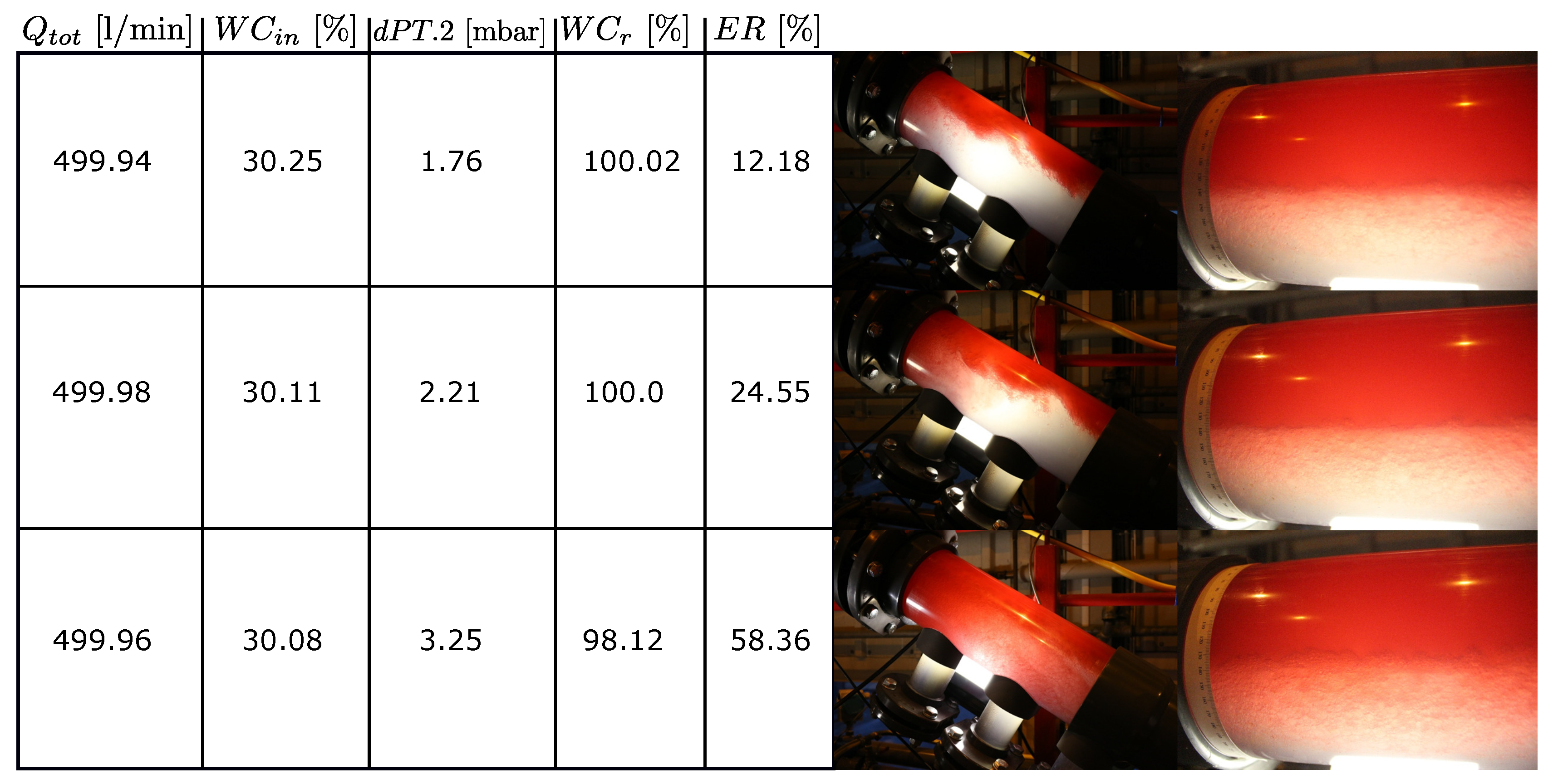
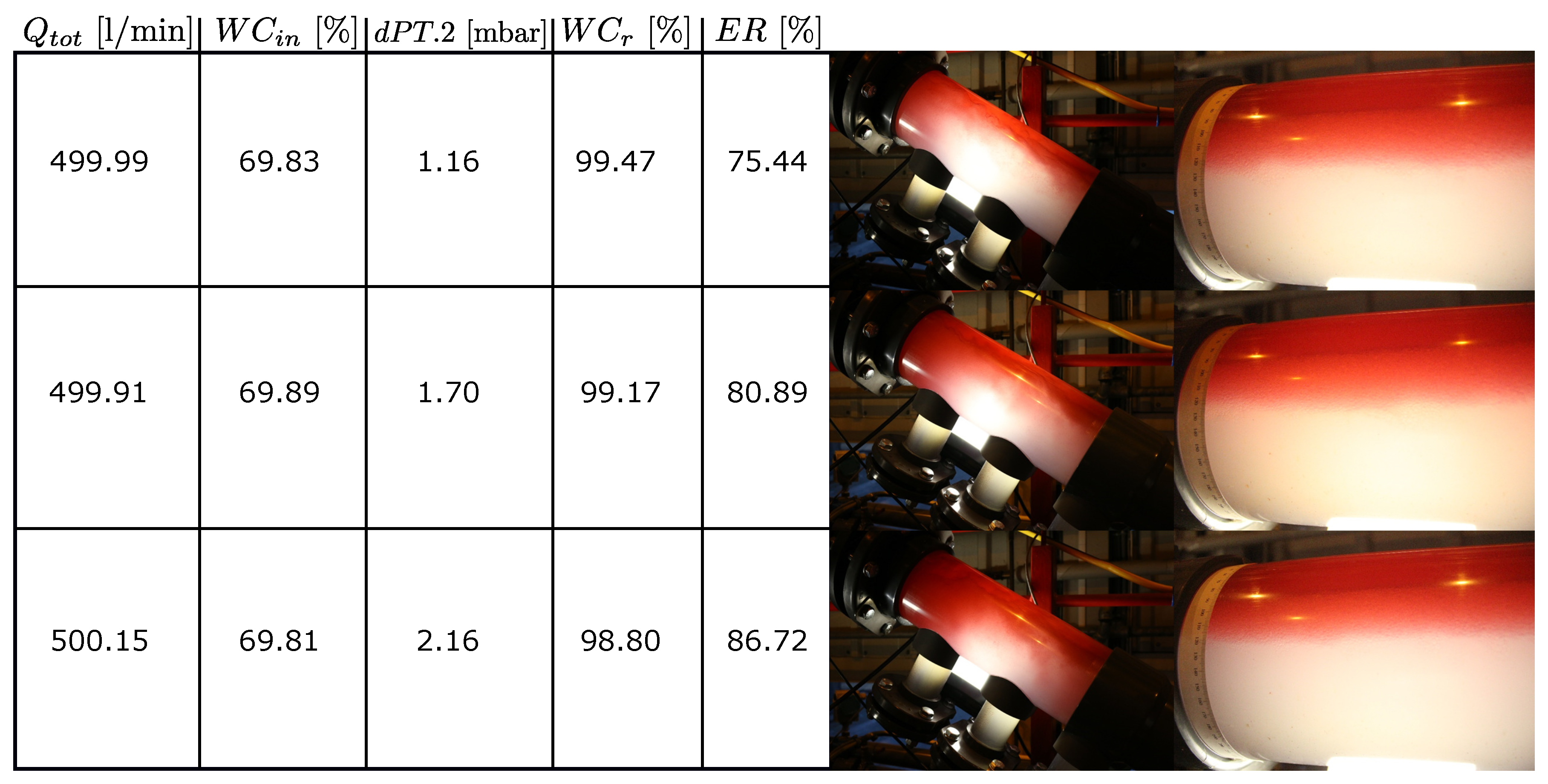
more robust to inlet variations. It was found through image analysis that a dP of 2 mbar gave stable oil and water layers (see the
Appendix A) and the buffer volume was assumed sufficient. Hence, this setpoint is used in the controllers.
Figure 6 shows a sketch of this.
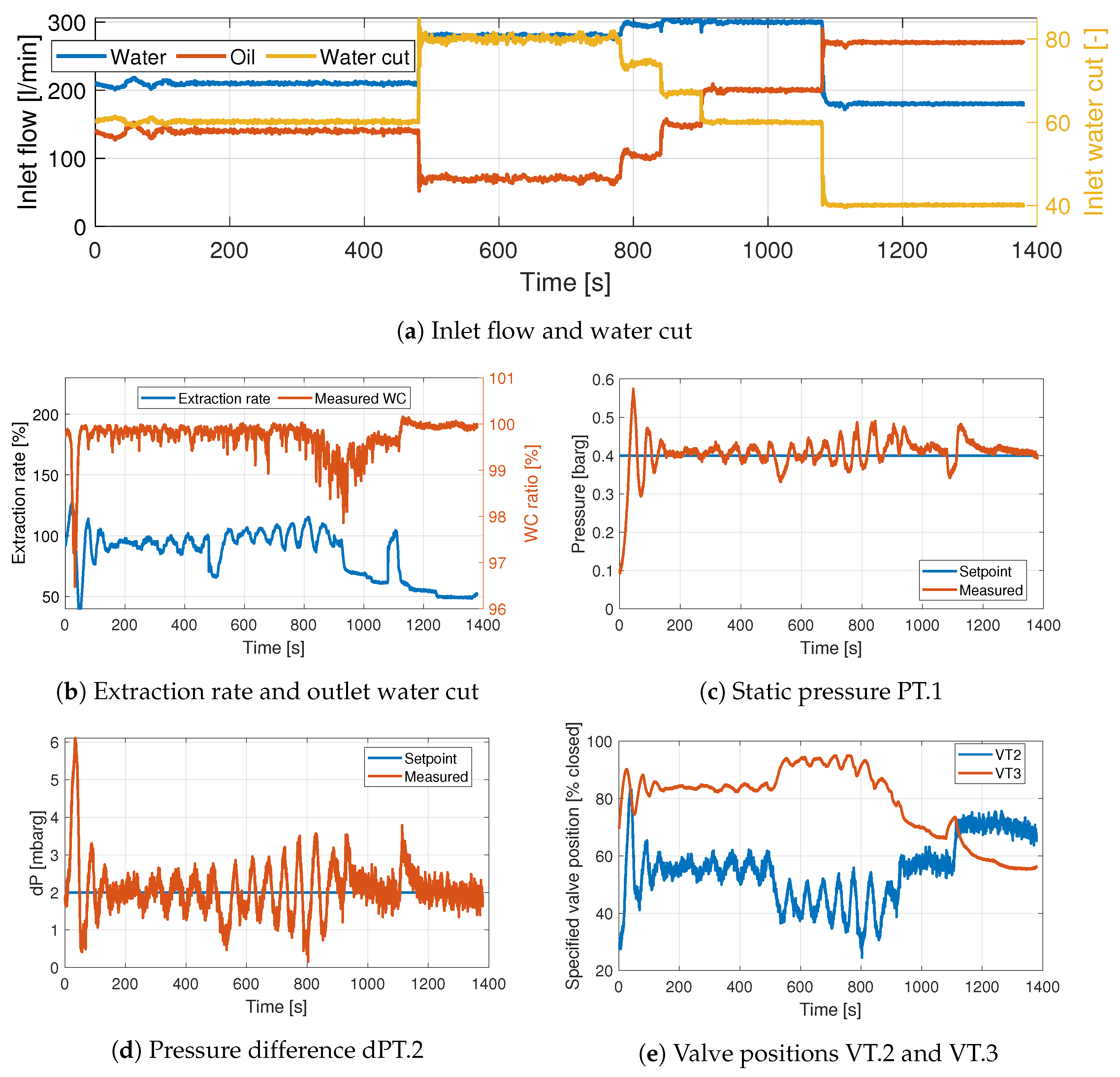
3.4. Experiment 1. PI Control VT.2–PT1, VT.3–
Figure 7 shows the results of Experiment 1 where the recommended pairings from the RGA analysis were not used. Since both outputs depend on both inputs, both controllers need to work continuously to counteract the effects caused by the other controller. Furthermore, when
is higher than the setpoint, the controller will close VT.3 to decrease
. This causes the ER to increase above 100% and oil starts flowing through the water outlet. Due to time delays, this effect suddenly causes a drop in
which then has to be counteracted. These drops in
are clearly seen in
Figure 7b.
The pressure controller is able to keep the pressure around the setpoint. The controller handles the steps in inlet flow and inlet WC quite well, but the effect of the other control loop is quite clear. Notice how the differential pressure dPT.2 oscillates (
Figure 7d) due to the lack of control. The dP is quite high, indicating a large amount of oil in the incline. Numerical values for the performance can be found in
Table 8.
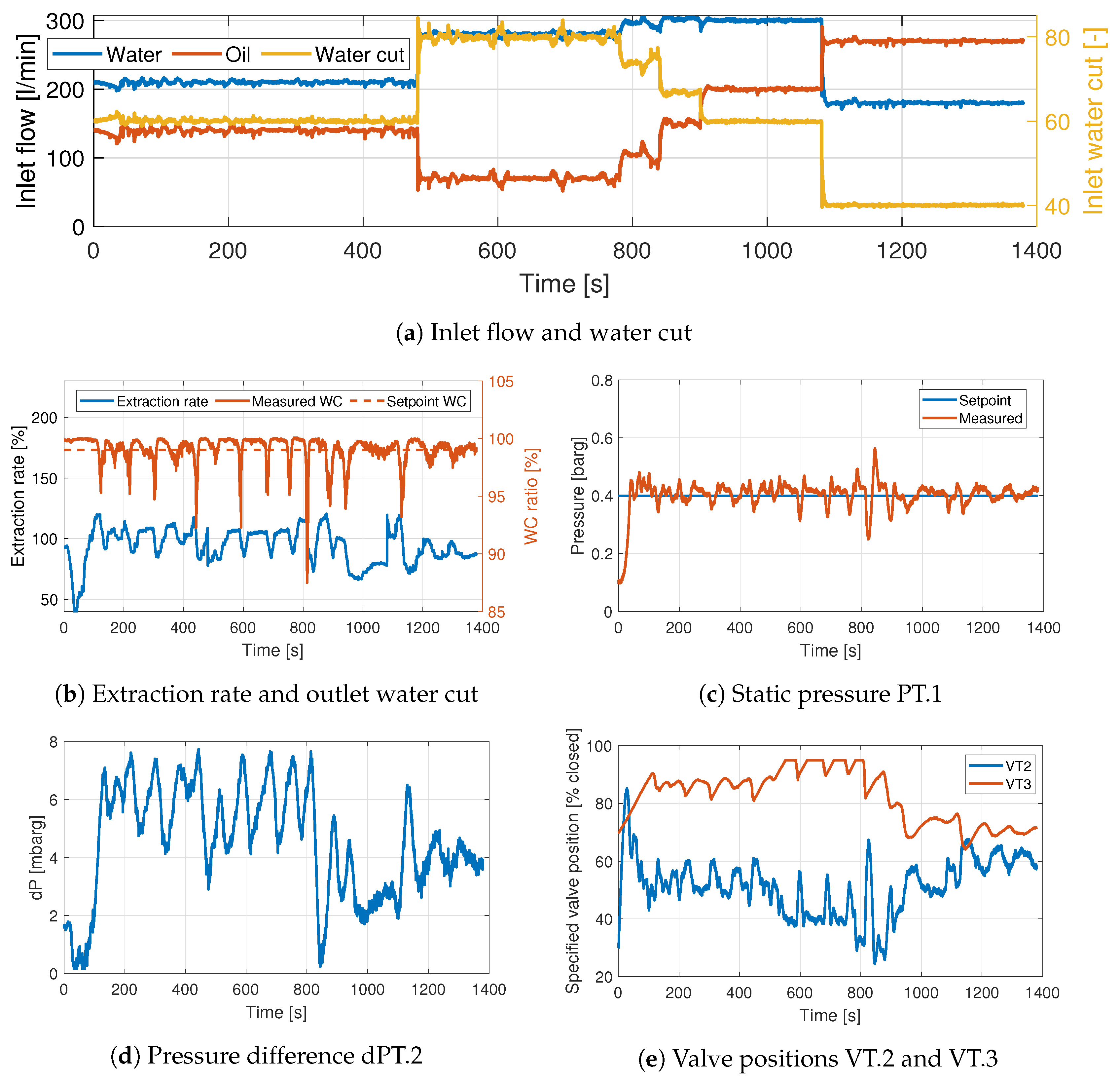
3.5. Experiment 2. PI Control VT.2–, VT.3–PT.1
Figure 8 shows the results of Experiment 2. Here, the recommended pairings from the RGA analysis were used, and the results show that PT.1 is controlled much better than in Experiment 1. The variations in
are less frequent, but this is caused by the slow controller operating VT.2. As can be seen in
Figure 8e, from
s to
s, the VT.2 valve opens very slowly. This causes the extraction rate to increase slowly (it increased much faster in Experiment 1) towards the point where a drop in
happens. This occurs at
s, causing the valve to close again. Since the variations in
happen less frequently, the effect on PT.1 from VT.2 opening and closing is also less than in Experiment 1, which may explain why PT.1 is better controlled in Experiment 2. It should be noted, however, that VT.3 is much faster than VT.2, hence the controller could possibly be able to counteract the influence of VT.2 even if the oscillations had been more frequent. The differential pressure dPT.2 oscillates here as well (
Figure 8d), due to the lack of control and the dP is quite high, indicating a large amount of oil in the incline. Numerical values for the performance can be found in
Table 8.
The initial transient is quite oscillatory. This is caused by the large initial error in the PT.1 and the fact that no reference filter is used. After PT.1 stabilizes, so does . During the steps in inlet conditions, both controllers are able to keep the controlled variable close to the setpoint. The variations in PT.1 are smaller than in Experiment 1.
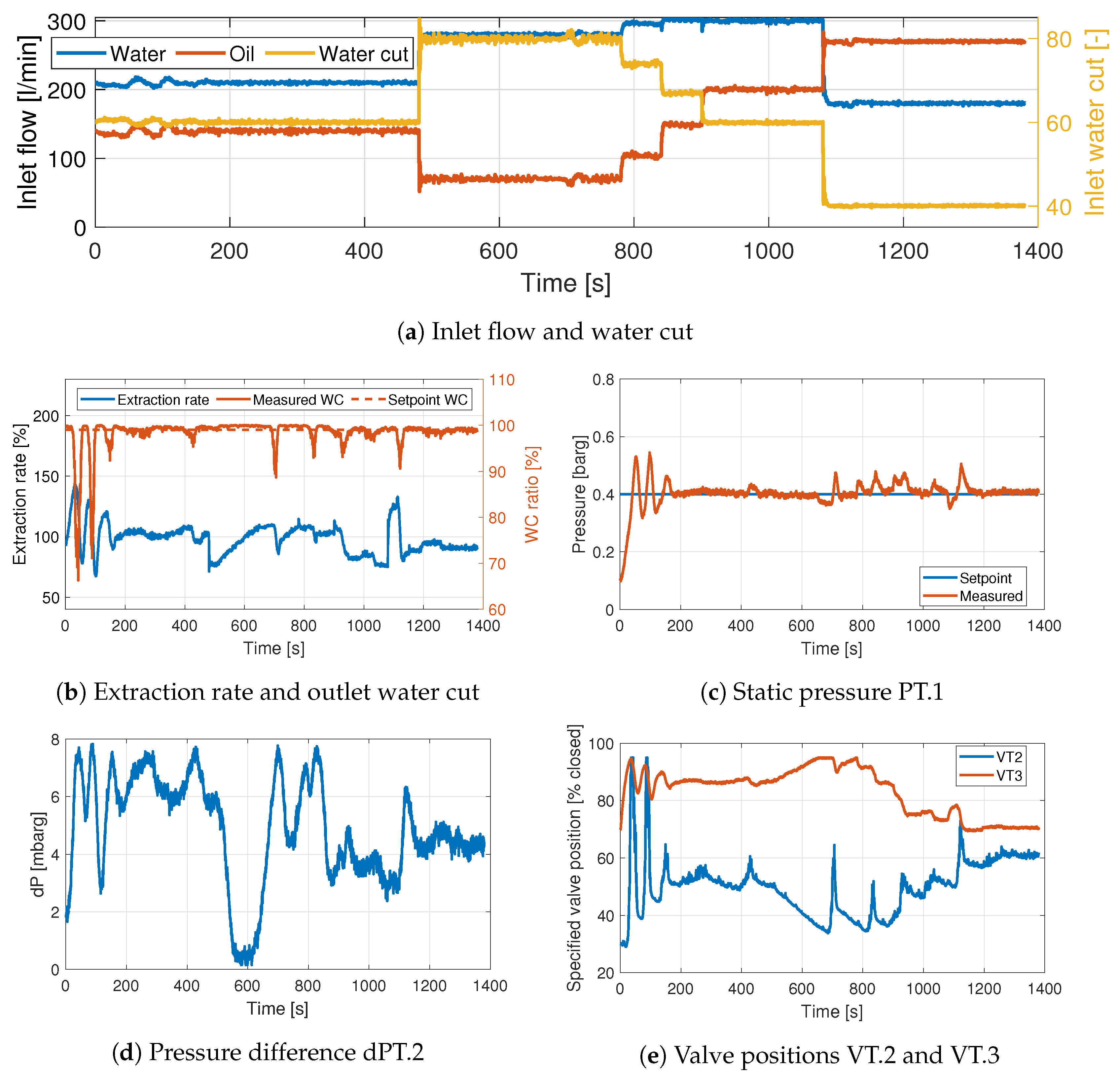
3.6. Experiment 3. PI Control VT.2–PT.1, VT.3–dPT.1
In this experiment,
is not used in the controller. Instead, the dP is controlled to a fixed setpoint.
Figure 9 shows the results. Here, we see that the behaviour of the
and the ER is not as in Experiments 1 and 2. Since the dP is controlled, a buffer volume is established in the incline. This buffer volume functions as a filter for the disturbances occurring at the inlet. The
has very few drops below 99% in this experiment (
Figure 9b). Numerical values for the performance can be found in
Table 8.
The effects of measurement noise in the dP transducer are clearly seen in
Figure 9d.
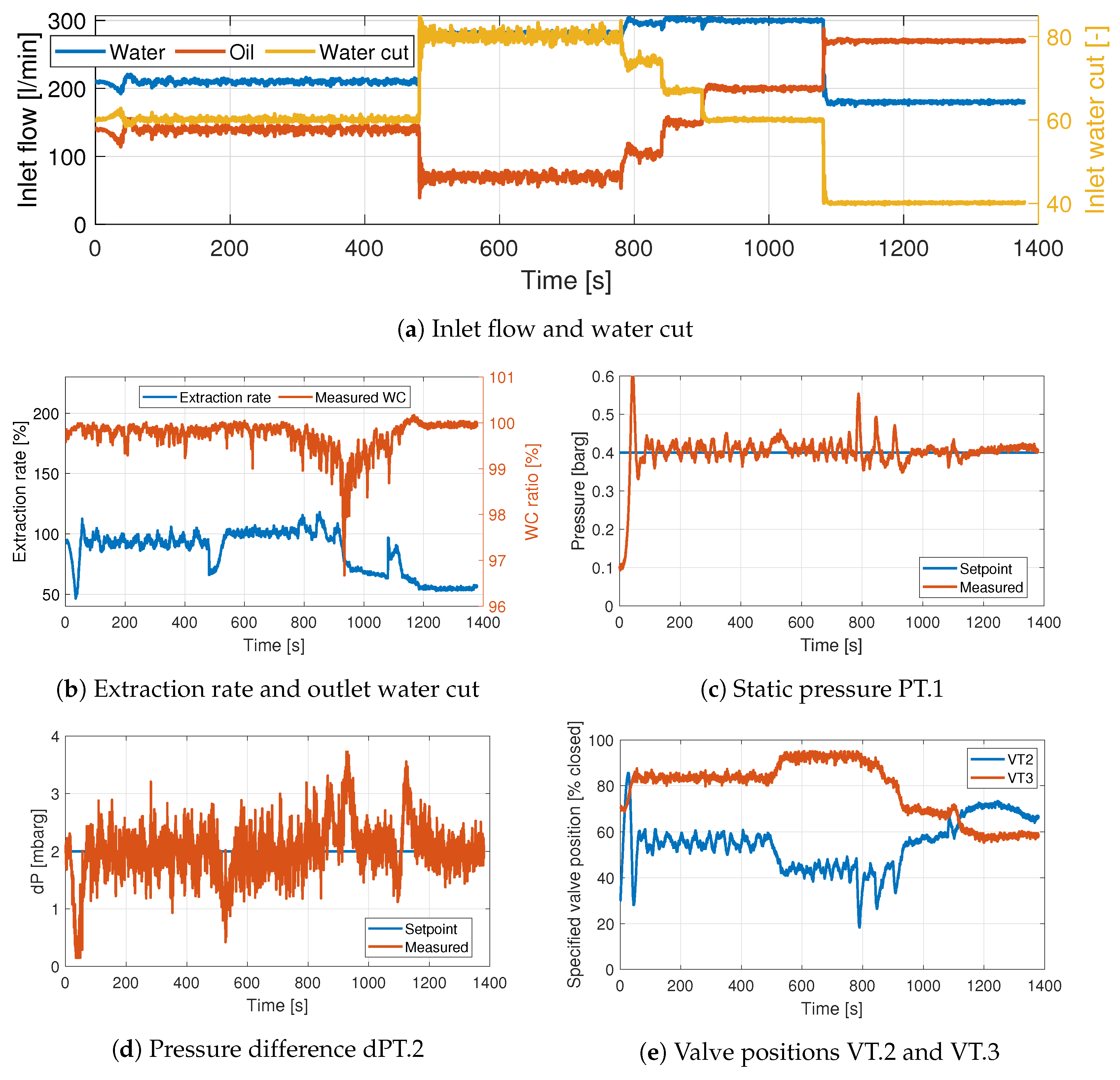
3.7. Experiment 4. PI Control VT.2–dPT.2, VT.3–PT.1
This experiment uses the control configuration recommended by the RGA analysis. The results of the experiment are shown in
Figure 10. The results are quite similar to those found in Experiment 3, but the oscillations in PT.1 during the disturbances are smaller. It is also clear that VT.2 is changing significantly more than VT.3 in Experiment 3. The variations and initial overshoot in dPT.2 are larger in this experiment, but this is caused by VT.2 being much slower than VT.3. The behaviour of the
and the ER is quite similar to Experiment 3, but the undershoot at
s is smaller in this experiment. Numerical values for the performance can be found in
Table 8.
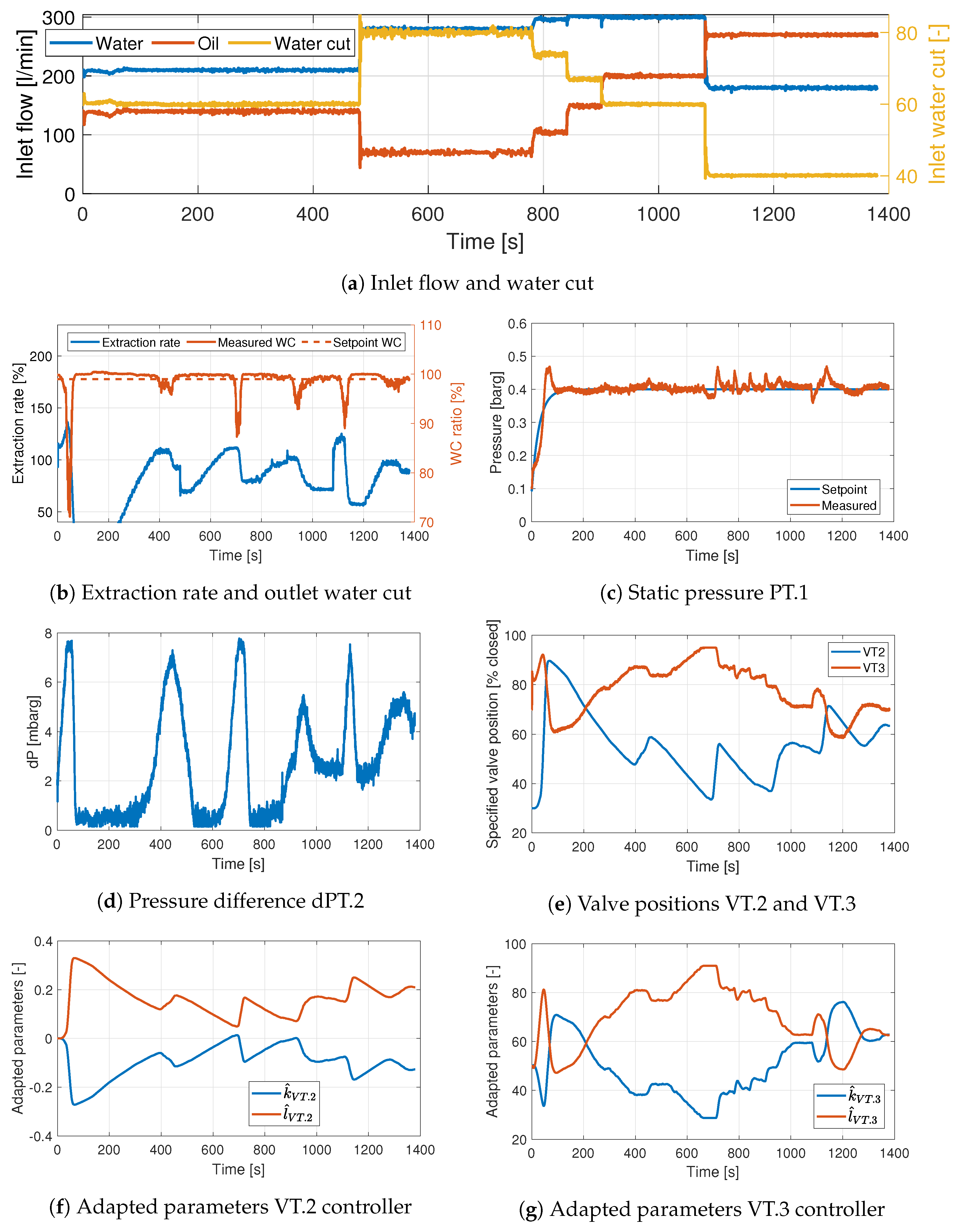
3.8. Experiment 5. Adaptive Control VT.2–, VT.3–PT.1
The model reference adaptive controller was first tested on the recommended control configuration with VT.2 controlling
and VT.3 controlling PT.1. The results are shown in
Figure 11. The pressure is controlled very well when using the MRAC. Note that the reference signal in
Figure 11c is the output of the reference model given in Equations (
22) and (
23), hence the signal is filtered and the initial response has much less overshoot compared to Experiment 2. The
controller is quite slow, hence the extraction rate increases slowly to the level where the drops in
occur. When the drops do happen, they are approximately equal to the drops experienced in Experiment 2.
The adaptive gains are shown in
Figure 11f,g. The gains for VT.2 are initialized at 0, but the gains for VT.3 are initialized at 50. This was found through trial and error to be a good initial value for VT.3. Numerical values for the performance can be found in
Table 8.
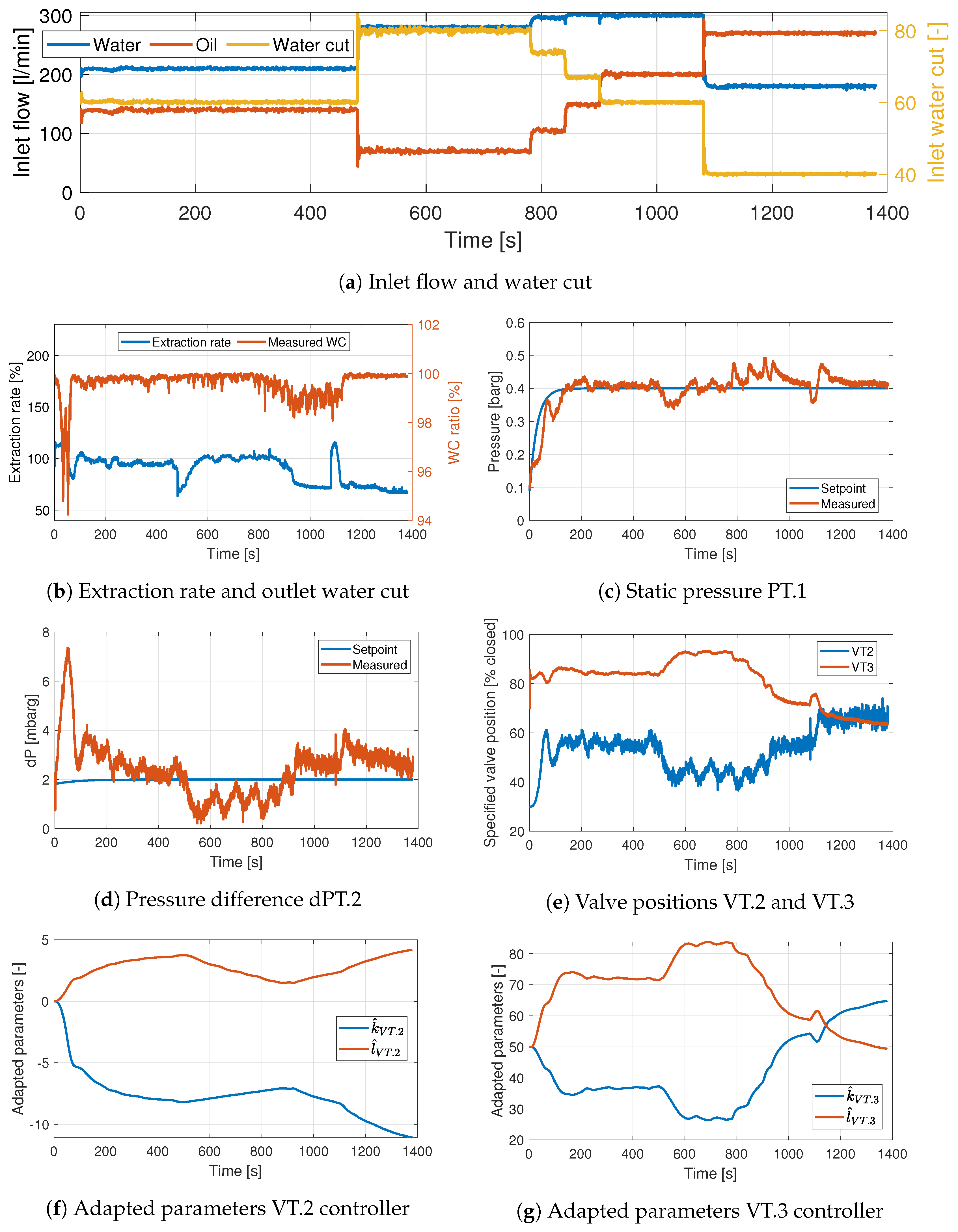
3.9. Experiment 6. Adaptive Control VT.2–dPT.2, VT.3–PT.1
The final experiment used MRAC for VT.2 and VT.3, with VT.2 controlling dPT.2 and VT.3 controlling PT.1. From
Figure 12b, it is clear that the
and ER have similar behaviour to that shown in Experiments 3 and 4. The pressure PT.1 is controlled quite well, though with some increases in oscillations compared to that observed in Experiment 5, caused by the need for a lower adaptation gain in this experiment.
The pressure difference controller has trouble bringing dPT.2 to the reference after the first change in inlet conditions happens at
s. This could be caused by the large initial overshoot caused by the zero initialization of the adaptive parameters. As can be seen from
Figure 12f,g, the adaptive parameters start changing direction at
s, but, since
and
had to be chosen to be quite small because of the slow valve, the adaptation takes a long time. Furthermore, the changes in PT.1 is causing the pressure difference dPT.2 to change. Since the VT.2 controller (and valve) is so slow, it is unable to bring dPT.2 to the reference as can be seen in
Figure 12d.
Numerical values for the performance can be found in
Table 8.
3.10. Numerical Comparison
Table 8 shows a numerical comparison of the values of interest from Experiments 1–6. The table includes the mean, root-mean-square (RMS), standard deviation (STD) and median, as well as the integrated absolute error (IAE) for the variables being controlled. The initial transient has an effect on all these numbers, hence the values are also calculated from
t = 200 s rather than from
t = 0 to exclude this effect. These values are showed in parentheses.
4. Discussion
From the RGA analysis, it was found that VT.3 should control PT.1 in all cases. The numerical data from Experiments 1 and 2 (
Table 8) shows that the control structure proposed by the RGA analysis improves the ER. The values for
is slightly worse in Experiment 2, but if the initial transient is ignored the difference is reduced. The slow valve VT.2 is controlling
in Experiment 2, which may explain why the values are worse, as it takes this valve more time to reduce the error compared to VT.3.
The numerical data from Experiments 3 and 4 (
Table 8) show that controlling dPT.2 rather than
improves the separator performance. The mean, median and RMS of the
are higher and the STD is much lower in both Experiments 3 and 4 compared to Experiments 1 and 2. This comes at the cost of a lower extraction rate. This could probably be improved by finding a better setpoint for dPT.2. The differences between Experiment 3 (not RGA) and Experiment 4 (RGA) are very small when looking at
. Experiment 4 has slightly lower values in mean, median and RMS and slightly higher in STD, but, if the initial transient is ignored, the values are slightly better than in Experiment 3 (except for median). Overall, Experiment 3 has slightly better values than Experiment 4. This is the opposite of what one might expect based on the results of the RGA analysis. The RGA analysis, however, is only based on steady state behaviour and does not consider time-delays or transients. The results may indicate that the transfer functions used in the RGA analysis are significantly different from the real dynamics, i.e., the model identification in
Section 2.4 may be insufficiently accurate.
The performance of the adaptive controllers are approximately equal to the performance of the PI controllers. Experiments 5 and 6 must be compared with Experiments 2 and 4, respectively.
The is slightly higher in Experiment 5 compared to Experiment 2, but the ER is much lower in Experiment 5. This is caused by the very low adaptation gains chosen in Experiment 5, which causes VT.2 to close very slowly and, hence, less variations are present in . The pressure control, however, is slightly improved when using the adaptive controller.
The values from Experiment 6 are very similar to those from Experiment 4. The is slightly worse, but the ER is higher. The adaptive gains for the dPT.2 controller again had to be chosen very low, which causes sluggish control of dPT.2. This again affects the static pressure due to the interactions between the two CVs, and hence the performance is reduced for both dPT.2 and PT.1. Comparing Experiments 5 and 6, it is again clear that controlling dPT.2 rather than improves the efficiency.
According to the information shown in
Table 8, the performance of the PI controller and the adaptive controller is approximately equal. However, aspects such as implementation and ease of operation should also be considered. The PI controllers could be easily implemented in the LabView block diagram, but the tuning required step response experiments and some trial and error. The MRAC, however, did not require a step response model, but the implementation required a custom script and the tuning was largely based on trial and error and the experience of the operators. The adaptation gain for the controller operating the slow valve VT.2 had to be very low, which may have negatively affected the end result. Improving the performance significantly with tuning, however, would be difficult due to the constraints imposed by the slow valve. Finding suitable adaptation gains and initial values for the MRAC was not trivial.
The SIMC tuning rules was chosen for the PI controllers, due to its simplicity and proven efficiency for first-order plus time delay systems [
16], but other tuning methods specifically designed for tuning decentralized PI controllers with two inputs and two inputs exist [
22,
23]. These methods may reduce the interactions between the control loops and lead to tighter control during transients, at the cost of a more complex tuning procedure.
A multivariable controller (adaptive or not) would probably outperform both controllers as it would better compensate for the interactions between the control loops. Implementing this is suggested as future work.
A model predictive controller (MPC) would also be a natural next step. The MPC can calculate the optimal setpoints and inputs while also handling the input and variable constraints. Implementing an MPC is also suggested as future work.
5. Conclusions
This paper presented a control structure analysis and controller design for a novel multi-pipe separator concept developed at the Department of Geoscience and Petroleum at the Norwegian University of Science and Technology. The control structure analysis gives an indication of which outputs to pair with which inputs, and the controller design for the conventional PI controllers is based on the well established SIMC tuning rules. Step response experiments were performed to gather data for the dynamic models of the different input/output relations in the separator. The dynamic models were assumed to be of first order with a time delay, but second order models and models accounting for the interactions between the states would probably yield better results, considering the measured system responses. Model reference adaptive controllers were also developed for the separator. The performances of the PI and adaptive controllers were quite similar, but the adaptive controller does not require a step response model in the tuning procedure. Due to a lack of tuning rules, however, the adaptive controller was quite difficult to tune. Furthermore, the adaptation gains in the MRAC had to be chosen very small due to the slow control valve VT.2. A faster valve would probably improve the results.
It was found that controlling the dP over the incline in the separator, and the water/oil interface level, by proxy, yielded a more stable water cut ratio on the water outlet, which was the primary control objective. This is due to dP control establishing a buffer volume of water in the incline, unlike when controlling directly.
The separator is a multiple input, multiple output (MIMO) system and would probably benefit from a multivariable controller rather than two decoupled controllers. Model predictive control could potentially improve the results even more, as the separator is subject to several constraints and control objectives. Finding the optimal setpoints and outputs within the constraints is key for efficient operation. This is suggested for future work.